Enhancing Grid Stability in Microgrid Systems with Vehicle-to-Grid Support and EDLC Supercapacitors
Abstract
1. Introduction
1.1. Background and Literature Review
1.2. Research Problem
2. Methodology
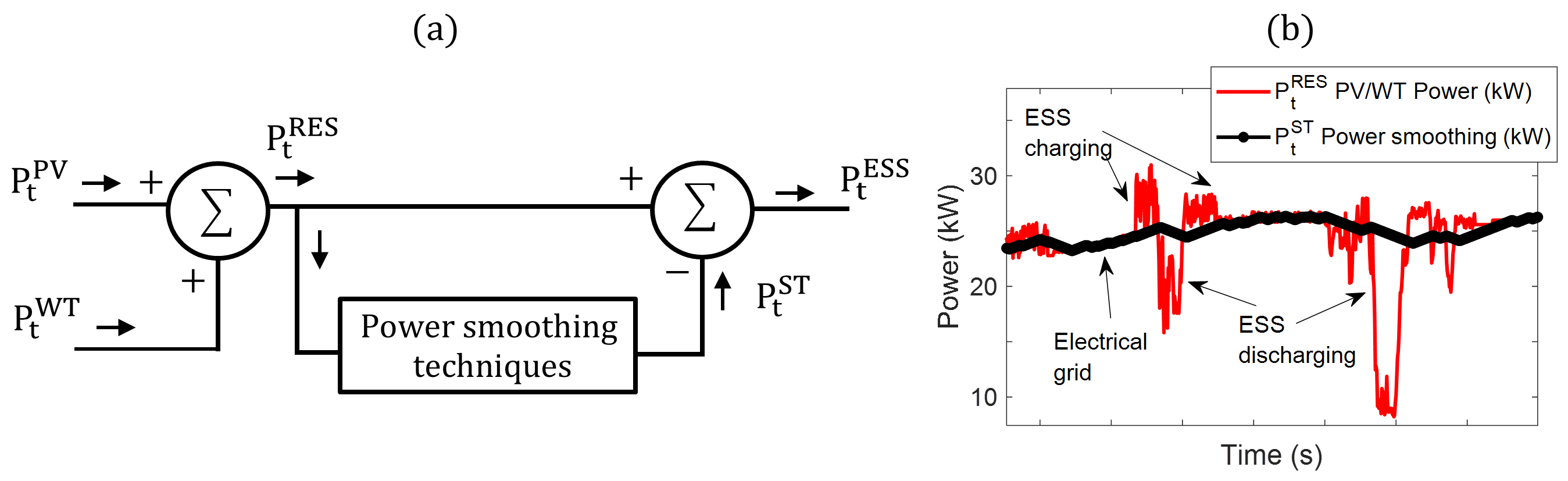
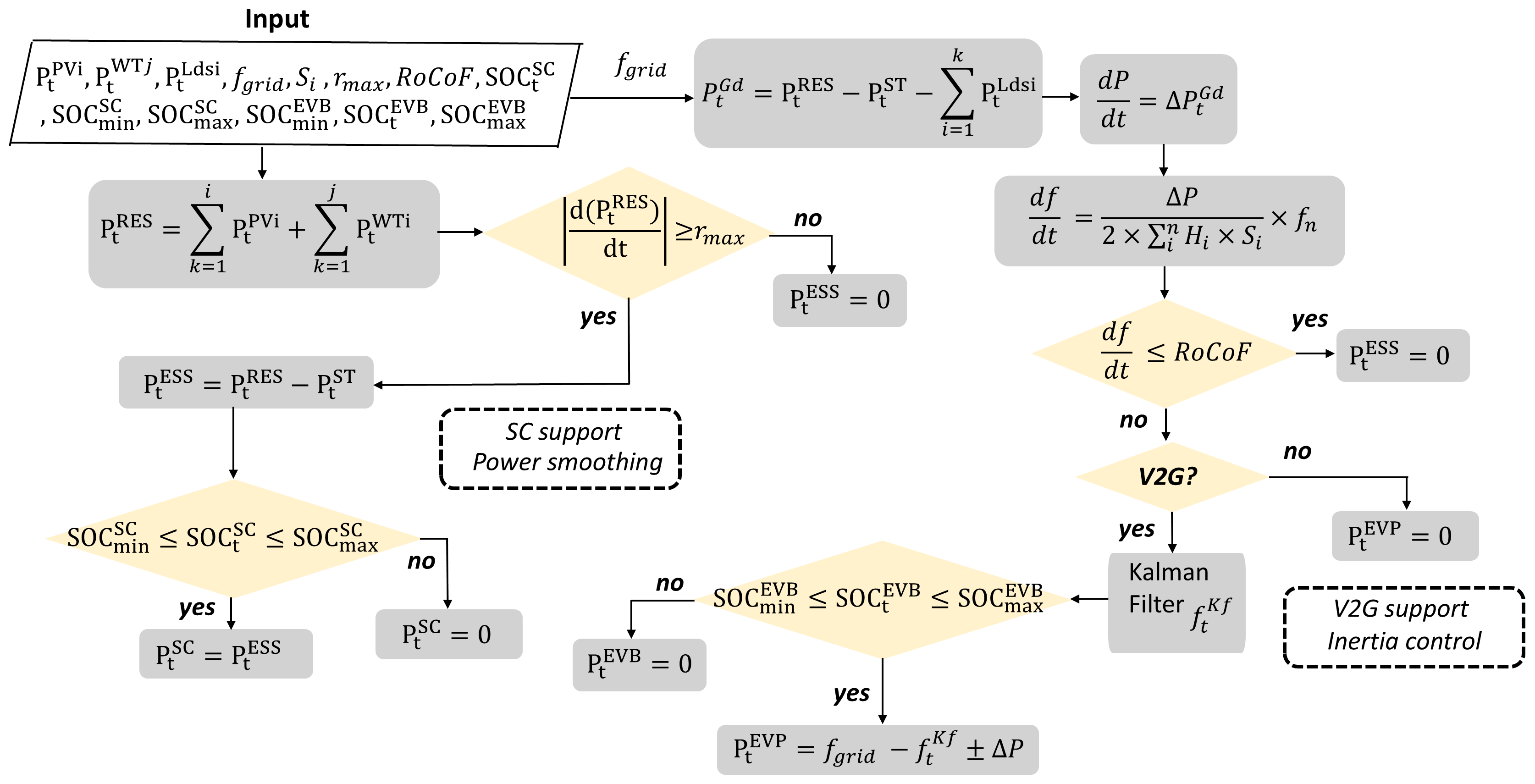
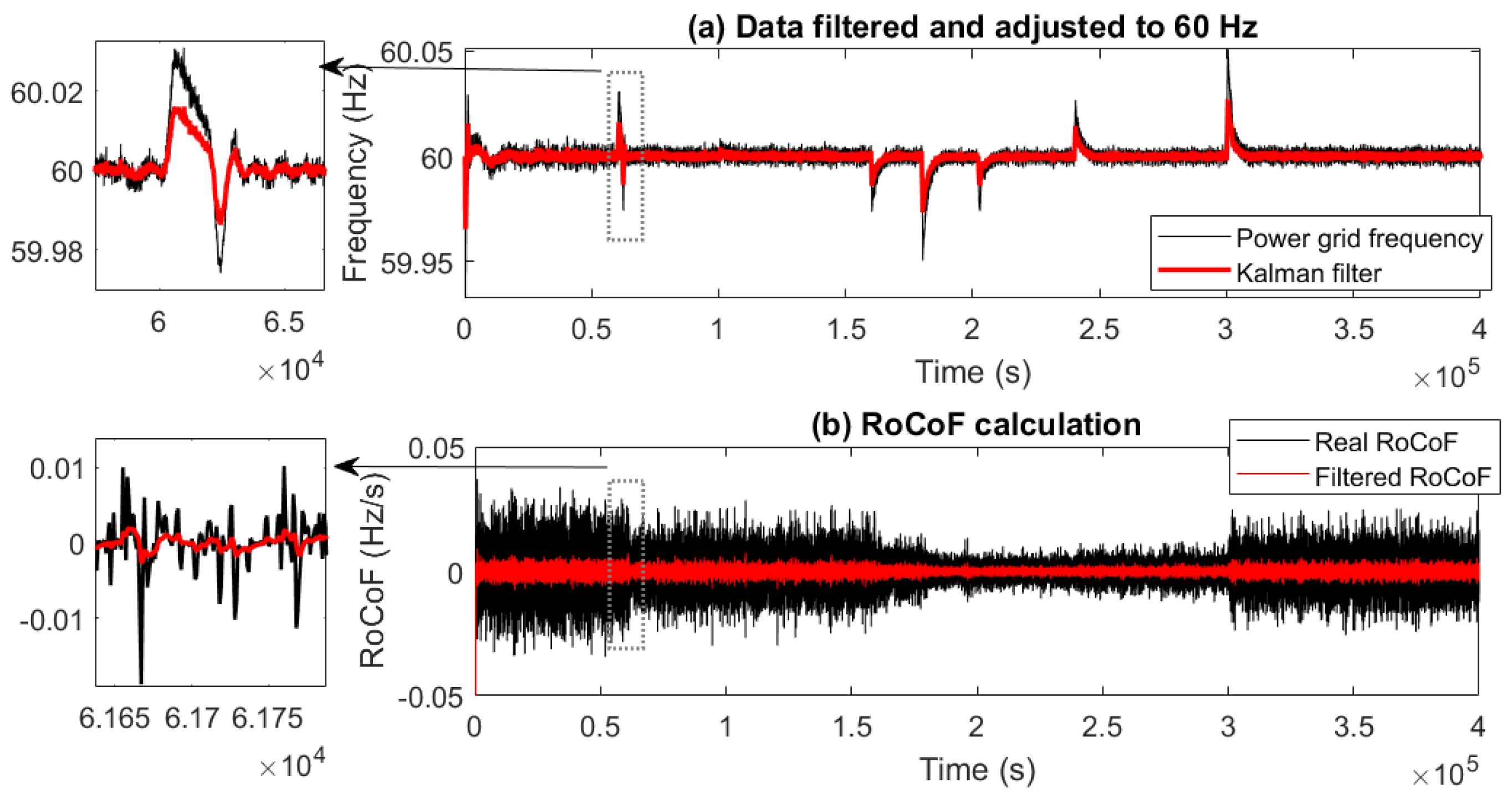
2.1. Power Smoothing Model and Rate of Change of Frequency (RoCoF)
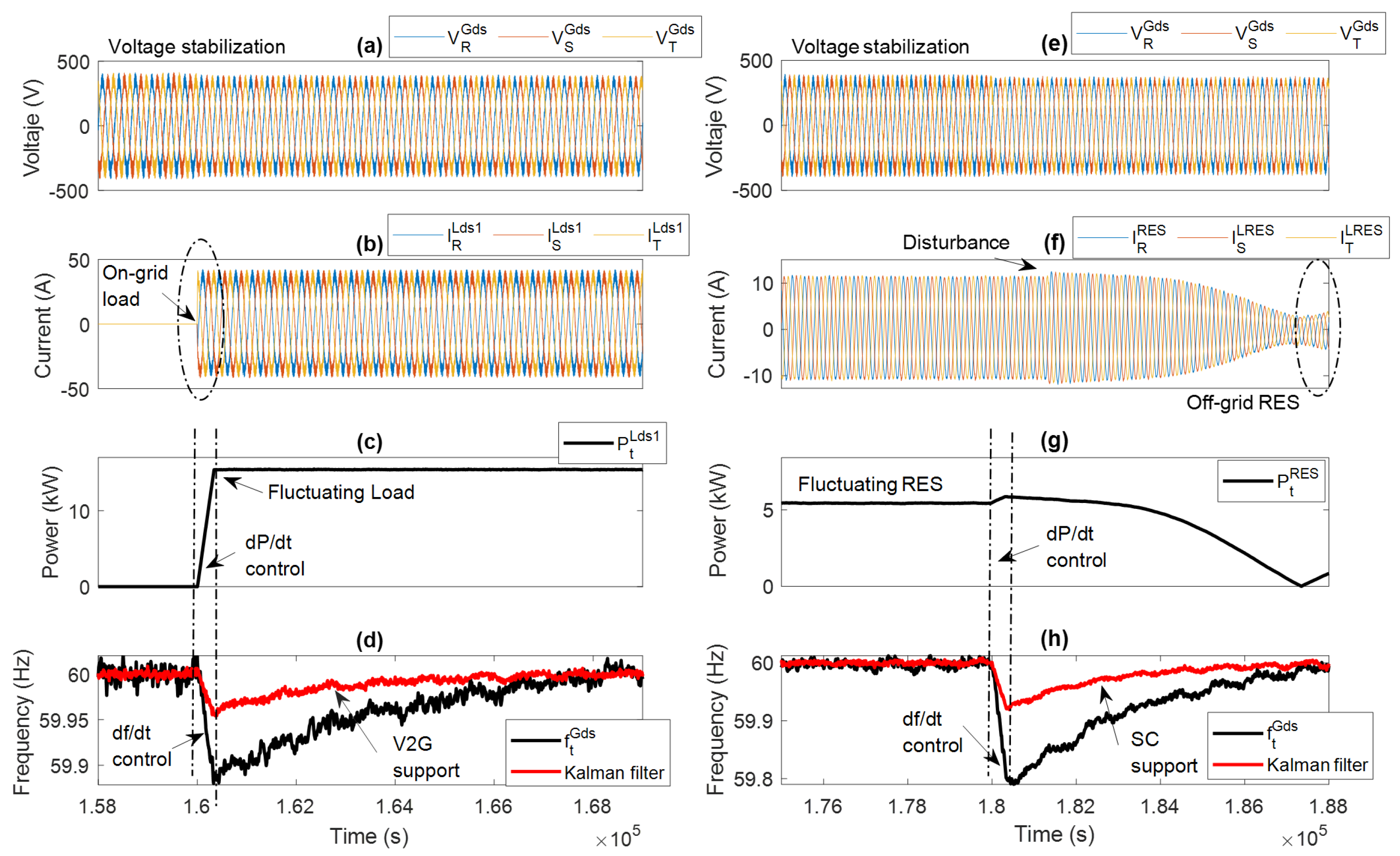
2.2. The V2G Strategy to Support the Power Grid
- is the state of charge at time n;
- i is the battery current;
- t is the time step;
- is the initial battery capacity.
- V is the terminal voltage;
- is the open-circuit voltage as a function of the SOC;
- R is the internal resistance, dependent on the SOC and temperature T;
- i is the current.
2.3. Battery Degradation Model
- is the actual degradation rate;
- is the reference degradation rate;
- is the stress factor.
2.4. Bidirectional AC/DC Converters
- are the grid voltages per phase;
- are the currents per phase;
- are the voltages between the midpoint of each phase and the neutral point;
- is the voltage between point N and point O;
- L, R are the inductance and resistance of the filter;
- is the DC bus voltage, is the DC bus current, and is the load current.
- are the currents in the frame;
- are the switching functions in the frame;
- is the angular frequency of the synchronous reference frame;
- are the components of grid voltage.
2.5. Storage Management Model
3. Results and Case Study
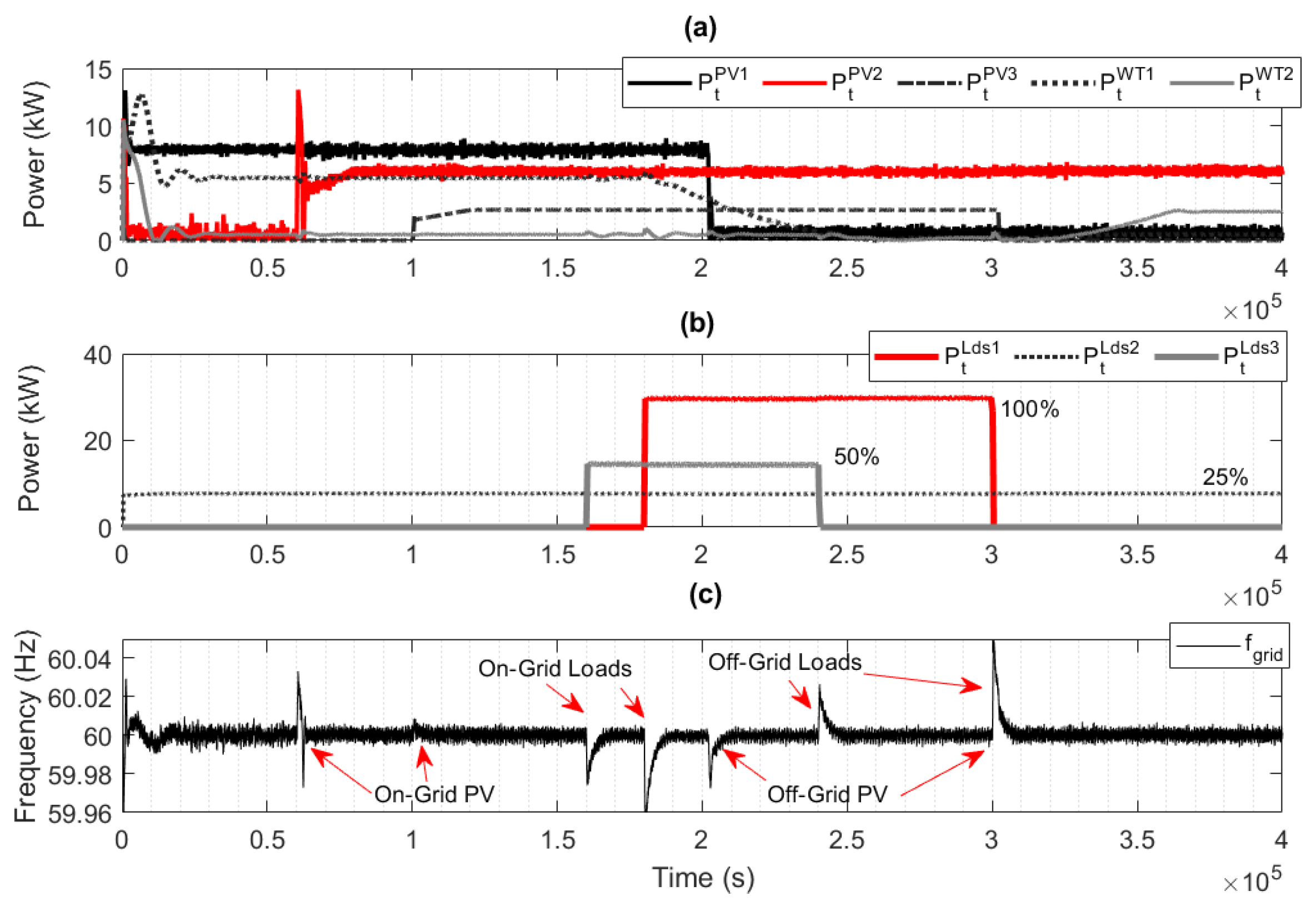
3.1. Microgrid Case Study
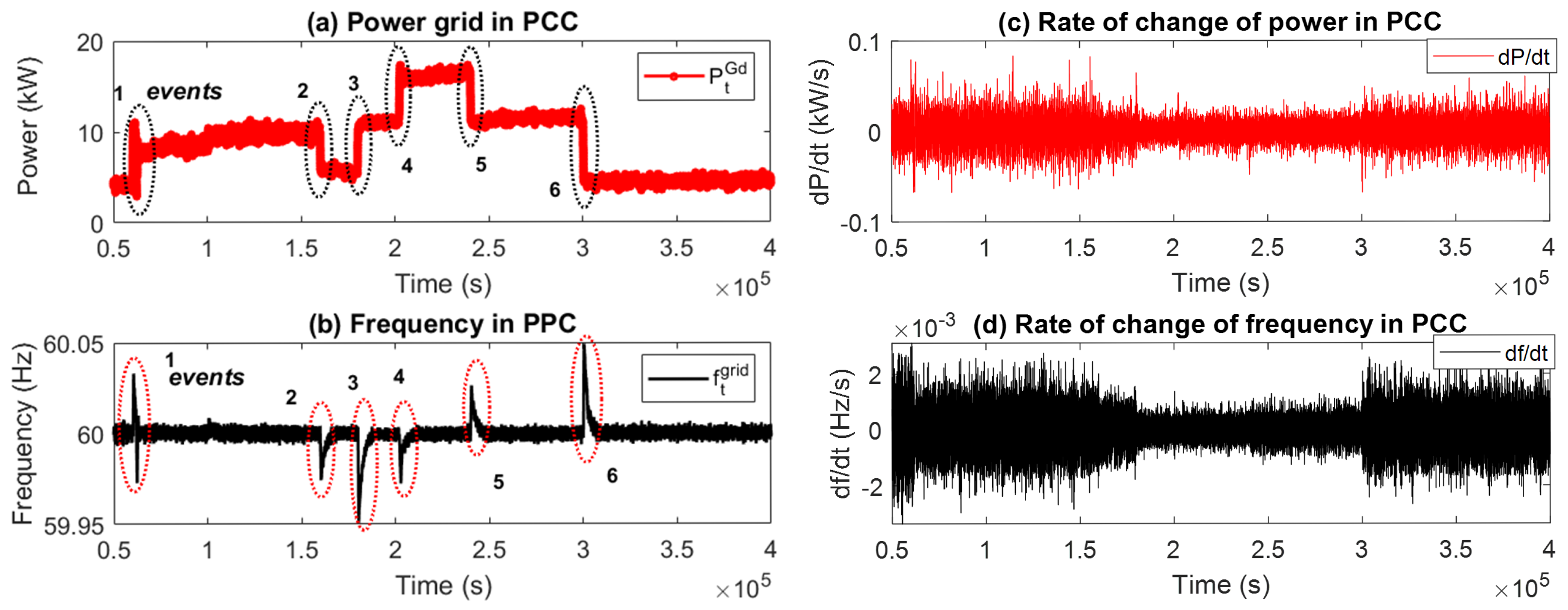
3.2. Power–Frequency Variability Analysis
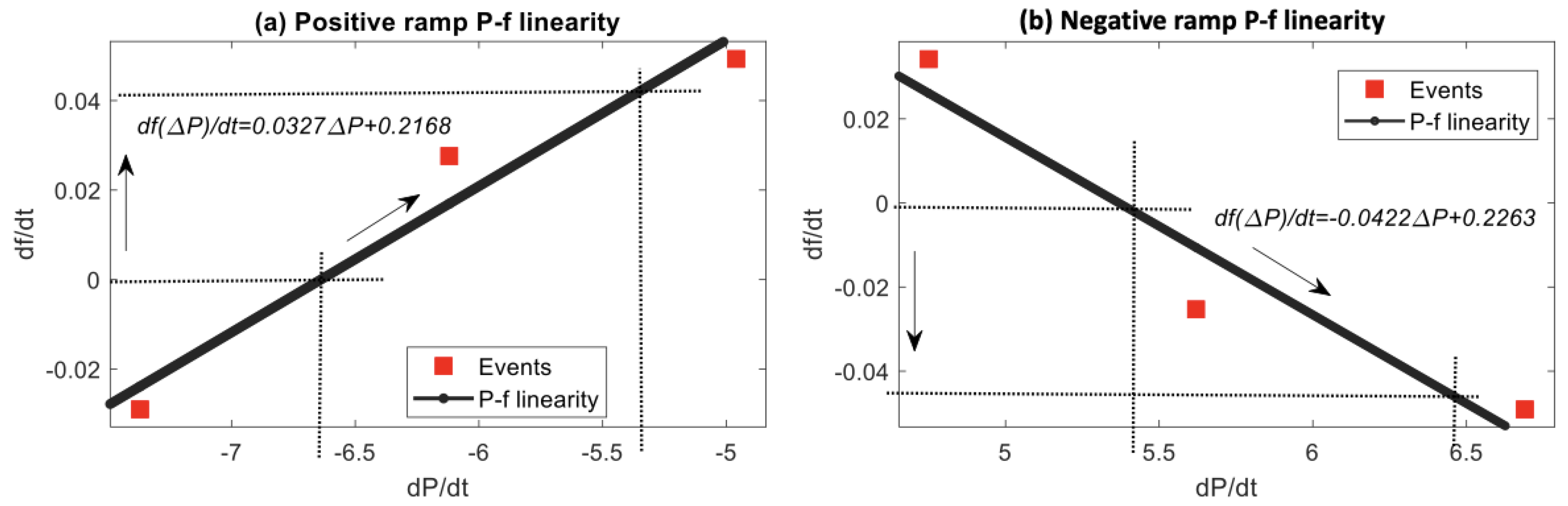
3.3. Power–Frequency Linear Estimation
3.4. Kalman Filter-Based Support
4. Discussion
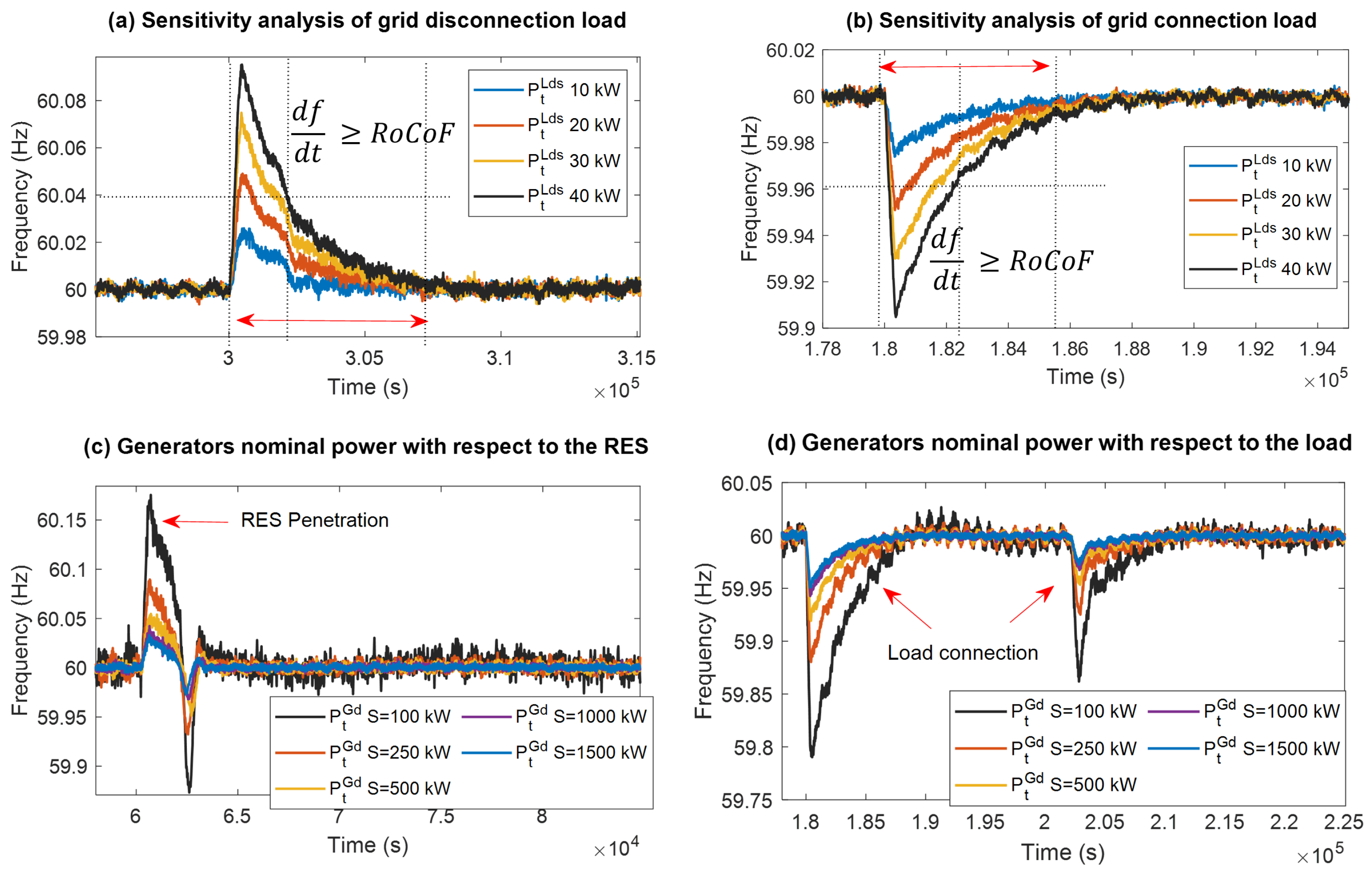
4.1. Sensitivity Analysis of System Power and Load
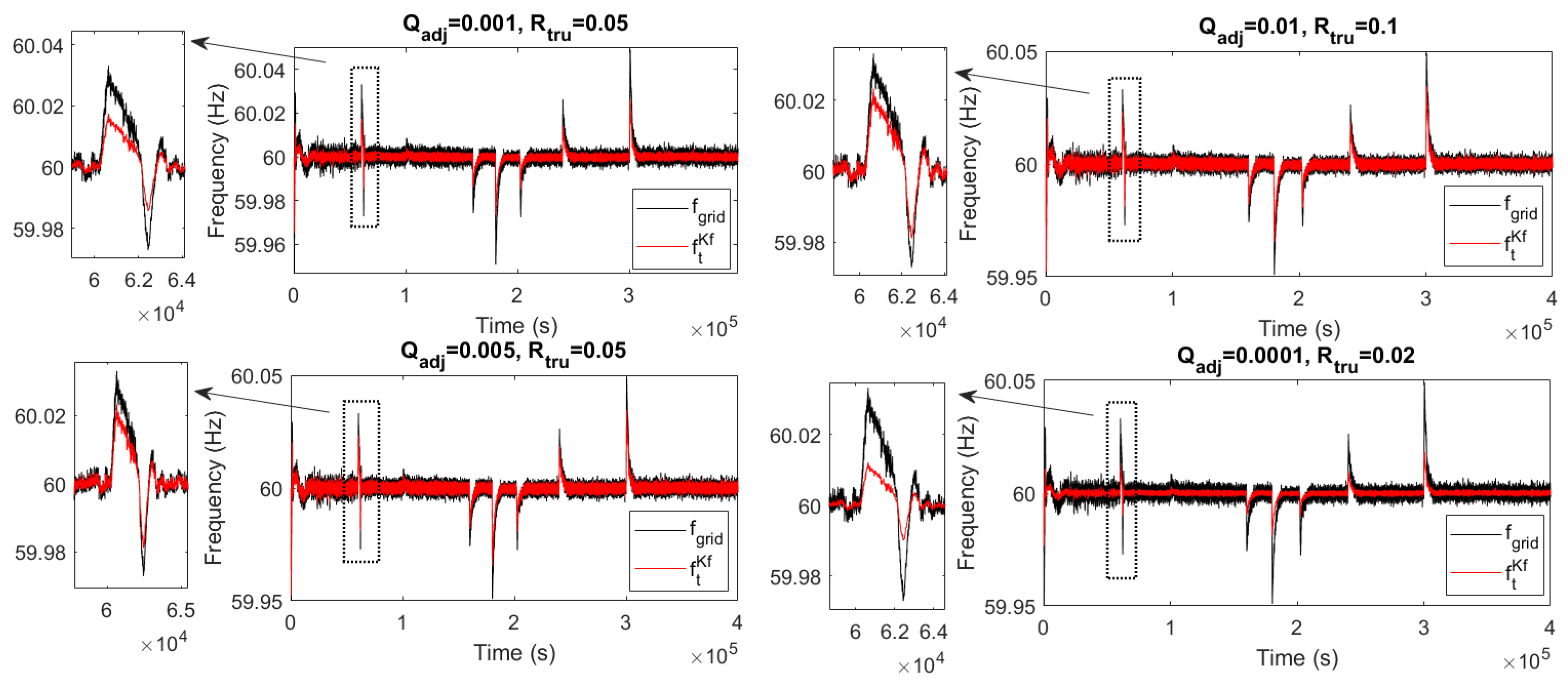
4.2. Sensitivity Analysis for Kalman Filter-Based Control
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Onishi, V.C.; Antunes, C.H.; Trovão, J.P.F. Optimal energy and reserve market management in renewable microgrid-PEVs parking lot systems: V2G, demand response and sustainability costs. Energies 2020, 13, 1884. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, Q.; Zhang, H.; Li, C. Optimal sizing of hybrid energy storage system considering power smoothing and transient frequency regulation. Int. J. Electr. Power Energy Syst. 2022, 142, 108227. [Google Scholar] [CrossRef]
- Vuić, L.; Hivziefendić, J.; Sarić, M.; Osmić, J. Voltage and frequency control of solar–battery–diesel based islanded microgrid. J. Electr. Eng. 2023, 74, 442–453. [Google Scholar] [CrossRef]
- satya nagasri Dangeti, L.; Marimuthu, R. Distributed model predictive control strategy for microgrid frequency regulation. Energy Rep. 2025, 13, 1158–1170. [Google Scholar] [CrossRef]
- Herzig, M.; Paetzold, J. Feasibility study on the Rate of Change of Frequency requirements in VDE-AR-N 4120. In Proceedings of the International ETG-Congress 2019; ETG Symposium, Esslingen, Germany, 8–9 May 2019; pp. 1–6. [Google Scholar]
- Grebla, M.; Yellajosula, J.R.A.K.; Høidalen, H.K. Adaptive Frequency Estimation Method for ROCOF Islanding Detection Relay. IEEE Trans. Power Deliv. 2020, 35, 1867–1875. [Google Scholar] [CrossRef]
- Javadi, M.; Gong, Y.; Chung, C.Y. Frequency Stability Constrained BESS Sizing Model for Microgrids. IEEE Trans. Power Syst. 2024, 39, 2866–2878. [Google Scholar] [CrossRef]
- Jan, M.U.; Xin, A.; Rehman, H.U.; Abdelbaky, M.A.; Iqbal, S.; Aurangzeb, M. Frequency regulation of an isolated microgrid with electric vehicles and energy storage system integration using adaptive and model predictive controllers. IEEE Access 2021, 9, 14958–14970. [Google Scholar] [CrossRef]
- Habib, H.U.R.; Subramaniam, U.; Waqar, A.; Farhan, B.S.; Kotb, K.M.; Wang, S. Energy cost optimization of hybrid renewables based V2G microgrid considering multi objective function by using artificial bee colony optimization. IEEE Access 2020, 8, 62076–62093. [Google Scholar] [CrossRef]
- Kisacikoglu, M.C.; Ozpineci, B.; Tolbert, L.M. EV/PHEV bidirectional charger assessment for V2G reactive power operation. IEEE Trans. Power Electron. 2013, 28, 5717–5727. [Google Scholar] [CrossRef]
- Villa-Ávila, E.; Arévalo, P.; Ochoa-Correa, D.; Espinoza, J.L.; Albornoz-Vintimilla, E.; Jurado, F. Improving V2G Systems Performance with Low-Pass Filter and Fuzzy Logic for PV Power Smoothing in Weak Low-Voltage Networks. Appl. Sci. 2025, 15, 1952. [Google Scholar] [CrossRef]
- Srihari, G.; Krishnam Naidu, R.; Falkowski-Gilski, P.; Bidare Divakarachari, P.; Kiran Varma Penmatsa, R. Integration of electric vehicle into smart grid: A meta heuristic algorithm for energy management between V2G and G2V. Front. Energy Res. 2024, 12, 1357863. [Google Scholar] [CrossRef]
- Zhang, C.; Kitamura, H.; Goto, M. Feasibility of vehicle-to-grid (V2G) implementation in Japan: A regional analysis of the electricity supply and demand adjustment market. Energy 2024, 311, 133317. [Google Scholar] [CrossRef]
- Janardhan, G.; Shanmugasundaram, R.; Narendar, R.; Kumar K, S. Modeling and Simulation of Vehicle to Grid (V2G) Integration. In Proceedings of the E3S Web of Conferences; EDP Sciences: Paris, France, 2025; Volume 616, p. 01016. [Google Scholar]
- Ellis, B.E.; Pearre, N.; Swan, L. Impact of residential photovoltaic systems on net load intermittency. Renew. Energy Focus 2023, 46, 377–384. [Google Scholar] [CrossRef]
- Jiang, H.; Lu, N.; Yao, L.; Qin, J.; Liu, T. Impact of climate changes on the stability of solar energy: Evidence from observations and reanalysis. Renew. Energy 2023, 208, 726–736. [Google Scholar] [CrossRef]
- Zhu, H.; Li, H.; Liu, G.; Ge, Y.; Shi, J.; Li, H.; Zhang, N. Energy Storage in High Variable Renewable Energy Penetration Power Systems: Technologies and Applications. CSEE J. Power Energy Syst. 2023, 9, 2099–2108. [Google Scholar] [CrossRef]
- Imtiaz, S.; Yang, L.; Munir, H.M.; Memon, Z.A.; Kilic, H.; Naz, M.N. DC-link voltage stability enhancement in intermittent microgrids using coordinated reserve energy management strategy. IET Renew. Power Gener. 2025, 19, e13197. [Google Scholar] [CrossRef]
- Frasetyo, M.B.; Wijaya, F.D.; Ali, H.R. Islanded Wind Farm Microgrid Stability Control using Synchronverter Algorithm. IEEJ J. Ind. Appl. 2023, 12, 603–612. [Google Scholar] [CrossRef]
- Wu, Z.H.; Yu, Y.X. Regulating the Electrochemical Performance of A2Ni2TeO6 (A = Na, K) as a Cathode of Alkali Metal Ion Battery by 3d Transition Metal Substitution from a Theoretical Perspective. ACS Appl. Energy Mater. 2024, 7, 8715–8725. [Google Scholar] [CrossRef]
- Cougnon, C. Impact of the Scan Rate on the Stability Window of an Electrical Double-Layer Capacitor. Energies 2023, 16, 5687. [Google Scholar] [CrossRef]
- Zeeshan, T.; Tahir, E.; Waseem, S.; Ali, M.D.; Anjum, S. Nickel substituted cobalt ferrites via ceramic rout approach: Exploration of structural, optical, dielectric and electrochemical behavior for pseudo-capacitors. Ceram. Int. 2025, 51, 5808–5820. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Y.; Kulaots, I.; Zhu, H.; Sheldon, B. Water-in-Salt Battery Electrolyte for High-Voltage Supercapacitors: A Fundamental Study on Biomass and Carbon Fiber Electrodes. J. Electrochem. Soc. 2024, 171, 110526. [Google Scholar] [CrossRef]
- Subasinghage, K.; Gunawardane, K.; Padmawansa, N.; Kularatna, N.; Moradian, M. Modern supercapacitors technologies and their applicability in mature electrical engineering applications. Energies 2022, 15, 7752. [Google Scholar] [CrossRef]
- Navarro, G.; Torres, J.; Blanco, M.; Nájera, J.; Santos-Herran, M.; Lafoz, M. Present and future of supercapacitor technology applied to powertrains, renewable generation and grid connection applications. Energies 2021, 14, 3060. [Google Scholar] [CrossRef]
- Fang, Z.; Shek, J.K.; Sun, W. A review of grid-connected hybrid energy storage systems: Sizing configurations, control strategies, and future directions. J. Energy Storage 2025, 118, 116226. [Google Scholar] [CrossRef]
- Luo, X.; Barreras, J.V.; Chambon, C.L.; Wu, B.; Batzelis, E. Hybridizing lead–acid batteries with supercapacitors: A methodology. Energies 2021, 14, 507. [Google Scholar] [CrossRef]
- Vasantharaj, S.; Indragandhi, V.; Subramaniyaswamy, V.; Teekaraman, Y.; Kuppusamy, R.; Nikolovski, S. Efficient control of dc microgrid with hybrid pv—fuel cell and energy storage systems. Energies 2021, 14, 3234. [Google Scholar] [CrossRef]
- Wu, X.; Wu, Y.; Tang, Z.; Kerekes, T. An adaptive power smoothing approach based on artificial potential field for PV plant with hybrid energy storage system. Sol. Energy 2024, 270, 112377. [Google Scholar] [CrossRef]
- Abadi, S.A.G.K.; Habibi, S.I.; Khalili, T.; Bidram, A. A model predictive control strategy for performance improvement of hybrid energy storage systems in DC microgrids. IEEE Access 2022, 10, 25400–25421. [Google Scholar] [CrossRef]
- Rajnarayanan, P.; Kathiravan, K. Supercapacitors as distributed energy storage systems for EV charging infrastructure. In Distributed Energy Storage Systems for Digital Power Systems; Elsevier: Amsterdam, The Netherlands, 2025; pp. 149–166. [Google Scholar]
- Lu, Q.; Yang, Y.; Chen, J.; Liu, Y.; Liu, N.; Cao, F. Capacity optimization of hybrid energy storage systems for offshore wind power volatility smoothing. Energy Rep. 2023, 9, 575–583. [Google Scholar] [CrossRef]
- Rimal, B.P.; Kong, C.; Poudel, B.; Wang, Y.; Shahi, P. Smart electric vehicle charging in the era of internet of vehicles, emerging trends, and open issues. Energies 2022, 15, 1908. [Google Scholar] [CrossRef]
- Shaker, Y.O.; Yousri, D.; Osama, A.; Al-Gindy, A.; Tag-Eldin, E.; Allam, D. Optimal charging/discharging decision of energy storage community in grid-connected microgrid using multi-objective hunger game search optimizer. IEEE Access 2021, 9, 120774–120794. [Google Scholar] [CrossRef]
- Suresh, V.; Janik, P.; Guerrero, J.M.; Leonowicz, Z.; Sikorski, T. Microgrid energy management system with embedded deep learning forecaster and combined optimizer. IEEE Access 2020, 8, 202225–202239. [Google Scholar] [CrossRef]
- Lazaroiu, G.C.; Roscia, M. Fuzzy logic strategy for priority control of electric vehicle charging. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19236–19245. [Google Scholar] [CrossRef]
- Benavides, D.; Arévalo, P.; Villa-Ávila, E.; Aguado, J.A.; Jurado, F. Predictive power fluctuation mitigation in grid-connected PV systems with rapid response to EV charging stations. J. Energy Storage 2024, 86, 111230. [Google Scholar] [CrossRef]
- Li, G.; Yang, Z.; Li, B.; Bi, H. Power allocation smoothing strategy for hybrid energy storage system based on Markov decision process. Appl. Energy 2019, 241, 152–163. [Google Scholar] [CrossRef]
- Benavides, D.; Arévalo, P.; Tostado-Véliz, M.; Vera, D.; Escamez, A.; Aguado, J.A.; Jurado, F. An Experimental Study of Power Smoothing Methods to Reduce Renewable Sources Fluctuations Using Supercapacitors and Lithium-Ion Batteries. Batteries 2022, 8, 228. [Google Scholar] [CrossRef]
- Zar, A.; Rehman, H.; Ahmad, I. Neural network based optimized barrier conditioned double super-twisting sliding mode controller of electric vehicle charger with grid to vehicle and vehicle to grid modes. J. Energy Storage 2023, 74, 109234. [Google Scholar] [CrossRef]
- Benavides, D.; Arévalo, P.; Criollo, A.; Tostado-Véliz, M.; Jurado, F. Multi-mode monitoring and energy management for photovoltaic-storage systems. Renew. Energy 2024, 230, 120820. [Google Scholar] [CrossRef]
- Review of PREPA Technical Requirements for Interconnecting Wind and Solar Generation | Search Results | IUCAT South Bend. Available online: https://docs.nrel.gov/docs/fy14osti/57089.pdf (accessed on 11 June 2025).
- Lamsal, D.; Sreeram, V.; Mishra, Y.; Kumar, D. Output power smoothing control approaches for wind and photovoltaic generation systems: A review. Renew. Sustain. Energy Rev. 2019, 113, 109245. [Google Scholar] [CrossRef]
- Mao, M.; Tang, Y.; Chen, J.; Ma, F.; Li, Z.; Ma, H.; Sun, H.; Yin, C.; Li, H. An Overview of Solar Photovoltaic Power Smoothing Control Strategies Based on Energy Storage Technology. Energies 2025, 18, 909. [Google Scholar] [CrossRef]
- Marcos, J.; Storkël, O.; Marroyo, L.; Garcia, M.; Lorenzo, E. Storage requirements for PV power ramp-rate control. Sol. Energy 2014, 99, 28–35. [Google Scholar] [CrossRef]
- Bašakarad, T.; Holjevac, N.; Kuzle, I.; ivanković, I.; Zovko, N. ROCOF importance in electric power systems with high renewables share: A simulation case for croatia. In Proceedings of the 12th Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MEDPOWER 2020), Virtual, 9–12 November 2020; Volume 2020, pp. 72–77. [Google Scholar] [CrossRef]
- Benavides, D.; Villa-Ávila, E.; Criollo, A.; Aguado, J.A. Optimal energy management of energy storage and electric vehicles in power systems. In Towards Future Smart Power Systems with High Penetration of Renewables; Elsevier: Amsterdam, The Netherlands, 2025; pp. 413–434. [Google Scholar]
- Han, J.; Zhou, X.; Lu, S.; Zhao, P. A Three-Phase Bidirectional Grid-Connected AC/DC Converter for V2G Applications. J. Control Sci. Eng. 2020, 2020, 8844073. [Google Scholar] [CrossRef]
- Espinoza, J.L.; González, L.G.; Sempértegui, R. Micro grid laboratory as a tool for research on non-conventional energy sources in Ecuador. In Proceedings of the 2017 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 8–10 November 2017; pp. 1–7. [Google Scholar] [CrossRef]


| Power Smoothing Techniques | Rate of Change of Frequency Control | Energy Demand Analysis | Vehicle-to-Grid Support | Supercapacitors | Experimental Validation | References |
|---|---|---|---|---|---|---|
| ✓ | ✓ | ✓ | ✓ | [2] | ||
| ✓ | ✓ | ✓ | [29,37] | |||
| ✓ | ✓ | ✓ | [11] | |||
| ✓ | ✓ | ✓ | [26,30,38] | |||
| ✓ | ✓ | ✓ | [39] | |||
| ✓ | ✓ | [31,40] | ||||
| ✓ | ✓ | ✓ | ✓ | [32,41] | ||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | This study |
| Symbol | Description | Model | Nominal Power | Energy/Day | Max. Voltage | Power Converter |
|---|---|---|---|---|---|---|
| PV System 1 | ATERSA A-250P | 15 kW | ≈50 kWh | 553 Vdc / 230 Vac | DC/AC | |
| PV System 2 | ATERSA A-250M | 15 kW | ≈50 kWh | 563 Vdc / 230 Vac | DC/AC | |
| PV System 3 | ATERSA A-250P | 5 kW | ≈20 kWh | 598 Vdc / 230 Vac | DC/AC | |
| WT System 1 | ATERSA A-250P | 5 kW | ≈30 kWh | 230 Vac | - | |
| WT System 2 | enair | 5 kW | ≈30 kWh | 230 Vac | - | |
| Lithium battery | Samsung ELPT392 | 50 kW | 44 kWh | 642 Vdc / 230 Vac | DC/AC-AC/DC | |
| Supercapacitors | Maxwell BMOD-0130 | 50 kW | 0.4 kWh | 560 Vdc / 230 Vac | DC/AC-AC/DC |
| Event | Parameter | |||
|---|---|---|---|---|
| 1 | Power (kW) | 3.44 | 10.81 | −7.37 |
| Frequency (Hz) | 60.0015 | 60.0305 | −0.029 | |
| 2 | Power (kW) | 10.32 | 5.57 | 4.75 |
| Frequency (Hz) | 60.0042 | 59.97 | 0.0342 | |
| 3 | Power (kW)r | 5.8 | 10.76 | −4.96 |
| Frequency (Hz) | 60.0002 | 59.9509 | 0.0493 | |
| 4 | Power (kW) | 11.19 | 17.31 | −6.12 |
| Frequency (Hz) | 60 | 59.9725 | 0.0276 | |
| 5 | Power (kW) | 16.88 | 11.26 | 5.62 |
| Frequency (Hz) | 60.0011 | 60.0264 | −0.0253 | |
| 6 | Power (kW) | 11.27 | 4.58 | 6.69 |
| Frequency (Hz) | 59.9992 | 60.0483 | −0.0491 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Criollo, A.; Benavides, D.; Arévalo, P.; Minchala-Avila, L.I.; Morales-Jadan, D. Enhancing Grid Stability in Microgrid Systems with Vehicle-to-Grid Support and EDLC Supercapacitors. Batteries 2025, 11, 231. https://doi.org/10.3390/batteries11060231
Criollo A, Benavides D, Arévalo P, Minchala-Avila LI, Morales-Jadan D. Enhancing Grid Stability in Microgrid Systems with Vehicle-to-Grid Support and EDLC Supercapacitors. Batteries. 2025; 11(6):231. https://doi.org/10.3390/batteries11060231
Chicago/Turabian StyleCriollo, Adrián, Dario Benavides, Paul Arévalo, Luis I. Minchala-Avila, and Diego Morales-Jadan. 2025. "Enhancing Grid Stability in Microgrid Systems with Vehicle-to-Grid Support and EDLC Supercapacitors" Batteries 11, no. 6: 231. https://doi.org/10.3390/batteries11060231
APA StyleCriollo, A., Benavides, D., Arévalo, P., Minchala-Avila, L. I., & Morales-Jadan, D. (2025). Enhancing Grid Stability in Microgrid Systems with Vehicle-to-Grid Support and EDLC Supercapacitors. Batteries, 11(6), 231. https://doi.org/10.3390/batteries11060231










