Measurement of Battery Aging Using Impedance Spectroscopy with an Embedded Multisine Coherent Measurement System
Abstract
1. Introduction
2. Electrochemical Impedance Spectroscopy
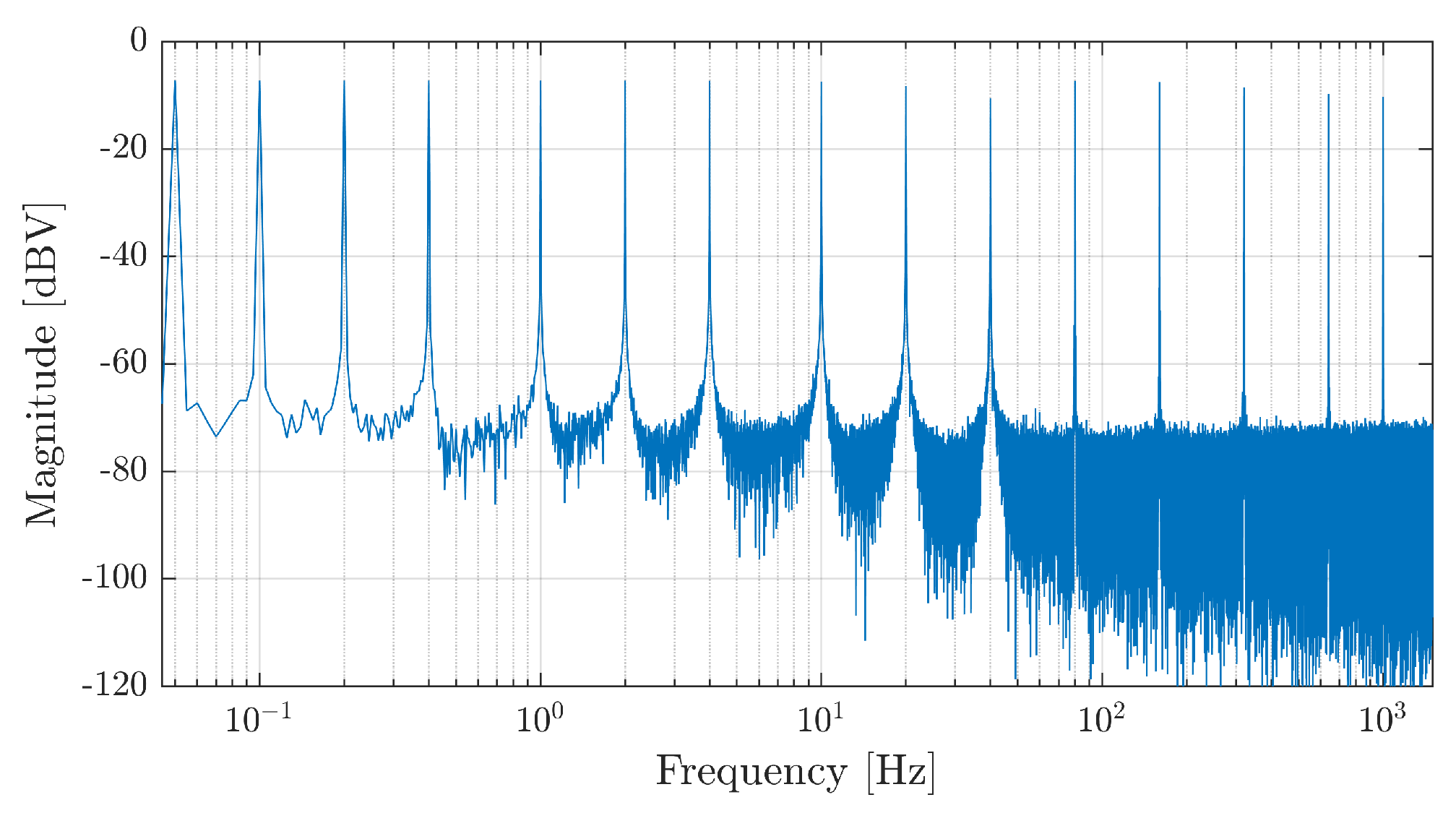
Excitation Signal Design
- Clip the time-domain voltage such that its amplitude is limited to a specified percentage of the current absolute peak value—the percentage starts at 75 % and is gradually increased to 99 % during the iterations, thus reducing the clipping.
- Determine the Discrete Fourier Transform (DFT) of the clipped voltage.
- Restore the amplitudes to the initial desired values while keeping the phases from the DFT result.
- Compute a new time-domain voltage using the Inverse DFT.
- Determine the new .
- If the reaches a desirable value, or there is no significant improvement, or the maximum number of iterations is reached, the algorithm is stopped. Otherwise, the algorithm returns to step 1.
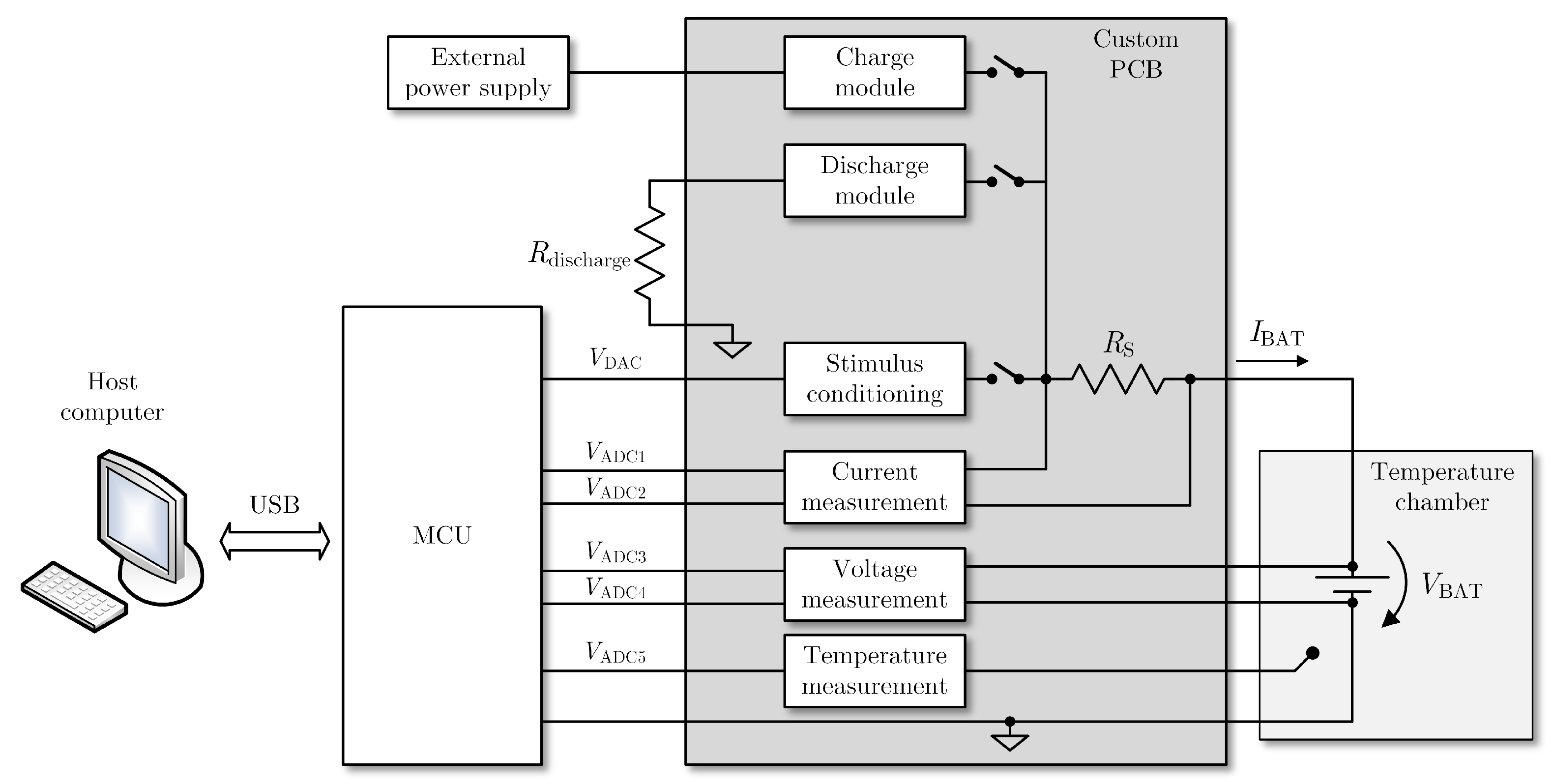
3. Embedded System Overview
3.1. Microcontroller Unit
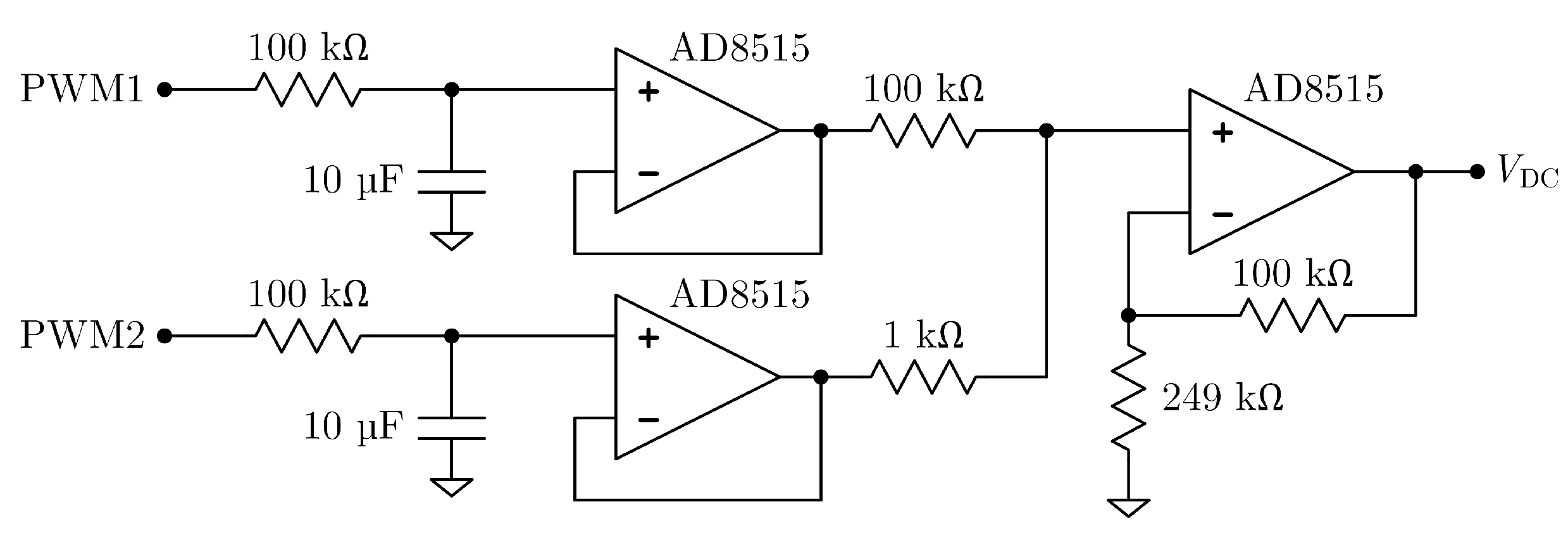
3.2. Excitation Current Source
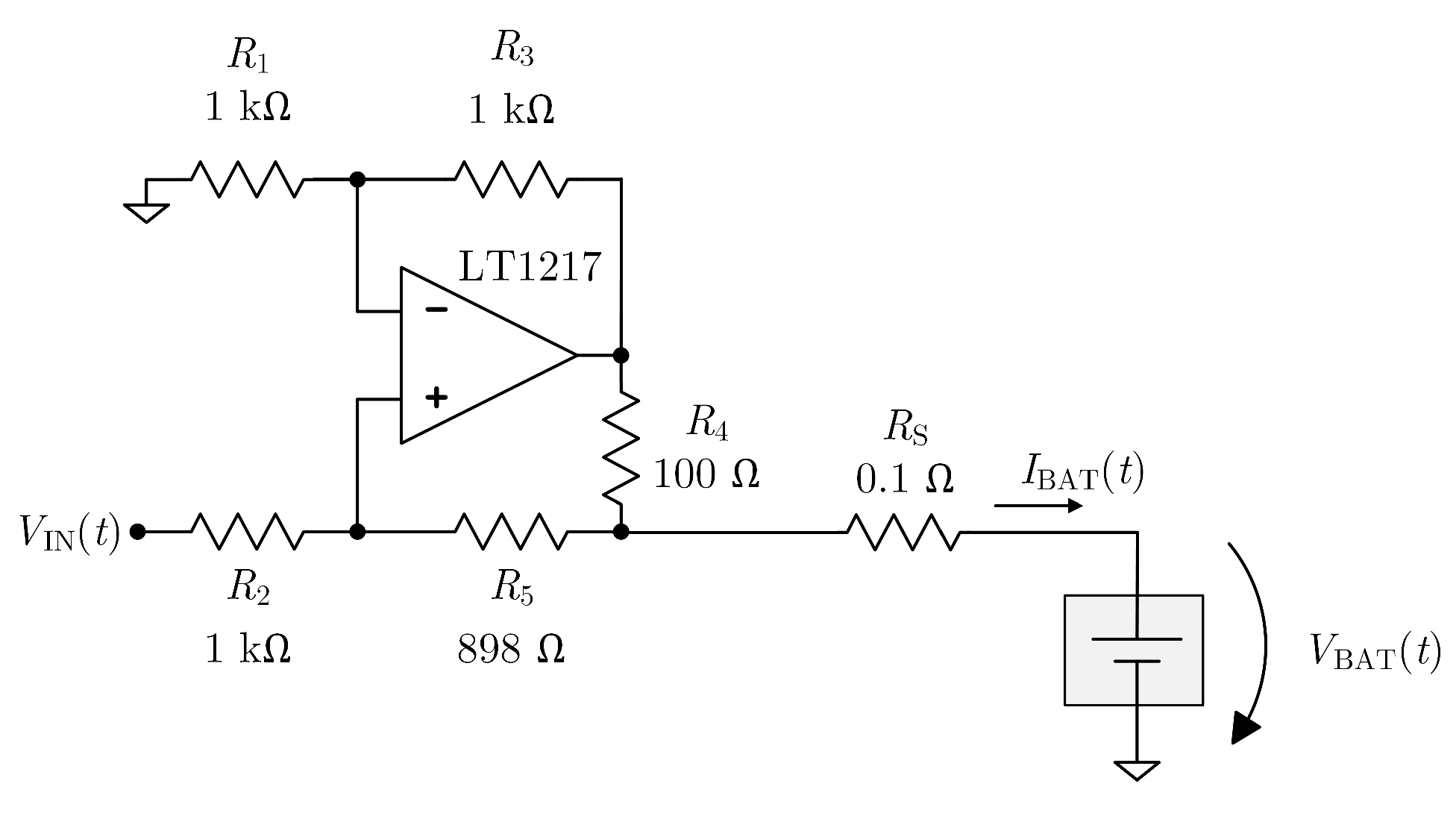
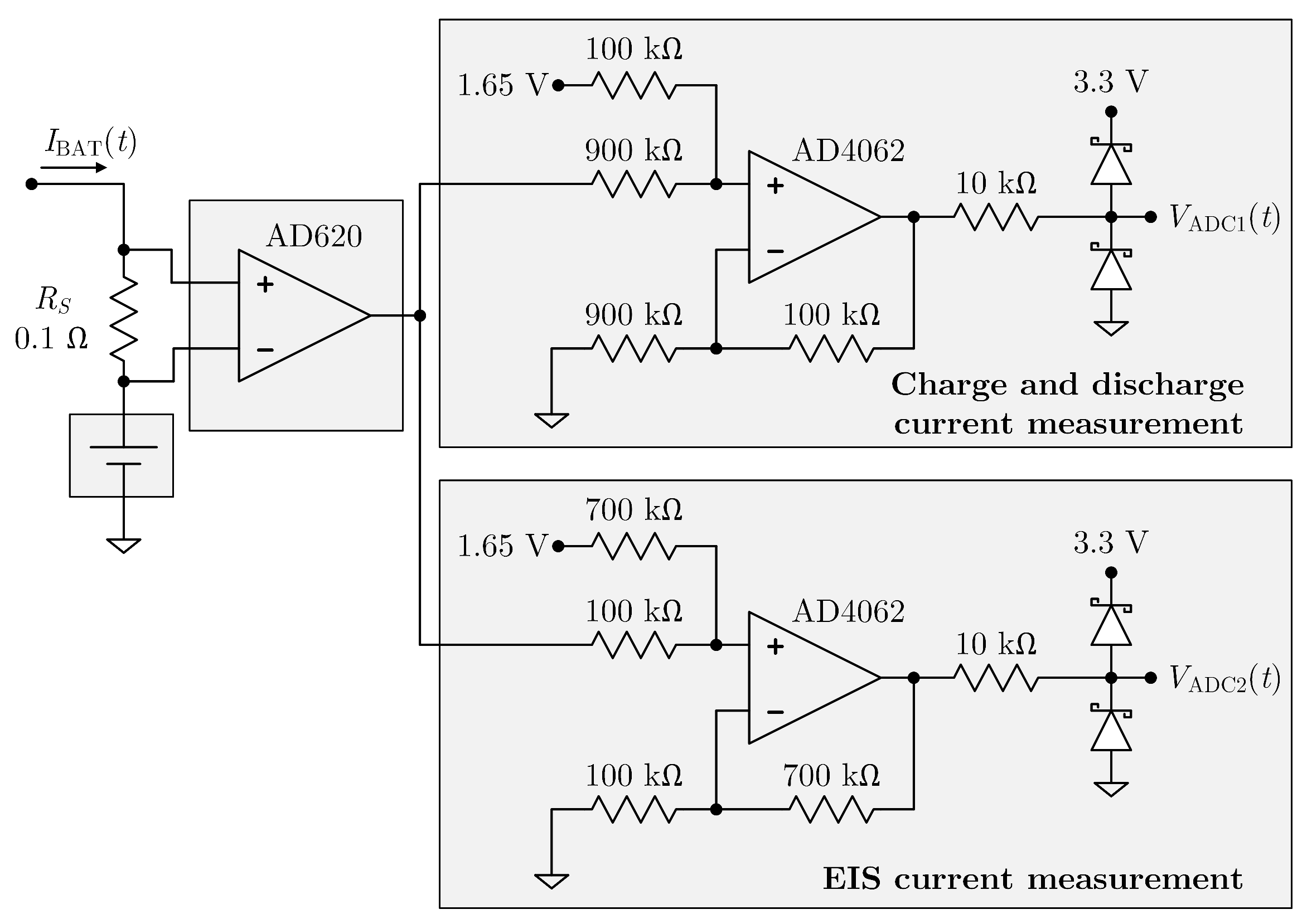
3.3. Current Measurement Circuit
3.4. Voltage Measurement Circuit
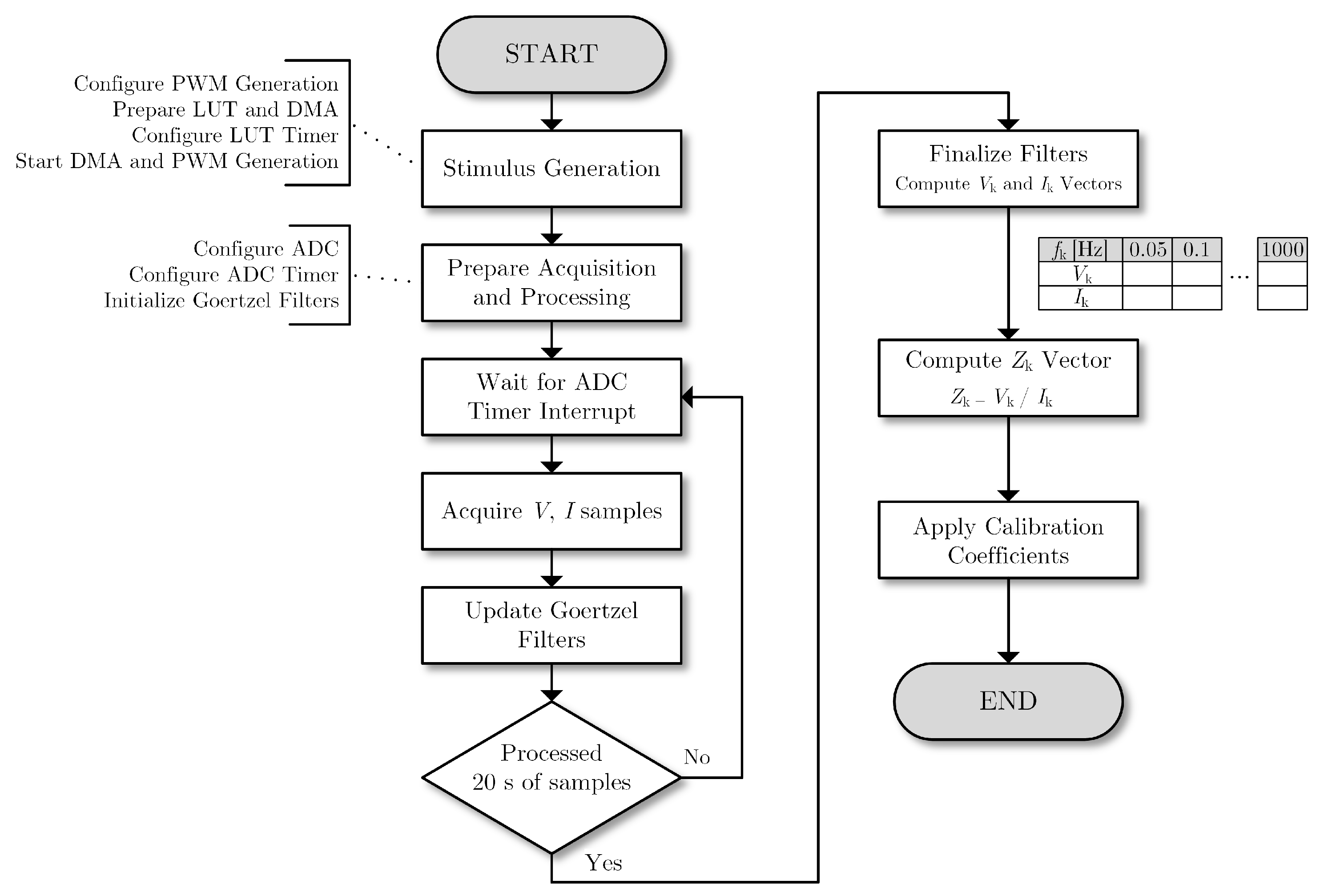
3.5. Impedance Estimation
4. Measurement Results
- Fully charge and discharge the battery 5 times, ending with it fully discharged (including rest periods after each charge and discharge).
- Perform EIS measurements with 12 repetitions to obtain the average impedance parameters for each of the 15 frequencies.
- If the battery was already fully charged, discharge it and go back to Step 1; otherwise, go to Step 4.
- Charge the battery up to 10 % of or until it is fully charged, wait for the battery to rest, and go to Step 2.
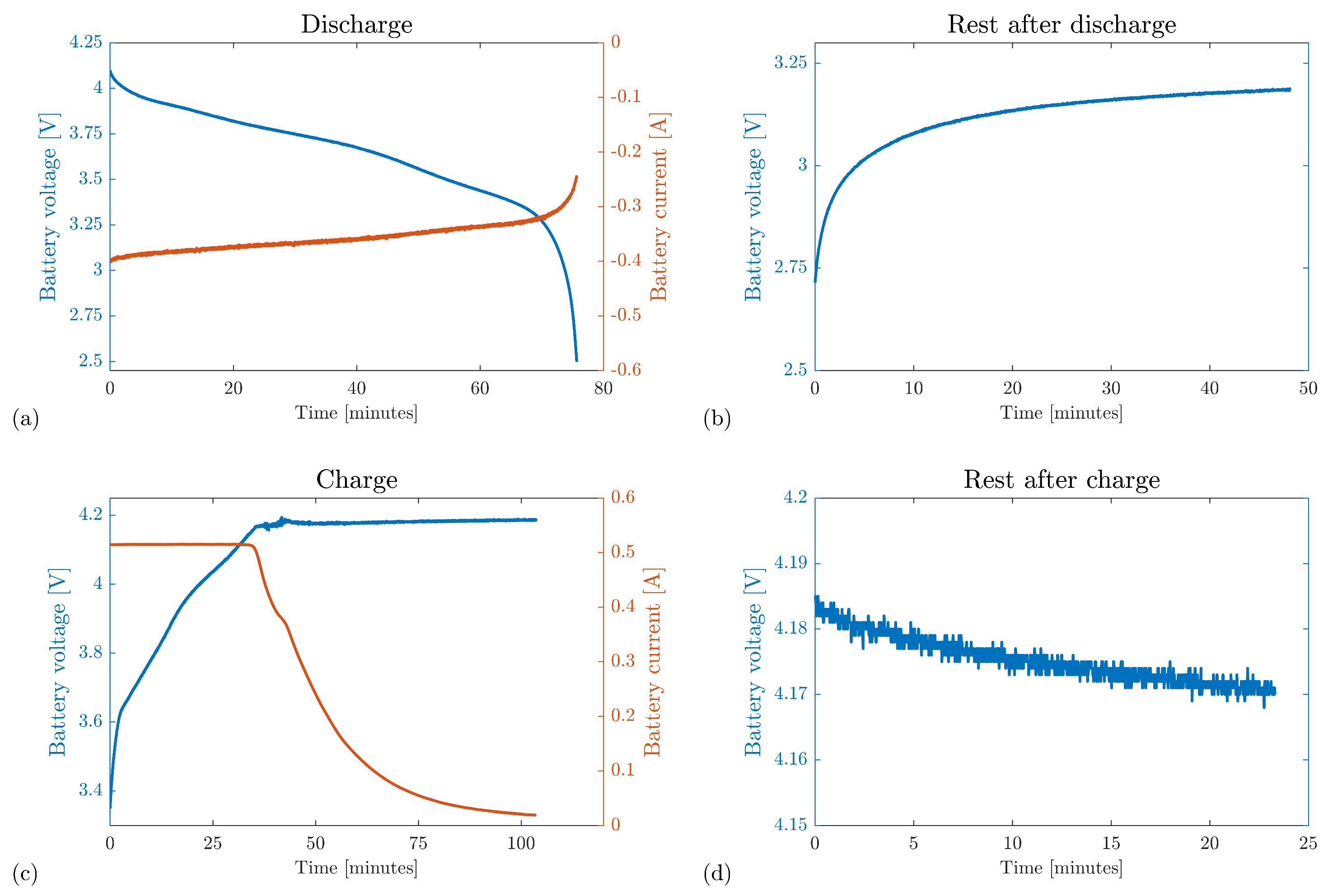
4.1. Charge/Discharge Cycling Procedure
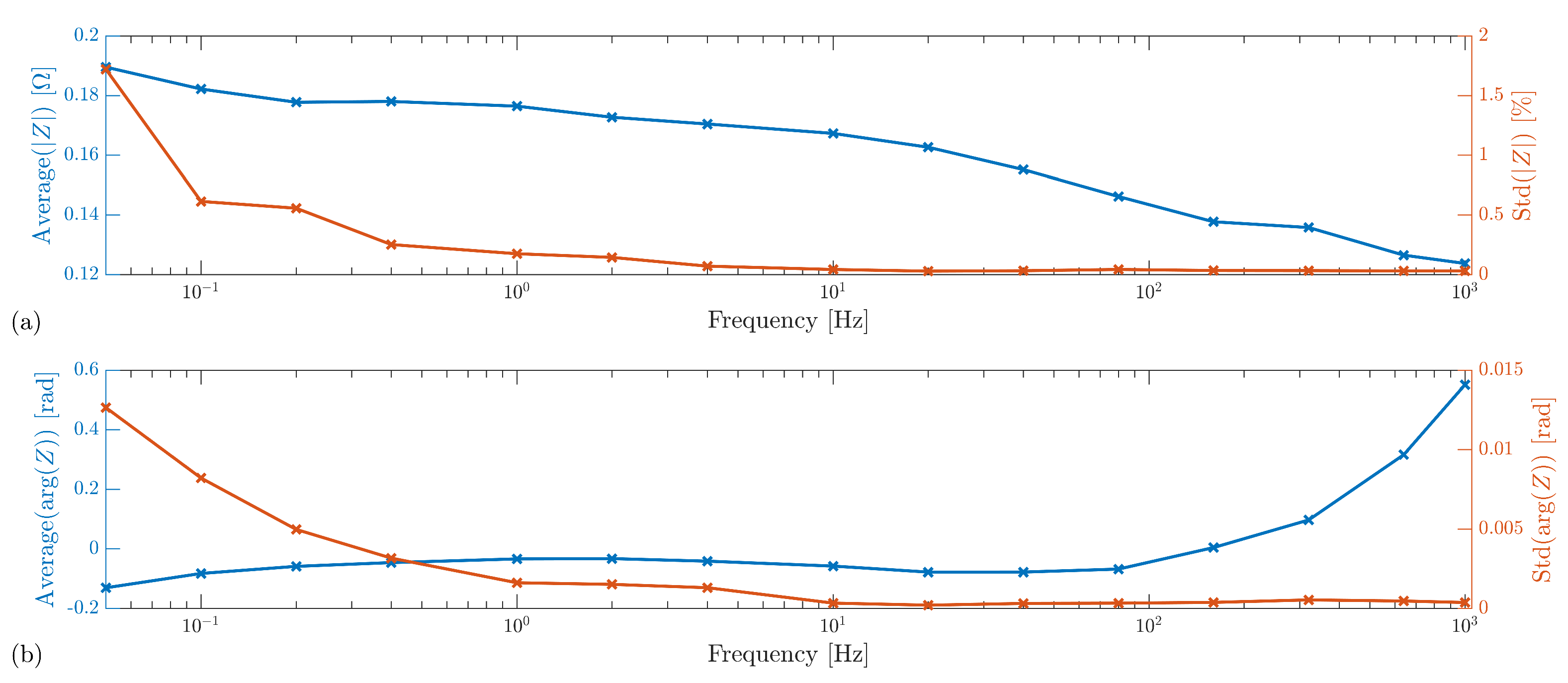
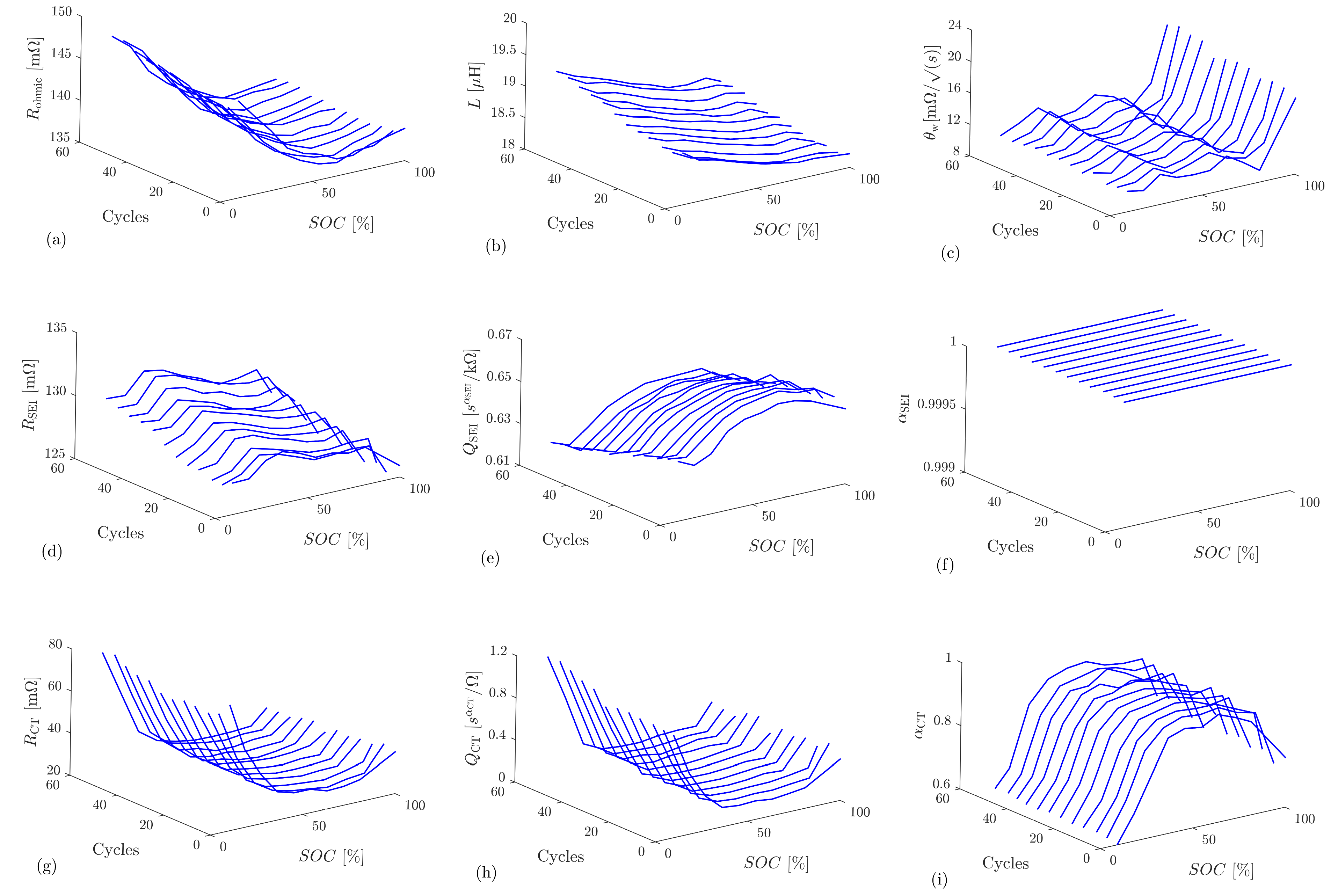
4.2. Measurements and Equivalent Circuit Model Fitting
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liang, Y.; Zhao, C.-Z.; Yuan, H.; Chen, Y.; Zhang, W.; Huang, J.-Q.; Yu, D.; Liu, Y.; Titirici, M.-M.; Chueh, Y.-L.; et al. A review of rechargeable batteries for portable electronic devices. InfoMat 2019, 1, 6–32. [Google Scholar] [CrossRef]
- Morris, M.; Tosunoglu, S. Comparison of rechargeable battery technologies. ASME Early Career Tech. J. 2012, 11, 148–155. [Google Scholar]
- Zhang, Y.; Zhang, C.; Zhang, X. State-of-charge estimation of the Lithium-ion battery system with time-varying parameter for hybrid electric vehicles. IET Control Theory 2014, 8, 160–167. [Google Scholar] [CrossRef]
- Hu, X.; Zou, C.; Zhang, C.; Li, Y. Technological developments in batteries: A survey of principal roles, types, and management needs. IEEE Power Energy Mag. 2014, 15, 20–31. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Mohamad, F.; Teh, J.; Lai, C.; Chen, L. Development of Energy Storage Systems for Power Network Reliability: A Review. Energies 2018, 11, 2278. [Google Scholar] [CrossRef]
- International Energy Agency. Global EV Outlook. 2024. Available online: https://iea.blob.core.windows.net/assets/a9e3544b-0b12-4e15-b407-65f5c8ce1b5f/GlobalEVOutlook2024.pdf (accessed on 10 April 2025).
- Rahmani, P.; Chakraborty, S.; Mele, I.; Katrašnik, T.; Bernhard, S.; Pruefling, S.; Wilkins, S.; Hegazy, O. Driving the Future: A Comprehensive Review of Automotive Battery Management System Technologies and Future Trends. J. Power Sources 2025, 629, 235827. [Google Scholar] [CrossRef]
- Garche, J.; Jossen, A. Battery Management Systems (BMS) for Increasing Battery Lifetime. In Proceedings of the TELESCON 2000—Third International Telecommunications Energy Special Conference, Dresden, Germany, 7–10 May 2000; pp. 81–88, IEEE Cat. No. 00EX424. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of Lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Huang, S.-C.; Tseng, K.-H.; Liang, J.-W.; Chang, C.-L.; Pecht, M.G. An online SoC and SoH estimation model for Lithium-ion batteries. Energies 2017, 10, 512. [Google Scholar] [CrossRef]
- Braun, J.A.; Behmann, R.; Schmider, D.; Bessler, W.G. State of charge and state of health diagnosis of batteries with voltage-controlled models. J. Power Sources 2022, 544, 231828. [Google Scholar] [CrossRef]
- Colarullo, L.; Thakur, J. Second-life EV batteries for stationary storage applications in local energy communities. Renew. Sustain. Energy Rev. 2022, 169, 112913. [Google Scholar] [CrossRef]
- Roy, P.M.; Sawant, H.H.; Shelar, P.P.; Sarode, P.U.; Gawande, S.H. Battery health management—A perspective of design, optimization, manufacturing, fault detection, and recycling. Energy Storage Sav. 2024, 3, 90–208. [Google Scholar] [CrossRef]
- Chang, W.-Y. The state of charge estimating methods for battery: A review. Int. Sch. Res. Not. 2013, 1, 953792. [Google Scholar] [CrossRef]
- Zhang, J.; Lee, J. A review on prognostics and health monitoring of Li-ion battery. J. Power Sources 2011, 196, 6007–6014. [Google Scholar] [CrossRef]
- Murnane, M.; Ghazel, A. A Closer Look at State of Charge (SOC) and State of Health (SOH) Estimation Techniques for Batteries; Analog Devices Technical Note. 2017. Available online: https://www.analog.com/media/en/technical-documentation/tech-articles/a-closer-look-at-state-of-charge-and-state-health-estimation-tech.pdf (accessed on 10 April 2025).
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.; Mekhilefb, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Hossain, M.; Haque, M.E.; Arif, M.T. Kalman filtering techniques for the online model parameters and state of charge estimation of the Li-ion batteries: A comparative analysis. J. Energy Storage 2022, 51, 104174. [Google Scholar] [CrossRef]
- Ren, Z.; Du, C. A review of machine learning state-of-charge and state-of-health estimation algorithms for lithium-ion batteries. Energy Rep. 2023, 9, 2993–3021. [Google Scholar] [CrossRef]
- Lee, S.; Lee, D. A novel battery state of charge estimation based on voltage relaxation curve. Batteries 2023, 9, 517. [Google Scholar] [CrossRef]
- Stiaszny, B.; Ziegler, J.C.; Krauß, E.E.; Zhang, M.; Schmidt, J.P.; Ivers-Tiffee, E. Electrochemical characterization and post-mortem analysis of aged LiMn2O4–NMC/graphite Lithium ion batteries part II: Calendar aging. J. Power Sources 2014, 258, 61–75. [Google Scholar] [CrossRef]
- Galeotti, M.; Cinà, L.; Giammanco, C.; Cordiner, S.; Di Carlo, A. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy. Energy 2015, 89, 678–686. [Google Scholar] [CrossRef]
- McCarthy, K.; Gullapalli, H.; Ryan, K.M.; Kennedy, T. Review—Use of Impedance Spectroscopy for the Estimation of Li-ion Battery State of Charge, State of Health and Internal Temperature. J. Electrochem. Soc. 2021, 168, 080517. [Google Scholar] [CrossRef]
- Kallel, A.Y.; Hu, Z.; Kanoun, O. Comparative Study of AC Signal Analysis Methods for Impedance Spectroscopy Implementation in Embedded Systems. Appl. Sci. 2022, 12, 591. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.-S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of electrochemical impedance spectroscopy to commercial li-ion cells: A review. J. Power Sources 2020, 480, 228742. [Google Scholar] [CrossRef]
- De Angelis, A.; Ramilli, R.; Crescentini, M.; Moschitta, A.; Carbone, P.; Traverso, P.A. In-situ electrochemical impedance spectroscopy of battery cells by means of binary sequences. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Kallel, A.Y.; Kanoun, O. On the design of multisine signals for maintaining stability condition in impedance spectroscopy measurements of batteries. J. Energy Storage 2023, 58, 106267. [Google Scholar] [CrossRef]
- Baccari, S.; Vasca, F.; Mostacciuolo, E.; Iannelli, L.; Sagnelli, S.; Luisi, R.; Stanzione, V. A characterization system for LEO satellites batteries. In Proceedings of the 2019 European Space Power Conference (ESPC), Juan-les-Pins, France, 30 September–4 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Miguel, E.; Plett, G.L.; Trimboli, M.S.; Oca, L.; Iraola, U.; Bekaert, E. Review of computational parameter estimation methods for electrochemical models. J. Energy Storage 2021, 44, 103388. [Google Scholar] [CrossRef]
- Cicioni, G.; De Angelis, A.; Janeiro, F.M.; Ramos, P.M.; Carbone, P. Battery impedance spectroscopy embedded measurement system. Batteries 2023, 9, 577. [Google Scholar] [CrossRef]
- Wei, X.; Wang, X.; Dai, H. Practical on-board measurement of Lithium Ion battery impedance based on distributed voltage and current sampling. Energies 2018, 11, 64. [Google Scholar] [CrossRef]
- Chen, H.; Bia, J.; Wu, Z.; Song, Z.; Zuo, B.; Fu, C.; Zhang, Y.; Wang, L. Rapid impedance measurement of Lithium-Ion batteries under pulse ex-citation and analysis of impedance characteristics of the regularization distributed relaxation time. Batteries 2025, 11, 91. [Google Scholar] [CrossRef]
- Chang, B.-Y.; Park, S.-M. Electrochemical impedance spectroscopy. Annu. Rev. Anal. Chem. 2010, 3, 207–229. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Q.; Wang, K. Revealing the degradation patterns of lithium-ion batteries from impedance spectroscopy using variational auto-encoders. Energy Storage Mater. 2024, 69, 103394. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef]
- De Angelis, A.; Buchicchio, E.; Santoni, F.; Moschitta, A.; Carbone, P. Practical broadband measurement of battery EIS. In Proceedings of the 2021 IEEE International Workshop on Metrology for Automotive (MetroAutomotive), Bologna, Italy, 1–2 July 2021; pp. 25–29. [Google Scholar] [CrossRef]
- Buchicchio, E.; De Angelis, A.; Santoni, F.; Carbone, P.; Bianconi, F.; Smeraldi, F. Dataset on broadband electrochemical impedance spectroscopy of Lithium-ion batteries for different values of the state-of-charge. Data Brief 2022, 45, 108589. [Google Scholar] [CrossRef]
- De Angelis, A.; Carbone, P.; Moschitta, A.; Crescentini, M.; Ramilli, R.; Traverso, P.A. A Fast and Simple Broadband EIS Measurement System for Li-ion Batteries. In Proceedings of the 24th IMEKO TC4 International Symposium, Pordenone, Italy, 20–21 September 2020; pp. 157–161. Available online: https://www.imeko.org/publications/tc4-2020/IMEKO-TC4-2020-30.pdf (accessed on 10 April 2025).
- Ojarand, J.; Min, M. Recent advances in crest factor minimization of multisine. Elektron. Elektrotech. 2017, 23, 59–62. [Google Scholar] [CrossRef]
- Janeiro, F.M.; Hu, Y.; Ramos, P.M. Peak factor optimization of multi-harmonic signals using artificial bee colony algorithm. Measurement 2020, 150, 107040. [Google Scholar] [CrossRef]
- Kallel, A.Y. Design of Optimized Broadband Excitation Signals for Consistent Impedance Spectroscopy Measurements. Ph.D. Thesis, Technische Universität Chemnitz, Chemnitz, Germany, 2024. [Google Scholar]
- Zhang, Z.; Jiang, L.; Zhang, L.; Huang, C. State-of-charge estimation of Lithium-ion battery pack by using an adaptive extended Kalman filter for electric vehicles. J. Energy Storage 2021, 37, 102457. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, L.; Hu, L.; Huang, C. Active cell balancing of Lithium-ion battery pack based on average state of charge. Int. J. Energ. Res. 2020, 44, 2535–2548. [Google Scholar] [CrossRef]
- Ningrum, P.; Windarko, N.A.; Suhariningsih, S. Estimation of state of charge (SoC) using modified coulomb counting method with open circuit compensation for battery management system (BMS). JAREE J. Adv. Res. Electr. Eng. 2021, 5, 15–20. [Google Scholar] [CrossRef]
- Rodrigues, N.M.; Janeiro, F.M.; Ramos, P.M. Implementation of Goertzel-based frequency estimation for power quality monitoring in embedded measurement systems. Metrol. Meas. Syst. 2022, 39, 142270. [Google Scholar] [CrossRef]
- Regnacq, L.; Wu, Y.; Neshatvar, N.; Jiang, D.; Demosthenous, A. A Goertzel filter-based system for fast simultaneous multi-frequency EIS. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3133–3137. [Google Scholar] [CrossRef]
- Kanoun, O.; Kallel, A.Y. High-performance efficient embedded systems for impedance spectroscopy: Challenges and potentials. Electrochim. Acta 2024, 492, 144351. [Google Scholar] [CrossRef]
- Orazem, M.E.; Ulgut, B. On the proper use of a Warburg impedance. J. Electrochem. Soc. 2024, 171, 040526. [Google Scholar] [CrossRef]
- Janeiro, F.M.; Ramos, P.M. Application of genetic algorithms for estimation of impedance parameters of two-terminal networks. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference, Singapore, 5–7 May 2009; pp. 602–606. [Google Scholar] [CrossRef]



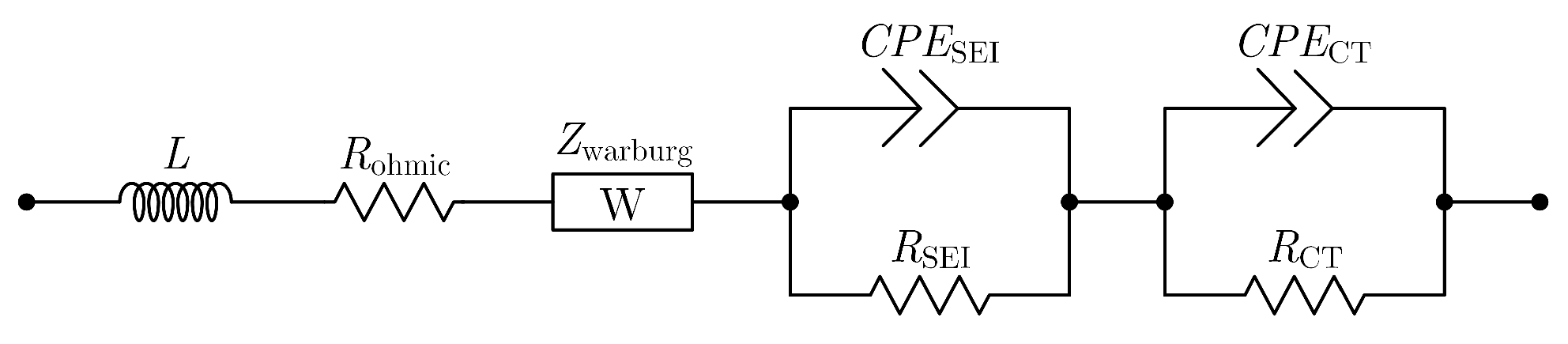

| Frequency Range | Measured Frequencies | Stimulus | Impedance Estimation Algorithm | Battery Charge/Discharge | |
|---|---|---|---|---|---|
| Proposed system | 0.05–1000 Hz | 15 | Multisine PWM-generated | Goertzel filters | Included |
| [32] | 0.5–5000 Hz | 39 | Sum of two PWM-generated multisine signals | FFT | External |
| [33] | 0.1–500 Hz | 16 | Sine-Sweep | Digital lock-in amplifier based on cross-correlation | Not Specified |
| [34] | 0.1–100 Hz | 24 | Sweep of a square signal using 3 frequency components for each input frequency | FFT | External |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lourenço, J.; Rosado, L.S.; Ramos, P.M.; Janeiro, F.M. Measurement of Battery Aging Using Impedance Spectroscopy with an Embedded Multisine Coherent Measurement System. Batteries 2025, 11, 227. https://doi.org/10.3390/batteries11060227
Lourenço J, Rosado LS, Ramos PM, Janeiro FM. Measurement of Battery Aging Using Impedance Spectroscopy with an Embedded Multisine Coherent Measurement System. Batteries. 2025; 11(6):227. https://doi.org/10.3390/batteries11060227
Chicago/Turabian StyleLourenço, Jorge, Luis S. Rosado, Pedro M. Ramos, and Fernando M. Janeiro. 2025. "Measurement of Battery Aging Using Impedance Spectroscopy with an Embedded Multisine Coherent Measurement System" Batteries 11, no. 6: 227. https://doi.org/10.3390/batteries11060227
APA StyleLourenço, J., Rosado, L. S., Ramos, P. M., & Janeiro, F. M. (2025). Measurement of Battery Aging Using Impedance Spectroscopy with an Embedded Multisine Coherent Measurement System. Batteries, 11(6), 227. https://doi.org/10.3390/batteries11060227









