Quantification of Degradation Processes in Lithium-Ion Batteries Through Internal Strain Measurement with Fiber Bragg Grating Sensors
Abstract
1. Introduction
2. Materials and Methods
2.1. Measuring Principle
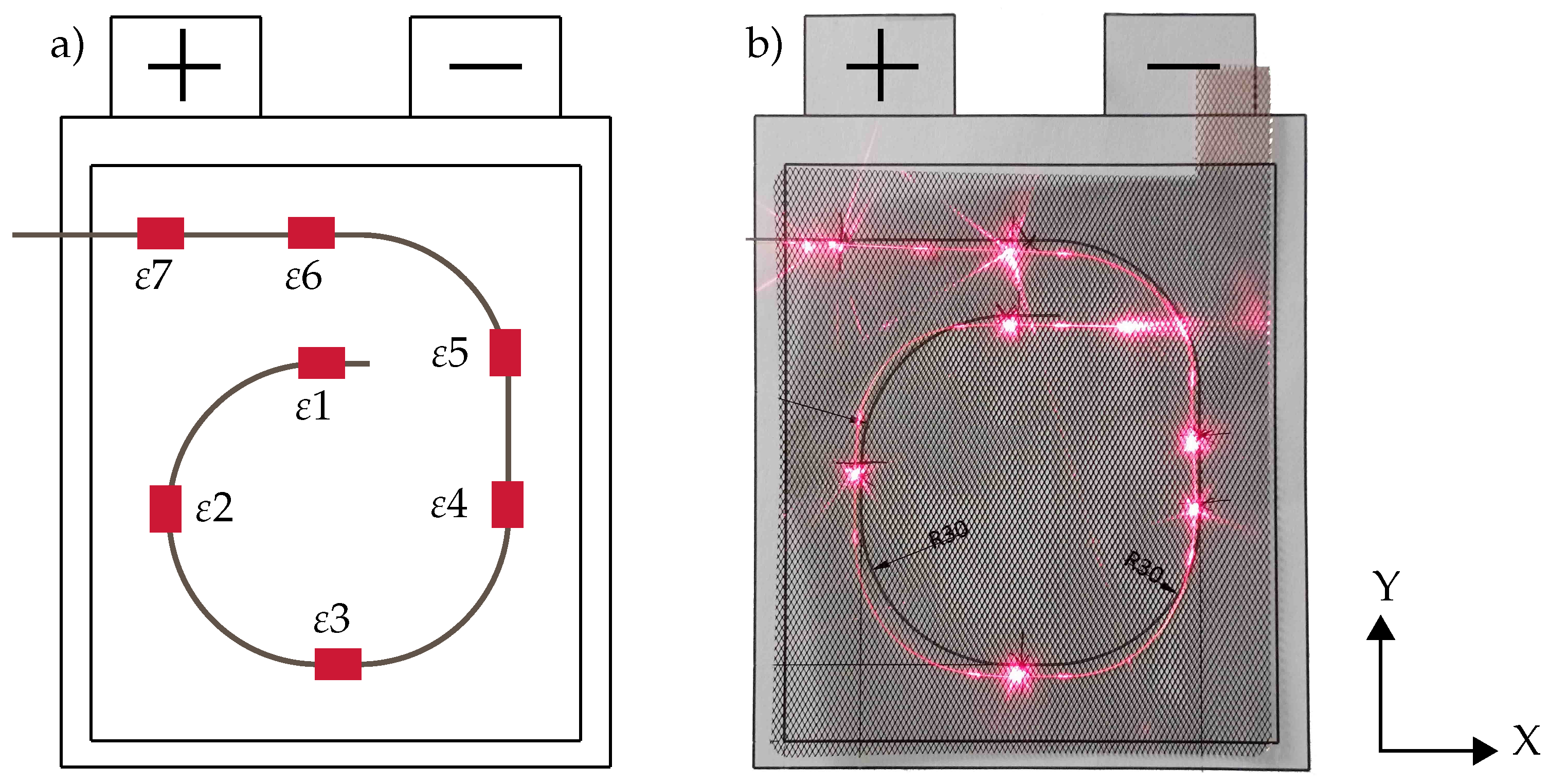
2.2. Device Under Test
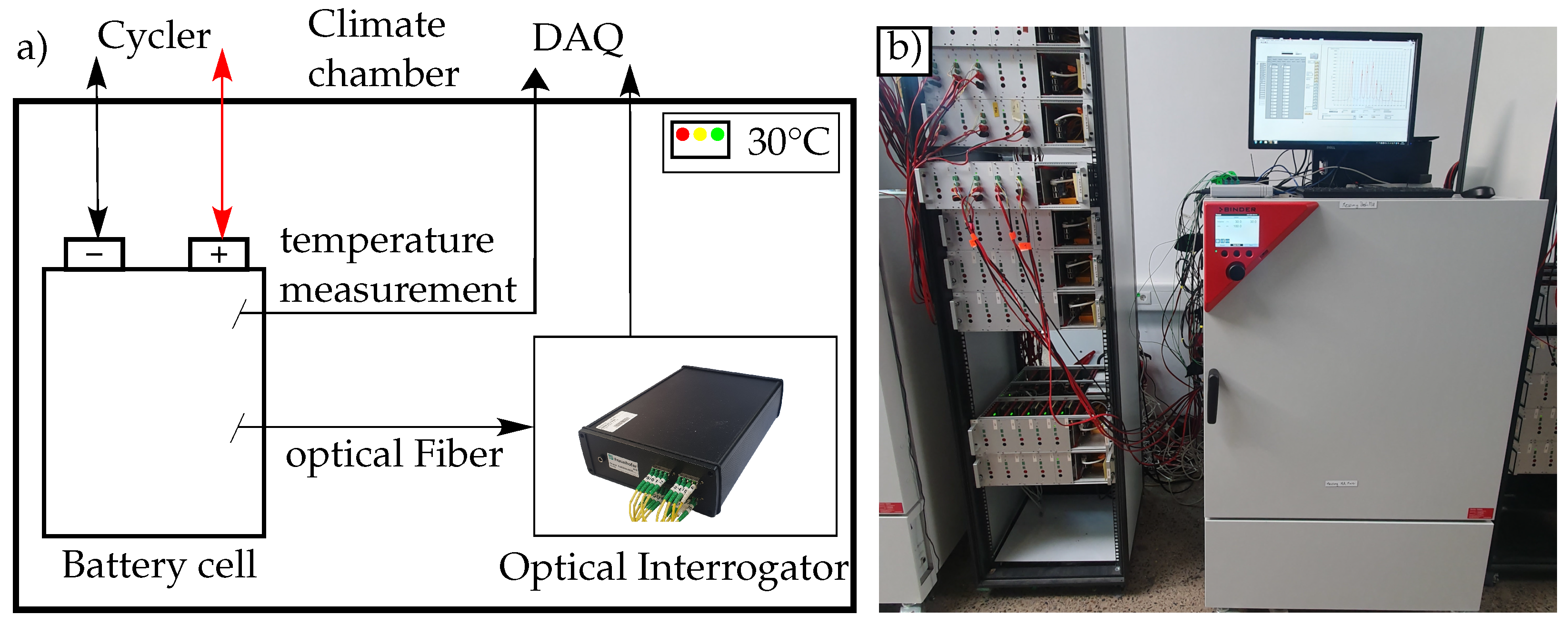
2.3. Experimental Setup
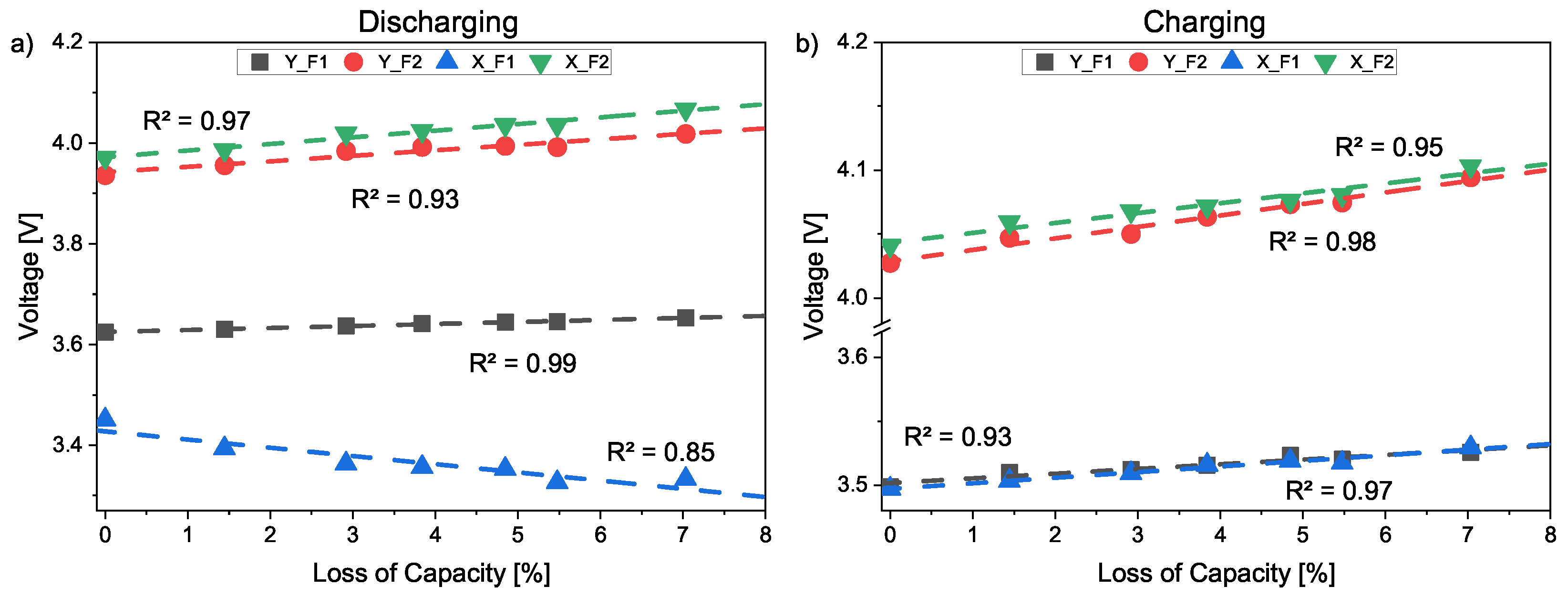
3. Results
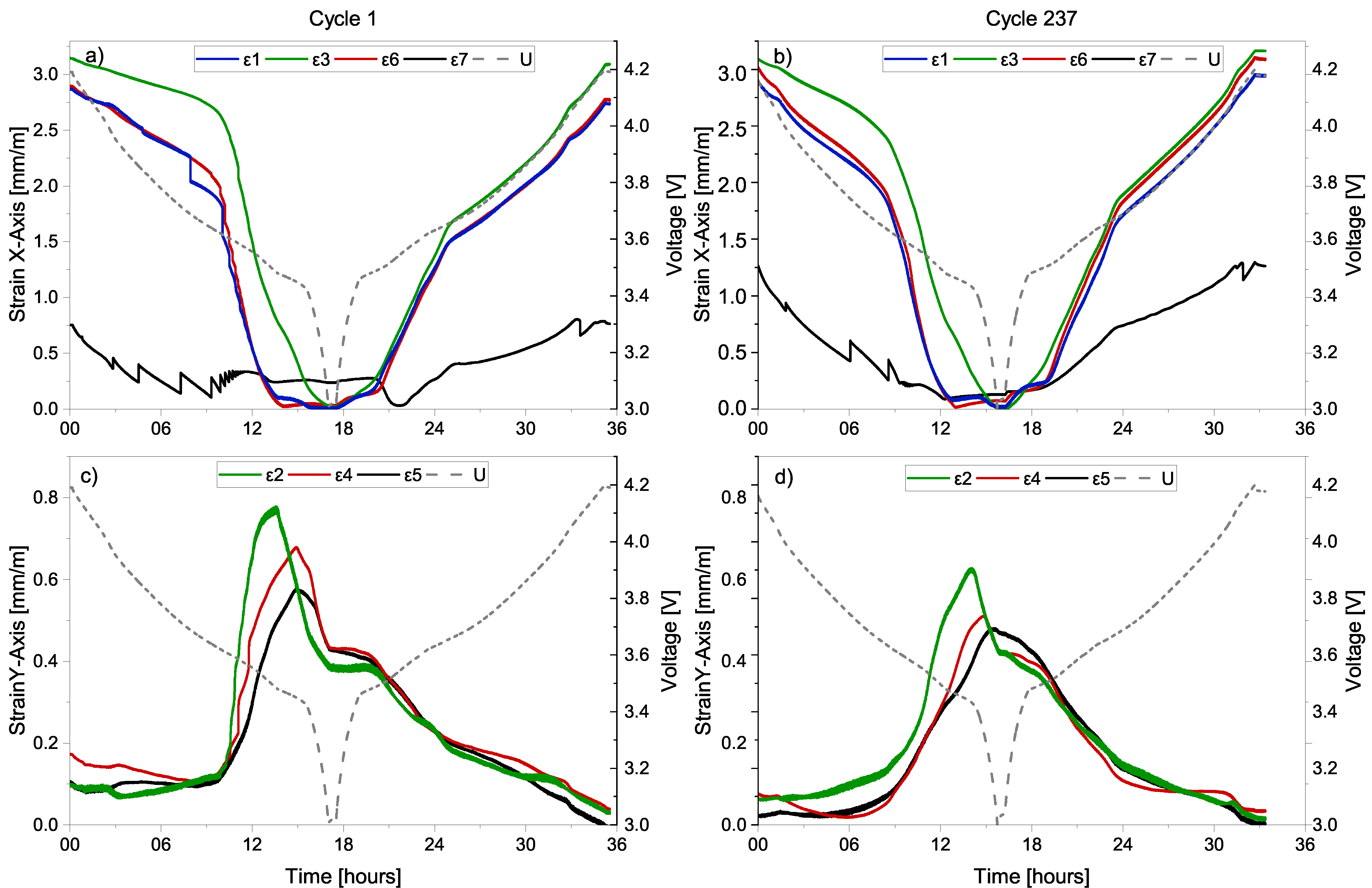
3.1. Cyclical Anode Strain Calculated from Wavelength Shift
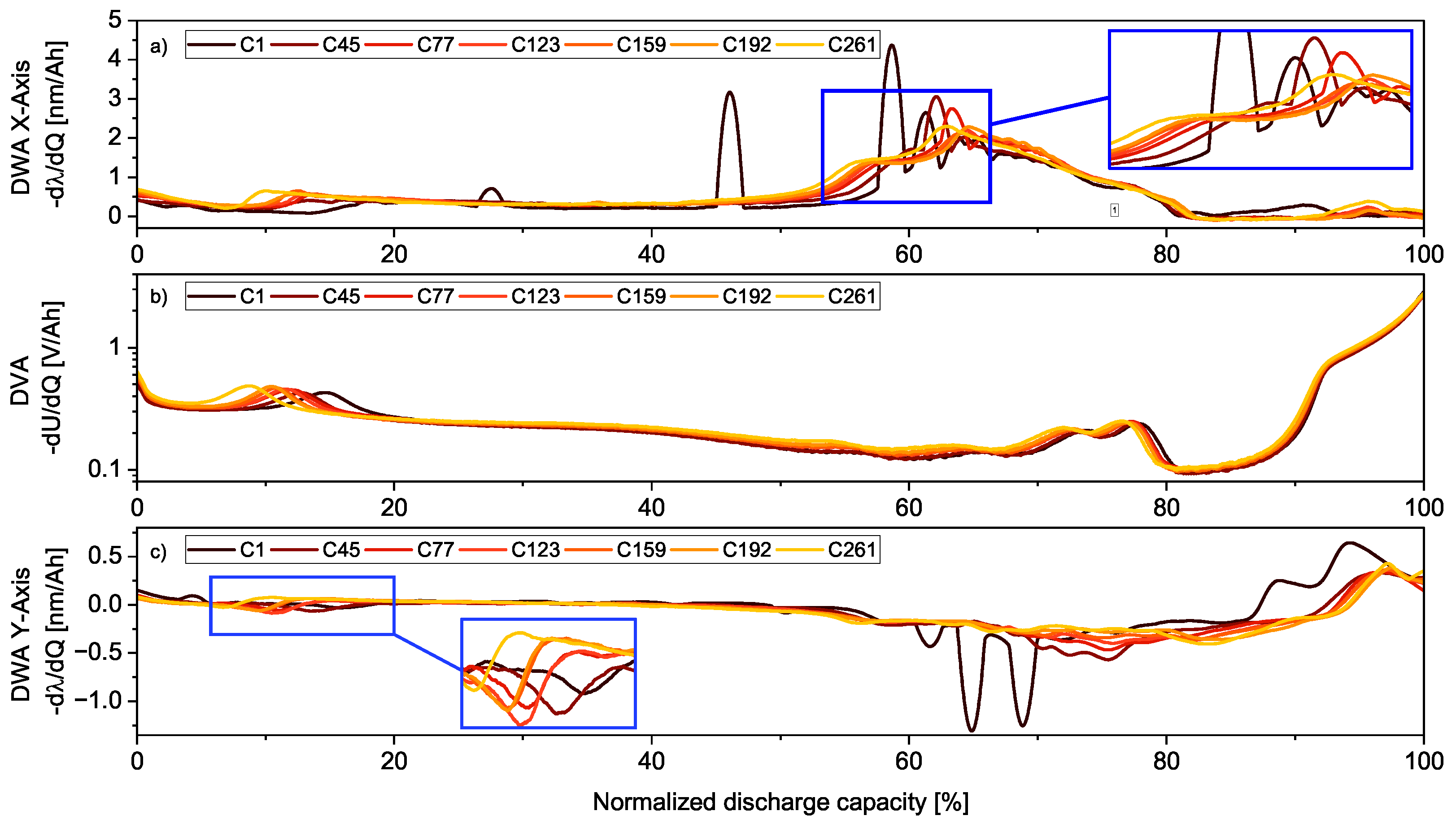
3.2. Differential Analysis
3.3. Incremental Analysis
3.4. Load Cycles
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DAQ | Data acquisition unit |
| DUT | Device under test |
| DVA | Differential voltage analysis |
| DWA | Differential wavelength analysis |
| FBG | Fiber Bragg grating |
| ICA | Incremental capacity analysis |
| IWA | Incremental wavelength analysis |
| LIB | Lithium-ion battery |
| LLI | Loss of lithium inventory |
| LAMne | Loss of active material (negative electrode) |
| LAMpe | Loss of active material (positive electrode) |
| NMC | Nickel-Manganese-Cobalt-oxide |
| SOC | State of charge |
References
- Deng, H.; Aifantis, K.E. Applications of Lithium Batteries; Wiley: Hoboken, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Xu, J.; Cai, X.; Cai, S.; Shao, Y.; Hu, C.; Lu, S.; Ding, S. High-Energy Lithium-Ion Batteries: Recent Progress and a Promising Future in Applications. Energy Environ. Mater. 2023, 6, e12450. [Google Scholar] [CrossRef]
- Dolotko, O.; Senyshyn, A.; Mühlbauer, M.J.; Nikolowski, K.; Scheiba, F.; Ehrenberg, H. Fatigue Process in Li-Ion Cells: An In Situ Combined Neutron Diffraction and Electrochemical Study. J. Electrochem. Soc. 2012, 159, A2082–A2088. [Google Scholar] [CrossRef]
- Darma, M.S.D.; Lang, M.; Kleiner, K.; Mereacre, L.; Liebau, V.; Fauth, F.; Bergfeldt, T.; Ehrenberg, H. The influence of cycling temperature and cycling rate on the phase specific degradation of a positive electrode in lithium ion batteries: A post mortem analysis. J. Power Sources 2016, 327, 714–725. [Google Scholar] [CrossRef]
- Iturrondobeitia, A.; Aguesse, F.; Genies, S.; Waldmann, T.; Kasper, M.; Ghanbari, N.; Wohlfahrt-Mehrens, M.; Bekaert, E. Post-Mortem Analysis of Calendar-Aged 16 Ah NMC/Graphite Pouch Cells for EV Application. J. Phys. Chem. C 2017, 121, 21865–21876. [Google Scholar] [CrossRef]
- Xiong, R.; Pan, Y.; Shen, W.; Li, H.; Sun, F. Lithium-ion battery aging mechanisms and diagnosis method for automotive applications: Recent advances and perspectives. Renew. Sustain. Energy Rev. 2020, 131, 110048. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. Stress evolution and capacity fade in constrained lithium-ion pouch cells. J. Power Sources 2014, 245, 745–751. [Google Scholar] [CrossRef]
- Clerici, D.; Mocera, F.; Somà, A. Experimental Characterization of Lithium-Ion Cell Strain Using Laser Sensors. Energies 2021, 14, 6281. [Google Scholar] [CrossRef]
- Jin, C.; Wang, Y.; Borujerdi, A.S.; Li, J. Stress evolution and thickness change of a lithium-ion pouch cell under various cycling conditions. J. Power Sources Adv. 2022, 16, 100103. [Google Scholar] [CrossRef]
- Krause, T.; Nusko, D.; Pitta Bauermann, L.; Vetter, M.; Schäfer, M.; Holly, C. Methods for Quantifying Expansion in Lithium-Ion Battery Cells Resulting from Cycling: A Review. Energies 2024, 17, 1566. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Sheldon, B.W. Deformation and stress in electrode materials for Li-ion batteries. Prog. Mater. Sci. 2014, 63, 58–116. [Google Scholar] [CrossRef]
- Wang, L.; Duan, X.; Liu, B.; Li, Q.; Yin, S.; Xu, J. Deformation and failure behaviors of anode in lithium-ion batteries: Model and mechanism. J. Power Sources 2020, 448, 227468. [Google Scholar] [CrossRef]
- Pistorio, F.; Clerici, D.; Mocera, F.; Somà, A. Review on the Experimental Characterization of Fracture in Active Material for Lithium-Ion Batteries. Energies 2022, 15, 9168. [Google Scholar] [CrossRef]
- Schulze, C.; Birke, K.P. Method for analyzing in-situ volume change of large format lithium-ion hard case cells. J. Energy Storage 2022, 55, 105736. [Google Scholar] [CrossRef]
- Xie, S.; Ren, L.; Yang, X.; Wang, H.; Sun, Q.; Chen, X.; He, Y. Influence of cycling aging and ambient pressure on the thermal safety features of lithium-ion battery. J. Power Sources 2020, 448, 227425. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Ansean, D.; Garcia, V.M.; Gonzalez, M.; Blanco-Viejo, C.; Viera, J.C.; Pulido, Y.F.; Sanchez, L. Lithium-Ion Battery Degradation Indicators Via Incremental Capacity Analysis. IEEE Trans. Ind. Appl. 2019, 55, 2992–3002. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Jiang, Y. Aging mechanisms under different state-of-charge ranges and the multi-indicators system of state-of-health for lithium-ion battery with Li(NiMnCo)O2 cathode. J. Power Sources 2018, 400, 641–651. [Google Scholar] [CrossRef]
- Zhu, J.; Dewi Darma, M.S.; Knapp, M.; Sørensen, D.R.; Heere, M.; Fang, Q.; Wang, X.; Dai, H.; Mereacre, L.; Senyshyn, A.; et al. Investigation of lithium-ion battery degradation mechanisms by combining differential voltage analysis and alternating current impedance. J. Power Sources 2020, 448, 227575. [Google Scholar] [CrossRef]
- Mohtat, P.; Lee, S.; Sulzer, V.; Siegel, J.B.; Stefanopoulou, A.G. Differential Expansion and Voltage Model for Li-ion Batteries at Practical Charging Rates. J. Electrochem. Soc. 2020, 167, 110561. [Google Scholar] [CrossRef]
- Kim, S.; Raj, A.; Li, B.; Dufek, E.J.; Dickerson, C.C.; Huang, H.Y.; Liaw, B.; Pawar, G.M. Correlation of electrochemical and mechanical responses: Differential analysis of rechargeable lithium metal cells. J. Power Sources 2020, 463, 228180. [Google Scholar] [CrossRef]
- Daubinger, P.; Ebert, F.; Hartmann, S.; Giffin, G.A. Impact of electrochemical and mechanical interactions on lithium-ion battery performance investigated by operando dilatometry. J. Power Sources 2021, 488, 229457. [Google Scholar] [CrossRef]
- Bezsonov, I.I.; Waller, G.H.; Ko, J.; Nadimpalli, S.P. In operando measurement of surface strain of 18650 Li-ion cells during cycling. J. Power Sources 2024, 592, 233915. [Google Scholar] [CrossRef]
- Han, G.; Yan, J.; Guo, Z.; Greenwood, D.; Marco, J.; Yu, Y. A review on various optical fibre sensing methods for batteries. Renew. Sustain. Energy Rev. 2021, 150, 111514. [Google Scholar] [CrossRef]
- Nedjalkov, A.; Meyer, J.; Gräfenstein, A.; Schramm, B.; Angelmahr, M.; Schwenzel, J.; Schade, W. Refractive Index Measurement of Lithium Ion Battery Electrolyte with Etched Surface Cladding Waveguide Bragg Gratings and Cell Electrode State Monitoring by Optical Strain Sensors. Batteries 2019, 5, 30. [Google Scholar] [CrossRef]
- Fortier, A.; Tsao, M.; Williard, N.; Xing, Y.; Pecht, M. Preliminary Study on Integration of Fiber Optic Bragg Grating Sensors in Li-Ion Batteries and In Situ Strain and Temperature Monitoring of Battery Cells. Energies 2017, 10, 838. [Google Scholar] [CrossRef]
- Nascimento, M.; Ferreira, M.; Pinto, J. Simultaneous Sensing of Temperature and Bi-Directional Strain in a Prismatic Li-Ion Battery. Batteries 2018, 4, 23. [Google Scholar] [CrossRef]
- Bae, C.; Manandhar, A.; Kiesel, P.; Raghavan, A. Monitoring the Strain Evolution of Lithium-Ion Battery Electrodes using an Optical Fiber Bragg Grating Sensor. Energy Technol. 2016, 4, 851–855. [Google Scholar] [CrossRef]
- Morey, W.W.; Meltz, G.; Glenn, W.H. Fiber Optic Bragg Grating Sensors. In Proceedings of the Fiber Optic and Laser Sensors VII, Boston, WA, USA, 5–7 September 1989; DePaula, R.P., Udd, E., Eds.; SPIE: Bellingham, WA, USA, 1990. [Google Scholar] [CrossRef]
- Rao, Y.J. In-fibre Bragg grating sensors. Meas. Sci. Technol. 1997, 8, 355–375. [Google Scholar] [CrossRef]
- Werneck, M.M.; Allil, R.C.S.B.; Ribeiro, B.A.; de Nazaré, F.V.B. A Guide to Fiber Bragg Grating Sensors. In Current Trends in Short- and Long-Period Fiber Gratings; InTech: London, UK, 2013. [Google Scholar] [CrossRef]
- Sahota, J.K.; Gupta, N.; Dhawan, D. Fiber Bragg grating sensors for monitoring of physical parameters: A comprehensive review. Opt. Eng. 2020, 59, 1. [Google Scholar] [CrossRef]
- O’Dwyer, M.J.; Ye, C.C.; James, S.W.; Tatam, R.P. Thermal dependence of the strain response of optical fibre Bragg gratings. Meas. Sci. Technol. 2004, 15, 1607–1613. [Google Scholar] [CrossRef]
- Frazão, O.; Santos, J.L. Simultaneous measurement of strain and temperature using a Bragg grating structure written in germanosilicate fibres. J. Opt. A Pure Appl. Opt. 2004, 6, 553–556. [Google Scholar] [CrossRef]
- Degen, F.; Winter, M.; Bendig, D.; Tübke, J. Energy consumption of current and future production of lithium-ion and post lithium-ion battery cells. Nat. Energy 2023, 8, 1284–1295. [Google Scholar] [CrossRef]
- Bosia, F.; Giaccari, P.; Botsis, J.; Facchini, M.; Limberger, H.G.; Salathé, R.P. Characterization of the response of fibre Bragg grating sensors subjected to a two-dimensional strain field. Smart Mater. Struct. 2003, 12, 925–934. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, L.; Fan, J.; Wen, J.; Feng, X.; Zhou, P.; Xie, F.; Zhou, J.; Wang, Y.N. In-situ obtained internal strain and pressure of the cylindrical Li-ion battery cell with silicon-graphite negative electrodes. J. Energy Storage 2021, 42, 103049. [Google Scholar] [CrossRef]
- Baccouche, I.; Jemmali, S.; Manai, B.; Nikolian, A.; Omar, N.; Essoukri Ben Amara, N. Li-ion battery modeling and characterization: An experimental overview on NMC battery. Int. J. Energy Res. 2021, 46, 3843–3859. [Google Scholar] [CrossRef]
- EL Aouam, A.; Sabi, N.; Aziam, H.; Touag, O.; Dolotko, O.; Mansori, M.; Dsoke, S.; Dollé, M.; Saadoune, I. Development and understanding of the lithiation/de-lithiation mechanism of a low cobalt and nickel-rich cathode material for lithium-ion batteries. J. Power Sources 2024, 606, 234551. [Google Scholar] [CrossRef]
- Li, W.; Xia, Y.; Zhu, J.; Luo, H. State-of-Charge Dependence of Mechanical Response of Lithium-Ion Batteries: A Result of Internal Stress. J. Electrochem. Soc. 2018, 165, A1537–A1546. [Google Scholar] [CrossRef]
- Qi, Y.; Guo, H.; Hector, L.G.; Timmons, A. Threefold Increase in the Young’s Modulus of Graphite Negative Electrode during Lithium Intercalation. J. Electrochem. Soc. 2010, 157, A558. [Google Scholar] [CrossRef]
- Schweidler, S.; de Biasi, L.; Schiele, A.; Hartmann, P.; Brezesinski, T.; Janek, J. Volume Changes of Graphite Anodes Revisited: A Combined Operando X-ray Diffraction and In Situ Pressure Analysis Study. J. Phys. Chem. C 2018, 122, 8829–8835. [Google Scholar] [CrossRef]
- Ovejas, V.; Cuadras, A. State of charge dependency of the overvoltage generated in commercial Li-ion cells. J. Power Sources 2019, 418, 176–185. [Google Scholar] [CrossRef]
- Bhattacharya, D.; Reese, C.W.; Bobel, A.; Kim, Y.; Toner, J.; Sayed, S.Y.; Sachdev, A.K. Mechanical performance of lithium metal anodes manufactured using two-dimensional and three-dimensional current collectors. J. Mater. Res. 2025. [Google Scholar] [CrossRef]
- Wang, L.; Yin, S.; Zhang, C.; Huan, Y.; Xu, J. Mechanical characterization and modeling for anodes and cathodes in lithium-ion batteries. J. Power Sources 2018, 392, 265–273. [Google Scholar] [CrossRef]
- Dubarry, M.; Beck, D. Analysis of Synthetic Voltage vs. Capacity Datasets for Big Data Li-ion Diagnosis and Prognosis. Energies 2021, 14, 2371. [Google Scholar] [CrossRef]
- Lee, S.; Siegel, J.B.; Stefanopoulou, A.G.; Lee, J.W.; Lee, T.K. Electrode State of Health Estimation for Lithium Ion Batteries Considering Half-cell Potential Change Due to Aging. J. Electrochem. Soc. 2020, 167, 090531. [Google Scholar] [CrossRef]
- Bloom, I.; Walker, L.K.; Basco, J.K.; Abraham, D.P.; Christophersen, J.P.; Ho, C.D. Differential voltage analyses of high-power lithium-ion cells. 4. Cells containing NMC. J. Power Sources 2010, 195, 877–882. [Google Scholar] [CrossRef]
- Guo, J.; Li, Y.; Meng, J.; Pedersen, K.; Gurevich, L.; Stroe, D.I. Understanding the mechanism of capacity increase during early cycling of commercial NMC/graphite lithium-ion batteries. J. Energy Chem. 2022, 74, 34–44. [Google Scholar] [CrossRef]
- Simolka, M.; Heger, J.F.; Traub, N.; Kaess, H.; Friedrich, K.A. Influence of Cycling Profile, Depth of Discharge and Temperature on Commercial LFP/C Cell Ageing: Cell Level Analysis with ICA, DVA and OCV Measurements. J. Electrochem. Soc. 2020, 167, 110502. [Google Scholar] [CrossRef]
- Deshpande, R.D.; Ridgway, P.; Fu, Y.; Zhang, W.; Cai, J.; Battaglia, V. The Limited Effect of VC in Graphite/NMC Cells. J. Electrochem. Soc. 2014, 162, A330–A338. [Google Scholar] [CrossRef]
- Bensaad, Y.; Friedrichs, F.; Sieg, J.; Bähr, J.; Fill, A.; Birke, K.P. Multidimensional estimation of inhomogeneous lithium-ion cell aging via modal differential voltage analysis. J. Energy Storage 2023, 63, 107108. [Google Scholar] [CrossRef]
- Tao, R.; Zhu, J.; Zhang, Y.; Song, W.L.; Chen, H.; Fang, D. Quantifying the 2D anisotropic displacement and strain fields in graphite-based electrode via in situ scanning electron microscopy and digital image correlation. Extrem. Mech. Lett. 2020, 35, 100635. [Google Scholar] [CrossRef]
- An, S.J.; Li, J.; Daniel, C.; Mohanty, D.; Nagpure, S.; Wood, D.L. The state of understanding of the lithium-ion-battery graphite solid electrolyte interphase (SEI) and its relationship to formation cycling. Carbon 2016, 105, 52–76. [Google Scholar] [CrossRef]
- Keil, P.; Schuster, S.F.; Wilhelm, J.; Travi, J.; Hauser, A.; Karl, R.C.; Jossen, A. Calendar Aging of Lithium-Ion Batteries: I. Impact of the Graphite Anode on Capacity Fade. J. Electrochem. Soc. 2016, 163, A1872–A1880. [Google Scholar] [CrossRef]
- Sommer, L.W.; Raghavan, A.; Kiesel, P.; Saha, B.; Schwartz, J.; Lochbaum, A.; Ganguli, A.; Bae, C.J.; Alamgir, M. Monitoring of Intercalation Stages in Lithium-Ion Cells over Charge-Discharge Cycles with Fiber Optic Sensors. J. Electrochem. Soc. 2015, 162, A2664–A2669. [Google Scholar] [CrossRef]
- Smith, A.J.; Smith, S.R.; Byrne, T.; Burns, J.C.; Dahn, J.R. Synergies in Blended LiMn2O4and Li[Ni1/3Mn1/3Co1/3]O2 Positive Electrodes. J. Electrochem. Soc. 2012, 159, A1696–A1701. [Google Scholar] [CrossRef]
- Dubarry, M.; Anseán, D. Best practices for incremental capacity analysis. Front. Energy Res. 2022, 10, 1023555. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, L.; Zou, C.; Dorrell, D.D. State-of-health estimation for Li-ion batteries by combing the incremental capacity analysis method with grey relational analysis. J. Power Sources 2019, 410–411, 106–114. [Google Scholar] [CrossRef]
- Huang, M. Incremental Capacity Analysis-Based Impact Study of Diverse Usage Patterns on Lithium-Ion Battery Aging in Electrified Vehicles. Batteries 2019, 5, 59. [Google Scholar] [CrossRef]
- Feng, X.; Merla, Y.; Weng, C.; Ouyang, M.; He, X.; Liaw, B.Y.; Santhanagopalan, S.; Li, X.; Liu, P.; Lu, L.; et al. A reliable approach of differentiating discrete sampled-data for battery diagnosis. eTransportation 2020, 3, 100051. [Google Scholar] [CrossRef]
- Plattard, T.; Barnel, N.; Assaud, L.; Franger, S.; Duffault, J.M. Combining a Fatigue Model and an Incremental Capacity Analysis on a Commercial NMC/Graphite Cell under Constant Current Cycling with and without Calendar Aging. Batteries 2019, 5, 36. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Monem, M.; Gopalakrishnan, R.; Berecibar, M.; Nanini-Maury, E.; Omar, N.; van den Bossche, P.; Van Mierlo, J. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter. J. Power Sources 2018, 373, 40–53. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Cugnet, M.; Liaw, B.Y.; Gering, K.; Sazhin, S.; Jamison, D.; Michelbacher, C. Evaluation of commercial lithium-ion cells based on composite positive electrode for plug-in hybrid electric vehicle applications. Part I: Initial characterizations. J. Power Sources 2011, 196, 10328–10335. [Google Scholar] [CrossRef]
- Riviere, E.; Venet, P.; Sari, A.; Meniere, F.; Bultel, Y. LiFePO4 Battery State of Health Online Estimation Using Electric Vehicle Embedded Incremental Capacity Analysis. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015. [Google Scholar] [CrossRef]
- Han, X.; Feng, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A Comparative Study of Charging Voltage Curve Analysis and State of Health Estimation of Lithium-ion Batteries in Electric Vehicle. Automot. Innov. 2019, 2, 263–275. [Google Scholar] [CrossRef]
- Spitthoff, L.; Vie, P.J.; Wahl, M.S.; Wind, J.; Burheim, O.S. Incremental capacity analysis (dQ/dV) as a tool for analysing the effect of ambient temperature and mechanical clamping on degradation. J. Electroanal. Chem. 2023, 944, 117627. [Google Scholar] [CrossRef]
- Fly, A.; Chen, R. Rate dependency of incremental capacity analysis (dQ/dV) as a diagnostic tool for lithium-ion batteries. J. Energy Storage 2020, 29, 101329. [Google Scholar] [CrossRef]
- Schiffer, Z.J.; Cannarella, J.; Arnold, C.B. Strain Derivatives for Practical Charge Rate Characterization of Lithium Ion Electrodes. J. Electrochem. Soc. 2015, 163, A427–A433. [Google Scholar] [CrossRef]
- Tavassol, H.; Jones, E.M.C.; Sottos, N.R.; Gewirth, A.A. Electrochemical stiffness in lithium-ion batteries. Nat. Mater. 2016, 15, 1182–1187. [Google Scholar] [CrossRef]
- Lewerenz, M.; Dechent, P.; Sauer, D.U. Investigation of capacity recovery during rest period at different states-of-charge after cycle life test for prismatic Li(Ni1/3Mn1/3Co1/3)O2-graphite cells. J. Energy Storage 2019, 21, 680–690. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kropkowski, L.; Oestreich, T.; Li, F.; Burger, A.; Nedjalkov, A.; Würsig, A.; Schade, W. Quantification of Degradation Processes in Lithium-Ion Batteries Through Internal Strain Measurement with Fiber Bragg Grating Sensors. Batteries 2025, 11, 218. https://doi.org/10.3390/batteries11060218
Kropkowski L, Oestreich T, Li F, Burger A, Nedjalkov A, Würsig A, Schade W. Quantification of Degradation Processes in Lithium-Ion Batteries Through Internal Strain Measurement with Fiber Bragg Grating Sensors. Batteries. 2025; 11(6):218. https://doi.org/10.3390/batteries11060218
Chicago/Turabian StyleKropkowski, Leonard, Tim Oestreich, Fangqi Li, Alexandra Burger, Antonio Nedjalkov, Andreas Würsig, and Wolfgang Schade. 2025. "Quantification of Degradation Processes in Lithium-Ion Batteries Through Internal Strain Measurement with Fiber Bragg Grating Sensors" Batteries 11, no. 6: 218. https://doi.org/10.3390/batteries11060218
APA StyleKropkowski, L., Oestreich, T., Li, F., Burger, A., Nedjalkov, A., Würsig, A., & Schade, W. (2025). Quantification of Degradation Processes in Lithium-Ion Batteries Through Internal Strain Measurement with Fiber Bragg Grating Sensors. Batteries, 11(6), 218. https://doi.org/10.3390/batteries11060218





