State of Health Estimation for Lithium-Ion Batteries Based on Transition Frequency’s Impedance and Other Impedance Features with Correlation Analysis
Abstract
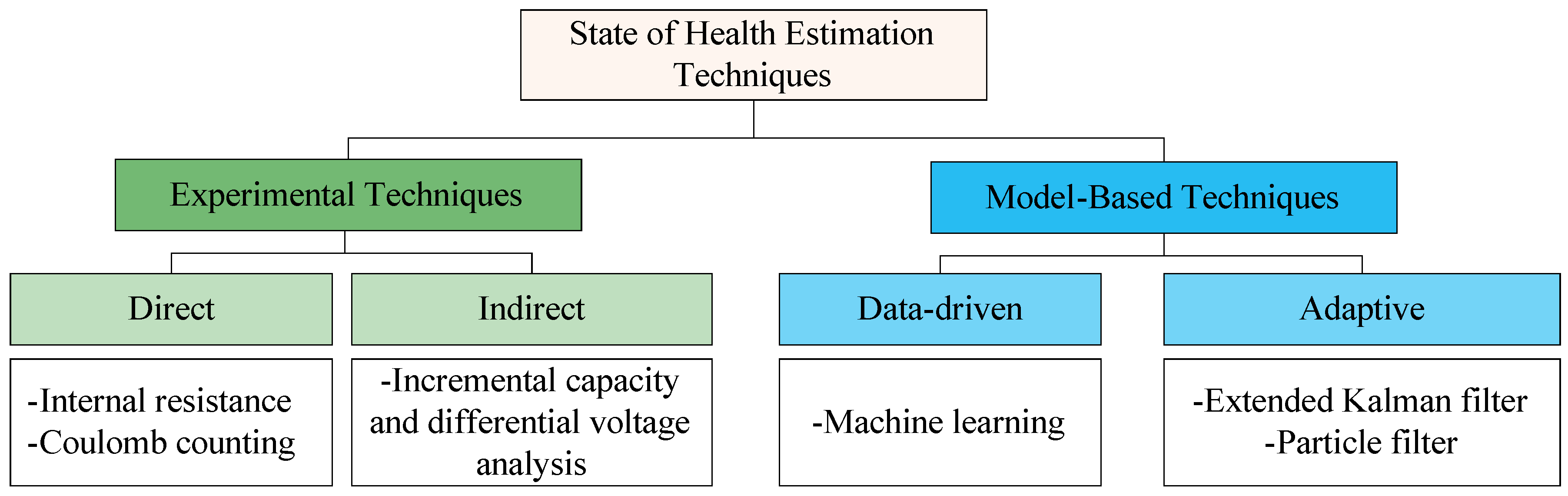
1. Introduction
- (1)
- Utilizing a broadband EIS curve to estimate the SOH value. The authors in [35] utilized the entire EIS curve of 60 frequency points (120 points of 60 real impedance values and 60 imaginary impedance values) to predict the SOH. However, this study was for 45 mAh coin cell batteries. Also, utilizing a high-dimensional input increases the computational cost.
- (2)
- Identifying specific points from the impedance curves to be utilized as SOH features:
- Non-fixed frequency points: features are identified from the pattern at which the impedance curves change at different SOH values, such as the minimum impedance magnitude [39], the impedance magnitude when the impedance phase is equal to 0° [33], and the value of the frequency at which the impedance phase is equal to 0° [40].
- Features from the Nyquist plot (the plot of the impedance real part against the impedance imaginary part): By studying how Nyquist plots change with SOH, various features can be extracted to be utilized for SOH estimation. For example, at the Nyquist plot’s peak point, the impedance real part, the impedance imaginary part, and the impedance vector amplitude were utilized for SOH estimation in [21].
- Features from the phase–magnitude plot: Another way to look at the battery’s impedance spectrum is to plot the phase against the magnitude [34]. From the phase–magnitude plot, some SOH features can be obtained, such as the differential impedance magnitude, which is the difference in the impedance magnitude at the valley and peak of the phase–magnitude plot [34].
- (3)
- Fitting the EIS curve to obtain values for the equivalent circuit model (ECM) parameters. For example, the EIS curve can be fit to obtain values for solid electrolyte interphase (SEI) resistance [41,42], diffusion constant phase elements [43], and charge transfer resistance [44]. The change in the ECM parameters is utilized for SOH estimation.
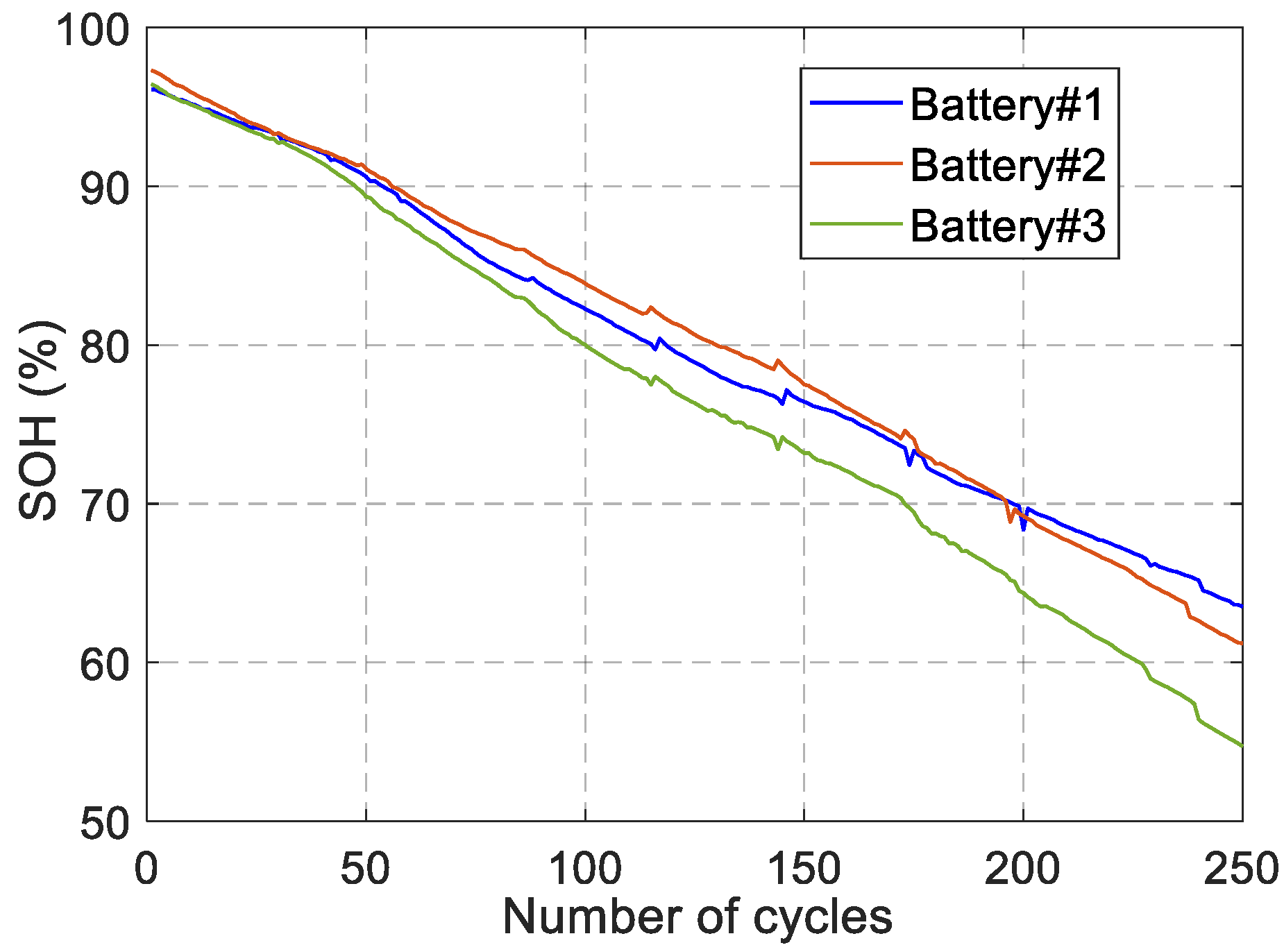
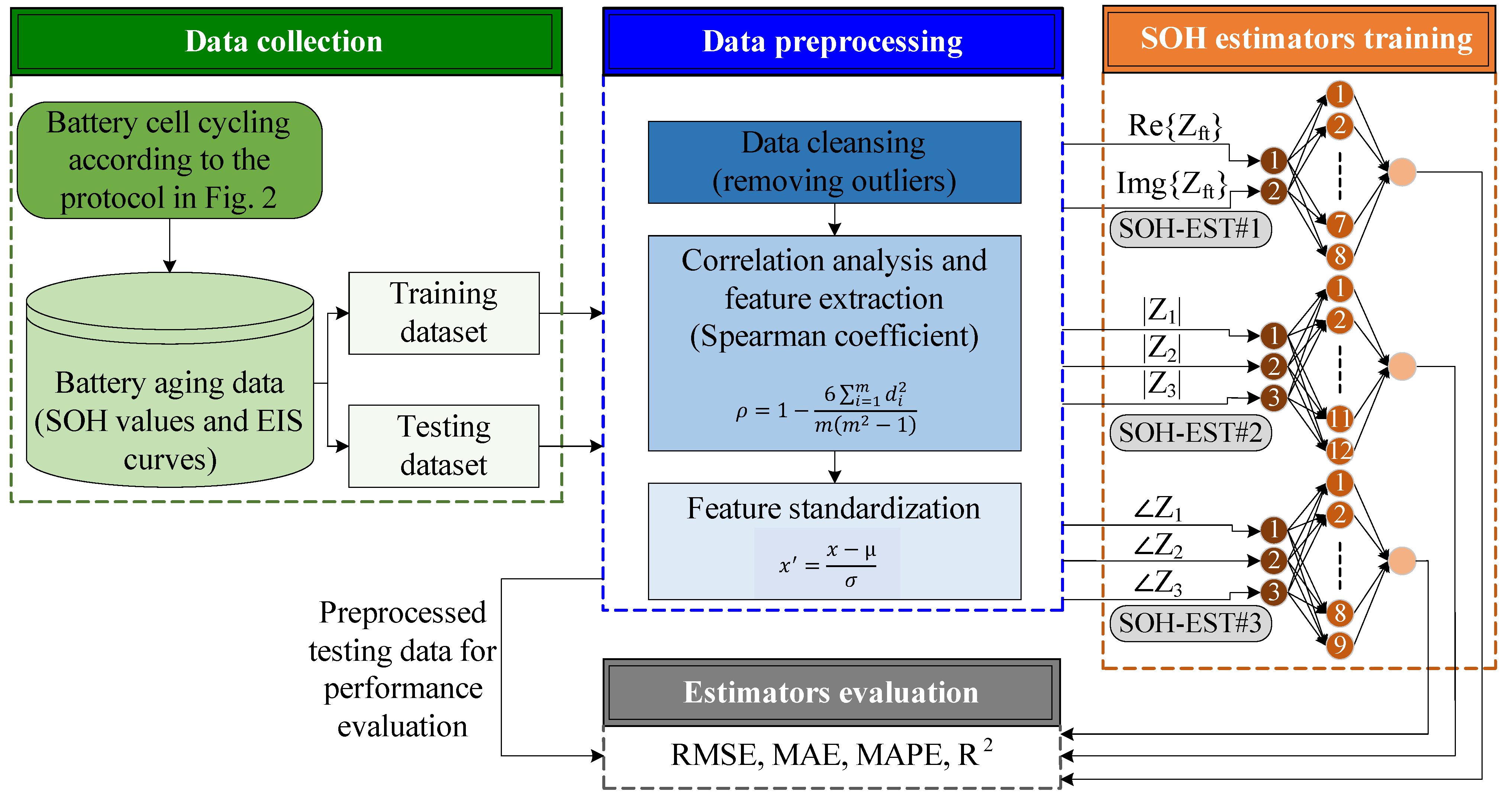
2. Battery Aging and Data Collection Protocol
3. SOH Indicators from the Electrochemical Impedance Spectrum
- (1)
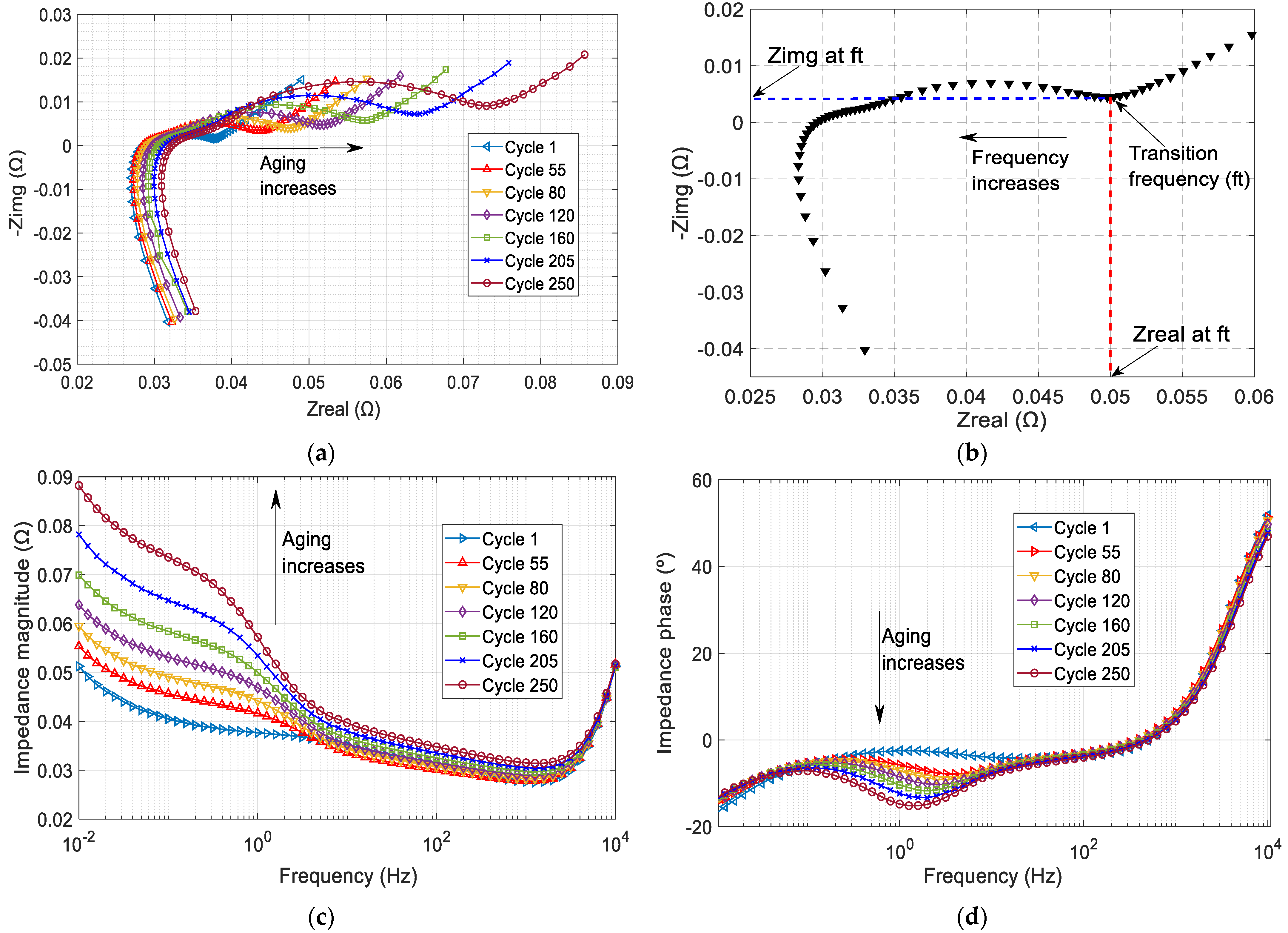
- SOHEST#1: This SOH estimator utilizes two indicators obtained from the complex impedance Nyquist plot. The two indicators are the impedance real part Re {Zft} and the impedance imaginary part Img {Zft} at the transition frequency ft. The transition frequency is the frequency at which the Nyquist plot moves from the diffusion region to the charge transfer region in the low-frequency range. Figure 4a shows sample Nyquist plots of BAT#1 at different aging cycles. As shown, as the battery ages (as the SOH value decreases), the Nyquist plot moves to the right (which means a larger Re {Zft}) and moves up (which means a larger Img {Zft}). A single Nyquist plot is shown in Figure 4b with the transition frequency ft, Re {Zft}, and Img {Zft} marked on the figure.
- (2)
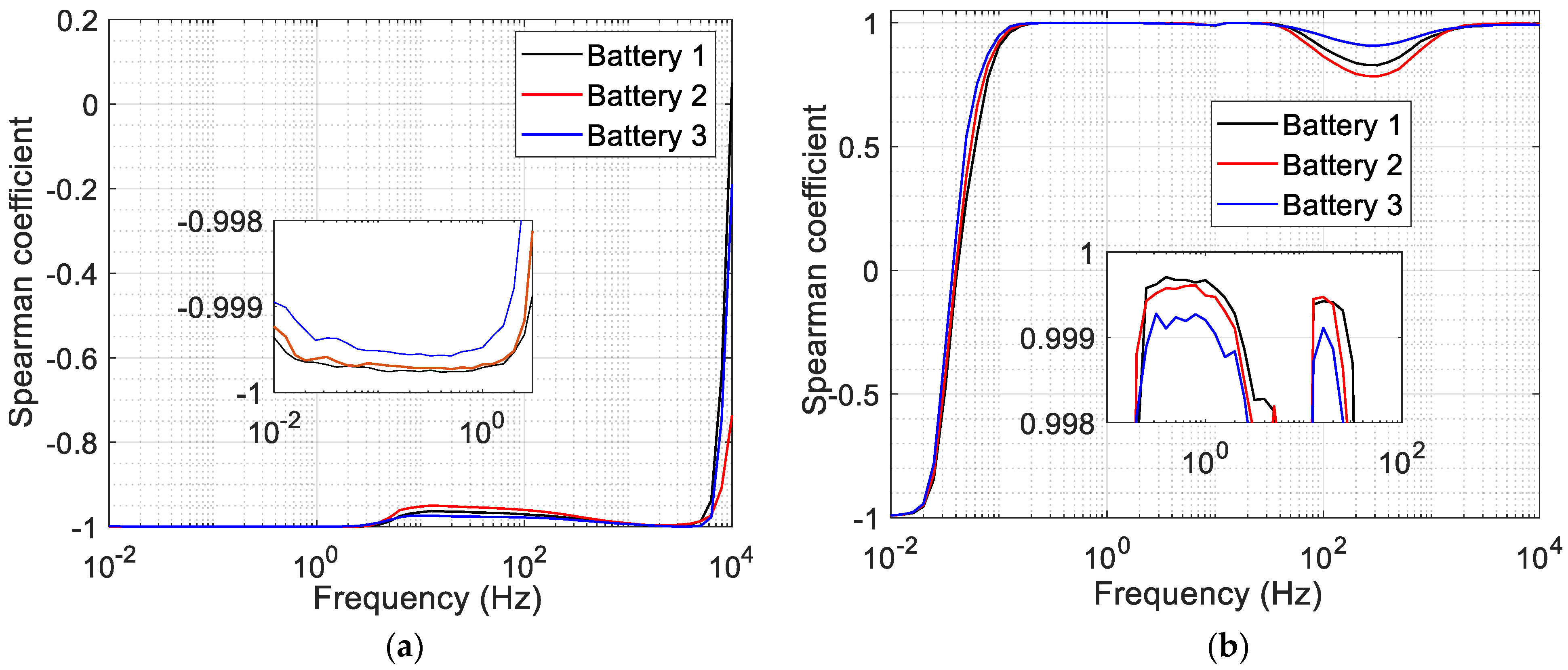
- SOHEST#2 and SOHEST#3: These estimators utilize certain impedance magnitude and phase values (respectively) within key frequency ranges in which the impedance magnitude and phase show strong correlations with the SOH value. From Figure 4c, it can be noticed that the impedance magnitude curves show a strong correlation with SOH values, especially in the low-frequency range. Therefore, impedance magnitude values at certain frequency points can be utilized for SOHEST#2. Similarly, from Figure 4d, it can be noticed that the impedance phase curves at different aging levels show a strong correlation with the SOH values in the low-frequency range. This means that impedance phase values at certain frequency points can be utilized for SOHEST#3.
4. Correlation Analysis
5. ANN-Based SOH Estimation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Manzetti, S.; Mariasiu, F. Electric vehicle battery technologies: From present state to future systems. Renew. Sustain. Energy Rev. 2015, 51, 1004–1012. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Li, P.; Lin, X.; Bian, X. Data-Driven Battery State of Health Estimation Based on Random Partial Charging Data. IEEE Trans. Power Electron. 2022, 37, 5021–5031. [Google Scholar] [CrossRef]
- Xia, Z.; Qahouq, J.A.A. Lithium-ion battery ageing behavior pattern characterization and state-of-health estimation using data-driven method. IEEE Access 2021, 9, 98287–98304. [Google Scholar]
- Lee, J.; Kwon, D.; Pecht, M.G. Reduction of li-ion battery qualification time based on prognostics and health management. IEEE Trans. Ind. Electron. 2018, 66, 7310–7315. [Google Scholar]
- Soyoye, B.D.; Bhattacharya, I.; Anthony Dhason, M.V.; Banik, T. State of Charge and State of Health Estimation in Electric Vehicles: Challenges, Approaches and Future Directions. Batteries 2025, 11, 32. [Google Scholar] [CrossRef]
- Nuroldayeva, G.; Serik, Y.; Adair, D.; Uzakbaiuly, B.; Bakenov, Z. State of Health Estimation Methods for Lithium-Ion Batteries. Int. J. Energy Res. 2023, 2023, 4297545. [Google Scholar]
- Akram, M.N.; Abdul-Kader, W. Repurposing Second-Life EV Batteries to Advance Sustainable Development: A Comprehensive Review. Batteries 2024, 10, 452. [Google Scholar] [CrossRef]
- Zhao, Y.; Qahouq, J.A.A. Second-Use Battery System for EV Charging Stations. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 2122–2126. [Google Scholar]
- Vignesh, S.; Che, H.S.; Selvaraj, J.; Tey, K.S.; Lee, J.W.; Shareef, H.; Errouissi, R. State of Health (SoH) estimation methods for second life lithium-ion battery—Review and challenges. Appl. Energy 2024, 369, 123542. [Google Scholar]
- Vermeer, W.; Mouli, G.R.C.; Bauer, P. A comprehensive review on the characteristics and modeling of lithium-ion battery aging. IEEE Trans. Transp. Electrif. 2021, 8, 2205–2232. [Google Scholar]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. ETransportation 2019, 1, 100005. [Google Scholar]
- Kumar, R.R.; Bharatiraja, C.; Udhayakumar, K.; Devakirubakaran, S.; Sekar, K.S.; Mihet-Popa, L. Advances in Batteries, Battery Modeling, Battery Management System, Battery Thermal Management, SOC, SOH, and Charge/Discharge Characteristics in EV Applications. IEEE Access 2023, 11, 105761–105809. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. Battery Health Monitoring and Remaining Useful Life Prediction Techniques: A Review of Technologies. Batteries 2025, 11, 31. [Google Scholar] [CrossRef]
- Yang, B.; Qian, Y.; Li, Q.; Chen, Q.; Wu, J.; Luo, E.; Xie, R.; Zheng, R.; Yan, Y.; Su, S. Critical summary and perspectives on state-of-health of lithium-ion battery. Renew. Sustain. Energy Rev. 2024, 190, 114077. [Google Scholar]
- Demirci, O.; Taskin, S.; Schaltz, E.; Demirci, B.A. Review of battery state estimation methods for electric vehicles-Part II: SOH estimation. J. Energy Storage 2024, 96, 112703. [Google Scholar]
- Yao, L.; Xu, S.; Tang, A.; Zhou, F.; Hou, J.; Xiao, Y.; Fu, Z. A review of lithium-ion battery state of health estimation and prediction methods. World Electr. Veh. J. 2021, 12, 113. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, C.; Jiang, J.; Zhang, W.; Zhang, L.; Wang, Y. Review on state-of-health of lithium-ion batteries: Characterizations, estimations and applications. J. Clean. Prod. 2021, 314, 128015. [Google Scholar]
- Guha, A.; Patra, A. State of health estimation of lithium-ion batteries using capacity fade and internal resistance growth models. IEEE Trans. Transp. Electrif. 2017, 4, 135–146. [Google Scholar]
- Zhang, C.; Liu, J.; Sharkh, S. Identification of dynamic model parameters for lithium-ion batteries used in hybrid electric vehicles. In Proceedings of the International Symposium on Electric Vehicles (ISEV), Beijing, China, 1 September 2009. [Google Scholar]
- Bao, Y.; Dong, W.; Wang, D. Online Internal Resistance Measurement Application in Lithium Ion Battery Capacity and State of Charge Estimation. Energies 2018, 11, 1073. [Google Scholar] [CrossRef]
- Fu, Y.; Xu, J.; Shi, M.; Mei, X. A fast impedance calculation-based battery state-of-health estimation method. IEEE Trans. Ind. Electron. 2021, 69, 7019–7028. [Google Scholar]
- Wang, D.; Bao, Y.; Shi, J. Online lithium-ion battery internal resistance measurement application in state-of-charge estimation using the extended Kalman filter. Energies 2017, 10, 1284. [Google Scholar] [CrossRef]
- Movassagh, K.; Raihan, A.; Balasingam, B.; Pattipati, K. A Critical Look at Coulomb Counting Approach for State of Charge Estimation in Batteries. Energies 2021, 14, 4074. [Google Scholar] [CrossRef]
- Schaltz, E.; Stroe, D.-I.; Nørregaard, K.; Ingvardsen, L.S.; Christensen, A. Incremental capacity analysis applied on electric vehicles for battery state-of-health estimation. IEEE Trans. Ind. Appl. 2021, 57, 1810–1817. [Google Scholar] [CrossRef]
- Xia, F.; Wang, K.; Chen, J. State of health and remaining useful life prediction of lithium-ion batteries based on a disturbance-free incremental capacity and differential voltage analysis method. J. Energy Storage 2023, 64, 107161. [Google Scholar] [CrossRef]
- Huang, Z.; Best, M.; Knowles, J.; Fly, A. Adaptive Piecewise Equivalent Circuit Model With SOC/SOH Estimation Based on Extended Kalman Filter. IEEE Trans. Energy Convers. 2023, 38, 959–970. [Google Scholar] [CrossRef]
- Andre, D.; Appel, C.; Soczka-Guth, T.; Sauer, D.U. Advanced mathematical methods of SOC and SOH estimation for lithium-ion batteries. J. Power Sources 2013, 224, 20–27. [Google Scholar] [CrossRef]
- Fang, F.; Ma, C.; Ji, Y. A Method for State of Charge and State of Health Estimation of Lithium Batteries Based on an Adaptive Weighting Unscented Kalman Filter. Energies 2024, 17, 2145. [Google Scholar] [CrossRef]
- Liu, D.; Yin, X.; Song, Y.; Liu, W.; Peng, Y. An On-Line State of Health Estimation of Lithium-Ion Battery Using Unscented Particle Filter. IEEE Access 2018, 6, 40990–41001. [Google Scholar] [CrossRef]
- Wu, T.; Liu, S.; Wang, Z.; Huang, Y. SOC and SOH joint estimation of lithium-ion battery based on improved particle filter algorithm. J. Electr. Eng. Technol. 2022, 17, 307–317. [Google Scholar] [CrossRef]
- Bi, J.; Zhang, T.; Yu, H.; Kang, Y. State-of-health estimation of lithium-ion battery packs in electric vehicles based on genetic resampling particle filter. Appl. Energy 2016, 182, 558–568. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, R.; Liu, X.; Zhang, C.; Sun, G.; Zhou, Y.; Yang, Z.; Liu, X.; Chen, S.; Dong, X.; et al. Advanced State-of-Health Estimation for Lithium-Ion Batteries Using Multi-Feature Fusion and KAN-LSTM Hybrid Model. Batteries 2024, 10, 433. [Google Scholar] [CrossRef]
- Al-Smadi, M.K.; Qahouq, J.A.A. SOH Estimation Algorithm and Hardware Platform for Lithium-ion Batteries. In Proceedings of the 2024 IEEE Vehicle Power and Propulsion Conference (VPPC), Washington DC, USA, 7–10 October 2024; pp. 1–5. [Google Scholar]
- Abu Qahouq, J. An Electrochemical Impedance Spectrum-Based State of Health Differential Indicator with Reduced Sensitivity to Measurement Errors for Lithium–Ion Batteries. Batteries 2024, 10, 368. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [PubMed]
- Xia, Z.; Qahouq, J.A.A. State of Health Estimation of Lithium-Ion Batteries Using Neuron Network and 1kHz Impedance Data. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA; 2020; pp. 1968–1972. [Google Scholar]
- Love, C.T.; Dubarry, M.; Reshetenko, T.; Devie, A.; Spinner, N.; Swider-Lyons, K.E.; Rocheleau, R. Lithium-ion cell fault detection by single-point impedance diagnostic and degradation mechanism validation for series-wired batteries cycled at 0 C. Energies 2018, 11, 834. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Woirgard, E.; Vinassa, J.M. Remaining useful life prediction of lithium batteries in calendar ageing for automotive applications. Microelectron. Reliab. 2012, 52, 2438–2442. [Google Scholar] [CrossRef]
- Xia, Z.; Qahouq, J.A.A. State-of-charge balancing of lithium-ion batteries with state-of-health awareness capability. IEEE Trans. Ind. Appl. 2020, 57, 673–684. [Google Scholar] [CrossRef]
- Xia, Z.; Qahouq, J.A.A. Adaptive and Fast State of Health Estimation Method for Lithium-ion Batteries Using Online Complex Impedance and Artificial Neural Network. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 3361–3365. [Google Scholar]
- Li, C.; Yang, L.; Li, Q.; Zhang, Q.; Zhou, Z.; Meng, Y.; Zhao, X.; Wang, L.; Zhang, S.; Li, Y. SOH estimation method for lithium-ion batteries based on an improved equivalent circuit model via electrochemical impedance spectroscopy. J. Energy Storage 2024, 86, 111167. [Google Scholar]
- Xiong, R.; Tian, J.; Mu, H.; Wang, C. A systematic model-based degradation behavior recognition and health monitoring method for lithium-ion batteries. Appl. Energy 2017, 207, 372–383. [Google Scholar]
- Luo, F.; Huang, H.; Ni, L.; Li, T. Rapid prediction of the state of health of retired power batteries based on electrochemical impedance spectroscopy. J. Energy Storage 2021, 41, 102866. [Google Scholar]
- Wang, X.; Wei, X.; Dai, H. Estimation of state of health of lithium-ion batteries based on charge transfer resistance considering different temperature and state of charge. J. Energy Storage 2019, 21, 618–631. [Google Scholar]
- LGChem. Product Specification: Rechargeable Lithium Ion Battery, Model: INR18650 MJ1 3500mAh; LGChem: Seoul, Republic of Korea, 2024. [Google Scholar]
- Admiral Instruments, “Squidstat Cycler—Base Model”. Available online: https://www.admiralinstruments.com/_files/ugd/dc5bf5_c4286dd7c5be411c9ad415c452fe5c88.pdf (accessed on 13 March 2025).
- Westerhoff, U.; Kroker, T.; Kurbach, K.; Kurrat, M. Electrochemical impedance spectroscopy based estimation of the state of charge of lithium-ion batteries. J. Energy Storage 2016, 8, 244–256. [Google Scholar]
- Messing, M.; Shoa, T.; Habibi, S. Electrochemical impedance spectroscopy with practical rest-times for battery management applications. IEEE Access 2021, 9, 66989–66998. [Google Scholar] [CrossRef]
- Li, Q.; Yi, D.; Dang, G.; Zhao, H.; Lu, T.; Wang, Q.; Lai, C.; Xie, J. Electrochemical Impedance Spectrum (EIS) Variation of Lithium-Ion Batteries Due to Resting Times in the Charging Processes. World Electr. Veh. J. 2023, 14, 321. [Google Scholar] [CrossRef]
- Spearman, C. The Proof and Measurement of Association Between Two Things; Appleton-Century-Crofts: East Norwalk, CT, USA, 1961; pp. 45–58. [Google Scholar]
- Berrar, D. Cross-Validation. In Encyclopedia of Bioinformatics and Computational Biology; Ranganathan, S., Gribskov, M., Nakai, K., Schönbach, C., Eds.; Academic Press: Oxford, UK, 2019; pp. 542–545. [Google Scholar]
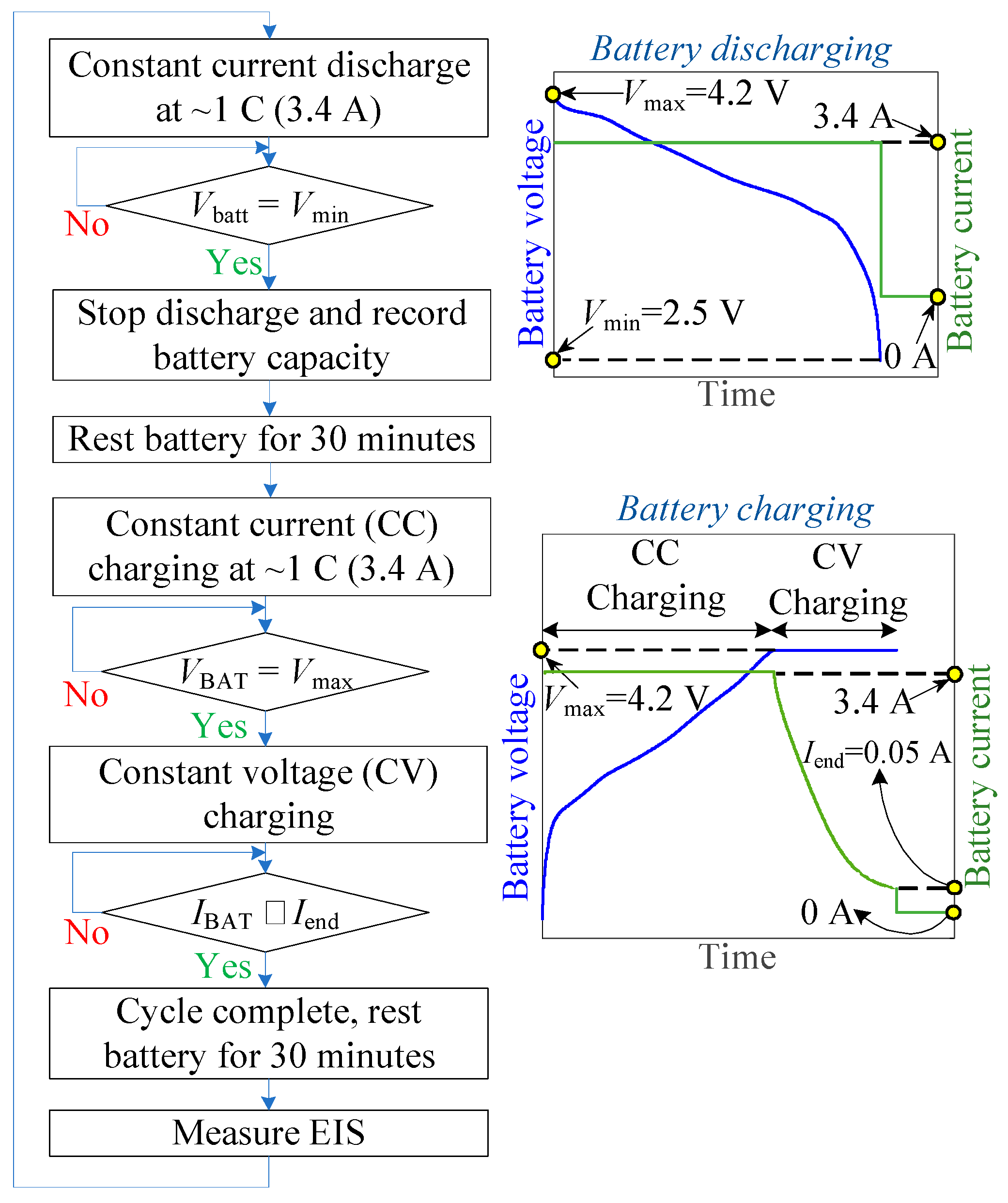

| Nominal capacity C | 3.5 Ah |
| Nominal voltage Vnom | 3.635 V |
| Minimum voltage Vmin | 2.50 V |
| Maximum voltage Vmax | 4.2 V |
| Maximum charging current | 3.4 A |
| Charing end current Iend | 0.05 A |
| Re {Zft} | Img {Zft} | |
|---|---|---|
| Battery#1 | −0.9996 | −0.9997 |
| Battery#2 | −0.9995 | −0.9996 |
| Battery#3 | −0.9993 | −0.9993 |
| SOH Estimator | SOH Estimation Model Designator | Training and Validation Data (Battery Numbers) | Performance Evaluation Data (Battery Number) | Frequency Points of Largest Correlation Coefficients |
|---|---|---|---|---|
| SOHEST#1 | SOHEST#1_12_3 | 1, 2 | 3 | Transition frequency ranges between 1.585 Hz and 0.079 Hz |
| SOHEST#1_13_2 | 1, 3 | 2 | ||
| SOHEST#1_23_1 | 2, 3 | 1 | ||
| SOHEST#2 | SOHEST#2_12_3 | 1, 2 | 3 | 0.079 Hz, 0.158 Hz, 0.2 Hz |
| SOHEST#2_13_2 | 1, 3 | 2 | 0.316 Hz, 0.398 Hz, 0.501 Hz | |
| SOHEST#2_23_1 | 2, 3 | 1 | 1.259 Hz, 1.585 Hz, 1.995 Hz | |
| SOHEST#3 | SOHEST#3_12_3 | 1, 2 | 3 | 12.59 Hz, 15.85 Hz, 19.95 Hz 12.59 Hz, 15.85 Hz, 19.95 Hz 12.59 Hz, 15.85 Hz, 19.95 Hz |
| SOHEST#3_13_2 | 1, 3 | 2 | ||
| SOHEST#3_23_1 | 2, 3 | 1 |
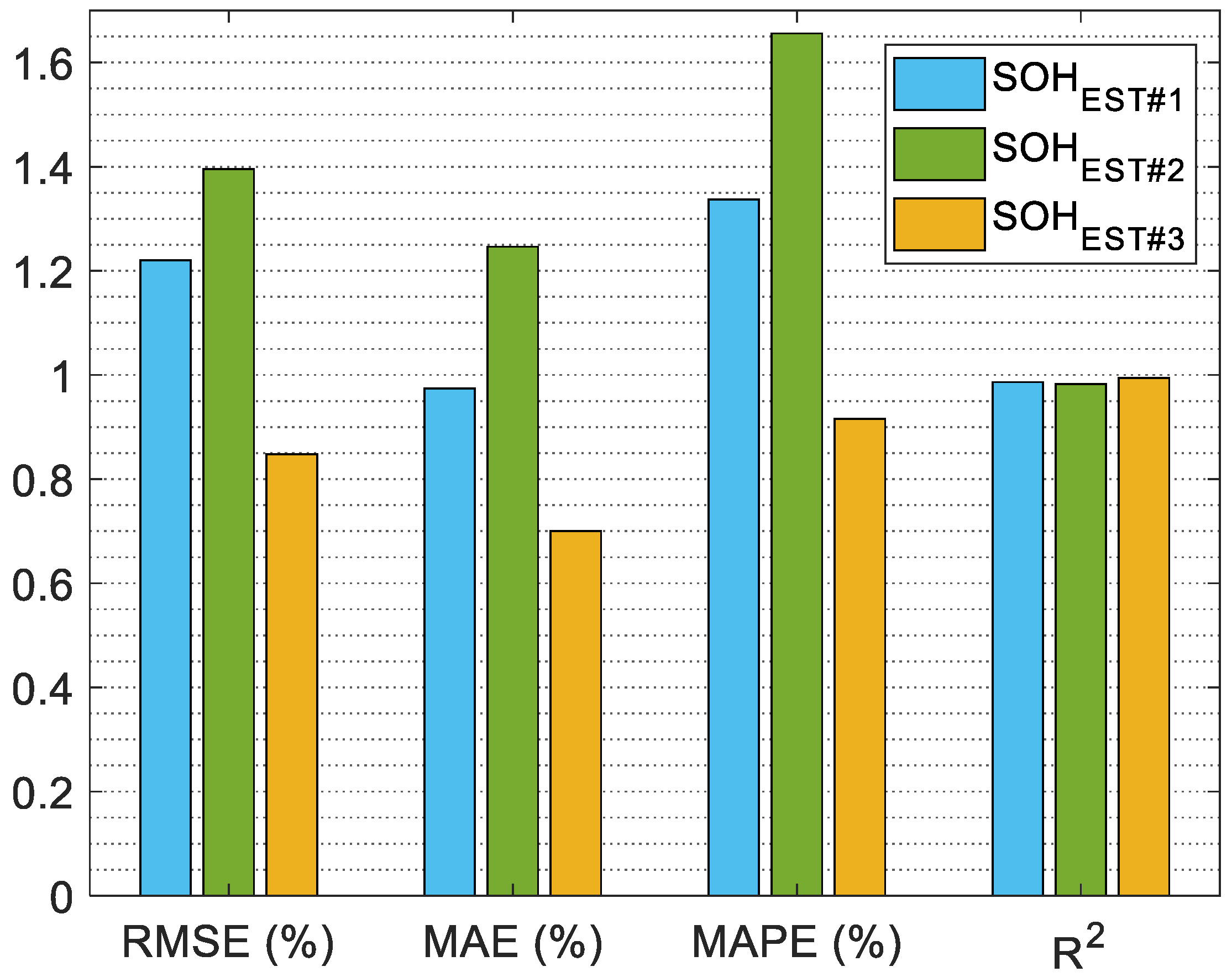
| SOH Estimator | SOH Estimation Model Designator | RMSE (%) | MAE (%) | MAPE (%) | R2 |
|---|---|---|---|---|---|
| SOHEST#1 | SOHEST#1_12_3 | 1.76 | 1.30 | 1.94 | 0.978 |
| SOHEST#1_13_2 | 1.24 | 1.08 | 1.39 | 0.986 | |
| SOHEST#1_23_1 | 0.67 | 0.54 | 0.68 | 0.995 | |
| Average | 1.22 | 0.97 | 1.34 | 0.986 | |
| SOHEST#2 | SOHEST#2_12_3 | 1.18 | 0.98 | 1.34 | 0.990 |
| SOHEST#2_13_2 | 1.40 | 1.29 | 1.66 | 0.986 | |
| SOHEST#2_23_1 | 1.60 | 1.47 | 1.94 | 0.973 | |
| Average | 1.39 | 1.25 | 1.55 | 0.983 | |
| SOHEST#3 | SOHEST#3_12_3 | 0.98 | 0.81 | 0.76 | 0.993 |
| SOHEST#3_13_2 | 0.74 | 0.60 | 0.90 | 0.996 | |
| SOHEST#3_23_1 | 0.82 | 0.69 | 0.98 | 0.993 | |
| Average | 0.85 | 0.70 | 0.88 | 0.994 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Smadi, M.K.; Abu Qahouq, J.A. State of Health Estimation for Lithium-Ion Batteries Based on Transition Frequency’s Impedance and Other Impedance Features with Correlation Analysis. Batteries 2025, 11, 133. https://doi.org/10.3390/batteries11040133
Al-Smadi MK, Abu Qahouq JA. State of Health Estimation for Lithium-Ion Batteries Based on Transition Frequency’s Impedance and Other Impedance Features with Correlation Analysis. Batteries. 2025; 11(4):133. https://doi.org/10.3390/batteries11040133
Chicago/Turabian StyleAl-Smadi, Mohammad K., and Jaber A. Abu Qahouq. 2025. "State of Health Estimation for Lithium-Ion Batteries Based on Transition Frequency’s Impedance and Other Impedance Features with Correlation Analysis" Batteries 11, no. 4: 133. https://doi.org/10.3390/batteries11040133
APA StyleAl-Smadi, M. K., & Abu Qahouq, J. A. (2025). State of Health Estimation for Lithium-Ion Batteries Based on Transition Frequency’s Impedance and Other Impedance Features with Correlation Analysis. Batteries, 11(4), 133. https://doi.org/10.3390/batteries11040133









