Abstract
Accurate estimation of the capacity of lithium-ion batteries is crucial for battery management and secondary utilization, which can ensure the healthy and efficient operation of the battery system. In this paper, we propose multiple machine learning algorithms to estimate the capacity using the incremental capacity (IC) curve features, including the adaptive moment estimation (Adam) model, root mean square propagation (RMSprop) model, and support vector regression (SVR) model. The Kalman filter algorithm is first used to construct the IC curve, and the peak and corresponding voltages correlated with battery life were analyzed and extracted as capacity estimation features. The three models were then used to learn the relationship between aging features and capacity. Finally, the lithium-ion battery cycle aging data were used to validate the capacity estimation performance of the three proposed machine learning models. The results show that the Adam model performs better than the other two models, balancing efficiency and accuracy in the capacity estimation of lithium-ion batteries throughout the entire lifecycle.
1. Introduction
In recent years, with the depletion of traditional fossil fuels and environmental degradation, energy conservation and environmental protection are the themes of the times. Currently, seeking safe, clean, and efficient energy conversion and storage technology is a research hotspot in science and technology [1,2,3]. The lithium-ion battery is a kind of energy storage and conversion carrier. With the advantages of large capacity, high operating voltage, large specific energy, long cycle life, good safety performance, small self-discharge, and fast charging, its application is expected to penetrate the fields of new energy vehicles and grid energy storage [4,5]. However, the lithium-ion battery is a dynamic and time-varying electrochemical system. It has nonlinear behavior and a complex internal reaction mechanism. The lithium-ion batteries undergo a continuous aging process once they are manufactured. If the capacity estimation of the battery is inaccurate, it may result in the inability to fully utilize the system’s functions or may lead to overcharging, over-discharging, or even fire accidents [6,7]. Therefore, effective evaluation of the capacity of lithium-ion batteries has become one of the core functions of the battery management system (BMS). It is of great significance to the reliability of energy systems, the use and maintenance of lithium-ion batteries, and safety.
The capacity of lithium-ion batteries can be evaluated by charge, internal resistance, cycle number, and peak power. Currently, the most commonly used estimation methods for battery life can be divided into two categories (model-based and data-driven methods), which have been extensively reviewed [8,9,10]. From the perspective of the battery model, due to its simple structure, low computational complexity, and ease of development, the equivalent-circuit model (ECM) is commonly used to estimate capacity and has achieved good results. For example, Yu et al. [11] achieved online estimation of battery capacity based on a second-order equivalent circuit model and Kalman filtering (KF) algorithm. Moreover, Zheng et al. [12] constructed a semi-empirical estimation model for battery capacity based on the Arrhenius model and KF algorithm. These KF-based methods can estimate battery SOC and SOH, but they heavily rely on ECM. When the battery ages, the parameters of the battery model drift, leading to a decrease in model and capacity estimation accuracy. However, due to the inability of ECM to consider the electrochemical parameters related to the battery aging mechanism in the model, the adaptability of ECM is poor during the battery cycling aging process, and large amounts of test data need to be used for calibration or correction to ensure the accuracy of battery capacity estimation under actual vehicle operating conditions.
Some scholars have quantitatively described the capacity degradation phenomenon caused by lithium deposition [13,14], SEI growth [15,16], and loss of active materials [17,18] in lithium-ion batteries by constructing electrochemical mechanism models, thus achieving estimations of battery capacity. For example, Wang et al. [19] analyzed the correlation between the cyclic voltammetry curve and increment capacity (IC) curve from the perspective of the internal chemical reaction mechanism of batteries, and proposed an online characterization method for battery aging based on the capacity increment curve. Atalay et al. [20] introduced the plating lithium mechanism in the pseudo-two-dimensional (P2D) model to study the effect of lithium plating on battery degradation and achieved capacity estimation in the long-term cycle modeling of the battery. Yang et al. [21,22] further combined the mechanism model with the thermodynamic behavior of batteries and constructed an electrochemical model that considers the influence of temperature field changes on internal reaction kinetics, thereby improving the simulation accuracy of the electrochemical model for temperature and aging processes. However, the construction of electrochemical models requires a deep understanding of the electrochemical processes and aging mechanisms of batteries, as well as a large amount of electrochemical testing and analysis work, to achieve accurate model construction. This is not easily achieved for capacity estimation in engineering applications such as electric vehicles and energy storage.
In recent years, with the development of computer and artificial intelligence technology, machine learning models have become increasingly popular because they do not require pre-defined complex mathematical, physical, or electrochemical models and can effectively handle nonlinear problems of battery aging [23,24]. For example, Fan et al. [25] established a basic bidirectional Long Short-Term Memory model and estimated the capacity and SOH of retired batteries based on the real part and amplitude features of electrochemical impedance spectroscopy (EIS). Liu et al. [26] used the Gaussian Process Regression (GPR) model to construct the mapping relationship between battery capacity, storage temperature, and state of charge and predicted battery life using nine different storage battery calendar-aging datasets. Similarly, Li et al. [27] proposed a method for short-term battery health status estimation and long-term remaining service life prediction based on the GPR model under a multi-time scale framework. However, the above machine learning methods heavily rely on the quality of feature selection. Recently, some scholars have proposed battery capacity estimation methods based on deep learning algorithms, such as Long Short-Term Memory (LSTM) [28], Convolutional Neural Networks (CNN) [29], Support Vector Machines [30], Random Forests [31], and others. Tian et al. [32] proposed a semi-supervised adversarial deep learning (SADL) method for lithium-ion battery capacity estimation, which is also a Deep Transfer Convolutional Neural Network (DTCNN) battery capacity estimation model based on IC features. Han et al. [33] proposed a deep transfer learning method that utilizes IC features. Zhang et al. [34] proposed an accurate estimation of battery capacity based on residual convolutional neural networks using only small pieces of raw measurement data, and the proposed model was validated using a common battery degradation dataset. Nagulapati et al. [35] studied battery capacity and health state estimation methods based on support vector machine (SVM) models and further compared the prediction accuracy of single-sensor and multi-sensor data. Lin et al. [36] proposed a SOH estimation method based on the fusion of annealing algorithm and support vector regression (SVR). Tian et al. [37] proposed a novel SOH estimation method using SVR based on the strong relationship between the differential temperature curves during constant charging and the SOH. Although these methods can extract features from raw data without additional processing, unfortunately, these deep learning methods consume huge amounts of computer memory space and computing resources and are not suitable for application in real vehicles and energy storage scenarios. Meanwhile, these methods do not take into account the aging mechanism of batteries. The above models and deep learning methods are not suitable for deployment and application in real electric vehicles.
The paper addresses the current problem of insufficient consideration of battery aging mechanisms and high computational resource consumption based on complex machine learning models, which lead to poor interpretability of capacity estimation methods. In this paper, three different machine learning models are proposed to estimate the capacity of batteries in their full life. The values corresponding to the peak height and the voltage of the IC curve are selected as input values. The remaining capacity of the battery is used as the output value, and the Adam optimization algorithm is used to estimate the capacity of the lithium-ion battery. The main contents of this study are as follows:
(1) The Kalman filter algorithm was used to construct the IC curve, and the correlation analysis was carried out by incorporating the aging mechanism. The peak values and corresponding voltages of IC curves that were highly correlated with battery capacity were extracted as input features for machine learning models.
(2) We compared the estimation performance of multiple machine learning models with IC features, including the adaptive moment estimation (Adam) model, root mean square propagation (RMSprop) model, and support vector regression (SVR) model.
(3) Finally, the proposed method was verified on the NASA lithium-ion cycle aging dataset, and Adam optimization algorithm demonstrated the fastest training speed and best capacity estimation performance.
The rest of the paper is structured as follows. The data for model training and validation are detailed in Section 2. Subsequently, the IC curve construction and capacity estimation methods are introduced in Section 3. The verification results of the proposed capacity estimation methods are presented in Section 4. Finally, Section 5 concludes this article.
2. Data Introduction
The aging data of lithium-ion batteries in this paper come from the battery aging dataset named Battery Aging ARC-FY08Q4 in NASA’s public dataset. Its lithium-ion battery numbers are Cell #05, Cell #06, Cell #07, and Cell #18 and comprise cycle aging data of batteries under normal conditions. The positive material of these batteries is LiNi0.8Co0.15Al0.05O2, and the negative electrode is graphite. The rated capacity is 2 Ah. The experimental temperature is 24 °C. The specific experimental steps are as follows: During the charging process, the lithium-ion battery is charged at a constant current of 1.5 A after the voltage rises to 4.2 V while keeping the voltage constant. Charging is continued and then stopped until the current drops to 20 mA. During discharge, the discharge current is 2 A. Four lithium-ion batteries are discharged to different cut-off voltages. Cell #05, Cell #06, Cell #07, and Cell #18 have discharge cut-off voltages of 2.7 V, 2.5 V, 2.2 V, and 2.5 V, respectively. One charging process and one discharging process constitute a complete cycle experiment.
3. Methods
3.1. Incremental Capacity Curve Acquisition
IC curves are currently widely used in the aging analysis of lithium-ion batteries. In the form of differential equations, the charging curve is transformed into an IC curve with more information [38]. To further extract the aging characteristics of the battery, the IC curve passes through the available equation, which is differentiated. The calculation method is divided into two categories: One is the charging capacity divided by equal time difference, named equal time interval (ETI). The other is the charging power divided by the terminal voltage change within the equal voltage difference, which is known as equal voltage interval (EVI) [39,40]. These are shown in (1) and (2):
where the charge capacity and cut-off voltage of lithium-ion battery are and , respectively. ic and t are the current and time in constant-current charging mode.
In practical application, when the sampling interval is small, the voltage difference in the denominator of Formula (1) is small. A small denominator will cause a huge fluctuation in the integral calculation results. The interval is small and the noise is large. With a too large interval, the features cannot be effectively extracted. Therefore, it is necessary to find an excellent filter for filtering. Common filtering algorithms are the Gaussian filter, maximum filter, particle filter, and Kalman filter. The first three filtering methods have high accuracy, but regarding computing resources and memory, they have high requirements for power consumption. The Kalman filter is a combination of optimal filtering theory and the state space idea, in which the optimal estimation in the sense of minimum variance for discrete stochastic linear systems is realized [41,42]. This method uses mean and variance to describe the noise and is calculated in recursive form. Therefore, the amount of calculation and memory space requirements are small and very suitable for online computing. Therefore, the Kalman filter is selected to clean and smooth the IC curve. The equation of state of the Kalman filter is as follows:
where is the noise pollution test value of , and Q and R are defined as the covariance of process noise and measurement noise. K is a Kalman gain, and P is defined as the estimated -covariance. The filtering algorithm based on the Equation (3) model can be expressed as follows:
3.2. Filtering Effect and Aging Introduction
This section selects a complete charging process of Cell #05, as shown in Figure 1a. A complete charging cycle includes a constant-current stage and a constant-voltage stage. The blue curve in Figure 1b is generated by calculating dQ/dV, but there is a lot of noise. We selected the Kalman filter with parameters of = 25 s, Q = 0.005%, and R = 0.000001% to process the original blue curve to obtain the red curve, where the noise is eliminated. Then, 168 cycles of charging voltage data for Cell #05 were extracted, and its IC curves were constructed using the same parameters, as shown in Figure 1c,d, respectively. With the continuous cycle experiment of the lithium-ion battery, the internal active material of the battery is gradually lost, leading to its capacity to decay continuously, the total charging time of the battery is gradually shortened, and the charging voltage curve shifts to the left, as shown in Figure 1c. For the IC curves, with the increase in the number of cycles, the IC curve gradually shrinks downwards.
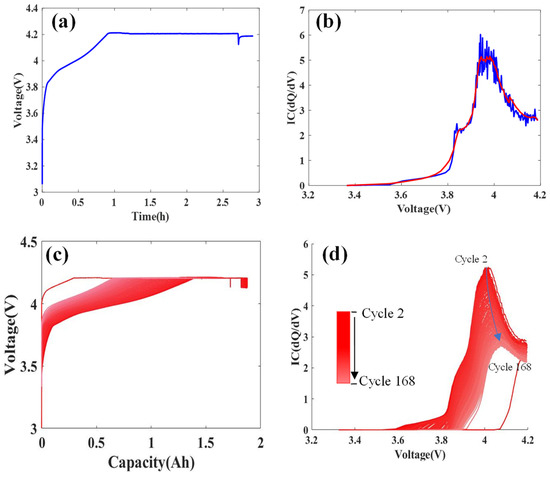
Figure 1.
IC curves under different cycles. (a) Constant-current and constant-voltage charging voltage curve; (b) IC curve; (c) charging voltage curves of battery cycle; (d) IC curves of battery cycle.
3.3. Correlation Model Analysis
To further verify the correlation accurately, we quantify the correlation. In this paper, the least squares algorithm is used to fit the peak height and peak position of the IC curve of Cell #05 with the capacity. Figure 2a,b give the calculation results of the correlation between the peak height and the peak position of the Cell # 05 IC curve and the capacity, respectively. It can be seen from Figure 2a that with the decrease in IC peak height, the battery capacity decreases. The peak height has a strong linear relationship with its capacity, (R2 = 0.99). The relative error is about 2%. The relationship between IC peak height and battery capacity is as follows:
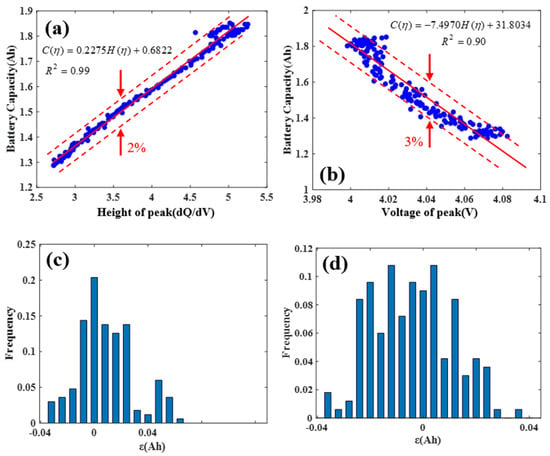
Figure 2.
The correlation between IC position features and capacity. (a) The correlation between the peak value of the IC curve and capacity. (b) The relationship between the voltage value of the IC curve and capacity. (c,d) Scatter distribution of the peak and voltage.
Figure 2b shows that as the peak position of the IC curve decreases, the battery capacity increases. The peak position has a slightly weaker correlation with its capacity than the peak height, but the correlation coefficient is greater than for the other factors (R2 = 0.90), and the relative error is about 3%. The peak position and battery capacity obey the following relationship:
Figure 2c,d show the scatter distribution of the peak height and peak position of the Cell #05 IC curve fitting with the capacity. The size of the error is determined by the distance from the point to the fitting line. The maximum value of the average distance is the gradient. It can be seen from Figure 2c that the scatter frequency of the IC curve peak height and capacity fitting obeys the normal distribution. There is a linear correlation between the peak height and peak position of the IC curve and the capacity. These phenomena indicate that, once the battery conforms to such a linear model, its electric quantity can be calculated quickly by voltage. Therefore, the two peak values and peak positions in the capacity increment curve are taken as the characteristic parameters of the IC curve and used as input variables in the subsequent lithium-ion battery capacity estimation model.
3.4. Adam Algorithm
The Adam algorithm was first proposed at the ICLR conference in 2015; it is an adaptive learning rate optimization algorithm [43,44], which is a widely used deep learning method. Compared with other gradient descent-based deep learning algorithms, the Adam algorithm adjusts the learning rate of different parameters by estimating the first and second moments of the gradient, introducing a constantly changing learning rate throughout the training process, thereby eliminating the need for one-dimensional search and significantly saving computational and storage resources. To date, the Adam algorithm has been widely applied in fields such as electronics and computer science [45,46], optoelectronic engineering [47,48], physical geography [49,50], and geotechnical engineering [51]. However, to the author’s knowledge, the application of the Adam algorithm in the battery capacity estimation problem has not been studied yet. The formula is as follows:
Learning rate : The decay rate of the first-order moment and second-order moment is , .
Hyperparameter ; initial weight parameter ; initialization iteration step .
We initialize the historical cumulative gradient ( represents zero vector), and initialize the historical cumulative gradient inner product .
While not meeting the stopping criteria do as follows:
Collect a small batch of k samples from the training set : .
Calculate the gradient information of the current iteration step parameter :
Iterative steps:
We update the historical cumulative gradient m using the index-weighted moving average method:
We update the historical cumulative gradient inner product R using the exponential weighted moving average method:
The deviation correction for historical cumulative gradient m is as follows:
We perform bias correction on the historical cumulative gradient inner product R:
We calculate the updated amount of the weight parameters for the current iteration step :
The application update is performed:
4. Results
4.1. Algorithm Verification
In this paper, four lithium-ion battery datasets (Cell #05, Cell #06, Cell #07, and Cell #18) published by NASA are used. Cell #05~Cell #07 are three batteries cycling 168 times, and Cell#18 cycles 132 times. After the battery cycle ends, the capacities of the four batteries are 1.32 Ah, 1.19 Ah, 1.43 Ah, and 1.33 Ah, respectively. It can be seen from Figure 3 that, as the number of cycles increases, the capacity of the four lithium-ion batteries gradually decreases but not constantly. There is a rebound phenomenon and random fluctuation components. At the same time, although the attenuation curve is similar, there are obvious differences in the state of fluctuation and speed during the capacity decay of the four batteries, which can provide support for the establishment and verification of the subsequent life estimation model.
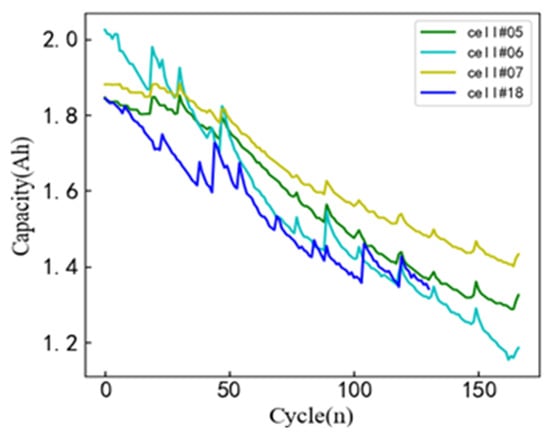
Figure 3.
NASA battery capacity degradation curve.
The aging features of batteries at peak values and peak positions extracted by Section 3 are analyzed, and the capacities of Cell #05, Cell #06, Cell #07, and Cell #18 were estimated online in real-time using the Adam, RMSProp, and SVR algorithms, in which Cell #18 was used for the training dataset and Cells #05–#07 were used for the validation dataset. The validated results show that the Adam, RMSProp, and SVR algorithms need to iterate 2000 times, 7000 times, and 8000 times, respectively. The loss values were 0.0027, 0.0054, and 0.061. The final diagnostic results and errors of the three machine learning algorithms are shown in Figure 4, Figure 5 and Figure 6, respectively. The green stars in these Figures represent the true capacity decay of the battery to the 80% SOH position.
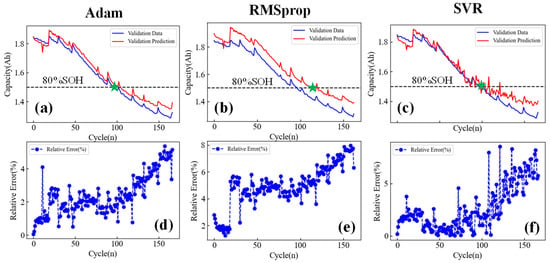
Figure 4.
Capacity estimation results of Cell #05. (a–c) Capacity estimation results of the Adam, RMSprop, and SVR algorithms. (d–f) Capacity estimation errors of the Adam, RMSprop, and SVR algorithms.
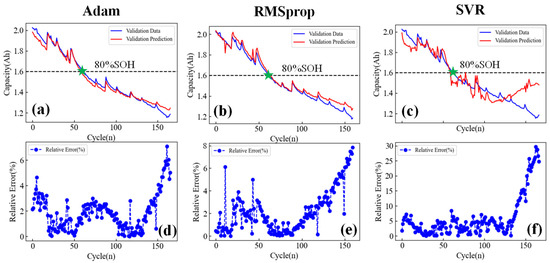
Figure 5.
Capacity estimation results of Cell #06. (a–c) Capacity estimation results of the Adam, RMSprop, and SVR algorithms. (d–f) Capacity estimation errors of the Adam, RMSprop, and SVR algorithms.
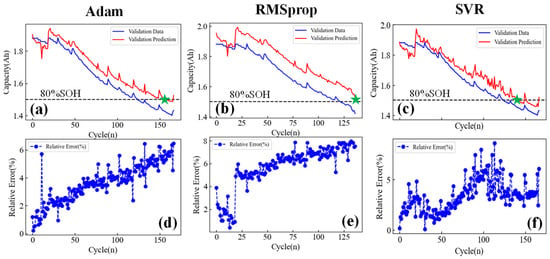
Figure 6.
Capacity estimation results of Cell #07. (a–c) Capacity estimation results of the Adam, RMSprop, and SVR algorithms. (d–f) Capacity estimation errors of the Adam, RMSprop, and SVR algorithms.
It can be seen from Figure 4, Figure 5 and Figure 6 that the three machine learning algorithms proposed can all achieve capacity estimation of lithium-ion batteries throughout the battery’s entire lifecycle. From the battery capacity estimation results in Figure 4, Figure 5 and Figure 6, it can be seen that the capacity estimation is more accurate in the early stages of battery decay. This may be because, in the early stages of battery aging, the nonlinearity of battery capacity decay is weak, while in the late stages of cycling, the battery shows an accelerated aging trend, resulting in a strong nonlinear trend and an increase in the capacity estimation error.
To better compare the differences in capacity estimation errors between different batteries and algorithms, we conducted a statistical analysis of the maximum estimation error results in Figure 4, Figure 5 and Figure 6, as shown in Table 1 and Table 2. Table 1 shows the estimation relative errors (RE) of capacity within the range of 80%~100% SOH. It can be seen from Table 1 that the maximum RE values of the Adam, RMSprop, and SVR algorithms are 5%, 8%, and 7%, respectively. Table 2 shows the estimation RE of capacity is within the range of 0%~80% SOH. It can be seen that the maximum RE values of the Adam, RMSprop, and SVR algorithms are 6.7%, 8.2%, and 5.1%, respectively. Comparing Table 1 and Table 2, the RE value of the Adam algorithm is small, and the estimation effect of the Adam algorithm is more stable than that of the two other algorithms. With strong anti-interference, the Adam algorithm has higher evaluation accuracy, and it shows good robustness under the aging characteristics of different linear correlations. In addition, it can be seen that we used the same capacity estimation model in the 80%~100% SOH and 0%~80% SOH ranges. However, the capacity estimation results in Table 2 are significantly lower than those in Table 1. This is mainly because, in the early stages of battery degradation from 0%~80% SOH, the battery capacity decay is slow, approximately explicit decay. When the battery life decays below 80% SOH, the internal active material decay mechanism of the battery changes, and significant nonlinear capacity decay characteristics appear, which leads to poor adaptability of the model and a decrease in the capacity estimation accuracy. This is also why replacement is needed when the capacity of the power battery decays to 80%; otherwise, the power battery decays to a nonlinear decay region, which results in a serious challenge to the battery management system.

Table 1.
Estimation results of capacity within the range of 80%~100% SOH.

Table 2.
Estimation results of capacity within the range of 0%~80% SOH.
Based on the working principles of the three models mentioned above, further theoretical analysis will be conducted here. The Adam optimization algorithm and RMSProp are both adaptive learning rate optimization algorithms, but Adam combines momentum and second-order moment estimation, usually providing better stability, so the Adam model exhibits faster capacity estimation speed and accuracy. SVR is a regression algorithm based on support vector machines, which constructs a separation hyperplane by finding support vectors to model the uncertain functional relationship between input IC features and battery capacity. However, the training process of SVR is relatively slow, especially when dealing with large-scale datasets, which is also the reason why the SVR model has the most iterations.
Comparing our diagnosis results with those of others, Tian et al. [32] conducted precise estimations with a root mean square error of approximately 2% based on the SADL model, and Han et al. [33] estimated the capacity of the Deep Transfer Convolutional Neural Network model to be approximately 0.0247. Moreover, some capacity estimation methods based on NASA’s public datasets have been proposed. For example, Huang et al. [52] used NASA’s public datasets to train and validate the temporal pattern attention mechanism and CNN-LSTM model, achieving an RMSE of 1.086%. Sun et al. [53] estimated SOH using gated recurrent units (GRUs) and validated it using a dataset published by NASA. The mean squared error (MSE) of their capacity estimation was 0.3%. Wang et al. [54] proposed an adaptive gated sequence network, recurrent neural network model, active state tracking Long Short-Term Memory model, and adaptive gating mechanism model, which were used to estimate battery capacity. The validation results of NASA’s publicly available dataset show that its absolute error is within 1%. However, these methods are all deep learning algorithms based on convolutional neural networks, which generate a large number of intermediate variables and parameters during network computation, making them unsuitable for application in real vehicle BMS. The deep learning-based optimizer Adam algorithm proposed in this paper can quickly converge the model through gradient optimization, which can significantly reduce its intermediate parameters. Therefore, the computational speed and memory dependency of this model are significantly lower than those of CNN models.
4.2. Lithium-Ion Battery Capacity Online Identification Scheme
From the perspective of the application of BMS, the future advanced BMS should have advantages such as high management accuracy, fast state estimation speed, strong robustness, and adaptability. To help achieve these goals, the capacity estimation method proposed in this article is summarized in Figure 7. The real-time voltage and current data of lithium-ion batteries are first obtained through voltage and current sampling sensors, and IC curves are constructed to extract the peak and valley features strongly related to battery aging. A small amount of peak and valley feature data is stored in the on-board memory. Then, the Adam model is used to estimate the battery capacity. In the future, transfer learning can also be introduced to train the Adam model with different types and regions of battery data to improve its adaptability and serve more battery management systems.
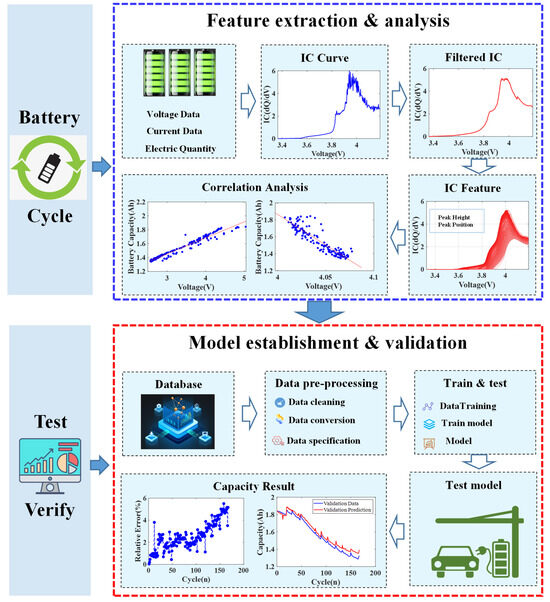
Figure 7.
Flowchart of identification of capacity estimation.
5. Conclusions
This paper proposes three different machine learning models that are widely used in the capacity prediction of lithium-ion batteries. Firstly, the Kalman filter algorithm was used to construct a smooth IC curve. The correlation between peak values and the corresponding voltage values of the IC curve and battery capacity were analyzed. The correlation coefficients are 99% and 90%, respectively. Then, the peak values and corresponding voltage values of the IC curve were selected to train the adaptive moment estimation (Adam) model, root mean square propagation (RMSprop) model, and support vector regression (SVR) model. The cycle life of the NASA lithium-ion battery dataset was tested and verified for its accuracy and robustness. The maximum error in capacity estimation for the Adam model within the 80–100% lifespan range was less than 5%. This method can automatically update the ownership weight, and it overcomes the problems of long calculation time and high calculation costs.
Author Contributions
Conceptualization and methodology: D.Q. and Y.L.; editing and project administration: D.Q.; Validation, writing and visualization: Y.L.; supervision and funding acquisition: D.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Sponsored by Shanghai Sailing Program under Grant (24YF2730300).
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gandoman, F.H.; Jaguemont, J.; Goutam, S.; Gopalakrishnan, R.; Firouz, Y.; Kalogiannis, T.; Omar, N.; Van Mierlo, J. Concept of reliability and safety assessment of lithium-ion batteries in electric vehicles: Basics, progress, and challenges. Appl. Energy 2019, 251, 113343. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, M.; Guo, P.; Gao, D.; Gao, Y. Numerical and Experimental-Based Framework for Fuel Cell System Fatigue Analysis in Frequency Domain. Machines 2025, 13, 18. [Google Scholar] [CrossRef]
- Qiao, D.; Wei, X.; Jiang, B.; Fan, W.; Gong, H.; Lai, X.; Zheng, Y.; Dai, H. Data-Driven Fault Diagnosis of Internal Short Circuit for Series-Connected Battery Packs Using Partial Voltage Curves. IEEE Trans. Ind. Inform. 2024, 20, 6751–6761. [Google Scholar] [CrossRef]
- Qiao, D.; Wei, X.; Jiang, B.; Fan, W.; Lai, X.; Zheng, Y.; Dai, H. Quantitative Diagnosis of Internal Short Circuit for Lithium-Ion Batteries Using Relaxation Voltage. IEEE Trans. Ind. Electron. 2024, 71, 13201–13210. [Google Scholar] [CrossRef]
- Qiao, D.; Wei, X.; Fan, W.; Jiang, B.; Lai, X.; Zheng, Y.; Tang, X.; Dai, H. Toward safe carbon-neutral transportation: Battery internal short circuit diagnosis based on cloud data for electric vehicles. Appl. Energy 2022, 317, 119168. [Google Scholar] [CrossRef]
- Gan, N.; Sun, Z.; Zhang, Z.; Xu, S.; Liu, P.; Qin, Z. Data-Driven Fault Diagnosis of Lithium-Ion Battery Overdischarge in Electric Vehicles. IEEE Trans. Power Electron. 2022, 37, 4575–4588. [Google Scholar] [CrossRef]
- Jin, Y.; Zheng, Z.K.; Wei, D.H.; Jiang, X.; Lu, H.F.; Sun, L.; Tao, F.B.; Guo, D.L.; Liu, Y.; Gao, J.F.; et al. Detection of Micro-Scale Li Dendrite via H2 Gas Capture for Early Safety Warning. Joule 2020, 4, 1714–1729. [Google Scholar] [CrossRef]
- Peng, J.; Meng, J.; Chen, D.; Liu, H.; Hao, S.; Sui, X.; Du, X. A Review of Lithium-Ion Battery Capacity Estimation Methods for Onboard Battery Management Systems: Recent Progress and Perspectives. Batteries 2022, 8, 229. [Google Scholar] [CrossRef]
- Dineva, A. Evaluation of Advances in Battery Health Prediction for Electric Vehicles from Traditional Linear Filters to Latest Machine Learning Approaches. Batteries 2024, 10, 356. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, R.; Yang, R.; Pecht, M.G. Online capacity estimation for lithium-ion batteries through joint estimation method. Appl. Energy 2019, 255, 113817. [Google Scholar] [CrossRef]
- Zheng, Y.; Qin, C.; Lai, X.; Han, X.; Xie, Y. A novel capacity estimation method for lithium-ion batteries using fusion estimation of charging curve sections and discrete Arrhenius aging model. Appl. Energy 2019, 251, 113327. [Google Scholar] [CrossRef]
- You, H.; Jiang, B.; Zhu, J.; Wang, X.; Shi, G.; Han, G.; Wei, X.; Dai, H. In-situ quantitative detection of irreversible lithium plating within full-lifespan of lithium-ion batteries. J. Power Sources 2023, 564, 232892. [Google Scholar] [CrossRef]
- Qiao, D.; Wei, X.; Zhu, J.; Wang, X.; Jiang, B.; Fan, W.; Wei, G.; Han, G.; Lai, X.; Zheng, Y.; et al. Unraveling the mechanism of non-uniform lithium deposition in liquid electrolytes. Cell Rep. Phys. Sci. 2024, 5, 101961. [Google Scholar] [CrossRef]
- Adenusi, H.; Chass, G.A.; Passerini, S.; Tian, K.V.; Chen, G. Lithium Batteries and the Solid Electrolyte Interphase (SEI)-Progress and Outlook. Adv. Energy Mater. 2023, 13, 2203307. [Google Scholar] [CrossRef]
- Zhu, J.; Darma, M.S.D.; Knapp, M.; Sorensen, D.R.; Heere, M.; Fang, Q.; Wang, X.; Dai, H.; Mereacre, L.; Senyshyn, A.; et al. Investigation of lithium-ion battery degradation mechanisms by combining differential voltage analysis and alternating current impedance. J. Power Sources 2020, 448, 227575. [Google Scholar] [CrossRef]
- Zhu, J.; Knapp, M.; Sorensen, D.R.; Heere, M.; Darma, M.S.D.; Mueller, M.; Mereacre, L.; Dai, H.; Senyshyn, A.; Wei, X.; et al. Investigation of capacity fade for 18650-type lithium-ion batteries cycled in different state of charge (SoC) ranges. J. Power Sources 2021, 489, 229422. [Google Scholar] [CrossRef]
- Jiang, B.; Zhu, J.; Wang, X.; Wei, X.; Shang, W.; Dai, H. A comparative study of different features extracted from electrochemical impedance spectroscopy in state of health estimation for lithium-ion batteries. Appl. Energy 2022, 322, 119502. [Google Scholar] [CrossRef]
- Wang, L.; Lu, D.; Song, M.; Zhao, X.; Li, G. Instantaneous estimation of internal temperature in lithium-ion battery by impedance measurement. Int. J. Energy Res. 2020, 44, 3082–3097. [Google Scholar] [CrossRef]
- Atalay, S.; Sheikh, M.; Mariani, A.; Merla, Y.; Bower, E.; Widanage, W.D. Theory of battery ageing in a lithium-ion battery: Capacity fade, nonlinear ageing and lifetime prediction. J. Power Sources 2020, 478, 229026. [Google Scholar] [CrossRef]
- Yang, X.-G.; Leng, Y.; Zhang, G.; Ge, S.; Wang, C.-Y. Modeling of lithium plating induced aging of lithium-ion batteries: Transition from linear to nonlinear aging. J. Power Sources 2017, 360, 28–40. [Google Scholar] [CrossRef]
- Yang, X.-G.; Wang, C.-Y. Understanding the trilemma of fast charging, energy density and cycle life of lithium-ion batteries. J. Power Sources 2018, 402, 489–498. [Google Scholar] [CrossRef]
- Liu, Q.; Shang, Z.; Lu, S.; Liu, Y.; Liu, Y.; Yu, S. Physics-guided TL-LSTM network for early-stage degradation trajectory prediction of lithium-ion batteries. J. Energy Storage 2025, 106, 114736. [Google Scholar] [CrossRef]
- Lu, S.; Gao, Z.-W.; Liu, Y. HFTL-KD: A new heterogeneous federated transfer learning approach for degradation trajectory prediction in large-scale decentralized systems. Control Eng. Pract. 2024, 153, 106098. [Google Scholar] [CrossRef]
- Fan, W.; Jiang, B.; Wang, X.; Yuan, Y.; Zhu, J.; Wei, X.; Dai, H. Enhancing capacity estimation of retired electric vehicle lithium-ion batteries through transfer learning from electrochemical impedance spectroscopy. Etransportation 2024, 22, 100362. [Google Scholar] [CrossRef]
- Liu, K.; Li, Y.; Hu, X.; Lucu, M.; Widanage, W.D. Gaussian Process Regression With Automatic Relevance Determination Kernel for Calendar Aging Prediction of Lithium-Ion Batteries. IEEE Trans. Ind. Inform. 2020, 16, 3767–3777. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z. Multi-time-scale framework for prognostic health condition of lithium battery using modified Gaussian process regression and nonlinear regression. J. Power Sources 2020, 467, 228358. [Google Scholar] [CrossRef]
- Kaur, K.; Garg, A.; Cui, X.; Singh, S.; Panigrahi, B.K. Deep learning networks for capacity estimation for monitoringSOHof Li-ion batteries for electric vehicles. Int. J. Energy Res. 2021, 45, 3113–3128. [Google Scholar] [CrossRef]
- Shen, S.; Sadoughi, M.; Chen, X.; Hong, M.; Hu, C. A deep learning method for online capacity estimation of lithium-ion batteries. J. Energy Storage 2019, 25, 100817. [Google Scholar] [CrossRef]
- Jiang, B.; Dai, H.; Wei, X.; Jiang, Z. Multi-kernel Relevance Vector Machine with Parameter Optimization for Cycling Aging Prediction of Lithium-ion Batteries. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 11, 175–186. [Google Scholar] [CrossRef]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.W.; Van Den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Yao, J.; Chang, Z.; Tian, J. Semi-supervised adversarial deep learning for capacity estimation of battery energy storage systems. Energy 2024, 294, 130882. [Google Scholar] [CrossRef]
- Yao, J.; Han, T. Data-driven lithium-ion batteries capacity estimation based on deep transfer learning using partial segment of charging/discharging data. Energy 2023, 271, 127033. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, G.; Zhou, B.; Chen, S.; Sun, Z.; Wang, Y.; Zhang, X. Rapid and flexible battery capacity estimation using random short-time charging segments based on residual convolutional networks. Appl. Energy 2023, 351, 121925. [Google Scholar] [CrossRef]
- Nagulapati, V.M.; Lee, H.; Jung, D.; Paramanantham, S.S.; Brigljevic, B.; Choi, Y.; Lim, H. A novel combined multi-battery dataset based approach for enhanced prediction accuracy of data driven prognostic models in capacity estimation of lithium ion batteries. Energy Ai 2021, 5, 100089. [Google Scholar] [CrossRef]
- Lin, M.; Yan, C.; Meng, J.; Wang, W.; Wu, J. Lithium-ion batteries health prognosis via differential thermal capacity with simulated annealing and support vector regression. Energy 2022, 250, 123829. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W. State-of-Health Estimation Based on Differential Temperature for Lithium Ion Batteries. IEEE Trans. Power Electron. 2020, 35, 10363–10373. [Google Scholar] [CrossRef]
- Tang, X.; Zou, C.; Yao, K.; Chen, G.; Liu, B.; He, Z.; Gao, F. A fast estimation algorithm for lithium-ion battery state of health. J. Power Sources 2018, 396, 453–458. [Google Scholar] [CrossRef]
- Jiang, B.; Dai, H.; Wei, X. Incremental capacity analysis based adaptive capacity estimation for lithium-ion battery considering charging condition. Appl. Energy 2020, 269, 115074. [Google Scholar] [CrossRef]
- Qiao, D.; Wang, X.; Lai, X.; Zheng, Y.; Wei, X.; Dai, H. Online quantitative diagnosis of internal short circuit for lithium-ion batteries using incremental capacity method. Energy 2022, 243, 123082. [Google Scholar] [CrossRef]
- Xie, J.; Wei, X.; Bo, X.; Zhang, P.; Chen, P.; Hao, W.; Yuan, M. State of charge estimation of lithium-ion battery based on extended Kalman filter algorithm. Front. Energy Res. 2023, 11, 012182. [Google Scholar] [CrossRef]
- Cui, Z.; Kang, L.; Li, L.; Wang, L.; Wang, K. A combined state-of-charge estimation method for lithium-ion battery using an improved BGRU network and UKF. Energy 2022, 259, 124933. [Google Scholar] [CrossRef]
- Yue, X.; Fu, Q.; Hu, H.; Wang, D. Hammerstein Model Based Battery SOC Estimation Considering Temperature Variation. J. Electrochem. Soc. 2024, 171, 030503. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, H.; Kang, L.; Zhang, Y.; Wang, L.; Wang, K. Prediction of Health Level of Multiform Lithium Sulfur Batteries Based on Incremental Capacity Analysis and an Improved LSTM. Prot. Control. Mod. Power Syst. 2024, 9, 21–31. [Google Scholar] [CrossRef]
- Reyad, M.; Sarhan, A.M.; Arafa, M. A modified Adam algorithm for deep neural network optimization. Neural Comput. Appl. 2023, 35, 17095–17112. [Google Scholar] [CrossRef]
- Zhang, W.; Niu, L.; Zhang, D.; Wang, G.; Farrukh, F.U.D.; Zhang, C. HW-ADAM: FPGA-Based Accelerator for Adaptive Moment Estimation. Electronics 2023, 12, 263. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, J.; Liu, W.; Li, J.; Huang, X.; Liu, L.; Liang, W.; Yu, C.; Li, F.; Li, Z. BGD-based Adam algorithm for time-domain equalizer in PAM-based optical interconnects. Opt. Lett. 2020, 45, 141–144. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, H.; Wei, J.; Liu, L.; Huang, X.; Gao, S.; Liu, W.; Li, J.; Yu, C.; Li, Z. Adaptive moment estimation for polynomial nonlinear equalizer in PAM8-based optical interconnects. Opt. Express 2019, 27, 32210–32216. [Google Scholar] [CrossRef]
- Bernal-Romero, M.; Iturraran-Viveros, U. Accelerating full-waveform inversion through adaptive gradient optimization methods and dynamic simultaneous sources. Geophys. J. Int. 2021, 225, 97–126. [Google Scholar] [CrossRef]
- Sun, J.; Niu, Z.; Innanen, K.A.; Li, J.; Trad, D.O. A theory-guided deep-learning formulation and optimization of seismic waveform inversion. Geophysics 2020, 85, R87–R99. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, R.; Chen, C.; Meng, F. Fast stability assessment of rock slopes subjected to flexural toppling failure using adaptive moment estimation (Adam) algorithm. Landslides 2022, 19, 2149–2158. [Google Scholar] [CrossRef]
- Huang, J.; He, T.; Zhu, W.; Liao, Y.; Zeng, J.; Xu, Q.; Niu, Y. A lithium-ion battery SOH estimation method based on temporal pattern attention mechanism and CNN-LSTM model. Comput. Electr. Eng. 2025, 122, 109930. [Google Scholar] [CrossRef]
- Sun, H.; Yang, D.; Du, J.; Li, P.; Wang, K. Prediction of Li-ion battery state of health based on data-driven algorithm. Energy Rep. 2022, 8, 442–449. [Google Scholar] [CrossRef]
- Wang, K.; Gao, Q.; Pang, X.; Li, H.; Liu, W. Estimating the Health State of Lithium-Ion Batteries Using an Adaptive Gated Sequence Network and Hierarchical Feature Construction. Batteries 2024, 10, 278. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).