Machine Learning-Assisted Design of Doping Strategies for High-Voltage LiCoO2: A Data-Driven Approach
Abstract
1. Introduction
2. Methods
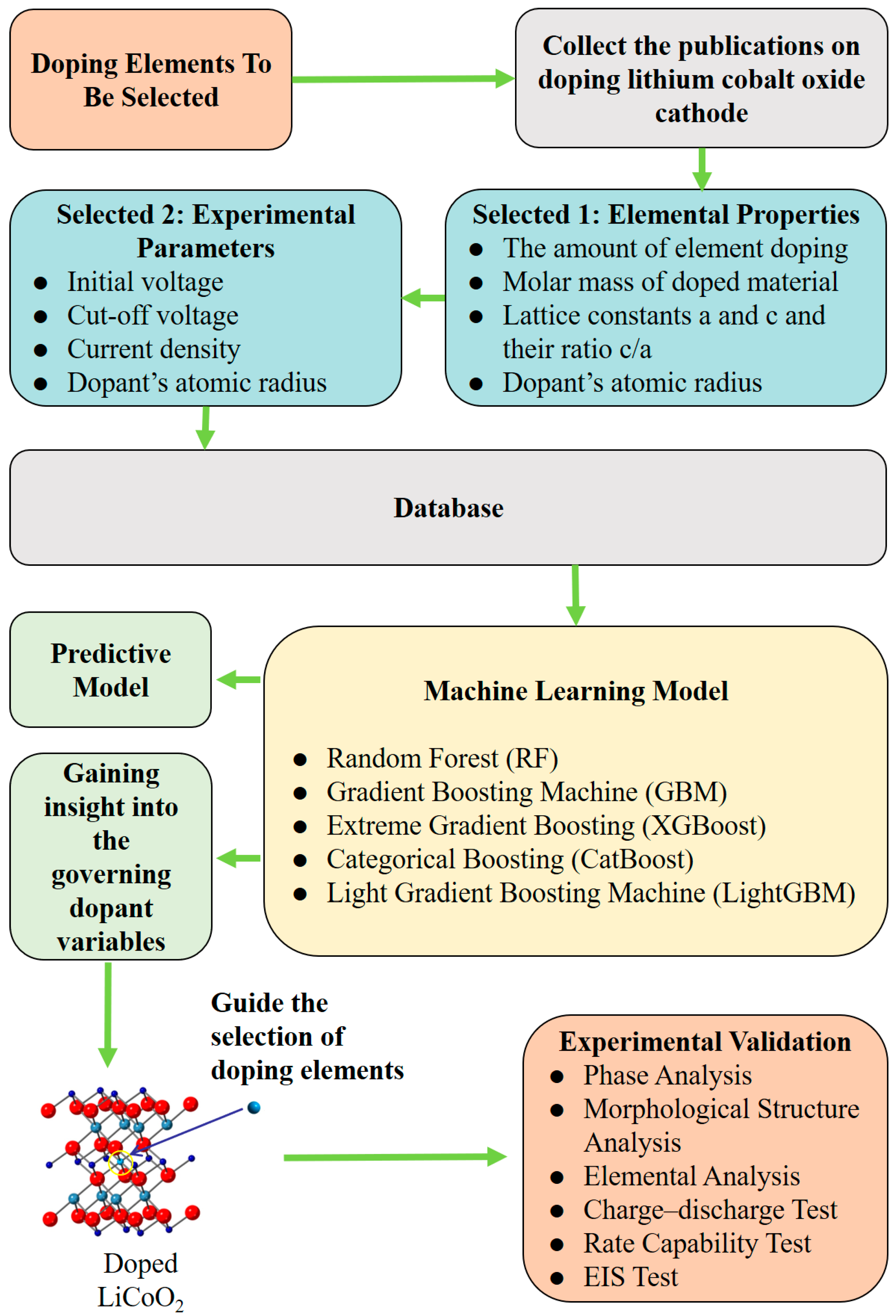
2.1. Data Collection and Features Selection
2.2. ML-Based Modeling
2.3. Analysis of Feature Importance and Design of Validation Experiment
2.4. Synthesis and Characterizations
3. Results and Discussion
3.1. Performance of ML-Based Models
3.2. Analysis of Feature Importance
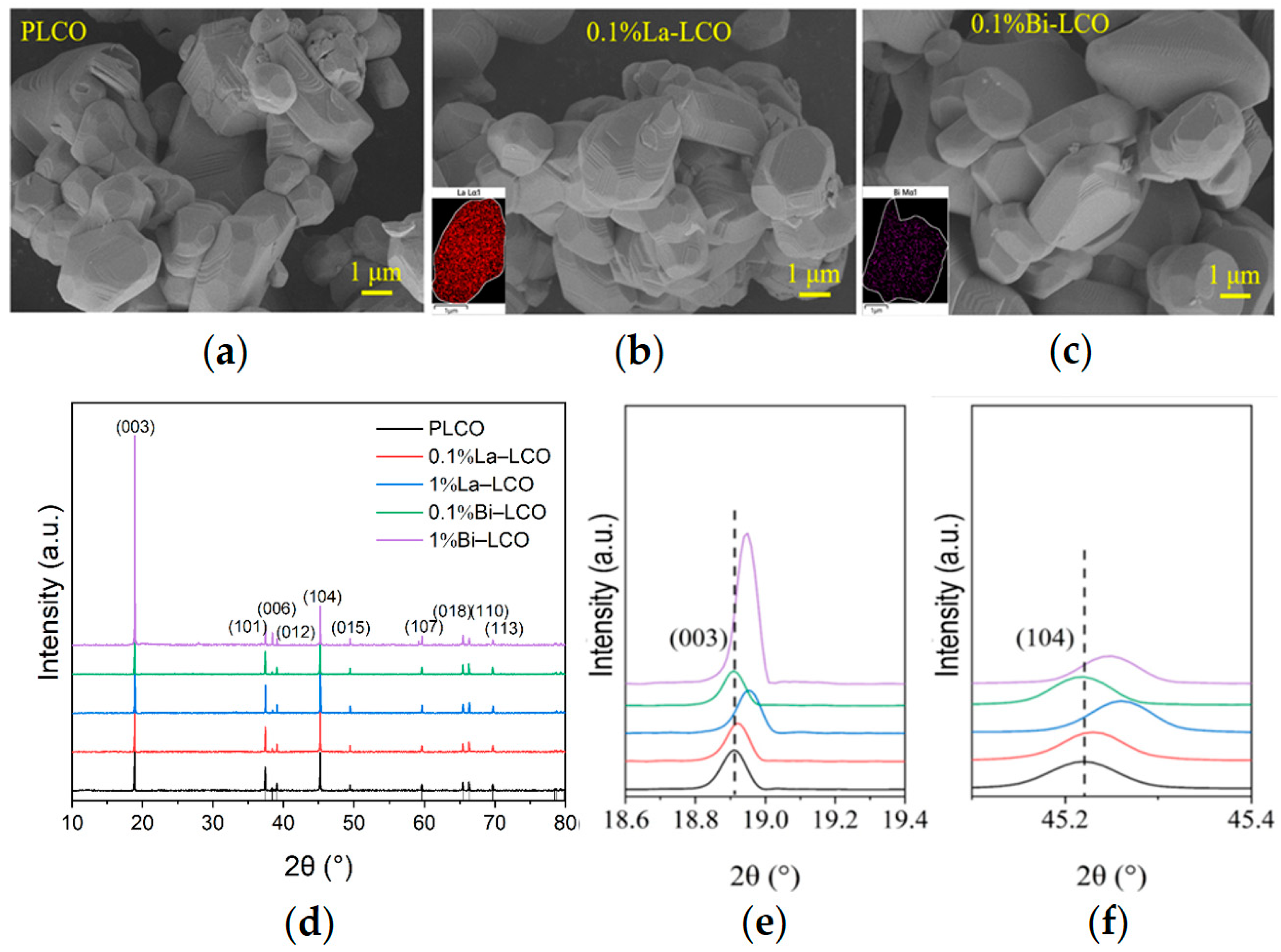
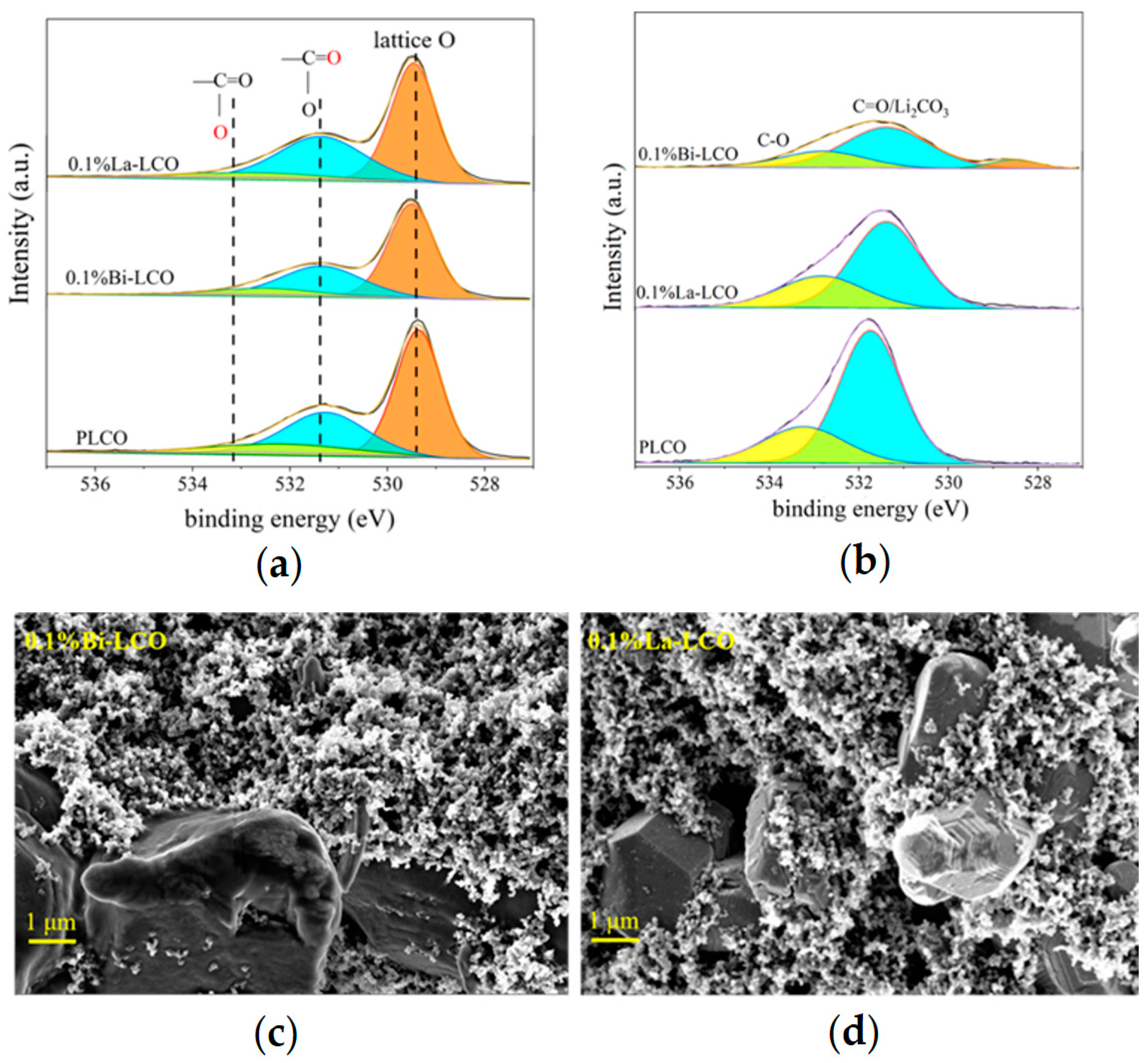
3.3. Experimentally Validation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dunn, B.; Kamath, H.; Tarascon, J.-M. Electrical Energy Storage for the Grid: A Battery of Choices. Science 2011, 334, 928–935. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Wan, J.; Xiang, Y.; Zhu, J.; Leng, Q.; Wang, M.; Xu, L.; Yang, Y. Recent advances and historical developments of high voltage lithium cobalt oxide materials for rechargeable Li-ion batteries. J. Power Sources 2020, 460, 228062. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, B.; Lu, Y. Progress and perspective of high-voltage lithium cobalt oxide in lithium-ion batteries. J. Energy Chem. 2022, 74, 283–308. [Google Scholar] [CrossRef]
- Amatucci, G.G.; Tarascon, J.M.; Klein, L.C. Cobalt dissolution in LiCoO2-based non-aqueous rechargeable batteries. Solid State Ion. 1996, 83, 167–173. [Google Scholar] [CrossRef]
- Sharifi-Asl, S.; Lu, J.; Amine, K.; Shahbazian-Yassar, R. Oxygen Release Degradation in Li-Ion Battery Cathode Materials: Mechanisms and Mitigating Approaches. Adv. Energy Mater. 2019, 9, 1900551. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, L.; Huang, X. Structural Design and Modification of Cathode Materials for Lithium Ion Batteries. Prog. Chem. 2011, 23, 284. [Google Scholar]
- Jena, A.; Lee, P.-H.; Pang, W.K.; Hsiao, K.-C.; Peterson, V.K.; Darwish, T.; Yepuri, N.; Wu, S.-H.; Chang, H.; Liu, R.-S. Monitoring the phase evolution in LiCoO2 electrodes during battery cycles using in-situ neutron diffraction technique. J. Chin. Chem. Soc. 2020, 67, 344–352. [Google Scholar] [CrossRef]
- Wang, L.; Chen, B.; Ma, J.; Cui, G.; Chen, L. Reviving lithium cobalt oxide-based lithium secondary batteries-toward a higher energy density. Chem. Soc. Rev. 2018, 47, 6505–6602. [Google Scholar] [CrossRef]
- Mou, S.; Huang, K.; Guan, M.; Ma, X.; Chen, J.s.; Xiang, Y.; Zhang, X. Reduced energy barrier for Li+ diffusion in LiCoO2 via dual doping of Ba and Ga. J. Power Sources 2021, 505, 230067. [Google Scholar] [CrossRef]
- Zhang, J.-N.; Li, Q.; Ouyang, C.; Yu, X.; Ge, M.; Huang, X.; Hu, E.; Ma, C.; Li, S.; Xiao, R.; et al. Trace doping of multiple elements enables stable battery cycling of LiCoO2 at 4.6 V. Nat. Energy 2019, 4, 594–603. [Google Scholar] [CrossRef]
- Cheng, Z.; Ma, X.; Mou, S.; Zhang, Y.; Wu, F.; Xiang, Y.; Zhang, X. The Synergetic Effects of Ru and Al Co-Doping for Improved Cyclability of LiCoO2 at High Voltages. Adv. Sustain. Syst. 2023, 2300325. [Google Scholar] [CrossRef]
- Chakraborty, A.; Dixit, M.; Aurbach, D.; Major, D.T. Predicting accurate cathode properties of layered oxide materials using the SCAN meta-GGA density functional. Npj Comput. Mater. 2018, 4, 60. [Google Scholar] [CrossRef]
- Hart, G.L.W.; Mueller, T.; Toher, C.; Curtarolo, S. Machine learning for alloys. Nat. Rev. Mater. 2021, 6, 730–755. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine learning in materials informatics: Recent applications and prospects. Npj Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, B.; Zou, X.; Li, Y.; Shi, S. Machine learning assisted materials design and discovery for rechargeable batteries. Energy Storage Mater. 2020, 31, 434–450. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, T.; Ju, W.; Shi, S. Materials discovery and design using machine learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Mao, J.; Miao, J.; Lu, Y.; Tong, Z. Machine learning of materials design and state prediction for lithium ion batteries. Chin. J. Chem. Eng. 2021, 37, 1–11. [Google Scholar] [CrossRef]
- Hautier, G.; Fischer, C.C.; Jain, A.; Mueller, T.; Ceder, G. Finding Nature’s Missing Ternary Oxide Compounds Using Machine Learning and Density Functional Theory. Chem. Mater. 2010, 22, 3762–3767. [Google Scholar] [CrossRef]
- Tao, K.; Wang, Z.; Han, Y.; Li, J. Rapid discovery of inorganic-organic solid composite electrolytes by unsupervised learning. Chem. Eng. J. 2023, 454, 140151. [Google Scholar] [CrossRef]
- Jalem, R.; Nakayama, M.; Kasuga, T. An efficient rule-based screening approach for discovering fast lithium ion conductors using density functional theory and artificial neural networks. J. Mater. Chem. A 2014, 2, 720–734. [Google Scholar] [CrossRef]
- Wang, G.; Fearn, T.; Wang, T.; Choy, K.L. Machine-Learning Approach for Predicting the Discharging Capacities of Doped Lithium Nickel-Cobalt-Manganese Cathode Materials in Li-Ion Batteries. ACS Cent. Sci. 2021, 7, 1551–1560. [Google Scholar] [CrossRef] [PubMed]
- Balachandran, P.V.; Theiler, J.; Rondinelli, J.M.; Lookman, T. Materials Prediction via Classification Learning. Sci. Rep. 2015, 5, 13285. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Guo, H.; Wang, Q.; Stuke, A.; Urban, A.; Artrith, N. Accelerated Atomistic Modeling of Solid-State Battery Materials With Machine Learning. Front. Energy Res. 2021, 9, 695902. [Google Scholar] [CrossRef]
- Sendek, A.D.; Cubuk, E.D.; Antoniuk, E.R.; Cheon, G.; Cui, Y.; Reed, E.J. Machine Learning-Assisted Discovery of Solid Li-Ion Conducting Materials. Chem. Mater. 2018, 31, 342–352. [Google Scholar] [CrossRef]
- Tao, Q.; Xu, P.; Li, M.; Lu, W. Machine learning for perovskite materials design and discovery. Npj Comput. Mater. 2021, 7, 23. [Google Scholar] [CrossRef]
- Min, K.; Choi, B.; Park, K.; Cho, E. Machine learning assisted optimization of electrochemical properties for Ni-rich cathode materials. Sci. Rep. 2018, 8, 15778. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2017. [Google Scholar]
- Ou, X.; Luo, J.; Zhang, J.; Chen, C.-L.; Yu, J.; Hu, J.; Chang, C.K.; Moudrakovski, I.; Lau, V.W.h.; Zhao, R. Reversible Li Intercalation in Layered Cathodes Enabled by Dopant-Induced Medium-Range Orders. Chem. Mater. 2023, 35, 7273–7282. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, Y.; Fu, H.; Ou, M.; Hu, C.; Yu, S.; Hu, Z.; Chen, C.-T.; Jiang, G.; Gu, H.; et al. Mg-Pillared LiCoO2: Towards Stable Cycling at 4.6 V. Angew. Chem. Int. Ed. 2021, 60, 4682–4688. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, W.; Tang, Z. Pillared layered Li1 − 2xCaxCoO2 cathode materials obtained by cationic exchange under hydrothermal conditions. J. Power Sources 2008, 184, 557–561. [Google Scholar] [CrossRef]
- Zhao, L.; Yan, P.; Liu, T.; Wang, X.; Wang, Z.; Wu, C.; Bao, W.; Zhu, H.; Zhang, Y.; Xie, J. Temperature-Driven Anisotropic Mg2+ Doping for a Pillared LiCoO2 Interlayer Surface in High-Voltage Applications. ACS Appl. Mater. Interfaces 2023, 15, 33132–33139. [Google Scholar] [CrossRef]
- Kim, C.H.; Rim, Y.S.; Kim, D.L.; Kim, H.J. Combined effect of the large ionic radius and low electronegativity of lanthanum additive on solution-processed zinc–tin–oxide thin-film transistors. Thin Solid Film. 2013, 536, 291–294. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhang, X.; Zhang, S. Insight into the mechanism of Sb promoted Cu(In,Ga)Se2 formation. J. Solid State Chem. 2013, 204, 278–282. [Google Scholar] [CrossRef]
- Zhang, Z.; Meng, Y.; Xiao, D. Tri-sites co-doping: An efficient strategy towards the realization of 4.6 V-LiCoO2 with cyclic stability. Energy Storage Mater. 2023, 56, 443–456. [Google Scholar] [CrossRef]
- Dahéron, L.; Martinez, H.; Dedryvère, R.; Baraille, I.; Ménétrier, M.; Denage, C.; Delmas, C.; Gonbeau, D. Surface Properties of LiCoO2 Investigated by XPS Analyses and Theoretical Calculations. J. Phys. Chem. C 2009, 113, 5843–5852. [Google Scholar] [CrossRef]
- Lu, Y.C.; Mansour, A.N.; Yabuuchi, N.; Shao-horn, Y. Probing the Origin of Enhanced Stability of AlPO4 Nanoparticle Coated LiCoO2 during Cycling to High Voltages: Combined XRD and XPS Studies. Chem. Mater. 2009, 21, 4408–4424. [Google Scholar] [CrossRef]
- Qian, J.; Liu, L.; Yang, J.; Li, S.; Wang, X.; Zhuang, H.L.; Lu, Y. Electrochemical surface passivation of LiCoO2 particles at ultrahigh voltage and its applications in lithium-based batteries. Nat. Commun. 2018, 9, 4918. [Google Scholar] [CrossRef]
- Zhang, P.; Xie, C.; Han, G.; Zhu, Q.; Chen, L.; Jin, M.; Liu, Q.; Zhou, Y.; Sun, Q.; Xie, J. Stable cycling of LiCoO2 at 4.55 V enabled by combined Mg doping and surface coating of NASICON-type electrolyte. Mater. Today Nano 2021, 15, 100122. [Google Scholar] [CrossRef]
- Xu, L.; Wang, K.; Gu, F.; Li, T.; Wang, Z. Determining the intrinsic role of Mg doping in LiCoO2. Mater. Lett. 2020, 277, 128407. [Google Scholar] [CrossRef]
- Kim, S.; Yang, D.-h.; Sohn, J.-S.; Jung, Y.C. Resynthesis of LiCo1 − xMnxO2 as a cathode material for lithium secondary batteries. Met. Mater. Int. 2012, 18, 321–326. [Google Scholar] [CrossRef]
- Konar, R.; Maiti, S.; Shpigel, N.; Aurbach, D. Reviewing failure mechanisms and modification strategies in stabilizing high-voltage LiCoO2 cathodes beyond 4.55 V. Energy Storage Mater. 2023, 63, 103001. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, T.; Yu, Z.-E.; Lyu, Y.; Guo, B. Study on the effect of Ni and Mn doping on the structural evolution of LiCoO2 under 4.6 V high-voltage cycling. J. Alloys Compd. 2020, 842, 155827. [Google Scholar] [CrossRef]
- Alcántara, R.; Lavela, P.; Tirado, J.L.; Stoyanova, R.; Zhecheva, E. Structure and Electrochemical Properties of Boron-Doped LiCoO2. J. Solid State Chem. 1997, 134, 265–273. [Google Scholar] [CrossRef]
- Shim, J.-H.; Lee, J.; Han, S.Y.; Lee, S. Synergistic effects of coating and doping for lithium ion battery cathode materials: Synthesis and characterization of lithium titanate-coated LiCoO2 with Mg doping. Electrochim. Acta 2015, 186, 201–208. [Google Scholar] [CrossRef]
- Needham, S.A.; Wang, G.X.; Liu, H.K.; Drozd, V.A.; Liu, R.S. Synthesis and electrochemical performance of doped LiCoO2 materials. J. Power Sources 2007, 174, 828–831. [Google Scholar] [CrossRef]
- Jia, Z.; Yang, P.; Li, Y.; Gao, D.; Xia, J.; Yang, Y.-J.; Wang, X.; Yang, Y. Enhancing the Structural Stability of LiCoO2 at Elevated Voltage via High-Valence Sb Doping. ACS Appl. Energy Mater. 2024, 7, 4207–4215. [Google Scholar] [CrossRef]
- Sathiyamoorthi, R.; Chandrasekaran, R.; Gopalan, A.; Vasudevan, T. Synthesis and electrochemical performance of high voltage cycling LiCo0.8M0.2O2 (M = Mg, Ca, Ba) as cathode material. Mater. Res. Bull. 2008, 43, 1401–1411. [Google Scholar] [CrossRef]
- Koyama, Y.; Arai, H.; Tanaka, I.; Uchimoto, Y.; Ogumi, Z. First principles study of dopant solubility and defect chemistry in LiCoO2. J. Mater. Chem. A 2014, 2, 11235–11245. [Google Scholar] [CrossRef]
- Jin, Y.; Xu, S.; Li, Z.; Xu, K.; Ding, W.; Song, J.; Wang, H.; Zhao, J. The Influence of Ni Doping on the Structure and Electrochemical Properties of LiCoO2 Materials. J. Electrochem. Soc. 2018, 165, A2267. [Google Scholar] [CrossRef]



| Covariate Variables | |||
|---|---|---|---|
| Publication Results | Elemental Properties | ||
| Name | Abbreviation | Name | Abbreviation |
| The amount of element doping | M | Molar mass of doped material | Mr |
| Lattice constants a and c | LC_a, LC_c | Dopant’s ionic radius | IR_dopant |
| Initial voltage and cut-off voltage | V_min, V_max | Dopant’s ionic electronegativity | EN_ionic_dopant |
| Experimental current density | CD | ||
| Response Variables | |||
| Name | Abbreviation | Name | Abbreviation |
| Initial discharge capacity | 1DC | 25th cycle end discharge capacity | 25DC |
| Model | 1DC R2 | 1DC RMSE (mAh/g) | 25DC R2 | 25DC RMSE (mAh/g) |
|---|---|---|---|---|
| RF | 0.8882 | 8.127 | 0.7371 | 13.49 |
| GBM | 0.7671 | 8.0597 | 0.5544 | 15.3106 |
| XGBoost | 0.8611 | 9.878 | 0.8318 | 13.49 |
| CatBoost | 0.8698 | 7.9806 | 0.6363 | 13.8317 |
| LightGBM | 0.4568 | 14.22 | 0.7065 | 15.00 |
| Element | Valence | Ionic Electronegativity | Ionic Radius (Å) |
|---|---|---|---|
| Co | +3 | 1.693 | 0.545 |
| La | +3 | 1.327 | 1.032 |
| Bi | +3 | 1.895 | 1.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, M.; Yao, Y.; Pang, C.; Chen, X.; Wei, Y.; Zhou, F.; Zhang, X.; Xiang, Y. Machine Learning-Assisted Design of Doping Strategies for High-Voltage LiCoO2: A Data-Driven Approach. Batteries 2025, 11, 100. https://doi.org/10.3390/batteries11030100
Fang M, Yao Y, Pang C, Chen X, Wei Y, Zhou F, Zhang X, Xiang Y. Machine Learning-Assisted Design of Doping Strategies for High-Voltage LiCoO2: A Data-Driven Approach. Batteries. 2025; 11(3):100. https://doi.org/10.3390/batteries11030100
Chicago/Turabian StyleFang, Man, Yutong Yao, Chao Pang, Xiehang Chen, Yutao Wei, Fan Zhou, Xiaokun Zhang, and Yong Xiang. 2025. "Machine Learning-Assisted Design of Doping Strategies for High-Voltage LiCoO2: A Data-Driven Approach" Batteries 11, no. 3: 100. https://doi.org/10.3390/batteries11030100
APA StyleFang, M., Yao, Y., Pang, C., Chen, X., Wei, Y., Zhou, F., Zhang, X., & Xiang, Y. (2025). Machine Learning-Assisted Design of Doping Strategies for High-Voltage LiCoO2: A Data-Driven Approach. Batteries, 11(3), 100. https://doi.org/10.3390/batteries11030100






