Polymer-BN Composites as Thermal Interface Materials for Lithium-Ion Battery Modules: Experimental and Simulation Insights
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Fabrication of Thermal Interface Materials
2.3. Characterization Techniques
2.4. COMSOL Modeling
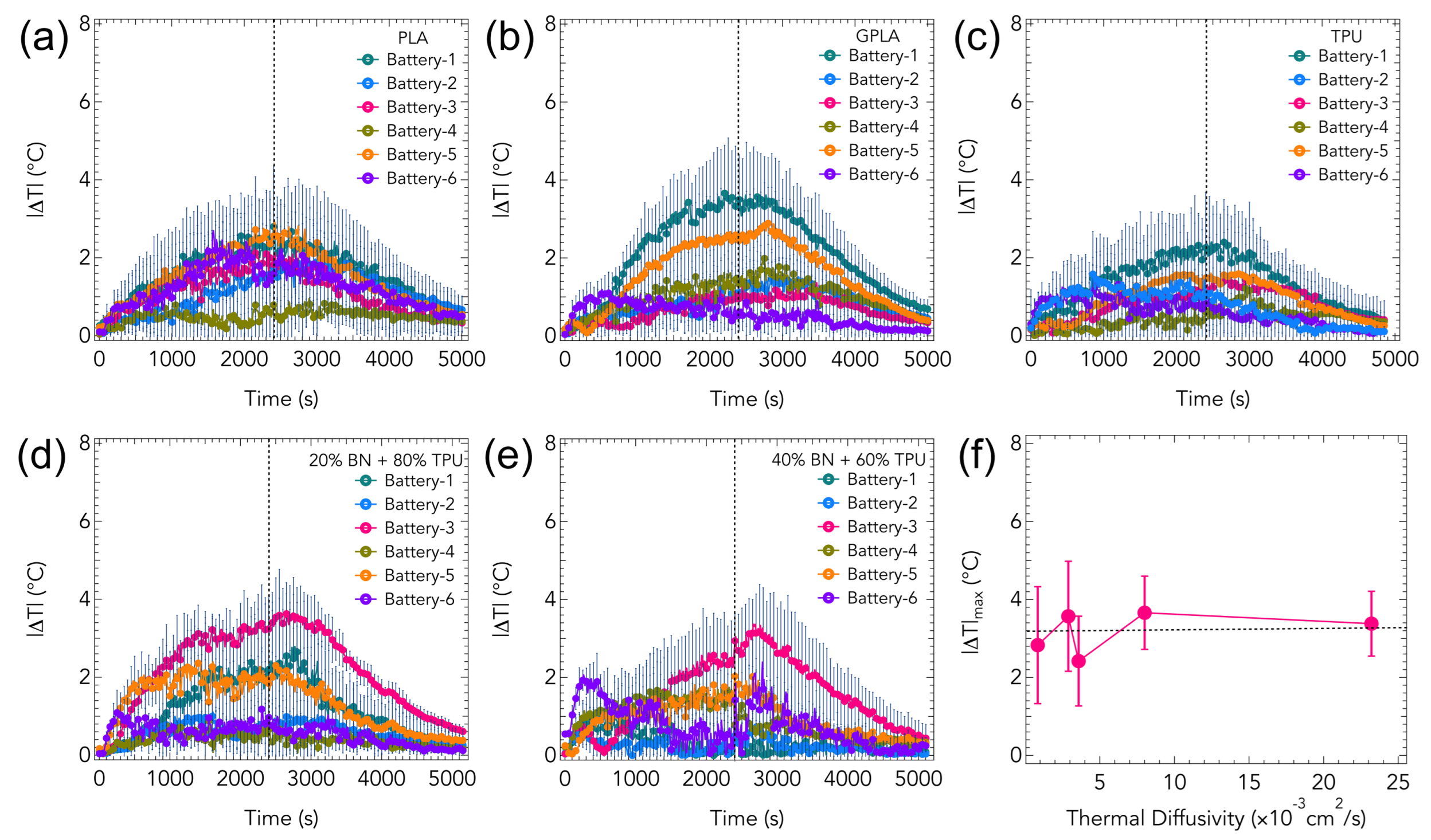
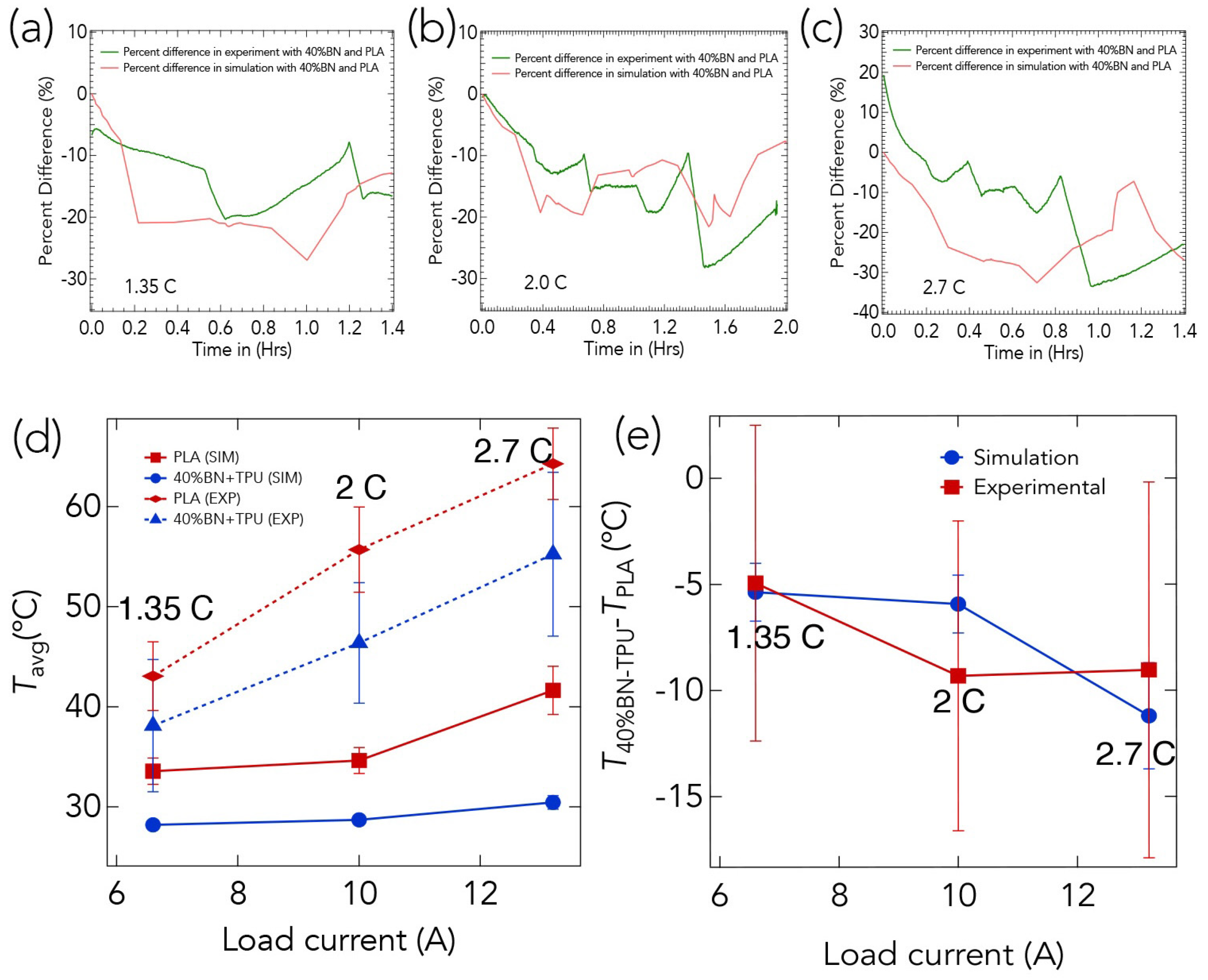
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LIB | Lithium-ion battery |
| TIMs | Thermal interface materials |
| PLA | Polylactic acid PLA |
| GPLA | Graphene-PLA |
| BN | Boron nitride |
| TPU | Thermoplastic polyurethane |
| EVs | Electric vehicles |
| BTMS | Battery thermal management systems |
| h-BN | Hexagonal boron nitride |
| TGA | Thermogravimetric analysis |
| DMF | N, N-dimethylformamide |
| XRD | X-ray diffraction |
| AFM | Atomic force microscopy |
| DSC | Differential scanning calorimetry |
| FEM | Finite element method |
References
- Kermani, J.R.; Taheri, M.M.; Pakzad, H.; Minaei, M.; Bijarchi, M.A.; Moosavi, A.; Shafii, M.B. Hybrid battery thermal management systems based on phase transition processes: A comprehensive review. J. Energy Storage 2024, 86, 111227. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.; Yang, B.; Cai, S. A review of battery thermal management systems using liquid cooling and PCM. J. Energy Storage 2024, 76, 109836. [Google Scholar] [CrossRef]
- Vikram, S.; Vashisht, S.; Rakshit, D.; Wan, M.P. Recent advancements and performance implications of hybrid battery thermal management systems for Electric Vehicles. J. Energy Storage 2024, 90, 111814. [Google Scholar] [CrossRef]
- Liu, J.; Yadav, S.; Salman, M.; Chavan, S.; Kim, S.C. Review of thermal coupled battery models and parameter identification for lithium-ion battery heat generation in EV battery thermal management system. Int. J. Heat Mass Transf. 2024, 218, 124748. [Google Scholar] [CrossRef]
- Hwang, F.S.; Confrey, T.; Reidy, C.; Picovici, D.; Callaghan, D.; Culliton, D.; Nolan, C. Review of battery thermal management systems in electric vehicles. Renew. Sustain. Energy Rev. 2024, 192, 114171. [Google Scholar] [CrossRef]
- Olabi, A.; Maghrabie, H.M.; Adhari, O.H.K.; Sayed, E.T.; Yousef, B.A.; Salameh, T.; Kamil, M.; Abdelkareem, M.A. Battery thermal management systems: Recent progress and challenges. Int. J. Thermofluids 2022, 15, 100171. [Google Scholar] [CrossRef]
- Lin, J.; Liu, X.; Li, S.; Zhang, C.; Yang, S. A review on recent progress, challenges and perspective of battery thermal management system. Int. J. Heat Mass Transf. 2021, 167, 120834. [Google Scholar] [CrossRef]
- Ghalkhani, M.; Habibi, S. Review of the Li-ion battery, thermal management, and AI-based battery management system for EV application. Energies 2022, 16, 185. [Google Scholar] [CrossRef]
- Longchamps, R.S.; Yang, X.G.; Wang, C.Y. Fundamental insights into battery thermal management and safety. ACS Energy Lett. 2022, 7, 1103–1111. [Google Scholar] [CrossRef]
- Li, H.; Wang, H.; Xu, Z.; Wang, K.; Ge, M.; Gan, L.; Zhang, Y.; Tang, Y.; Chen, S. Thermal-responsive and fire-resistant materials for high-safety lithium-ion batteries. Small 2021, 17, 2103679. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z.; Weng, L.; Ge, S.; Jiang, D.; Huang, M.; Mulvihill, D.M.; Chen, Q.; Guo, Z.; Jazzar, A.; et al. A roadmap review of thermally conductive polymer composites: Critical factors, progress, and prospects. Adv. Funct. Mater. 2023, 33, 2301549. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, Z.; Wu, B.; Song, M.; Wu, X. An air-cooled system with a control strategy for efficient battery thermal management. Appl. Therm. Eng. 2024, 236, 121578. [Google Scholar] [CrossRef]
- Kalaf, O.; Solyali, D.; Asmael, M.; Zeeshan, Q.; Safaei, B.; Askir, A. Experimental and simulation study of liquid coolant battery thermal management system for electric vehicles: A review. Int. J. Energy Res. 2021, 45, 6495–6517. [Google Scholar] [CrossRef]
- Yu, W.; Liu, C.; Qiu, L.; Zhang, P.; Ma, W.; Yue, Y.; Xie, H.; Larkin, L.S. Advanced thermal interface materials for thermal management. Eng. Sci. 2018, 2, 1–3. [Google Scholar] [CrossRef]
- Guo, H.; Zhao, H.; Niu, H.; Ren, Y.; Fang, H.; Fang, X.; Lv, R.; Maqbool, M.; Bai, S. Highly thermally conductive 3D printed graphene filled polymer composites for scalable thermal management applications. Acs Nano 2021, 15, 6917–6928. [Google Scholar] [CrossRef]
- Ma, H.; Gao, B.; Wang, M.; Yuan, Z.; Shen, J.; Zhao, J.; Feng, Y. Strategies for enhancing thermal conductivity of polymer-based thermal interface materials: A review. J. Mater. Sci. 2021, 56, 1064–1086. [Google Scholar] [CrossRef]
- Lin, Y.; Li, P.; Liu, W.; Chen, J.; Liu, X.; Jiang, P.; Huang, X. Application-driven high-thermal-conductivity polymer nanocomposites. ACS Nano 2024, 18, 3851–3870. [Google Scholar] [CrossRef]
- Lewis, J.S.; Perrier, T.; Barani, Z.; Kargar, F.; Balandin, A.A. Thermal interface materials with graphene fillers: Review of the state of the art and outlook for future applications. Nanotechnology 2021, 32, 142003. [Google Scholar] [CrossRef] [PubMed]
- Akula, R.; Balaji, C. Thermal management of 18650 Li-ion battery using novel fins–PCM–EG composite heat sinks. Appl. Energy 2022, 316, 119048. [Google Scholar] [CrossRef]
- Yuan, Z.; Ma, H.; Hussien, M.A.; Feng, Y. Development and challenges of thermal interface materials: A review. Macromol. Mater. Eng. 2021, 306, 2100428. [Google Scholar] [CrossRef]
- Chen, J.; Xu, X.; Zhou, J.; Li, B. Interfacial thermal resistance: Past, present, and future. Rev. Mod. Phys. 2022, 94, 025002. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, J.; Wei, N.; Yang, J.; Pei, Q.X. Recent progress in the development of thermal interface materials: A review. Phys. Chem. Chem. Phys. 2021, 23, 753–776. [Google Scholar] [CrossRef]
- Shahil, K.M.; Balandin, A.A. Graphene–multilayer graphene nanocomposites as highly efficient thermal interface materials. Nano Lett. 2012, 12, 861–867. [Google Scholar] [CrossRef] [PubMed]
- Naghibi, S.; Kargar, F.; Wright, D.; Huang, C.Y.T.; Mohammadzadeh, A.; Barani, Z.; Salgado, R.; Balandin, A.A. Noncuring graphene thermal interface materials for advanced electronics. Adv. Electron. Mater. 2020, 6, 1901303. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Han, D.; Zhao, Y.H.; Bai, S.L. High-performance thermal interface materials consisting of vertically aligned graphene film and polymer. Carbon 2016, 109, 552–557. [Google Scholar] [CrossRef]
- Yun, J.; Lee, J.; Kim, J.; Lee, J.; Choi, W. Hexagonal boron nitride nanosheets/graphene nanoplatelets/cellulose nanofibers-based multifunctional thermal interface materials enabling electromagnetic interference shielding and electrical insulation. Carbon 2024, 228, 119397. [Google Scholar] [CrossRef]
- Chung, D. Performance of thermal interface materials. Small 2022, 18, 2200693. [Google Scholar] [CrossRef] [PubMed]
- Luo, T.; Lloyd, J.R. Enhancement of thermal energy transport across graphene/graphite and polymer interfaces: A molecular dynamics study. Adv. Funct. Mater. 2012, 22, 2495–2502. [Google Scholar] [CrossRef]
- Huang, J.; Zhu, Y.; Xu, L.; Chen, J.; Jiang, W.; Nie, X. Massive enhancement in the thermal conductivity of polymer composites by trapping graphene at the interface of a polymer blend. Compos. Sci. Technol. 2016, 129, 160–165. [Google Scholar] [CrossRef]
- Li, A.; Zhang, C.; Zhang, Y.F. Thermal conductivity of graphene-polymer composites: Mechanisms, properties, and applications. Polymers 2017, 9, 437. [Google Scholar] [CrossRef]
- Zhang, P.; Zeng, J.; Zhai, S.; Xian, Y.; Yang, D.; Li, Q. Thermal properties of graphene filled polymer composite thermal interface materials. Macromol. Mater. Eng. 2017, 302, 1700068. [Google Scholar] [CrossRef]
- Lu, X.H.; Liu, J.; Shu, C.; Zhang, S.C.; Zhao, H.Y.; Zhang, Y.; Wang, Q.; Yu, Z.Z.; Li, X. Densifying conduction networks of vertically aligned carbon fiber arrays with secondary graphene networks for highly thermally conductive polymer composites. Adv. Funct. Mater. 2025, 35, 2417324. [Google Scholar] [CrossRef]
- Dai, W.; Wang, Y.; Li, M.; Chen, L.; Yan, Q.; Yu, J.; Jiang, N.; Lin, C.T. 2D materials-based thermal Interface materials: Structure, properties, and applications. Adv. Mater. 2024, 36, 2311335. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Han, S.; Dan, C.; Wu, T.; You, F.; Jiang, X.; Wu, Y.; Dang, Z.M. Boron Nitride-Polymer Composites with High Thermal Conductivity: Preparation, Functionalization Strategy and Innovative Structural Regulation. Small 2025, 21, 2412447. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; An, L.; Yu, L.; Pan, Y.; Fan, H.; Qin, L. Strategies for optimizing interfacial thermal resistance of thermally conductive hexagonal boron nitride/polymer composites: A review. Polym. Compos. 2024, 45, 10587–10618. [Google Scholar] [CrossRef]
- Hu, J.; Huang, Y.; Yao, Y.; Pan, G.; Sun, J.; Zeng, X.; Sun, R.; Xu, J.B.; Song, B.; Wong, C.P. Polymer composite with improved thermal conductivity by constructing a hierarchically ordered three-dimensional interconnected network of BN. ACS Appl. Mater. Interfaces 2017, 9, 13544–13553. [Google Scholar] [CrossRef]
- Ravichandran, V.; Varrla, E. Sustainable high-yield h-BN nanosheet production by liquid exfoliation for thermal interface materials. RSC Appl. Interfaces 2025, 2, 534–549. [Google Scholar] [CrossRef]
- Xu, L.; Zhan, K.; Ding, S.; Zhu, J.; Liu, M.; Fan, W.; Duan, P.; Luo, K.; Ding, B.; Liu, B.; et al. A Malleable Composite Dough with Well-Dispersed and High-Content Boron Nitride Nanosheets. ACS Nano 2023, 17, 4886–4895. [Google Scholar] [CrossRef]
- Liang, Z.; Pei, Y.; Chen, C.; Jiang, B.; Yao, Y.; Xie, H.; Jiao, M.; Chen, G.; Li, T.; Yang, B.; et al. General, Vertical, Three-Dimensional Printing of Two-Dimensional Materials with Multiscale Alignment. ACS Nano 2019, 13, 12653–12661. [Google Scholar] [CrossRef]
- Liu, G.; Ding, A.; Xu, P.; Zhu, M.; Zhang, H.; Zheng, Y.; Luo, Y.; Zhang, L.; Zhang, P.; Chen, A.; et al. Thermal conductivity of epoxy composites containing 3D honeycomb boron nitride filler. Chem. Eng. J. 2024, 489, 151170. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.; Sun, B.; Wang, Y.; Zhu, Y.; Jiang, P. Vertically Aligned and Interconnected Boron Nitride Nanosheets for Advanced Flexible Nanocomposite Thermal Interface Materials. ACS Appl. Mater. Interfaces 2017, 9, 30909–30917. [Google Scholar] [CrossRef]
- Hong, H.; Jung, Y.H.; Lee, J.S.; Jeong, C.; Kim, J.U.; Lee, S.; Ryu, H.; Kim, H.; Ma, Z.; Kim, T. Anisotropic Thermal Conductive Composite by the Guided Assembly of Boron Nitride Nanosheets for Flexible and Stretchable Electronics. Adv. Funct. Mater. 2019, 29, 1902575. [Google Scholar] [CrossRef]
- Song, Q.; Zhu, W.; Deng, Y.; Hai, F.; Wang, Y.; Guo, Z. Enhanced through-plane thermal conductivity and high electrical insulation of flexible composite films with aligned boron nitride for thermal interface material. Compos. Part A Appl. Sci. Manuf. 2019, 127, 105654. [Google Scholar] [CrossRef]
- Gao, C.; Zhu, Z.; Shen, Y.; Wang, T.; Xiang, D. Efficient construction of boron nitride network in epoxy composites combining reaction-induced phase separation and three-roll milling. Compos. Part B Eng. 2020, 198, 108232. [Google Scholar] [CrossRef]
- Yuan, W.; Li, W.; Zhu, S.; Chu, Z.; Gan, W. 3D-network of hybrid epoxy-boron nitride microspheres leading to epoxy composites of high thermal conductivity. J. Mater. Sci. 2022, 57, 11698–11713. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Zhang, Z.; Liang, L.; Zhao, Z.; Shi, J. Preparation of a 3D BN network structure by a salt template assisted method filled with epoxy resin to obtain high thermal conductivity nanocomposites. Polym. Compos. 2023, 44, 3610–3621. [Google Scholar] [CrossRef]
- Leng, X.; Xiao, C.; Chen, L.; Su, Z.; Zheng, K.; Zhang, X.; Tian, X. An efficient approach for constructing 3-D boron nitride networks with epoxy composites to form materials with enhanced thermal, dielectric, and mechanical properties. High Perform. Polym. 2019, 31, 350–358. [Google Scholar] [CrossRef]
- Jung, D.W.; Kim, J.M.; Yoon, H.W.; Nam, K.M.; Kwon, Y.E.; Jeong, S.; Baek, Y.H.; Choi, Y.S.; Chang, S.J.; Yi, G.R.; et al. Solution-processable thermally conductive polymer composite adhesives of benzyl-alcohol-modified boron nitride two-dimensional nanoplates. Chem. Eng. J. 2019, 361, 783–791. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, Z.; Li, X.; Hu, J.; Liao, Y.; Liu, Y.; Li, L.; Wei, S.; Li, Z. Improved out-of-plane thermal conductivity of boron nitride nanosheet-filled polyamide 6/polyethylene terephthalate composites by a rapid solidification method. Mater. Adv. 2023, 4, 1490–1501. [Google Scholar] [CrossRef]
- Zhao, N.; Li, J.; Wang, W.; Gao, W.; Bai, H. Isotropically Ultrahigh Thermal Conductive Polymer Composites by Assembling Anisotropic Boron Nitride Nanosheets into a Biaxially Oriented Network. ACS Nano 2022, 16, 18959–18967. [Google Scholar] [CrossRef]
- Zhan, K.; Chen, Y.; Xiong, Z.; Zhang, Y.; Ding, S.; Zhen, F.; Liu, Z.; Wei, Q.; Liu, M.; Sun, B.; et al. Low thermal contact resistance boron nitride nanosheets composites enabled by interfacial arc-like phonon bridge. Nat. Commun. 2024, 15, 2905. [Google Scholar] [CrossRef]
- Chen, X.; Lim, J.; Yan, W.; Guo, F.; Liang, Y.; Chen, H.; Lambourne, A.; Hu, X. Salt template assisted BN scaffold fabrication toward highly thermally conductive epoxy composites. ACS Appl. Mater. Interfaces 2020, 12, 16987–16996. [Google Scholar] [CrossRef]
- Pan, D.; Li, Q.; Zhang, W.; Dong, J.; Su, F.; Murugadoss, V.; Liu, Y.; Liu, C.; Naik, N.; Guo, Z. Highly thermal conductive epoxy nanocomposites filled with 3D BN/C spatial network prepared by salt template assisted method. Compos. Part B Eng. 2021, 209, 108609. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Y.; Li, M.; Qin, Y.; Yang, R.; Xu, K.; Guo, Y.; Li, L.; Zhang, Z.; Zhang, J.; et al. Ultra-high thermal conductivity multifunctional composites with uniaxially oriented boron nitride sheets for future wireless charging technology. Adv. Compos. Hybrid Mater. 2025, 8, 237. [Google Scholar] [CrossRef]
- Yu, C.; Gong, W.; Tian, W.; Zhang, Q.; Xu, Y.; Lin, Z.; Hu, M.; Fan, X.; Yao, Y. Hot-pressing induced alignment of boron nitride in polyurethane for composite films with thermal conductivity over 50 W/mK. Compos. Sci. Technol. 2018, 160, 199–207. [Google Scholar] [CrossRef]
- Ravichandran, V.; Chandrashekar, A.; Prabhu, T.N.; Varrla, E. SPI-modified h-BN nanosheets-based thermal interface materials for thermal management applications. ACS Appl. Mater. Interfaces 2024, 16, 34367–34376. [Google Scholar] [CrossRef] [PubMed]
- Arora, P.; Doyle, M.; Gozdz, A.S.; White, R.E.; Newman, J. Comparison between computer simulations and experimental data for high-rate discharges of plastic lithium-ion batteries. J. Power Sources 2000, 88, 219–231. [Google Scholar] [CrossRef]
- Ekström, H.; Fridholm, B.; Lindbergh, G. Comparison of lumped diffusion models for voltage prediction of a lithium-ion battery cell during dynamic loads. J. Power Sources 2018, 402, 296–300. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J.; Gozdz, A.S.; Schmutz, C.N.; Tarascon, J. Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells. J. Electrochem. Soc. 1996, 143, 1890. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, B.; Chen, S.; Li, P. Lithium-ion battery pack thermal management under high ambient temperature and cyclic charging-discharging strategy design. J. Energy Storage 2024, 80, 110391. [Google Scholar] [CrossRef]
- Mahmood, A.; Cockerill, T.; de Boer, G.; Voss, J.; Thompson, H. Heat Transfer Modeling and Optimal Thermal Management of Electric Vehicle Battery Systems. Energies 2024, 17, 4575. [Google Scholar] [CrossRef]
- Smith, K.; Wang, C.Y. Power and thermal characterization of a lithium-ion battery pack for hybrid-electric vehicles. J. Power Sources 2006, 160, 662–673. [Google Scholar] [CrossRef]
- Cai, L.; White, R.E. Mathematical modeling of a lithium ion battery with thermal effects in COMSOL Inc. Multiphysics (MP) software. J. Power Sources 2011, 196, 5985–5989. [Google Scholar] [CrossRef]
- Srinivasan, V.; Wang, C.Y. Analysis of electrochemical and thermal behavior of Li-ion cells. J. Electrochem. Soc. 2002, 150, A98. [Google Scholar] [CrossRef]
- Weragoda, D.M.; Tian, G.; Burkitbayev, A.; Lo, K.H.; Zhang, T. A comprehensive review on heat pipe based battery thermal management systems. Appl. Therm. Eng. 2023, 224, 120070. [Google Scholar] [CrossRef]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. Origins and accommodation of cell variations in Li-ion battery pack modelling. Int. J. Energy Res. 2010, 34, 216–231. [Google Scholar] [CrossRef]
- Beck, D.D.P.; Junker, M.; Sauer, D.U.; Dubarry, M. Inhomogeneities and cell-to-cell variations in lithium-ion batteries: A review. Energies 2021, 14, 3276. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohonta, S.K.; Francis, S.M.; Ferebee, A.; Bohara, G.; Puneet, P.; Ding, Y.; Podila, R. Polymer-BN Composites as Thermal Interface Materials for Lithium-Ion Battery Modules: Experimental and Simulation Insights. Batteries 2025, 11, 431. https://doi.org/10.3390/batteries11120431
Mohonta SK, Francis SM, Ferebee A, Bohara G, Puneet P, Ding Y, Podila R. Polymer-BN Composites as Thermal Interface Materials for Lithium-Ion Battery Modules: Experimental and Simulation Insights. Batteries. 2025; 11(12):431. https://doi.org/10.3390/batteries11120431
Chicago/Turabian StyleMohonta, Sajib Kumar, Shinto Mundackal Francis, Andrew Ferebee, Gajendra Bohara, Pooja Puneet, Yi Ding, and Ramakrishna Podila. 2025. "Polymer-BN Composites as Thermal Interface Materials for Lithium-Ion Battery Modules: Experimental and Simulation Insights" Batteries 11, no. 12: 431. https://doi.org/10.3390/batteries11120431
APA StyleMohonta, S. K., Francis, S. M., Ferebee, A., Bohara, G., Puneet, P., Ding, Y., & Podila, R. (2025). Polymer-BN Composites as Thermal Interface Materials for Lithium-Ion Battery Modules: Experimental and Simulation Insights. Batteries, 11(12), 431. https://doi.org/10.3390/batteries11120431







