The Impact of C-Rate, Float Charging and Temperature on Pouch Lithium-Ion Battery Swelling
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Charge–Discharge Cycling Test Results
3.2. Float Charging Test Results
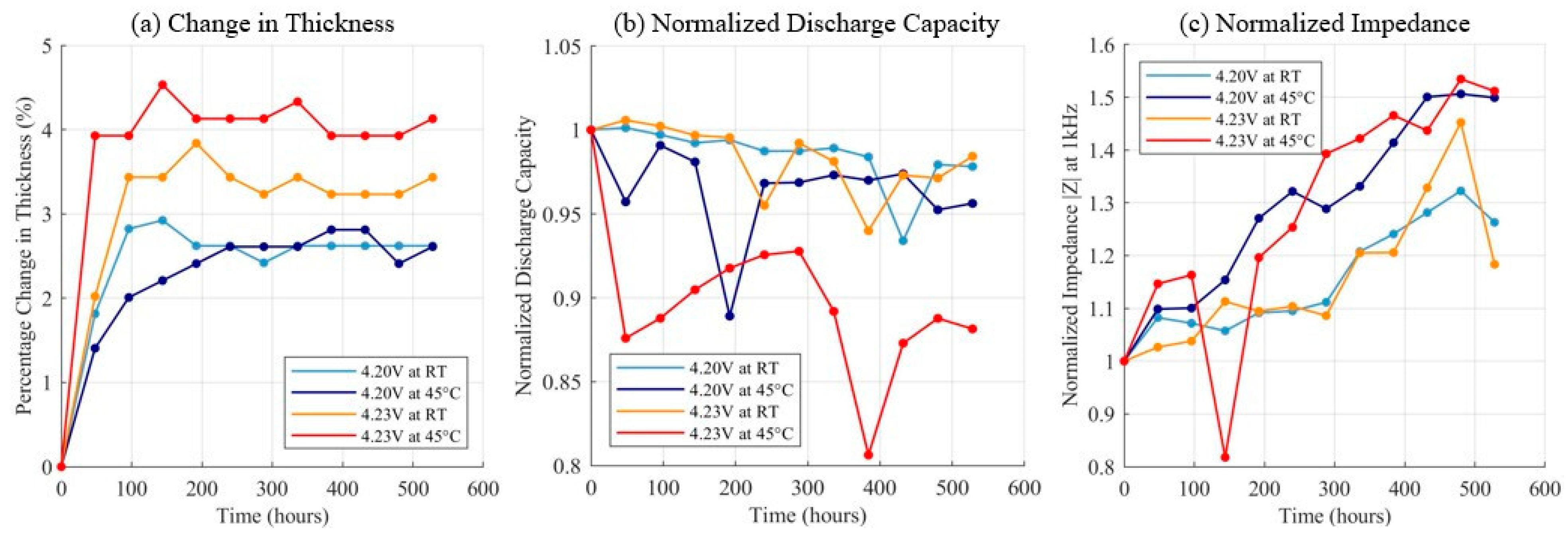
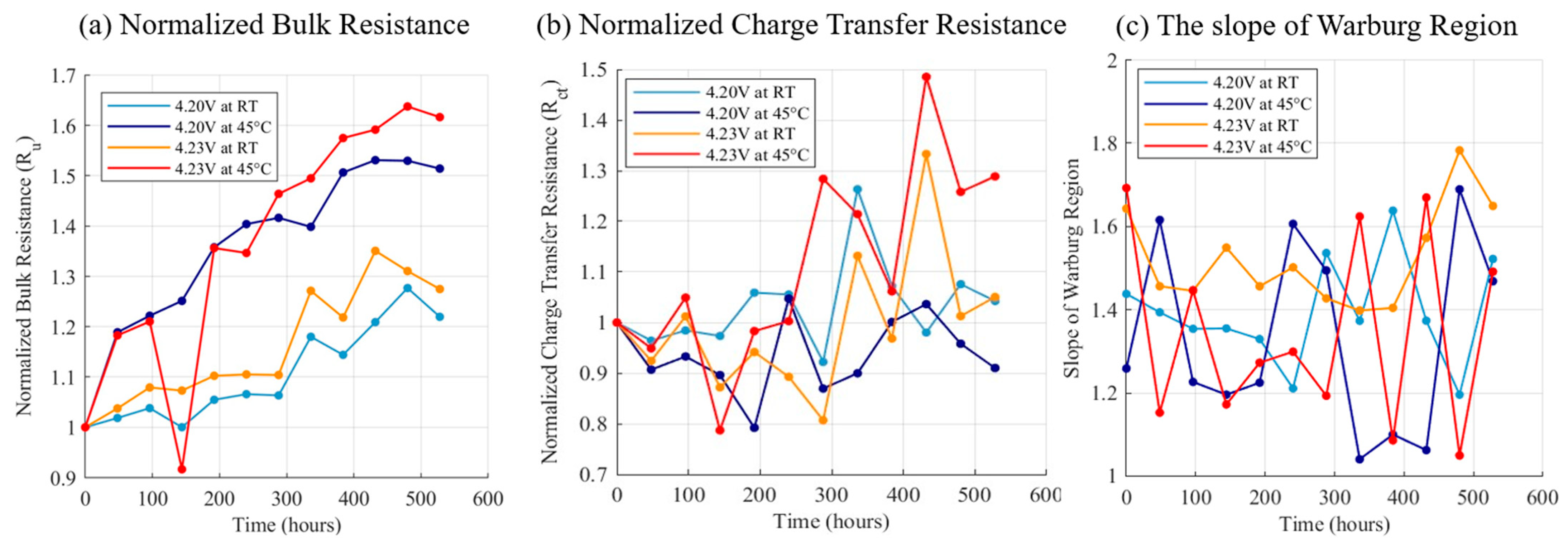
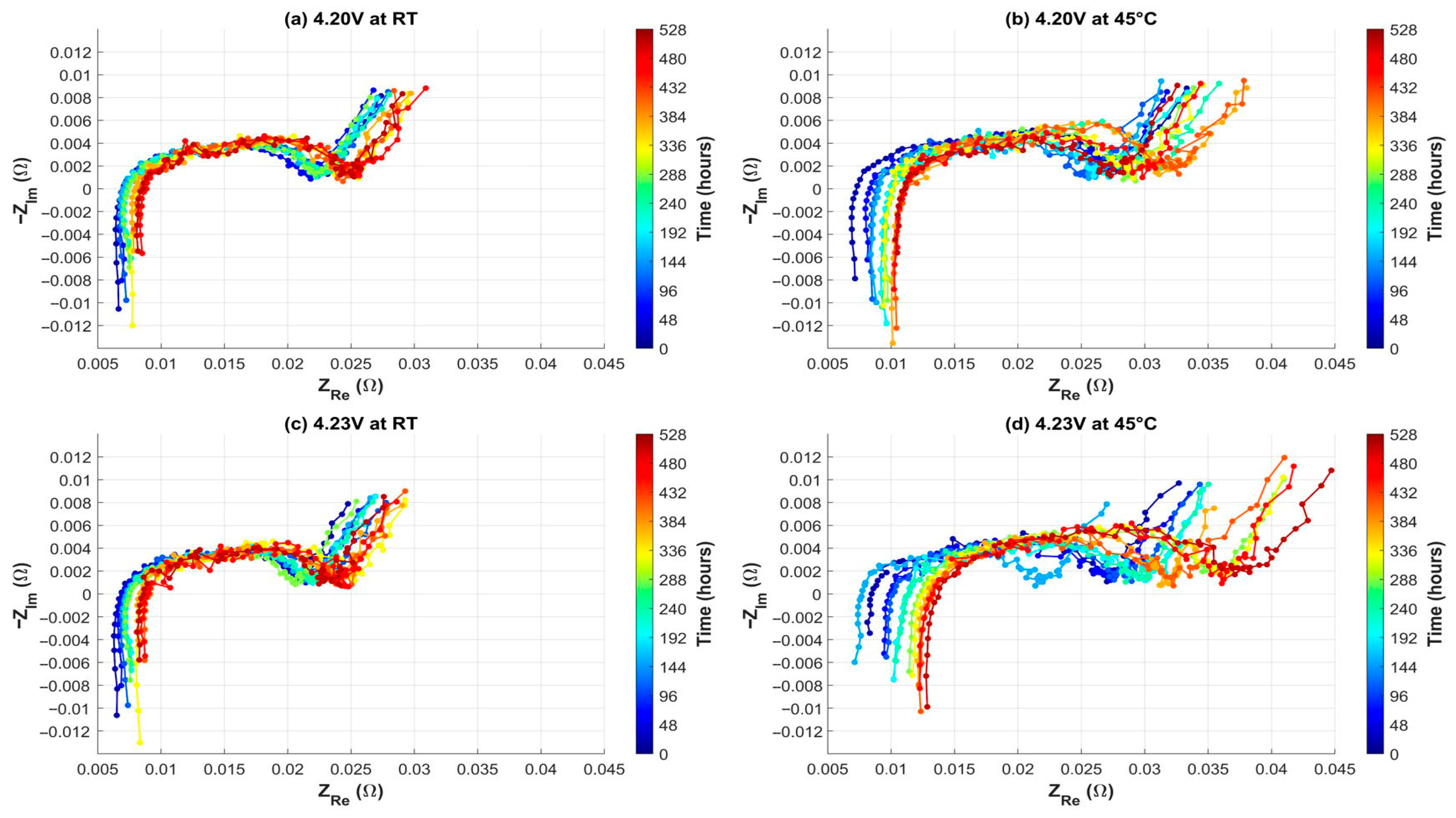
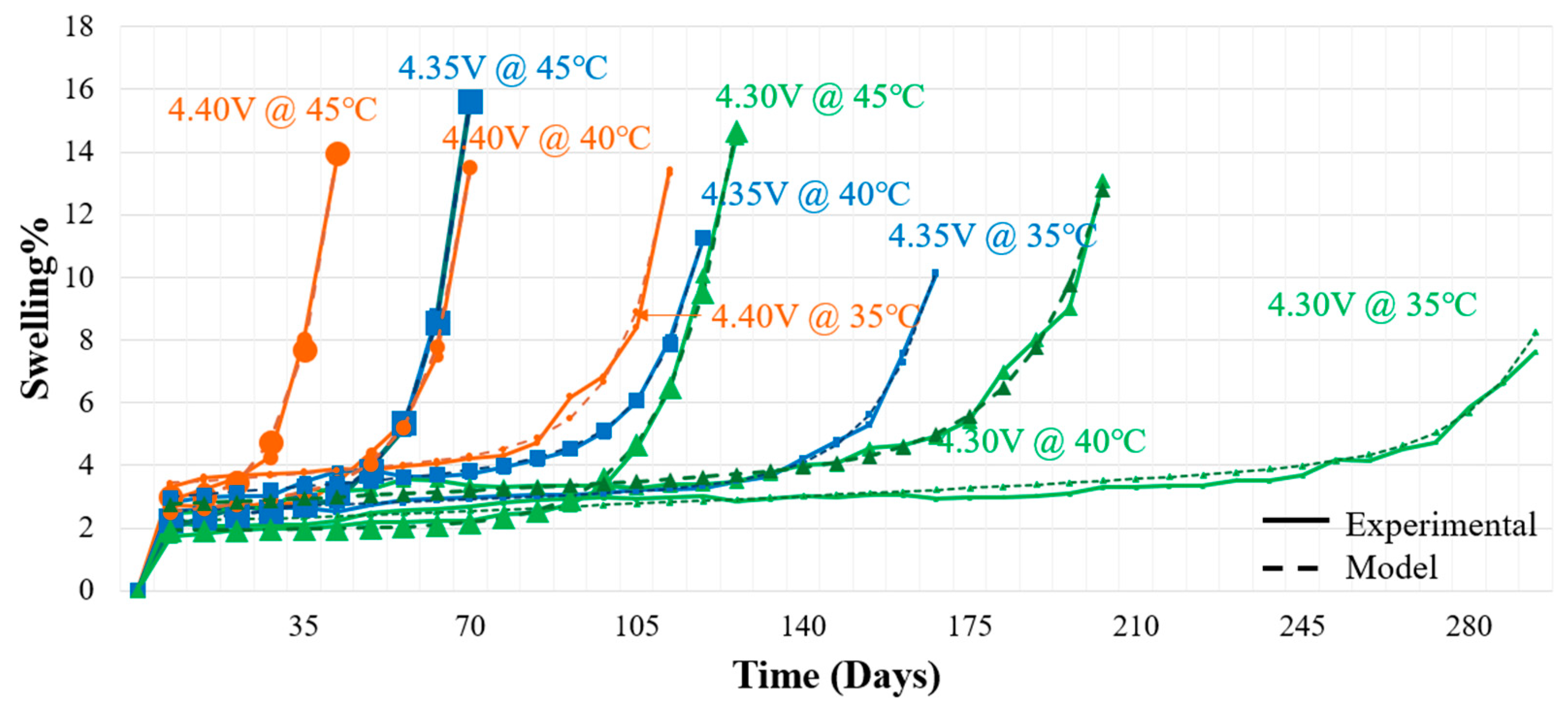
3.3. Float Charging Test Results at Elevated Voltage and Temperature
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SEI | Solid electrolyte interphase |
| NMC | Lithium nickel manganese cobalt oxide |
| BMS | Battery management system |
| EIS | Electrochemical Impedance Spectroscopy |
| ECM | Equivalent circuit model |
| 1RC | One-resistor-capacitor pair |
| NCA | Lithium nickel cobalt aluminum oxide |
| RT | Room temperature |
| CC | Constant current |
| CV | Constant voltage |
References
- Maddipatla, S.; Rauf, H.; Osterman, M.; Arshad, N.; Pecht, M. Swelling Mechanisms, Diagnostic Applications, and Mitigation Strategies in Lithium-Ion Batteries. Batteries 2025, 11, 356. [Google Scholar] [CrossRef]
- Li, X.; Zeng, T.; Qin, H.; Huo, R.; Liu, Y.; Wei, D.; Ding, X. Investigation of Inhomogeneous Degradation in Large-Format Lithium-Ion Batteries. J. Energy Storage 2021, 42, 103113. [Google Scholar] [CrossRef]
- Aiken, C.P.; Self, J.; Petibon, R.; Xia, X.; Paulsen, J.M.; Dahn, J.R. A Survey of In Situ Gas Evolution during High Voltage Formation in Li-Ion Pouch Cells. J. Electrochem. Soc. 2015, 162, A760–A767. [Google Scholar] [CrossRef]
- Renfrew, S.E.; McCloskey, B.D. Residual Lithium Carbonate Predominantly Accounts for First Cycle CO2 and CO Outgassing of Li-Stoichiometric and Li-Rich Layered Transition-Metal Oxides. J. Am. Chem. Soc. 2017, 139, 17853–17860. [Google Scholar] [CrossRef]
- An, S.J.; Li, J.; Daniel, C.; Mohanty, D.; Nagpure, S.; Wood, D.L. The State of Understanding of the Lithium-Ion-Battery Graphite Solid Electrolyte Interphase (SEI) and Its Relationship to Formation Cycling. Carbon 2016, 105, 52–76. [Google Scholar] [CrossRef]
- Peled, E.; Menkin, S. Review—SEI: Past, Present and Future. J. Electrochem. Soc. 2017, 164, A1703–A1719. [Google Scholar] [CrossRef]
- Bernhard, R.; Metzger, M.; Gasteiger, H.A. Gas Evolution at Graphite Anodes Depending on Electrolyte Water Content and SEI Quality Studied by On-Line Electrochemical Mass Spectrometry. J. Electrochem. Soc. 2015, 162, A1984–A1989. [Google Scholar] [CrossRef]
- Metzger, M.; Strehle, B.; Solchenbach, S.; Gasteiger, H.A. Origin of H2 Evolution in LIBs: H2O Reduction vs. Electrolyte Oxidation. J. Electrochem. Soc. 2016, 163, A798–A809. [Google Scholar] [CrossRef]
- Mao, Z.; Farkhondeh, M.; Pritzker, M.; Fowler, M.; Chen, Z. Calendar Aging and Gas Generation in Commercial Graphite/NMC-LMO Lithium-Ion Pouch Cell. J. Electrochem. Soc. 2017, 164, A3469–A3483. [Google Scholar] [CrossRef]
- Lu, D.; Lin, S.; Cui, W.; Hu, S.; Zhang, Z.; Peng, W. Swelling Mechanism of 0%SOC Lithium Iron Phosphate Battery at High Temperature Storage. J. Energy Storage 2020, 32, 101791. [Google Scholar] [CrossRef]
- Jung, R.; Metzger, M.; Maglia, F.; Stinner, C.; Gasteiger, H.A. Oxygen Release and Its Effect on the Cycling Stability of LiNixMnyCozO2 (NMC) Cathode Materials for Li-Ion Batteries. J. Electrochem. Soc. 2017, 164, A1361–A1377. [Google Scholar] [CrossRef]
- Zhang, S.S. Insight into the Gassing Problem of Li-Ion Battery. Front. Energy Res. 2014, 2, 59. [Google Scholar] [CrossRef]
- Belharouak, I.; Koenig, G.M.; Tan, T.; Yumoto, H.; Ota, N.; Amine, K. Performance Degradation and Gassing of Li4Ti5O12/LiMn2O4 Lithium-Ion Cells. J. Electrochem. Soc. 2012, 159, A1165–A1170. [Google Scholar] [CrossRef]
- Berkes, B.B.; Schiele, A.; Sommer, H.; Brezesinski, T.; Janek, J. On the Gassing Behavior of Lithium-Ion Batteries with NCM523 Cathodes. J. Solid State Electrochem. 2016, 20, 2961–2967. [Google Scholar] [CrossRef]
- Mao, C.; Ruther, R.E.; Geng, L.; Li, Z.; Leonard, D.N.; Meyer, H.M.; Sacci, R.L.; Wood, D.L. Evaluation of Gas Formation and Consumption Driven by Crossover Effect in High-Voltage Lithium-Ion Batteries with Ni-Rich NMC Cathodes. ACS Appl. Mater. Interfaces 2019, 11, 43235–43243. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Liu, F.; Fang, Z.; Gu, N.; Chen, B.; Yang, N.; Jia, Y. A Comparative Study of Overcharge Thermal Runaway Force-Electrical-Thermal Characteristics and Safety Assessment of Lithium Batteries with Different Cathode Materials. Appl. Therm. Eng. 2024, 256, 124092. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal Runaway Mechanism of Lithium Ion Battery for Electric Vehicles: A Review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Xiong, D.J.; Petibon, R.; Nie, M.; Ma, L.; Xia, J.; Dahn, J.R. Interactions between Positive and Negative Electrodes in Li-Ion Cells Operated at High Temperature and High Voltage. J. Electrochem. Soc. 2016, 163, A546–A551. [Google Scholar] [CrossRef]
- Oh, K.-Y.; Epureanu, B.I. A Novel Thermal Swelling Model for a Rechargeable Lithium-Ion Battery Cell. J. Power Sources 2016, 303, 86–96. [Google Scholar] [CrossRef]
- Oh, K.-Y.; Siegel, J.B.; Secondo, L.; Kim, S.U.; Samad, N.A.; Qin, J.; Anderson, D.; Garikipati, K.; Knobloch, A.; Epureanu, B.I.; et al. Rate Dependence of Swelling in Lithium-Ion Cells. J. Power Sources 2014, 267, 197–202. [Google Scholar] [CrossRef]
- Oh, K.-Y.; Samad, N.A.; Kim, Y.; Siegel, J.B.; Stefanopoulou, A.G.; Epureanu, B.I. A Novel Phenomenological Multi-Physics Model of Li-Ion Battery Cells. J. Power Sources 2016, 326, 447–458. [Google Scholar] [CrossRef]
- Sauerteig, D.; Hanselmann, N.; Arzberger, A.; Reinshagen, H.; Ivanov, S.; Bund, A. Electrochemical-Mechanical Coupled Modeling and Parameterization of Swelling and Ionic Transport in Lithium-Ion Batteries. J. Power Sources 2018, 378, 235–247. [Google Scholar] [CrossRef]
- Li, Y.; Wei, C.; Sheng, Y.; Jiao, F.; Wu, K. Swelling Force in Lithium-Ion Power Batteries. Ind. Eng. Chem. Res. 2020, 59, 12313–12318. [Google Scholar] [CrossRef]
- Mohtat, P.; Lee, S.; Siegel, J.B.; Stefanopoulou, A.G. Reversible and Irreversible Expansion of Lithium-Ion Batteries Under a Wide Range of Stress Factors. J. Electrochem. Soc. 2021, 168, 100520. [Google Scholar] [CrossRef]
- Lin, X.; Khosravinia, K.; Hu, X.; Li, J.; Lu, W. Lithium Plating Mechanism, Detection, and Mitigation in Lithium-Ion Batteries. Prog. Energy Combust. Sci. 2021, 87, 100953. [Google Scholar] [CrossRef]
- Juarez-Robles, D.; Vyas, A.A.; Fear, C.; Jeevarajan, J.A.; Mukherjee, P.P. Overcharge and Aging Analytics of Li-Ion Cells. J. Electrochem. Soc. 2020, 167, 090547. [Google Scholar] [CrossRef]
- Sauerteig, D.; Ivanov, S.; Reinshagen, H.; Bund, A. Reversible and Irreversible Dilation of Lithium-Ion Battery Electrodes Investigated by in-Situ Dilatometry. J. Power Sources 2017, 342, 939–946. [Google Scholar] [CrossRef]
- Stravova, Z.; Klvac, O.; Bana, J.; Anothumakkool, B.; Zikmund, T.; Blazek, P.; Kaiser, J.; Kazda, T. Comprehensive Study of Rapid Capacity Fade in Prismatic Li-Ion Cells with Flexible Packaging. Sci. Rep. 2024, 14, 28546. [Google Scholar] [CrossRef]
- Wu, L.; Wei, X.; Lin, C.; Huang, Z.; Fan, Y.; Liu, C.; Fang, S. Battery SOC Estimation with Physics-Constrained BiLSTM under Different External Pressures and Temperatures. J. Energy Storage 2025, 117, 116205. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, Y.; Song, Y.; Wang, W.; Yang, L.; Du, X. Capacity Degradation of NMC/Graphite Battery Based on Electrochemical-Mechanical-Thermal Coupling Aging Model. J. Energy Storage 2025, 135, 118249. [Google Scholar] [CrossRef]
- Tian, Y.; Lin, C.; Li, H.; Du, J.; Xiong, R. Detecting Undesired Lithium Plating on Anodes for Lithium-Ion Batteries—A Review on the in-Situ Methods. Appl. Energy 2021, 300, 117386. [Google Scholar] [CrossRef]
- Cai, T.; Pannala, S.; Stefanopoulou, A.G.; Siegel, J.B. Battery Internal Short Detection Methodology Using Cell Swelling Measurements. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 1143–1148. [Google Scholar]
- Zhao, Y.; Spingler, F.B.; Patel, Y.; Offer, G.J.; Jossen, A. Localized Swelling Inhomogeneity Detection in Lithium Ion Cells Using Multi-Dimensional Laser Scanning. J. Electrochem. Soc. 2019, 166, A27–A34. [Google Scholar] [CrossRef]
- Choi, W.; Shin, H.-C.; Kim, J.M.; Choi, J.-Y.; Yoon, W.-S. Modeling and Applications of Electrochemical Impedance Spectroscopy (EIS) for Lithium-Ion Batteries. J. Electrochem. Sci. Technol. 2020, 11, 1–13. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.-S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of Electrochemical Impedance Spectroscopy to Commercial Li-Ion Cells: A Review. J. Power Sources 2020, 480, 228742. [Google Scholar] [CrossRef]
- Hahn, M.; Buqa, H.; Ruch, P.W.; Goers, D.; Spahr, M.E.; Ufheil, J.; Novák, P.; Kötz, R. A Dilatometric Study of Lithium Intercalation into Powder-Type Graphite Electrodes. Electrochem. Solid-State Lett. 2008, 11, A151. [Google Scholar] [CrossRef]
- Li, R.; Li, W.; Singh, A.; Ren, D.; Hou, Z.; Ouyang, M. Effect of External Pressure and Internal Stress on Battery Performance and Lifespan. Energy Storage Mater. 2022, 52, 395–429. [Google Scholar] [CrossRef]
- Leonard, A.; Planden, B.; Lukow, K.; Morrey, D. Investigation of Constant Stack Pressure on Lithium-Ion Battery Performance. J. Energy Storage 2023, 72, 108422. [Google Scholar] [CrossRef]
- Leung, P.K.; Moreno, C.; Masters, I.; Hazra, S.; Conde, B.; Mohamed, M.R.; Dashwood, R.J.; Bhagat, R. Real-Time Displacement and Strain Mappings of Lithium-Ion Batteries Using Three-Dimensional Digital Image Correlation. J. Power Sources 2014, 271, 82–86. [Google Scholar] [CrossRef]
- Cheng, X.; Pecht, M. In Situ Stress Measurement Techniques on Li-Ion Battery Electrodes: A Review. Energies 2017, 10, 591. [Google Scholar] [CrossRef]
- Plotnikov, Y.; Karp, J.; Knobloch, A.; Kapusta, C.; Lin, D. Eddy Current Sensor for In-Situ Monitoring of Swelling of Li-Ion Prismatic Cells. AIP Conf. Proc. 2015, 1650, 434–442. [Google Scholar]
- Bonefacino, J.; Ghashghaie, S.; Zheng, T.; Lin, C.-P.; Zheng, W.; Blanquer, L.A.; Huang, J.; Gervillié, C.; Tam, H.-Y.; Tarascon, J.-M.; et al. High-Fidelity Strain and Temperature Measurements of Li-Ion Batteries Using Polymer Optical Fiber Sensors. J. Electrochem. Soc. 2022, 169, 100508. [Google Scholar] [CrossRef]
- Wang, X.; Sone, Y.; Segami, G.; Naito, H.; Yamada, C.; Kibe, K. Understanding Volume Change in Lithium-Ion Cells during Charging and Discharging Using In Situ Measurements. J. Electrochem. Soc. 2007, 154, A14. [Google Scholar] [CrossRef]
- Hendricks, C.; Sood, B.; Pecht, M. Lithium-Ion Battery Strain Gauge Monitoring and Depth of Discharge Estimation. J. Electrochem. Energy Convers. Storage 2023, 20, 011008. [Google Scholar] [CrossRef]
- Willenberg, L.K.; Dechent, P.; Fuchs, G.; Sauer, D.U.; Figgemeier, E. High-Precision Monitoring of Volume Change of Commercial Lithium-Ion Batteries by Using Strain Gauges. Sustainability 2020, 12, 557. [Google Scholar] [CrossRef]
- Osterman, M.; Maddipatla, S. Swelling in Lithium-Ion Pouch Batteries. In Proceedings of the 2024 Pan Pacific Strategic Electronics Symposium (Pan Pacific), Kona, Big Island, HI, USA, 29 January–1 February 2024; IEEE: New York, NY, USA, 2024; pp. 1–4. [Google Scholar]
- Lazanas, A.C.; Prodromidis, M.I. Electrochemical Impedance Spectroscopy—A Tutorial. ACS Meas. Sci. Au 2023, 3, 162–193. [Google Scholar] [CrossRef]
- Hu, W.; Peng, Y.; Wei, Y.; Yang, Y. Application of Electrochemical Impedance Spectroscopy to Degradation and Aging Research of Lithium-Ion Batteries. J. Phys. Chem. C 2023, 127, 4465–4495. [Google Scholar] [CrossRef]
- Wu, X.; He, Z.; Wang, T.; Li, X.; Yang, D.; Wang, Q.; Li, Y. Effects of Temperature on Electrochemical Impedance Spectroscopy of the LiFePO4 Battery. IOP Conf. Ser. Earth Environ. Sci. 2021, 675, 012220. [Google Scholar] [CrossRef]
- Zhu, X.; Soult, M.C.; Wouters, B.; Mamme, M.H. Study of Solid-State Diffusion Impedance in Li-Ion Batteries Using Parallel-Diffusion Warburg Model. J. Electrochem. Soc. 2024, 171, 060539. [Google Scholar] [CrossRef]
- Maheshwari, A.; Heck, M.; Santarelli, M. Cycle Aging Studies of Lithium Nickel Manganese Cobalt Oxide-Based Batteries Using Electrochemical Impedance Spectroscopy. Electrochim. Acta 2018, 273, 335–348. [Google Scholar] [CrossRef]
- Chung, H.-C. The Long-Term Usage of an Off-Grid Photovoltaic System with a Lithium-Ion Battery-Based Energy Storage System on High Mountains: A Case Study in Paiyun Lodge on Mt. Jade in Taiwan. Batteries 2024, 10, 202. [Google Scholar] [CrossRef]
- Diao, W.; Kim, J.; Azarian, M.H.; Pecht, M. Degradation Modes and Mechanisms Analysis of Lithium-Ion Batteries with Knee Points. Electrochim. Acta 2022, 431, 141143. [Google Scholar] [CrossRef]
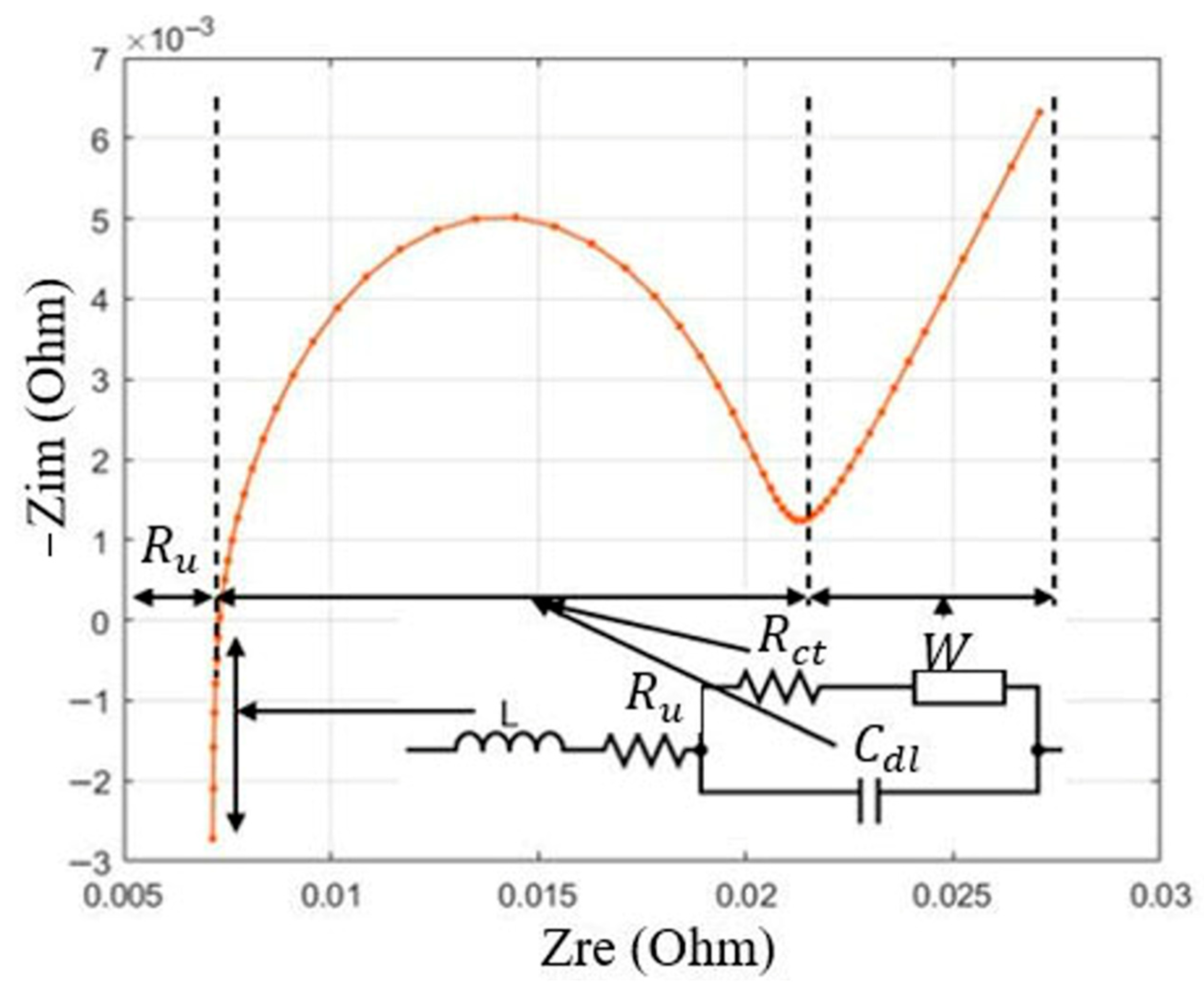

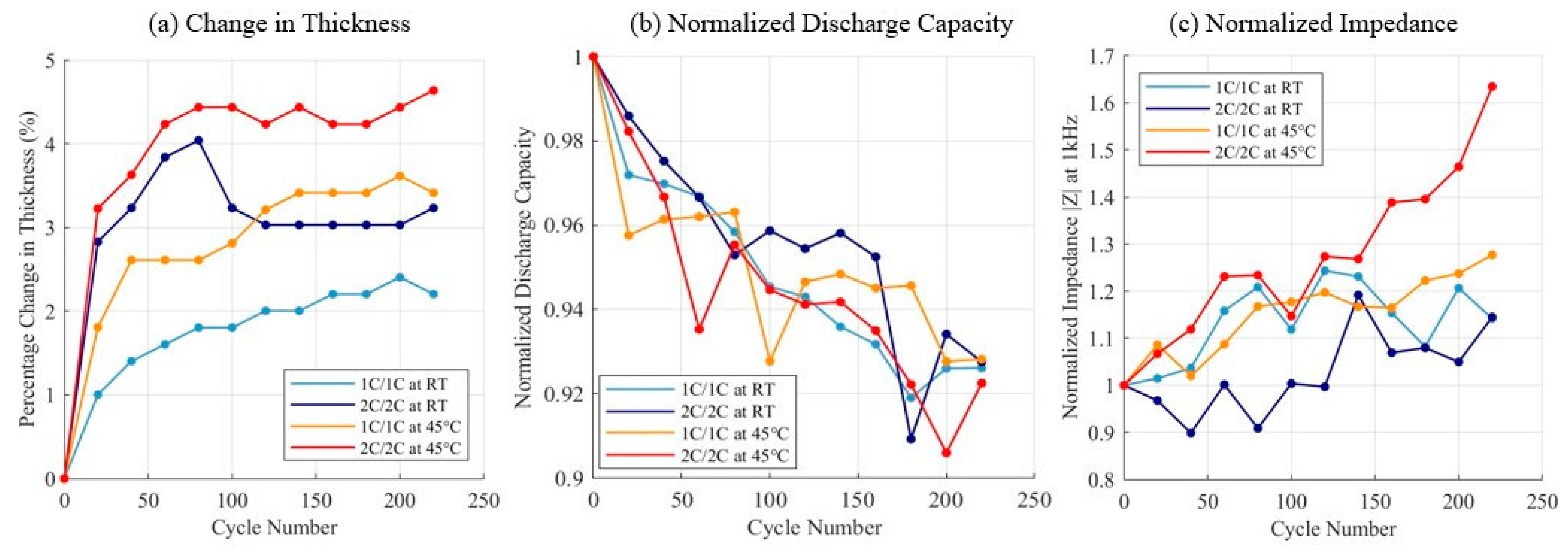
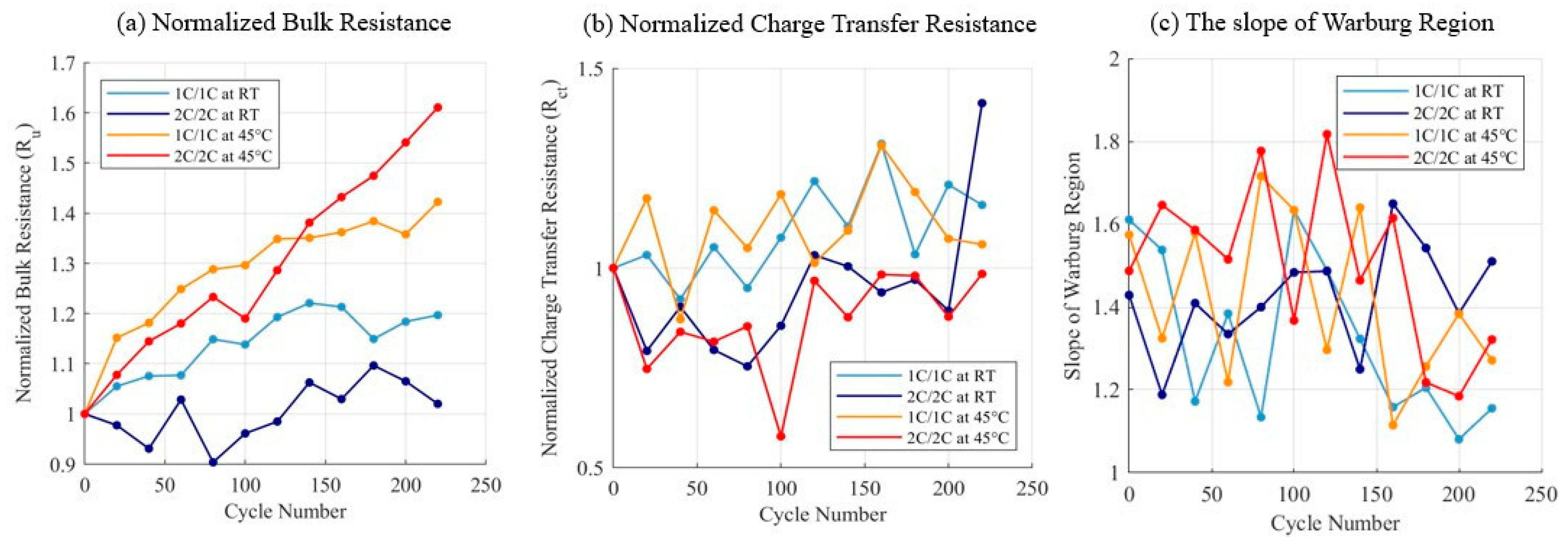
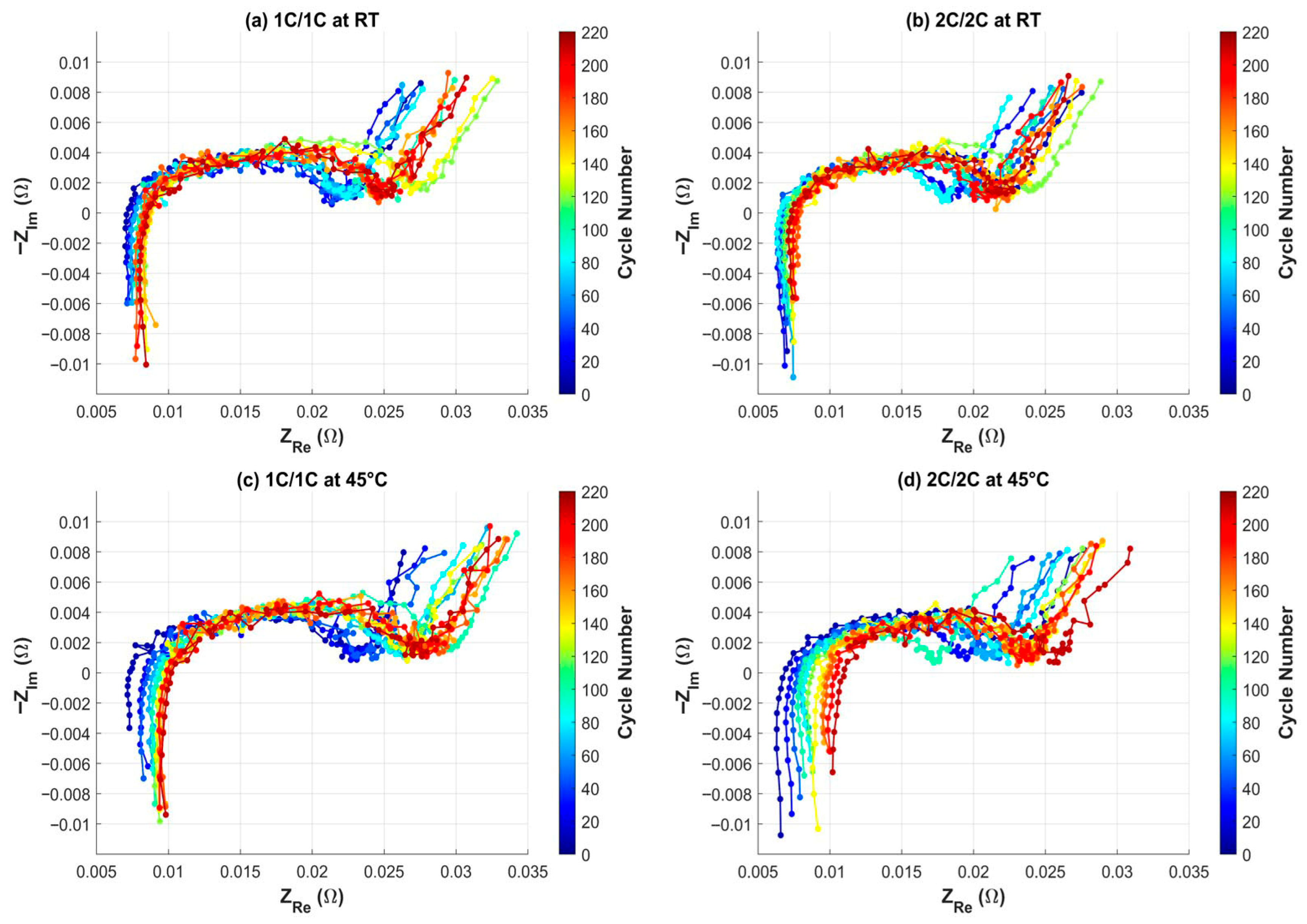
| Test Name | Voltage Limits | C-Rate | Temperature |
|---|---|---|---|
| Charge Discharge Cycling | 3.0 V to 4.20 V | 1 C | 25 ± 3 °C |
| 3.0 V to 4.20 V | 2 C | 25 ± 3 °C | |
| 3.0 V to 4.20 V | 1 C | 45 °C | |
| 3.0 V to 4.20 V | 2 C | 45 °C | |
| Constant Voltage Charging | 3.0 V to 4.20 V–Hold at 4.20 V | 0.5 C | 25 ± 3 °C |
| 3.0 V to 4.20 V–Hold at 4.20 V | 0.5 C | 45 °C | |
| 3.0 V to 4.23 V–Hold at 4.23 V | 0.5 C | 25 ± 3 °C | |
| 3.0 V to 4.23 V–Hold at 4.23 V | 0.5 C | 45 °C |
| Test Name | Voltage Limits | Temperature |
|---|---|---|
| Constant High Voltage Charging | 3.0 V to 4.30 V–Hold at 4.30 V | 35 °C |
| 3.0 V to 4.30 V–Hold at 4.30 V | 40 °C | |
| 3.0 V to 4.30 V–Hold at 4.30 V | 45 °C | |
| 3.0 V to 4.35 V–Hold at 4.35 V | 35 °C | |
| 3.0 V to 4.35 V–Hold at 4.35 V | 40 °C | |
| 3.0 V to 4.35 V–Hold at 4.35 V | 45 °C | |
| 3.0 V to 4.40 V–Hold at 4.40 V | 35 °C | |
| 3.0 V to 4.40 V–Hold at 4.40 V | 40 °C | |
| 3.0 V to 4.40 V–Hold at 4.40 V | 45 °C |
| ECM Parameters | Swelling Pearson’s Correlation Coefficient |
|---|---|
| Bulk Resistance | 0.50 |
| Charge Transfer Resistance | −0.03 |
| Double Layer Capacitance | −0.25 |
| Slope of Warburg Region | 0.16 |
| ECM Parameters | Swelling Pearson’s Correlation Coefficient |
|---|---|
| Bulk Resistance | 0.36 |
| Charge Transfer Resistance | 0.09 |
| Double Layer Capacitance | −0.25 |
| Slope of Warburg Region | −0.52 |
| Temperature | Voltage | R2 | |||||
|---|---|---|---|---|---|---|---|
| 35 °C | 4.40 V | −2.38 | −0.19 | 8.59 × 10−15 | 7.33 | 4.84 | 0.98 |
| 35 °C | 4.35 V | −2.04 | −0.61 | 1.03 × 10−14 | 6.65 | 2.82 | 0.95 |
| 35 °C | 4.30 V | −1.56 | −0.33 | 9.04 × 10−21 | 8.42 | 3.04 | 0.93 |
| 45 °C | 4.40 V | −0.90 | −0.04 | 4.84 × 10−10 | 6.39 | 3.83 | 0.97 |
| 45 °C | 4.35 V | −1.17 | −0.26 | 6.68 × 10−13 | 7.21 | 2.84 | 1.00 |
| 45 °C | 4.30 V | −1.33 | −0.17 | 1.67 × 10−14 | 7.07 | 2.54 | 0.99 |
| 40 °C | 4.40 V | −2.10 | −0.42 | 8.93 × 10−13 | 7.08 | 3.33 | 0.99 |
| 40 °C | 4.35 V | −1.96 | −0.55 | 8.85 × 10−15 | 7.19 | 3.59 | 0.98 |
| 40 °C | 4.30 V | −1.86 | −0.64 | 2.90 × 10−16 | 7.14 | 3.12 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maddipatla, S.; Kong, L.; Osterman, M.; Kim, J.; Pecht, M. The Impact of C-Rate, Float Charging and Temperature on Pouch Lithium-Ion Battery Swelling. Batteries 2025, 11, 419. https://doi.org/10.3390/batteries11110419
Maddipatla S, Kong L, Osterman M, Kim J, Pecht M. The Impact of C-Rate, Float Charging and Temperature on Pouch Lithium-Ion Battery Swelling. Batteries. 2025; 11(11):419. https://doi.org/10.3390/batteries11110419
Chicago/Turabian StyleMaddipatla, Sahithi, Lingxi Kong, Michael Osterman, Jonghoon Kim, and Michael Pecht. 2025. "The Impact of C-Rate, Float Charging and Temperature on Pouch Lithium-Ion Battery Swelling" Batteries 11, no. 11: 419. https://doi.org/10.3390/batteries11110419
APA StyleMaddipatla, S., Kong, L., Osterman, M., Kim, J., & Pecht, M. (2025). The Impact of C-Rate, Float Charging and Temperature on Pouch Lithium-Ion Battery Swelling. Batteries, 11(11), 419. https://doi.org/10.3390/batteries11110419











