Abstract
The exponential growth of lithium-ion battery consumption has amplified the urgency of identifying sustainable and economically viable recycling solutions. This study proposes an integrated decision-making framework based on the T-Spherical Fuzzy Einstein Interaction Aggregator DEMATEL-CoCoSo approach to comprehensively evaluate and rank battery recycling technologies under uncertainty. Ten key evaluation criteria—encompassing environmental, economic, and technological dimensions—were identified through expert consultation and literature synthesis. The T-Spherical Fuzzy DEMATEL method was first applied to analyze the causal interdependencies among criteria and determine their relative weights, revealing that environmental drivers such as energy consumption, greenhouse gas emissions, and waste generation exert the most systemic influence. Subsequently, six recycling alternatives were assessed and ranked using the CoCoSo method enhanced by Einstein-based aggregation, which captured the complex interactions present in the experts’ evaluations and assessments. Results indicate that Direct Recycling is the most favorable option, followed by the Hydrometallurgical and Bioleaching methods, while Pyrometallurgical Recycling ranked lowest due to its high energy demands and environmental burden. The proposed hybrid model effectively handles linguistic uncertainty, expert variability, and interdependent evaluation structures, offering a robust decision-support tool for sustainable technology selection in the circular battery economy. The framework is adaptable to other domains requiring structured expert-based evaluations under fuzzy environments.
1. Introduction
The exponential growth in the deployment of lithium-ion batteries has become one of the defining features of the 21st-century energy landscape. With global efforts directed at decarbonizing transport systems and integrating renewable energy sources, the demand for lithium-ion batteries is projected to increase by over 17-fold between 2019 and 2030, reaching more than 3.5 terawatt-hours of annual production [1]. This surge, while beneficial for climate goals, has triggered an equally pressing challenge: the accumulation of spent batteries. According to BloombergNEF, over 11 million metric tons of end-of-life lithium-ion batteries are expected to be retired globally by 2030, with projections reaching 29 million tons by 2040 [2]. If improperly managed, these batteries can leach toxic substances such as lithium, cobalt, and manganese into the environment, posing severe risks to ecosystems and human health. Furthermore, the flammable organic electrolytes they contain raise fire hazards during storage and disposal.
At the same time, spent batteries represent a significant secondary source of critical raw materials. As geopolitical competition over lithium, cobalt, and nickel intensifies—especially among nations with limited domestic reserves—the economic incentive to recover these materials through efficient recycling processes has grown sharply. It has been reported that the recovery of metals from used lithium-ion batteries could reduce mining needs by up to 25% for lithium and 35% for cobalt over the next decade [3]. Recycling also supports the circular economy by decreasing the carbon footprint associated with raw material extraction and battery manufacturing, contributing to long-term environmental and resource sustainability.
Beyond the techno-environmental arguments, the feasibility and prioritization of recycling routes are also strongly conditioned by geopolitical and macroeconomic realities. Trade partnerships, supply-chain dependencies, and policy instruments that respond to strategic vulnerabilities in lithium, cobalt, and nickel markets can reweight national preferences over recycling pathways, even when environmental criteria dominate in principle. For instance, countries with limited access to primary raw materials may emphasize technologies that maximize domestic material recovery and strategic autonomy, whereas jurisdictions with entrenched high-temperature metallurgical infrastructure may continue to rely on mature but emission-intensive routes in the short to medium term. Likewise, export restrictions, critical-minerals strategies, and industrial policy incentives can shift the relative attractiveness of capital-intensive versus low-emission technologies. Acknowledging these contextual forces underscores the value of a flexible decision framework that can incorporate heterogeneous weights and expert perceptions across jurisdictions, while still transparently revealing the trade-offs among environmental, economic, and technological objectives.
Given these stakes, the selection of an appropriate battery recycling technology has emerged as a strategic decision for governments, manufacturers, and recycling enterprises. A wide array of recycling technologies (RT) has been developed and is currently under evaluation, including pyrometallurgical, hydrometallurgical, direct recycling, mechanical processing, cryogenic treatment, and bioleaching techniques. These technologies vary greatly in terms of their environmental impact, material recovery rates, capital investment, operational costs, scalability, and technological readiness [4,5]. For instance, pyrometallurgical processes, while widely adopted, are highly energy-intensive—consuming more than 3.5 MWh per ton of batteries—and generate significant greenhouse gas emissions, often exceeding 2.9 tons of CO2 per ton [6]. On the other hand, hydrometallurgical processes use chemical leaching agents to recover metals with relatively lower emissions but require hazardous reagents and generate secondary liquid waste [7]. Novel approaches like direct recycling and bioleaching promise environmental advantages, but their industrial feasibility and maturity remain under question.
Evaluating these diverse technologies under conflicting criteria demands a rigorous decision-making framework. To this end, Multi-Criteria Decision-Making (MCDM) approaches have gained prominence for structuring complex evaluation problems in sustainability, resource management, and environmental engineering [8,9]. These methods enable the simultaneous consideration of multiple quantitative and qualitative criteria and allow expert judgments to guide the selection process. In the context of battery recycling, MCDM provides a mechanism to weigh the trade-offs between economic feasibility and environmental performance.
Among MCDM techniques, the Decision-Making Trial and Evaluation Laboratory (DEMATEL) and the Combined Compromise Solution (CoCoSo) methods are particularly well-suited for integrated use. DEMATEL enables the modeling of interdependencies and feedback relationships among evaluation criteria, distinguishing between cause and effect factors [10,11]. This capability is crucial when evaluating technologies that exhibit system-wide implications—for instance, how material recovery efficiency influences both capital cost and emissions [12,13]. On the other hand, CoCoSo provides a flexible yet comprehensive mechanism for aggregating weighted performance data and generating rankings of alternatives [14,15]. Unlike traditional scoring methods, CoCoSo synthesizes simple additive weighting, multiplicative utility, and compromise programming, producing robust and interpretable outcomes [16,17]. The combination of DEMATEL and CoCoSo thus delivers both structural insight and outcome prioritization in a single unified framework.
Despite their strength, traditional MCDM models typically rely on crisp numerical inputs or classical fuzzy sets, which may fail to adequately capture the linguistic ambiguity and hesitation inherent in expert judgments [18,19]. To overcome these challenges, the current study employs the T-Spherical Fuzzy Set (T-SFS) framework, a powerful generalization of fuzzy logic that introduces a tunable parameter to flexibly model the degrees of membership , hesitation , and non-membership () for each evaluation [20,21]. The constraint defines a hyperspherical boundary, capturing complex uncertainty in human reasoning beyond the capabilities of intuitionistic or traditional spherical fuzzy models. In addition to fuzzy modeling, this study incorporates Einstein aggregation operators, which are non-linear and interaction-aware—making them better suited for integrating expert evaluations than conventional arithmetic means. Two aggregation mechanisms are applied: the T-Spherical Fuzzy Weighted Einstein Interactive Geometric Aggregator (TSFWEIGA) and the T-Spherical Fuzzy Weighted Einstein Interactive Arithmetic Aggregator (TSFWEIAA). These operators account for interaction effects between membership, hesitancy, and non-membership components, yielding results that are more stable and expressive under uncertainty.
By integrating these components, a novel T-SFS DEMATEL-CoCoSo model with Einstein aggregation is proposed. In the first stage, the T-SFS-based DEMATEL is applied to quantify interdependencies among environmental and economic criteria, and derive their relative influence weights. In the second stage, these weights are fed into the CoCoSo method, which evaluates and ranks battery recycling technologies using expert assessments expressed as T-spherical fuzzy numbers. Both the DEMATEL and CoCoSo phases are conducted under the T-SFS environment with Einstein interaction operations to preserve the richness of expert information throughout the decision-making process.
The objectives of this study are as follows:
- To identify and structure the key environmental and economic evaluation criteria relevant to battery recycling technologies.
- To develop and apply a hybrid T-SFS DEMATEL-CoCoSo decision-making framework utilizing Einstein aggregation to address both interdependence and uncertainty.
- To demonstrate the model’s effectiveness in capturing ambiguous judgments and enabling the robust evaluation of battery recycling alternatives.
The remainder of this paper is structured as follows:
Section 2 presents the materials and methods, including the mathematical formulation of the T-SFS, the development of the DEMATEL and CoCoSo methods under the fuzzy environment, and the evaluation framework for battery recycling. Section 3 reports the results of the case application. Section 4 discusses the key insights and policy implications. Section 5 concludes the study and outlines avenues for future research.
2. Materials and Methods
2.1. Preliminaries
Definition 1
([22]). A T-spherical fuzzy set on the universe of discourse is defined as follows:
The notations and are the degree of membership, hesitancy, and non-membership of to , respectively. The refusal degree of in is defined as follows:
and the formula is known as the T-spherical number (T-SFN).
Definition 2
([22]). The score value of the T-SFN is defined as follows:
and the accuracy value of the T-SFN is defined as follows:
Remark 1.
Definitions 1 and 2 can be reduced for the following:
| (1) | PFS if t = 1; |
| (2) | SFS if t = 2; |
| (3) | q-ROFS if γ = 0; |
| (4) | PyFS if t = 2 and γ = 0; |
| (5) | IFS if t = 1 and γ = 0; |
| (6) | FS if t = 1, γ = 0, and β = 0. |
Definition 3
([22]). Consider two equations T-SFN and ; the comparison is defined as follows:
Definition 4
([23]). Consider two equations T-SFN and ; the Einstein interaction operations are defined as follows:
Remark 2.
Definition 3 can be reduced for the following:
| (1) | PFSs if t = 1; |
| (2) | SFSs if t = 2; |
| (3) | q-ROFSs if γ = 0; |
| (4) | PyFSs if t = 2 and γ = 0; |
| (5) | IFSs if t = 1 and γ = 0; |
| (6) | FSs if t = 1, γ = 0, and β = 0. |
Definition 5
([23]). Consider T-SFNs with ; the T-spherical fuzzy weighted Einstein interactive geometric aggregator (TSFWEIGA) and the T-spherical fuzzy weighted Einstein interactive arithmetic aggregator (TSFWEIAA) with the weight vector are defined as follows:
2.2. The T-Spherical Fuzzy Einstein Interaction Aggregator DEMATEL-CoCoSo
To evaluate complex decision problems under uncertainty, this study introduces an integrated approach that combines the T-Spherical Fuzzy Set theory with the DEMATEL and CoCoSo methods. The proposed framework, named the T-Spherical Fuzzy Einstein Interaction Aggregator DEMATEL-CoCoSo, enables the simultaneous analysis of interdependencies among evaluation criteria and the comprehensive ranking of alternatives under fuzzy and ambiguous information. The method incorporates the non-linear Einstein aggregation operator to effectively capture expert hesitation and interaction effects among fuzzy components. The complete evaluation process consists of 17 structured steps below:
Step 1. A group of decision-makers is identified, and their expertise is quantified using T-SFNs as shown Table 1. Each expert is assigned a normalized weight () based on the linguistic evaluation of their competence as Equation (15).

Table 1.
Linguistic terms for the expert decision-makers.
Step 2. Decision-makers define and validate the evaluation criteria . They then perform pairwise comparisons of these criteria using linguistic terms, which are converted into T-SFNs as shown in Table 2. As a result, the individual T-SFN direct influence matrices ( are established as Equation (16).

Table 2.
Linguistic terms for criteria influence.
Step 3. Individual direct influence matrices from each expert are aggregated into a single matrix as the T-SFN direct influence matrix using the TSFWEIAA, incorporating their respective weights :
where the following applies:
Step 4. The aggregated T-SFNs in the direct influence matrix are defuzzified using the T-SFS score function to obtain a crisp matrix suitable for linear algebraic operations:
where the following applies:
Step 5. The initial direct influence matrix is normalized as Equation (23):
where the following applies:
Step 6. The total influence matrix is derived, capturing both direct and indirect relationships among criteria according to Equation (25):
Step 7. In this step, the row sum and the column sum of the total influence matrix are computed according to Equations (26) and (27). The prominence and relation values for each criterion are calculated from the total influence matrix. The criterion can be grouped into the cause group if is positive. Conversely, if is negative, the criterion is influenced by the other criteria. Then, it can be grouped into the effect group. The prominence represents the strength of influence that is received or given by the criterion.
Step 8. A four-quadrant Network Relation Map (NRM) is constructed based on prominence and relation values, helping visualize the causal structure of criteria. By calculating the mean of prominence , the NRM can be divided into four quadrants as illustrated in Figure 1. Based on the criteria’s position on four-quadrant NRM, decision-makers can visually detect the complex causal relationships among criteria and further spotlight valuable insights for decision-making.
Figure 1.
The four-quadrant NRM.
Step 9. The weight of each criterion is determined by normalizing the prominence value across all criteria, forming the final importance vector.
Step 10. Experts evaluate each alternative against each criterion using linguistic terms, which are transformed into T-SFNs as shown in Table 3 to form T-SFN individual decision matrices ().

Table 3.
Linguistics terms and corresponding T-SFNs for the decision matrix.
Step 11. These matrices are aggregated using TSFWEIAA based on expert weights, resulting in the final fuzzy decision matrix:
where the following applies:
Step 12. Based on the Einstein T-SFN aggregated decision matrix and obtained the criteria weight , the T-spherical fuzzy weighted Einstein interactive arithmetic mean sequence and the T-spherical fuzzy weighted Einstein interactive geometric mean sequence of each alternative are determined as follows:
Step 13. The score values of and are calculated according to Equation (4).
Step 14. The additive normalized importance , the relative importance , and the trade-off importance of each alternative with the trade-off coefficient are determined.
Step 17. Based on the final score (, alternatives are ranked in order of priority to support strategic decision-making.
3. Results
3.1. Problem Description
The rapid advancement of electric vehicles and portable electronic devices has resulted in a substantial increase in lithium-ion battery consumption worldwide. As these batteries reach their end-of-life phase, a significant challenge arises in managing the resultant battery waste. Recycling technologies (RTs) offer an effective pathway not only to reduce environmental burdens but also to recover valuable materials such as lithium, cobalt, and nickel. However, selecting the most appropriate recycling method involves complex trade-offs among technical, environmental, and economic factors, often complicated by expert subjectivity and imprecision. To address this multi-faceted decision-making problem, the present study employs a T-Spherical Fuzzy Einstein Interaction Aggregator DEMATEL-CoCoSo approach to evaluate and rank six prominent battery recycling technologies.
Six recycling technology alternatives have been identified for this study based on their technological maturity, industrial relevance, and potential contribution to sustainability goals. These alternatives span a spectrum from established large-scale processes to novel experimental methods still under development. Their selection is grounded in both current industrial applications and state-of-the-art academic research on battery recycling, as documented in recent studies by Harper et al. (2019), Lv et al. (2018), and more recently by the IEA Global EV Outlook (2023) [1,3,24].
RT1, Mechanical Processing, represents one of the most conventional and widely used recycling methods. It involves the physical disassembly and separation of battery components through crushing, shredding, sieving, and magnetic sorting. This approach is generally employed as a preliminary stage before other chemical or thermal treatments and is favored for its operational simplicity, low energy requirements, and compatibility with automated systems. However, its standalone recovery rates for critical metals such as lithium and cobalt are low, making it insufficient without downstream processing [25,26].
RT2, Direct Recycling, is an innovative method that seeks to preserve and rejuvenate the original cathode material without decomposing it into elemental metals. By maintaining the crystal structure of the active materials, this approach reduces energy consumption and chemical use compared to hydrometallurgical and pyrometallurgical methods. Although it offers substantial environmental advantages, its commercial adoption remains limited due to challenges in adapting the process to a variety of battery chemistries, formats, and degradation states [27].
RT3, Hydrometallurgical Recycling, is a chemical extraction method in which metals such as lithium, nickel, and cobalt are leached from battery components using acid or base solutions. This process has gained attention for its relatively high recovery efficiency and lower greenhouse gas emissions compared to pyrometallurgical methods. Nevertheless, it requires substantial water and chemical input and generates hazardous liquid waste that must be managed responsibly [7,27].
RT4, Pyrometallurgical Recycling, is among the most mature and industrially deployed methods. It involves high-temperature smelting, often above 1500 °C, to recover metals by reducing battery materials into alloy forms. While it is advantageous in terms of processing mixed or contaminated batteries, it suffers from several drawbacks—high energy consumption, poor lithium recovery, and significant CO2 emissions. Consequently, it is increasingly scrutinized for its environmental burden [3,6].
RT5, Bioleaching, utilizes specific microorganisms to biologically extract metals from battery waste through natural metabolic processes. This method is environmentally friendly and avoids the use of aggressive acids, but it is considerably slower than other chemical processes and remains in the pilot or laboratory testing phase. Scaling up for industrial applications poses both economic and logistical challenges [28,29].
RT6, Cryogenic Recycling, is a relatively novel technique in which batteries are cooled to extremely low temperatures using substances like liquid nitrogen. Once frozen, the batteries become brittle and can be fractured safely with minimal fire or explosion risk. This method offers promising safety benefits, especially for end-of-life batteries with unknown charge states. However, its commercial deployment is rare, and its cost-effectiveness and processing throughput require further validation [30,31].
The assessment of these recycling technologies is guided by a panel of ten experts, as presented in Table 4. The experts were selected based on their diverse academic backgrounds and industrial experience in environmental engineering, battery manufacturing, waste management, and sustainable materials. Their profiles represent a balance between practical implementation knowledge and theoretical insight. The group includes individuals with doctoral and master’s degrees as well as senior engineers and managers from research institutions, policy consultancy, and industry operations. Their professional experience ranges from 11 to 28 years, ensuring comprehensive and balanced perspectives on both current capabilities and future trends in battery recycling.

Table 4.
Expert profiles.
The evaluation framework employed in this study is based on ten comprehensive criteria, which were defined through expert consultation and an extensive review of contemporary academic literature and industrial guidelines in the fields of battery recycling, sustainability assessment, and circular economy. These criteria collectively reflect three primary dimensions: technical performance, environmental impact, and economic feasibility [3,5,19,24,30,31,32].
C1, Material Recovery Efficiency, quantifies the percentage of valuable materials successfully extracted from spent batteries. This indicator is central to assessing the recycling method’s contribution to material circularity. C2, Energy Consumption, captures the total energy required to process a unit of battery waste (e.g., kWh/ton), serving as a proxy for environmental and economic efficiency. C3, Operating Cost, includes recurring expenses such as energy use, labor, chemicals, and maintenance, and directly affects the economic viability of a recycling facility. C4, Greenhouse Gas Emissions, reflects the climate change impact of each technology, typically measured in CO2-equivalent emissions, and is a critical sustainability performance metric.
C5, Technological Maturity, indicates how advanced technology is on the scale from research development to commercial deployment. High maturity reduces uncertainty and facilitates rapid scaling. C6, Capital Investment, denotes the upfront infrastructure cost required to implement the recycling facility and is often a barrier for new entrants or emerging methods. C7, Market Value of Recovered Materials, considers the revenue potential based on the economic worth of extracted outputs such as lithium, cobalt, and nickel. This criterion is influenced by both material purity and market demand. C8, Payback Period, represents the duration needed to recoup capital investment and reflects long-term economic feasibility.
C9, Toxic Chemical Usage, assesses the degree to which a recycling process depends on hazardous substances, which can pose operational and regulatory risks. Finally, C10, Waste Generation, accounts for the quantity and type of byproducts—solid, liquid, or gaseous—that must be handled post-process. Minimizing waste output is essential for reducing the ecological footprint of battery recycling technologies.
3.2. The T-SFN DEMATEL-CoCoSo Results
In this section, the results of the integrated decision-making process are presented, applying the T-Spherical Fuzzy Number (T-SFN) based DEMATEL-CoCoSo methodology to evaluate the interrelations among criteria and the overall performance of battery recycling technologies. The analysis was conducted using expert assessments, aggregated under T-SFN representations, to capture the inherent uncertainty and hesitation in linguistic judgments. First, the DEMATEL component identifies the causal relationships and weights among the ten evaluation criteria, supporting the construction of a four-quadrant Network Relation Map (NRM). Subsequently, the CoCoSo method ranks the six recycling technologies based on aggregated performance values across all criteria. This dual-phase process facilitates a comprehensive understanding of both the structural influence of decision criteria and the relative desirability of each alternative. The following subsections detail the computational results and corresponding interpretations derived from the hybrid model.
Based on the expert profiles outlined in Section 3.1, linguistic qualifications representing each expert’s level of expertise were assigned by the authors, in consultation with domain-specific benchmarks in battery recycling and environmental systems engineering.
In total, ten experts were selected to participate in the linguistic evaluation and influence matrix construction process. These individuals represent a broad spectrum of expertise across environmental engineering, battery recycling operations, life cycle assessment, and policy advisory roles. While the number of experts might appear limited, it is consistent with established guidelines in fuzzy decision-making research, where expert panels typically range from five to fifteen members to ensure a balance between judgment diversity and result coherence.
Moreover, the selected panel includes individuals with varying academic qualifications (Ph.D., M.Sc., M.Eng., etc.) and professional experiences ranging from 11 to 28 years, enhancing the credibility and generalizability of the input data. This size also allowed for effective computation within the T-Spherical Fuzzy framework, ensuring the manageable aggregation of expert opinions without introducing excessive variability.
These qualifications were expressed using T-SFNs, allowing for the nuanced incorporation of partial belief, uncertainty, and hesitation in expert judgment. Utilizing Equation (15), the individual weights of the ten decision-makers were then calculated to reflect their relative influence in the aggregation process. This weighting ensures that experts with more substantial domain experience and academic or industrial standing contribute proportionally to the final decision matrix. The computed weights for each expert, along with their corresponding linguistic terms and fuzzy parameters, are summarized in Table 5, forming the foundational input for the subsequent aggregation of influence and evaluation matrices.

Table 5.
Experts’ linguistic qualifications and weights.
After assigning weights to the experts, each decision-maker was asked to provide linguistic evaluations of the degree of influence among the ten assessment criteria. Table 6 presents the linguistic judgments made by Expert 1. These pairwise evaluations reflect the perceived causal relationships—indicating how one criterion may impact another—in the context of assessing battery recycling technologies. The linguistic terms used by the experts, such as “No Influence,” “Weak Influence,” “Moderate Influence,” and “Strong Influence,” were systematically translated into T-SFNs based on the scale outlined in Table 2. This conversion enables the inherently imprecise and subjective expert assessments to be expressed and analyzed mathematically. The matrix provided by Expert 1 is shown in Table 7, while the corresponding matrices from Experts 2 to 10 are detailed in Tables S1–S9 in the Supplementary Materials.

Table 6.
The criteria influencing the linguistic judgment of Expert 1.

Table 7.
The individual T-SFN direct influence matrix by Expert 1.
To consolidate the diverse perspectives of the expert panel, the individual T-SFN direct influence matrices were aggregated using the T-Spherical Fuzzy Weighted Einstein Interaction Averaging Aggregator (TSFWEIAA), which integrates the expert weights derived in Equation (15). This aggregation was performed according to Equations (18)–(20), where each element of the final T-SFN direct influence matrix was computed as the weighted average of the corresponding elements across all expert matrices. Specifically, the , , and components of each fuzzy number were aggregated using the respective expert weights, ensuring that the more experienced and knowledgeable experts exerted a proportionally greater influence on the resulting matrix as shown in Table 8.

Table 8.
The T-SFN direct influence matrix.
Once the aggregated T-SFN direct influence matrix was established, defuzzification was performed to convert the fuzzy values into crisp scores suitable for quantitative analysis. According to Equation (22), the defuzzification of each T-SFN element was calculated by taking the difference between the powered truth-membership degree () and the powered falsity-membership degree (), where is the parameter that determines the defuzzification sensitivity. This scalar transformation enables the interpretation of fuzzy relationships in a numerical form while preserving the essence of uncertainty embedded in the original linguistic judgments. The result of this operation is the defuzzified direct influence matrix, which quantifies the intensity of influence from each criterion to another in crisp numerical terms as shown in Table 9. The defuzzified matrix is presented in Table 9, providing a clear and interpretable structure that facilitates further analysis in the DEMATEL methodology, including normalization and total influence computation.

Table 9.
The direct influence matrix.
Following defuzzification, the direct influence matrix was normalized to ensure comparability across all criteria. This was achieved by applying Equation (24), which scales the influence values based on the maximum row and column sums of the defuzzified matrix. The normalization process guarantees that all influence scores remain within a standardized range, preserving proportional relationships while avoiding dominance by any particular criterion. The resulting normalized matrix is presented in Table 10, serving as the basis for the subsequent total influence calculations. Subsequently, the total influence matrix was derived using Equation (25), which integrates both direct and indirect influences among criteria as shown in Table 11. This matrix reflects the complete influence of each criterion on every other, including all intermediate pathways of impact, thereby capturing the systemic nature of interdependencies.

Table 10.
The initial direct influence matrix.

Table 11.
The total influence matrix.
Using the total influence matrix derived in the previous step, the prominence and relation values of each criterion were computed in accordance with Equations (28) and (29), respectively. The prominence value represents the total strength of influence (both given and received) of a criterion, indicating its overall centrality within the decision-making system. Conversely, the relation value determines whether a criterion primarily acts as a cause (positive value) or effect (negative value) in the network of interrelations. The calculated values for all ten criteria are presented in Table 12.

Table 12.
The prominence and relation value of the criteria.
To further visualize the causal relationships among the criteria, a Network Relations Map (NRM) was constructed based on the computed prominence and relation values as shown in Figure 2. The NRM utilizes a Cartesian coordinate system in which each criterion is plotted according to its prominence (r + c) on the horizontal axis and its relation (r − c) on the vertical axis. This allows for the categorization of criteria into two distinct groups: the cause group (positive relation values) and the effect group (negative relation values). The cause group comprises the criteria that exert a stronger influence on others, making them pivotal levers for strategic decision-making, whereas the effect group contains those more influenced by external factors. The mean of the prominence values was used as the threshold to divide the map into four quadrants, highlighting the relative impact and influence dynamics of each criterion.
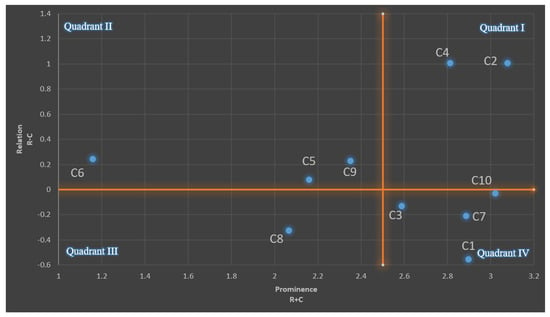
Figure 2.
The network relations map.
Criteria located in Quadrant I, namely C2 (Energy Consumption) and C4 (Greenhouse Gas Emissions), exhibit high prominence and positive relation scores, signifying that they are key causal drivers in the evaluation system. Their positions indicate a strong influence over other criteria, reaffirming their critical roles in the environmental sustainability assessments of recycling technologies. In contrast, C6 (Capital Investment) is located in Quadrant II, implying it functions as a cause but with relatively lower systemic influence—often serving as an enabler rather than a central determinant. Meanwhile, C8 (Payback Period), positioned in Quadrant III, represents a downstream criterion with low prominence and a negative relation, suggesting that it is influenced by other factors but does not substantially affect the system itself. Most notably, Quadrant IV contains a cluster of high-prominence but negative-relation criteria, including C1 (Material Recovery Efficiency), C3 (Operating Cost), C7 (Market Value of Recovered Materials), and C10 (Technological Maturity). These criteria act primarily as effect variables, indicating they are strongly influenced by the system’s causal dynamics. Lastly, C5 (Technological Maturity) and C9 (Toxic Chemical Usage) appear near the origin, suggesting a more balanced role, where they exhibit moderate bidirectional influence.
Based on these results, the normalized weight (as illustrate in Figure 3) for each criterion was determined using Equation (30). Among all criteria, Energy Consumption (0.123) and Waste Generation (0.121) received the highest weights, indicating that environmental performance factors are prioritized by experts when evaluating alternative technologies. This aligns with the findings of recent studies emphasizing the central role of energy efficiency and waste minimization in sustainable recycling systems [1,2]. Closely following is Material Recovery Efficiency (0.116) and Market Value of Recovered Materials (0.115), reflecting a balanced emphasis on both environmental and economic outcomes—specifically, how effectively and profitably that valuable materials such as lithium, cobalt, and nickel can be recovered. The weight for Greenhouse Gas Emissions (0.112) further confirms the significant concern among experts regarding climate impacts, underscoring the necessity to evaluate emissions-intensive methods like pyrometallurgy with caution.
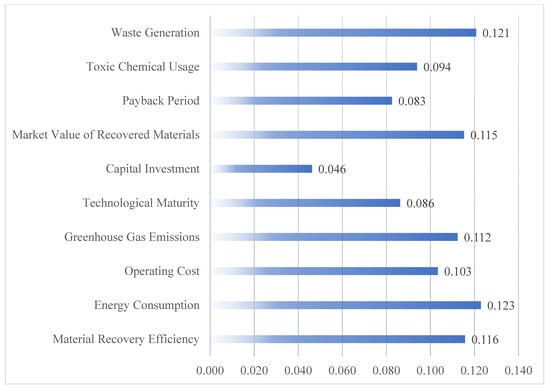
Figure 3.
The criteria weights.
Operating Cost (0.103) and Toxic Chemical Usage (0.094) hold moderate importance, suggesting that while economic efficiency and chemical safety are valued, they are not considered as critical as recovery effectiveness or energy-related impacts. Interestingly, Technological Maturity (0.086) and Payback Period (0.083) were assigned comparatively lower weights. This may reflect a growing willingness among experts to tolerate developmental uncertainty or delayed returns in favor of long-term environmental benefits. Capital Investment (0.046) received the lowest weight, indicating that initial cost alone is not a dominant consideration in the decision-making process—likely due to expectations of scale economies or public subsidies in the context of circular economy initiatives.
In Step 10, each of the ten experts was asked to evaluate the six battery recycling technologies across the ten previously defined criteria using linguistic terms that reflect their judgment of each alternative’s performance. These linguistic evaluations—ranging from “Extremely Low” to “Extremely High”—were converted into T-SFNs based on the standardized scale presented in Table 3. The linguistic evaluations by Expert 1 are shown in Table 13. This process enabled the incorporation of uncertainty, hesitation, and partial truth into the decision model, offering a richer and more realistic representation of expert opinions. The resulting evaluations formed ten individual T-SFN decision matrices. These matrices capture the nuanced expert assessments of the performance of each recycling technology with respect to each criterion under the T-SFS framework. The decision matrix of Expert 1 is presented in Table 14, while the matrices for Experts 2 through 10 are provided in Tables S10–S18 in the Supplementary Materials.

Table 13.
The individual linguistic decision matrix for Expert 1.

Table 14.
The individual T-SFN decision matrix for Expert 1.
In Step 11, the individual T-SFN decision matrices provided by each expert were aggregated to form a unified evaluation matrix that captures the collective judgment of the decision-making group. This aggregation was performed using the TSFWEIAA, as defined in Equation (12), where the previously determined expert weights were used to account for the varying levels of expertise across participants. For each element in the decision matrix, the (membership), (hesitation), and (non-membership) values were aggregated across all experts using Equations (33)–(35). This process preserved the interaction among fuzzy components and ensured that more credible expert evaluations exerted a stronger influence on the aggregated result. The output is a comprehensive aggregated T-SFN decision matrix, denoted by , which synthesizes performance assessments of all six recycling technologies across the ten criteria under fuzzy uncertainty. The aggregated matrix is presented in Table 15.

Table 15.
The T-SFN decision matrix.
In the next step, the aggregated T-Spherical Fuzzy Decision Matrix and the criteria weights derived from the T-SFN DEMATEL process were used to compute the T-Spherical Fuzzy Weighted Einstein Interactive Arithmetic Mean sequence () and Geometric Mean sequence () for each recycling technology alternative. The Einstein interaction operators enable a more robust handling of the interaction effects between criteria and preserve the non-linear relationships in fuzzy information. Specifically, for each alternative, the arithmetic sequence was calculated by applying the weighted Einstein summation across all criteria, as defined in Equation (36), while the geometric sequence was derived using the weighted Einstein product, as shown in Equation (37).
These fuzzy outputs were then defuzzified using the score function defined in Equation (4), resulting in crisp scores that reflect both the additive and multiplicative aggregation perspectives of the alternatives’ performance. The resulting , , , and values for each recycling technology are presented in Table 16, laying the foundation for the final ranking procedure.

Table 16.
Mean sequences of CoCoSo.
In Step 14, the additive normalized importance (), relative importance (), and trade-off importance () scores were computed for each recycling technology alternative to facilitate a comprehensive evaluation. The score, determined using Equation (38), represents the normalized aggregation of both arithmetic and geometric scores and reflects the overall magnitude of performance. The score, calculated through Equation (39), evaluates each alternative’s performance relative to the minimum observed AS and GS values, thereby emphasizing deviation from the least desirable performance. The score incorporates a trade-off coefficient = 0.5 (representing an equal balance between AS and GS) and is computed using Equation (40) to reflect the weighted preference between additive and multiplicative information aggregation. These three indicators offer a well-rounded view of each alternative’s performance under various analytical perspectives. The resulting values for , , and are summarized in Table 17, which forms the basis for deriving the final composite score.

Table 17.
The additive normalized importance, relative importance, and trade-off importance.
In the last step, the final evaluation score () for each recycling technology was calculated by combining the additive normalized importance (), relative importance (), and trade-off importance () using Equation (41). This scoring approach captures both linear and non-linear aggregation perspectives by averaging the three components and incorporating the cube root of their sum to emphasize balanced performance. The resulting κi scores represent a synthesized evaluation index that supports robust ranking among the six considered recycling technology alternatives. As summarized in Figure 4, the highest score corresponds to the most preferred alternative under the T-Spherical Fuzzy Einstein Aggregator DEMATEL-CoCoSo framework.
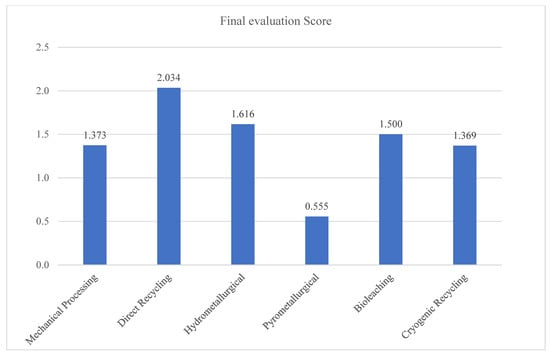
Figure 4.
The final score of RT by the T-Spherical Fuzzy Einstein Interaction Aggregator DEMATEL-CoCoSo.
The final evaluation results, summarized in Figure 4, provide a comprehensive ranking of six prominent battery recycling technologies based on the T-Spherical Fuzzy DEMATEL-CoCoSo methodology. The findings reflect a multi-dimensional synthesis of technical, environmental, and economic criteria under expert uncertainty, with each technology evaluated against ten strategically weighted factors. The highest-ranked alternative is Direct Recycling ( = 2.034), which outperforms all others in terms of overall performance. This result strongly aligns with its conceptual advantages, namely, its ability to retain the functional structure of cathode materials, reduce processing complexity, and minimize both energy consumption and chemical usage. While Direct Recycling still faces challenges in commercial scalability, standardization, and adaptation to various chemistries, the model clearly indicates its high potential under sustainability and circular economic objectives. The method’s top position suggests that, with continued research and industrial refinement, it could serve as a core technology for future battery recycling frameworks, especially in closed-loop systems.
The second-ranked technology, Hydrometallurgical Recycling (= 1.616), also demonstrates strong performance. This method has become increasingly popular due to its ability to extract high-purity metals using aqueous chemistry, with relatively lower energy requirements compared to pyrometallurgy. Its placement reflects a balanced trade-off between technical maturity, high recovery efficiency, and acceptable environmental impacts. However, concerns over chemical waste generation and complex process control remain key limitations that prevent it from surpassing direct recycling in this evaluation. Bioleaching ranks third (= 1.500), affirming its recognition as a promising green alternative. Its environmentally benign nature—operating without high temperatures or toxic reagents—contributes positively to criteria such as greenhouse gas emissions and toxic chemical usage. Nonetheless, its lower technological maturity and slower kinetics restrict its current viability at industrial scale, and these constraints are reflected in its mid-tier score.
Mechanical Processing ( = 1.373) ranks fourth, highlighting its role as a cost-effective and energy-efficient option, particularly as a pre-treatment step in integrated recycling systems. Despite these advantages, its inability to recover valuable elements such as lithium and cobalt in their pure forms places a ceiling on its overall utility. The marginal difference in score between mechanical processing and Cryogenic Recycling ( = 1.369), which ranks fifth, suggests comparable but distinct trade-offs. Cryogenic methods offer enhanced safety and fire mitigation—particularly valuable when dealing with unstable or unknown battery states—but suffer from high capital and operational costs as well as limited throughput, which hinder broader industrial adoption. The proximity of their scores indicates that both methods may serve niche roles depending on specific operational contexts.
At the bottom of the ranking is Pyrometallurgical Recycling ( = 0.555), a result that is consistent with growing criticism in both academic and industrial circles. Although this method is technologically mature and widely implemented, it is penalized in this evaluation due to its severe environmental drawbacks, including excessive energy use, high greenhouse gas emissions, and limited recovery of lithium—a metal that is increasingly prioritized due to its strategic importance. Its placement suggests that, while reliable and established, pyrometallurgy is no longer aligned with modern sustainability standards and must be complemented or replaced by cleaner and more efficient alternatives.
4. Discussion
This study aimed to provide a comprehensive evaluation and prioritization of six major battery recycling technologies under a multi-criteria framework, integrating both expert judgment and uncertainty modeling. By employing the T-Spherical Fuzzy Einstein Interaction Aggregator DEMATEL-CoCoSo approach, the methodology enabled a two-phase analysis—first, to determine the causal relationships and relative importance of ten evaluation criteria using T-SFN DEMATEL, and second, to aggregate expert assessments of each alternative using the CoCoSo method under a fuzzy decision-making environment. The findings reveal significant insights into both the structure of decision criteria and the comparative performance of the recycling technologies.
The results of the DEMATEL phase indicate that Energy Consumption, Greenhouse Gas Emissions, and Waste Generation are among the most influential criteria in the decision model, placing environmental sustainability at the forefront of expert concerns. These criteria not only received high prominence scores but were also positioned in the cause group of the NRM, confirming their role as primary drivers in the evaluation structure. This supports previous findings in the literature that emphasize the urgent need to decarbonize recycling processes and minimize resource use and emissions in end-of-life battery treatment [24,33]. Conversely, criteria such as Payback Period and Operating Cost were classified as effect criteria, suggesting that economic performance is more a consequence of technological and environmental characteristics than a determinant of them. This structural understanding is critical for strategic planning and highlights where intervention and innovation should be prioritized.
The CoCoSo phase further confirms these insights by revealing Direct Recycling as the most favorable alternative. Its top rank reflects its strong performance across environmental, economic, and technical dimensions, particularly in material recovery efficiency, low energy use, and minimal emissions. Although it is not yet fully commercialized, its conceptual advantages signal that it may serve as a future benchmark for sustainable battery recycling practices. Hydrometallurgical and Bioleaching methods also performed well, suggesting that wet-chemical and biological recovery processes offer balanced trade-offs in terms of recovery efficiency and environmental compliance. However, their limitations in chemical usage and processing speed, respectively, underscore the need for ongoing research and process optimization.
In contrast, Pyrometallurgical Recycling, despite its wide industrial adoption, ranked last due to its high energy demands, low lithium recovery, and substantial greenhouse gas emissions. This result is consistent with recent sustainability assessments that question the long-term viability of thermal recovery methods in a low-carbon economy [6]. Interestingly, Mechanical Processing and Cryogenic Recycling occupied the mid-range positions, indicating potential utility as support technologies, particularly in hybrid or pre-treatment configurations. Their relative strength lies in safety and cost-effectiveness, though their standalone material recovery capabilities are limited.
Furthermore, the integration of the T-SFS theory and Einstein aggregation operators offered a distinct methodological advantage. This combination allowed the model to better handle the linguistic uncertainty and interaction effects inherent in group decision-making processes. The approach also preserved the richness of expert input without reducing complex subjective evaluations to single crisp values prematurely, a limitation common in conventional MCDM models. The use of both arithmetic and geometric aggregation in CoCoSo enabled a balanced consideration of additive and multiplicative utility, increasing the robustness of the final ranking outcomes.
Despite the robust performance of the proposed T-Spherical Fuzzy DEMATEL-CoCoSo framework, several limitations warrant consideration. First, the model relies on expert judgment for both the weighting of criteria and the evaluation of alternatives. While a diverse panel of experts was selected and weighted to mitigate bias, subjectivity remains an inherent limitation that could influence outcomes, especially in domains with limited empirical data. Second, the model assumes consistency in expert assessments, yet varying cognitive biases and contextual backgrounds may introduce uncertainty. Third, although the Direct Recycling and Hydrometallurgical methods rank highest in this analysis, their scalability and industrial readiness may vary significantly across regions depending on regulatory environments, infrastructure, and supply-chain integration. These contextual factors could limit the generalizability of the findings. Lastly, while T-spherical fuzzy logic improves the handling of ambiguity and hesitancy in linguistic inputs, its mathematical complexity may pose a barrier to broader adoption without computational support tools. Future research may explore the integration of probabilistic sensitivity analysis or cross-validation using empirical performance data to further enhance model robustness and applicability.
5. Conclusions
This study proposed and applied an integrated T-Spherical Fuzzy Einstein Interaction Aggregator DEMATEL-CoCoSo framework to evaluate and rank six prominent battery recycling technologies under uncertain and subjective expert assessments. Recognizing the growing environmental and economic significance of end-of-life battery management, the research addressed the complex, interrelated nature of evaluation criteria while incorporating linguistic ambiguity and decision-maker expertise diversity.
The model was executed in two major phases. First, the T-Spherical Fuzzy DEMATEL method was used to identify causal relationships among ten key evaluation criteria across environmental, economic, and technological dimensions. Results revealed that Energy Consumption, Greenhouse Gas Emissions, and Waste Generation were the most influential drivers—reflecting the increasing priority of environmental sustainability in battery recycling decisions. Second, the CoCoSo method—enhanced with Einstein-based aggregation—was employed to derive final performance scores. This phase synthesized expert evaluations with criteria weights to produce a robust, transparent ranking of technologies.
Key findings include the following:
- Direct Recycling emerged as the most favorable method, offering superior performance in energy efficiency, material recovery, and low emissions.
- Hydrometallurgical and Bioleaching ranked second and third, balancing environmental performance with operational feasibility.
- Pyrometallurgical Recycling, despite its maturity, ranked lowest due to its high energy demands and low lithium recovery, underscoring the misalignment between industrial prevalence and environmental sustainability.
- Mechanical Processing and Cryogenic Recycling occupied middle ranks, showing promise as niche or pre-treatment options.
Beyond empirical results, this study demonstrates the utility of T-Spherical Fuzzy logic and Einstein aggregation in capturing expert hesitation, preserving information richness, and modeling interdependencies. The unified causal-performance framework offers enhanced interpretability and decision confidence.
These insights have practical significance. For policymakers, the results support prioritizing low-emission technologies through targeted incentives and regulatory strategies. For industry stakeholders, the ranking highlights scalable and sustainable investment directions. For researchers, the framework offers a flexible, uncertainty-aware approach applicable to other complex sustainability decisions.
Future research may extend this framework along several concrete directions. First, incorporating real-world operational data—such as lifecycle CO2 emissions, metal recovery yields, reagent consumption, and processing costs from pilot-scale recycling plants—would enhance the empirical robustness of evaluation results. Such integration can refine assumptions and reduce reliance on purely expert-based assessments. Second, the methodology is well-suited for adaptation to electronic waste (e-waste) recycling decisions, where similar multi-criteria trade-offs between material recovery, hazardous waste management, and cost efficiency exist. Third, the framework can be applied to electric vehicle (EV) supply-chain resilience analysis, assessing recycling strategies as a mitigation mechanism for material criticality and geopolitical supply risks. Finally, the model could be expanded to include scenario analysis or dynamic criteria weighting, enabling decision-makers to simulate the impact of shifting policy, market, or technological conditions. These directions would not only improve the model’s fidelity but also broaden its relevance to sustainable transition planning across interconnected domains.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/batteries11080294/s1.
Author Contributions
Conceptualization, N.-L.N. and Y.-H.W.; methodology, N.-L.N. and Y.-H.W.; software, N.-L.N.; validation, N.-L.N., Y.-H.W., and C.-N.W.; formal analysis, N.-L.N.; investigation, N.-L.N.; re-sources, N.-L.N.; data curation, N.-L.N.; writing—original draft preparation, N.-L.N. and Y.-H.W.; writing—review and editing, N.-L.N., Y.-H.W., and C.-N.W.; visualization, N.-L.N.; supervision, C.-N.W.; project administration, C.-N.W.; funding acquisition, C.-N.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study is partially funded by the University of Economics Ho Chi Minh City (UEH), Ho Chi Minh City, Vietnam.
Data Availability Statement
The original contributions presented in this study are included in the article and Supplementary Material. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- International Energy Agency. Global Ev Outlook 2023; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Colin, M. Electric Vehicle Outlook 2024; BloombergNEF: London, UK, 2024. [Google Scholar]
- Harper, G.; Sommerville, R.; Kendrick, E.; Driscoll, L.; Slater, P.; Stolkin, R.; Walton, A.; Christensen, P.; Heidrich, O.; Lambert, S.; et al. Recycling Lithium-Ion Batteries from Electric Vehicles. Nature 2019, 575, 75–86. [Google Scholar] [CrossRef]
- Gaines, L. The Future of Automotive Lithium-Ion Battery Recycling: Charting a Sustainable Course. Sustain. Mater. Technol. 2014, 1–2, 2–7. [Google Scholar] [CrossRef]
- Liu, C.; Lin, J.; Cao, H.; Zhang, Y.; Sun, Z. Recycling of Spent Lithium-Ion Batteries in View of Lithium Recovery: A Critical Review. J. Clean. Prod. 2019, 228, 801–813. [Google Scholar] [CrossRef]
- Rajaeifar, M.A.; Raugei, M.; Steubing, B.; Hartwell, A.; Anderson, P.A.; Heidrich, O. Life Cycle Assessment of Lithium—Ion Battery Recycling Using Pyrometallurgical Technologies. J. Ind. Ecol. 2021, 25, 1560–1571. [Google Scholar] [CrossRef]
- Chen, Q.; Lai, X.; Chen, J.; Yao, Y.; Guo, Y.; Zhai, M.; Han, X.; Lu, L.; Zheng, Y. Comparative Environmental Impacts of Different Hydrometallurgical Recycling and Remanufacturing Technologies of Lithium-Ion Batteries Considering Multi-Recycling-Approach and Temporal-Geographical Scenarios in China. Sep. Purif. Technol. 2023, 324, 124642. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Goswami, S.S. A Comprehensive Review of Multiple Criteria Decision-Making (Mcdm) Methods: Advancements, Applications, and Future Directions. Decis. Mak. Adv. 2023, 1, 25–48. [Google Scholar] [CrossRef]
- Magableh, G.M.; Bazel, N.K. Exploring Future Renewable Energy Technologies Using a Developed Model and a Variety of Mcdm Approaches. Sustainability 2025, 17, 3057. [Google Scholar] [CrossRef]
- Gül, S. Spherical Fuzzy Extension of Dematel (Sf-Dematel). Int. J. Intell. Syst. 2020, 35, 1329–1353. [Google Scholar] [CrossRef]
- Eti, S.; Dinçer, H.; Yüksel, S.; Gökalp, Y. Analysis of the Suitability of the Solar Panels for Hospitals: A New Fuzzy Decision-Making Model Proposal with the T-Spherical Top-Dematel Method. J. Intell. Fuzzy Syst. 2023, 44, 4613–4625. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, T.-D.; Nhieu, N.-L.; Hsueh, M.-H. A Novel Psychological Decision-Making Approach for Healthcare Digital Transformation Benchmarking in Asean. Appl. Sci. 2023, 13, 3711. [Google Scholar] [CrossRef]
- Kim, D.; Kim, M. Hybrid Analysis of the Decision-Making Factors for Software Upgrade Based on the Integration of Ahp and Dematel. Symmetry 2022, 14, 172. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nhieu, N.-L.; Tran, H.-V. Wave Energy Site Location Optimizing in Chile: A Fuzzy Serial Linear Programming Decision-Making Approach. Environ. Dev. Sustain. 2024, 1–25. [Google Scholar] [CrossRef]
- Nhieu, N.-L.; Dang, T.D. Harnessing Vietnam’s Coastal Potential: Prioritizing Marine Energy Technologies with an Objectively Weighting Decision-Making Approach. Renew. Energy 2024, 230, 120881. [Google Scholar] [CrossRef]
- Yazdani, M.; Zarate, P.; Zavadskas, E.K.; Turskis, Z. A Combined Compromise Solution (Cocoso) Method for Multi-Criteria Decision-Making Problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar] [CrossRef]
- Kumar, V.; Kalita, K.; Chatterjee, P.; Zavadskas, E.K.; Chakraborty, S. A Swara-Cocoso-Based Approach for Spray Painting Robot Selection. Informatica 2022, 33, 35–54. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nhieu, N.-L.; Liu, W.-L. Unveiling the Landscape of Fintech in Asean: Assessing Development, Regulations, and Economic Implications by Decision-Making Approach. Humanit. Soc. Sci. Commun. 2024, 11, 100. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nhieu, N.-L.; Wang, Y.-H. The Future of Energy Storage in Vietnam: A Fuzzy Multi-Criteria Decision-Making Approach to Metal-Ion Battery Assessments. Batteries 2024, 10, 130. [Google Scholar] [CrossRef]
- Nhieu, N.-L. The T-Spherical Fuzzy Einstein Interaction Operation Matrix Energy Decision-Making Approach: The Context of Vietnam Offshore Wind Energy Storage Technologies Assessment. Mathematics 2024, 12, 2498. [Google Scholar] [CrossRef]
- Khan, M.R.; Ullah, K.; Khan, Q. Multi-Attribute Decision-Making Using Archimedean Aggregation Operator in T-Spherical Fuzzy Environment. Rep. Mech. Eng. 2023, 4, 18–38. [Google Scholar] [CrossRef]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An Approach toward Decision-Making and Medical Diagnosis Problems Using the Concept of Spherical Fuzzy Sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Zeng, S.; Munir, M.; Mahmood, T.; Naeem, M. Some T-Spherical Fuzzy Einstein Interactive Aggregation Operators and Their Application to Selection of Photovoltaic Cells. Math. Probl. Eng. 2020, 2020, 1904362. [Google Scholar] [CrossRef]
- Ren, Z.; Li, H.; Yan, W.; Lv, W.; Zhang, G.; Lv, L.; Sun, L.; Sun, Z.; Gao, W. Comprehensive Evaluation on Production and Recycling of Lithium-Ion Batteries: A Critical Review. Renew. Sustain. Energy Rev. 2023, 185, 113585. [Google Scholar] [CrossRef]
- Wang, M.-M.; Zhang, C.-C.; Zhang, F.-S. Recycling of Spent Lithium-Ion Battery with Polyvinyl Chloride by Mechanochemical Process. Waste Manag. 2017, 67, 232–239. [Google Scholar] [CrossRef]
- Wang, M.; Liu, K.; Yu, J.; Zhang, C.-C.; Zhang, Z.; Tan, Q. Recycling Spent Lithium-Ion Batteries Using a Mechanochemical Approach. Circ. Econ. 2022, 1, 100012. [Google Scholar] [CrossRef]
- Toro, L.; Moscardini, E.; Baldassari, L.; Forte, F.; Falcone, I.; Coletta, J.; Toro, L. A Systematic Review of Battery Recycling Technologies: Advances, Challenges, and Future Prospects. Energies 2023, 16, 6571. [Google Scholar] [CrossRef]
- Roy, J.J.; Cao, B.; Madhavi, S. A Review on the Recycling of Spent Lithium-Ion Batteries (Libs) by the Bioleaching Approach. Chemosphere 2021, 282, 130944. [Google Scholar] [CrossRef]
- Moosakazemi, F.; Ghassa, S.; Jafari, M.; Chelgani, S.C. Bioleaching for Recovery of Metals from Spent Batteries—A Review. Miner. Process. Extr. Metall. Rev. 2023, 44, 511–521. [Google Scholar] [CrossRef]
- Fang, Z.; Wu, Z.; Zeng, W.; Bontempi, E.; Duan, Q.; Sun, J.; Wang, Q. Exploring the Viability of Cryogenic Freezing for Safe Pretreatment in Lithium-Ion Battery Recycling. Renew. Energy 2025, 252, 123481. [Google Scholar] [CrossRef]
- Grandjean, T.R.B.; Groenewald, J.; Marco, J. The Experimental Evaluation of Lithium Ion Batteries after Flash Cryogenic Freezing. J. Energy Storage 2019, 21, 202–215. [Google Scholar] [CrossRef]
- Li, L.; Zhang, X.; Li, M.; Chen, R.; Wu, F.; Amine, K.; Lu, J. The Recycling of Spent Lithium-Ion Batteries: A Review of Current Processes; Technologies. Electrochem. Energy Rev. 2018, 1, 461–482. [Google Scholar] [CrossRef]
- Shahjalal, M.; Roy, P.K.; Shams, T.; Fly, A.; Chowdhury, J.I.; Ahmed, M.R.; Liu, K. A Review on Second-Life of Li-Ion Batteries: Prospects, Challenges, and Issues. Energy 2022, 241, 122881. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).