A Smart Evolving Fuzzy Predictor with Customized Firefly Optimization for Battery RUL Prediction
Abstract
1. Introduction
2. The Proposed SEFP-FO Technique
2.1. Evolving Fuzzy Rule Structure
2.2. The Proposed Activation- and Distance-Aware Penalization (ADAP) Method
2.2.1. The Geometric Proximity Indicator
2.2.2. The Activation Confidence Indicator
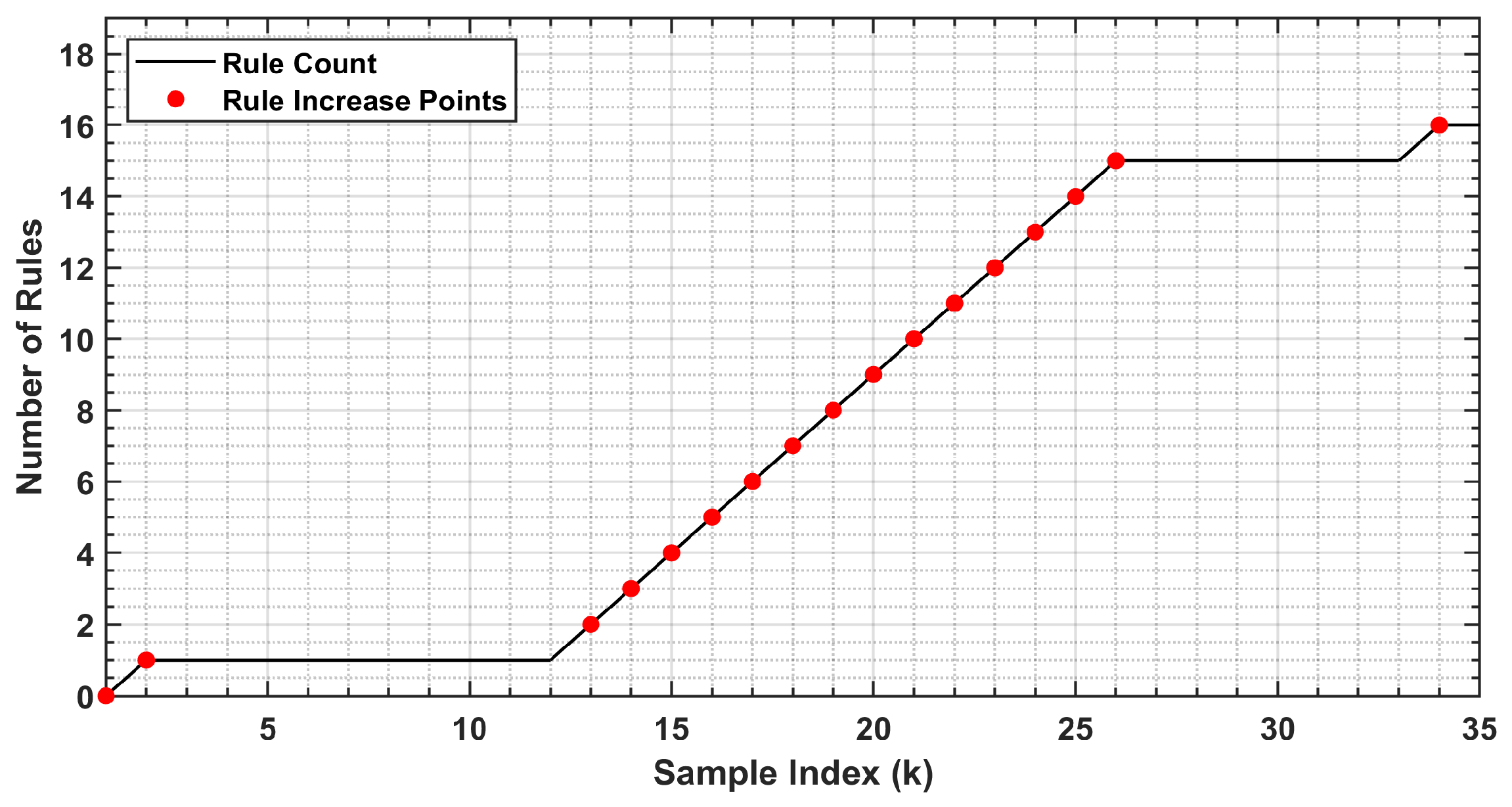
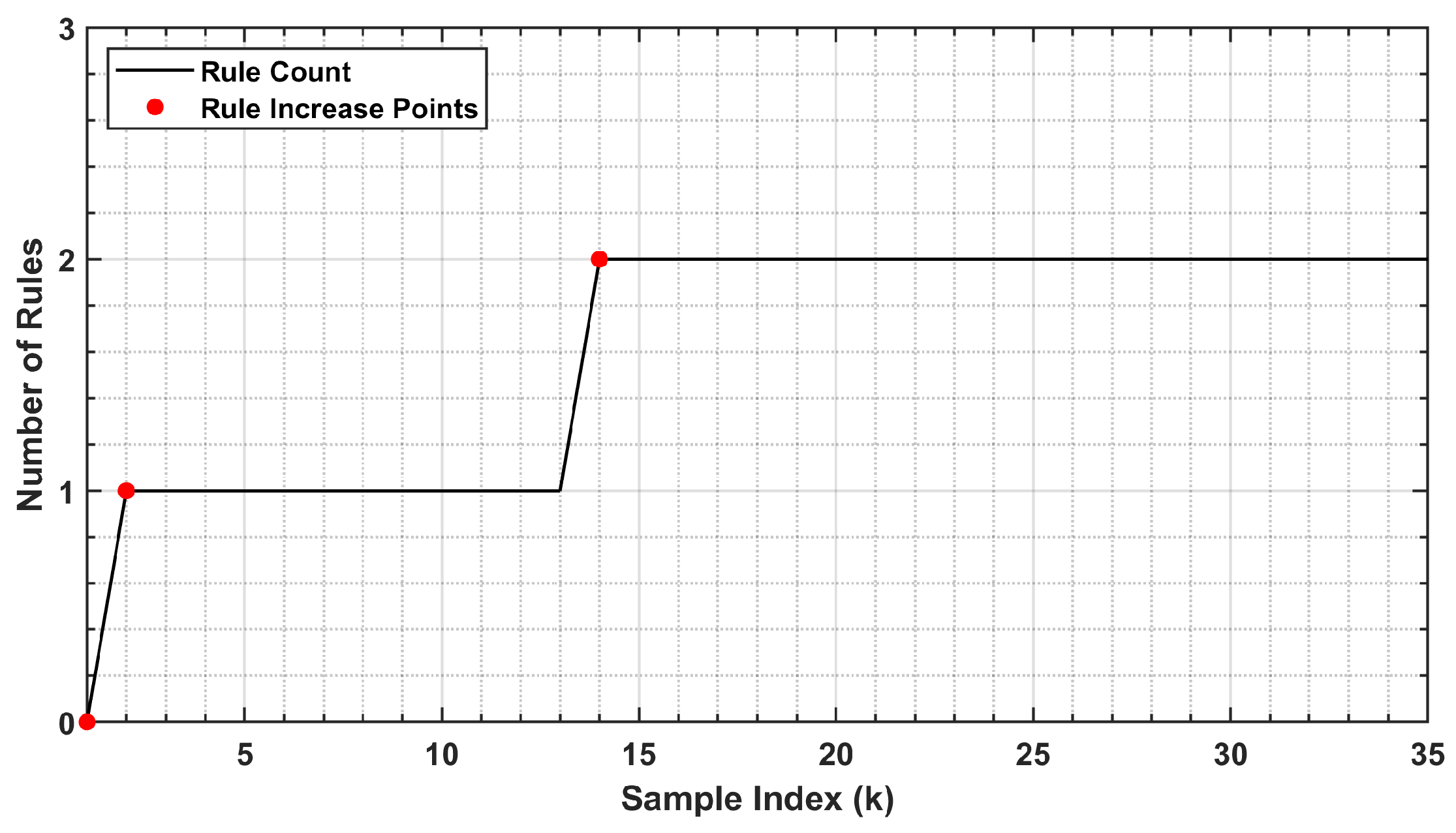
2.2.3. Rule Evolution Decision Mechanism
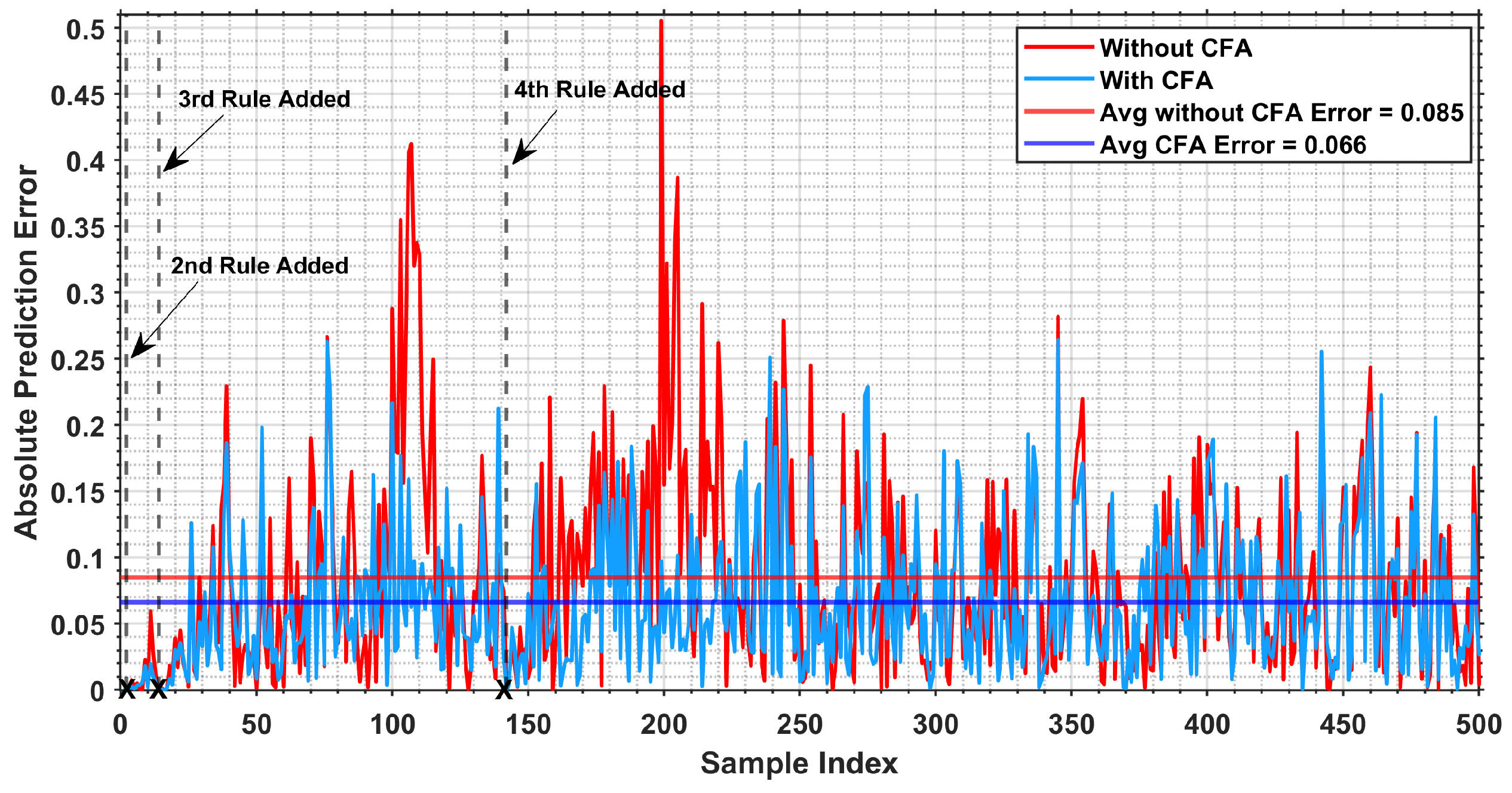
2.3. The Proposed Customized Firefly Algorithm (CFA) for Rule Optimization
- (1)
- One-to-one movement: Each candidate firefly compares itself with other candidates with lower prediction errors and moves toward them. This allows the candidate to improve by learning from better solutions in its local population.
- (2)
- Global guidance: Each firefly is softly attracted to the best-performing candidate found so far. This introduces a global guidance to improve convergence and stabilize the search toward a better solution.
3. Simulation Results and Performance Evaluation
3.1. Simulation Tests Using Benchmark Datasets
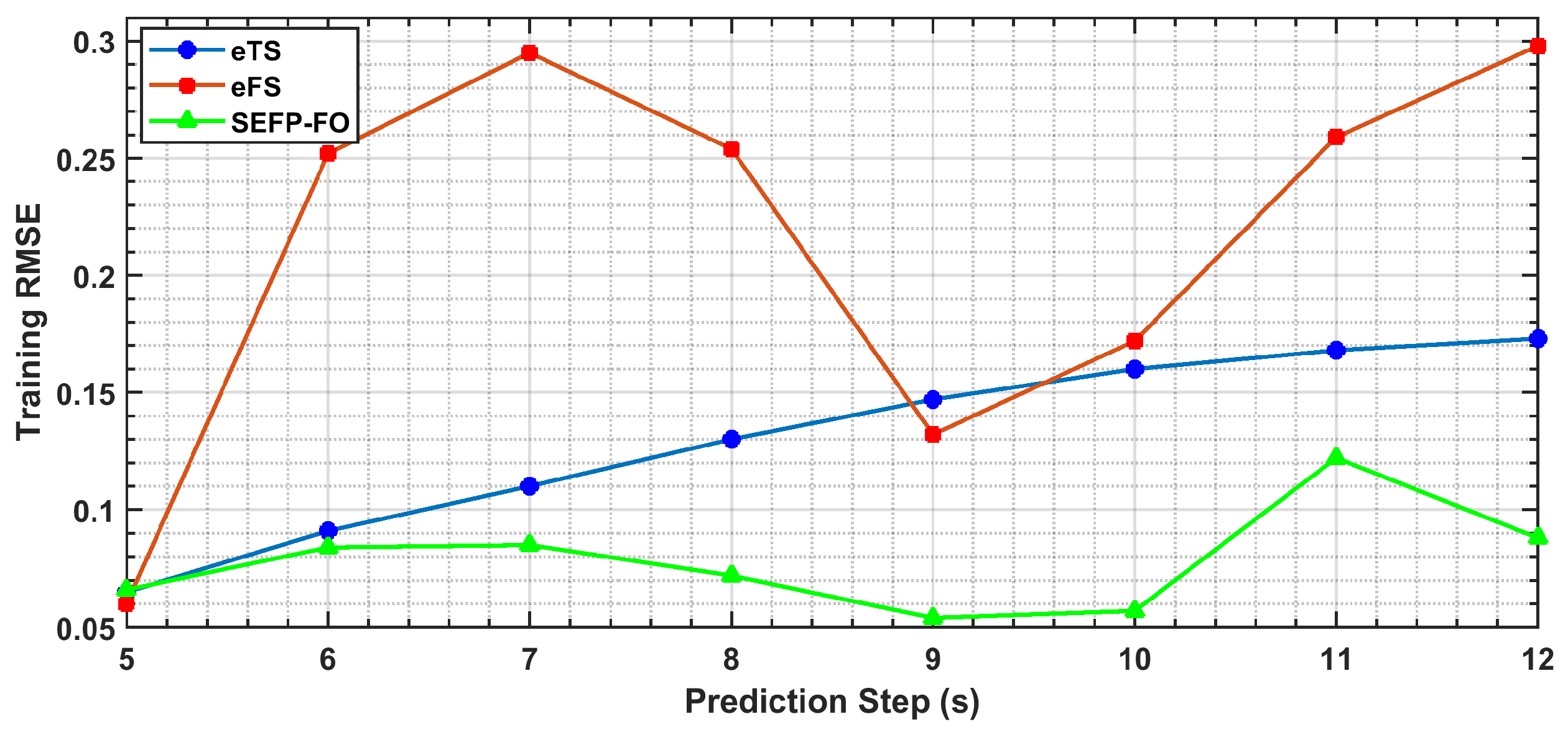
3.1.1. Performance Evaluation for Long-Term Predictions Under Strong Nonlinearity
3.1.2. Performance Evaluation Under Noisy Conditions
- (A).
- Performance under mild noise
- (B).
- Performance under moderate noise
- (C).
- Performance under high noise
3.2. Performance Evaluation for Battery RUL Prediction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RUL | Remaining useful life |
| Li-ion | Lithium-ion |
| SEFP-FO | Smart evolving fuzzy predictor with customized firefly optimization |
| EOL | End-of-life |
| PFs | Particle filters |
| SOH | State-of-health |
| eFS | evolving fuzzy system |
| ADAP | Activation- and distance-aware penalization |
| FA | Firefly algorithm |
| CFA | Customized firefly algorithm |
| TS-1 | First-order Takagi-Sugeno |
| MFs | Membership functions |
| RLSE | Recursive least squares estimator |
| RMSE | Root-mean-square error |
| eTS | evolving Takagi-Sugeno |
| NASA | National Aeronautics and Space Administration |
References
- Wang, J.; Liu, P.; Yi, T.; Zhang, J.; Zhang, C. A review on modeling of lithium-ion batteries for electric vehicles. Renew. Sustain. Energy Rev. 2016, 64, 106–128. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Ge, M.-F.; Liu, Y.; Jiang, X.; Liu, J. A review on state of health estimations and remaining useful life prognostics of lithium-ion batteries. Measurement 2021, 174, 109057. [Google Scholar] [CrossRef]
- Xiong, R.; Pan, Y.; Shen, W.; Li, H.; Sun, F. Lithium-ion battery aging mechanisms and diagnosis method for automotive applications: Recent advances and perspectives. Renew. Sustain. Energy Rev. 2020, 131, 110048. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Kordestani, M.; Saif, M.; Orchard, M.E.; Razavi-Far, R.; Khorasani, K. Failure prognosis and applications—A survey of recent literature. IEEE Trans. Reliab. 2019, 70, 728–748. [Google Scholar] [CrossRef]
- Elmahallawy, M.; Elfouly, T.; Alouani, A.; Massoud, A.M. A Comprehensive Review of Lithium-Ion Batteries Modeling, and State of Health and Remaining Useful Lifetime Prediction. IEEE Access 2022, 10, 119040–119070. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Dong, H.; Hu, Q.; Li, D.; Li, Z.; Song, Z. Predictive battery thermal and energy management for connected and automated electric vehicles. IEEE Trans. Intell. Transp. Syst. 2024, 26, 2144–2156. [Google Scholar] [CrossRef]
- Reza, M.; Mannan, M.; Mansor, M.; Ker, P.J.; Mahlia, T.M.I.; Hannan, M. Recent advancement of remaining useful life prediction of lithium-ion battery in electric vehicle applications: A review of modelling mechanisms, network configurations, factors, and outstanding issues. Energy Rep. 2024, 11, 4824–4848. [Google Scholar] [CrossRef]
- Liu, X.; Hu, Z.; Wang, X.; Xie, M. Capacity Degradation Assessment of Lithium-Ion Battery Considering Coupling Effects of Calendar and Cycling Aging. IEEE Trans. Autom. Sci. Eng. 2023, 21, 3052–3064. [Google Scholar] [CrossRef]
- Seaman, A.; Dao, T.-S.; McPhee, J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. J. Power Sources 2014, 256, 410–423. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. An AI-driven particle filter technology for battery system state estimation and RUL prediction. Batteries 2024, 10, 437. [Google Scholar] [CrossRef]
- Meng, H.; Li, Y.-F. A review on prognostics and health management (PHM) methods of lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 116, 109405. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. Battery Health Monitoring and Remaining Useful Life Prediction Techniques: A Review of Technologies. Batteries 2025, 11, 31. [Google Scholar] [CrossRef]
- Hu, X.; Xu, L.; Lin, X.; Pecht, M. Battery Lifetime Prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Beelen, H.; Bergveld, H.J.; Donkers, M.C.F. Joint Estimation of Battery Parameters and State of Charge Using an Extended Kalman Filter: A Single-Parameter Tuning Approach. IEEE Trans. Control. Syst. Technol. 2020, 29, 1087–1101. [Google Scholar] [CrossRef]
- He, H.; Qin, H.; Sun, X.; Shui, Y. Comparison study on the battery SoC estimation with EKF and UKF algorithms. Energies 2013, 6, 5088–5100. [Google Scholar] [CrossRef]
- Partovibakhsh, M.; Liu, G. An Adaptive Unscented Kalman Filtering Approach for Online Estimation of Model Parameters and State-of-Charge of Lithium-Ion Batteries for Autonomous Mobile Robots. IEEE Trans. Control. Syst. Technol. 2014, 23, 357–363. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Zhang, X. An improved adaptive unscented kalman filtering for state of charge online estimation of lithium-ion battery. J. Energy Storage 2020, 32, 101980. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. An Adaptive Particle Filter Technique for System State Estimation and Prognosis. IEEE Trans. Instrum. Meas. 2020, 69, 6756–6765. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. Modeling Li-ion battery capacity depletion in a particle filtering framework. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, San Diego, CA, USA, 27 September–1 October 2009; pp. 1–10. [Google Scholar]
- Saha, B.; Goebel, K.; Poll, S.; Christophersen, J. An integrated approach to battery health monitoring using Bayesian regression and state estimation. In Proceedings of the IEEE Autotestcon, Baltimore, MD, USA, 17–20 September 2007; pp. 646–653. [Google Scholar]
- Li, D.Z.; Wang, W.; Ismail, F. A mutated particle filter technique for system state estimation and battery life prediction. IEEE Trans. Instrum. Meas. 2014, 63, 2034–2043. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, C.; Wang, Z.; Tao, L. Artificial Fish Swarm Algorithm-Based Particle Filter for Li-Ion Battery Life Prediction. Math. Probl. Eng. 2014, 2014, 564894. [Google Scholar] [CrossRef]
- Liu, D.; Luo, Y.; Liu, J.; Peng, Y.; Guo, L.; Pecht, M. Lithium-ion battery remaining useful life estimation based on fusion nonlinear degradation AR model and RPF algorithm. Neural Comput. Appl. 2013, 25, 557–572. [Google Scholar] [CrossRef]
- Ren, Y.; Tang, T.; Xia, Q.; Zhang, K.; Tian, J.; Hu, D.; Yang, D.; Sun, B.; Feng, Q.; Qian, C. A data and physical model joint driven method for lithium-ion battery remaining useful life prediction under complex dynamic conditions. J. Energy Storage 2024, 79, 110065. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, S.; He, Y. An Integrated Method of the Future Capacity and RUL Prediction for Lithium-Ion Battery Pack. IEEE Trans. Veh. Technol. 2021, 71, 2601–2613. [Google Scholar] [CrossRef]
- Tian, H.; Qin, P.; Li, K.; Zhao, Z. A review of the state of health for lithium-ion batteries: Research status and suggestions. J. Clean. Prod. 2020, 261, 120813. [Google Scholar] [CrossRef]
- Du, Z.; Zuo, L.; Li, J.; Liu, Y.; Shen, H.T. Data-Driven Estimation of Remaining Useful Lifetime and State of Charge for Lithium-Ion Battery. IEEE Trans. Transp. Electrif. 2021, 8, 356–367. [Google Scholar] [CrossRef]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M.; Dietmayer, K. Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods. J. Power Sources 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Atiya, A. A Comprehensive Review of Neural Network-based Prediction Intervals and New Advances. IEEE Trans. Neural Netw. 2011, 22, 1341–1356. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Z.; Pan, J.; Zhang, Z.; Cheng, X. A data-driven fault tracing of lithium-ion batteries in electric vehicles. IEEE Trans. Power Electron. 2024, 39, 16609–16621. [Google Scholar] [CrossRef]
- Catelani, M.; Ciani, L.; Fantacci, R.; Patrizi, G.; Picano, B. Remaining Useful Life Estimation for Prognostics of Lithium-Ion Batteries Based on Recurrent Neural Network. IEEE Trans. Instrum. Meas. 2021, 70, 3524611. [Google Scholar] [CrossRef]
- Zheng, X.; Deng, X. State-of-Health Prediction For Lithium-Ion Batteries With Multiple Gaussian Process Regression Model. IEEE Access 2019, 7, 150383–150394. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, Y.; Lu, S.; Wang, J.; Zhang, X. Remaining Useful Life Prediction of Lithium-Ion Batteries Using Support Vector Regression Optimized by Artificial Bee Colony. IEEE Trans. Veh. Technol. 2019, 68, 9543–9553. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Ayob, A.; Lipu, M.S.H.; Ansari, S.; Kiong, T.S.; Saad, M.H.M.; Ustun, T.S.; Kalam, A. Advanced data-driven fault diagnosis in lithium-ion battery management systems for electric vehicles: Progress, challenges, and future perspectives. eTransportation. 2024, 22, 100374. [Google Scholar] [CrossRef]
- Qu, J.; Liu, F.; Ma, Y.; Fan, J. A Neural-Network-Based Method for RUL Prediction and SOH Monitoring of Lithium-Ion Battery. IEEE Access 2019, 7, 87178–87191. [Google Scholar] [CrossRef]
- Zhou, D.; Li, Z.; Zhu, J.; Zhang, H.; Hou, L. State of Health Monitoring and Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Temporal Convolutional Network. IEEE Access 2020, 8, 53307–53320. [Google Scholar] [CrossRef]
- Zraibi, B.; Okar, C.; Chaoui, H.; Mansouri, M. Remaining Useful Life Assessment for Lithium-Ion Batteries Using CNN-LSTMDNN Hybrid Method. IEEE Trans. Veh. Technol. 2021, 70, 4252–4261. [Google Scholar] [CrossRef]
- Li, Y.; Li, L.; Mao, R.; Zhang, Y.; Xu, S.; Zhang, J. Hybrid Data-Driven Approach for Predicting the Remaining Useful Life of Lithium-Ion Batteries. IEEE Trans. Transp. Electrif. 2023, 10, 2789–2805. [Google Scholar] [CrossRef]
- Cartagena, O.; Parra, S.; Muñoz-Carpintero, D.; Marín, L.G.; Sáez, D. Review on Fuzzy and Neural Prediction Interval Modelling for Nonlinear Dynamical Systems. IEEE Access 2021, 9, 23357–23384. [Google Scholar] [CrossRef]
- Jafari, S.; Byun, Y.C. A CNN-GRU Approach to the Accurate Prediction of Batteries’ Remaining Useful Life from Charging Profiles. Computers 2023, 12, 219. [Google Scholar] [CrossRef]
- He, W.; Li, Z.; Liu, T.; Liu, Z.; Guo, X.; Du, J.; Li, X.; Sun, P.; Ming, W. Research progress and application of deep learning in remaining useful life, state of health and battery thermal management of lithium batteries. J. Energy Storage 2023, 70, 107868. [Google Scholar] [CrossRef]
- Oji, T.; Zhou, Y.; Ci, S.; Kang, F.; Chen, X.; Liu, X. Data-driven methods for battery soh estimation: Survey and a critical analysis. IEEE Access 2021, 10, 126903–126916. [Google Scholar] [CrossRef]
- Škrjanc, I.; Iglesias, J.A.; Sanchis, A.; Leite, D.; Lughofer, E.; Gomide, F. Evolving fuzzy and neuro-fuzzy approaches in clustering, regression, identification, and classification: A survey. Inf. Sci. 2019, 490, 344–368. [Google Scholar] [CrossRef]
- Lughofer, E.; Skrjanc, I. Evolving Error Feedback Fuzzy Model for Improved Robustness under Measurement Noise. IEEE Trans. Fuzzy Syst. 2022, 31, 997–1008. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. An Adaptive Evolving Fuzzy Technique for Prognosis of Dynamic Systems. IEEE Trans. Fuzzy Syst. 2021, 30, 841–849. [Google Scholar] [CrossRef]
- Juang, C.F.; Tsao, Y.W. A Self-evolving interval type-2 fuzzy neural network with online structure and parameter learning. IEEE Trans. Fuzzy Syst. 2008, 16, 1411–1424. [Google Scholar] [CrossRef]
- Angelov, P.; Buswell, R. Identification of evolving rule-based models. IEEE Trans. Fuzzy Syst. 2002, 10, 667–677. [Google Scholar] [CrossRef]
- Angelov, P.; Filev, D.P. An approach to online identification of Takagi-Sugeno fuzzy models. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 484–498. [Google Scholar] [CrossRef]
- Angelov, P. Fuzzily connected multimodel systems evolving autonomously from data streams. IEEE Trans. Syst. Man Cybern. Part B 2011, 41, 898–910. [Google Scholar] [CrossRef]
- Wang, W.; Li, D.Z.; Vrbanek, J. An evolving neuro-fuzzy technique for system state forecasting. Neurocomputing 2012, 87, 111–119. [Google Scholar] [CrossRef]
- Lughofer, E.D. FLEXFIS: A robust incremental learning approach for evolving Takagi–Sugeno fuzzy models. IEEE Trans. Fuzzy Syst. 2008, 16, 1393–1410. [Google Scholar] [CrossRef]
- Li, D.; Wang, W.; Ismail, F. An evolving fuzzy neural predictor for multi-dimensional system state forecasting. Neurocomputing 2014, 145, 381–391. [Google Scholar] [CrossRef]
- Lughofer, E.; Cernuda, C.; Kindermann, S.; Pratama, M. Generalized smart evolving fuzzy systems. Evol. Syst. 2015, 6, 269–292. [Google Scholar] [CrossRef]
- Maciel, L.; Ballini, R.; Gomide, F. An evolving possibilistic fuzzy modeling approach for value-at-risk estimation. Appl. Soft Comput. 2017, 60, 820–830. [Google Scholar] [CrossRef]
- Wang, W.; Vrbanek, J. An evolving fuzzy predictor for industrial applications. IEEE Trans. Fuzzy Syst. 2008, 16, 1439–1449. [Google Scholar] [CrossRef]
- Ge, D.; Zeng, X.J. Learning data streams online—An evolving fuzzy system approach with self-learning/adaptive thresholds. Inf. Sci. 2020, 507, 172–184. [Google Scholar] [CrossRef]
- Nguyen, N.N.; Zhou, W.J.; Quek, C. GSETSK: A generic self-evolving TSK fuzzy neural network with a novel Hebbian-based rule reduction approach. Appl. Soft Comput. 2015, 35, 29–42. [Google Scholar] [CrossRef]
- Lughofer, E.; Zavoianu, A.; Pollak, R.; Pratama, M.; Meyer-Heye, P.; Zorrer, H.; Eitzinger, C.; Haim, J.; Radauer, T. Self-adaptive evolving forecast models with incremental PLS space updating for on-line prediction of micro-fluidic chip quality. Eng. Appl. Artif. Intell. 2018, 68, 131–151. [Google Scholar] [CrossRef]
- Cartagena, O.; Trovò, F.; Roveri, M.; Sáez, D. Evolving fuzzy prediction intervals in nonstationary environments. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 903–916. [Google Scholar] [CrossRef]
- Baruah, R.D.; Angelov, P. DEC: Dynamically evolving clustering and its application to structure identification of evolving fuzzy models. IEEE Trans. Cybern. 2014, 44, 1619–1631. [Google Scholar] [CrossRef]
- Mei, Z.; Zhao, T.; Gu, X. A dynamic evolving fuzzy system for streaming data prediction. IEEE Trans. Fuzzy Syst. 2024, 32, 4324–4337. [Google Scholar] [CrossRef]
- Angelov, P. Evolving fuzzy systems. In Computational Complexity; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2012; pp. 1053–1065. [Google Scholar]
- Yang, X.-S. Firefly algorithms for multimodal optimization. In Stochastic Algorithms: Foundations and Applications; Springer: Berlin, Germany, 2009; Volume 9, pp. 169–178. [Google Scholar]
- Li, J.; Wei, X.Y.; Li, B.; Zeng, Z.G. A survey on firefly algorithms. Neurocomputing 2022, 500, 662–678. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. Battery Data Set. In NASA Prognostics Data Repository; NASA Ames Research Center: Moffett Field, CA, USA, 2024; Available online: https://phm-datasets.s3.amazonaws.com/NASA/5.+Battery+Data+Set.zip (accessed on 1 May 2024).



| Approach | Accuracy | Interpretability | Adaptiveness/Online Use | Robustness to Noise | Computational Cost |
|---|---|---|---|---|---|
| Model-based [9,12,14,15] | Good when model is accurate | High | Limited; often fixed parameters; sensitive to assumptions | Handles some noise but sensitive to non-Gaussian errors | Moderate–High |
| Hybrid [16,17,18] | Often improved accuracy | Medium | Limited by integration of components | Sensitive to noise; improved with denoising | High |
| Classical ML [19,20,21] | Works well in stable or short-horizon predictions | Medium | Low; retraining needed under drift | Sensitive to noise; limited robustness | Low–Moderate |
| Deep learning [22,23,24,25] | High with large, labeled datasets | Low (“black box”) | Low online adaptiveness; prone to overfitting and drift | Moderate; needs regularization | High (training), Moderate (inference) |
| Evolving fuzzy systems [26,27,28,29,30] | Effective on nonlinear, time-varying data | High | High; structure evolves online | Medium; sensitive to thresholds and noise | Moderate; costly if many rules created |
| No. of Steps | eTS | eFS | SEFP-FO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training RMSE | Testing RMSE | No. of Rules | Training RMSE | Testing RMSE | No. of Rules | Training RMSE | Testing RMSE | No. of Rules | |
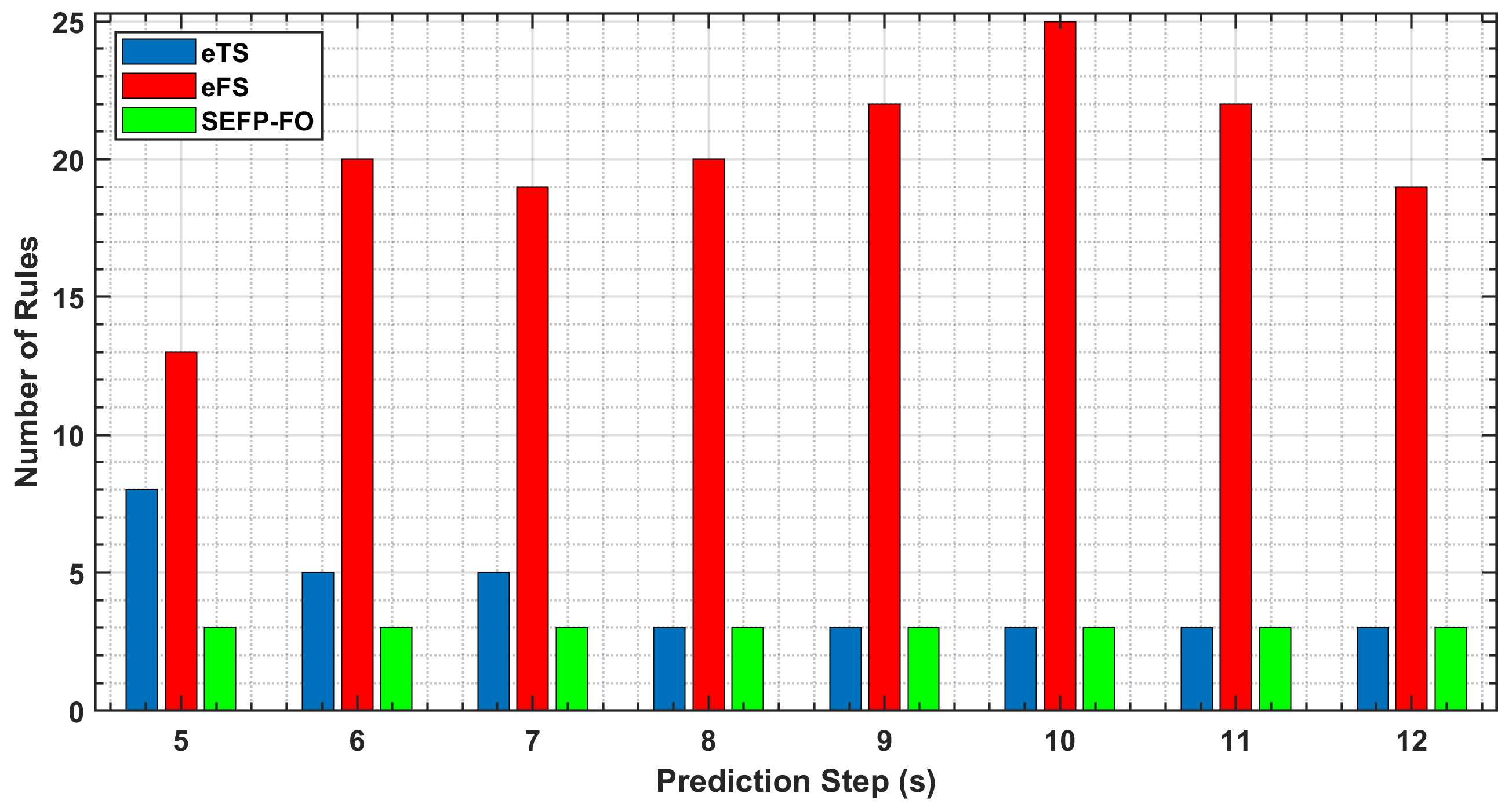
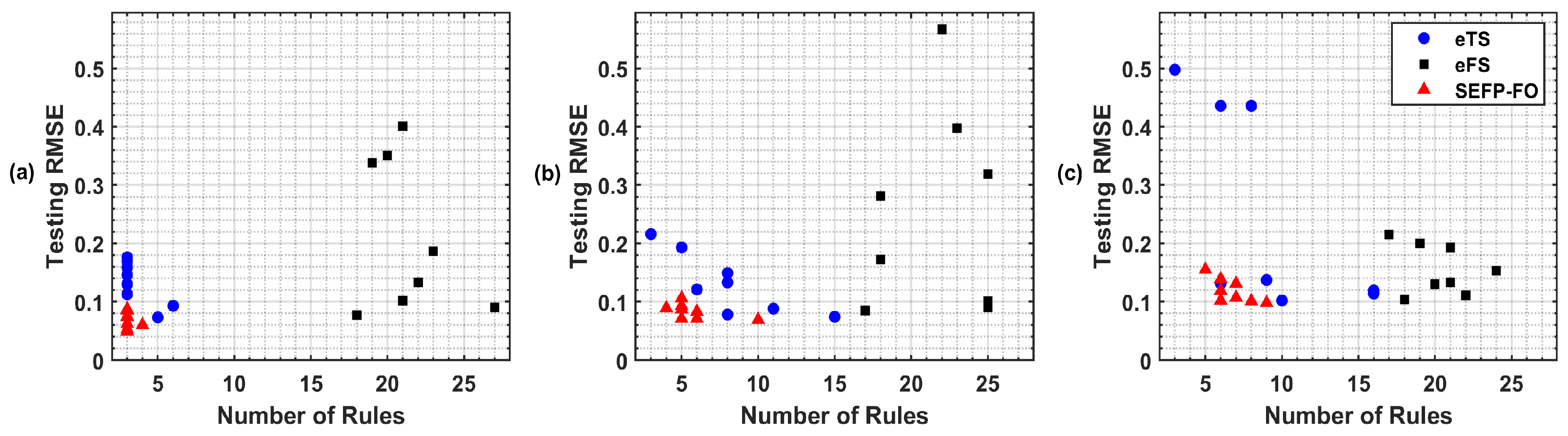
| 5 | 0.065 | 0.063 | 8 | 0.060 | 0.060 | 13 | 0.066 | 0.063 | 3 |
| 6 | 0.091 | 0.093 | 5 | 0.252 | 0.114 | 20 | 0.084 | 0.085 | 3 |
| 7 | 0.110 | 0.111 | 5 | 0.295 | 0.278 | 19 | 0.085 | 0.086 | 3 |
| 8 | 0.130 | 0.132 | 3 | 0.254 | 0.192 | 20 | 0.072 | 0.071 | 3 |
| 9 | 0.147 | 0.150 | 3 | 0.132 | 0.061 | 22 | 0.054 | 0.055 | 3 |
| 10 | 0.160 | 0.164 | 3 | 0.172 | 0.076 | 25 | 0.057 | 0.057 | 3 |
| 11 | 0.168 | 0.176 | 3 | 0.259 | 0.335 | 22 | 0.122 | 0.129 | 3 |
| 12 | 0.173 | 0.183 | 3 | 0.298 | 0.309 | 19 | 0.088 | 0.092 | 3 |
| No. of Steps | eTS | eFS | SEFP-FO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training RMSE | Testing RMSE | No. of Rules | Training RMSE | Testing RMSE | No. of Rules | Training RMSE | Testing RMSE | No. of Rules | |
| 5 | 0.075 | 0.073 | 5 | 0.067 | 0.077 | 18 | 0.074 | 0.074 | 3 |
| 6 | 0.093 | 0.093 | 6 | 0.321 | 0.338 | 19 | 0.085 | 0.085 | 3 |
| 7 | 0.110 | 0.113 | 3 | 0.169 | 0.133 | 22 | 0.086 | 0.087 | 3 |
| 8 | 0.127 | 0.130 | 3 | 0.219 | 0.102 | 21 | 0.074 | 0.075 | 3 |
| 9 | 0.141 | 0.146 | 3 | 0.211 | 0.187 | 23 | 0.051 | 0.053 | 3 |
| 10 | 0.153 | 0.159 | 3 | 0.155 | 0.090 | 27 | 0.060 | 0.062 | 3 |
| 11 | 0.161 | 0.170 | 3 | 0.238 | 0.351 | 20 | 0.050 | 0.049 | 3 |
| 12 | 0.167 | 0.176 | 3 | 0.218 | 0.401 | 21 | 0.059 | 0.060 | 4 |
| No. of Steps | eTS | eFS | SEFP-FO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training RMSE | Testing RMSE | No. of Rules | Training RMSE | Testing RMSE | No. of Rules | Training RMSE | Testing RMSE | No. of Rules | |
| 5 | 0.087 | 0.088 | 11 | 0.084 | 0.085 | 17 | 0.089 | 0.089 | 4 |
| 6 | 0.190 | 0.193 | 5 | 0.253 | 0.281 | 18 | 0.116 | 0.093 | 5 |
| 7 | 0.205 | 0.216 | 3 | 0.147 | 0.172 | 18 | 0.120 | 0.083 | 6 |
| 8 | 0.128 | 0.121 | 6 | 0.196 | 0.090 | 25 | 0.106 | 0.069 | 10 |
| 9 | 0.081 | 0.074 | 15 | 0.223 | 0.319 | 25 | 0.073 | 0.071 | 5 |
| 10 | 0.152 | 0.078 | 8 | 0.194 | 0.101 | 25 | 0.139 | 0.087 | 5 |
| 11 | 0.193 | 0.149 | 8 | 0.211 | 0.398 | 23 | 0.119 | 0.071 | 6 |
| 12 | 0.125 | 0.133 | 8 | 0.248 | 0.567 | 22 | 0.097 | 0.106 | 5 |
| No. of Steps | eTS | eFS | SEFP-FO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training RMSE | Testing RMSE | No. of Rules | Training RMSE | Testing RMSE | No. of Rules | Training RMSE | Testing RMSE | No. of Rules | |
| 5 | 0.100 | 0.102 | 10 | 0.098 | 0.104 | 18 | 0.100 | 0.102 | 6 |
| 6 | 0.287 | 0.498 | 3 | 0.200 | 0.200 | 19 | 0.153 | 0.119 | 6 |
| 7 | 0.191 | 0.119 | 16 | 0.196 | 0.215 | 17 | 0.134 | 0.107 | 7 |
| 8 | 0.267 | 0.436 | 6 | 0.169 | 0.130 | 20 | 0.164 | 0.155 | 5 |
| 9 | 0.238 | 0.436 | 8 | 0.187 | 0.111 | 22 | 0.147 | 0.098 | 9 |
| 10 | 0.260 | 0.114 | 16 | 0.168 | 0.153 | 24 | 0.129 | 0.101 | 8 |
| 11 | 0.130 | 0.131 | 6 | 0.161 | 0.133 | 21 | 0.119 | 0.131 | 7 |
| 12 | 0.130 | 0.137 | 9 | 0.205 | 0.193 | 21 | 0.129 | 0.139 | 6 |
| Prediction Starting Point | Technique | Prediction Result (Cycle) | Error (Cycle) | Relative Error | Testing RMSE |
|---|---|---|---|---|---|
| 81 | eTS | 133 | 28 | 17.39% | 0.067 |
| eFS | - | - | - | 0.478 | |
| SEFP-FO | 144 | 17 | 10.56% | 0.031 | |
| 101 | eTS | 148 | 13 | 8.07% | 0.030 |
| eFS | 130 | 31 | 19.25% | 0.180 | |
| SEFP-FO | 152 | 9 | 5.59% | 0.025 | |
| 121 | eTS | 151 | 10 | 6.21% | 0.022 |
| eFS | 139 | 22 | 13.66% | 0.114 | |
| SEFP-FO | 154 | 7 | 4.35% | 0.020 | |
| 141 | eTS | 158 | 3 | 1.86% | 0.013 |
| eFS | 151 | 10 | 6.21% | 0.053 | |
| SEFP-FO | 160 | 1 | 0.62% | 0.008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahwiadi, M.; Wang, W. A Smart Evolving Fuzzy Predictor with Customized Firefly Optimization for Battery RUL Prediction. Batteries 2025, 11, 362. https://doi.org/10.3390/batteries11100362
Ahwiadi M, Wang W. A Smart Evolving Fuzzy Predictor with Customized Firefly Optimization for Battery RUL Prediction. Batteries. 2025; 11(10):362. https://doi.org/10.3390/batteries11100362
Chicago/Turabian StyleAhwiadi, Mohamed, and Wilson Wang. 2025. "A Smart Evolving Fuzzy Predictor with Customized Firefly Optimization for Battery RUL Prediction" Batteries 11, no. 10: 362. https://doi.org/10.3390/batteries11100362
APA StyleAhwiadi, M., & Wang, W. (2025). A Smart Evolving Fuzzy Predictor with Customized Firefly Optimization for Battery RUL Prediction. Batteries, 11(10), 362. https://doi.org/10.3390/batteries11100362










