Hardware Implementation of Hybrid Data Driven-PI Control Scheme for Resilient Operation of Standalone DC Microgrid
Abstract
1. Introduction
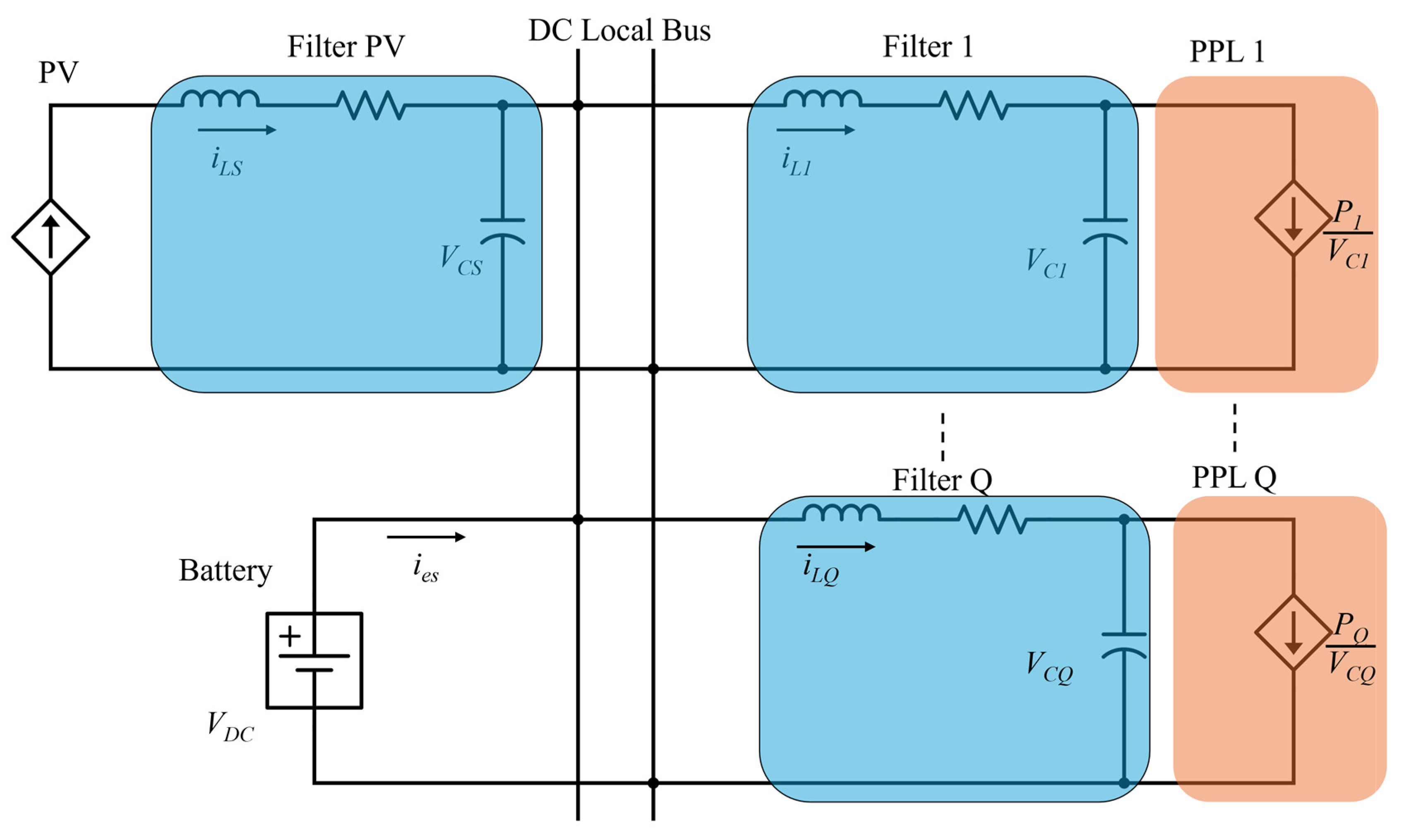
2. Microgrid System Architecture and Description
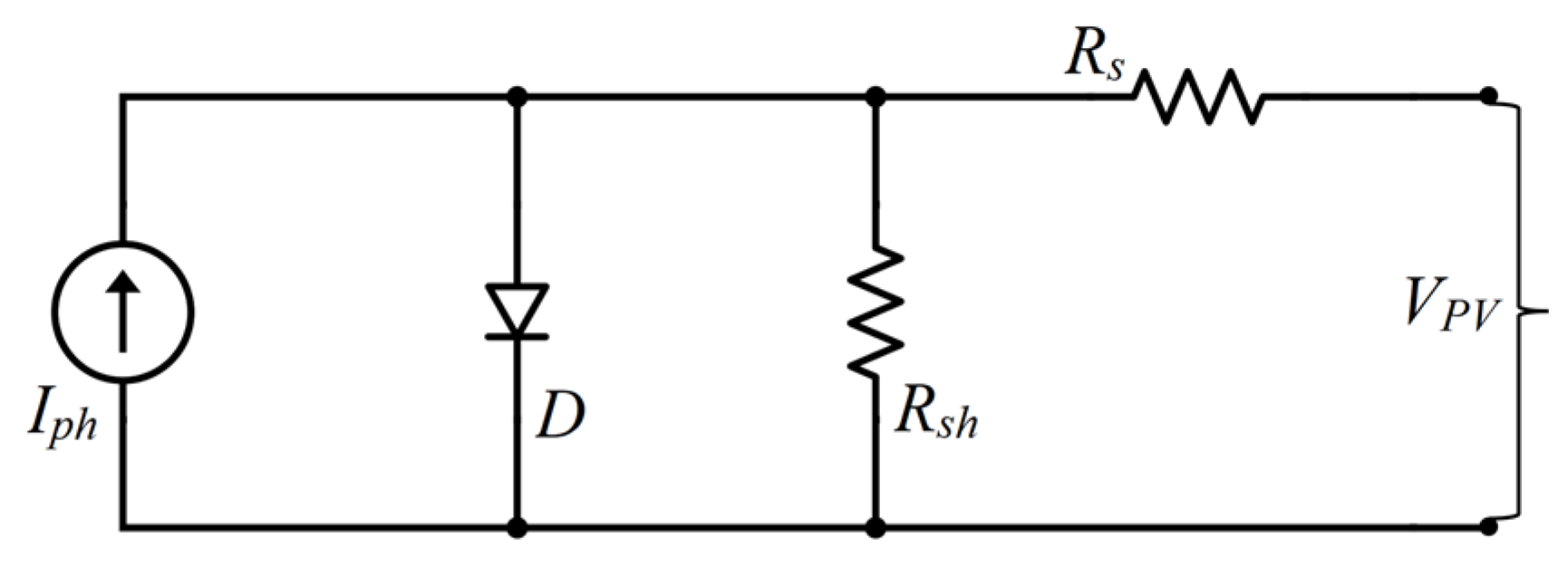
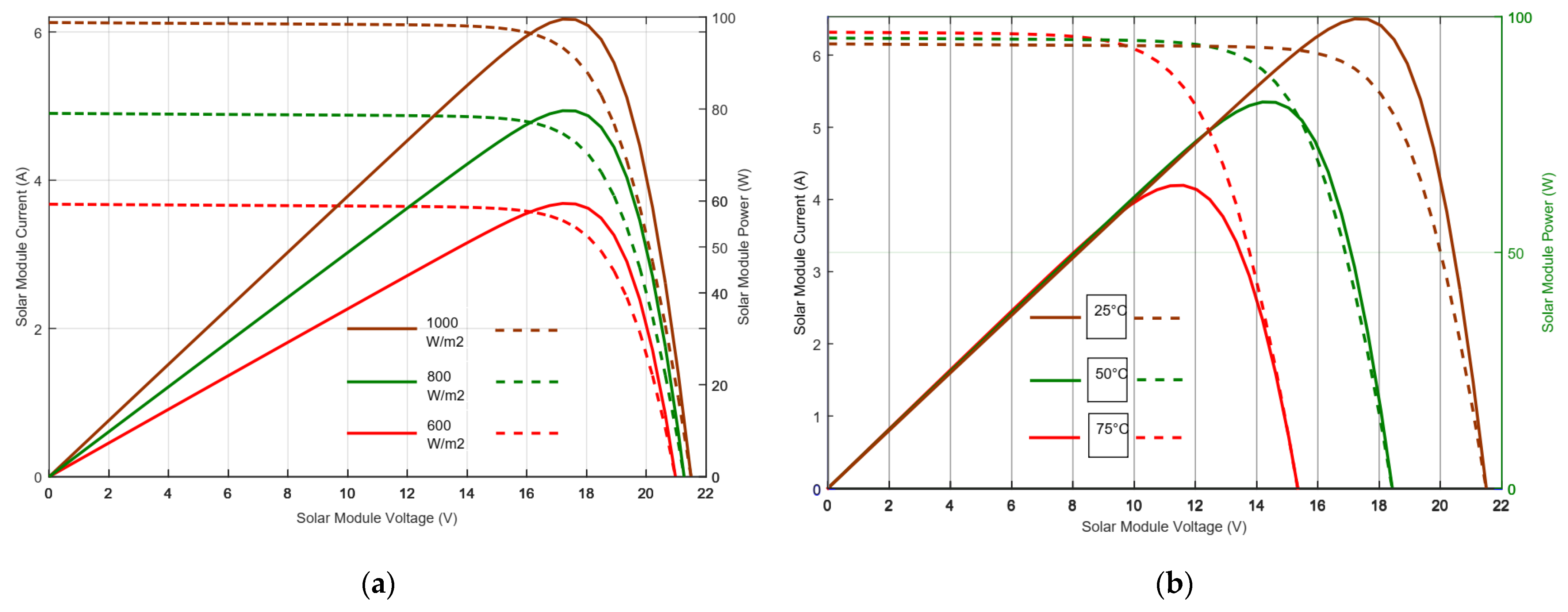
2.1. Photovoltaic System
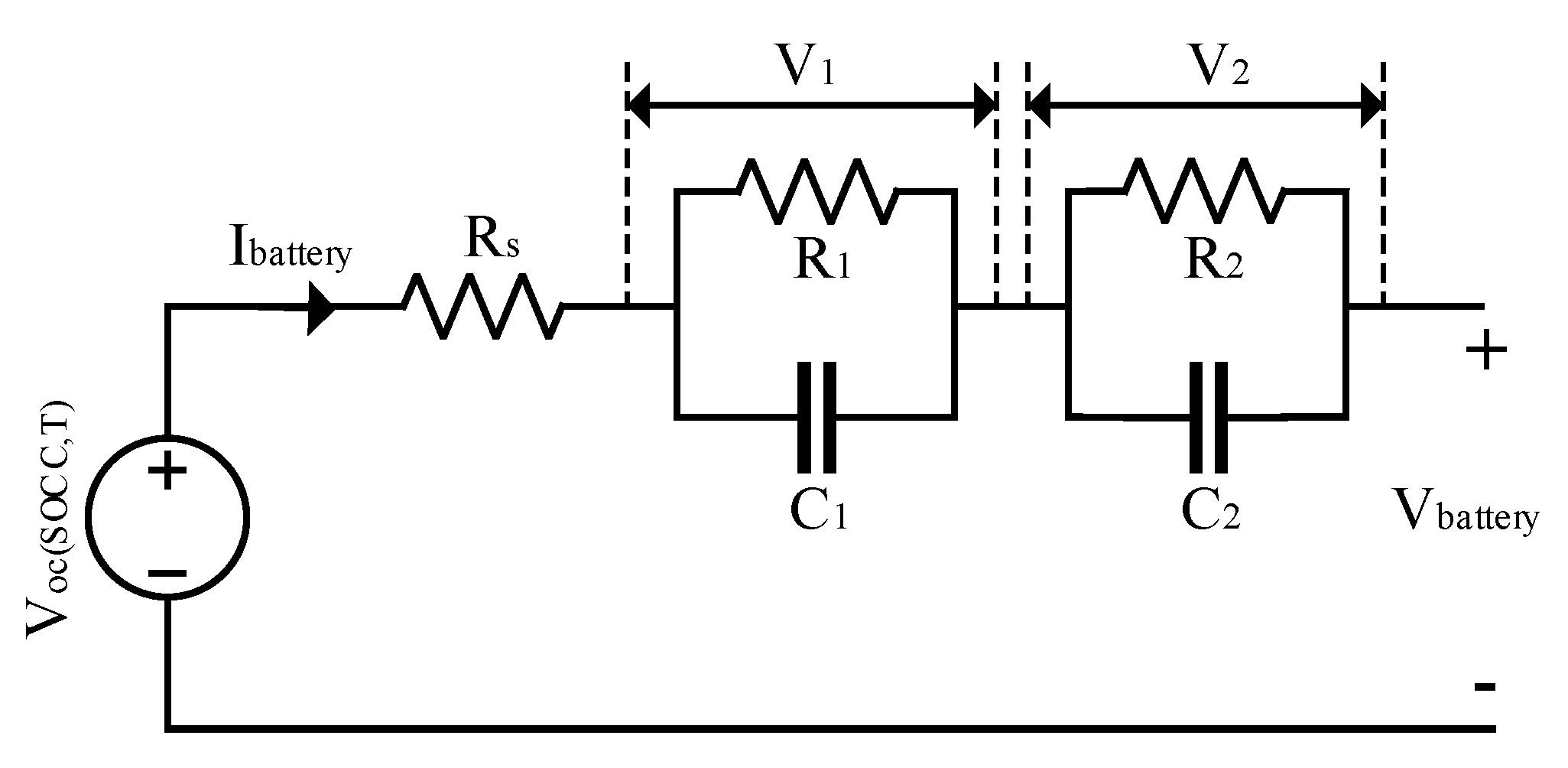
2.2. Battery Energy Storage System
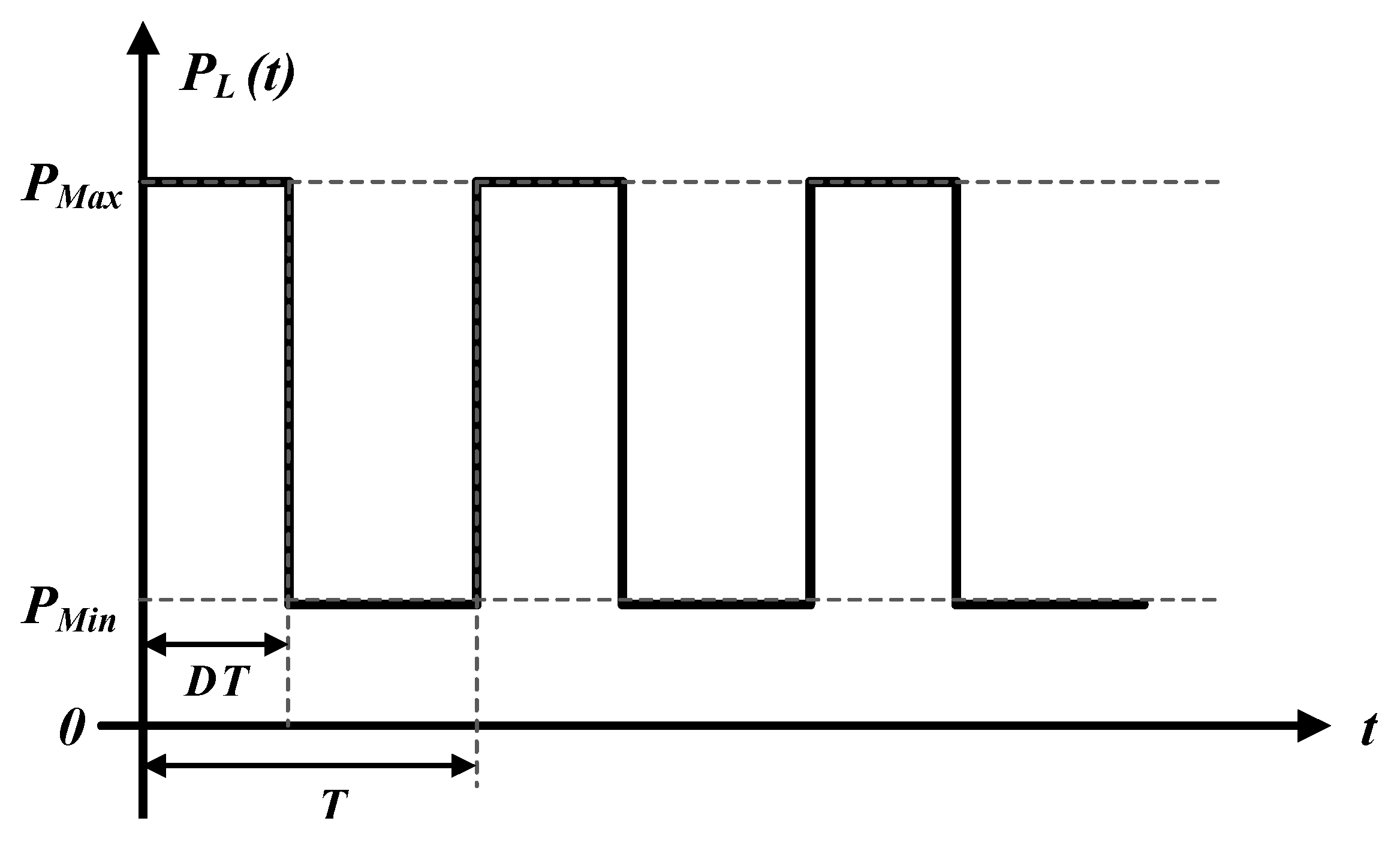
2.3. Load Model
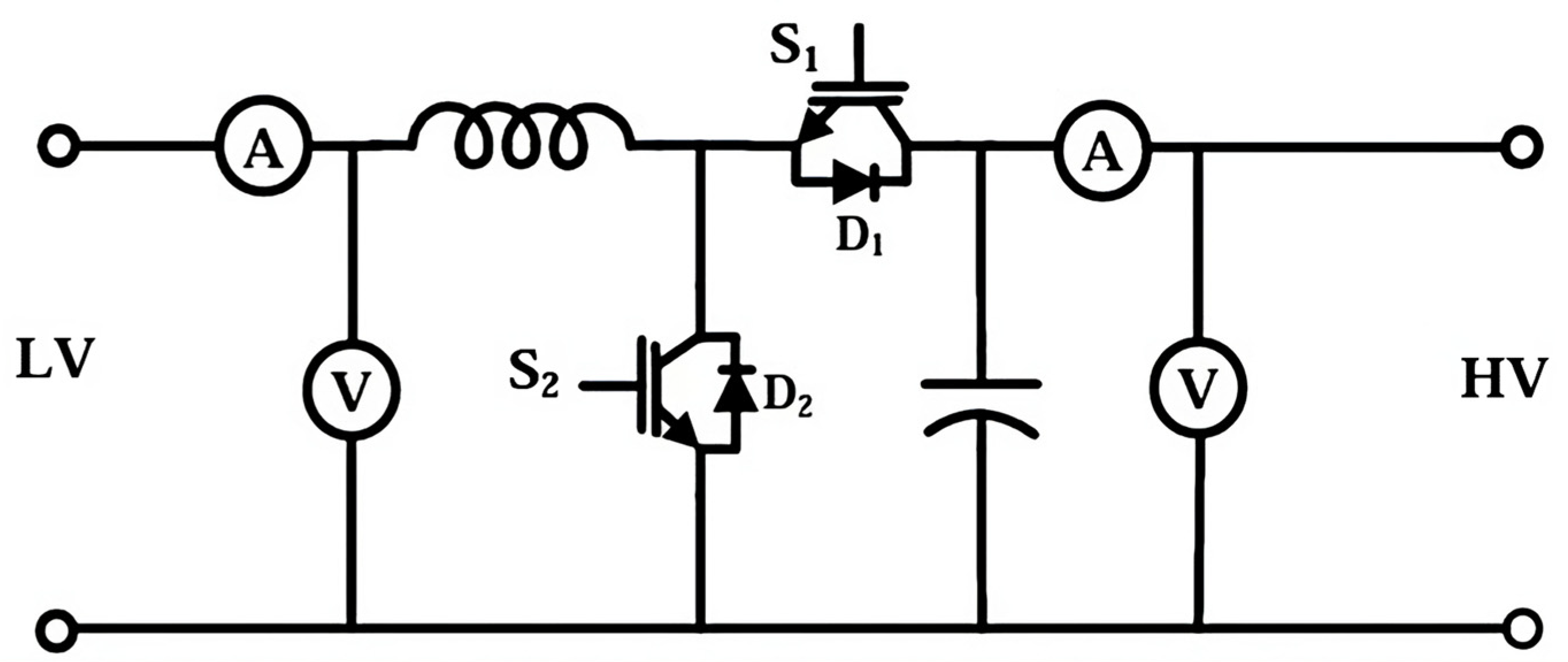
2.4. DC-DC Bidirectional Structure
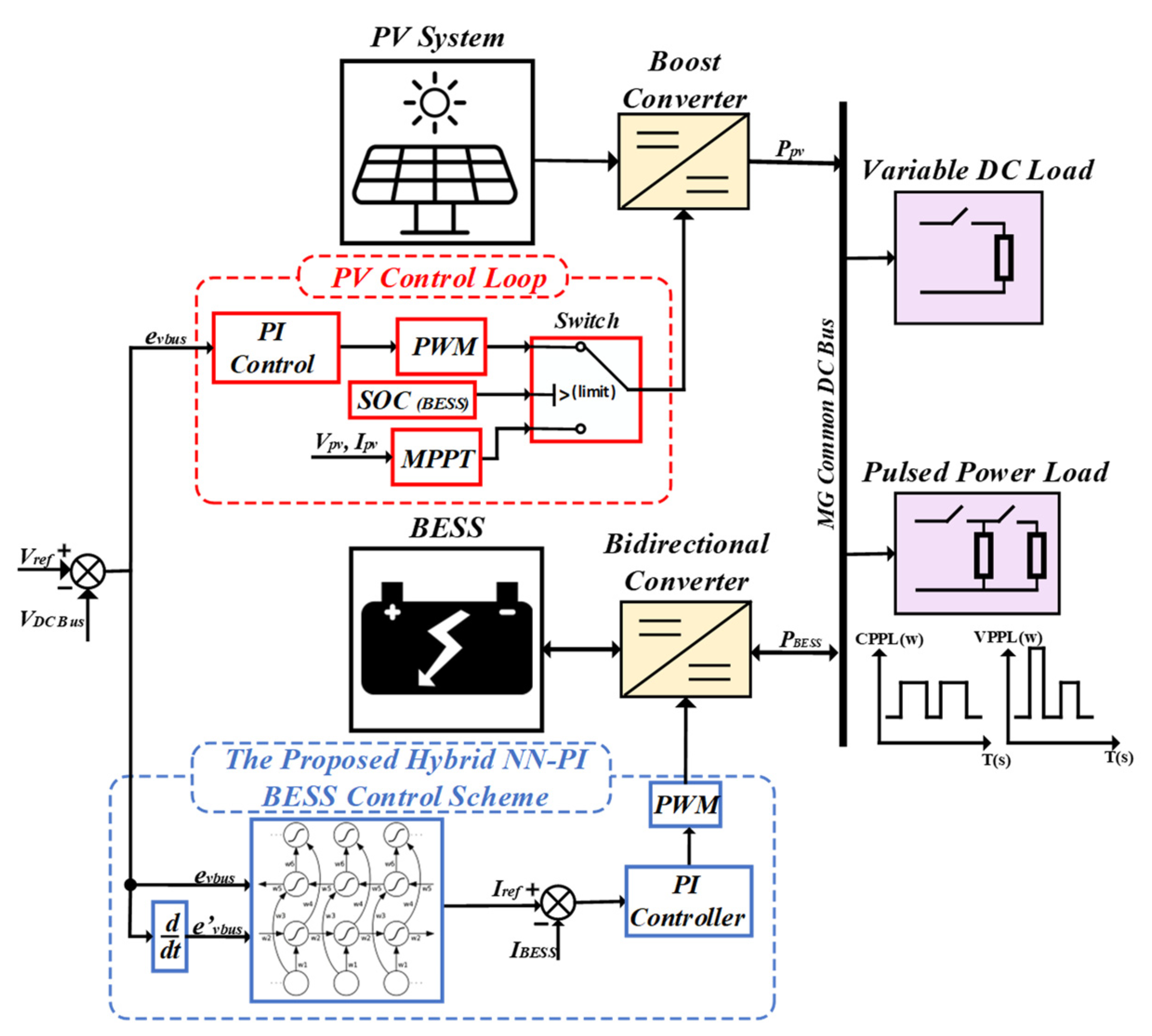
3. Proposed Control Scheme
3.1. Photovoltaic Control Scheme
- Proportional Integral (PI) Control Loop: This loop takes over when the battery reaches its maximum charge. The PI controller manages the PV array boost converter, which supplies the power required to adjust voltage levels. This regulation is crucial for assuring the stability of the DC bus voltage, preventing battery overcharging, and keeping the voltage within acceptable limits.
- Maximum Power Point Tracking (MPPT) Control Loop: This loop activates when the battery is not fully charged. The MPPT controller employs the “Perturb and Observe” algorithm to constantly modify the operating point of the PV array to harvest the most feasible power. This power is utilized to satisfy the current load requirements. If the PV array produces any excess electricity, it recharges the battery.
3.2. Conventional PI-PI Control Scheme
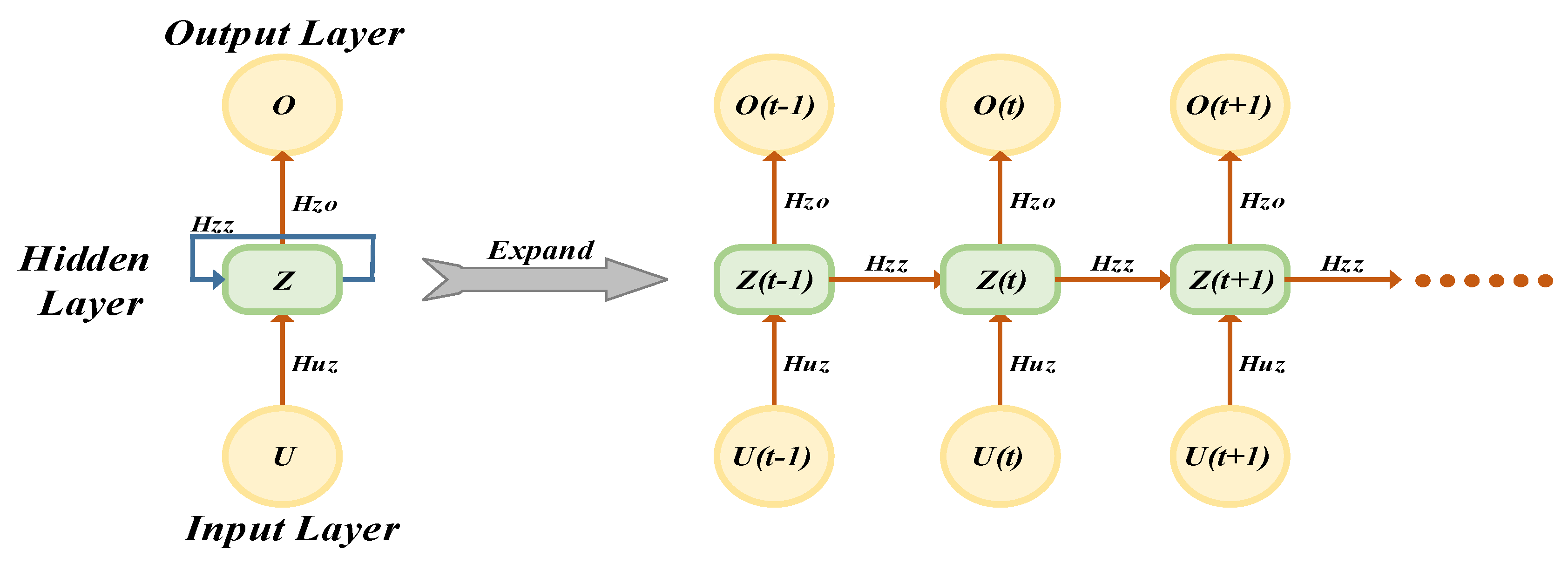
3.3. Neural Network Structure
3.4. PI-NN Control and Operation
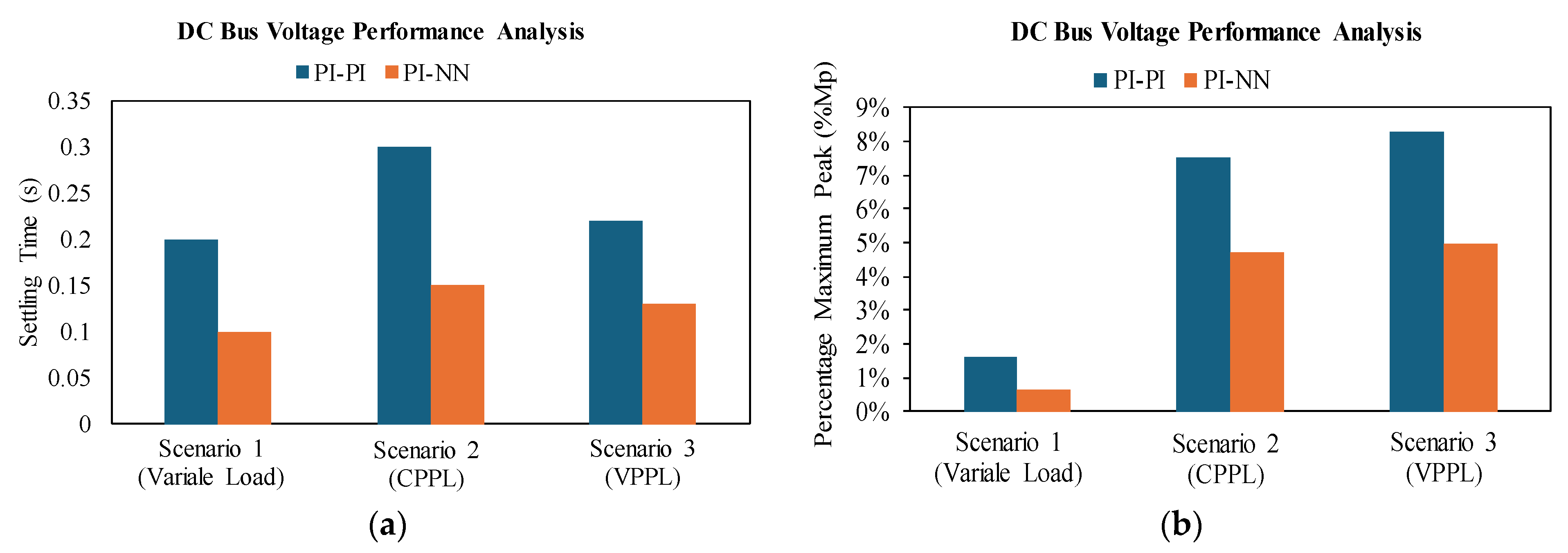
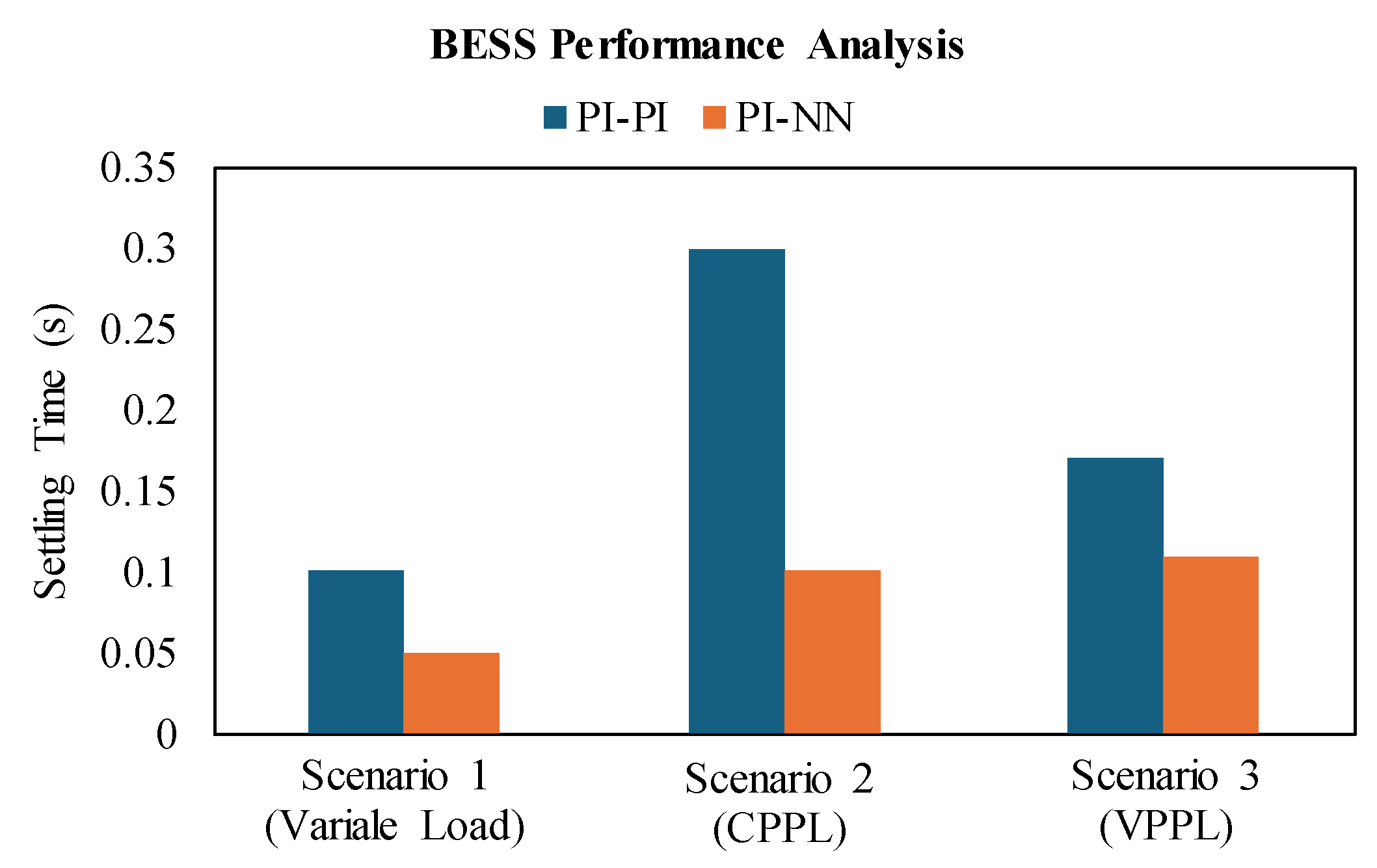
4. Simulation Results
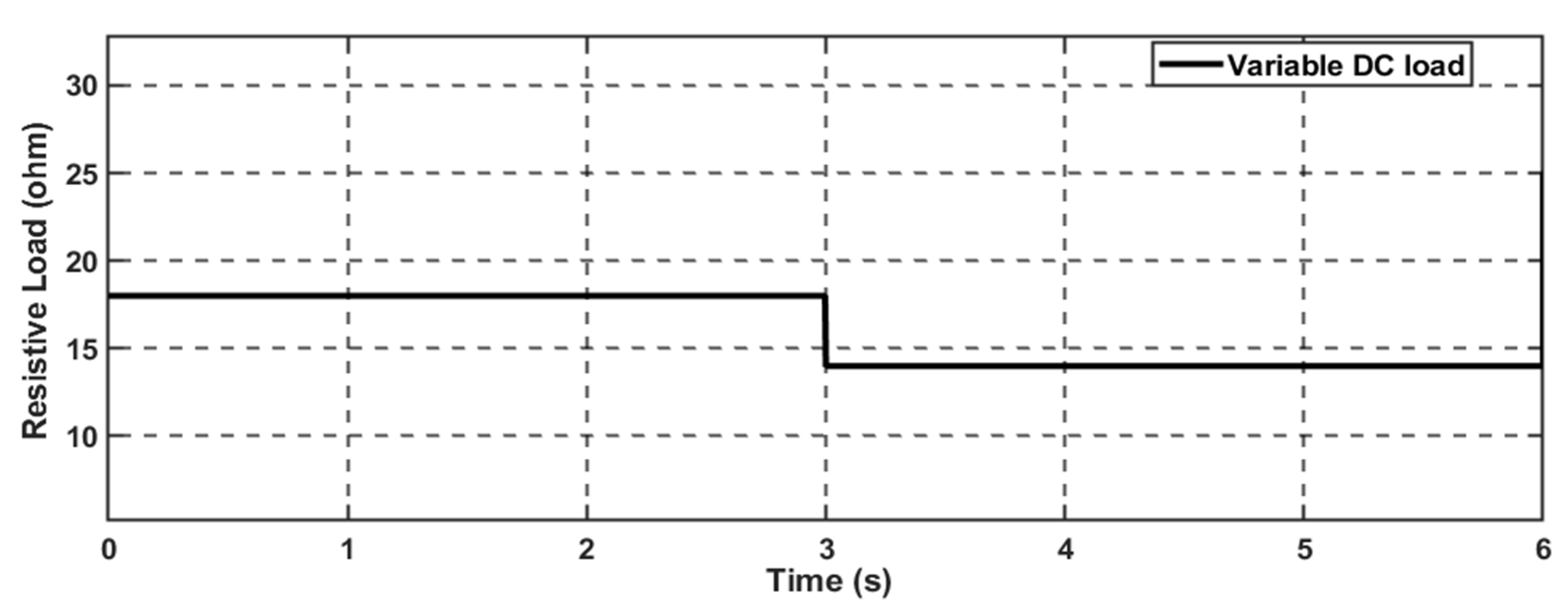
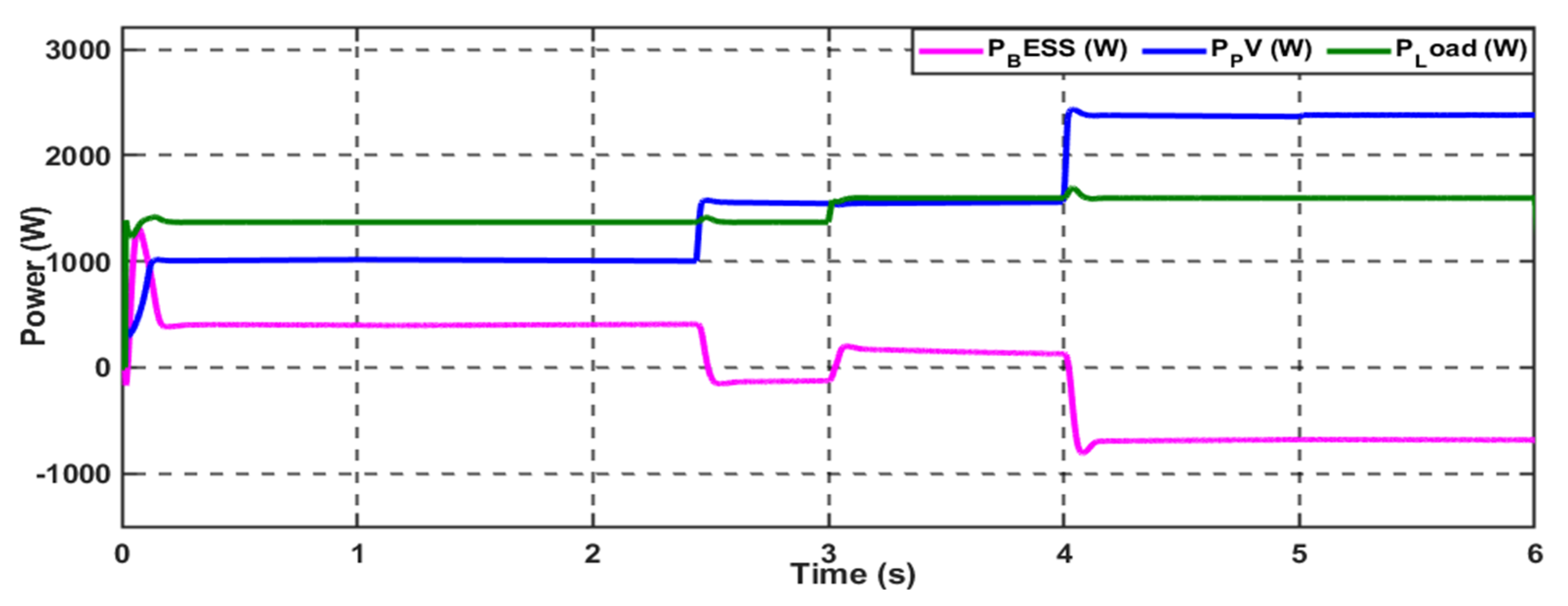
4.1. Scenario 1: Variable DC Load
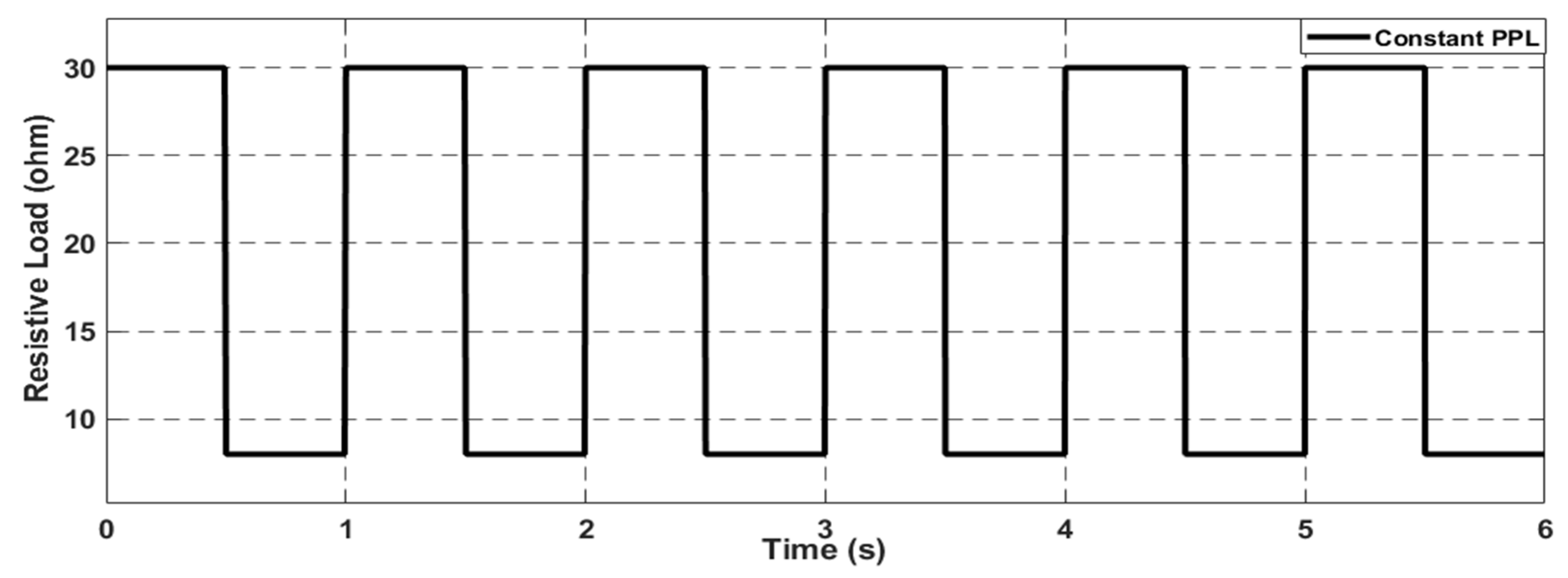
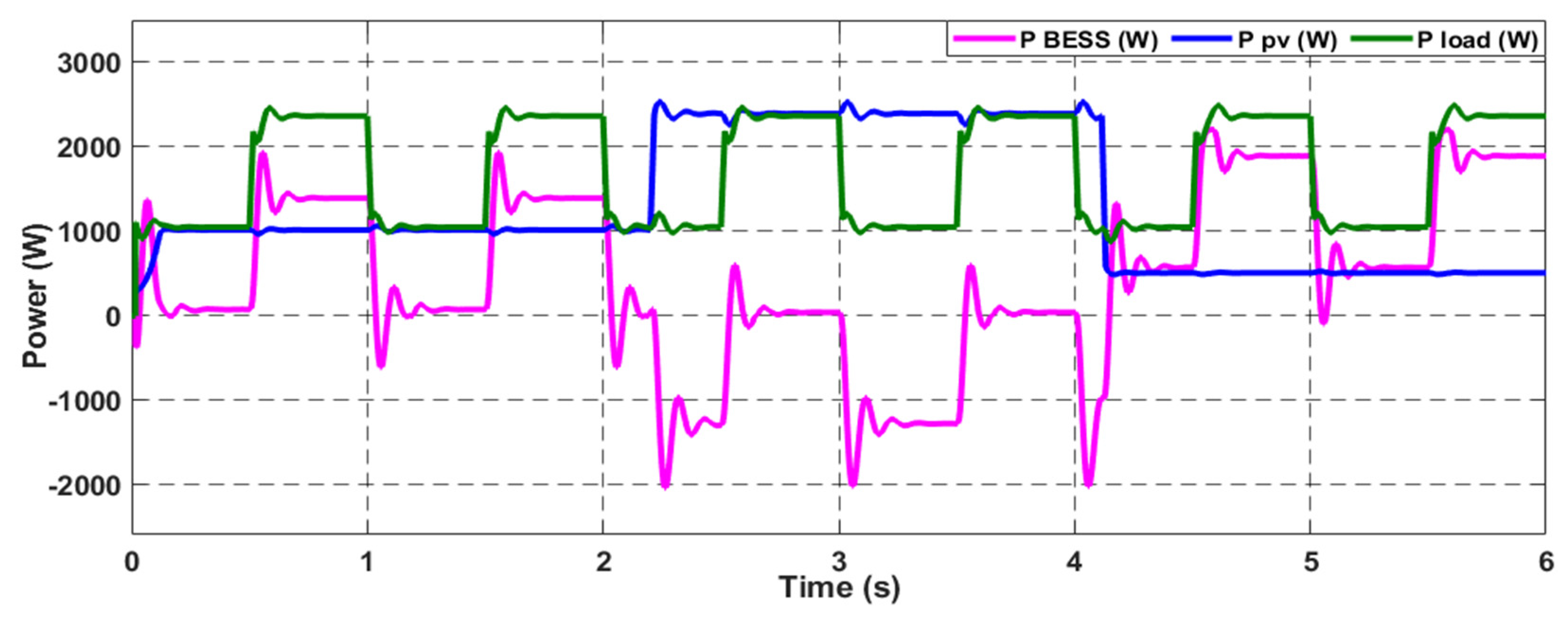
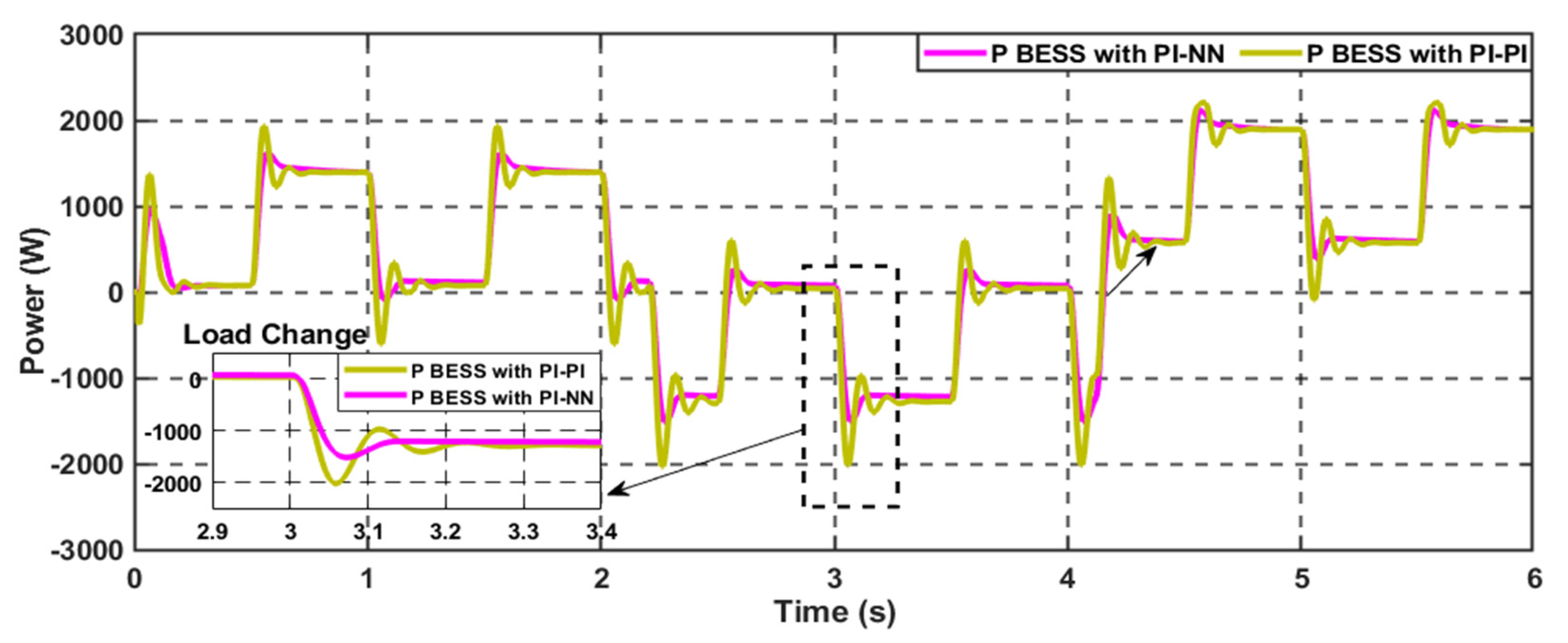
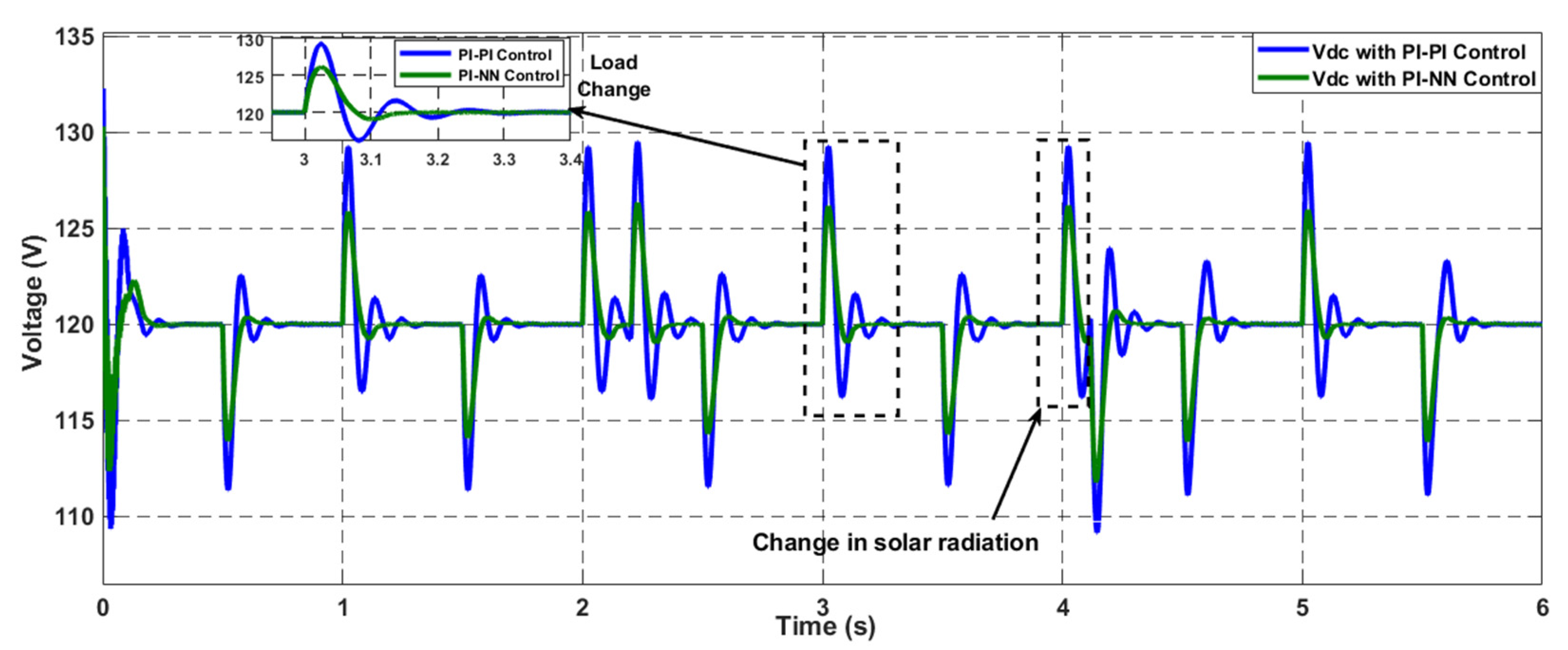
4.2. Scenario 2: Constant Pulsed Power Load (CPPL)
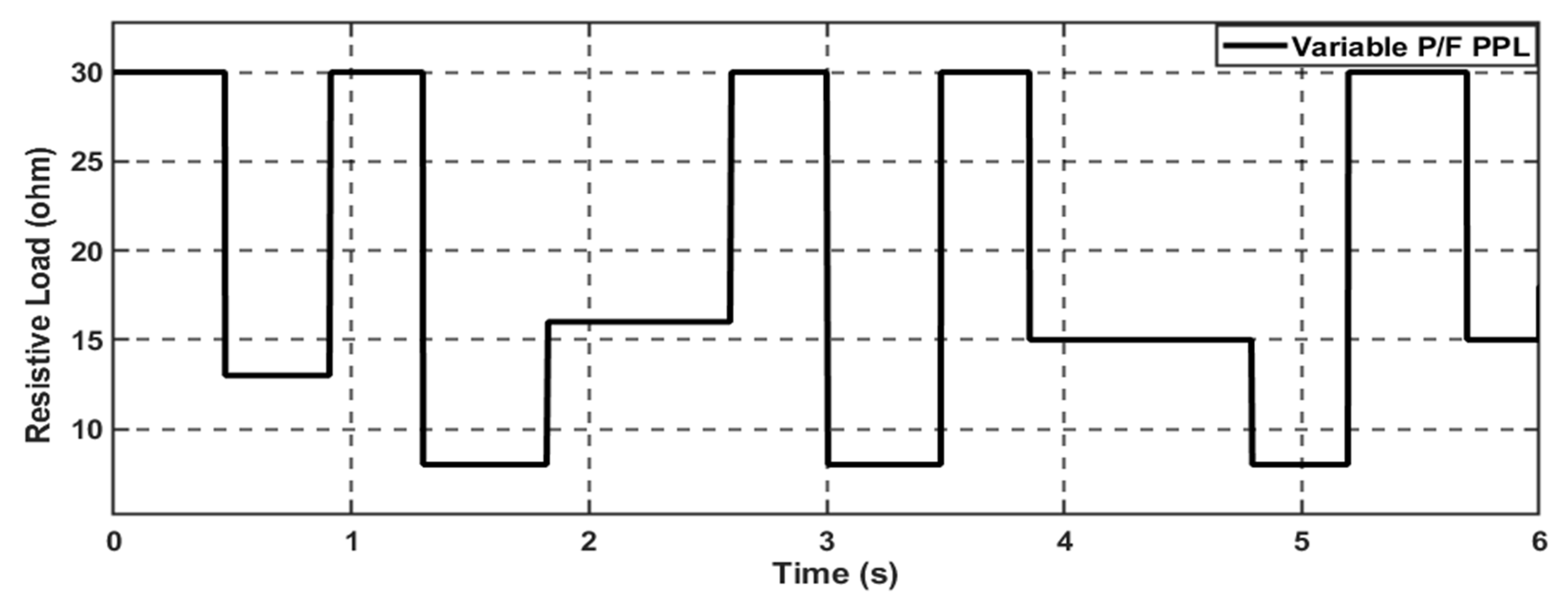
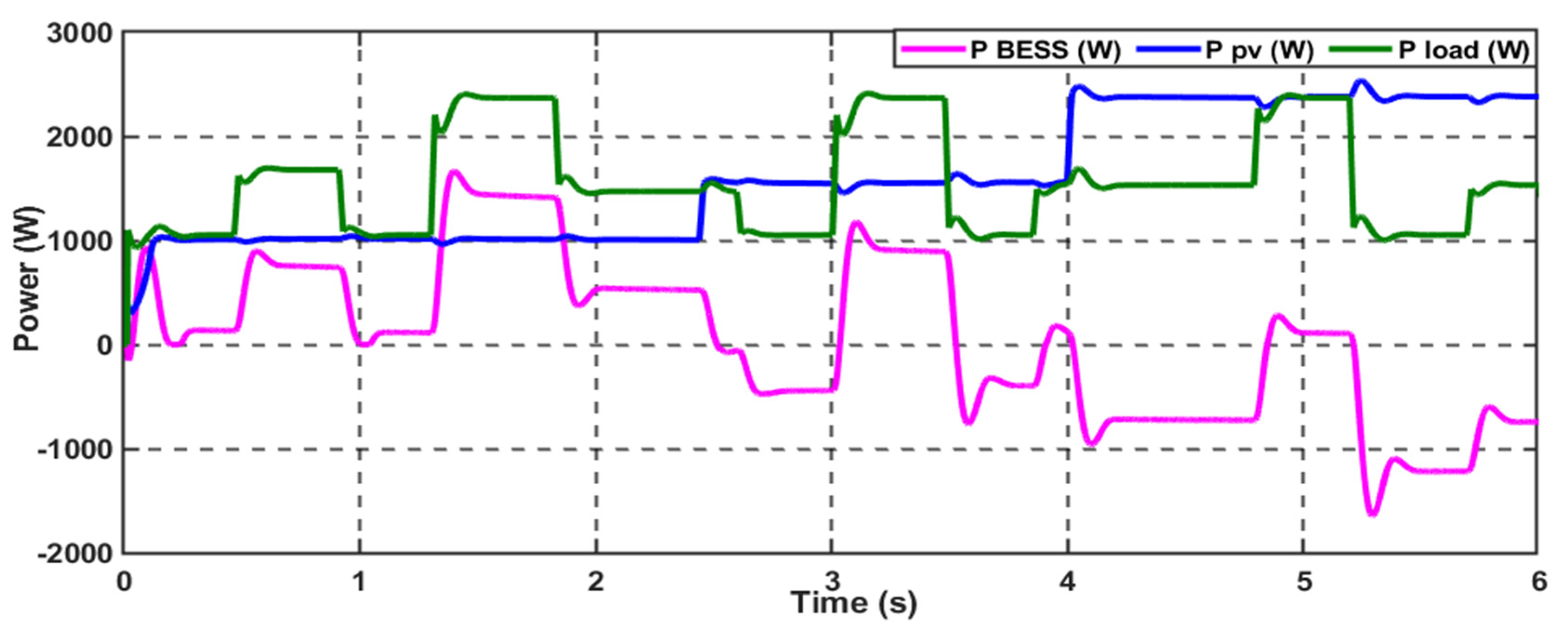
4.3. Scenario 3: Variable Power/Frequency Pulsed Power Load (VPPL)
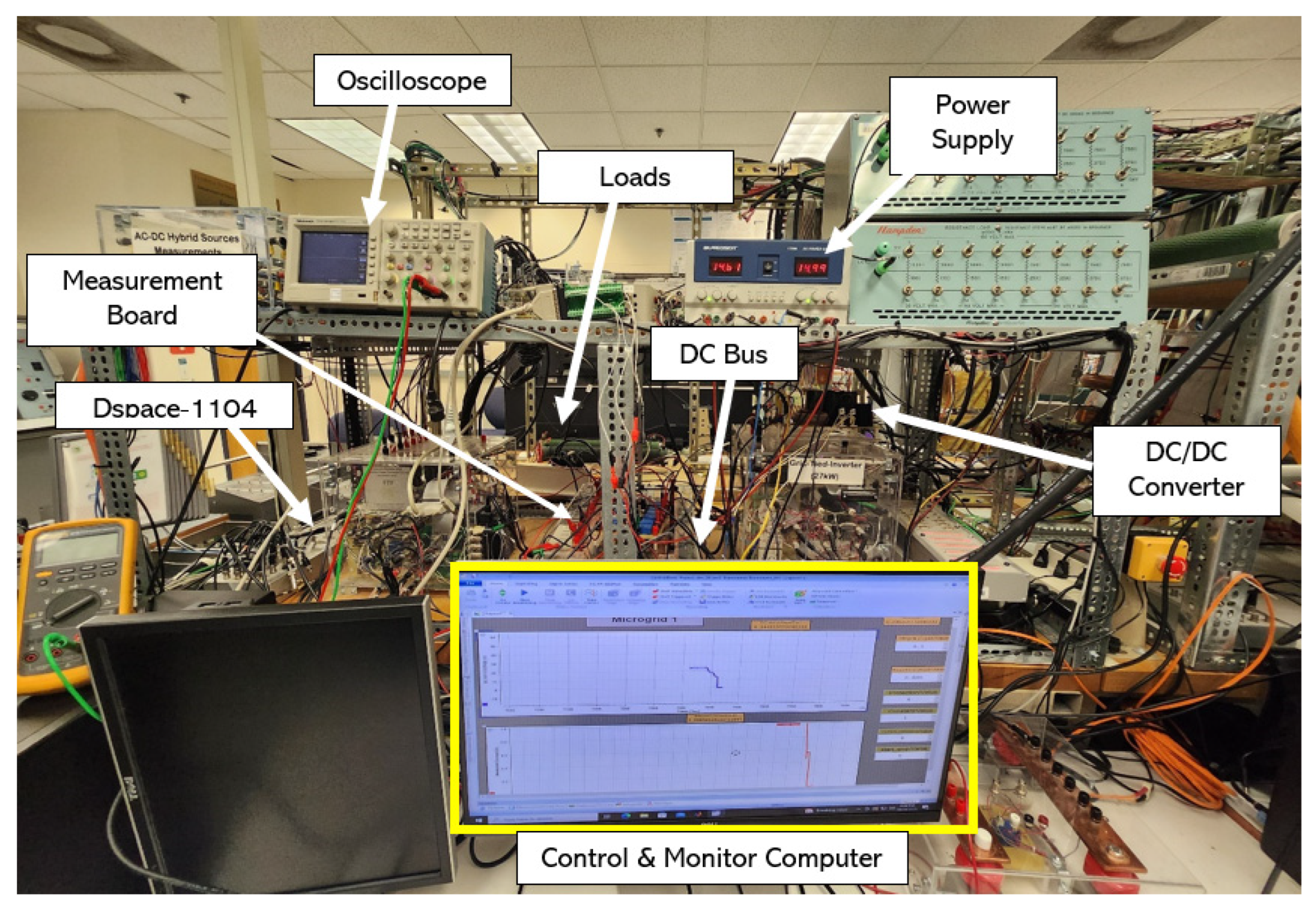
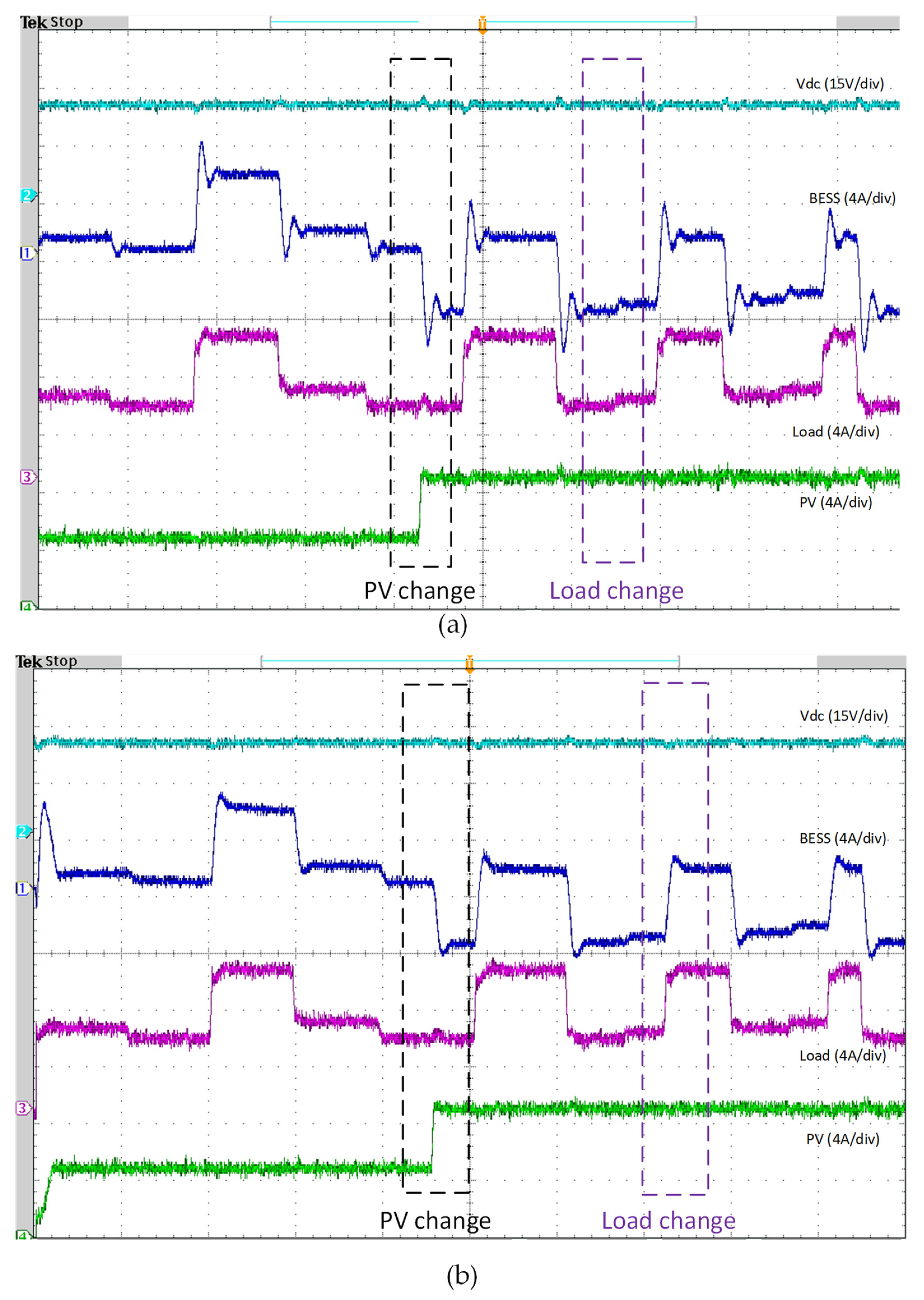
5. Hardware and Experimental Results
5.1. Experiment Setup
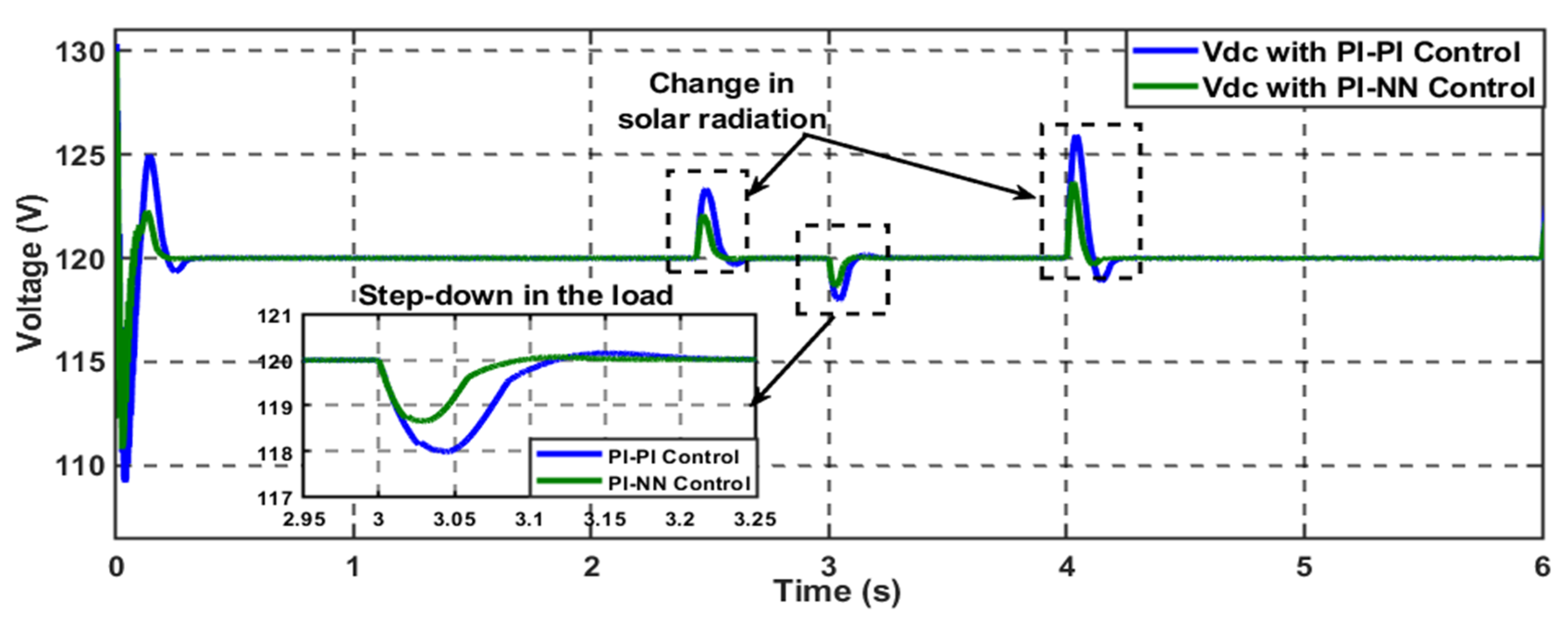
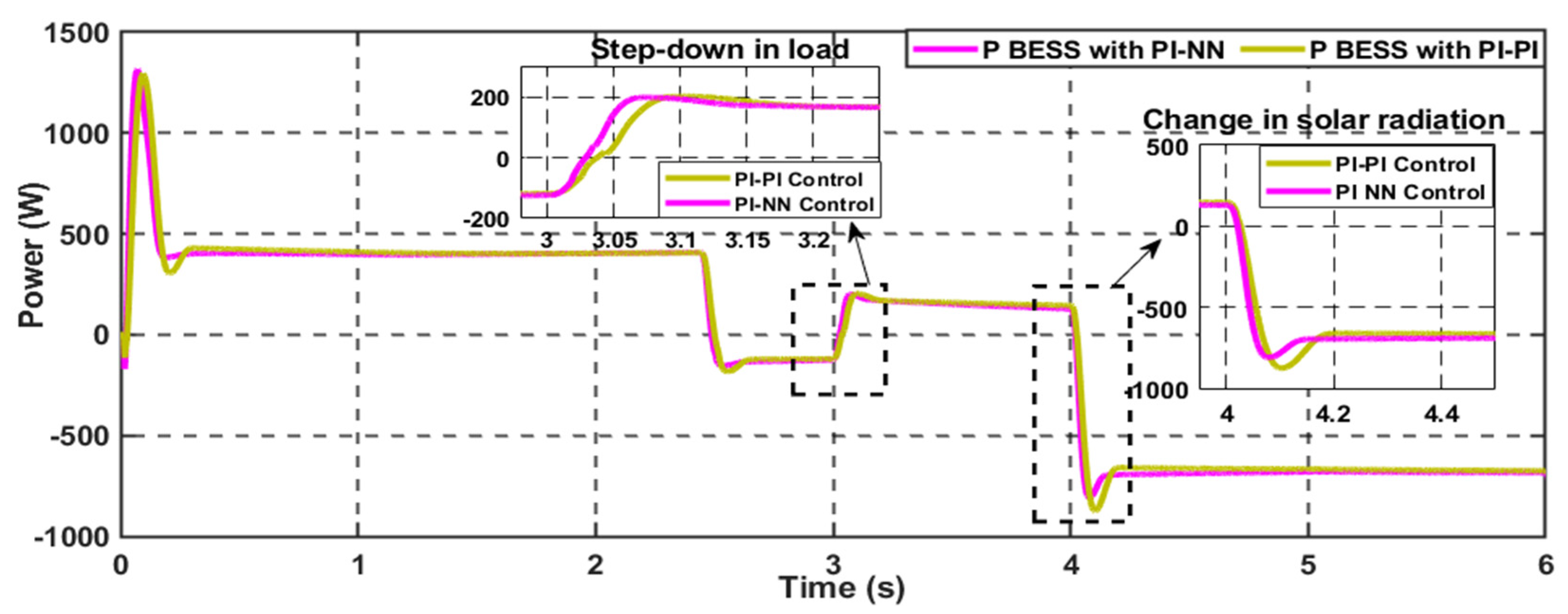
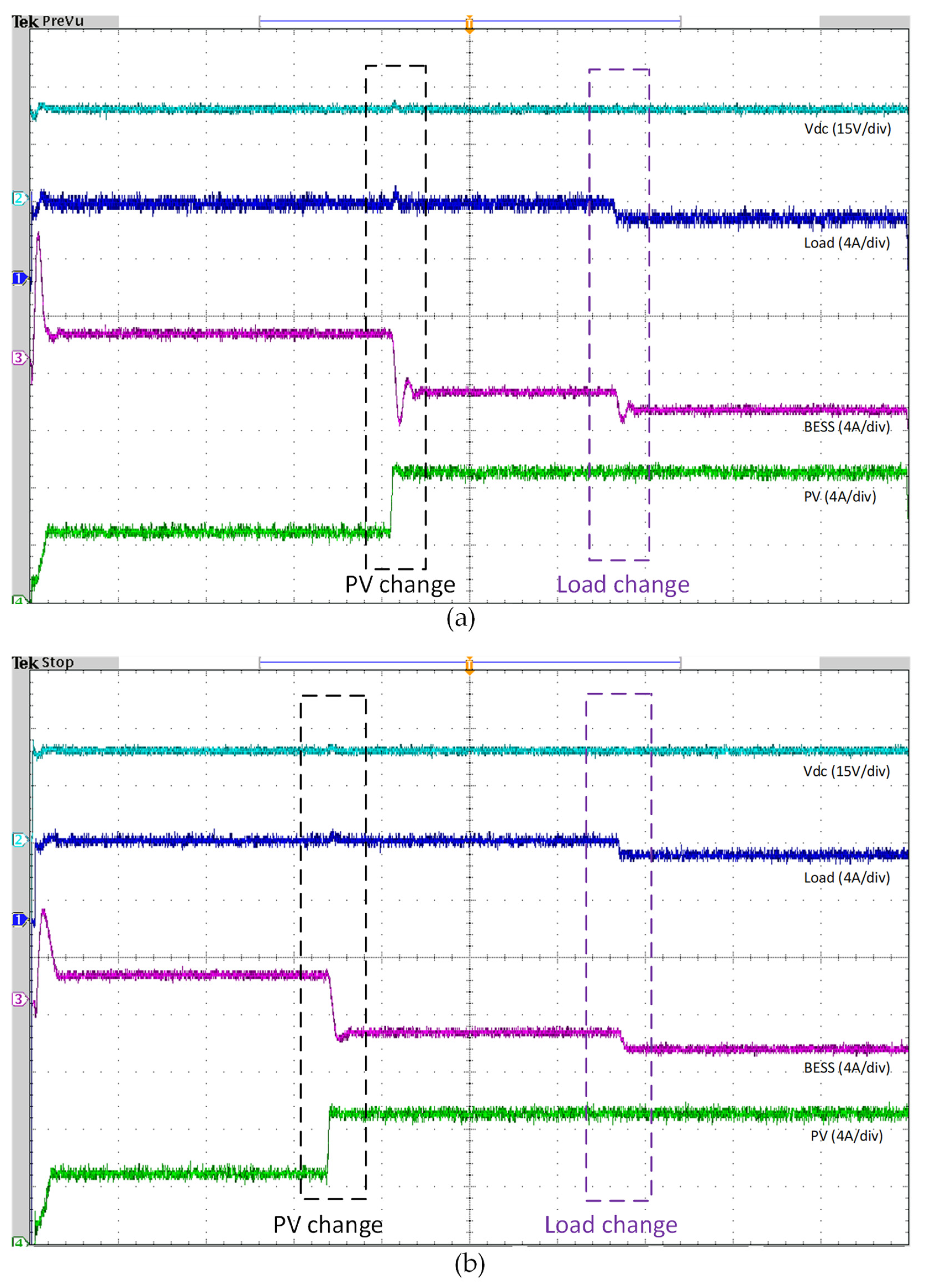
5.2. Scenario 1: Load Step Change—PV Step Change
5.3. Scenario 2: Constant Pulsed Load
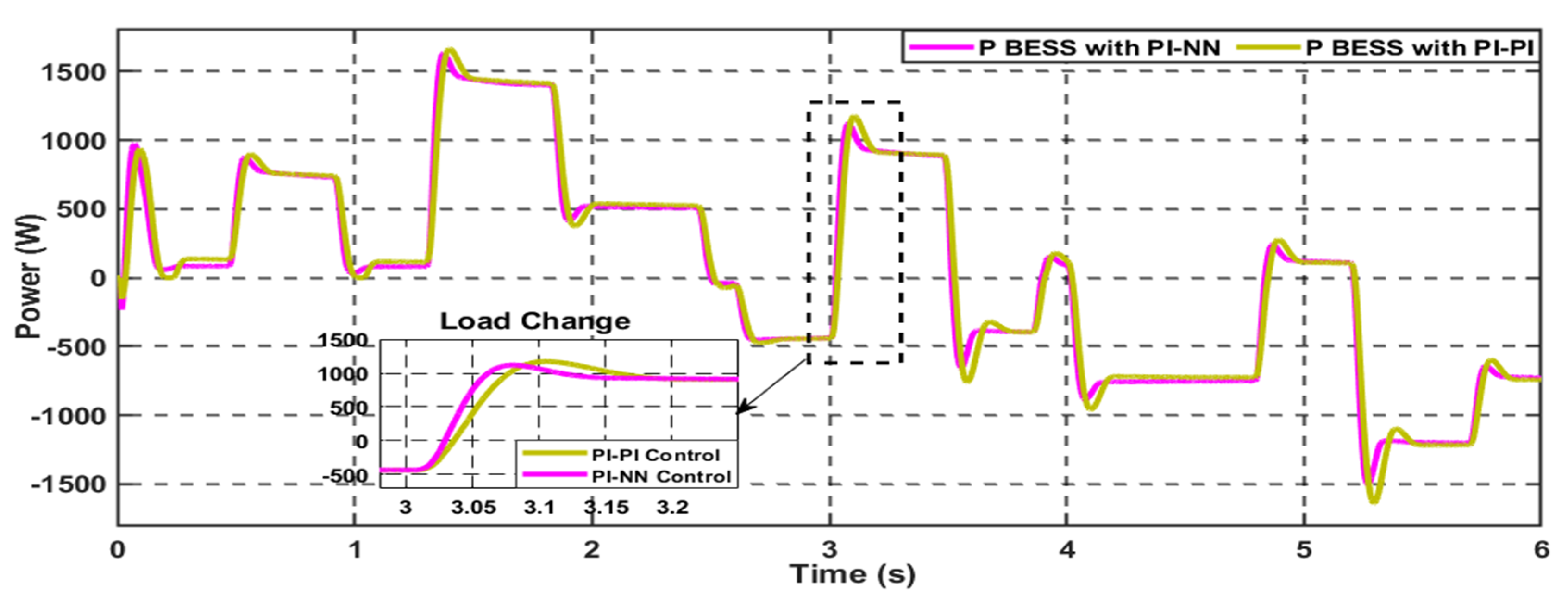
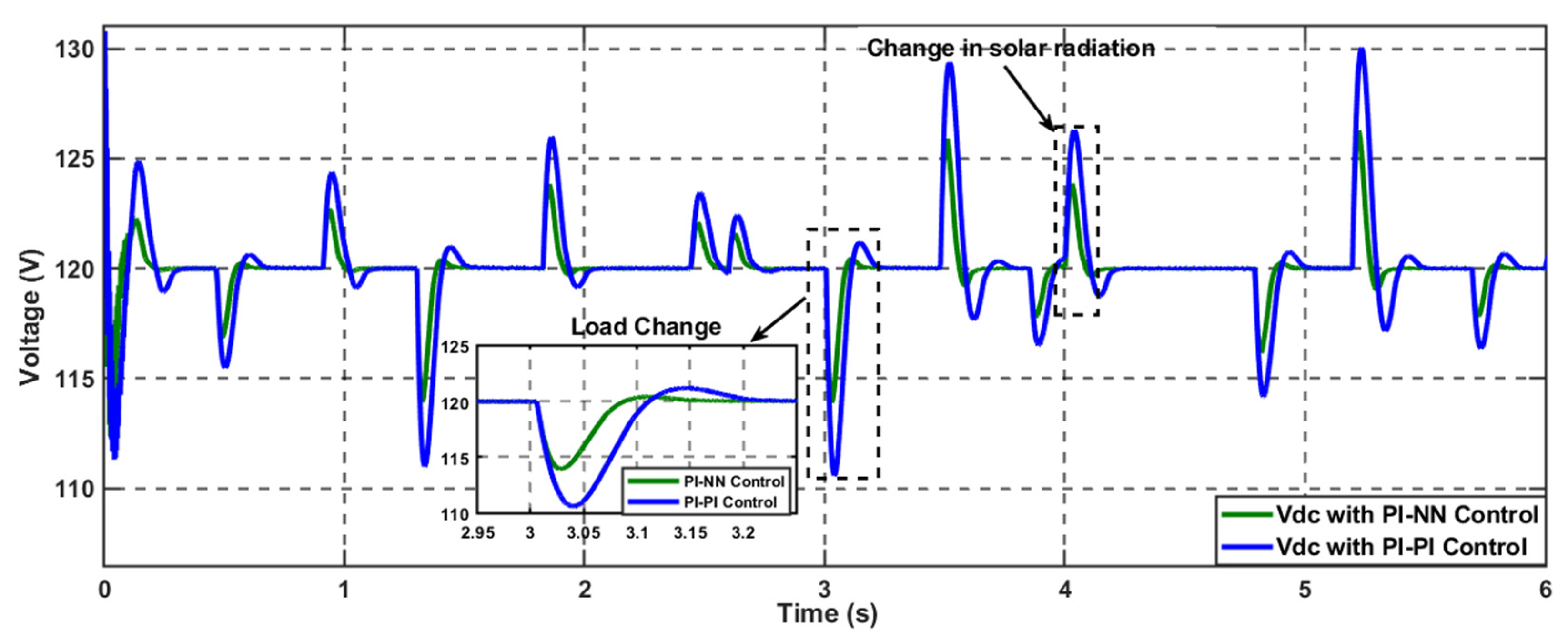
5.4. Scenario 3: Variable Pulsed Load
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RES | Renewable Energy Source |
| MG | Microgrid |
| ESS | Energy Storage System |
| BESS | Battery Energy Storage System |
| PV | Photovoltaic |
| SC | Supercapacitor |
| MPPT | Maximum Power Point Tracking |
| DER | Distributed Energy Resource |
| DC | Direct Current |
| AC | Alternative Current |
| PI | Proportional Integral |
| ML | Machine Learning |
| ANN | Artificial Neural Network |
| HLRNN | Hidden Layer Recurrent Neural Network |
| FLC | Fuzzy Logic Control |
| HESS | Hybrid Energy Storage System |
| NVSP | New Voltage Stability Pointer |
| FFNN | Feedforward Neural Network |
| CFNN | Cascade-Forward Neural Network |
| LRNN | Layer Recurrent Neural Network |
| LLNN | linear layer Neural Network |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| ABC | Artificial Bee Colony |
| BSA | Backtracking Search Algorithm |
| MPC | Model Predictive Control |
| LFC | Load Frequency Control |
| LV | Low Voltage |
| HV | High Voltage |
| RNN | Recurrent Neural Network |
| SM | Sliding Mode |
| PPL | Pulsed Power Load |
| CPPL | Constant Pulsed Power Load |
| VPPL | Variable Power/Frequency Pulsed Power Load |
| SOC | State Of Charge |
| P&O | Perturb and observe |
| Ts | Settling Time |
| %Mp | Percentage Maximum Peak |
References
- Blaabjerg, F.; Yang, Y.; Ma, K. Power Electronics—The Key Technology for Renewable Energy System Integration. In Proceedings of the 2013 3rd International Conference on Electric Power and Energy Conversion Systems, EPECS 2013, Istanbul, Turkey, 2–4 October 2013; IEEE: Palermo, Italy, 2013. [Google Scholar] [CrossRef]
- Aghmadi, A.; Hussein, H.; Polara, K.H.; Mohammed, O. A Comprehensive Review of Architecture, Communication, and Cybersecurity in Networked Microgrid Systems. Inventions 2023, 8, 84. [Google Scholar] [CrossRef]
- Eghtedarpour, N.; Farjah, E. Distributed charge/discharge control of energy storages in a renewable-energy-based DC micro-grid. IET Renew. Power Gener. 2014, 8, 45–57. [Google Scholar] [CrossRef]
- Zheng, J.; Liang, Z.T.; Li, Y.; Li, Z.; Wu, Q.H. Multi-Agent Reinforcement Learning With Privacy Preservation for Continuous Double Auction-Based P2P Energy Trading. IEEE Trans. Ind. Inform. 2024, 20, 6582–6590. [Google Scholar] [CrossRef]
- Shahgholian, G. A brief review on microgrids: Operation, applications, modeling, and control. Int. Trans. Electr. Energy Syst. 2021, 31, e12885. [Google Scholar] [CrossRef]
- Korompili, A.; Monti, A. Review of Modern Control Technologies for Voltage Regulation in DC/DC Converters of DC Microgrids. Energies 2023, 16, 4563. [Google Scholar] [CrossRef]
- Joshi, A.; Capezza, S.; Alhaji, A.; Chow, M.Y. Survey on AI and Machine Learning Techniques for Microgrid Energy Management Systems. IEEE/CAA J. Autom. Sin. 2023, 10, 1513–1529. [Google Scholar] [CrossRef]
- Aghmadi, A.; Ali, O.; Mohammed, O.A. Enhancing DC Microgrid Stability under Pulsed Load Conditions through Hybrid Energy Storage Control Strategy. In Proceedings of the 2023 IEEE Industry Applications Society Annual Meeting, (IAS), Nashville, TN, USA; 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Ma, T.; Cintuglu, M.H.; Mohammed, O.A. Control of a hybrid AC/DC microgrid involving energy storage and pulsed loads. IEEE Trans. Ind. Appl. 2017, 53, 567–575. [Google Scholar] [CrossRef]
- Li, H.; Yun, Z.; Liang, J.; Zhang, F. Optimized Operation Mode of Coordination between the Flywheel Energy Storage and Generators for Pulsed Loads in Micro-grid. In Proceedings of the 2017 2nd International Conference on Power and Renewable Energy, Chengdu, China, 20–23 September 2017; IEEE: Chengdu, China, 2017. [Google Scholar]
- Aghmadi, A.; Mohammed, O.A. Operation and Coordinated Energy Management in Multi-Microgrids for Improved and Resilient Distributed Energy Resource Integration in Power Systems. Electronics 2024, 13, 358. [Google Scholar] [CrossRef]
- Elbeshbeshy, A.M.; Ghanem, A.; Abulanwar, S.; Deng, F.; Kaddah, S.S.; Rizk, M.E.M. Enhanced Stability in Hybrid AC/DC Microgrids with Controlled Magnetic Energy Router. In Proceedings of the 2023 24th International Middle East Power System Conference, MEPCON 2023, Mansoura, Egypt, 19–21 December 2023; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Badrudeen, T.U.; Nwulu, N.I.; Gbadamosi, S.L. Neural Network Based Approach for Steady-State Stability Assessment of Power Systems. Sustainability 2023, 15, 1667. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, Y.; Wang, A.; Zhang, J. Neural network modeling and dynamic behavior prediction of nonlinear dynamic systems. Nonlinear Dyn. 2023, 111, 11335–11356. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial Neural Networks Based Optimization Techniques: A Review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Akpolat, A.N.; Habibi, M.R.; Baghaee, H.R.; Dursun, E.; Kuzucuoğlu, A.E.; Yang, Y.; Dragičević, T.; Blaabjerg, F. Dynamic Stabilization of DC Microgrids Using ANN-Based Model Predictive Control. IEEE Trans. Energy Convers. 2022, 37, 999–1010. [Google Scholar] [CrossRef]
- Rehimi, S.; Mirzaei, R.; Bevrani, H. ANN-Based Frequency and Tie-Line Power Control in Interconnected Microgrids. In Proceedings of the 2019 6th International Conference on Control, Instrumentation and Automation, ICCIA 2019, Sanandaj, Iran, 30–31 October 2019. [Google Scholar] [CrossRef]
- Rafikiran, S.; Devadasu, G.; Basha, C.H.; Tom, P.M.; Prashanth, V.; Dhanamjayulu, C.; Kumbhar, A.; Muyeen, S.M. Design and performance analysis of hybrid MPPT controllers for fuel cell fed DC-DC converter systems. Energy Rep. 2023, 9, 5826–5842. [Google Scholar] [CrossRef]
- Chetouani, E.; Errami, Y.; Obbadi, A.; Sahnoun, S. Self-adapting PI controller for grid-connected DFIG wind turbines based on recurrent neural network optimization control under unbalanced grid faults. Electr. Power Syst. Res. 2023, 214, 108829. [Google Scholar] [CrossRef]
- Zdiri, M.A.; Guesmi, T.; Alshammari, B.M.; Alqunun, K.; Almalaq, A.; Salem, F.M.; Hadj Abdallah, H.; Toumi, A. Design and Analysis of Sliding-Mode Artificial Neural Network Control Strategy for Hybrid PV-Battery-Supercapacitor System. Energies 2022, 15, 4099. [Google Scholar] [CrossRef]
- Aghmadi, A.; Ali, O.; Hussein, H.; Mohammed, O.A. Dynamic Pulsed Load Mitigation in PV-Battery-Supercapacitor Systems: A Hybrid PI-NN Controller Approach. In Proceedings of the 2023 IEEE Design Methodologies Conference, DMC 2023, Miami, FL, USA, 24–26 September 2023; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Idrissi, Y.E.A.; Assalaou, K.; Elmahni, L.; Aitiaz, E. New improved MPPT based on artificial neural network and PI controller for photovoltaic applications. Int. J. Power Electron. Drive Syst. 2022, 13, 1791–1801. [Google Scholar] [CrossRef]
- Depuru, S.R.; Mahankali, M. Performance analysis of a maximum power point tracking technique using silver mean method. Adv. Electr. Electron. Eng. 2018, 16, 25–35. [Google Scholar] [CrossRef]
- Rezkallah, M.; Singh, S.; Chandra, A.; Singh, B.; Tremblay, M.; Saad, M.; Geng, H. Comprehensive Controller Implementation for Wind-PV-Diesel Based Standalone Microgrid. IEEE Trans. Ind. Appl. 2019, 55, 5416–5428. [Google Scholar] [CrossRef]
- Sharma, R.K.; Mishra, S. Dynamic Power Management and Control of a PV PEM Fuel-Cell-Based Standalone ac/dc Microgrid Using Hybrid Energy Storage. IEEE Trans. Ind. Appl. 2018, 54, 526–538. [Google Scholar] [CrossRef]
- Mardani, M.M.; Vafamand, N.; Khooban, M.H.; Dragičević, T.; Blaabjerg, F. Design of Quadratic D-Stable Fuzzy Controller for DC Microgrids With Multiple CPLs. IEEE Trans. Ind. Electron. 2019, 66, 4805–4812. [Google Scholar] [CrossRef]
- Herrera, L.; Zhang, W.; Wang, J. Stability Analysis and Controller Design of DC Microgrids with Constant Power Loads. IEEE Trans. Smart Grid 2017, 8, 881–888. [Google Scholar] [CrossRef]
- Kardan, M.A.; Asemani, M.H.; Khayatian, A.; Vafamand, N.; Khooban, M.H.; Dragičević, T.; Blaabjerg, F. Improved Stabilization of Nonlinear DC Microgrids: Cubature Kalman Filter Approach. IEEE Trans. Ind. Appl. 2018, 54, 5104–5112. [Google Scholar] [CrossRef]
- Vafamand, N.; Khooban, M.H.; Dragičević, T.; Blaabjerg, F. Networked Fuzzy Predictive Control of Power Buffers for Dynamic Stabilization of DC Microgrids. IEEE Trans. Ind. Electron. 2019, 66, 1356–1362. [Google Scholar] [CrossRef]
- Su, M.; Liu, Z.; Sun, Y.; Han, H.; Hou, X. Stability analysis and stabilization methods of DC microgrid with multiple parallel-connected DC-DC converters loaded by CPLs. IEEE Trans. Smart Grid 2018, 9, 132–142. [Google Scholar] [CrossRef]
- Xu, Q.; Vafamand, N.; Chen, L.; Dragicevic, T.; Xie, L.; Blaabjerg, F. Review on Advanced Control Technologies for Bidirectional DC/DC Converters in DC Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1205–1221. [Google Scholar] [CrossRef]
- Gonzatti, R.B.; Li, Y.; Amirabadi, M.; Lehman, B.; Peng, F.Z. An Overview of Converter Topologies and Their Derivations and Interrelationships. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6417–6429. [Google Scholar] [CrossRef]
- Abdullah, A.M.; Yatim, Y.A.H.M.; Tan, C.W.; Samosir, A.S. Control of a Bidirectional Converter to Interface Ultracapacitor with Renewable Energy Sources. In Proceedings of the 2013 IEEE international conference on industrial technology (ICIT), Cape Town, South Africa, 25–28 February 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Junhong, Z.; Jih-Sheng, L.; Wensong, Y. Bidirectional DC-DC converter modeling and unified controller with digital implementation. In Proceedings of the 2008 Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 24–28 February 2008; IEEE: Piscataway, NJ, USA, May, 2008. [Google Scholar]
- Lopez-Garcia, T.B.; Coronado-Mendoza, A.; Domínguez-Navarro, J.A. Artificial neural networks in microgrids: A review. Eng. Appl. Artif. Intell. 2020, 95, 103894. [Google Scholar] [CrossRef]
- Urias, M.E.G.; Sanchez, E.N.; Ricalde, L.J. Electrical Microgrid Optimization via a New Recurrent Neural Network. IEEE Syst. J. 2015, 9, 945–953. [Google Scholar] [CrossRef]
- Habibi, M.R.; Baghaee, H.R.; Dragičević, T.; Blaabjerg, F. Detection of false data injection cyber-attacks in DC microgrids based on recurrent neural networks. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5294–5310. [Google Scholar] [CrossRef]
- Zeng, P.; Li, H.; He, H.; Li, S. Dynamic Energy Management of a Microgrid Using Approximate Dynamic Programming and Deep Recurrent Neural Network Learning. IEEE Trans. Smart Grid 2019, 10, 4435–4445. [Google Scholar] [CrossRef]
- Mao, S.; Sejdic, E. A Review of Recurrent Neural Network-Based Methods in Computational Physiology. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 6983–7003. [Google Scholar] [CrossRef] [PubMed]
- Long, D.; Zhang, R.; Mao, Y. Recurrent Neural Networks with Finite Memory Length. IEEE Access 2019, 7, 12511–12520. [Google Scholar] [CrossRef]
- Husein, M.; Chung, I.Y. Day-ahead solar irradiance forecasting for microgrids using a long short-term memory recurrent neural network: A deep learning approach. Energies 2019, 12, 1856. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning Long-Term Dependencies with Gradient Descent is Difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]

| [Ref] | Control Strategy | Key Features | Validation |
|---|---|---|---|
| [13] | ANN employs different algorithms |
| Simulation |
| [14] | NN |
| Simulation |
| [15] | ANN with optimization techniques |
| Simulation |
| [16] | ANN-MPC |
| Experimental |
| [17] | ANN |
| Simulation |
| [18] | Hybrid MPPT |
| Simulation |
| [19] | Hidden Layer Recurrent Neural Network (HLRNN) |
| Simulation |
| [20] | Fuzzy Logic Control (FLC) and Sliding-mode and ANN controllers |
| Simulation |
| [21] | Hybrid PI-NN |
| Simulation |
| [22] | ANN-MPPT |
| Simulation |
| Parameter | Value |
|---|---|
| Common DC bus voltage | 120 V |
| Rating of the PV generation System | 2.5 KW |
| Rating of the BESS | 51.8 V, 100 Ah |
| Converter’s switching frequency | 5 kHz |
| Pulsed Power Load (PPL) demand | 480–2400 W |
| Parameter | Value |
|---|---|
| Common DC bus voltage | 25 V |
| Rating of the PV generation System | 1.5 KW |
| Rating of the BESS | 12 V, 100 Ah |
| Converter’s switching frequency | 5 kHz |
| Pulsed Power Load (PPL) demand | 150~400 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aghmadi, A.; Ali, O.; Sajjad Hossain Rafin, S.M.; Taha, R.A.; Ibrahim, A.M.; Mohammed, O.A. Hardware Implementation of Hybrid Data Driven-PI Control Scheme for Resilient Operation of Standalone DC Microgrid. Batteries 2024, 10, 297. https://doi.org/10.3390/batteries10090297
Aghmadi A, Ali O, Sajjad Hossain Rafin SM, Taha RA, Ibrahim AM, Mohammed OA. Hardware Implementation of Hybrid Data Driven-PI Control Scheme for Resilient Operation of Standalone DC Microgrid. Batteries. 2024; 10(9):297. https://doi.org/10.3390/batteries10090297
Chicago/Turabian StyleAghmadi, Ahmed, Ola Ali, S. M. Sajjad Hossain Rafin, Rawan A. Taha, Ahmed M. Ibrahim, and Osama A. Mohammed. 2024. "Hardware Implementation of Hybrid Data Driven-PI Control Scheme for Resilient Operation of Standalone DC Microgrid" Batteries 10, no. 9: 297. https://doi.org/10.3390/batteries10090297
APA StyleAghmadi, A., Ali, O., Sajjad Hossain Rafin, S. M., Taha, R. A., Ibrahim, A. M., & Mohammed, O. A. (2024). Hardware Implementation of Hybrid Data Driven-PI Control Scheme for Resilient Operation of Standalone DC Microgrid. Batteries, 10(9), 297. https://doi.org/10.3390/batteries10090297










