Review of Photovoltaic–Battery Energy Storage Systems for Grid-Forming Operation
Abstract
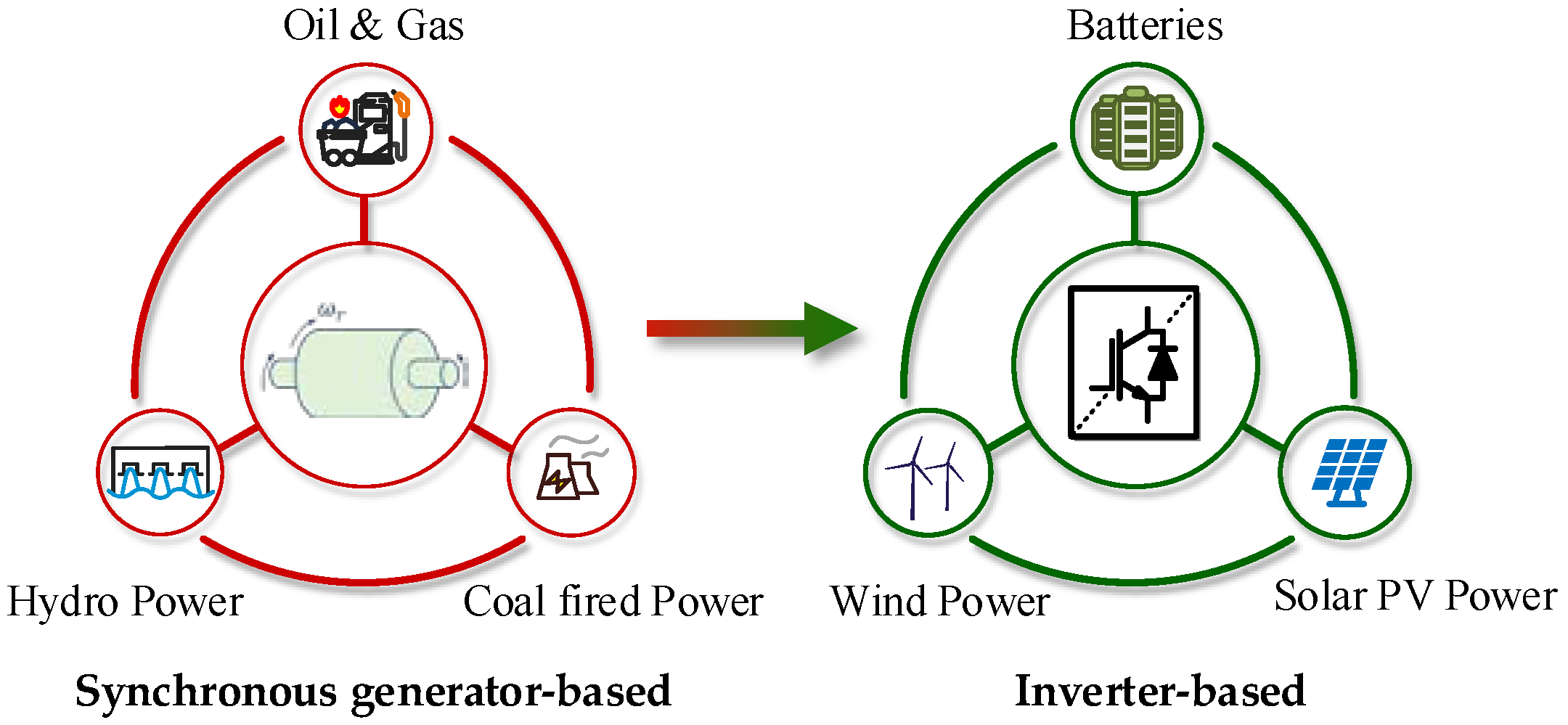
1. Introduction
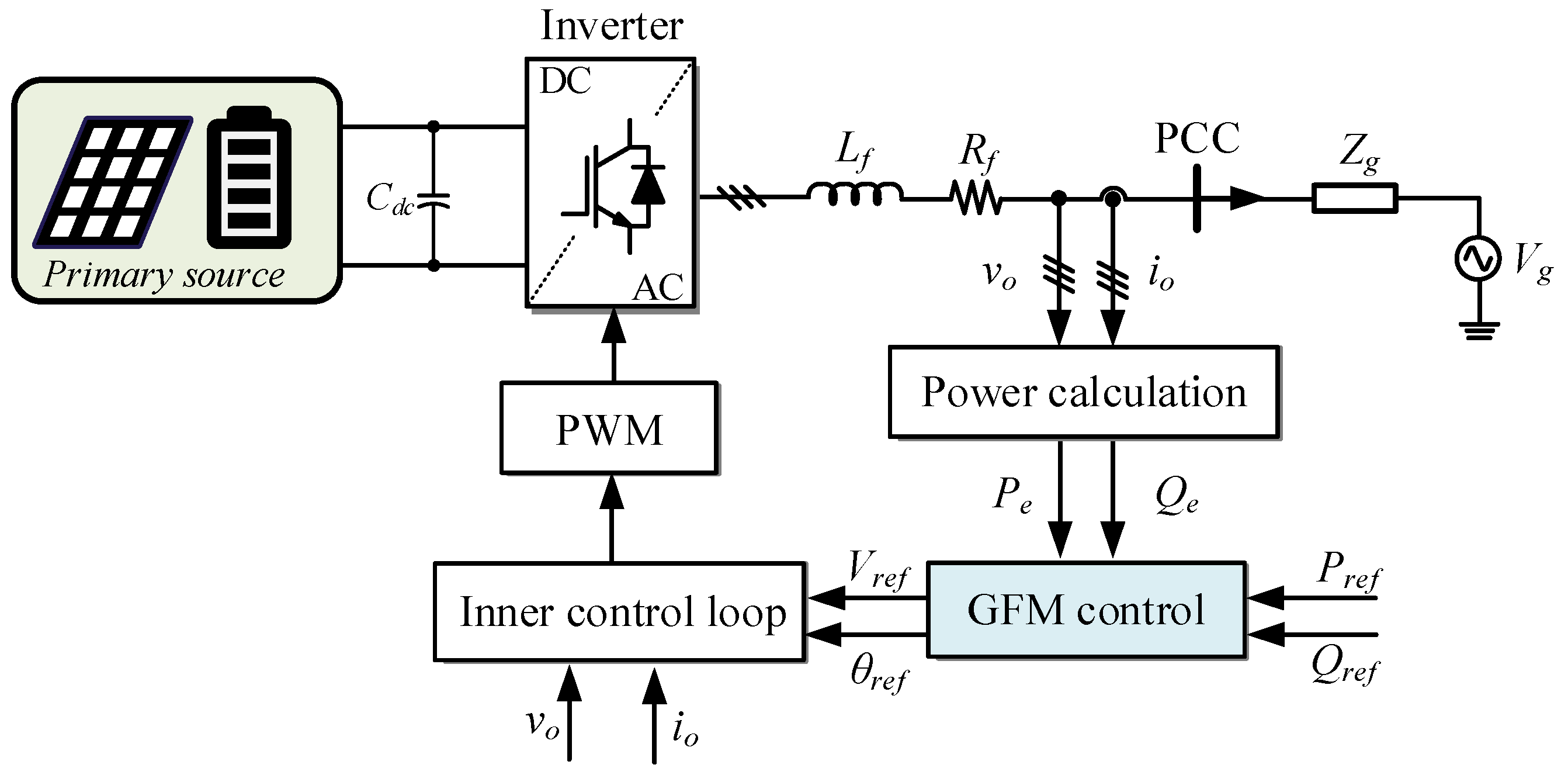
2. Typical Configuration of the PV-BES System
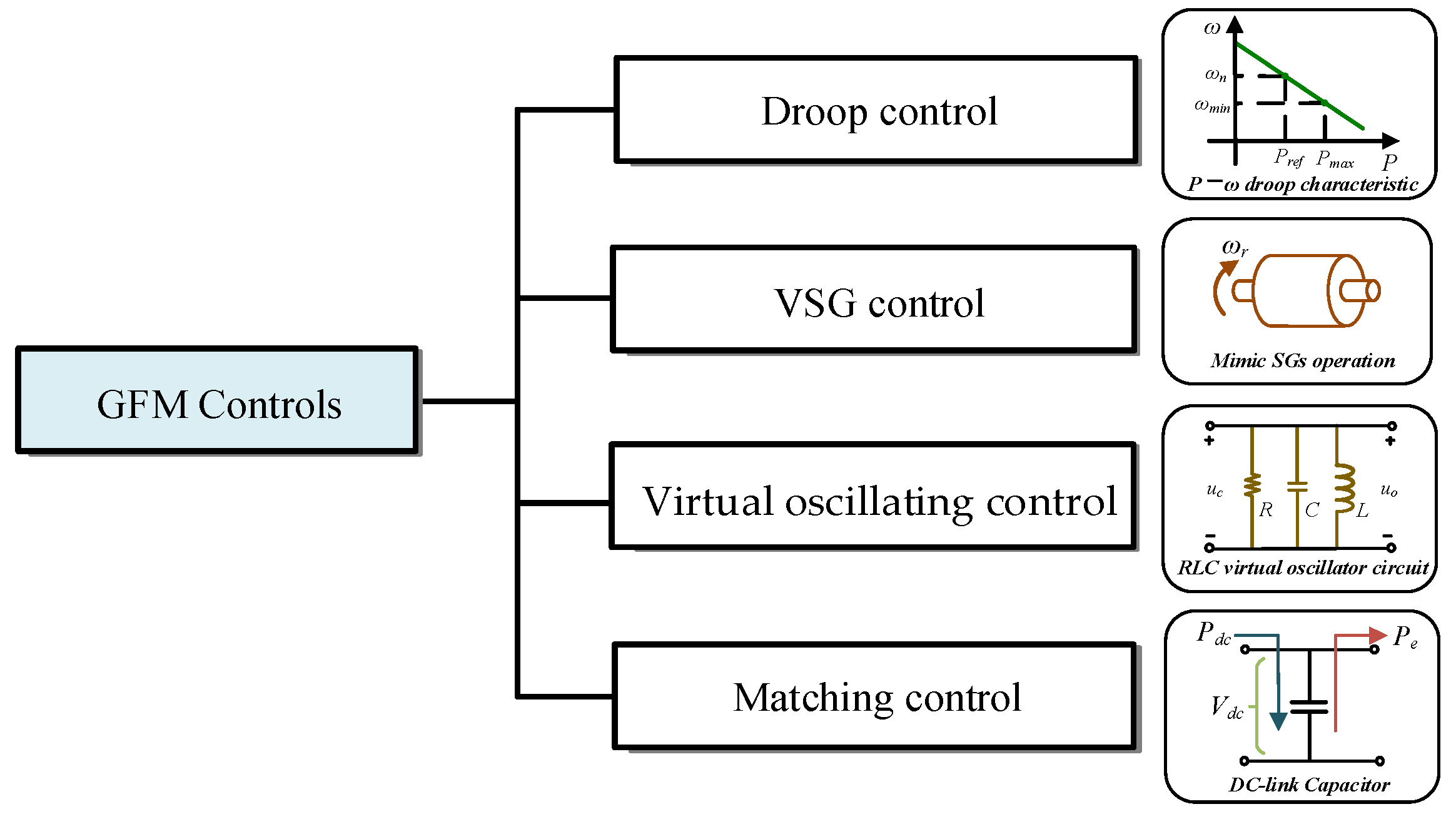
3. Typical GFM Controls in PV-BES System
3.1. Droop Control
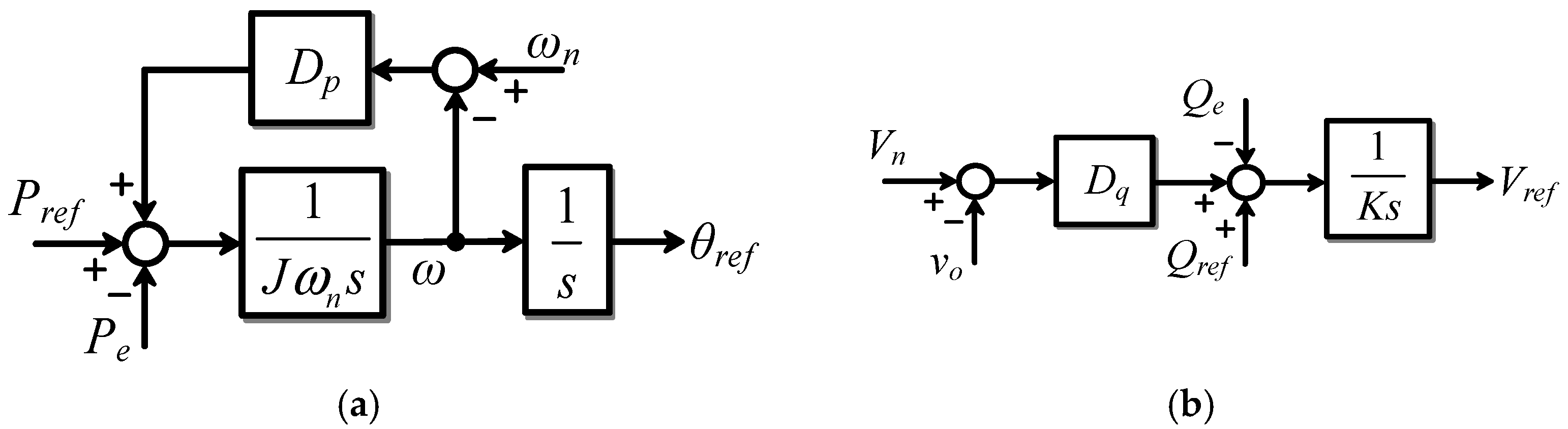
3.2. Virtual Synchronous Generator Control
3.3. Virtual Oscillator Control
3.4. Matching Control
4. Coordinated Control of the PV-BES System
4.1. Unified Mode Division and Switching Method
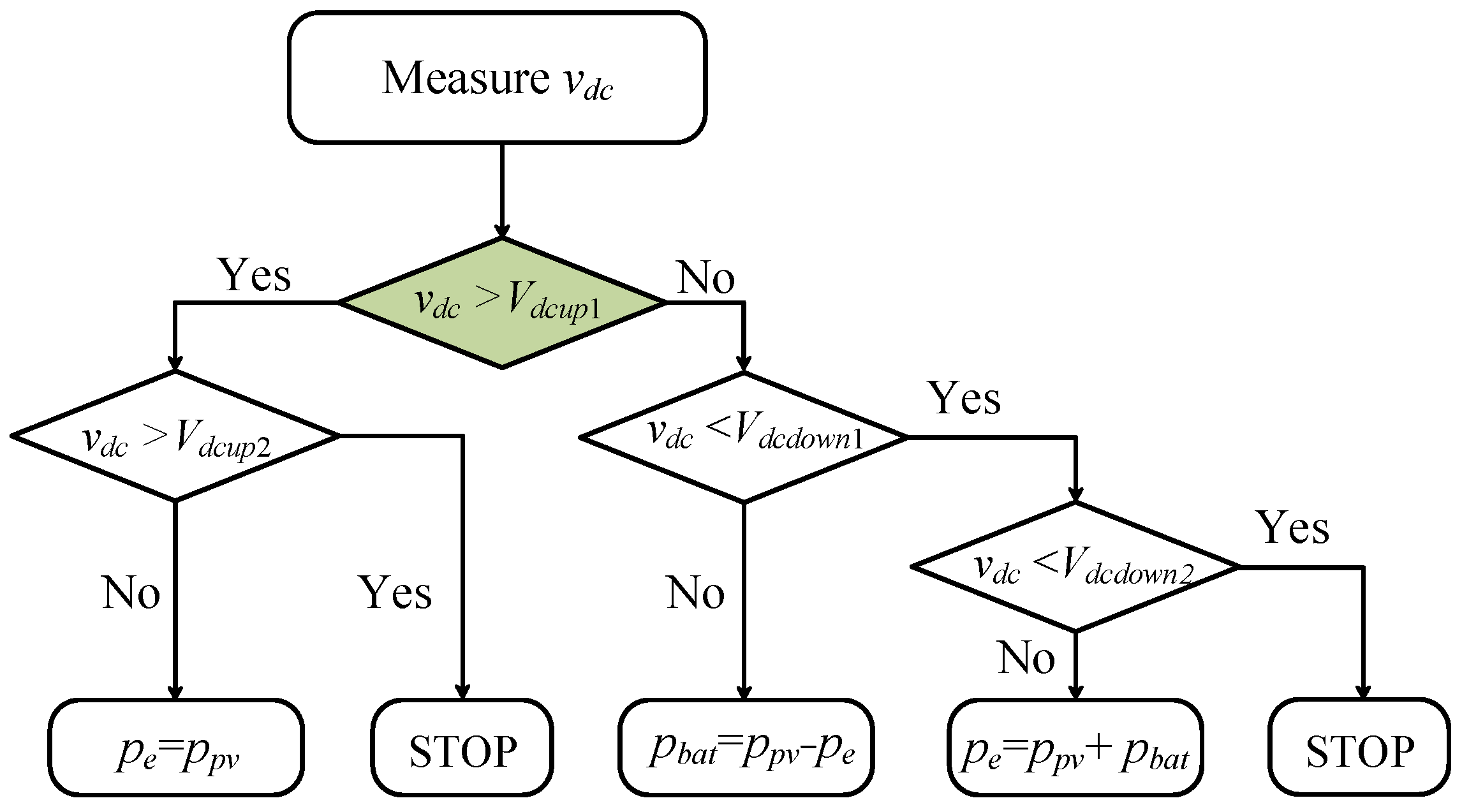
4.2. Specific Mode Switching and Division Methods
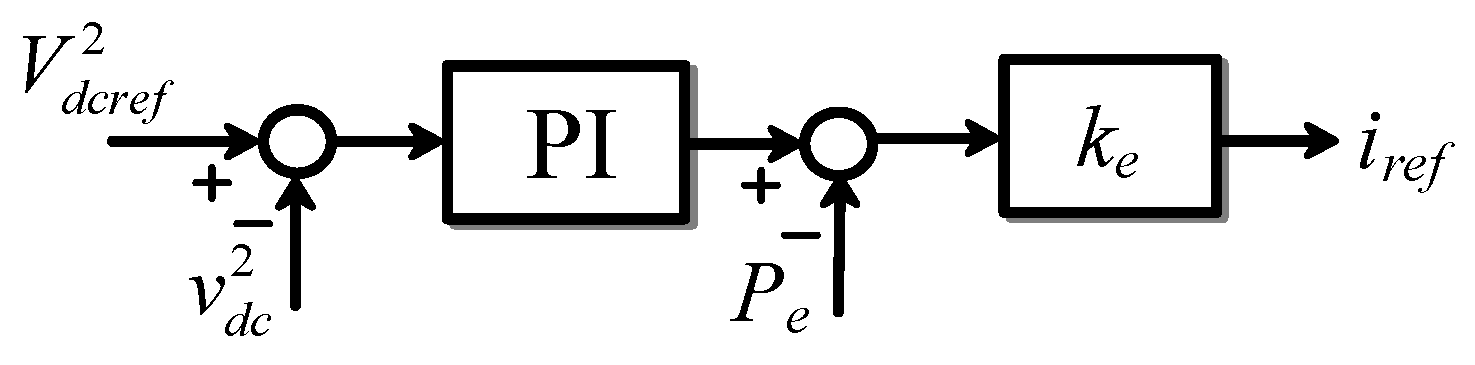
4.3. Coordinated Control Strategies to Improve the Power Flow Performance
4.4. Challenges and Prospects of Coordinated GFM Control in PV-BES Systems
- (1)
- Seamless mode transitions: develop coordinated control strategies to enable seamless mode transitions, minimizing power losses and transient times.
- (2)
- Transient stability: consider transient stability during PV-BES system mode switching.
- (3)
- System modeling and parameter design: model the PV-BES system and design control parameters to ensure system stability.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blaabjerg, F.; Yang, Y.; Kim, K.A.; Rodriguez, J. Power electronics technology for large-scale renewable energy generation. Proc. IEEE 2023, 111, 335–355. [Google Scholar] [CrossRef]
- Liu, Y.; You, S.; Tan, J.; Zhang, Y.; Liu, Y. Frequency response assessment and enhancement of the U.S. power grids toward extra-high photovoltaic generation penetrations-an industry perspective. IEEE Trans. Power Syst. 2018, 33, 3438–3449. [Google Scholar] [CrossRef]
- Zhu, Y.; Wen, H.; Chu, G.; Hu, Y.; Li, X.; Ma, J. High-Performance Photovoltaic Constant Power Generation Control with Rapid Maximum Power Point Estimation. IEEE Trans. Ind. Appl. 2021, 57, 714–729. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Pattabiraman, D.; Lasseter, R.H.; Jahns, T.M. Comparison of grid following and grid forming control for a high inverter penetration power system. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- White Paper: Grid Forming Functional Specifications for BPS-Connected Battery Energy Storage Systems. Available online: www.nerc.com (accessed on 6 June 2023).
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison between Traditional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Qu, Z.; Peng, J.C.-H.; Yang, H.; Srinivasan, D. Modeling and Analysis of Inner Controls Effects on Damping and Synchronizing Torque Components in VSG-Controlled Converter. IEEE Trans. Energy Convers. 2021, 36, 488–499. [Google Scholar] [CrossRef]
- Zhu, Y.; Wen, H.; Bu, Q.; Wang, X.; Hu, Y.; Chen, G. An Improved Photovoltaic Power Reserve Control with Rapid Real-Time Available Power Estimation and Drift Avoidance. IEEE Trans. Ind. Electron. 2023, 70, 11287–11298. [Google Scholar] [CrossRef]
- Sreedevi, J.; Ashwin, N.; Raju, M.N. A study on grid connected PV system. In Proceedings of the 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19–21 December 2016; pp. 1–6. [Google Scholar]
- Shi, B.; Zhao, Z.; Yuan, L. A Novel Coordinated Control Strategy for Energy Storage System in DC Microgrid with Weak Communication. IEEE Trans. Ind. Appl. 2020, 56, 800–814. [Google Scholar] [CrossRef]
- Babaei, E.; Abu-Rub, H.; Suryawanshi, H.M. Z-Source Converters: Topologies, Modulation Techniques, and Application–Part I. IEEE Trans. Ind. Electron. 2018, 65, 5092–5095. [Google Scholar] [CrossRef]
- Alsiraji, H.A.; ElShatshat, R.; Radwan, A.A. A novel control strategy for the interlinking converter in hybrid microgrid. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Lasseter, R.H.; Chen, Z.; Pattabiraman, D. Grid-Forming Inverters: A Critical Asset for the Power Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 925–935. [Google Scholar] [CrossRef]
- Luo, H.; Xiao, Y.; Zhu, Y.; Yang, Y.; Papanikolaou, N.P.; Molinas, M. A Review of Recent Requirements for Inverter-Based Resources and Grid-Forming Technologies. In Proceedings of the 2023 25th European Conference on Power Electronics and Applications (EPE’23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023; pp. 1–9. [Google Scholar]
- Liu, P.; Sun, S.; Guan, Y.; Wang, Y.; Xie, X. An overview of hybrid control strategy presenting grid-following and grid-forming capabilities. In Proceedings of the 12th International Conference on Renewable Power Generation (RPG 2023), Shanghai, China, 14–15 October 2023; pp. 567–572. [Google Scholar]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-Forming Converters: Control Approaches, Grid-Synchronization, and Future Trends—A Review. IEEE Open J. Ind. Appl IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, X.; Jin, Z. Flexible Synchronization Control for Grid-Forming Converters with Regulated DC-Link Dynamics. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–8. [Google Scholar]
- Hazra, P.; Hadidi, R.; Makram, E. Dynamic study of virtual oscillator-controlled inverter based distributed energy source. In Proceedings of the 015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015; pp. 1–6. [Google Scholar]
- Lu, M.; Dhople, S.; Johnson, B. Benchmarking Nonlinear Oscillators for Grid-Forming Inverter Control. IEEE Trans. Power Electron. 2022, 37, 10250–10266. [Google Scholar] [CrossRef]
- Khalilpour, R.; Vassallo, A. Planning and operation scheduling of PV-battery systems: A novel methodology. Renew. Sustain. Energy Rev. 2016, 53, 194–208. [Google Scholar] [CrossRef]
- Nottrott, A.; Kleissl, J.; Washom, B. Storage dispatch optimization for grid-connected combined photovoltaic-battery storage systems. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R.C. Integration of PV and BES units in commercial distribution systems considering energy loss and voltage stability. Appl. Energy 2014, 113, 1162–1170. [Google Scholar] [CrossRef]
- Alhatlani, A.; Batarseh, I. Review of Partially Isolated Three-Port Converters for PV-Battery Systems That Interface a PV, Bidirectional Battery, and Load. In Proceedings of the 2019 IEEE Conference on Power Electronics and Renewable Energy (CPERE), Aswan, Egypt, 23–25 October 2019; pp. 465–472. [Google Scholar]
- Sharma, R.K.; Mudaliyar, S.; Mishra, S. Power management and economic load dispatch-based control of hybrid PV-battery-diesel standalone AC system. In Proceedings of the 2018 IEEMA Engineer Infinite Conference (eTechNxT), New Delhi, India, 13–14 March 2018; pp. 1–6. [Google Scholar]
- Narayanan, V.; Kewat, S.; Singh, B. Control and Implementation of a Multifunctional Solar PV-BES-DEGS Based Microgrid. IEEE Trans. Ind. Electron. 2021, 68, 8241–8252. [Google Scholar] [CrossRef]
- Naqvi, S.B.Q.; Singh, B. Weak Grid Integrated Improved Power Quality PV-Battery System with Controlled Power Flow and Grid Assistive Capabilities. IEEE Trans. Ind. Appl. 2024, 60, 4517–4529. [Google Scholar] [CrossRef]
- Mitali, J.; Dhinakaran, S.; Mohamad, A.A. Energy storage systems: A review. Energy Storage Sav. 2022, 1, 166–216. [Google Scholar] [CrossRef]
- Choi, J.; Lee, J.I.; Lee, I.W.; Cha, S.W. Robust PV-BESS Scheduling for a Grid with Incentive for Forecast Accuracy. IEEE Trans. Sustain. Energy 2022, 13, 567–578. [Google Scholar] [CrossRef]
- Joshi, J.; Swami, A.K.; Jately, V.; Azzopardi, B. A Comprehensive Review of Control Strategies to Overcome Challenges During LVRT in PV Systems. IEEE Access 2021, 9, 121804–121834. [Google Scholar] [CrossRef]
- Yang, X.; Ren, J.; Li, X. Slope Control Method with Variable Coefficients of Battery Energy Storage System for Smoothing Photovoltaic Power Fluctuation. Autom. Electr. Power Syst. 2016, 40, 56–63. [Google Scholar]
- Mishra, J.; Behera, P.K.; Pattnaik, M.; Samanta, S. An Efficient Supervisory Power Management Scheme for a Wind–Battery-Assisted Hybrid Autonomous System. IEEE Syst. J. 2023, 17, 768–779. [Google Scholar] [CrossRef]
- Liu, J.; Hou, Y.; Guo, J.; Liu, X.; Liu, J. A Cost-Efficient Virtual Synchronous Generator System Based on Coordinated Photovoltaic and Supercapacitor. IEEE Trans. Power Electron. 2023, 38, 16219–16229. [Google Scholar] [CrossRef]
- Qian, Z.; Abdel-Rahman, O.; Hu, H.; Batarseh, I. An integrated three-port inverter for stand-alone PV applications. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 1471–1478. [Google Scholar]
- Zhang, Z.; Fang, J.; Dong, C.; Jin, C.; Tang, Y. Enhanced Grid Frequency and DC-Link Voltage Regulation in Hybrid AC/DC Microgrids Through Bidirectional Virtual Inertia Support. IEEE Trans. Ind. Electron. 2023, 70, 6931–6940. [Google Scholar] [CrossRef]
- Gupta, Y.; Amin, M. Adaptive Droop Controller for PV—Battery Based Microgrids. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–6. [Google Scholar]
- Rajabinezhad, M.A.; Guerrero, J.M. A Three-Level Control Strategy for Battery Energy Storage System to Mitigate Power fluctuations and Compensate Reactive Power of Distributed Generators in a Microgrid. In Proceedings of the 2020 10th Smart Grid Conference (SGC), Kashan, Iran, 16–17 December 2020; pp. 1–6. [Google Scholar]
- Mahmood, H.; Blaabjerg, F. Autonomous Power Management of Distributed Energy Storage Systems in Islanded Microgrids. IEEE Trans. Sustain. Energy 2022, 13, 1507–1522. [Google Scholar] [CrossRef]
- Al-Obaidi, N.A.; Abbas, R.A.; Khazaal, H.F. A Review of Non-Isolated Bidirectional DC-DC Converters for Hybrid Energy Storage System. In Proceedings of the 2022 5th International Conference on Engineering Technology and its Applications (IICETA), Al-Najaf, Iraq, 31 May–1 June 2022; pp. 248–253. [Google Scholar]
- Lithesh, G.; Krishna, B.; Karthikeyan, V. Review and Comparative Study of Bi-Directional DC-DC Converters. In Proceedings of the 2021 IEEE International Power and Renewable Energy Conference (IPRECON), Kollam, India, 24–26 September 2021; pp. 1–6. [Google Scholar]
- Kanaparthi, R.K.; Singh, J.P.; Ballal, M.S. A Review on Multi-Port Bidirectional Isolated and Non-Isolated DC-DC Converters for Renewable Applications. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022; pp. 1–6. [Google Scholar]
- Yang, S.; Shoyama, M.; Zaitsu, T.; Yamamoto, J.; Abe, S.; Ninomiya, T. Detail operating characteristics of Bi-directional LLC resonant converter. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; pp. 1–6. [Google Scholar]
- Kim, E.-S.; Park, J.-H.; Jeon, Y.-S.; Kong, Y.-S.; Lee, S.-M.; Kim, K. Bidirectional secondary LLC resonant converter using auxiliary switches and inductor. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 1941–1947. [Google Scholar]
- Doncker, R.W.D.; Divan, D.M.; Kheraluwala, M.H. A three-phase soft-switched high power density DC/DC converter for high power applications. IEEE Trans. Ind. Appl. 1991, 27, 63–73. [Google Scholar] [CrossRef]
- Shao, S.; Chen, L.; Shan, Z.; Gao, F.; Chen, H.; Sha, D.; Dragičević, T. Modeling and Advanced Control of Dual-Active-Bridge DC–DC Converters: A Review. IEEE Trans. Power Electron. 2022, 37, 1524–1547. [Google Scholar] [CrossRef]
- Qin, H.; Kimball, J.W. Generalized Average Modeling of Dual Active Bridge DC–DC Converter. IEEE Trans. Power Electron. 2012, 27, 2078–2084. [Google Scholar]
- Tavakoli, S.D.; Kadkhodaei, G.; Mahdavyfakhr, M.; Hamzeh, M.; Sheshyekani, K. Interlinking converters in application of bipolar dc microgrids. In Proceedings of the 2017 8th Power Electronics, Drive Systems & Technologies Conference (PEDSTC), Mashhad, Iran, 14–16 February 2017; pp. 37–42. [Google Scholar]
- Peng, F.Z. Z-source inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Peng, F.Z. Z-source inverter. In Proceedings of the IAS Annual Meeting, Pittsburgh, PA, USA, 13–18 October 2002; Volume 2, pp. 775–781. [Google Scholar]
- Nguyen, M.-K.; Jung, Y.-G.; Lim, Y.-C. Single-Phase AC–AC Converter Based on Quasi-Z-Source Topology. IEEE Trans. Power Electron. 2010, 25, 2200–2210. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Lim, Y.-C.; Cho, G.-B. Switched-Inductor Quasi-Z-Source Inverter. IEEE Trans. Power Electron. 2011, 26, 3183–3191. [Google Scholar] [CrossRef]
- Vinnikov, D.; Roasto, I. Quasi-Z-Source-Based Isolated DC/DC Converters for Distributed Power Generation. IEEE Trans. Ind. Electron. 2011, 58, 192–201. [Google Scholar] [CrossRef]
- Liang, W.; Liu, Y.; Shen, Y. Active Power Control Integrated with Reactive Power Compensation of Battery Energy Stored Quasi-Z Source Inverter PV Power System Operating in VSG Mode. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 339–350. [Google Scholar] [CrossRef]
- Tang, Z.; Yang, Y.; Blaabjerg, F. An interlinking converter for renewable energy integration into hybrid grids. IEEE Trans. Power Electron. 2021, 36, 2499–2504. [Google Scholar] [CrossRef]
- Sun, D.; Du, L.; Lu, X.; He, L. An Energy-Stored Quasi-Z Source Converter Based Interlinking Converter for Hybrid AC/DC Microgrids. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 3821–3826. [Google Scholar]
- Wang, L.; Lee, M.-F.; Zhang, C.-D.; Lin, J.-J.; Tseng, C.-C. Frequency Control of a Bidirectional Interlinking Converter in an Islanded Hybrid AC/DC Microgrid. In Proceedings of the 2022 IET International Conference on Engineering Technologies and Applications (IET-ICETA), Changhua, Taiwan, 14–16 October 2022; pp. 1–2. [Google Scholar]
- Bose, U.; Chattopadhyay, S.; Chakraborty, C. Topological investigation on interlinking converter in a hybrid microgrid. In Proceedings of the 2018 IEEE International Conference on Industrial Electronics for Sustainable Energy Systems (IESES), Hamilton, New Zealand, 31 January–2 February 2018; pp. 62–67. [Google Scholar]
- Hema, V.K.; Dhanalakshmi, R. Operation of hybrid AC-DC microgrid with an interlinking converter. In Proceedings of the 2014 IEEE International Conference on Advanced Communications, Control and Computing Technologies, Ramanathapuram, India, 8–10 May 2014; pp. 38–42. [Google Scholar]
- Huang, L.; Xin, H.; Wang, Z.; Zhang, L.; Wu, K.; Hu, J. Transient stability analysis and control design of droop-controlled voltage source converters considering current limitation. IEEE Trans. Smart Grid 2019, 10, 578–591. [Google Scholar] [CrossRef]
- Zhu, Y.; Wen, H.; Chu, G.; Wang, X.; Peng, Q.; Hu, Y.; Jiang, L. Power-Rating Balance Control and Reliability Enhancement in Mismatched Photovoltaic Differential Power Processing Systems. IEEE Trans. Power Electron. 2022, 37, 879–895. [Google Scholar] [CrossRef]
- Singhal, A.; Vu, T.L.; Du, W. Consensus Control for Coordinating Grid-Forming and Grid-Following Inverters in Microgrids. IEEE Trans. Smart Grid. 2022, 13, 4123–4133. [Google Scholar] [CrossRef]
- Mejbaul, M.H.; Wolfs, P.J.; Alahakoon, S.; Islam, M.A.; Nadarajah, M.; Zare, F.; Omar, F. Three-Port Converters for Energy Conversion of PV-BES Integrated Systems—A Review. IEEE Access 2023, 11, 6551–6573. [Google Scholar]
- Ling, Y.; Li, Y.; Yang, Z.; Xiang, J. A Dispatchable Droop Control Method for Distributed Generators in Islanded AC Microgrids. IEEE Trans. Ind. Electron. 2021, 68, 8356–8366. [Google Scholar] [CrossRef]
- Sun, Y.; Hou, X.; Yang, J.; Han, H.; Su, M.; Guerrero, J.M. New Perspectives on Droop Control in AC Microgrid. IEEE Trans. Ind. Electron. 2017, 64, 5741–5745. [Google Scholar] [CrossRef]
- Eajal, A.A.; Yazdavar, A.H.; El-Saadany, E.F.; Salama, M.M.A. Optimizing the Droop Characteristics of AC/DC Hybrid Microgrids for Precise Power Sharing. IEEE Syst. J 2021, 15, 560–569. [Google Scholar] [CrossRef]
- Majumder, R.; Chaudhuri, B.; Ghosh, A.; Majumder, R.; Ledwich, G.; Zare, F. Improvement of Stability and Load Sharing in an Autonomous Microgrid Using Supplementary Droop Control Loop. IEEE Trans. Power Syst. 2010, 25, 796–808. [Google Scholar] [CrossRef]
- Vasquez, J.C.; Guerrero, J.M.; Savaghebi, M.; Eloy-Garcia, J.; Teodorescu, R. Modeling, Analysis, and Design of Stationary-Reference-Frame Droop-Controlled Parallel Three-Phase Voltage Source Inverters. IEEE Trans. Ind. Electron. 2013, 60, 1271–1280. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Q.; Lin, S.; Bian, X.Y. A Self-Adaptive Inertia and Damping Combination Control of VSG to Support Frequency Stability. IEEE Trans. Energy Convers. 2017, 32, 397–398. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, D.; Yin, S.; Lei, Y.; He, T. Improved Adaptive Inertia and Damping Coefficient Control Strategy of VSG Based on Optimal Damping Ratio. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022- ECCE Asia), Himeji, Japan, 15–19 May 2022; pp. 102–107. [Google Scholar]
- Dhople, S.V.; Johnson, B.B.; Hamadeh, A.O. Virtual Oscillator Control for voltage source inverters. In Proceedings of the 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–4 October 2013; pp. 1359–1363. [Google Scholar]
- Johnson, B.B.; Dhople, S.V.; Hamadeh, A.O.; Krein, P.T. Synchronization of Nonlinear Oscillators in an LTI Electrical Power Network. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 834–844. [Google Scholar] [CrossRef]
- Lu, M. Virtual Oscillator Grid-Forming Inverters: State of the Art, Modeling, and Stability. IEEE Trans. Power Electron. 2022, 37, 11579–11591. [Google Scholar] [CrossRef]
- Lu, M.; Dutta, S.; Purba, V.; Dhople, S.; Johnson, B. A grid-compatible virtual oscillator controller: Analysis and design. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 2643–2649. [Google Scholar]
- Johnson, B.B.; Sinha, M.; Ainsworth, N.G.; Dörfler, F.; Dhople, S.V. Synthesizing virtual oscillators to control islanded inverters. IEEE Trans. Power Electron. 2016, 31, 6002–6015. [Google Scholar] [CrossRef]
- Gurugubelli, V.; Ghosh, A.; Panda, A.K.; Behera, B.P. Fuzzy-Based Adaptive VOC Methods for Parallel Inverters. IEEE Trans. Power Electron. 2024, 39, 3956–3961. [Google Scholar] [CrossRef]
- Arghir, C.; Dörfler, F. The Electronic Realization of Synchronous Machines: Model Matching, Angle Tracking, and Energy Shaping Techniques. IEEE Trans. Power Electron. 2020, 35, 4398–4410. [Google Scholar] [CrossRef]
- Zhao, L.; Jin, Z.; Wang, X. Small-Signal Synchronization Stability of Grid-Forming Converters with Regulated DC-Link Dynamics. IEEE Trans. Ind. Electron. 2023, 70, 12399–12409. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, X.; Jin, Z. Impedance-Based Dynamics Analysis for DC-Link Voltage-Synchronized Voltage-Source Converters. IEEE Trans. Power Electron. 2023, 38, 10829–10844. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-Synchronization Control of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Mahmood, H.; Michaelson, D.; Jiang, J. Decentralized power management of a PV/battery hybrid unit in a droop-controlled islanded microgrid. IEEE Trans. Power Electron. 2015, 30, 7215–7229. [Google Scholar] [CrossRef]
- Yang, Y.; Qin, Y.; Tan, S.; Hui, S.Y.R. Efficient improvement of photovoltaic-battery systems in standalone dc microgrids using a local hierarchical control for the battery system. IEEE Trans. Power Electron. 2019, 34, 10796–10807. [Google Scholar] [CrossRef]
- Merabet, A.; Ahmed, K.T.; Ibrahim, H.; Beguenane, R.; Ghias, A.M.Y.M. Energy management and control system for laboratory scale microgrid based wind-PV-battery. IEEE Trans. Sustain. Energy 2017, 8, 145–154. [Google Scholar] [CrossRef]
- Tofighi, A.; Kalantar, M. Power management of PV/battery hybrid power source via passivity-based control. Renew. Energy 2011, 36, 2440–2450. [Google Scholar] [CrossRef]
- Zhou, H.; Bhattacharya, T.; Tran, D.; Siew, T.S.T.; Khambadkone, A.M. Composite Energy Storage System Involving Battery and Ultracapacitor with Dynamic Energy Management in Microgrid Applications. IEEE Trans. Power Electron. 2011, 26, 923–930. [Google Scholar] [CrossRef]
- Li, D.; Ho, C.N.M. Decentralized PV–BES Coordination Control with Improved Dynamic Performance for Islanded Plug-Play DC Microgrid. IEEE J. Sel. Top. Power Electron. 2021, 9, 4992–5001. [Google Scholar] [CrossRef]
- Wang, L.; Bai, F.; Yan, R.; Saha, T.K. Real-Time Coordinated Voltage Control of PV Inverters and Energy Storage for Weak Networks with High PV Penetration. IEEE Trans. Power Syst. 2018, 33, 3383–3395. [Google Scholar] [CrossRef]
- Yin, K.; Xiao, Y.; Yang, Y. A Coordinated PV-Battery GFM Control for Power Management and Frequency Support. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; pp. 797–802. [Google Scholar]
- Liu, Y.; Wang, Y.; Wang, M.; Xu, Z.; Peng, Y.; Li, M. Coordinated VSG Control of Photovoltaic/Battery System for Maximum Power Output and Grid Supporting. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 301–309. [Google Scholar] [CrossRef]
- Mao, M.; Qian, C.; Ding, Y. Decentralized coordination power control for islanding microgrid based on PV/BES-VSG. IEEE CPSS 2018, 3, 14–24. [Google Scholar] [CrossRef]
- Fang, J.; Tang, Y.; Li, H.; Li, X. A Battery/Ultracapacitor Hybrid Energy Storage System for Implementing the Power Management of Virtual Synchronous Generators. IEEE Trans. Power Electron. 2018, 33, 2820–2824. [Google Scholar] [CrossRef]
- Quan, X.; Yu, R.; Zhao, X.; Lei, Y.; Chen, T.; Li, C.; Huang, A.Q. Photovoltaic Synchronous Generator: Architecture and Control Strategy for a Grid-Forming PV Energy System. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 936–948. [Google Scholar] [CrossRef]
- Tafti, H.; Townsend, C.D.; Farivar, G.; Sangwongwanich, A.; Yang, Y.; Pou, J.; Blaabjerg, F. Extended Functionalities of Photovoltaic Systems With Flexible Power Point Tracking: Recent Advances. IEEE Trans. Power Electron. 2020, 35, 9342–9356. [Google Scholar] [CrossRef]
- Zhu, Y.; Wen, H.; Tafti, H.D.; Wang, G.; Bu, Q.; Chu, G.; Shi, H.; Hu, Y.; Jiang, L. Novel Fast-Speed Partial-Shading-Tolerant Flexible Power Point Tracking for Photovoltaic Systems With Explicit Key Points Estimation. IEEE Trans. Sustain. Energy 2024, 15, 466–485. [Google Scholar] [CrossRef]
- Shukl, P.; Singh, B. Dual Mode Operation of PV-BES Based Microgrid with Seamless Transition Capability. In Proceedings of the 2021 IEEE 2nd International Conference on Smart Technologies for Power, Energy and Control (STPEC), Bilaspur, Chhattisgarh, India, 19–22 December 2021; pp. 1–6. [Google Scholar]
- Kanchev, H.; Lu, D.; Colas, F.; Lazarov, V.; Francois, B. Energy Management and Operational Planning of a Microgrid With a PV-Based Active Generator for Smart Grid Applications. IEEE Trans. Ind. Electron. 2011, 58, 4583–4592. [Google Scholar] [CrossRef]
- Riffonneau, Y.; Bacha, S.; Barruel, F.; Ploix, S. Optimal Power Flow Management for Grid Connected PV Systems with Batteries. IEEE Trans. Sustain. Energy 2011, 2, 309–320. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, L.; Xing, Y.; Guerrero, J.M. A Distributed Control Strategy Based on DC Bus Signaling for Modular Photovoltaic Generation Systems with Battery Energy Storage. IEEE Trans. Power Electron. 2011, 26, 3032–3045. [Google Scholar] [CrossRef]
- Ashtiani, N.A.; Azizi, S.M.; Khajehoddin, S.A. Robust Control Design for High-Power Density PV Converters in Weak Grids. IEEE Trans. Control Syst. Technol. 2019, 27, 2361–2373. [Google Scholar] [CrossRef]
- Wu, F.; Fan, S.; Luo, S. Small-Signal Modeling and Closed-Loop Control of Bidirectional Buck-Boost Current-Fed Isolated DC-DC Converter. IEEE Trans. Ind. Electron. 2021, 68, 4036–4045. [Google Scholar] [CrossRef]
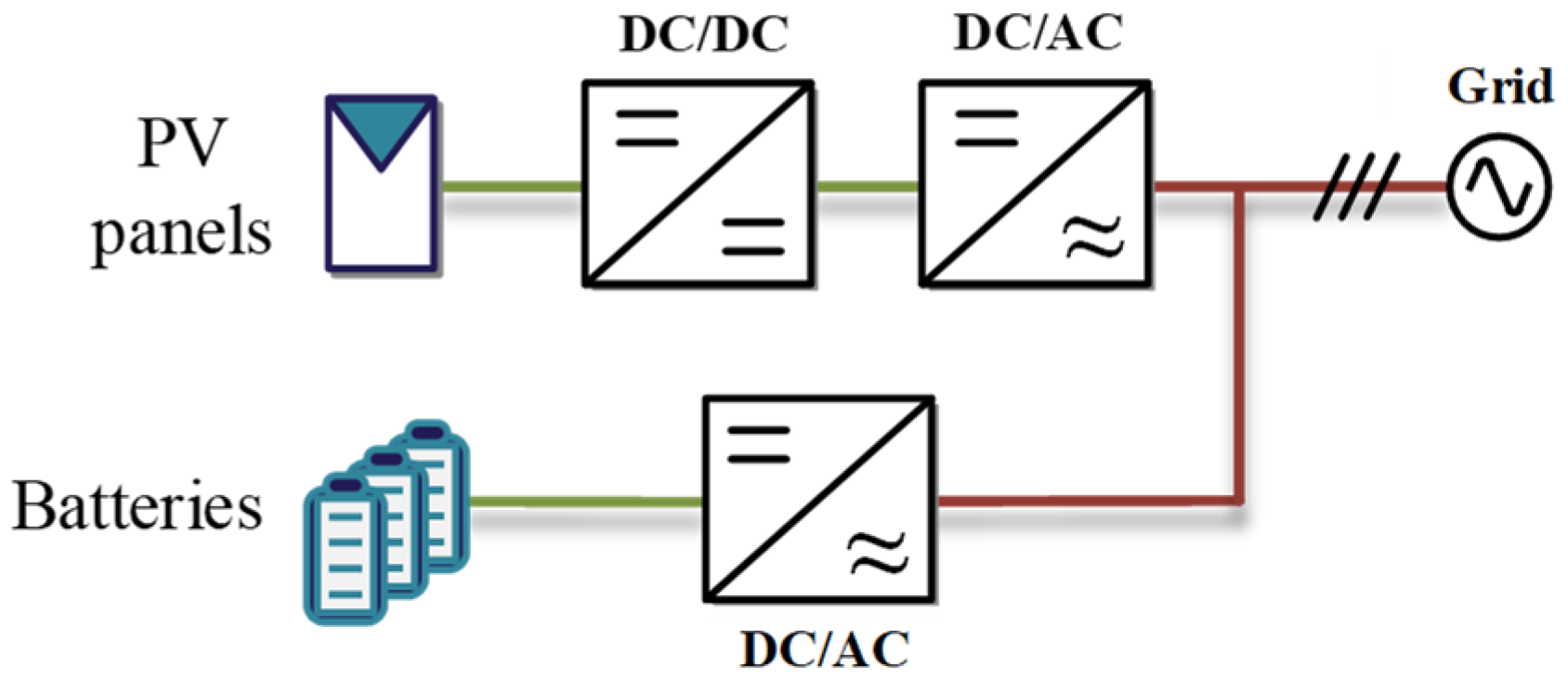

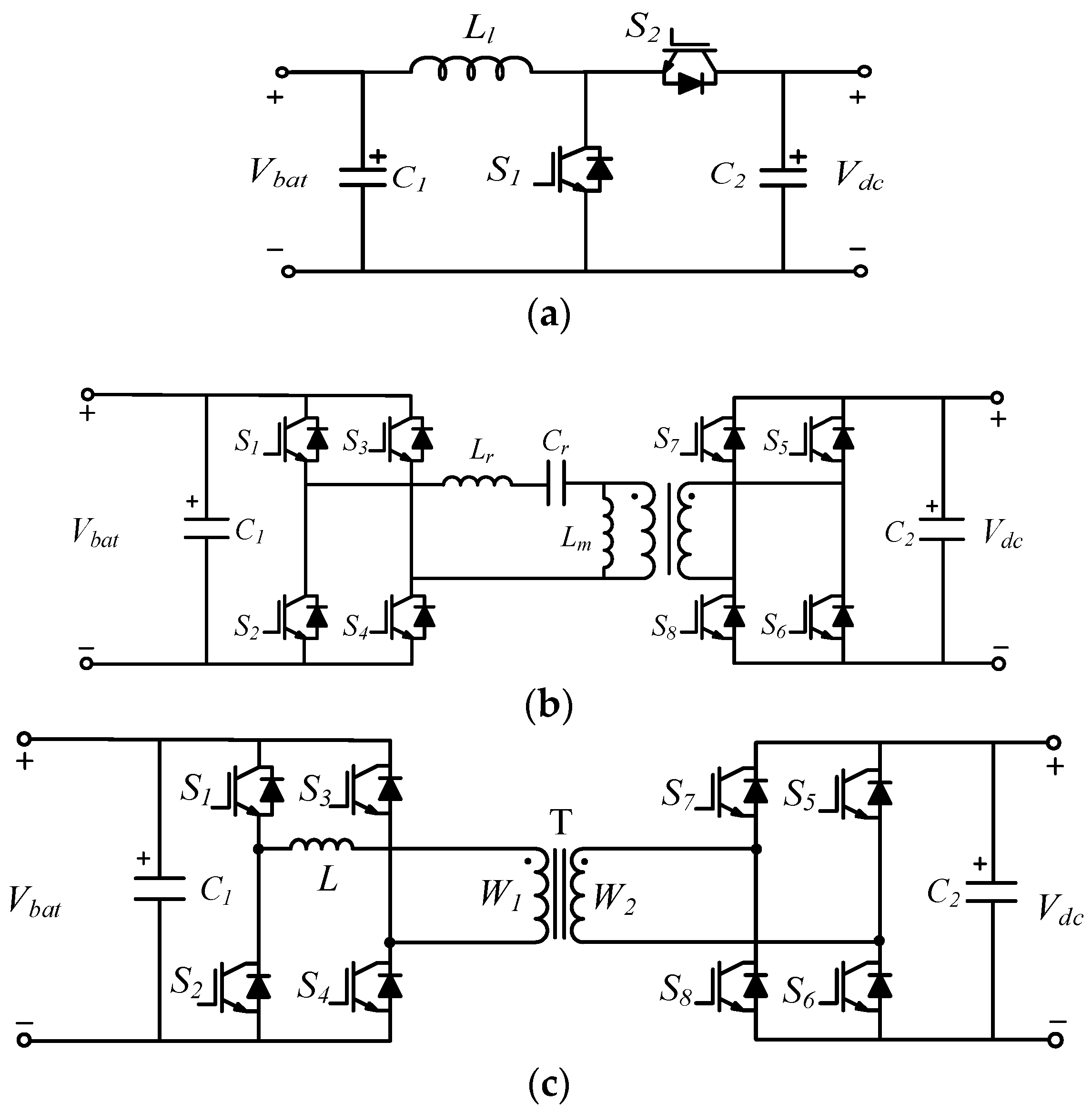

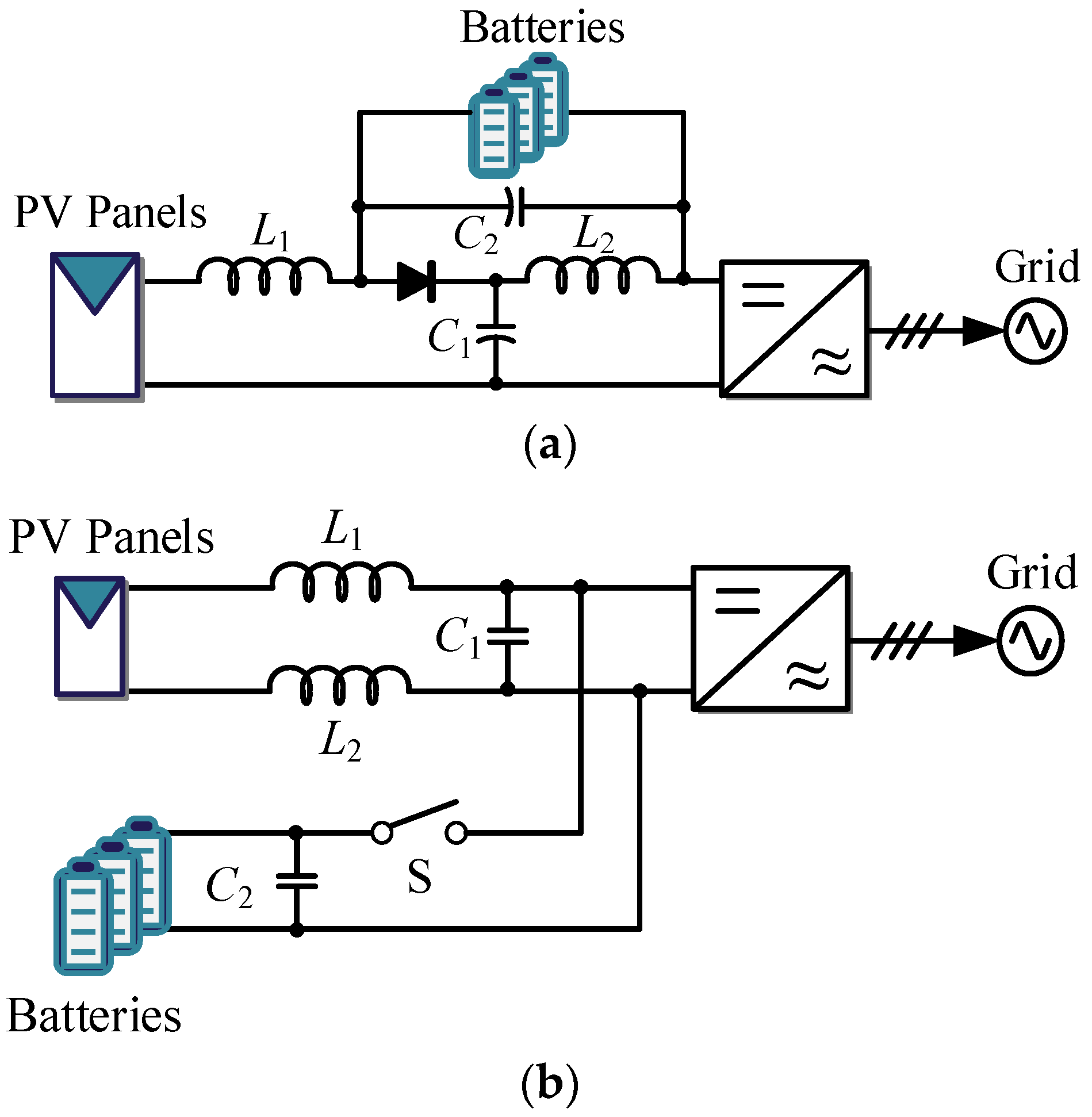



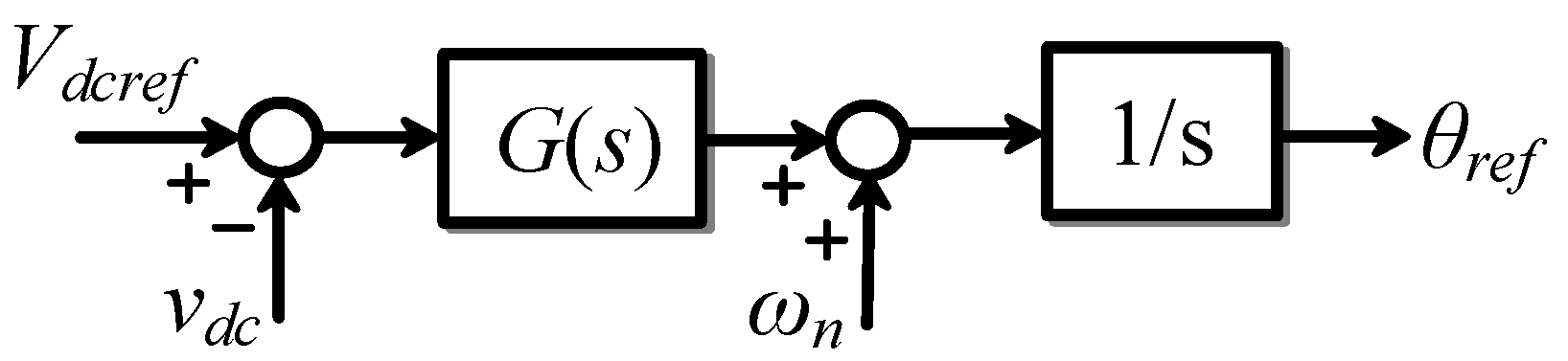
| Configuration | Common AC-Bus | Common DC-Bus | TPCs | |
|---|---|---|---|---|
| Structure scalability | Easy | Difficult | Difficult | |
| Control degrees | Less | More | More | |
| Efficiency | PV to batteries | Low | High | Highest |
| PV to the grid | High | Low | Highest | |
| Batteries to the grid | High | High | Highest | |
| Cost | High | Low | Highest | |
| GFM Control | Advantages | Disadvantages |
|---|---|---|
| Droop control |
|
|
| VSG control |
|
|
| VOC control |
|
|
| Matching control |
|
|
| Control | Configuration | Characteristics |
|---|---|---|
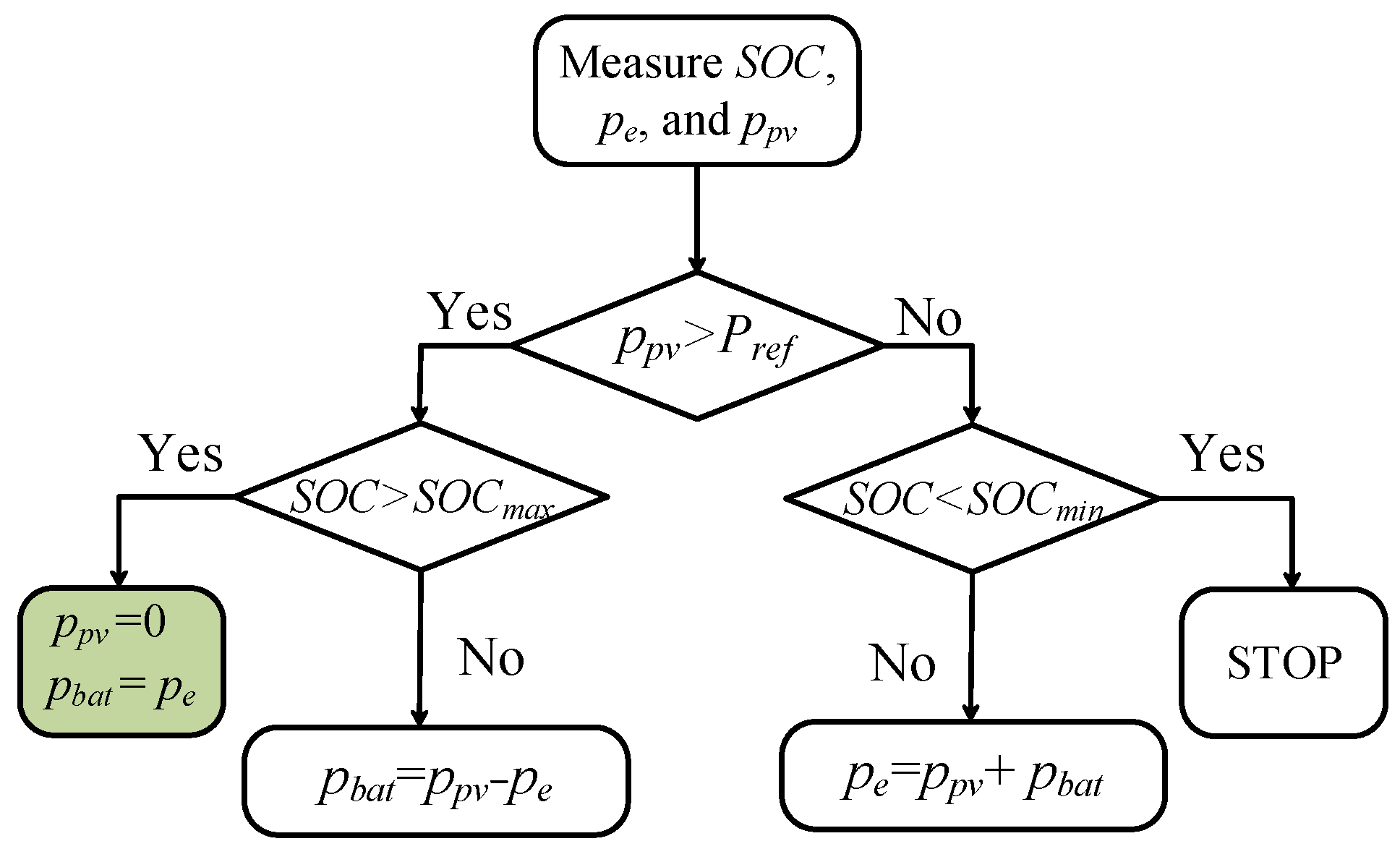
| Coordinated control I |
| PV system always works at MPP. |
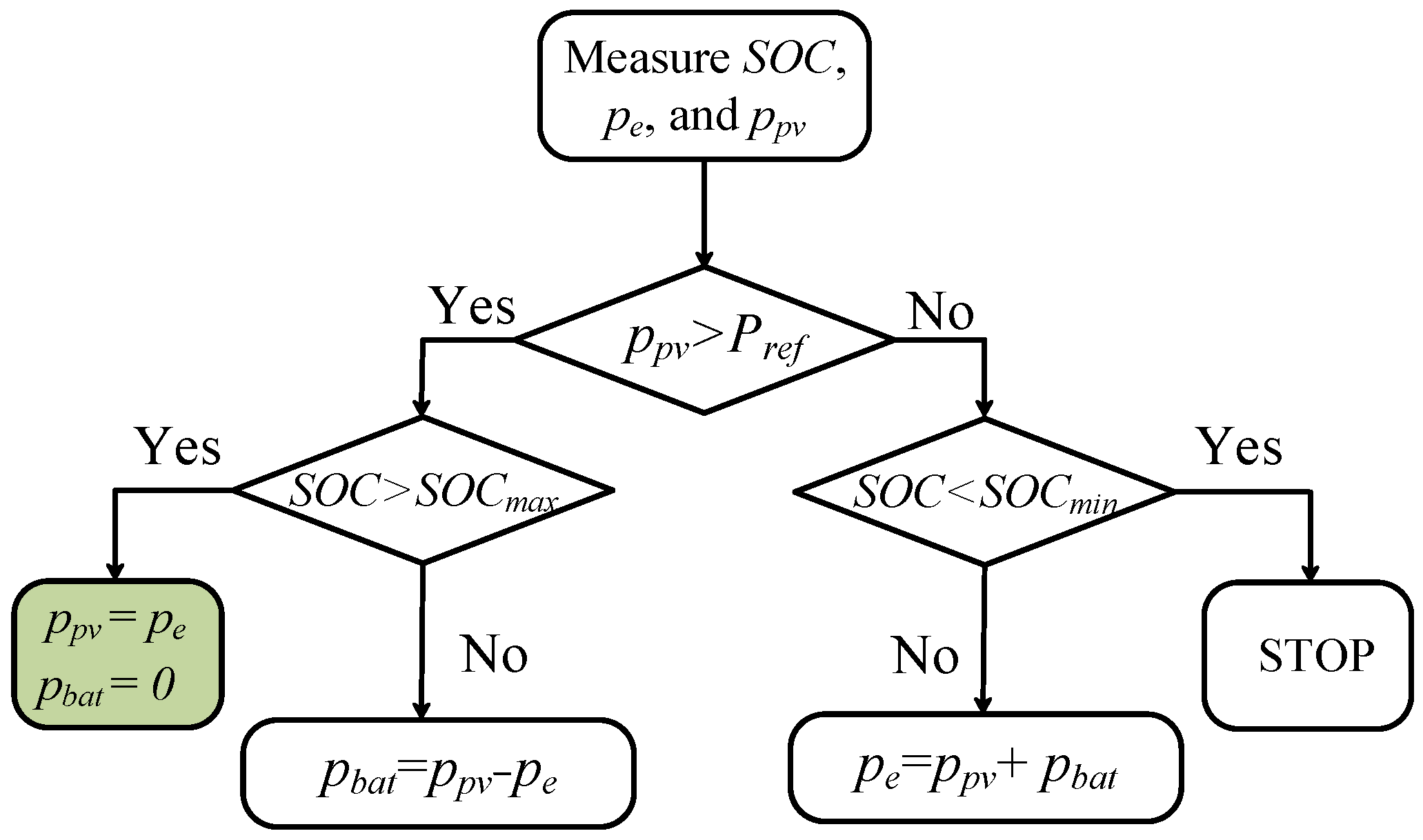
| Coordinated control II |
| PV system works at MPP or reduced power. |
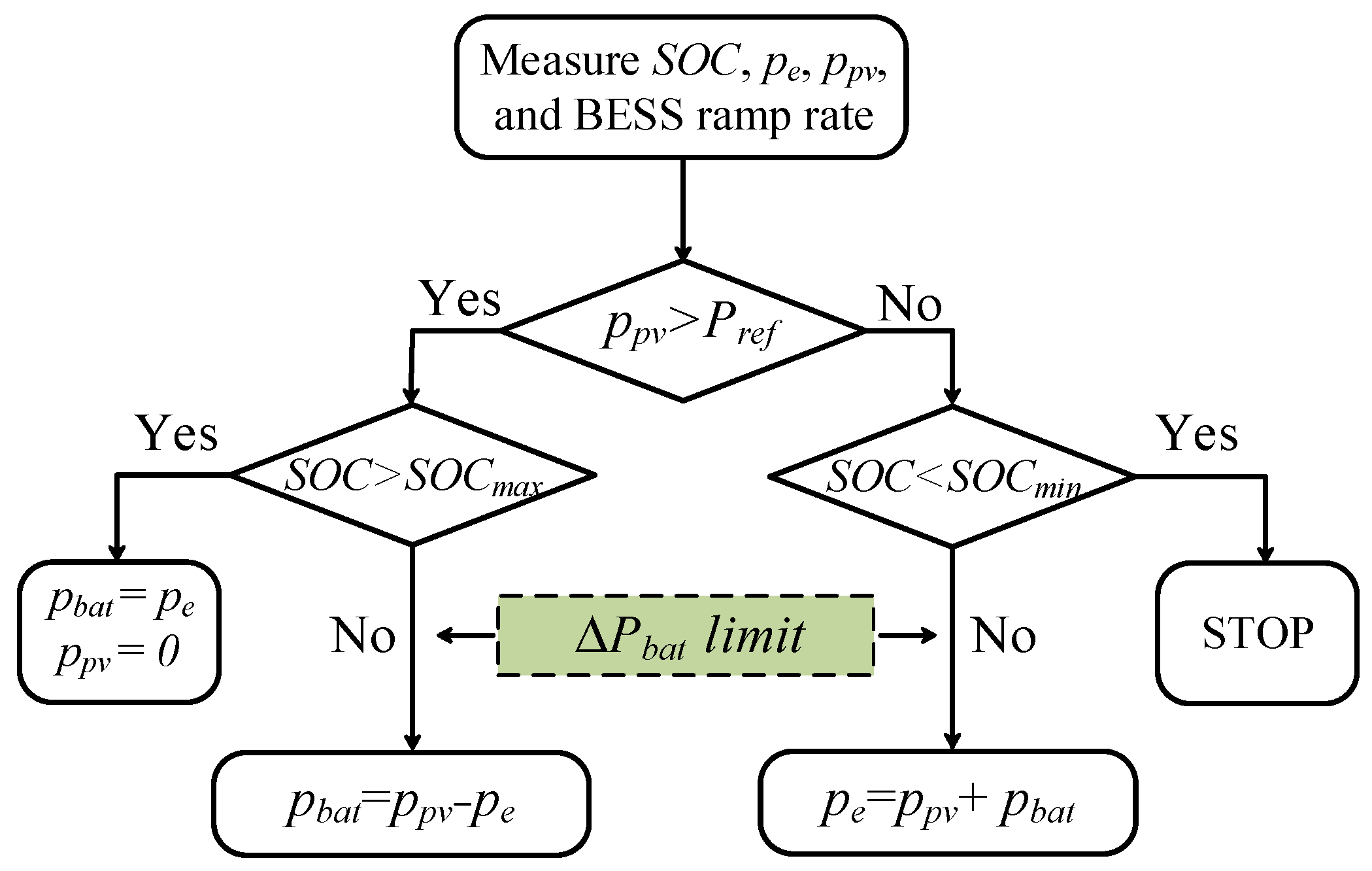
| Coordinated control III |
| The battery ramp rate is considered. |
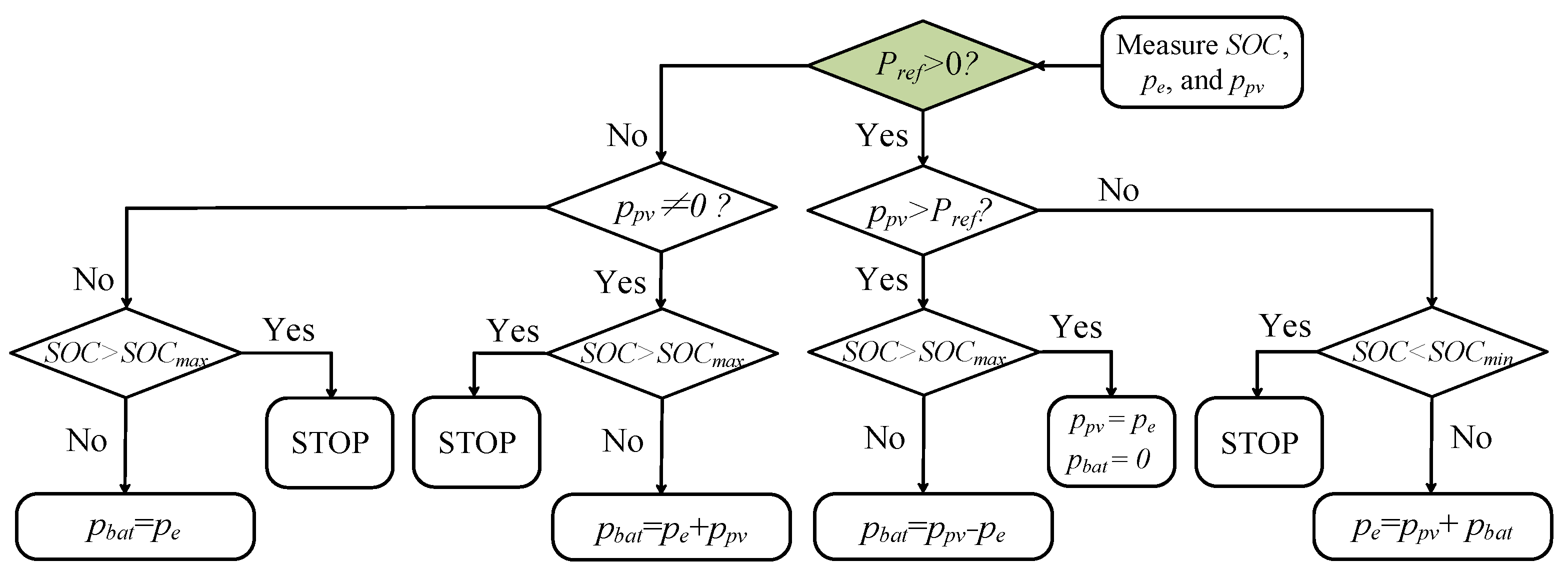
| Coordinated control IV |
| The scenario in which the grid supplies energy to the source has been considered. |
| Coordinated control V | Common DC bus connection | The DC-link voltage is employed to regulate the power flow. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, K.; Xiao, Y.; Shen, X.; Zhu, Y.; Yang, Y. Review of Photovoltaic–Battery Energy Storage Systems for Grid-Forming Operation. Batteries 2024, 10, 288. https://doi.org/10.3390/batteries10080288
Yin K, Xiao Y, Shen X, Zhu Y, Yang Y. Review of Photovoltaic–Battery Energy Storage Systems for Grid-Forming Operation. Batteries. 2024; 10(8):288. https://doi.org/10.3390/batteries10080288
Chicago/Turabian StyleYin, Kai, Yi Xiao, Xiaomeng Shen, Yinxiao Zhu, and Yongheng Yang. 2024. "Review of Photovoltaic–Battery Energy Storage Systems for Grid-Forming Operation" Batteries 10, no. 8: 288. https://doi.org/10.3390/batteries10080288
APA StyleYin, K., Xiao, Y., Shen, X., Zhu, Y., & Yang, Y. (2024). Review of Photovoltaic–Battery Energy Storage Systems for Grid-Forming Operation. Batteries, 10(8), 288. https://doi.org/10.3390/batteries10080288








