Diffusion-Equation-Based Electrical Modeling for High-Power Lithium Titanium Oxide Batteries

Abstract

Lithium titanium oxide (LTO) batteries offer superior performance compared to graphite-based anodes in terms of rapid charge/discharge capability and chemical stability, making them promising candidates for fast-charging and power-assist vehicle applications. However, commonly used battery models often struggle to accurately describe the current–voltage characteristics of LTO batteries, particularly before the charge/discharge cutoff conditions. In this work, a novel electrical model based on the solid-phase diffusion equation is proposed to capture the unique electrochemical phenomena arising from the diffusion mismatch between the positive and negative electrodes in high-power LTO batteries. The robustness of the proposed model is evaluated under various loading conditions, including constant current and dynamic current tests, and the results are compared against experimental data. The experimental results for LTO batteries exhibit remarkable alignment with the model estimation, demonstrating a maximum voltage error below 3%.

1. Introduction

Lithium-ion batteries have become ubiquitous in a wide range of electrical devices and systems, including telephones, electric vehicles, and renewable energy generation, owing to their high power density, high energy density, and excellent reliability [1,2,3,4]. To meet the diverse power and energy requirements of different applications, lithium-ion batteries can be categorized into two broad types: high-power designs and high-energy designs. Lithium titanium oxide (LTO) batteries utilizing Li₄Ti₅O₁₂ as the anode material have exhibited remarkable battery performance, encompassing excellent rate capabilities and chemical stability. Consequently, LTO batteries have emerged as a leading candidate for fast-charging and power-assist vehicle applications [5,6]. LTO batteries demonstrate pronounced advantages over conventional lead–acid batteries for starting or regenerative braking applications, which is primarily attributed to their superior power density and significantly extended service life [7,8,9,10]. LTO batteries have been used in a wide range of applications, including all-electric buses and high-speed rail trains. Highly accurate battery models are essential for ensuring safe battery operation and enhancing battery management systems [11,12,13,14].

In recent decades, various battery models have been reported to address the critical requirements of diverse scenarios. These models can be broadly categorized into three groups: electrochemical models, analytical models, and circuit models [15,16,17,18]. Electrochemical modeling is based on electrochemical equations and thermodynamic principles and represents the chemical reaction processes inside the battery numerically through partial differential equations of electrode and electrolyte kinetics [16,18]. Analytical models are founded upon the same fundamental principles as electrochemical models, with a simplification of the computational equations [11]. However, these models involve complex nonlinear differential equations and numerous unknown variables, increasing their complexity and making them challenging to integrate into battery management systems.

Circuit models, on the other hand, can capture a battery’s current–voltage characteristics through a combination of electrical components such as voltage sources, resistors, and capacitors [17,19,20]. These models have a simpler structure and fewer unknown variables compared to the other two model types and can be easily incorporated into the control model of a battery-powered system. For example, Low et al. [21] proposed an improved model consisting of two resistance–capacitance (RC) parallel networks, which can predict the behavior of lithium iron phosphate (LFP) batteries with sufficient accuracy. Hu et al. [17] compared twelve circuit models using the same data, finding that a single RC parallel network model is more suitable for lithium–nickel–manganese–cobalt oxide batteries, while a first-order RC model with a single-state hysteresis is more suitable for LFP cells. Philipp et al. [22] provide a comprehensive analysis of modeling techniques for high-power LTO batteries, noting that accurately modeling battery performance at the high current rate (C-rate), extreme temperatures, and state-of-charge (SOC) boundaries are the main challenges. In addition, they conclude that second- or third-order RC equivalent circuits are best suited as LTO battery models. Many studies have also reported modeling LTO batteries with equivalent circuits, but the performance of these models is poor at high C-rates [23,24,25].

To improve the feasibility of high-power battery models, researchers have developed several enhanced circuit models. SOC estimation at different C-rates has been achieved using a normalization method based on the definition of the rate factor [26]. More comprehensively, Zhang et al. proposed an integrated approach combining a circuit model and a Rakhmatov diffusion model, which is capable of capturing the recovery effect [27]. However, this improved model has a complex structure that can be difficult to configure. In addition, Kim et al. used a kinetic model rather than a diffusion model to represent the rate–capacity effect to enhance the model’s adaptability to high C-rates [28]. It is worth noting that the above approaches rarely discuss the variation in model parameters with current flow rate and direction, although they are sufficiently accurate from a quantitative perspective.

Lam et al. proposed an empirical formulation using curve fitting to describe the current dependence of the model parameters [29]. However, the generalization of this approach is limited due to the lack of theoretical derivation and the fact that the model validation was only achieved at rates below 2 C.

Liu et al. modeled LTO batteries in high-power applications based on the Butler–Volmer equation with a correction for the electrochemical polarization in the model [30]. Chen et al. modeled LTO batteries at different temperatures by correcting the open-circuit voltage and ohmic resistance based on the Nernst and Arrhenius equations [31]. However, these models have poor accuracy at SOC boundaries such as 0–20% SOC or 80–100% SOC. The main reason for this is caused by the deviation of the material surface SOC from the cell SOC due to the diffusion process [32].

There are several studies that have considered the effect of the diffusion process and made corrections based on diffusion equations to improve the model accuracy [27,28,32]. However, the difference in diffusion ability of positive and negative electrodes and the effect at different C-rates are not considered.

This work presents a novel electrical model for high-power LTO batteries based on the diffusion equation. The model accurately simulates the diffusive polarization of the electrodes under high C-rate operation scenarios. The accuracy and reliability of the proposed battery model across the full SOC range are validated by testing the lithium titanate battery at various C-rates and dynamic operating conditions, demonstrating a maximum error within 3%.

The remainder of this paper is structured as follows. Section 2 presents the related work, encompassing commonly utilized electrical circuit models and derivations of the diffusion equation. Section 3 details the experimental setup and procedures. The modeling process of the proposed model is outlined in Section 4. Section 5 outlines the steps for parameter extraction. Model verification results are discussed in Section 6. Finally, Section 7 concludes the work.

2. Related Work

2.1. Equivalent Circuit Model

The equivalent circuit model is a widely adopted approach for simplifying the complex electrochemical dynamics of batteries. This modeling technique leverages the electrical properties of circuit elements, such as resistors, capacitors, and voltage sources, to represent the underlying electrochemical processes within the battery. A commonly used variant is the second-order equivalent circuit model, as illustrated in Figure 1.

The model consists of a controlled voltage source that is primarily governed by the battery’s SOC, a series resistance to account for the energy losses in the electrodes, electrolyte, and other cell components, and two parallel RC networks. These RC branches are used to simulate the electrochemical polarization and concentration polarization phenomena, respectively, which are fundamental to the battery’s transient behavior.

In practice, the values of the resistances and capacitances within this equivalent circuit model are dependent on the battery’s SOC and differ between charging and discharging operations. This adaptability allows the model to capture the complex and nonlinear electrochemical dynamics of the battery. However, conventional equivalent circuit models may be insufficient to accurately characterize the battery’s performance under high-power applications, due to their limited ability to represent the intricate internal reaction mechanisms.

2.2. Solid-Phase Diffusion Equation

To better simulate the voltage response in high-power application scenarios, this work analyzes the effect of different polarization processes on the battery voltage. The analysis is based on the results of electrochemical impedance spectroscopy (EIS) from our previous study [33], in conjunction with analytical methods from the literature [34].

As shown in Figure 2, the various polarization losses are separated using curves simulated with parameters identified from the EIS data. Among the polarization effects, diffusion polarization has the greatest impact on the voltage, followed by ohmic polarization and interfacial polarization. The voltage losses for ohmic and interfacial polarization are fully developed within a few seconds. Therefore, the prolonged voltage loss is primarily caused by diffusion polarization. Additionally, while the interfacial polarization differs for the positive electrode (PE) and negative electrode (NE) at different SOCs, the combined effect of these two polarizations remains relatively constant. In contrast, the effects of diffusive polarization vary significantly at different SOCs.

The results shown in Figure 2 indicate that diffusion polarization has a greater impact than interfacial polarization on the LTO battery. Specifically, the voltage drop caused by diffusion polarization is 1.07 to 1.75 times that caused by interfacial polarization. This finding highlights the urgent need for methods that can effectively characterize the diffusive polarization resulting from concentration changes within the cell.

During the establishment of the diffusion process in the spherical electrode particles, the diffusion of lithium ions within the material follows Fick’s law [35], which can be expressed as follows:

$$\frac{\partial c_s\left(r,t\right)}{\partial t}=\frac{D}{r^2}\frac{\partial }{\partial r}\left[r^2\cdot \frac{\partial c_s\left(r,t\right)}{\partial r}\right]$$

(1)

where $c_s$ is the solid-phase lithium-ion concentration, $r$ is the distance from the center of the spherical particles, and $D$ is the diffusion coefficient. Additionally, the following boundary conditions must be satisfied:

$$\frac{\partial c_s}{\partial r}{|}_{r=0}=0,$$

(2)

$$\frac{\partial c_s}{\partial r}{|}_{r=R_s}=-\frac{i\left(t\right)}{nFD}$$

(3)

where n is the number of charges carried by a single charged particle and F is Faraday’s constant. However, it seems impractical to directly obtain the concentration difference by integration, as Equation (1) cannot be solved without a known initial concentration value, which is typically unavailable. Fortunately, the initial concentration value does not affect the concentration difference between the material concentration and the average concentration. Wang and Srinivasan [36] proposed an empirical equation to describe the evolution of the concentration gradient within a spherical particle under constant current, which provides a valuable tool for characterizing the diffusive polarization in LTO cells.

$$c_s\left(r,t\right)=c_{avg}\left(t\right)+\frac{i\left(t\right)r}{nFD}\left(1-e^{-\frac{4\sqrt{Dt}}{3r}}\right)$$

(4)

3. Experimental Setup and Procedures

The experimental test platform is depicted in Figure 3, comprising a battery charge/discharge test system and a temperature-controlled test chamber. The battery charge/discharge test system is a multi-channel 5V-100A tester manufactured by Arbin, featuring a voltage accuracy of ±0.02% and a current accuracy of ±0.05%. The temperature-controlled thermal chamber was provided by GIANT FORCE CO., with a temperature range of −60 °C to 100 °C and a temperature resolution of 0.1 °C. In this study, the thermal chamber was kept at a constant temperature of 25 °C.

The basic parameters of the LTO battery investigated for this study are summarized in

Table 1. The basic parameters of LTO batteries investigated.

Battery Parameters	Characteristics
Nominal capacity	25 Ah
Voltage range	1.8~2.8 V
Max. charge current	8 C (200 A)
Max. discharge current	12 C (300 A)
Cathode material	LiCoO2
Anode material	Li4Ti5O12

. Compared to lithium-ion batteries with graphite negative electrodes, LTO batteries are preferred for high-power applications in electric vehicles due to their superior rate capabilities. Accordingly, the reference rate for the maximum current of the battery is provided in Table 1.

To evaluate the battery’s performance under different charge/discharge rates, a series of constant-current charge/discharge tests were conducted. The battery was first charged or discharged at a 1 C rate until the cutoff voltage was reached. Subsequently, the battery was then charged and discharged in the opposite direction at five different current rates: 1 C, 2 C, 4 C, 6 C, and 8 C. This experimental protocol allowed for the assessment of the battery’s performance as a function of the applied current rates.

For internal resistance characterization, the test conditions were based on the Japanese electric vehicle standard (JEVS). The procedure involved the following steps between 10% and 90% SOC at 10% SOC intervals:

(1)

1 C charging for 60 s;

(2)

0.1 C discharging until the discharged capacity equals the charging capacity of the previous step;

(3)

Resting for 10 min;

(4)

1 C discharging for 60 s;

(5)

0.1 C charging until the charging capacity equals the charging capacity of the previous step;

(6)

Repeat steps (1) to (5) after replacing 1 C with 2 C, 4 C, 6 C, and 8 C, respectively.

Additionally, the battery was subjected to dynamic stress test (DST) and federal urban dynamic schedule (FUDS) profiles to provide a comprehensive dataset for model validation. Typical current curves for the DST and FUDS tests are shown in Figure 4.

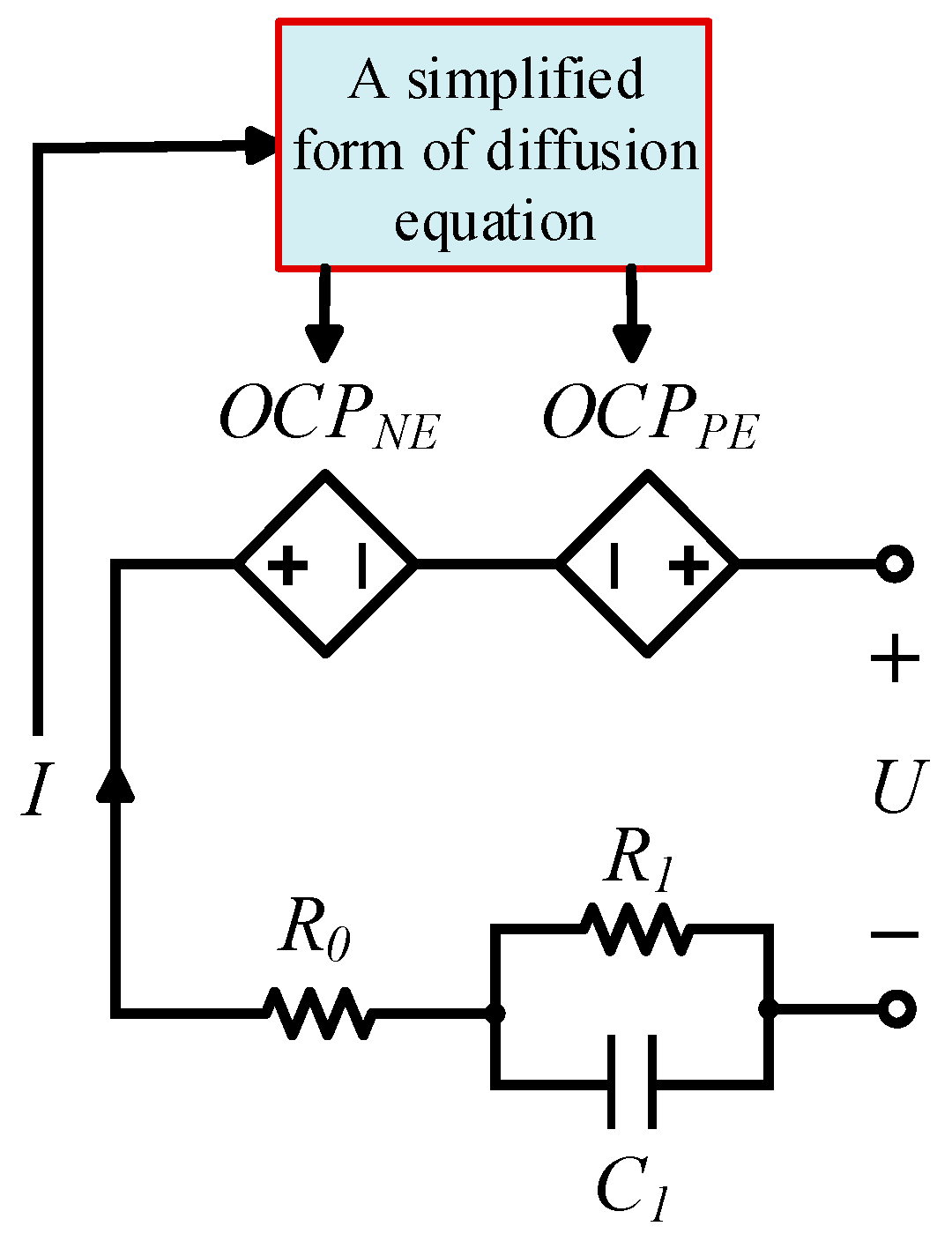
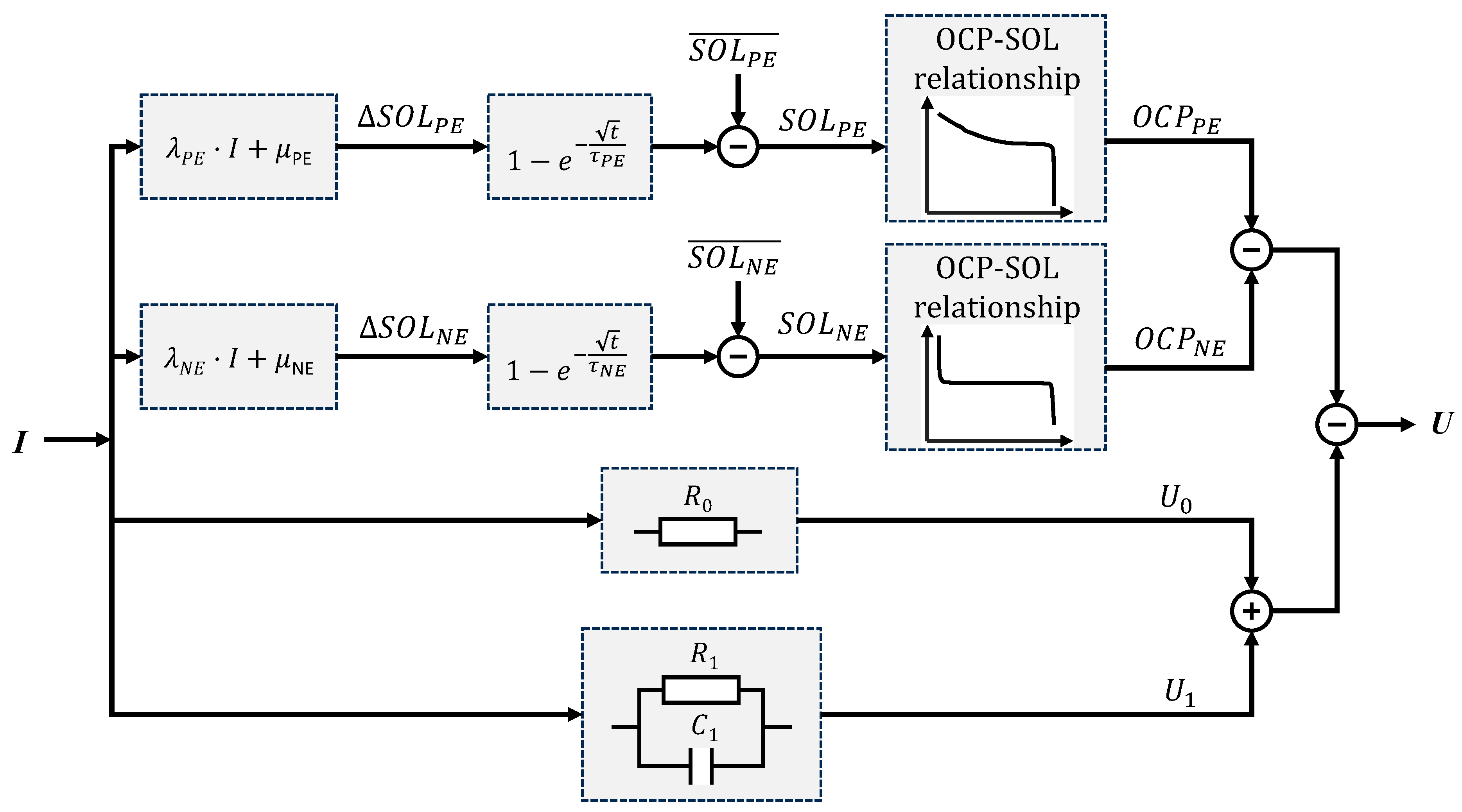
4. Diffusion Equation Based Electrical Model

Figure 5 shows the diffusion-equation-based electrical model. It employs two controlled voltage sources to simulate the positive and negative open-circuit potential (OCP), respectively, and uniquely embeds a simplified form of the diffusion equation to simulate diffusion polarization. In addition, parallel branches of $R_0$ and $R_1,C_1$ are used to simulate ohmic and interfacial polarization, respectively. As a result, the proposed model is sufficient to characterize the integrated battery behavior, especially for lithium titanate batteries applied to high-rate applications.

Assuming that the battery is discharged with current I from the equilibrium state at the moment $t_0$, the proposed model is described as

$$U=OC{P}_{PE}\left[SO{L}_{PE}\left(t\right)\right]-OC{P}_{NE}\left[SO{L}_{NE}\left(t\right)\right]-R_{0}I-R_{1}I\left(1-e^{-\frac{t}{R_1{C}_1}}\right)$$

(5)

where $OC{P}_{PE}$ and $OC{P}_{NE}$ are functions of positive and negative electrode OCP with respect to the state of lithiation (SOL). Since only the lithium-ion concentration on the surface of the electrode material affects the OCP of the electrode, the expression of the electrode SOL can be obtained according to the diffusion Equation (4) as

$$SOL\left(t\right)=\overline{SOL}\left(t\right)+\mathsf{\Delta }SOL\left[I\left(t\right)\right]\cdot \left(1-e^{-\frac{\sqrt{t}}{\tau }}\right)$$

(6)

where $SOL\left(t\right)$ denotes the lithiation state on the surface of the electrode material; $\overline{SOL}\left(t\right)$ denotes the average lithiation state of the electrode material; $\mathsf{\Delta }SOL\left[I\left(t\right)\right]$denotes the shift of the lithiation state of the electrode due to diffusive polarization; and τ is the corresponding time constant. The $\overline{SOL}\left(t\right)$ can be calculated by integrating the current over time as shown in Equation (7), where $Q$ is the capacity of the electrode.

$$\overline{SOL}\left(t\right)=\overline{SOL}\left(t_0\right)-\frac{1}{Q}{\int }_{t_0}^{t}I\left(t\right)dt$$

(7)

As derived in Section 2.2, the proposed model differs from other methods that aim to improve model accuracy by correcting the model parameters. In the case of the presented approach, none of the circuit elements ($R_0$, $R_1,$ and $C_1$) within the model vary with the SOC of the battery. Instead, the diverse polarization behaviors exhibited by the cell at different SOC levels are all represented by the diffusion-based polarization term. Specifically, SOL(t) can be calculated using Equation (8) since the diffusion polarization is also changed at different current rates:

$$\mathsf{\Delta }SOL\left[I\left(t\right)\right]=\lambda \cdot I\left(t\right)+\mu$$

(8)

where λ and µ are the parameters to be identified. The diffusion Equation (6) can be further morphed into

$$SOL\left(t\right)=\overline{SOL}\left(t\right)+\left[\lambda \cdot I\left(t\right)+\mu \right]\cdot \left(1-e^{-\frac{\sqrt{t}}{\tau }}\right).$$

(9)

By directly incorporating diffusion-based polarization into the model structure, the proposed model is able to accurately capture the battery’s performance characteristics across a wide range of SOC and current conditions without the need for extensive parameter tuning. The complete schematic for calculating the output voltage is shown in Figure 6. The $U_0$ and $U_1$ are the voltages induced by the current across $R_0$ and $R_1/C_1$, respectively.

5. Model Extraction

5.1. Full Cell OCV-SOC and Electrode OCP-SOL

As an integral part of the proposed model, the full-cell, open-circuit voltage (OCV) as a function of SOC can be obtained by averaging the battery’s charge and discharge curves measured at low current rates. This approach ensures that the full-cell OCV-SOC relationship captures the underlying electrochemical equilibrium behavior of the battery. To further characterize the model, the relationship between the OCP and the SOL for the positive and negative electrodes can be determined through half-cell testing. The positive material of the half-cell is the positive and negative materials obtained from the disassembled full cell, and the negative material of the half-cell is lithium metal. Then, according to the method in the literature [37], the OCV curves of the full battery are matched using the OCP curve, and the matching relationship between the positive and negative electrodes and the full battery is obtained as shown in Figure 7.

The matching process involves scaling and offsetting the electrode OCP-SOL curves to align with the OCV curve. Specifically, the scaling factors ${\alpha }_{PE}$ and ${\alpha }_{NE}$are used to stretch or shrink the OCP curves of the positive and negative electrodes, respectively, while the offsets ${\beta }_{PE}$ and ${\beta }_{NE}$ are used to shift the OCP curves to lower SOC levels to match the full-cell behavior.

When $SOL=0$, it indicates that the electrode is completely delithiated, and the electrode OCP is the highest; when $SOL=1$, it indicates that the electrode is completely embedded in lithium, and the electrode OCP is the lowest. Finally, the relationship between the full-cell capacity ($Q_{Full}$) and the individual electrode capacities ($Q_{PE}$ and $Q_{NE}$) can be calculated using the following equation:

$$Q_{Full}=\frac{Q_{PE}}{{\alpha }_{PE}}=\frac{Q_{NE}}{{\alpha }_{NE}}.$$

(10)

5.2. Parameter Identification

Depending on the parameter type, the parameter identification process can be divided into three parts:

(1)

The OCV curves of the full cell were reconstructed using the OCP data of the half-cells based on the methodology presented in the literature [33,38], to obtain the correspondence parameters between the electrode and the full cell (${\alpha }_{PE}$, ${\alpha }_{NE},$ ${\beta }_{PE}$, and ${\beta }_{NE}$), as well as the ohmic resistance ($R_0$). These parameters and Equation (10) were then used to calculate the capacity of the electrode ($Q_{PE}$, $Q_{NE}$).

(2)

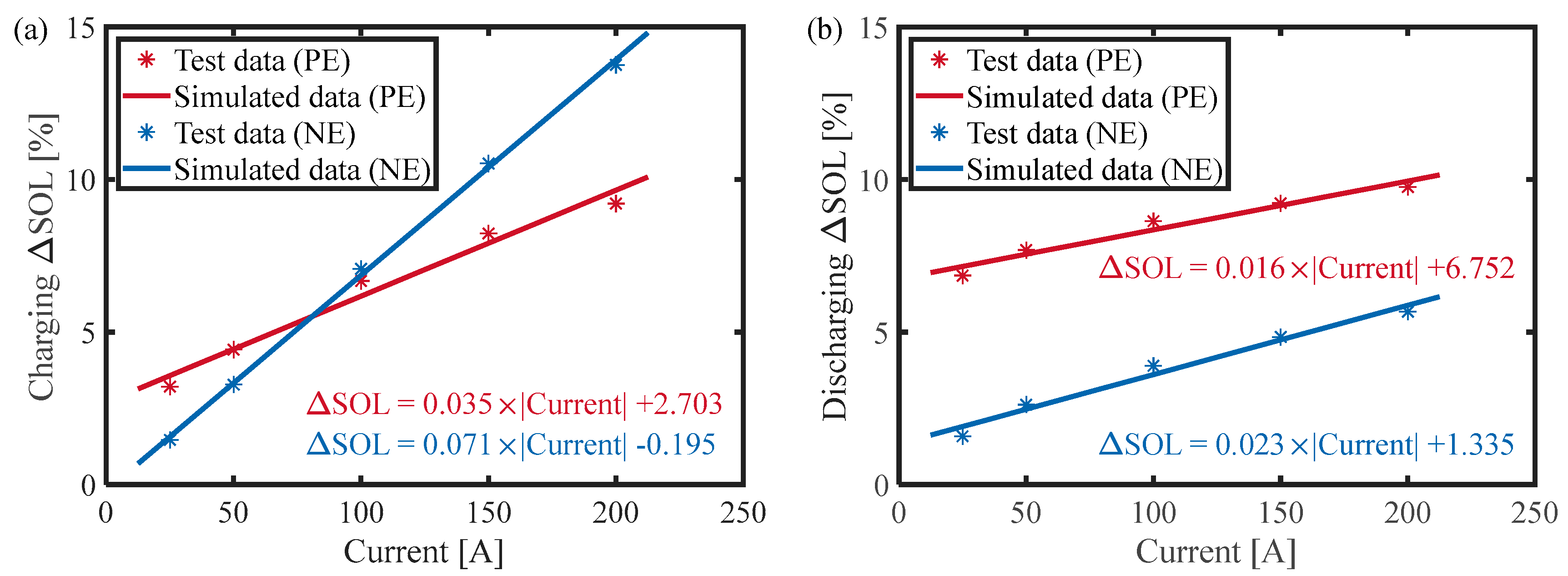
Based on the three-electrode battery configuration, the battery was subjected to constant-current charge/discharge experiments at different C-rates. The parameters ($\lambda ,\mu$) in the diffusion Equation (9) were identified based on the difference between the diffusion polarization of the positive and negative electrodes. In addition, the parameter $R_1$ was determined by ohmic and interfacial polarization.

(3)

Based on the JEVS experiments with different SOCs, the parameters ($C_1,\tau$) were obtained by least-squares fitting of different pulses according to the different magnitudes of the time constant. The final parameters were obtained by averaging the parameters at different SOCs.

To investigate the SOL shift that occurs at the positive and negative electrodes due to the diffusion polarization under different current rates, this study employed a three-electrode cell configuration. As shown in Figure 8, the positive electrode is LiCoO₂, the negative electrode is Li₄Ti₅O₁₂, and a lithium metal electrode serves as the reference electrode. The inclusion of the reference electrode allowed for a clear distinction between the voltages of the positive and negative electrodes. Specifically, the voltage of the positive electrode with respect to the reference electrode is denoted as $U_{PE}$, while the voltage of the negative electrode with respect to the reference electrode is denoted as $U_{NE}$. The voltage of the full battery can be expressed as the sum of these two electrode potentials, as shown in the following equation:

$$U=U_{PE}-U_{NE}.$$

(11)

After assembling the three-electrode lithium titanate battery, charging and discharging experiments were conducted at different current rates to highlight the distinct effects of positive and negative electrode polarization on the full-cell voltage. Two representative current conditions were selected for this analysis: the OCV test under 0.1 C (2.5A), which minimizes the influence of polarization on the electrodes; and a high-rate 8 C (200A) test, which emphasizes the impact of polarization on the electrodes. Through these experiments, the performance differences between the positive and negative electrodes under varying polarization levels could be more clearly analyzed. The experimental setup utilized three test channels: one channel measured and controlled the full-cell voltage during charging and discharging, while the other two channels independently monitored the voltages between the positive electrode and the reference electrode and between the negative electrode and the reference electrode, respectively.

Figure 9 illustrates the correlation between the positive electrode voltage, negative electrode voltage, and full-cell voltage under various charging and discharging current conditions. As observed in the OCV test, the rapid rise in the full-cell voltage near the charging cutoff is primarily attributed to a significant drop in the negative electrode voltage, indicating that the negative electrode becomes the dominant factor in determining the voltage cutoff of the full battery under these quasi-equilibrium conditions. In contrast, under the high-rate 8 C charging condition, the rapid increase in the full-cell voltage before the cutoff is mainly driven by a rapid rise in the positive electrode voltage, suggesting that the positive electrode becomes the primary influence on the full-cell voltage cutoff. The voltage difference in the vertical direction at a steady state is caused by a combination of ohmic polarization and interface polarization. The polarization resistance $R_1$ can be obtained by dividing this voltage difference by the current and subtracting the ohmic resistance.

By fitting the OCP curves of the positive and negative electrodes to the measured three-electrode voltages, the diffusion polarization at the positive and negative electrodes can be separately quantified. Additionally, the shift in the voltage direction of the full-cell curve represents the combined effects of ohmic and interfacial polarization. Similar observations can be made for the OCV and 8 C discharge tests, as shown in Figure 10. Compared to the charging process, the diffusion polarization at the positive electrode remains relatively unchanged, while the diffusion polarization at the negative electrode is significantly reduced, which may be attributable to the differences in the material properties between the positive and negative electrodes.

By matching the positive and negative electrode voltage curves obtained during constant-current charging and discharging at different current rates, the offset ${\beta }^{rate}$ under various current rates can be obtained and used to calculate the $∆SO{L}^{rate}$ of the electrodes, where the subscript “rate” denotes the specific current rate applied during the charging and discharging processes. It is important to note that during the curve-matching process, the parameters ${\alpha }_{PE}$ and ${\alpha }_{NE}$should be constrained to ensure consistency with the identified OCP curves. This approach ensures that the positive and negative electrodes have the same capacity. According to the matching results, the $∆SO{L}^{rate}$ of the positive and negative electrodes can be calculated using Equation (12):

$$∆SO{L}^{rate}={\beta }^{OCV}-{\beta }^{rate}$$

(12)

where ${\beta }^{OCV}$ represents the offset obtained from the OCV test. The experimentally determined $∆SOL$ of the positive and negative electrodes as a function of the current rate is shown in Figure 11.

After the ∆SOL has been determined, the parameters ($C_1,\tau$) can be identified separately according to the differences in the time constants of interfacial and diffusion polarization. In general, the time constant of the diffusion process is much larger than that of the interfacial process. Therefore, the particle swarm algorithm was fitted to the model using the voltage response under the complete 60 s current pulse from the JEVS test to identify the parameter $\tau$. It is worth noting that parameter C was set to infinity during the identification process to ignore the effect of the interfacial process. Then, the voltage response of the first 10 s of the pulse in the JEVS test was used to identify parameter $C_1$, which characterizes the interfacial process. All the identified model parameters at 25 °C are summarized in

Table 2. Identification results of equivalent circuit model parameters for LTO battery.

Parameters	Current Direction	Positive Electrode	Negative Electrode	Full Cell
$R_0$	-	-	-	0.8 mΩ
$R_1$	-	-	-	0.4 mΩ
$C_1$	-	-	-	27,732 F
${\alpha }^{OCV}$	-	1.239	1.023	-
${\beta }^{OCV}$	-	−0.064	−0.003	-
$\lambda$	Charge	0.009	0.018	-
	Discharge	0.004	0.006	-
$\mu$	Charge	0.027	−0.002	-
	Discharge	0.068	0.013	-
$\tau$	Charge	116.6 s	106.1 s	-
	Discharge	123.2 s	102.0 s	-

.

6. Model Verification

To validate the proposed model, constant current tests and dynamic current tests with different current rates were carried out for LTO batteries, respectively. The superiority of the proposed model was then quantitatively assessed by comparing the simulation results against the experimental data. In this study, the proposed model was implemented using MATLAB, which ensures its potential for generalization and application in high-power applications.

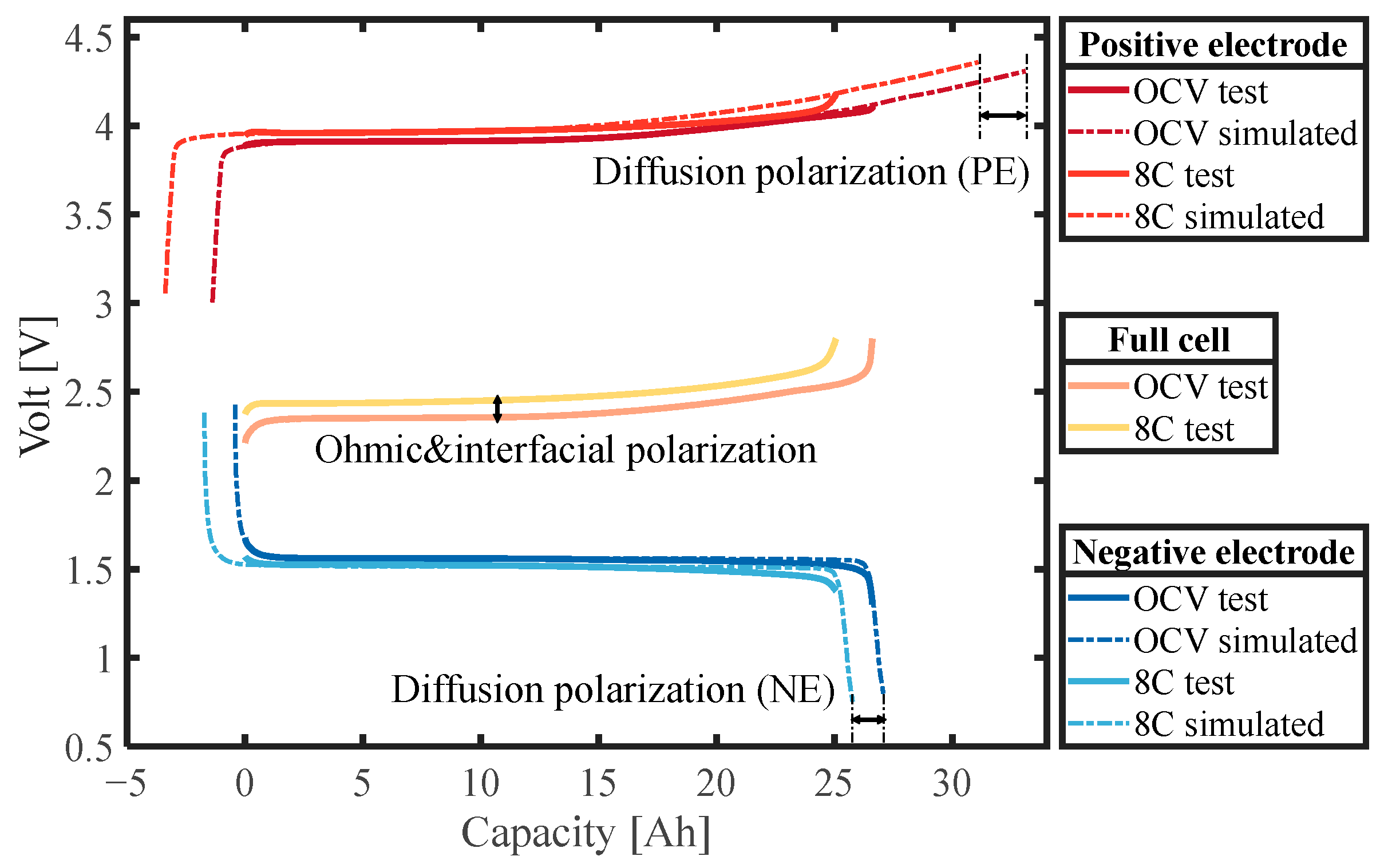
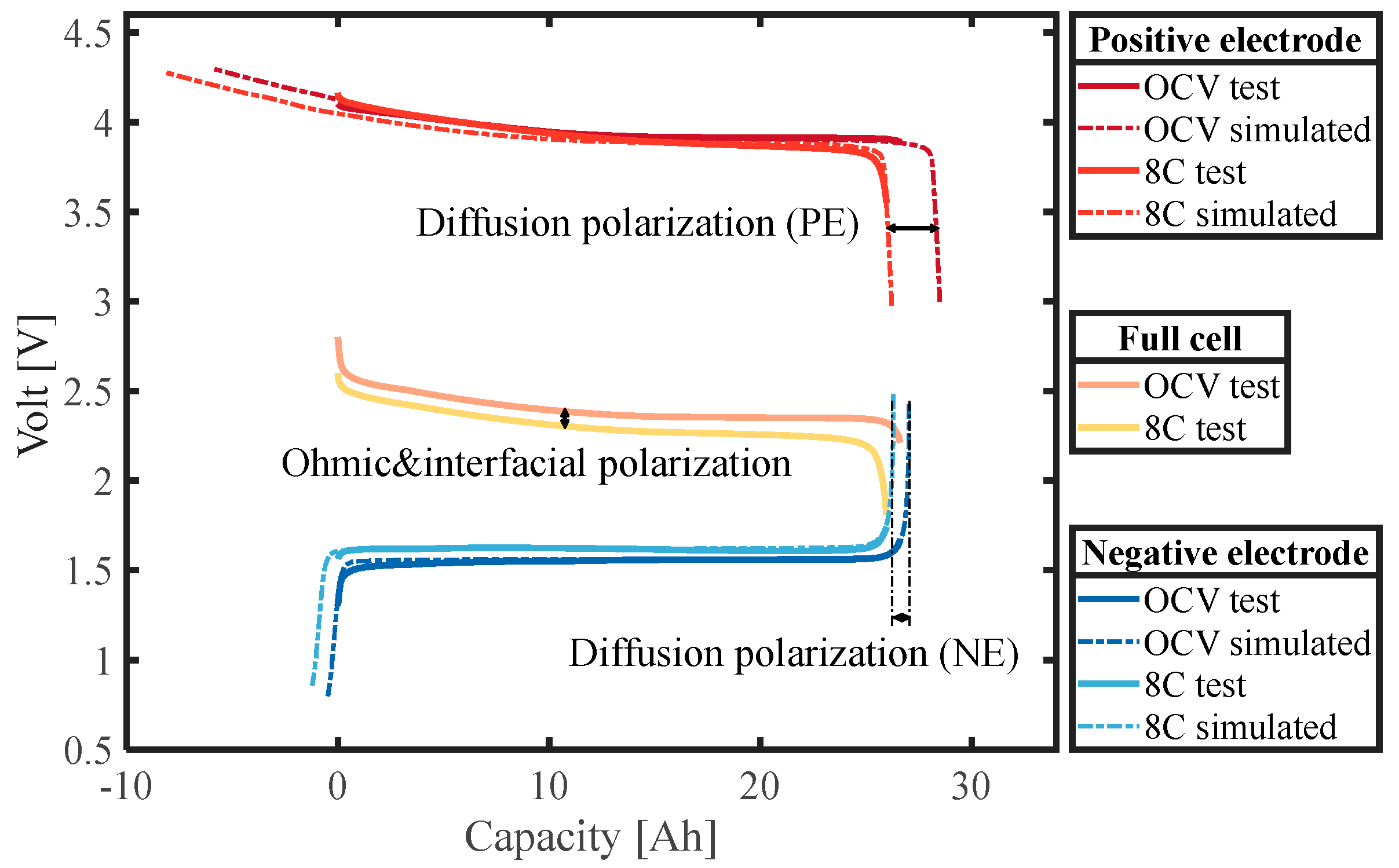
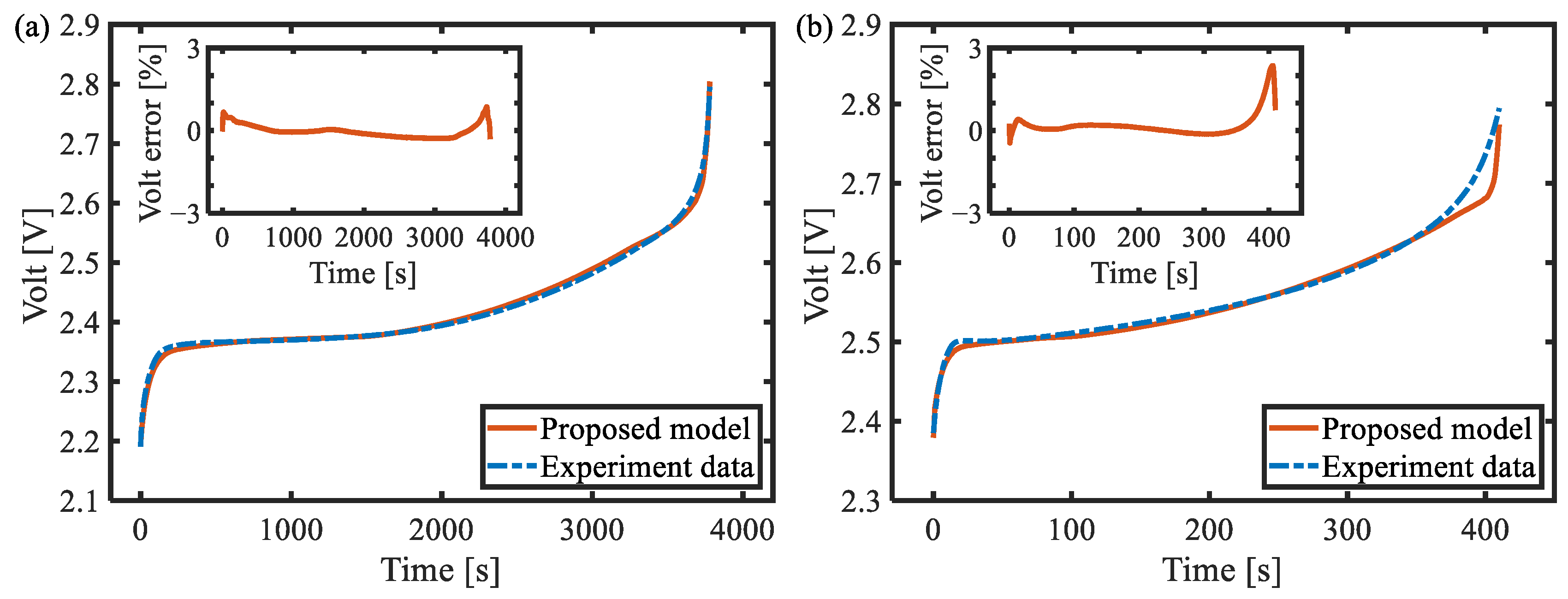
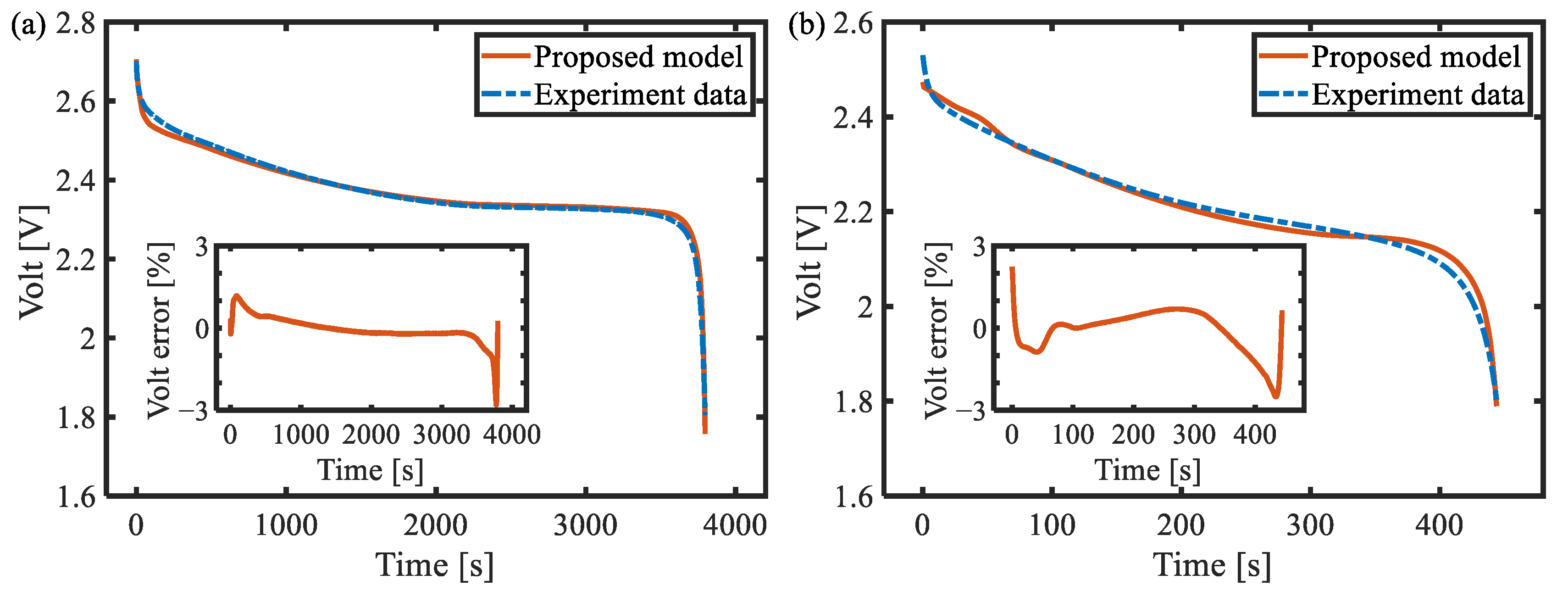
6.1. Galvanostatic Test at Different Rates

Figure 12 presents the validation results of the lithium titanate battery model under constant current charging conditions with varying current multiplication factors. As shown, the simulated voltage results of the proposed model closely align with the experimental test data, despite the differences in current multiplication. Specifically, when the current was 1 C, the error throughout the entire charging process was less than 1%, as shown in Figure 12a. Similarly, for an 8 C current, the error remained below 1% for the first 350 s of charging, though it exhibited an upward trend towards the end, with a maximum error of less than 3%, as shown in Figure 12b.

On the other hand, Figure 13 compares the simulation results and experimental data for constant-current discharge under different current multiplication factors. Analogous to the charging performance, the model’s errors were less than 1% for the majority of the discharge cycle. Larger errors, not exceeding 3%, were observed only at the beginning and end of discharge. These results demonstrate that the proposed model can accurately capture the constant-current discharge and charging behavior of lithium titanate batteries.

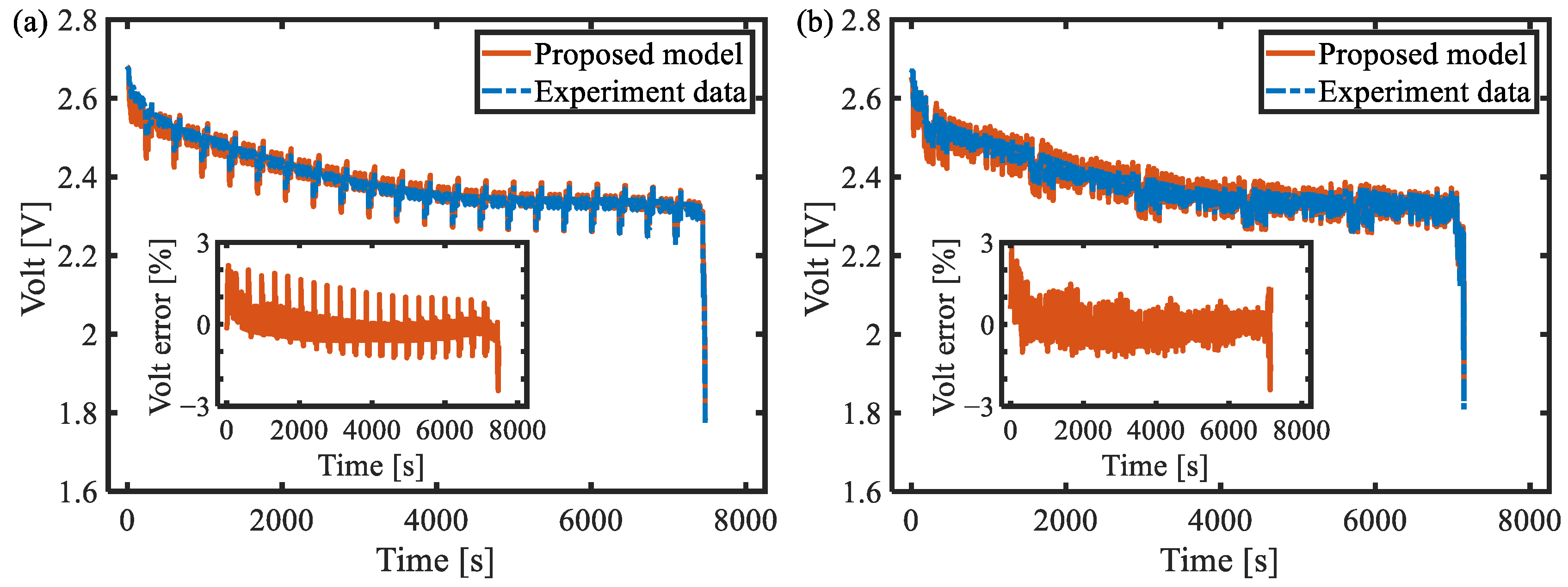
6.2. Dynamic Current Testing Using DST and FUDS Profiles

In addition to the galvanostatic validation, the proposed model was further assessed under DST and FUDS operating conditions. For the DST, as shown in Figure 14a, the error between the model-simulated voltage and the experimental data were less than 2% for the majority of the time range. This demonstrates the simulation accuracy of the model at continuous, steadily varying currents. It is worth noting that even though the error increased towards the end of the discharge period, the maximum error remained within 3%, reflecting the model’s stability and reliability throughout the discharge process.

In addition, the battery model also performs well under more complex FUDS conditions, as shown in Figure 14b. In this case, the battery’s voltage response underwent drastic oscillations due to the frequent changes in current. Nevertheless, the proposed model was still able to accurately simulate the voltage response under such dynamic conditions. Even during the most violent current fluctuations, the maximum error in the model prediction was less than 3%, proving the model’s accuracy and reliability in capturing complex dynamic behavior.

6.3. Comparison against Second-Order RC Model

To better illustrate the advantages of using diffusion equation modeling, the second-order RC model and the model proposed in this paper were used to describe the performance of the battery at different conditions.

In order to compare the errors of the models under different C-rates, the errors distributed by time were transformed into errors distributed by SOC, as shown in Figure 15. The SOC was calculated based on the capacity at different C-rates, respectively. The voltage error of the second-order RC model rises continuously, exceeding 6% by the end of charge in Figure 15a. And, the error increases at a higher C-rate. Similarly, the second-order RC model also exhibits low accuracy in the galvanostatic discharging with large C-rates, as shown in Figure 15b. In contrast, the voltage error of the proposed model remains lower than 3%, demonstrating the diffusion equation’s ability to better characterize the integrated battery behavior, enhancing the model’s applicability for high C-rate operations.

Figure 16 shows the error analysis of the battery under DST and FUDS operating conditions. The voltage error of the second-order RC model increases rapidly, exceeding 18% before the discharge cutoff, while the error of the model proposed in this paper is always less than 3%. This indicates that the diffusion equation accurately captures the battery characteristics, particularly during rapid voltage changes near the charging and discharging cutoffs. The high agreement between the simulation results and experimental data for LTO batteries verifies the accuracy and reliability of the model proposed in this paper, which outperforms the second-order RC model.

7. Conclusions

In this paper, a simplified diffusion equation was used to establish an electrical model for high-power LTO batteries, and the main contributions are as follows:

(1)

By comparing the polarization distribution of the battery, it was found that the effect of diffusion polarization on the LTO battery is more serious than that of interfacial polarization, and it is the diffusion polarization rather than the interfacial polarization that will change with SOC. Specifically, the effect of diffusion polarization is 1.07 to 1.75 times that of interfacial polarization.

(2)

A simplified diffusion equation related to SOL that can be directly added to the circuit model was elaborately derived, which has more physical significance than the mathematical solution, and gives an ideal expression for the lithiation state of the positive and negative electrodes in the steady state.

(3)

Through the three-electrode battery architecture, the degree of diffusion polarization of the positive and negative electrodes under high-power conditions was decoupled and analyzed, and the model based on the simplified diffusion equation was established with high accuracy in the full SOC range, with a maximum voltage error of less than 3%.

Compared with the second-order RC model, the model implemented in MATLAB embeds the simplified form of the diffusion equation, which reduces the model estimation error under different loading profiles. Comparative analysis of simulation and experimental data for LTO batteries shows that the proposed model has the advantage of accurately and reliably estimating the terminal voltage. In this paper, a modeling method for lithium titanate batteries is provided for the first time from the perspective of diffusion polarization and will contribute to the optimization of management strategies for battery management systems in future fast charging and electric vehicles.