Robust Online Estimation of State of Health for Lithium-Ion Batteries Based on Capacities under Dynamical Operation Conditions
Abstract
1. Introduction
2. Mathematical Modeling of Lithium-Ion Batteries
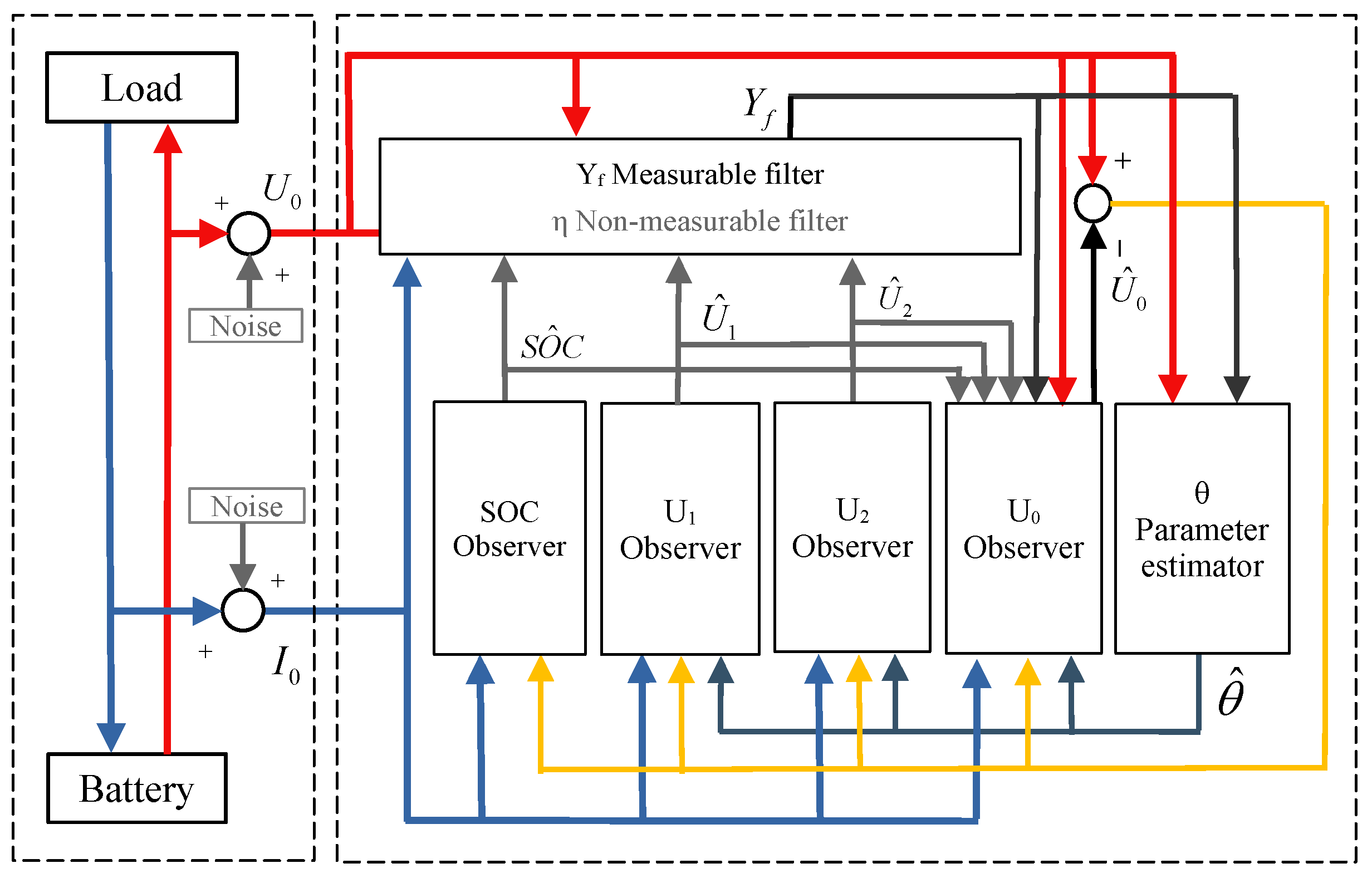
3. Filter-Based Co-Estimation Method of SOH
4. Stability Analysis
5. Simulation Analysis and Experimental Results
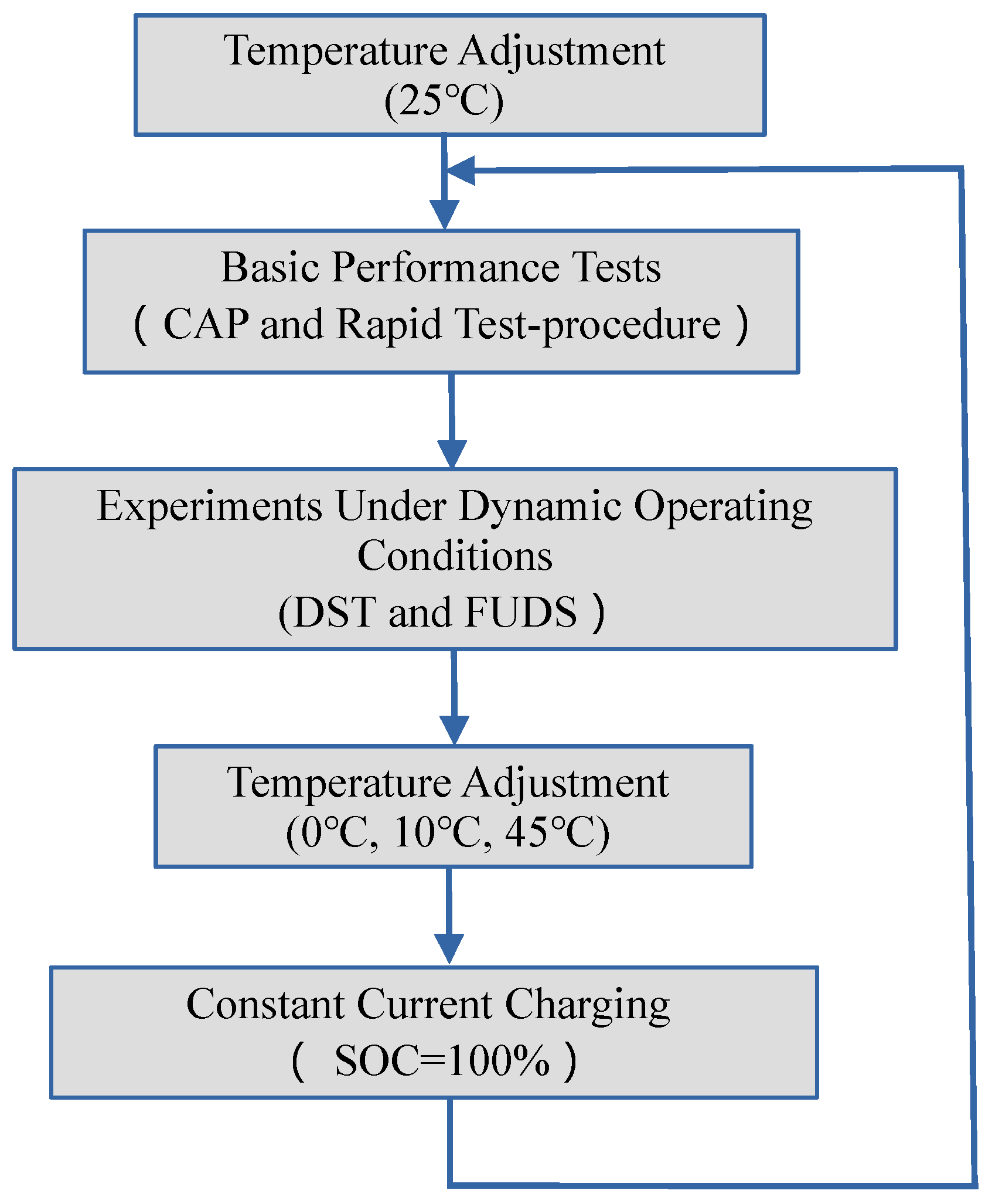
5.1. Experimental Setup
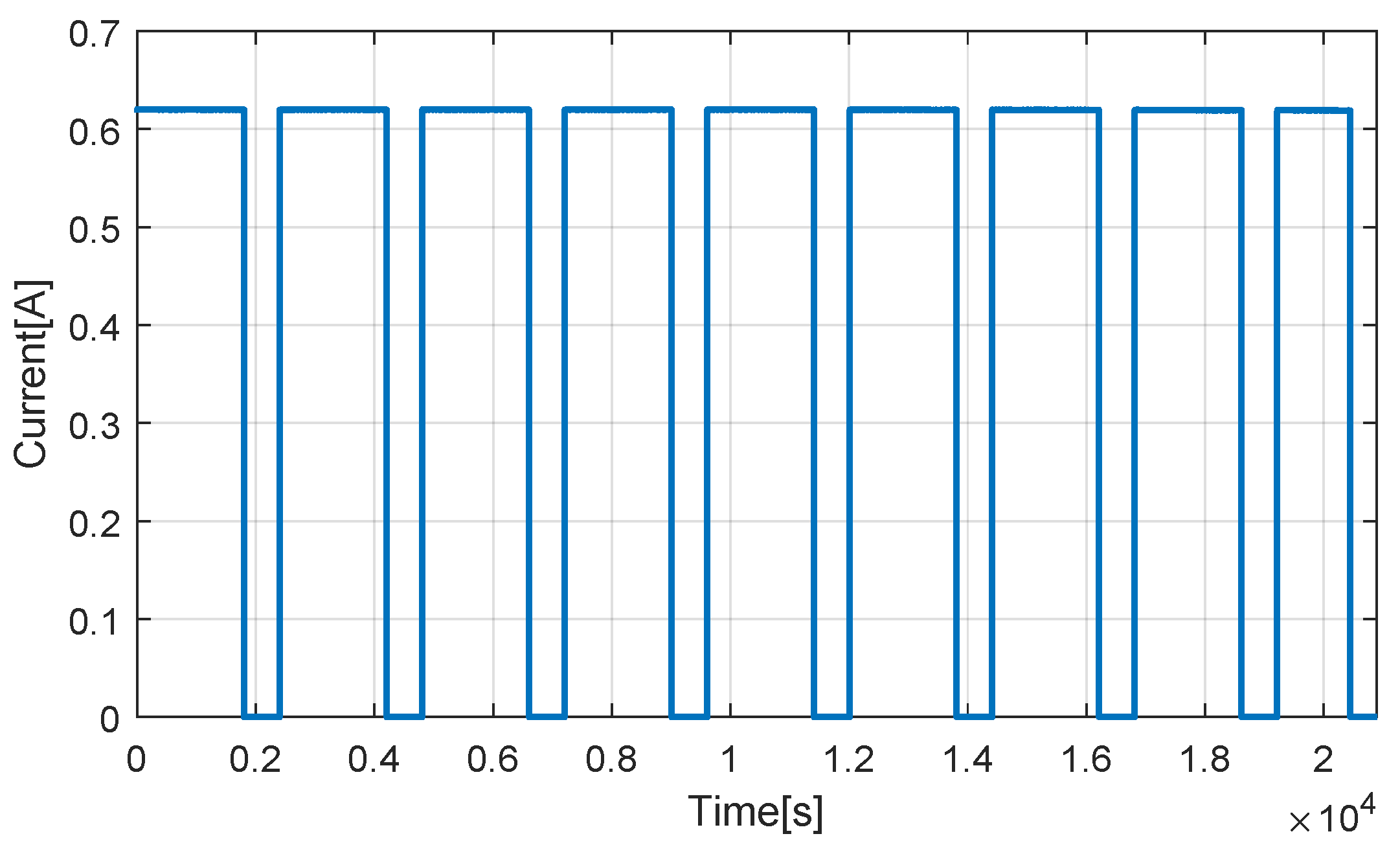
5.2. Lithium-Ion Battery Basic Performance Test
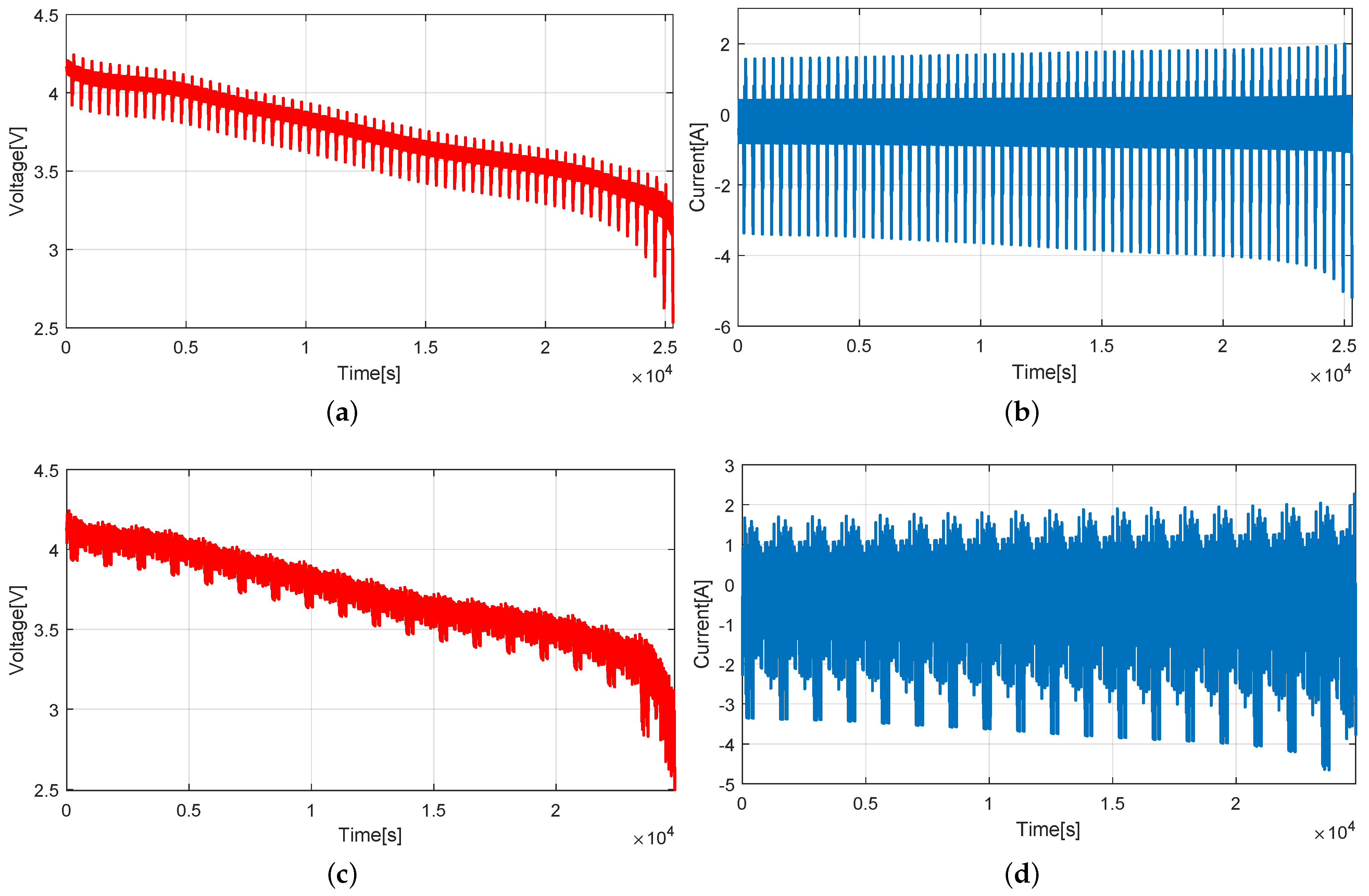
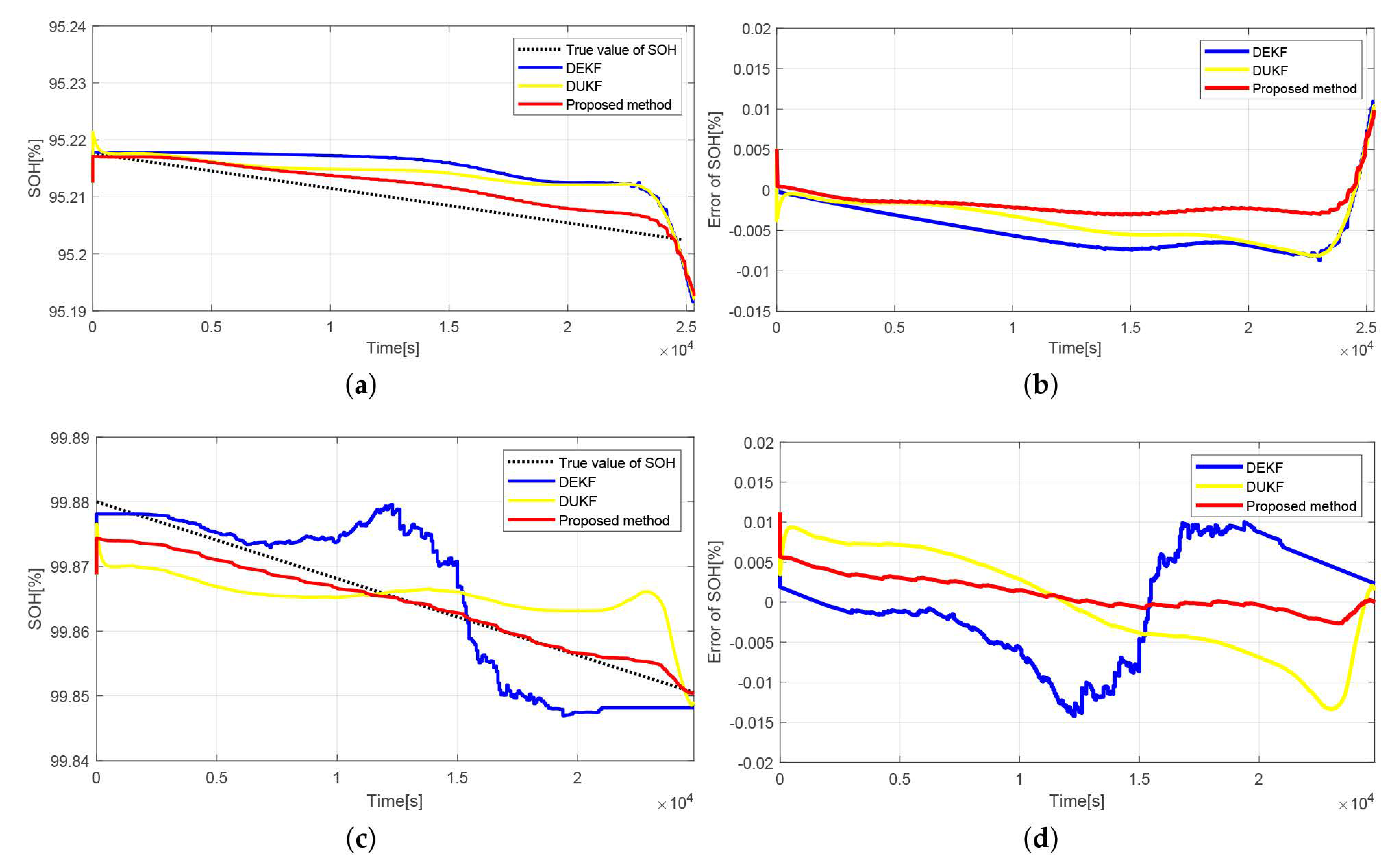
5.3. Experiment under Dynamic Operating Conditions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, B.; Qian, Y.; Li, Q.; Chen, Q.; Wu, J.; Luo, E.; Xie, R.; Zheng, R.; Yan, Y.; Su, S.; et al. Critical summary and perspectives on state-of-health of lithium-ion battery. Renew. Sustain. Energy Rev. 2024, 190, 114077. [Google Scholar] [CrossRef]
- Xiong, R.; Pan, Y.; Shen, W.; Li, H.; Sun, F. Lithium-ion battery aging mechanisms and diagnosis method for automotive applications: Recent advances and perspectives. Renew. Sustain. Energy Rev. 2020, 131, 110048. [Google Scholar] [CrossRef]
- Liu, D.; Xie, W.; Liao, H.; Peng, Y. An integrated probabilistic approach to lithium-ion battery remaining useful life estimation. IEEE Trans. Instrum. Meas. 2014, 64, 660–670. [Google Scholar]
- Dai, H.; Wei, X.; Sun, Z. A new SOH prediction concept for the power lithium-ion battery used on HEVs. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1649–1653. [Google Scholar]
- Samadani, E.; Mastali, M.; Farhad, S.; Fraser, R.A.; Fowler, M. Li-ion battery performance and degradation in electric vehicles under different usage scenarios. Int. J. Energy Res. 2016, 40, 379–392. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Chakraborty, B. Battery management strategies: An essential review for battery state of health monitoring techniques. J. Energy Storage 2022, 51, 104427. [Google Scholar] [CrossRef]
- Waag, W.; Käbitz, S.; Sauer, D.U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Appl. Energy 2013, 102, 885–897. [Google Scholar] [CrossRef]
- Choi, W.; Shin, H.C.; Kim, J.M.; Choi, J.Y.; Yoon, W.S. Modeling and applications of electrochemical impedance spectroscopy (EIS) for lithium-ion batteries. J. Electrochem. Sci. Technol. 2020, 11, 1–13. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A comparative study of commercial lithium ion battery cycle life in electrical vehicle: Aging mechanism identification. J. Power Sources 2014, 251, 38–54. [Google Scholar] [CrossRef]
- Meng, K.; Chen, X.; Zhang, W.; Chang, W.; Xu, J. A robust ultrasonic characterization methodology for lithium-ion batteries on frequency-domain damping analysis. J. Power Sources 2022, 547, 232003. [Google Scholar] [CrossRef]
- Schaltz, E.; Stroe, D.I.; Nørregaard, K.; Ingvardsen, L.S.; Christensen, A. Incremental capacity analysis applied on electric vehicles for battery state-of-health estimation. IEEE Trans. Ind. Appl. 2021, 57, 1810–1817. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Dou, X.; Zhang, X. A rapid online calculation method for state of health of lithium-ion battery based on coulomb counting method and differential voltage analysis. J. Power Sources 2020, 479, 228740. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Energy Storage 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Fu, Y.; Xu, J.; Gong, X. Online battery state of health estimation based on Genetic Algorithm for electric and hybrid vehicle applications. J. Power Sources 2013, 240, 184–192. [Google Scholar] [CrossRef]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.; Dechent, P.; Sauer, D.U. Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data. J. Power Sources 2012, 215, 248–257. [Google Scholar] [CrossRef]
- Jia, S.; Ma, B.; Guo, W.; Li, Z.S. A sample entropy based prognostics method for lithium-ion batteries using relevance vector machine. J. Manuf. Syst. 2021, 61, 773–781. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, Y.; Wang, C.; Tian, J.; Chen, X.; Li, H.; Zhang, Q. A data-driven method for extracting aging features to accurately predict the battery health. Energy Storage Mater. 2023, 57, 460–470. [Google Scholar] [CrossRef]
- Manoharan, A.; Begam, K.; Aparow, V.R.; Sooriamoorthy, D. Artificial Neural Networks, Gradient Boosting and Support Vector Machines for electric vehicle battery state estimation: A review. J. Energy Storage 2022, 55, 105384. [Google Scholar] [CrossRef]
- Zhao, J.; Han, X.; Ouyang, M.; Burke, A.F. Specialized deep neural networks for battery health prognostics: Opportunities and challenges. J. Energy Chem. 2023, 87, 416–438. [Google Scholar] [CrossRef]
- Wu, L.; Lyu, Z.; Huang, Z.; Zhang, C.; Wei, C. Physics-based battery SOC estimation methods: Recent advances and future perspectives. J. Energy Chem. 2023, 89, 27–40. [Google Scholar] [CrossRef]
- Vaghela, R.; Ramani, P.; Sarda, J.; Hui, K.L.; Sain, M. Analysis of State-of-Health Estimation Approaches and Constraints for Lithium-Ion Batteries in Electric Vehicles. Int. J. Energy Res. 2024, 2024, 6488186. [Google Scholar] [CrossRef]
- Sarkar, S.; Halim, S.Z.; El-Halwagi, M.M.; Khan, F.I. Electrochemical models: Methods and applications for safer lithium-ion battery operation. J. Electrochem. Soc. 2022, 169, 100501. [Google Scholar] [CrossRef]
- Naseri, F.; Schaltz, E.; Stroe, D.I.; Gismero, A.; Farjah, E. An enhanced equivalent circuit model with real-time parameter identification for battery state-of-charge estimation. IEEE Trans. Ind. Electron. 2021, 69, 3743–3751. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, C. An Extended Kalman Filter Design for State-of-Charge Estimation Based on Variational Approach. Batteries 2023, 9, 583. [Google Scholar] [CrossRef]
- Tian, Y.; Xia, B.; Sun, W.; Xu, Z.; Zheng, W. A modified model based state of charge estimation of power lithium-ion batteries using unscented Kalman filter. J. Power Sources 2014, 270, 619–626. [Google Scholar] [CrossRef]
- Schwunk, S.; Armbruster, N.; Straub, S.; Kehl, J.; Vetter, M. Particle filter for state of charge and state of health estimation for lithium–iron phosphate batteries. J. Power Sources 2013, 239, 705–710. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Chen, Z.; He, H. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476. [Google Scholar] [CrossRef]
- Xiong, R.; Mu, H. Accurate state of charge estimation for lithium-ion battery using dual Uncsented Kalman filters. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 5484–5487. [Google Scholar]
- Yu, Q.; Xiong, R.; Yang, R.; Pecht, M.G. Online capacity estimation for lithium-ion batteries through joint estimation method. Appl. Energy 2019, 255, 113817. [Google Scholar] [CrossRef]
- Lai, X.; Yuan, M.; Tang, X.; Yao, Y.; Weng, J.; Gao, F.; Ma, W.; Zheng, Y. Co-estimation of state-of-charge and state-of-health for lithium-ion batteries considering temperature and ageing. Energies 2022, 15, 7416. [Google Scholar] [CrossRef]
- Zhou, M.; Wei, K.; Wu, X.; Weng, L.; Su, H.; Wang, D.; Zhang, Y.; Li, J. Fractional-Order Sliding-Mode Observers for the Estimation of State-of-Charge and State-of-Health of Lithium Batteries. Batteries 2023, 9, 213. [Google Scholar] [CrossRef]
- Chen, J.; Chitrakaran, V.K.; Dawson, D.M. Range identification of features on an object using a single camera. Automatica 2011, 47, 201–206. [Google Scholar] [CrossRef]
- Wu, X.; Chen, J.; Wang, D.; Xu, K.; Shao, M.; Wang, Y.; Long, Y. Filter-Based Co-estimation of State-of-Charge and State-of-Health for Lithium-ion Batterie. IEEE Trans. Ind. Electron. 2024; submitted. [Google Scholar]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and IV performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Chen, J.; Ouyang, Q.; Xu, C.; Su, H. Neural network-based state of charge observer design for lithium-ion batteries. IEEE Trans. Control Syst. Technol. 2018, 26, 313–320. [Google Scholar] [CrossRef]
- Chaoui, H.; Mandalapu, S. Comparative study of online open circuit voltage estimation techniques for state of charge estimation of lithium-ion batteries. Batteries 2017, 3, 12. [Google Scholar] [CrossRef]
- Rahman, M.A.; Anwar, S.; Izadian, A. Electrochemical model parameter identification of a lithium-ion battery using particle swarm optimization method. J. Power Sources 2016, 307, 86–97. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Pan, R.; Chen, Z. Experimental data of lithium-ion battery and ultracapacitor under DST and UDDS profiles at room temperature. Data Brief 2017, 12, 161–163. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Yang, F.; Xu, Y.; Su, L.; Yang, Z.; Feng, Y.; Zhang, C.; Shao, T. State of charge and state of health estimation of lithium-ion battery packs with inconsistent internal parameters using dual extended Kalman filter. J. Electrochem. Energy Convers. Storage 2024, 21, 011004. [Google Scholar] [CrossRef]
- Mahboubi, D.; Gavzan, I.J.; Saidi, M.H.; Ahmadi, N. State of charge estimation for lithium-ion batteries based on square root sigma point Kalman filter considering temperature variations. IET Electr. Syst. Transp. 2022, 12, 165–180. [Google Scholar] [CrossRef]




| Parameters | Specification |
|---|---|
| Rated capacity | 3200 mAh |
| Nominal voltage | 3.63 V |
| Maximum charge voltage | 4.2 V |
| Discharge cut-off voltage | 2.5 V |
| Working temperature | 0∼45 °C |
| Battery weight | 49 g |
| Temperature | () | () | () | (F) | (F) | (F) |
|---|---|---|---|---|---|---|
| 0 °C | 0.053 | 0.022 | 0.034 | 2.764 | 46.429 | 9263.228 |
| 10 °C | 0.042 | 0.099 | 0.043 | 2.970 | 5.482 | 2747.428 |
| 25 °C | 0.029 | 0.056 | 0.054 | 3.047 | 12.443 | 2462.632 |
| 40 °C | 0.013 | 0.077 | 0.041 | 3.179 | 6.99 | 3905.739 |
| Temperature | Algorithm Type | DST Condition | FUDS Condition |
|---|---|---|---|
| 0 °C | Filter-Based Observer | MAE: 1.1296% | MAE: 1.5110% |
| RMSE: 0.5123% | RMSE: 0.8781% | ||
| DUKF | MAE: 9.0690% | MAE: 6.0277% | |
| RMSE: 3.2567% | RMSE: 2.6664% | ||
| DEKF | MAE: 8.4087% | MAE: 6.1495% | |
| RMSE: 2.3025% | RMSE: 3.2103% | ||
| 10 °C | Filter-Based Observer | MAE: 1.4766% | MAE: 1.0435% |
| RMSE: 0.8685% | RMSE: 0.7620% | ||
| DUKF | MAE: 9.6849% | MAE: 9.5598% | |
| RMSE: 4.0638% | RMSE: 3.9750% | ||
| DEKF | MAE: 9.1705% | MAE: 5.8272% | |
| RMSE: 5.3467% | RMSE: 3.6444% | ||
| 25 °C | Filter-Based Observer | MAE: 1.2475% | MAE: 1.7281% |
| RMSE: 0.5517% | RMSE: 0.4770% | ||
| DUKF | MAE: 3.2238% | MAE: 3.5548% | |
| RMSE: 0.8014% | RMSE: 1.1321% | ||
| DEKF | MAE: 3.2698% | MAE: 4.1347% | |
| RMSE: 1.6472% | RMSE: 2.1402% | ||
| 40 °C | Filter-Based Observer | MAE: 1.2621% | MAE: 0.3129% |
| RMSE: 0.7205% | RMSE: 0.0975% | ||
| DUKF | MAE: 2.3814% | MAE: 3.4679% | |
| RMSE: 0.9114% | RMSE: 0.9373% | ||
| DEKF | MAE: 2.9840% | MAE: 3.2516% | |
| RMSE: 1.8293% | RMSE: 0.7150% |
| Temperature | Algorithm Type | DST Condition | FUDS Condition |
|---|---|---|---|
| 0 °C | Filter-Based Observer | MAE: 0.0360% | MAE: 0.0112% |
| RMSE: 0.0196% | RMSE: 0.0085% | ||
| DUKF | MAE: 0.0788% | MAE: 0.0478% | |
| RMSE: 0.0372% | RMSE: 0.0246% | ||
| DEKF | MAE: 0.0732% | MAE: 0.0705% | |
| RMSE: 0.0278% | RMSE: 0.0325% | ||
| 10 °C | Filter-Based Observer | MAE: 0.0239% | MAE: 0.0345% |
| RMSE: 0.0183% | RMSE: 0.0054% | ||
| DUKF | MAE: 0.0292% | MAE: 0.0457% | |
| RMSE: 0.0200% | RMSE: 0.0098% | ||
| DEKF | MAE: 0.0350% | MAE: 0.1429% | |
| RMSE: 0.0207% | RMSE: 0.0215% | ||
| 25 °C | Filter-Based Observer | MAE: 0.0099% | MAE: 0.0078% |
| RMSE: 0.0024% | RMSE: 0.0061% | ||
| DUKF | MAE: 0.0104% | MAE: 0.0186% | |
| RMSE: 0.0046% | RMSE: 0.0089% | ||
| DEKF | MAE: 0.0109% | MAE: 0.0213% | |
| RMSE: 0.0057% | RMSE: 0.0103% | ||
| 40 °C | Filter-Based Observer | MAE: 0.0383% | MAE: 0.0311% |
| RMSE: 0.0116% | RMSE: 0.0168% | ||
| DUKF | MAE: 0.0227% | MAE: 0.0424% | |
| RMSE: 0.0119% | RMSE: 0.0196% | ||
| DEKF | MAE: 0.0540% | MAE: 0.0499% | |
| RMSE: 0.0184% | RMSE: 0.0225% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Chen, J.; Tang, H.; Xu, K.; Shao, M.; Long, Y. Robust Online Estimation of State of Health for Lithium-Ion Batteries Based on Capacities under Dynamical Operation Conditions. Batteries 2024, 10, 219. https://doi.org/10.3390/batteries10070219
Wu X, Chen J, Tang H, Xu K, Shao M, Long Y. Robust Online Estimation of State of Health for Lithium-Ion Batteries Based on Capacities under Dynamical Operation Conditions. Batteries. 2024; 10(7):219. https://doi.org/10.3390/batteries10070219
Chicago/Turabian StyleWu, Xiaoxuan, Jian Chen, Hu Tang, Ke Xu, Mingding Shao, and Yu Long. 2024. "Robust Online Estimation of State of Health for Lithium-Ion Batteries Based on Capacities under Dynamical Operation Conditions" Batteries 10, no. 7: 219. https://doi.org/10.3390/batteries10070219
APA StyleWu, X., Chen, J., Tang, H., Xu, K., Shao, M., & Long, Y. (2024). Robust Online Estimation of State of Health for Lithium-Ion Batteries Based on Capacities under Dynamical Operation Conditions. Batteries, 10(7), 219. https://doi.org/10.3390/batteries10070219








