Comparative Study-Based Data-Driven Models for Lithium-Ion Battery State-of-Charge Estimation
Abstract
1. Introduction
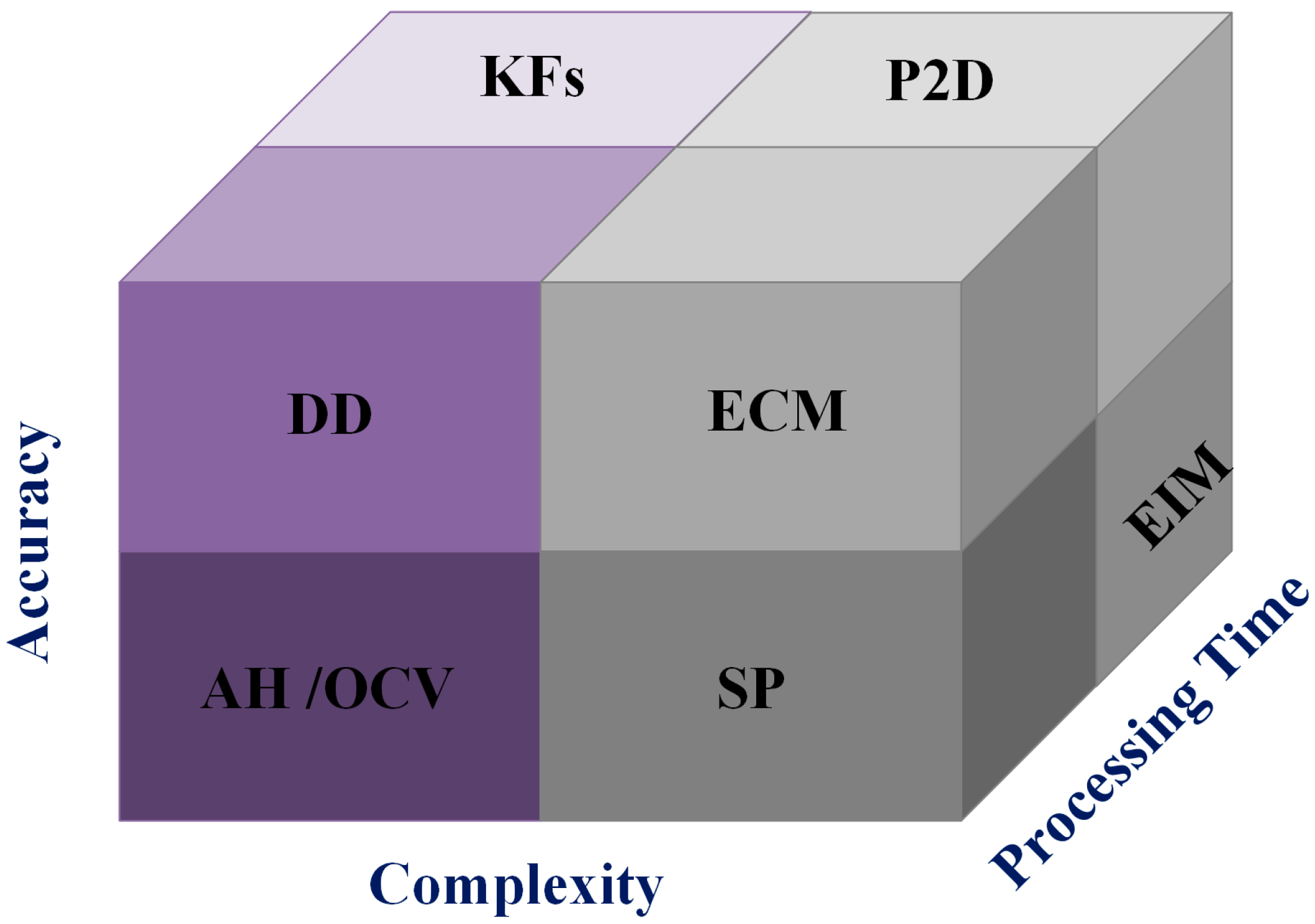
2. State-of-Charge Estimation Approaches
3. Proposed Data-Driven Approaches
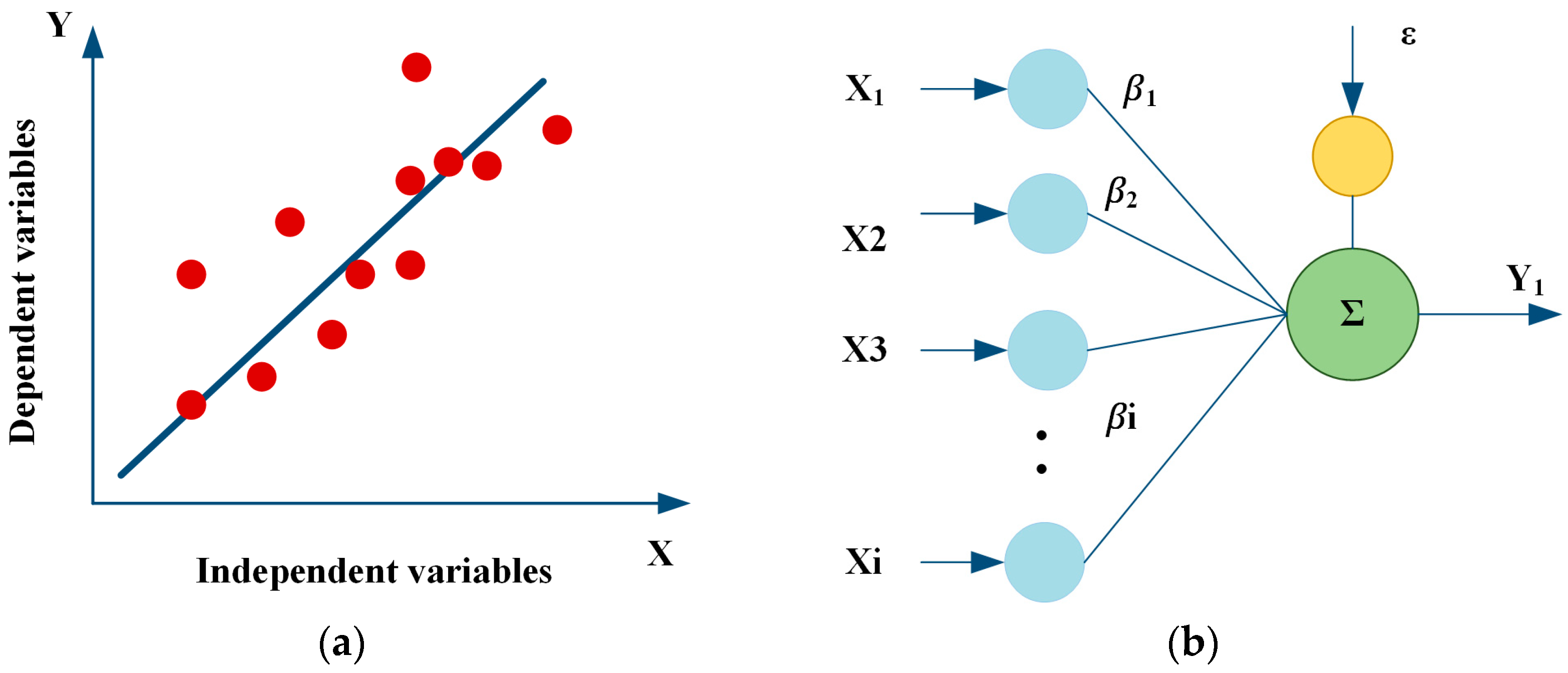
3.1. Linear Regression (LR) Models
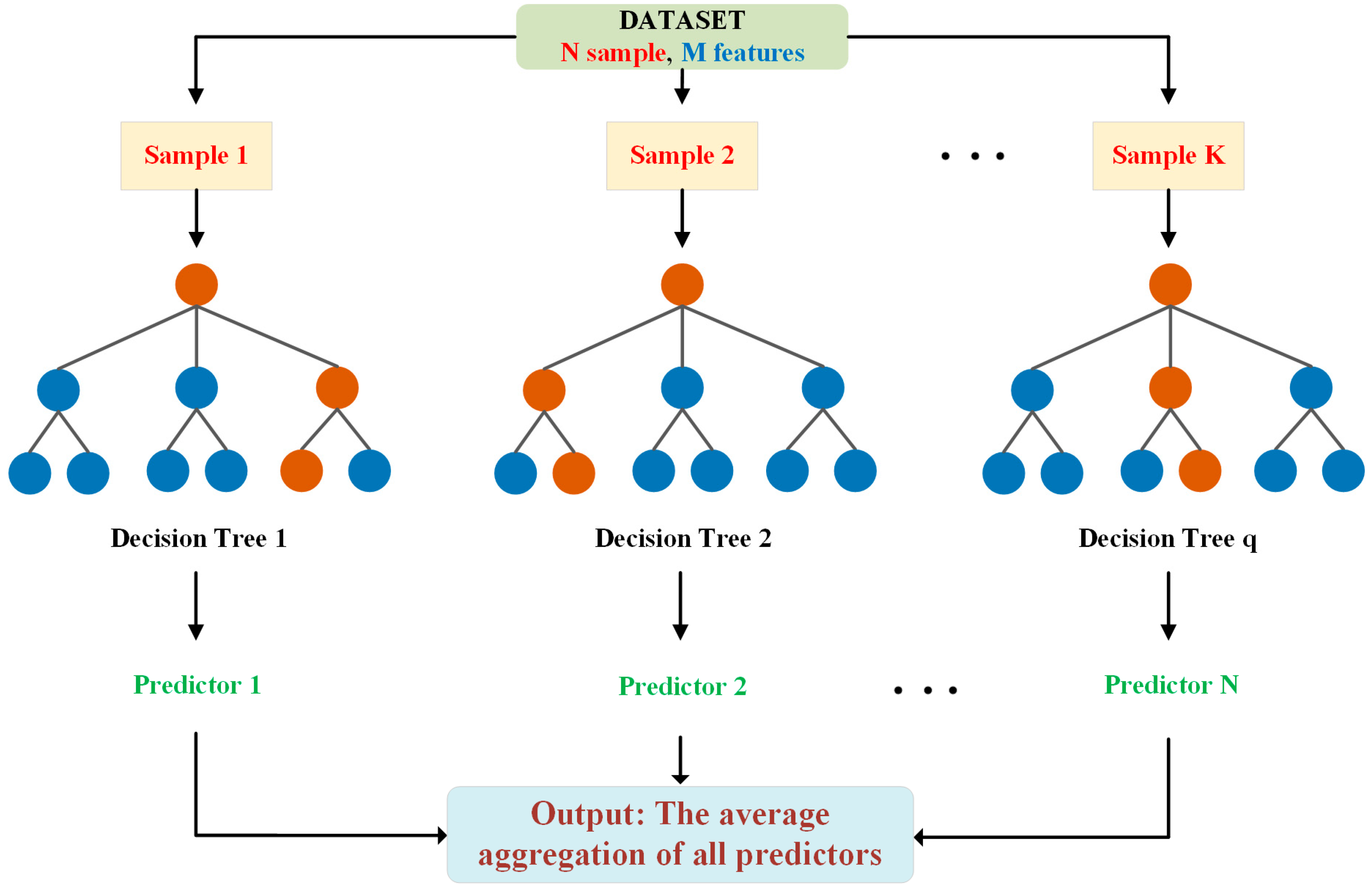
3.2. Random Forest Regression (RFR)
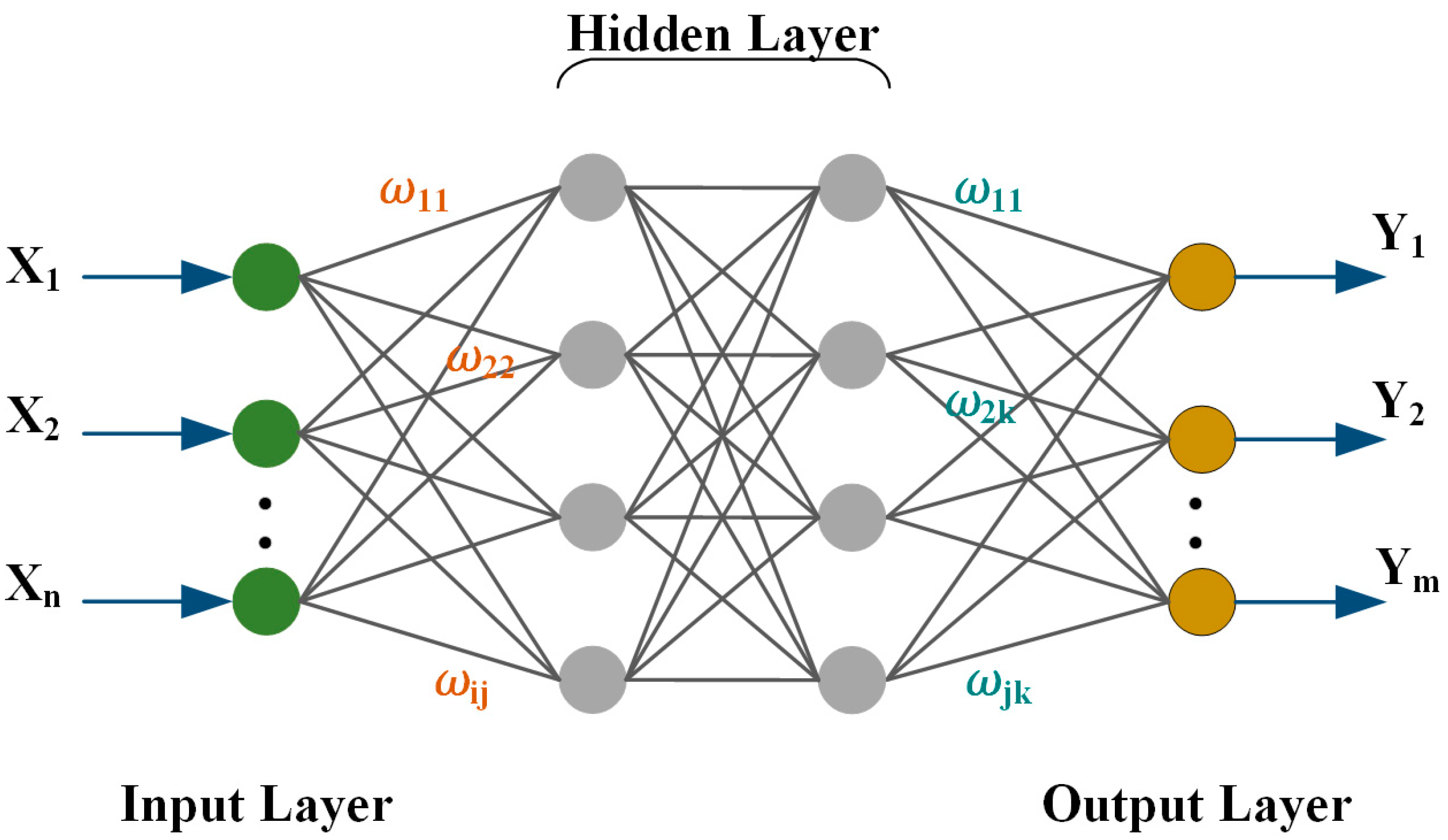
3.3. Neural Networks (NNs)
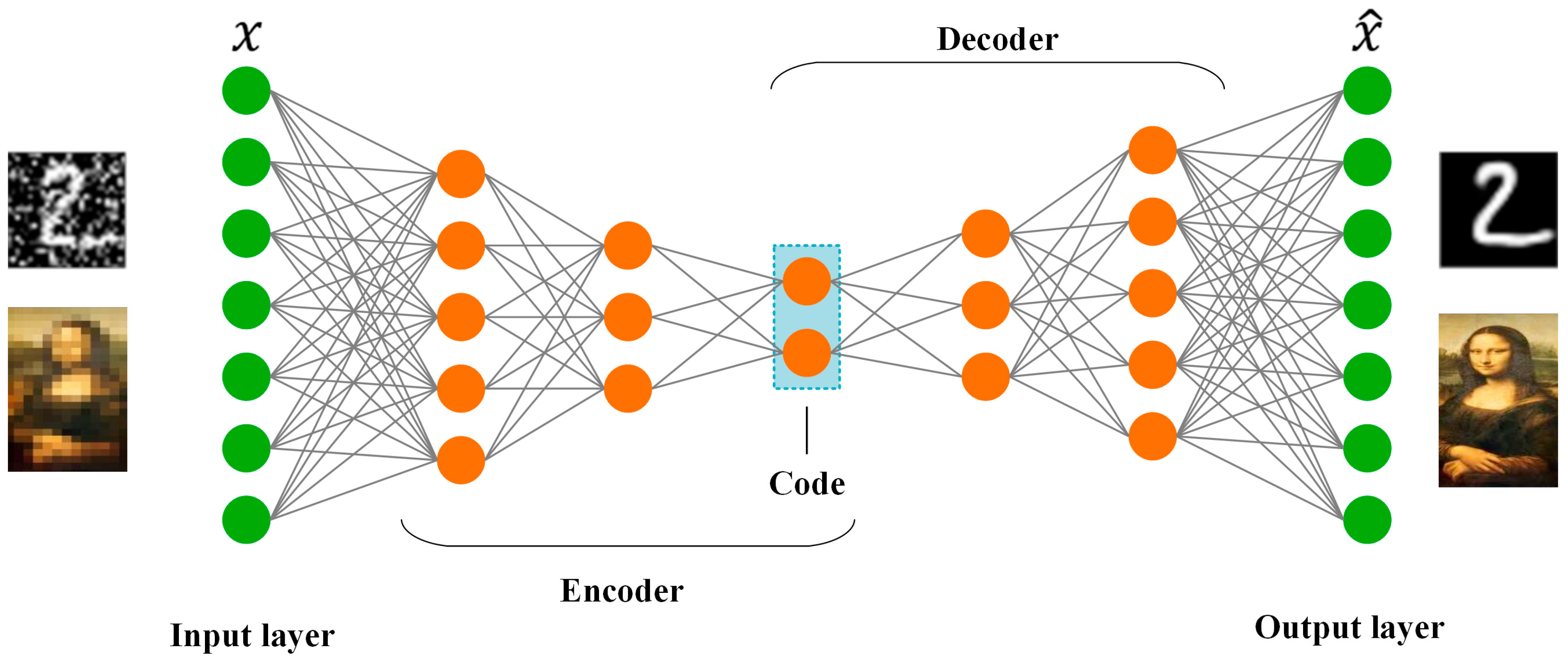
3.4. Autoencoders (AEs)
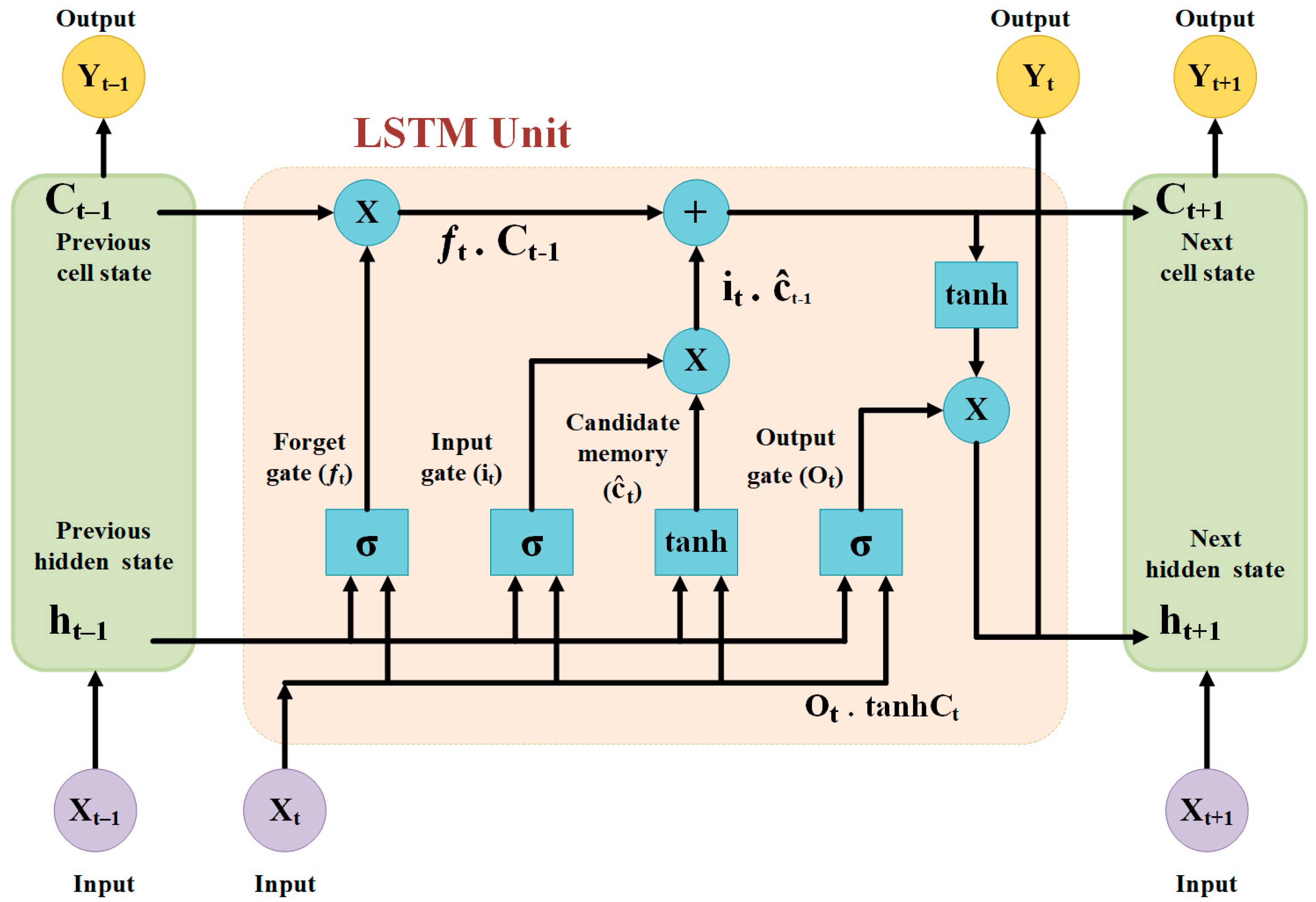
3.5. Long Short-Term Memory (LSTM)
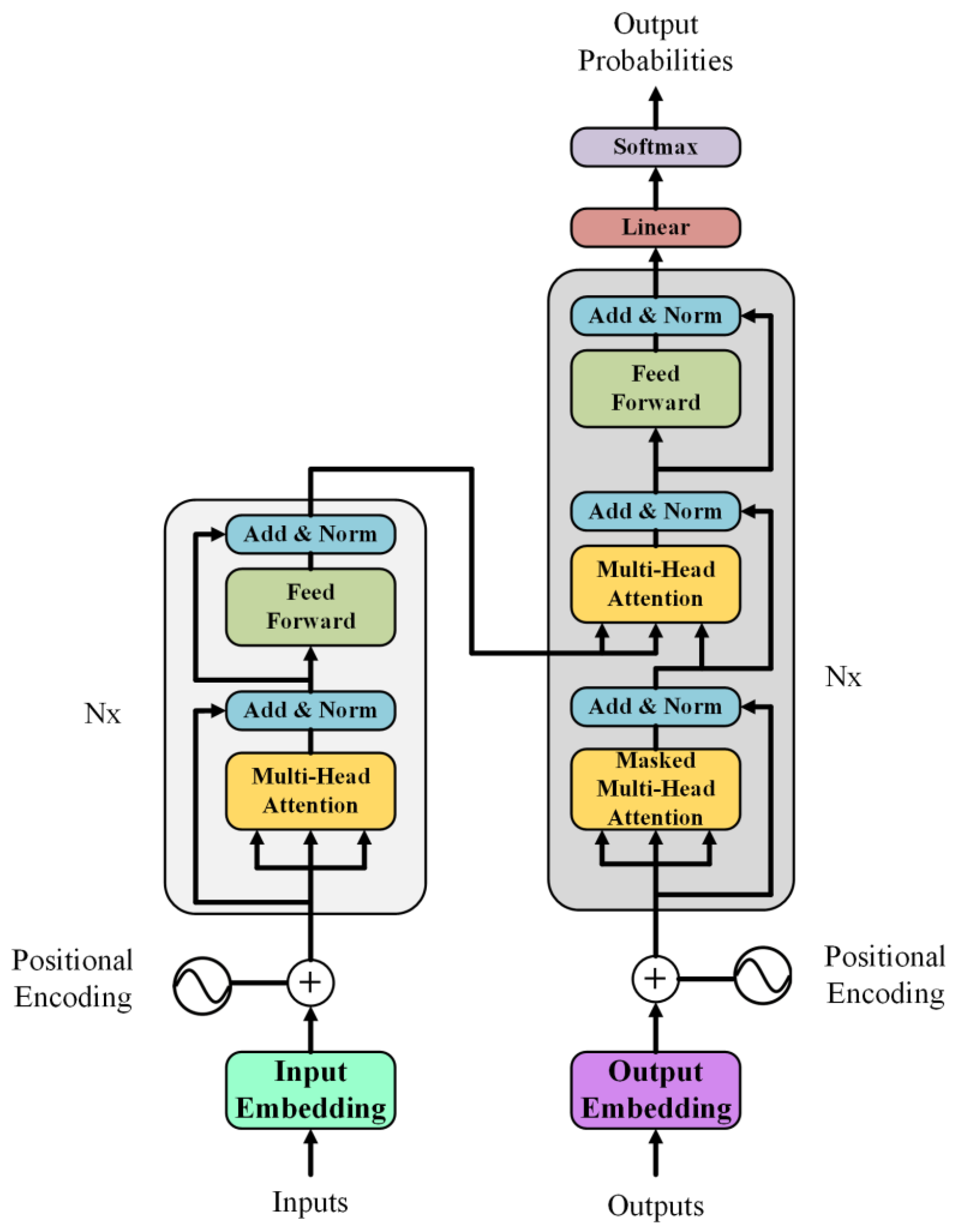
3.6. Transformer (TR)
4. System Configuration
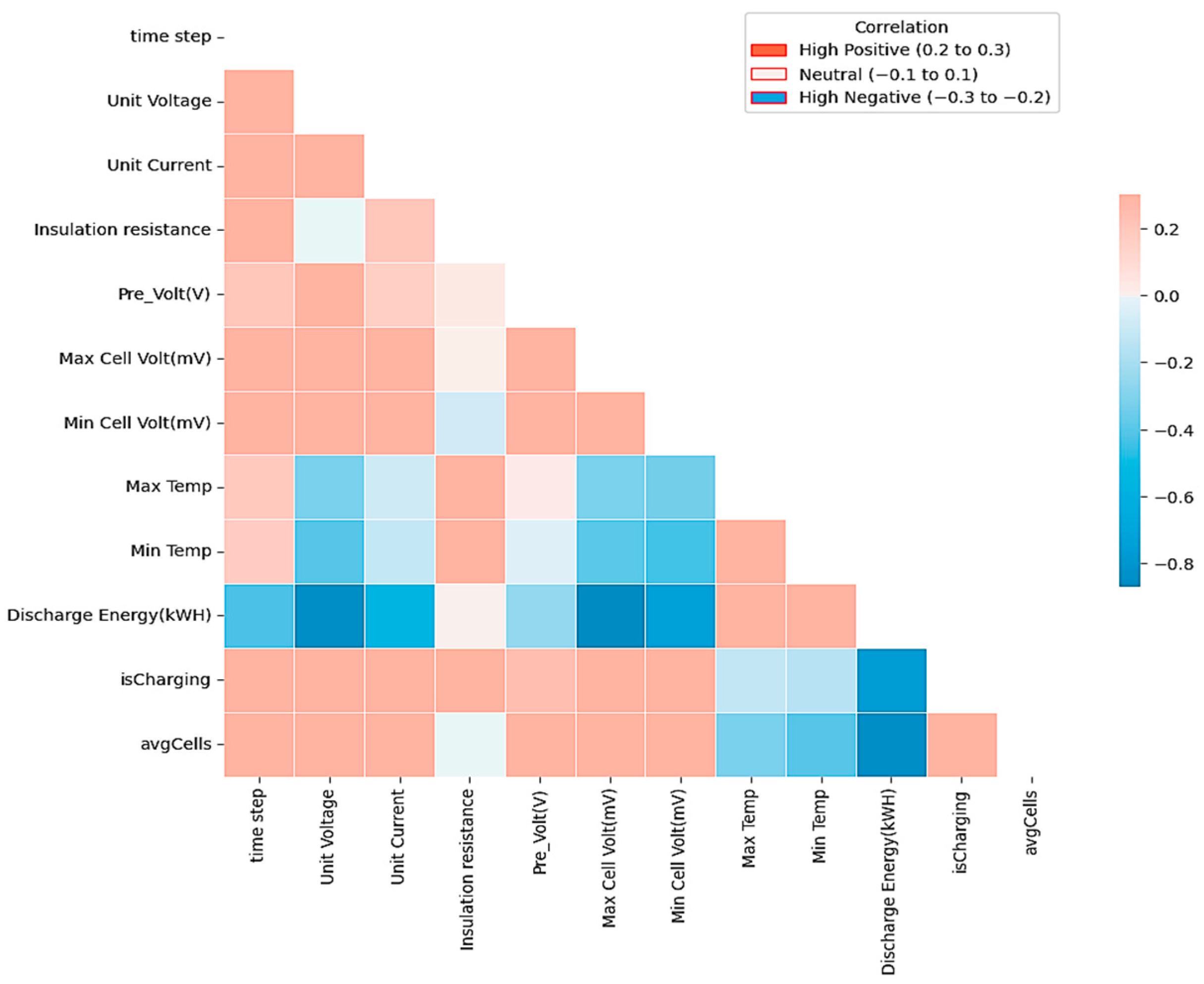
4.1. Data Preprocessing
4.2. Linear Regression Model
4.3. Random Forest Regression Model
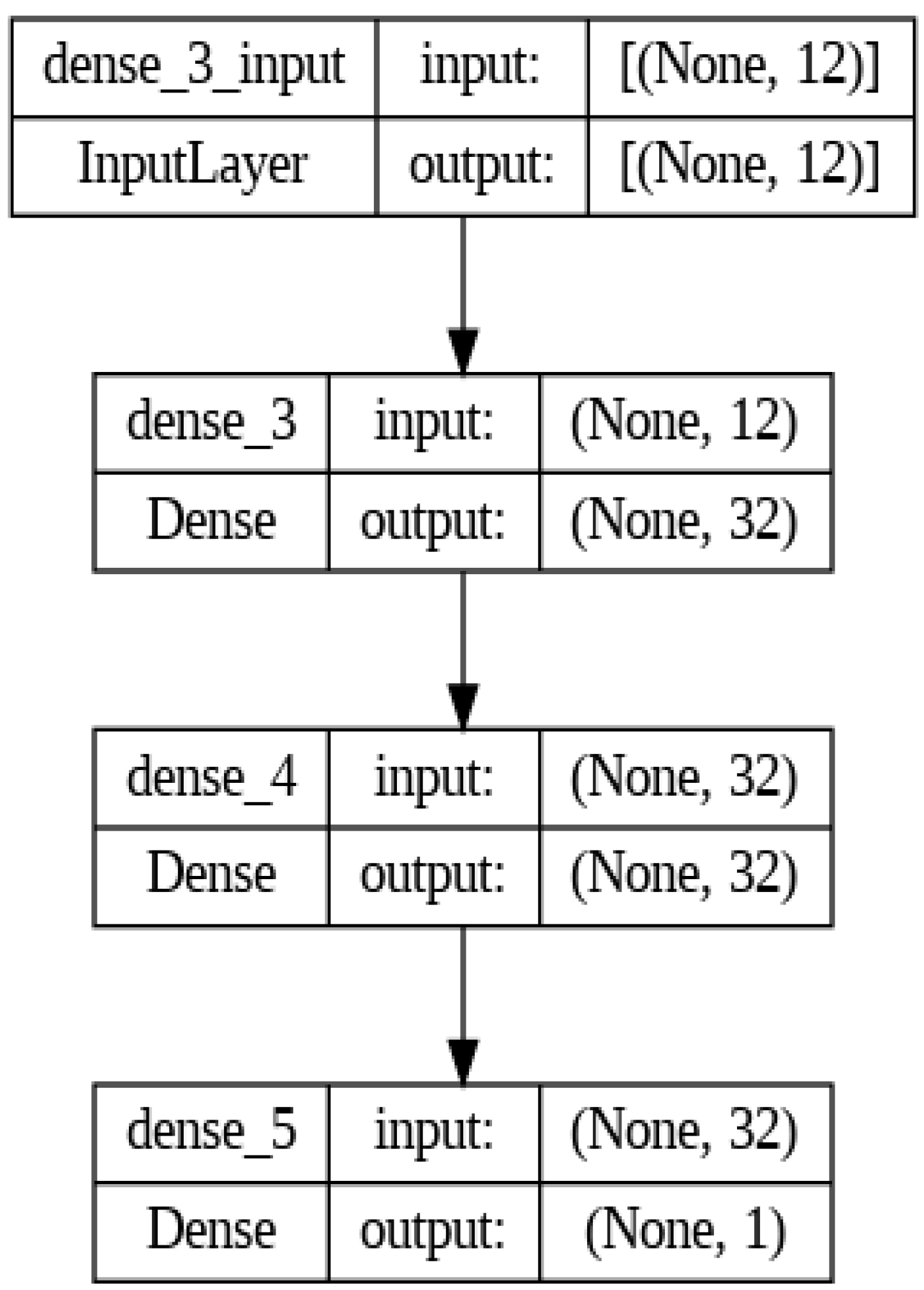
4.4. Neural Network Model
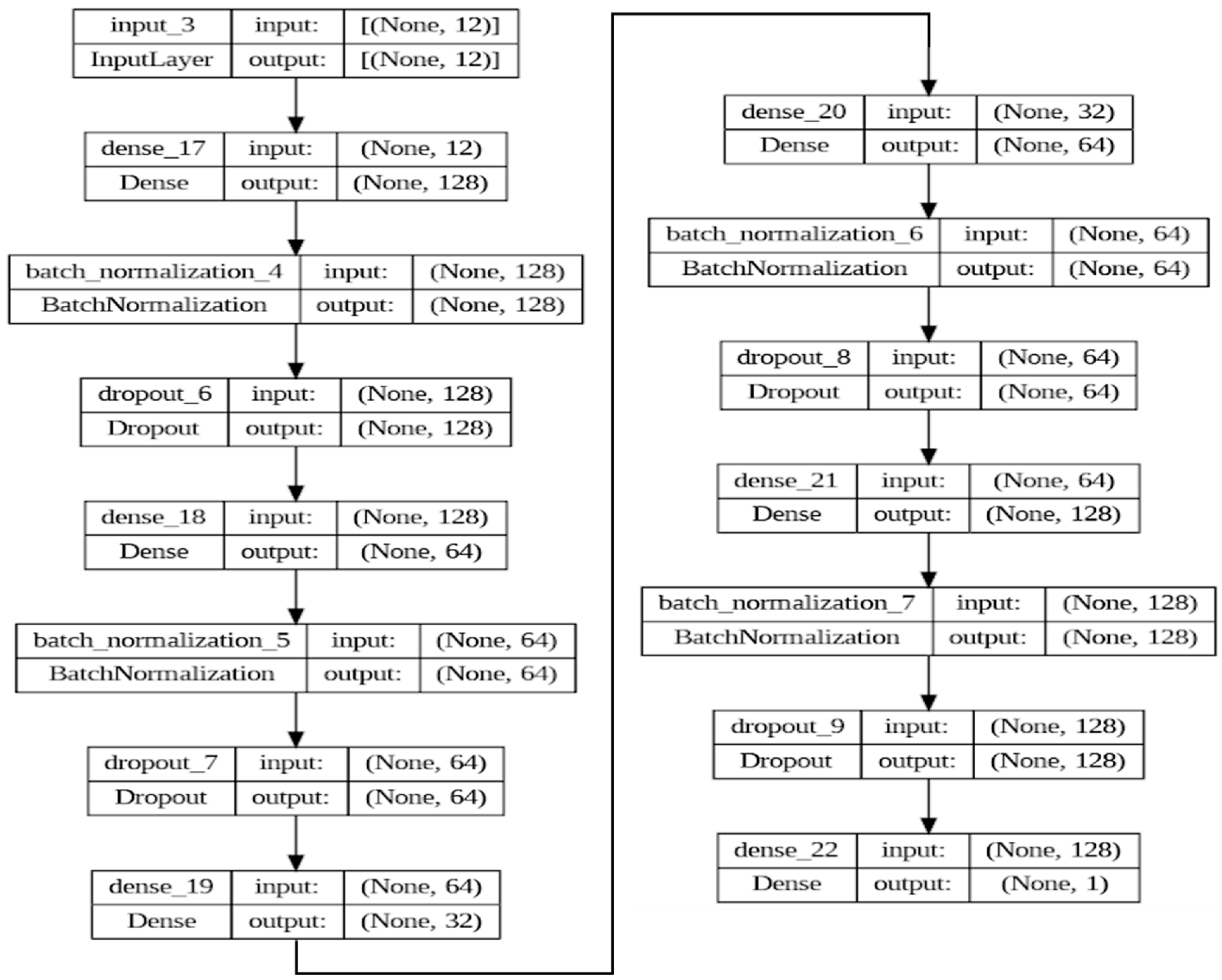
4.5. Autoencoder Model
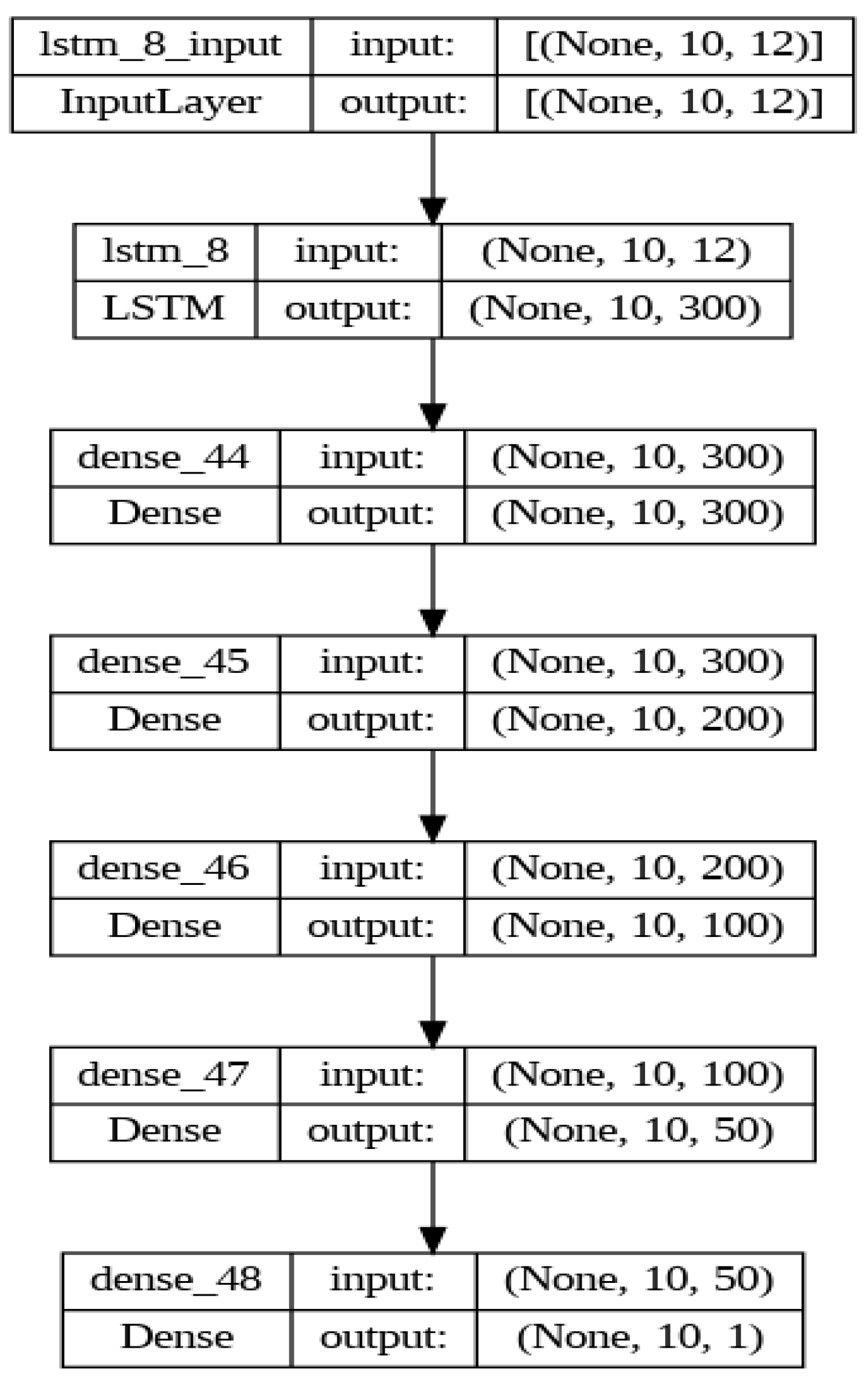
4.6. LSTM Model
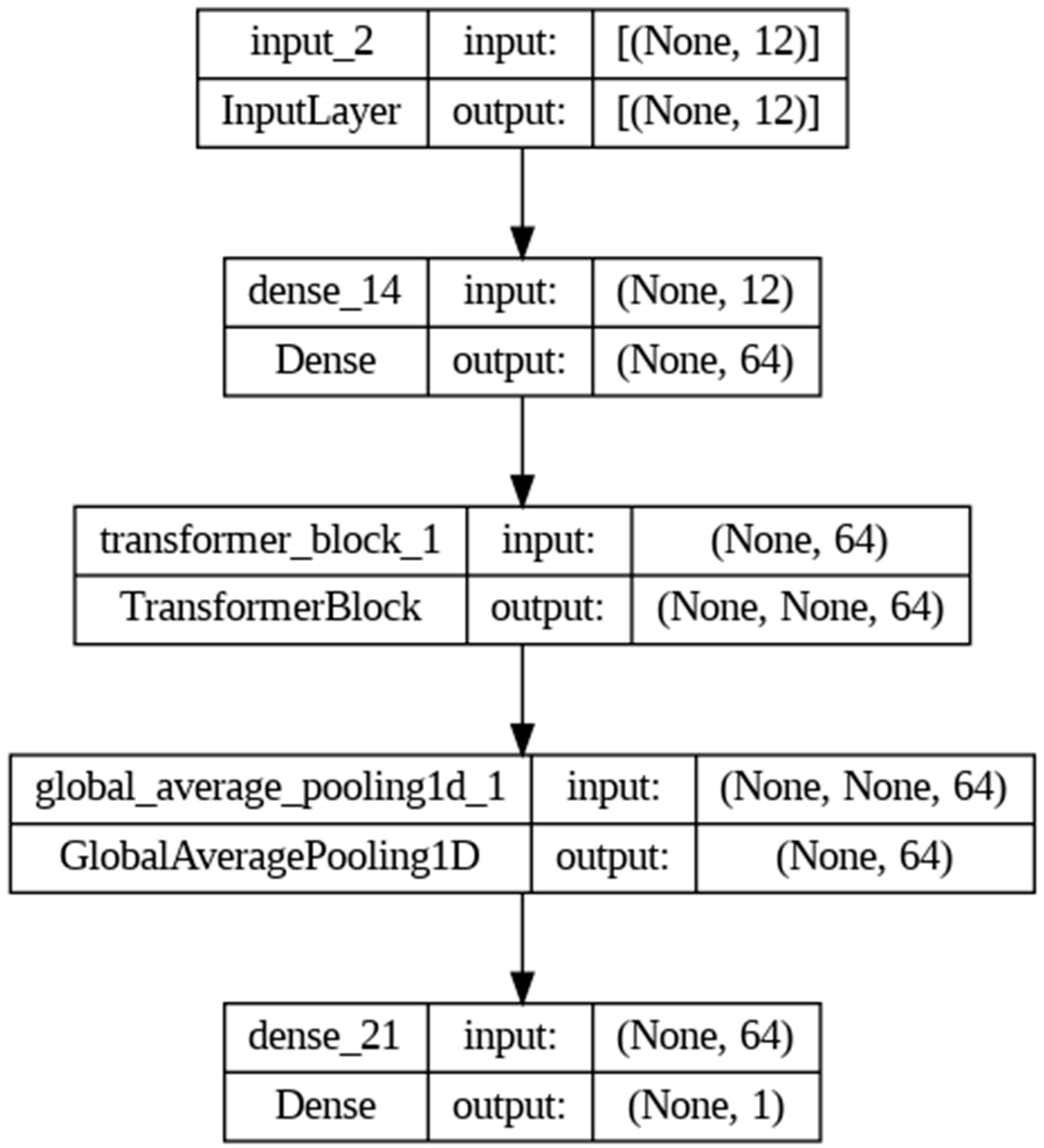
4.7. Transformer Model
- Number of Attention Heads: This dictates how many different parts of the input sequence are attended to simultaneously. Set at 32, this allows the model to simultaneously attend to various segments of the input sequence, providing a rich and diverse representation of the input space.
- Embedding Dimensionality (d_model): This determines the size of the input projection space, impacting the model’s capacity to capture information. With a value of 64, it provides a balance between model complexity and computational efficiency, ensuring sufficient representation capacity without incurring prohibitive computational costs.
- Feedforward Network Dimensionality (dff): This influences the complexity of transformations within the feedforward network.
- Dropout Rate: This controls the dropout regularization technique to prevent overfitting. The dimensionality of 32 allows the network to perform a series of transformations that are complex enough to capture non-linear relationships but not so complex as to overfit the training data.
- Learning Rate: This affects the rate at which the model updates its parameters during training. A dropout rate of 0.1 helps in regularizing the model, encouraging the development of more robust features that are not reliant on any small subset of the neurons.
- Batch Size: This specifies the number of samples that are propagated through the network before the model’s parameters are updated. We use a smaller batch size of 32 because it is less demanding on memory resources and makes it feasible to train a complex model such as a transformer.
- Epochs: This defines the number of complete passes through the entire training dataset. We use 10 epochs as it is less demanding on memory resources and makes it feasible to train a complex model such as a transformer.
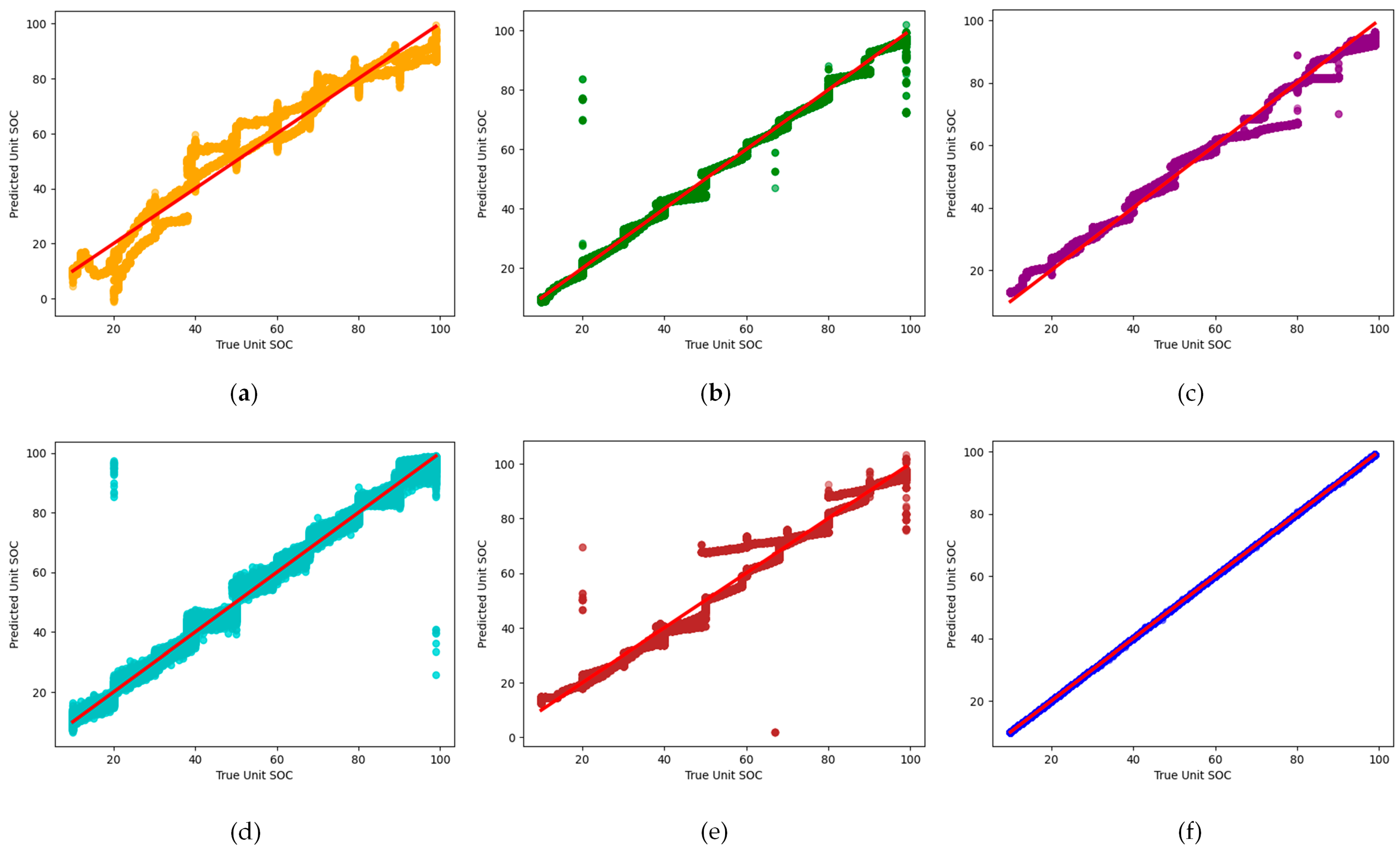
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hussein, H.; Aghmadi, A.; Mohammed, O.A. Design and Analysis of Voltage Control for Islanded DC Microgrids Based on a Fuzzy-PI Controller. In Proceedings of the 2023 IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 19–21 April 2023; pp. 229–233. [Google Scholar]
- Hussein, H.; Aghmadi, A.; Nguyen, T.L.; Mohammed, O. Hardware-in-the-Loop Implementation of a Battery System Charging/Discharging in Islanded DC Micro-Grid. In Proceedings of the SoutheastCon 2022, Mobile, AL, USA, 26 March–3 April 2022; IEEE: Mobile, AL, USA, 2022; pp. 496–500. [Google Scholar]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Hu, X.; Zou, C.; Zhang, C.; Li, Y. Technological developments in batteries: A survey of principal roles, types, and management needs. IEEE Power Energy Mag. 2017, 15, 20–31. [Google Scholar] [CrossRef]
- Ng, M.-F.; Zhao, J.; Yan, Q.; Conduit, G.J.; Seh, Z.W. Predicting the state of charge and health of batteries using data-driven machine learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar] [CrossRef]
- Aghmadi, A.; Hussein, H.; Mohammed, O.A. Enhancing Energy Management System for a Hybrid Wind Solar Battery Based Standalone Microgrid. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 6–9 June 2023; pp. 1–6. [Google Scholar]
- Abdelrahman, M.S.; Hussein, H.; Mohammed, O.A. Rule-Based Power and Energy Management System for Shipboard Microgrid with HESS To Mitigate Propulsion and Pulsed Load Fluctuations. In Proceedings of the 2023 IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 19–21 April 2023; pp. 224–228. [Google Scholar]
- Yang, R.; Xiong, R.; He, H.; Mu, H.; Wang, C. A novel method on estimating the degradation and state of charge of lithium-ion batteries used for electrical vehicles. Appl. Energy 2017, 207, 336–345. [Google Scholar] [CrossRef]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Alvi, M.J.; Kim, H.-J. Towards a smarter battery management system for electric vehicle applications: A critical review of lithium-ion battery state of charge estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W. State of the art of lithium-ion battery SOC estimation for electrical vehicles. Energies 2018, 11, 1820. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.P.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H.O. SoC estimation for lithium-ion batteries: Review and future challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef]
- Wu, B.; Widanage, W.D.; Yang, S.; Liu, X. Battery digital twins: Perspectives on the fusion of models, data and artificial intelligence for smart battery management systems. Energy AI 2020, 1, 100016. [Google Scholar] [CrossRef]
- Hussein, H.; Aghmadi, A.; Abdelrahman, M.S.; Rafin, S.M.S.H.; Mohammed, O. A review of battery state of charge estimation and management systems: Models and future prospective. WIREs Energy Environ. 2024, 13, e507. [Google Scholar] [CrossRef]
- Vidal, C.; Malysz, P.; Kollmeyer, P.; Emadi, A. Machine learning applied to electrified vehicle battery state of charge and state of health estimation: State-of-the-art. IEEE Access 2020, 8, 52796–52814. [Google Scholar] [CrossRef]
- Lipu, M.H.; Hannan, M.A.; Hussain, A.; Ayob, A.; Saad, M.H.; Karim, T.F.; How, D.N. Data-driven state of charge estimation of lithium-ion batteries: Algorithms, implementation factors, limitations and future trends. J. Clean. Prod. 2020, 277, 124110. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Hossain Lipu, M.S.; Ker, P.J. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: A review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Ren, L.; Dong, J.; Wang, X.; Meng, Z.; Zhao, L.; Deen, M.J. A Data-Driven Auto-CNN-LSTM Prediction Model for Lithium-Ion Battery Remaining Useful Life. IEEE Trans. Ind. Inform. 2021, 17, 3478–3487. [Google Scholar] [CrossRef]
- Vidal, C.; Kollmeyer, P.; Naguib, M.; Malysz, P.; Gross, O.; Emadi, A. Robust xev battery state-of-charge estimator design using a feedforward deep neural network. SAE Int. J. Adv. Curr. Pract. Mobil. 2020, 2, 2872–2880. [Google Scholar] [CrossRef]
- Jiao, M.; Wang, D.; Qiu, J. A GRU-RNN based momentum optimized algorithm for SOC estimation. J. Power Sources 2020, 459, 228051. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, E.; Jiang, K.; Wang, K. Dual fuzzy-based adaptive extended Kalman filter for state of charge estimation of liquid metal battery. Appl. Energy 2022, 327, 120091. [Google Scholar] [CrossRef]
- Tan, X.; Zhan, D.; Lyu, P.; Rao, J.; Fan, Y. Online state-of-health estimation of lithium-ion battery based on dynamic parameter identification at multi timescale and support vector regression. J. Power Sources 2021, 484, 229233. [Google Scholar] [CrossRef]
- Liu, K.; Hu, X.; Zhou, H.; Tong, L.; Widanalage, D.; Marco, J. Feature analyses and modeling of lithium-ion battery manufacturing based on random forest classification. IEEE/ASME Trans. Mechatron. 2021, 26, 2944–2955. [Google Scholar] [CrossRef]
- Shen, H.; Zhou, X.; Wang, Z.; Wang, J. State of charge estimation for lithium-ion battery using Transformer with immersion and invariance adaptive observer. J. Energy Storage 2022, 45, 103768. [Google Scholar] [CrossRef]
- Bosello, M.; Falcomer, C.; Rossi, C.; Pau, G. To Charge or to Sell? EV Pack Useful Life Estimation via LSTMs, CNNs, and Autoencoders. Energies 2023, 16, 2837. [Google Scholar] [CrossRef]
- Audin, P.; Jorge, I.; Mesbahi, T.; Samet, A.; Beuvron, F.D.B.D.; Bone, R. Auto-encoder LSTM for Li-ion SOH prediction: A comparative study on various benchmark datasets. In Proceedings of the 20th IEEE International Conference on Machine Learning and Applications (ICMLA), Pasadena, CA, USA, 13–16 December 2021; pp. 1529–1536. [Google Scholar]
- Hossain Lipu, M.S.; Karim, T.F.; Ansari, S.; Miah, M.S.; Rahman, M.S.; Meraj, S.T.; Vijayaraghavan, R.R. Intelligent SOX estimation for automotive battery management systems: State-of-the-art deep learning approaches, open issues, and future research opportunities. Energies 2022, 16, 23. [Google Scholar] [CrossRef]
- Yang, K.; Tang, Y.; Zhang, S.; Zhang, Z. A deep learning approach to state of charge estimation of lithium-ion batteries based on dual-stage attention mechanism. Energy 2022, 244, 123233. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical review on the battery state of charge estimation methods for electric vehicles. IEEE Access 2017, 6, 1832–1843. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Amir, U.; Tao, L.; Zhang, X.; Saeed, M.; Hussain, M. A novel SOC estimation method for lithium ion battery based on improved adaptive PI observer. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference, Nottingham, UK, 7–9 November 2018; pp. 1–5. [Google Scholar]
- Ghaeminezhad, N.; Ouyang, Q.; Wei, J.; Xue, Y.; Wang, Z. Review on state of charge estimation techniques of lithium-ion batteries: A control-oriented approach. J. Energy Storage 2023, 72, 108707. [Google Scholar] [CrossRef]
- Barai, A.; Chouchelamane, G.H.; Guo, Y.; McGordon, A.; Jennings, P. A study on the impact of lithium-ion cell relaxation on electrochemical impedance spectroscopy. J. Power Sources 2015, 280, 74–80. [Google Scholar] [CrossRef]
- Wu, L.; Lyu, Z.; Huang, Z.; Zhang, C.; Wei, C. Physics-based battery SOC estimation methods: Recent advances and future perspectives. J. Energy Chem. 2023, 89, 27–40. [Google Scholar] [CrossRef]
- Waag, W.; Kabitz, S.; Sauer, D.U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Appl. Energy 2013, 102, 885–897. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, J.; Lund, P.D.; Zhang, Y. Co-estimating the state of charge and health of lithium batteries through combining a minimalist electrochemical model and an equivalent circuit model. Energy 2022, 240, 122815. [Google Scholar] [CrossRef]
- Yang, C.; Wang, X.; Fang, Q.; Dai, H.; Cao, Y.; Wei, X. An online SOC and capacity estimation method for aged lithium-ion battery pack considering cell inconsistency. J. Energy Storage 2020, 29, 101250. [Google Scholar] [CrossRef]
- Luzi, M.; Mascioli, F.M.F.; Paschero, M.; Rizzi, A. A white-box equivalent neural network circuit model for SoC estimation of electrochemical cells. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 371–382. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Luo, J.; He, H.; Lu, B. An improved state of charge estimation method based on cubature Kalman filter for lithium-ion batteries. Appl. Energy 2019, 253, 113520. [Google Scholar] [CrossRef]
- Fleischer, C.; Waag, W.; Heyn, H.M.; Sauer, D.U. On-line adaptive battery impedance parameter and state estimation considering physical principles in reduced order equivalent circuit battery models part 2. Parameter and state estimation. J. Power Sources 2014, 262, 457–482. [Google Scholar] [CrossRef]
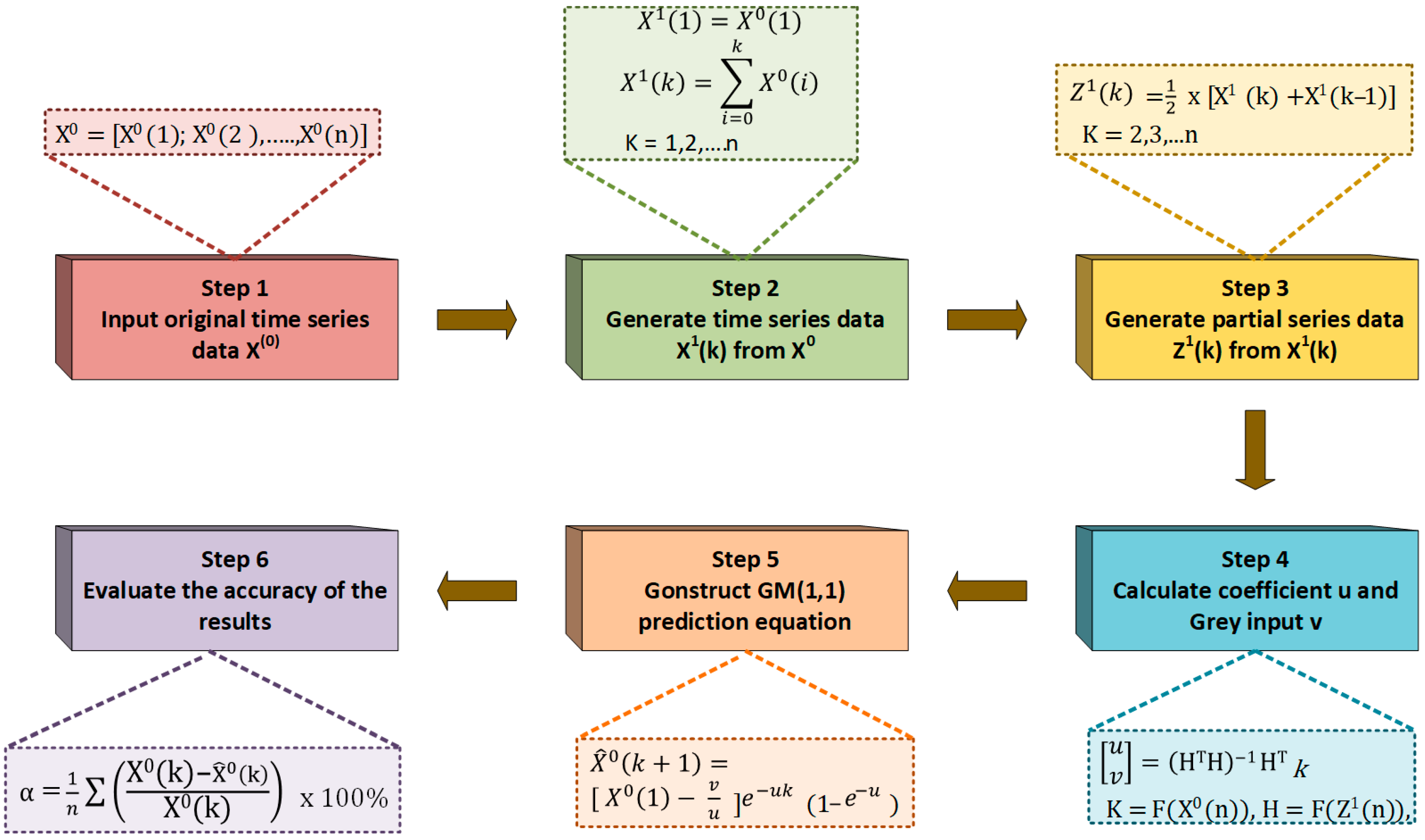
- Chen, L.; Tian, B.; Lin, W.; Ji, B.; Li, J.; Pan, H. Analysis and prediction of the discharge characteristics of the lithium–ion battery based on the Grey system theory. IET Power Electron. 2015, 8, 2361–2369. [Google Scholar] [CrossRef]
- Sun, Q.; Wang, S.; Gao, S.; Lv, H.; Liu, J.; Wang, L.; Du, J.; Wei, K. A State of Charge Estimation Approach for Lithium-Ion Batteries Based on the Optimized Metabolic EGM (1, 1) Algorithm. Batteries 2022, 8, 260. [Google Scholar] [CrossRef]
- Wang, C.-N.; Dang, T.-T.; Nguyen, N.-A.; Le, T.-T. Supporting better decision-making: A combined grey model and data envelopment analysis for efficiency evaluation in e-commerce marketplaces. Sustainability 2020, 12, 10385. [Google Scholar] [CrossRef]
- Kumar, A.S.; Aher, P.K.; Patil, S.L. SOC Estimation using Coulomb Counting and Fuzzy Logic in Lithium Battery. In Proceedings of the 2022 International Conference on Industry 4.0 Technology (I4Tech), Pune, India, 23–24 September 2022; pp. 1–5. [Google Scholar]
- Manoharan, A.; Sooriamoorthy, D.; Begam, K.; Aparow, V.R. Electric vehicle battery pack state of charge estimation using parallel artificial neural networks. J. Energy Storage 2023, 72, 108333. [Google Scholar] [CrossRef]
- Liu, B.; Wang, H.; Tseng, M.-L.; Li, Z. State of charge estimation for lithium-ion batteries based on improved barnacle mating optimizer and support vector machine. J. Energy Storage 2022, 55, 105830. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Lü, Z.; Li, J.; Ji, B.; Wei, H.; Pan, H. A novel state-of-charge estimation method of lithium-ion batteries combining the grey model and genetic algorithms. IEEE Trans. Power Electron. 2017, 33, 8797–8807. [Google Scholar] [CrossRef]
- Lucaferri, V.; Quercio, M.; Laudani, A.; Riganti Fulginei, F. A Review on Battery Model-Based and Data-Driven Methods for Battery Management Systems. Energies 2023, 16, 7807. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y.; Huang, Y.; Bhushan Gopaluni, R.; Cao, Y.; Heere, M.; Mühlbauer, M.J.; Ehrenberg, H. Data-driven capacity estimation of commercial lithium-ion batteries from voltage relaxation. Nat. Commun. 2022, 13, 2261. [Google Scholar] [CrossRef]
- Sesidhar, D.V.S.R.; Badachi, C.; Green, R.C., II. A review on data-driven SOC estimation with Li-Ion batteries: Implementation methods & future aspirations. J. Energy Storage 2023, 72, 108420. [Google Scholar]
- Chen, J.; Zhang, Y.; Wu, J.; Cheng, W.; Zhu, Q. SOC estimation for lithium-ion battery using the LSTM-RNN with extended input and constrained output. Energy 2023, 262, 125375. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, Z.; Liu, K.; Zhang, Y.; Feng, W. A compact and optimized neural network approach for battery state-of-charge estimation of energy storage system. Energy 2021, 219, 119529. [Google Scholar] [CrossRef]
- Chandran, V.; Patil, C.K.; Karthick, A.; Ganeshaperumal, D.; Rahim, R.; Ghosh, A. State of Charge Estimation of Lithium-Ion Battery for Electric Vehicles Using Machine Learning Algorithms. World Electr. Veh. J. 2021, 12, 38. [Google Scholar] [CrossRef]
- Sahinoglu, G.O.; Pajovic, M.; Sahinoglu, Z.; Wang, Y.; Orlik, P.V.; Wada, T. Battery state-of-charge estimation based on regular/recurrent Gaussian process regression. IEEE Trans. Ind. Electron. 2017, 65, 4311–4321. [Google Scholar] [CrossRef]
- Hasan, A.S.M.J.; Yusuf, J.; Faruque, R.B. Performance comparison of machine learning methods with distinct features to estimate battery SOC. In Proceedings of the 2019 IEEE Green Energy and Smart Systems Conference (IGESSC), Long Beach, CA, USA, 4–5 November 2019; pp. 1–5. [Google Scholar]
- Babaeiyazdi, I.; Rezaei-Zare, A.; Shokrzadeh, S. State of charge prediction of EV Li-ion batteries using EIS: A machine learning approach. Energy 2021, 223, 120116. [Google Scholar] [CrossRef]
- Çelik, M.; Tanağardıgil, İ.; Soydemir, M.U.; Şahin, S. Battery Charge and Health Evaluation for Defective UPS Batteries via Machine Learning Methods. In The International Conference on Artificial Intelligence and Applied Mathematics in Engineering; Springer International Publishing: Cham, Switzerland, 2022; pp. 298–308. [Google Scholar]
- Hong, J.; Wang, Z.; Chen, W.; Wang, L.-Y.; Qu, C. Online joint-prediction of multi-forward-step battery SOC using LSTM neural networks and multiple linear regression for real-world electric vehicles. J. Energy Storage 2020, 30, 101459. [Google Scholar] [CrossRef]
- Vilsen, S.B.; Stroe, D.-I. Battery state-of-health modelling by multiple linear regression. J. Clean. Prod. 2021, 290, 125700. [Google Scholar] [CrossRef]
- Wu, T.; Wu, Q.; Zhuang, Q.; Li, Y.; Yao, Y.; Zhang, L.; Xing, S. Optimal Sample Size for SOC Content Prediction for Mapping Using the Random Forest in Cropland in Northern Jiangsu, China. Eurasian Soil Sci. 2022, 55, 1689–1699. [Google Scholar] [CrossRef]
- Yang, N.; Song, Z.; Hofmann, H.; Sun, J. Robust State of Health estimation of lithium-ion batteries using convolutional neural network and random forest. J. Energy Storage 2022, 48, 103857. [Google Scholar] [CrossRef]
- Castanho, D.; Guerreiro, M.; Silva, L.; Eckert, J.; Alves, T.A.; Tadano, Y.d.S.; Stevan, S.L., Jr.; Siqueira, H.V.; Corrêa, F.C. Method for SoC estimation in lithium-ion batteries based on multiple linear regression and particle swarm optimization. Energies 2022, 15, 6881. [Google Scholar] [CrossRef]
- Manriquez-Padilla, C.G.; Cueva-Perez, I.; Dominguez-Gonzalez, A.; Elvira-Ortiz, D.A.; Perez-Cruz, A.; Saucedo-Dorantes, J.J. State of Charge Estimation Model Based on Genetic Algorithms and Multivariate Linear Regression with Applications in Electric Vehicles. Sensors 2023, 23, 2924. [Google Scholar] [CrossRef] [PubMed]
- Manoharan, A.; Begam, K.M.; Aparow, V.R.; Sooriamoorthy, D. Artificial Neural Networks, Gradient Boosting and Support Vector Machines for electric vehicle battery state estimation: A review. J. Energy Storage 2022, 55, 105384. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, K.; Yu, X.; Wang, Y. State-of-health estimation for lithium-ion batteries based on historical dependency of charging data and ensemble SVR. Electrochim. Acta 2022, 428, 140940. [Google Scholar] [CrossRef]
- Zhi, Y.; Wang, H.; Wang, L. A state of health estimation method for electric vehicle Li-ion batteries using GA-PSO-SVR. Complex Intell. Syst. 2022, 8, 2167–2182. [Google Scholar] [CrossRef]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.-W.; van den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Li, C.; Chen, Z.; Cui, J.; Wang, Y.; Zou, F. The lithium-ion battery state-of-charge estimation using random forest regression. In Proceedings of the 2014 Prognostics and System Health Management Conference (PHM-2014 Hunan), Zhangjiajie, China, 24–27 August 2014; pp. 336–339. [Google Scholar]
- Lipu, M.S.H.; Hannan, M.A.; Hussaion, A.; Ansari, S.S.; Rahman, S.A.; Saad, M.H.; Muttaqi, K. Real-time state of charge estimation of lithium-ion batteries using optimized random forest regression algorithm. IEEE Trans. Intell. Veh. 2022, 8, 639–648. [Google Scholar] [CrossRef]
- Lamprecht, A.; Riesterer, M.; Steinhorst, S. Random forest regression of charge balancing data: A state of health estimation method for electric vehicle batteries. In Proceedings of the 2020 International Conference on Omni-layer Intelligent Systems (coins), Barcelona, Spain, 31 August–2 September 2020; pp. 1–6. [Google Scholar]
- Sidhu, M.S.; Ronanki, D.; Williamson, S. State of charge estimation of lithium-ion batteries using hybrid machine learning technique. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 2732–2737. [Google Scholar]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Ansari, S.; Ayob, A.; Saad, M.H.; Muttaqi, K.M. Differential search optimized random forest regression algorithm for state of charge estimation in electric vehicle batteries. In Proceedings of the 2021 IEEE Industry Applications Society Annual Meeting (IAS), Vancouver, BC, Canada, 10–14 October 2021; pp. 1–8. [Google Scholar]
- Chen, Z.; Sun, M.; Shu, X.; Shen, J.; Xiao, R. On-board state of health estimation for lithium-ion batteries based on random forest. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 1754–1759. [Google Scholar]
- Khawaja, Y.; Shankar, N.; Qiqieh, I.; Alzubi, J.; Alzubi, O.; Nallakaruppan, M.; Padmanaban, S. Battery management solutions for li-ion batteries based on artificial intelligence. Ain Shams Eng. J. 2023, 14, 102213. [Google Scholar] [CrossRef]
- Lipu, M.H.; Ayob, A.; Saad, M.H.M.; Hussain, A.; Hannan, M.A.; Faisal, M. State of charge estimation for lithium-ion battery based on random forests technique with gravitational search algorithm. In Proceedings of the 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Sabah, Malaysia, 7–10 October 2018; pp. 45–50. [Google Scholar]
- Hussein, H.; Donekal, A.; Aghmadi, A.; Rafin, S.M.S.H.; Mohammed, O.A. State of Charge Estimation Using Data-Driven Models for Inverter-Based Systems. In Proceedings of the 2023 IEEE Design Methodologies Conference (DMC), Miami, FL, USA, 24–26 September 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Mawonou, K.S.; Eddahech, A.; Dumur, D.; Beauvois, D.; Godoy, E. State-of-health estimators coupled to a random forest approach for lithium-ion battery aging factor ranking. J. Power Sources 2021, 484, 229154. [Google Scholar] [CrossRef]
- Deb, S.; Goswami, A.K.; Chetri, R.L.; Roy, R. Prediction of plug-in electric vehicle’s state-of-charge using gradient boosting method and random forest method. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and energy Systems (PEDES), Jaipur, India, 16–19 December 2020; pp. 1–6. [Google Scholar]
- MayilvahaMayilvahanan, K.S.; Takeuchi, K.J.; Takeuchi, E.S.; Marschilok, A.C.; West, A.C. Supervised learning of synthetic big data for Li-ion battery degradation diagnosis. Batter. Supercaps 2022, 5, e202100166. [Google Scholar] [CrossRef]
- Lin, C.; Xu, J.; Shi, M.; Mei, X. Constant current charging time based fast state-of-health estimation for lithium-ion batteries. Energy 2022, 247, 123556. [Google Scholar] [CrossRef]
- Tran, M.K.; Panchal, S.; Chauhan, V.; Brahmbhatt, N.; Mevawalla, A.; Fraser, R.; Fowler, M. Python-based scikit-learn machine learning models for thermal and electrical performance prediction of high-capacity lithium-ion battery. Int. J. Energy Res. 2022, 46, 786–794. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, L.; Li, Q.; Wang, K. A comprehensive review on the state of charge estimation for lithium-ion battery based on neural network. Int. J. Energy Res. 2022, 46, 5423–5440. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Lipu, M.S.H.; Sahari, K.S.M.; Ker, P.J.; Muttaqi, K.M. State-of-charge estimation of li-ion battery in electric vehicles: A deep neural network approach. IEEE Trans. Ind. Appl. 2020, 56, 5565–5574. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Ayob, A.; Saad, M.H.M.; Muttaqi, K.M. State of charge estimation in lithium-ion batteries: A neural network optimization approach. Electronics 2020, 9, 1546. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Yang, R.; Shen, W.; Sun, F. State-of-charge estimation of lithium-ion battery using an improved neural network model and extended Kalman filter. J. Clean. Prod. 2019, 234, 1153–1164. [Google Scholar] [CrossRef]
- Sun, W.; Qiu, Y.; Sun, L.; Hua, Q. Neural network-based learning and estimation of battery state-of-charge: A comparison study between direct and indirect methodology. Int. J. Energy Res. 2020, 44, 10307–10319. [Google Scholar] [CrossRef]
- Baldi, P. Autoencoders, unsupervised learning, and deep architectures. In Proceedings of the ICML Workshop on Unsupervised and Transfer Learning, Irvine, CA, USA, 27 June 2012; JMLR Workshop and Conference Proceedings. pp. 37–49. [Google Scholar]
- Zhai, J.; Zhang, S.; Chen, J.; He, Q. Autoencoder and its various variants. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 415–419. [Google Scholar]
- Dor, B.; Koenigstein, N.; Giryes, R. Autoencoders. In Machine Learning for Data Science Handbook: Data Mining and Knowledge Discovery Handbook; Springer Nature: Berlin/Heidelberg, Germany, 2023; pp. 353–374. [Google Scholar]
- Cheng, Z.; Wang, S.; Zhang, P.; Wang, S.; Liu, X.; Zhu, E. Improved autoencoder for unsupervised anomaly detection. Int. J. Intell. Syst. 2021, 36, 7103–7125. [Google Scholar] [CrossRef]
- Jeng, S.-L.; Chieng, W.-H. Evaluation of Cell Inconsistency in Lithium-Ion Battery Pack Using the Autoencoder Network Model. IEEE Trans. Ind. Inform. 2022, 19, 6337–6348. [Google Scholar] [CrossRef]
- Ahmed, I.; Galoppo, T.; Hu, X.; Ding, Y. Graph Regularized Autoencoder and its Application in Unsupervised Anomaly Detection. Trans. Pattern Anal. Mach. Intell. 2022, 44, 4110–4124. [Google Scholar] [CrossRef] [PubMed]
- Rhodes, T.; Lee, D. Local Disentanglement in Variational Auto-Encoders Using Jacobian L1 Regularization. Adv. Neural Inf. Process. Syst. 2021, 34, 22708–22719. [Google Scholar]
- Savargaonkar, M.; Oyewole, I.; Chehade, A.; Hussein, A.A. Uncorrelated Sparse Autoencoder With Long Short-Term Memory for State-of-Charge Estimations in Lithium-Ion Battery Cells. IEEE Trans. Autom. Sci. Eng. 2022, 21, 15–26. [Google Scholar] [CrossRef]
- Pinaya; Lopez, W.H.; Vieira, S.; Garcia-Dias, R.; Mechelli, A. Autoencoders. In Machine Learning; Academic Press: Cambridge, MA, USA, 2020; pp. 193–208. [Google Scholar]
- Sun, Y.; Zhang, J.; Zhang, K.; Qi, H.; Zhang, C. Battery state of health estimation method based on sparse auto-encoder and backward propagation fading diversity among battery cells. Int. J. Energy Res. 2021, 45, 7651–7662. [Google Scholar] [CrossRef]
- Zhang, H.; Bai, Y.; Yang, S.; Li, C. State-of-Charge Prediction of Lithium-Ion Batteries Based on Sparse Autoencoder and Gated Recurrent Unit Neural Network. Energy Technol. 2023, 11, 2201510. [Google Scholar] [CrossRef]
- Sun, G.; Wang, X.; Zhang, X.; Wang, J.; Li, Z. Autoencoder-Enhanced Regularized Prototypical Network for New Energy Vehicle battery fault detection. Control Eng. Pract. 2023, 141, 105738. [Google Scholar] [CrossRef]
- Hong, S.; Kang, M.; Kim, J.; Baek, J. Investigation of denoising autoencoder-based deep learning model in noise-riding experimental data for reliable state-of-charge estimation. J. Energy Storage 2023, 72, 108421. [Google Scholar] [CrossRef]
- Chen, J.; Feng, X.; Jiang, L.; Zhu, Q. State of charge estimation of lithium-ion battery using denoising autoencoder and gated recurrent unit recurrent neural network. Energy 2021, 227, 120451. [Google Scholar] [CrossRef]
- Xu, F.; Yang, F.; Fei, Z.; Huang, Z.; Tsui, K.-L. Life prediction of lithium-ion batteries based on stacked denoising autoencoders. Reliab. Eng. Syst. Saf. 2021, 208, 107396. [Google Scholar] [CrossRef]
- Sudarshan, M.; Serov, A.; Jones, C.; Ayalasomayajula, S.M.; García, R.E.; Tomar, V. Data-driven autoencoder neural network for onboard BMS Lithium-ion battery degradation prediction. J. Energy Storage 2024, 82, 110575. [Google Scholar] [CrossRef]
- Valant, C.J.; Wheaton, J.D.; Thurston, M.G.; McConky, S.P.; Nenadic, N.G. Evaluation of 1D CNN autoencoders for lithium-ion battery condition assessment using synthetic data. In Proceedings of the Annual Conference of the Prognostics and Health Management Society 2019, 11th PHM Conference, Scottsdale, AZ, USA, 21–26 September 2019; Volume 11, pp. 1–11. [Google Scholar]
- Wu, J.; Chen, J.; Feng, X.; Xiang, H.; Zhu, Q. State of health estimation of lithium-ion batteries using Autoencoders and Ensemble Learning. J. Energy Storage 2022, 55, 105708. [Google Scholar] [CrossRef]
- Fasahat, M.; Manthouri, M. State of charge estimation of lithium-ion batteries using hybrid autoencoder and Long Short Term Memory neural networks. J. Power Sources 2020, 469, 228375. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, Y.; Zhang, C.; Shen, W.; Xiong, R. Deep neural network-enabled battery open-circuit voltage estimation based on partial charging data. J. Energy Chem. 2024, 90, 120–132. [Google Scholar] [CrossRef]
- Jiao, R.; Peng, K.; Dong, J. Remaining useful life prediction of lithium-ion batteries based on conditional variational autoencoders-particle filter. IEEE Trans. Instrum. Meas. 2020, 69, 8831–8843. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, L.; Hong, S.; Zhao, S.; Wang, H.; Zhang, L. Remaining useful life prediction for lithium-ion battery: A deep learning approach. IEEE Access 2018, 6, 50587–50598. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural. Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural. Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Landi, F.; Baraldi, L.; Cornia, M.; Cucchiara, R. Working memory connections for LSTM. Neural Networks. 2021, 144, 334–341. [Google Scholar] [CrossRef]
- Gers, F.; Schmidhuber, J. Recurrent nets that time and count. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27 July 2000; Volume 3, pp. 189–194. [Google Scholar] [CrossRef]
- Olah, C. Understanding LSTM Networks. GitHub Repository. 2015. Available online: https://github.com/colah/LSTM (accessed on 27 August 2015).
- Graves, A.; Mohamed, A.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Jozefowicz, R.; Zaremba, W.; Sutskever, I. An empirical exploration of recurrent network architectures. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37, pp. 2342–2350. [Google Scholar]
- Cho, K.; van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Zhou, D.; Zuo, X.; Zhao, Z. Constructing a large-scale urban land subsidence prediction method based on neural network algorithm from the perspective of multiple factors. Remote Sens. 2022, 14, 1803. [Google Scholar] [CrossRef]
- Ren, X.; Liu, S.; Yu, X.; Dong, X. A method for state-of-charge estimation of lithium-ion batteries based on PSO-LSTM. Energy 2021, 234, 121236. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Y. Attention-based encoder-decoder networks for state of charge estimation of lithium-ion battery. Energy 2023, 268, 126665. [Google Scholar] [CrossRef]
- Almaita, E.; Alshkoor, S.; Abdelsalam, E.; Almomani, F. State of charge estimation for a group of lithium-ion batteries using long short-term memory neural network. J. Energy Storage 2022, 52, 104761. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long Short-Term Memory Recurrent Neural Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Tang, A.; Huang, Y.; Liu, S.; Yu, Q.; Shen, W.; Xiong, R. A novel lithium-ion battery state of charge estimation method based on the fusion of neural network and equivalent circuit models. Appl. Energy 2023, 348, 121578. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Dong, L.; Xu, S.; Xu, B. Speech-Transformer: A No-Recurrence Sequence-to-Sequence Model for Speech Recognition. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 5884–5888. [Google Scholar] [CrossRef]
- Dai, Z.; Yang, Z.; Yang, Y.; Carbonell, J.G.; Le, Q.V.; Salakhutdinov, R. Transformer-XL: Attentive language models beyond a fixed-length context. arXiv 2019, arXiv:1901.02860. [Google Scholar]
- Ott, M.; Edunov, S.; Grangier, D.; Auli, M. Scaling neural machine translation. arXiv 2018, arXiv:1806.00187. [Google Scholar]
- Chi, L.; Yuan, Z.; Mu, Y.; Wang, C. Non-local neural networks with grouped bilinear attentional transforms. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11804–11813. [Google Scholar]
- Weston, J.; Chopra, S.; Bordes, A. Memory networks. arXiv 2014, arXiv:1410.3916. [Google Scholar]
- Child, R.; Gray, S.; Radford, A.; Sutskever, I. Generating long sequences with sparse transformers. arXiv 2019, arXiv:1904.10509. [Google Scholar]
- Ke, G.; He, D.; Liu, T. Rethinking the Position Encoding in Vision Transformer. arXiv 2021, arXiv:2107.14222. [Google Scholar]
- Salman, K.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in vision: A survey. ACM Comput. Surv. 2022, 54, 1–41. [Google Scholar]
- Shi, D.; Zhao, J.; Wang, Z.; Zhao, H.; Wang, J.; Lian, Y.; Burke, A.F. Spatial-Temporal Self-Attention Transformer Networks for Battery State of Charge Estimation. Electronics 2023, 12, 2598. [Google Scholar] [CrossRef]
- Karita, S.; Chen, N.; Hayashi, T.; Hori, T.; Inaguma, H.; Jiang, Z.; Someki, M.; Zhang, W. A comparative study on transformer vs. rnn in speech applications. In Proceedings of the 2019 IEEE Automatic Speech Recognition and Understanding Workshop (ASRU), Singapore, 14–18 December 2019; pp. 449–456. [Google Scholar]
- Ahn, H.; Shen, H.; Zhou, X.; Kung, Y.-C.; Wang, J. State of Charge Estimation of Lithium-Ion Batteries Using Physics-Informed Transformer for Limited Data Scenarios. ASME Lett. Dyn. Syst. Control 2023, 3, 041002. [Google Scholar] [CrossRef]
- Almarzooqi, A.H.; Alhusin, M.O.; Nikolakakos, I.P.; Husnain, A.; Albeshr, H.M. Improved NaS Battery State of Charge Estimation by Means of Temporal Fusion Transformer. In Proceedings of the 2023 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 13–14 February 2023; pp. 1–6. [Google Scholar]
- Stensson, J.; Svantesson, K. Physics Informed Neural Network for Thermal Modeling of an Electric Motor. 2023. Available online: https://odr.chalmers.se/items/03b63aad-812d-4ec3-9679-1aa65981eff6 (accessed on 27 August 2015).



| LR | RFR | NN | AE | LSTM | TR | |
|---|---|---|---|---|---|---|
| Layer types | N/A | Decision trees | Dense | Dense, input, dropout, batch normalization | LSTM | MultiHeadAttention |
| Number of layers | N/A | N/A | 2 dense layers | Multiple (encoder, decoder, dropout, normalization) | Multiple with sequential model | Custom layers in transformer |
| Neurons per layer | N/A | N/A | 32 neurons each | Varies per layer | Varies per layer | - |
| Core parameters | - | N estimation = 100 | Dense layers with 32 neurons each | Input, dense, dropout, batch normalization layers | LSTM layer | D_model. Num_heads in MultiHeadAttention |
| Activation functions | - | - | ReLU | ReLU | Sigmoid | Not used |
| Regularization | - | - | - | Dropout, batch normalization | - | - |
| Learning rate optimizer | - | - | Adam | rmsprop | - | |
| Loss function | - | - | MSE | MSE | MSE | MSE |
| Dropout/batch normalization | N/A | N/A | Both used | N/A | N/A | |
| Hyperparameter tunability | Limited (mostly data preprocessing) | High (number of trees, depth, etc.) | High (layer types, number of neurons, activations) | High (layer types, encoding, decoding, activations) | High (number of units, return sequences, etc.) | High (attention heads, model size, etc.) |
| Model size (memory) | Amall | Large (due to multiple trees) | Varies (depends on the number of layers and neurons) | Varies (complex architecture) | Varies (depends on sequence length and complexity) | Large (due to complex architecture) |
| LR | NN | AE | TR | LSTM | RFR | |
|---|---|---|---|---|---|---|
| MSE | 33.7637442 | 19.1336108 | 13.328750 | 4.4526869 | 3.5021456 | 0.0002765 |
| MAE | 4.5823155 | 2.63253629 | 2.1715623 | 1.1486983 | 0.0139719 | 0.0007379 |
| R-squared | 0.9491749 | 0.97119789 | 0.9833935 | 0.9931919 | 0.9989747 | 0.9999996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussein, H.M.; Esoofally, M.; Donekal, A.; Rafin, S.M.S.H.; Mohammed, O. Comparative Study-Based Data-Driven Models for Lithium-Ion Battery State-of-Charge Estimation. Batteries 2024, 10, 89. https://doi.org/10.3390/batteries10030089
Hussein HM, Esoofally M, Donekal A, Rafin SMSH, Mohammed O. Comparative Study-Based Data-Driven Models for Lithium-Ion Battery State-of-Charge Estimation. Batteries. 2024; 10(3):89. https://doi.org/10.3390/batteries10030089
Chicago/Turabian StyleHussein, Hossam M., Mustafa Esoofally, Abhishek Donekal, S M Sajjad Hossain Rafin, and Osama Mohammed. 2024. "Comparative Study-Based Data-Driven Models for Lithium-Ion Battery State-of-Charge Estimation" Batteries 10, no. 3: 89. https://doi.org/10.3390/batteries10030089
APA StyleHussein, H. M., Esoofally, M., Donekal, A., Rafin, S. M. S. H., & Mohammed, O. (2024). Comparative Study-Based Data-Driven Models for Lithium-Ion Battery State-of-Charge Estimation. Batteries, 10(3), 89. https://doi.org/10.3390/batteries10030089









