First Principles Study of the Phase Stability, the Li Ionic Diffusion, and the Conductivity of the Li10GexMo1−xP2S12 of Superionic Conductors
Abstract
:1. Introduction
2. Computational Details
2.1. Modeling and Structure Optimization
2.2. Binding Energy
2.3. Intrinsic Redox Stability
2.4. Lithium-Ion Transport Capabilities
- The Li10GexMo1−xP2S12 (x = 0~1) samples are assigned an initial temperature of 100 K based on a Boltzmann distribution at the start of the MD simulations.
- The samples are then heated to the required temperature (600 to 1200 K) by velocity scaling over 1000 time steps (2 ps) in the NVT ensemble with a constant volume and a Nosé–Hoover thermostat, and then equilibrated at the equilibrium temperature for 5000 time steps (10 ps) in the NVT ensemble with a constant volume and a Nosé–Hoover thermostat.
- The MD simulations for diffusion are then run in the NVT ensemble for 40 ps to 100 ps until the diffusion coefficient converges.
3. Results and Discussion
3.1. Relaxed Structural and Parameters
3.2. Phase Stability
3.3. Bandgaps and Intrinsic Redox Stability
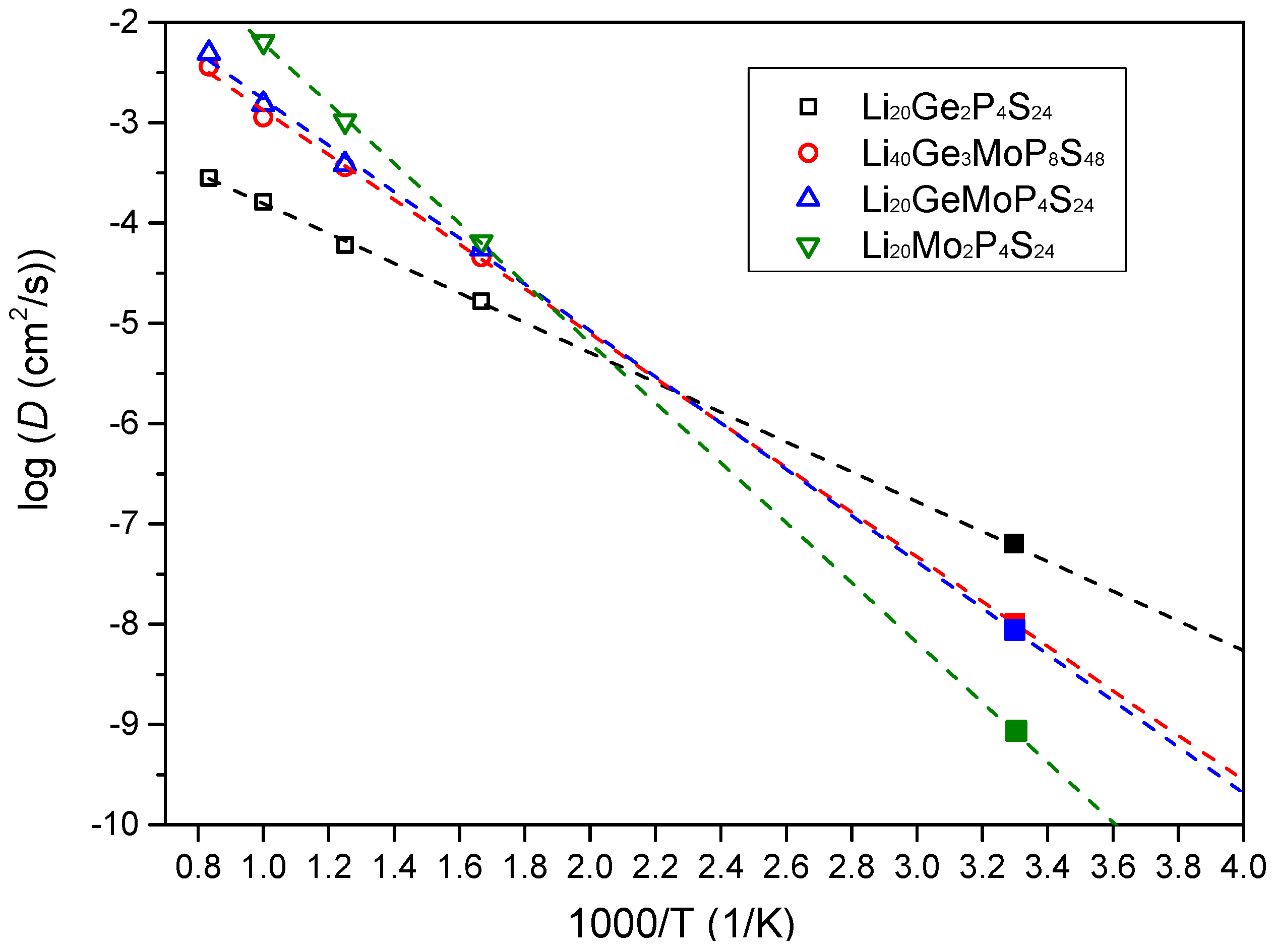
3.4. Li+ Diffusivity and Conductivity
3.5. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, S.Y.; Gu, K.H.; Lu, B.A.; Han, J.W.; Zhou, J. Hydrometallurgical Processes on Recycling of Spent Lithium-lon Battery Cathode: Advances and Applications in Sustainable Technologies. Acta Phys.-Chim. Sin. 2024, 40, 2309028. [Google Scholar] [CrossRef]
- Zhang, J.K.; Lv, J.C.; Lu, W.; Li, X.; Liu, Y.; Lang, J.H.; Liu, J.; Wang, Z.; Lu, M.; Sun, H. Li10GeP2S12-based solid electrolyte induced by high pressure for all-solid-state batteries: A facile strategy of low-grain-boundary-resistance. Chem. Eng. J. 2024, 487, 150452. [Google Scholar] [CrossRef]
- Kamaya, N.; Homma, K.; Yamakawa, Y.; Hirayama, M.; Kanno, R.; Yonemura, M.; Kamiyama, T.; Kato, Y.; Hama, S.; Kawamoto, K.; et al. A lithium superionic conductor. Nat. Mater. 2011, 10, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Hwang, T.; Conlin, P.; Cho, M.; Cho, K. Electrochemical Stability and Li Ion Diffusion Kinetics of Grain Boundaries in Li10GeP2S12 Solid Electrolyte. J. Phys. Chem. C 2023, 127, 7528–7535. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, L.; Gu, X. Failure mechanism of solid-state electrolyte Li10GeP2S12 in a moist atmosphere: A first-principles study. Mater. Adv. 2022, 3, 3143–3150. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, D.; Ma, X.; Liu, Q.; Zhou, X.; Lei, Z. Sb-doped Li10GeP2S12-type electrolyte Li10SnP2-xSbxS12 with enhanced ionic conductivity and lower lithium-ion migration barrier. J. Colloid Interface Sci. 2022, 627, 1039–1046. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, C.; Zhu, J.P.; Liu, X.S.; Yao, J.M.; Wang, B.; Dai, Q.S.; Wang, Z.F.; Chen, J.Z.; Jia, P.; et al. Size-Dependent Chemomechanical Failure of Sulfide Solid Electrolyte Particles during Electrochemical Reaction with Lithium. Nano Lett. 2022, 22, 411–418. [Google Scholar] [CrossRef]
- Ong, S.P.; Mo, Y.F. William Davidson Richards, Lincoln Miara, Hyo Sug Leeb and Gerbrand Ceder. Phase stability, electrochemical stability and ionic conductivity of the (M=Ge, Si, Sn, Al or P, and X=O, S or Se) family of superionic conductors. Energy Environ. Sci. 2013, 6, 148–156. [Google Scholar] [CrossRef]
- Sahu, G.; Lin, Z.; Liu, J.; Dudney, N.; Liang, C. Air-stable, high-conduction solid electrolytes of arsenic-substituted Li4SnS4. Energy Environ. Sci. 2014, 7, 1053–1058. [Google Scholar] [CrossRef]
- Yang, M.; Chen, L.Q.; Li, H.; Wu, F. Air/Water Stability Problems and Solutions for Lithium Batteries. Energy Mater. Adv. 2022, 2022, 9842651. [Google Scholar]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2006, 124, 219906, Erratum in J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E. Efficient hybrid density functional calculations in solids: Assessment of the Heyd-Scuseria-Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 2004, 121, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Henderson, T.M.; Paier, J.; Scuseria, G.E. Accurate treatment of solids with the HSE screened hybrid. Phys. Status Solidi B 2011, 248, 767–774. [Google Scholar] [CrossRef]
- Ong, S.P.; Andreussi, O.; Wu, Y.; Marzari, N.; Ceder, G. Electrochemical windows of room-temperature ionic liquids from molecular dynamics and density functional theory calculations. Chem. Mater. 2011, 23, 2979–2986. [Google Scholar] [CrossRef]
- Jian, Y.; Huang, Z.; Xing, J.; Sun, L.; Liu, Y.; Gao, P. Phase stability, mechanical properties and electronic structures of TiAl binary compounds by first principles calculations. Mater. Chem. Phys. 2019, 221, 311–321. [Google Scholar] [CrossRef]
- Yang, J.; Huang, J.; Ye, Z.; Fan, D.; Chen, S.; Zhao, Y. First-principles calculations on structural energetics of Cu-Ti binary system intermetallic compounds in Ag-Cu-Ti and Cu-Ni-Ti active filler metals. Ceram. Int. 2017, 43, 7751–7761. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Nachimuthu, S.; Cheng, H.-J.; Lai, H.-J.; Cheng, Y.-H.; Kuo, R.T.; Zeier, W.G.; Hwang, B.J.; Jiang, J.-C. First-principles study on selenium-doped Li10GeP2S12 solid electrolyte: Effects of doping on moisture stability and Li-ion transport properties. Mater. Today Chem. 2022, 26, 101223. [Google Scholar] [CrossRef]
- Kuhn, A.; Duppel, V.; Lotsch, B.V. Tetragonal Li10GeP2S12 and Li7GePS8-exploring the Li ion dynamics in LGPS Li electrolytes. Energy Environ. Sci. 2013, 6, 3548–3552. [Google Scholar] [CrossRef]
- Mo, Y.F.; Ong, S.P.; Ceder, G. First Principles Study of the Li10GeP2S12 Lithium Super Ionic Conductor Material. Chem. Mater. 2012, 24, 15–17. [Google Scholar] [CrossRef]
- Wang, Z.; Shao, G. Theoretical design of solid electrolytes with superb ionic conductivity: Alloying effect on Li+ transportation in cubic Li6PA5X chalcogenides. J. Mater. Chem. A 2017, 5, 21846–21857. [Google Scholar] [CrossRef]
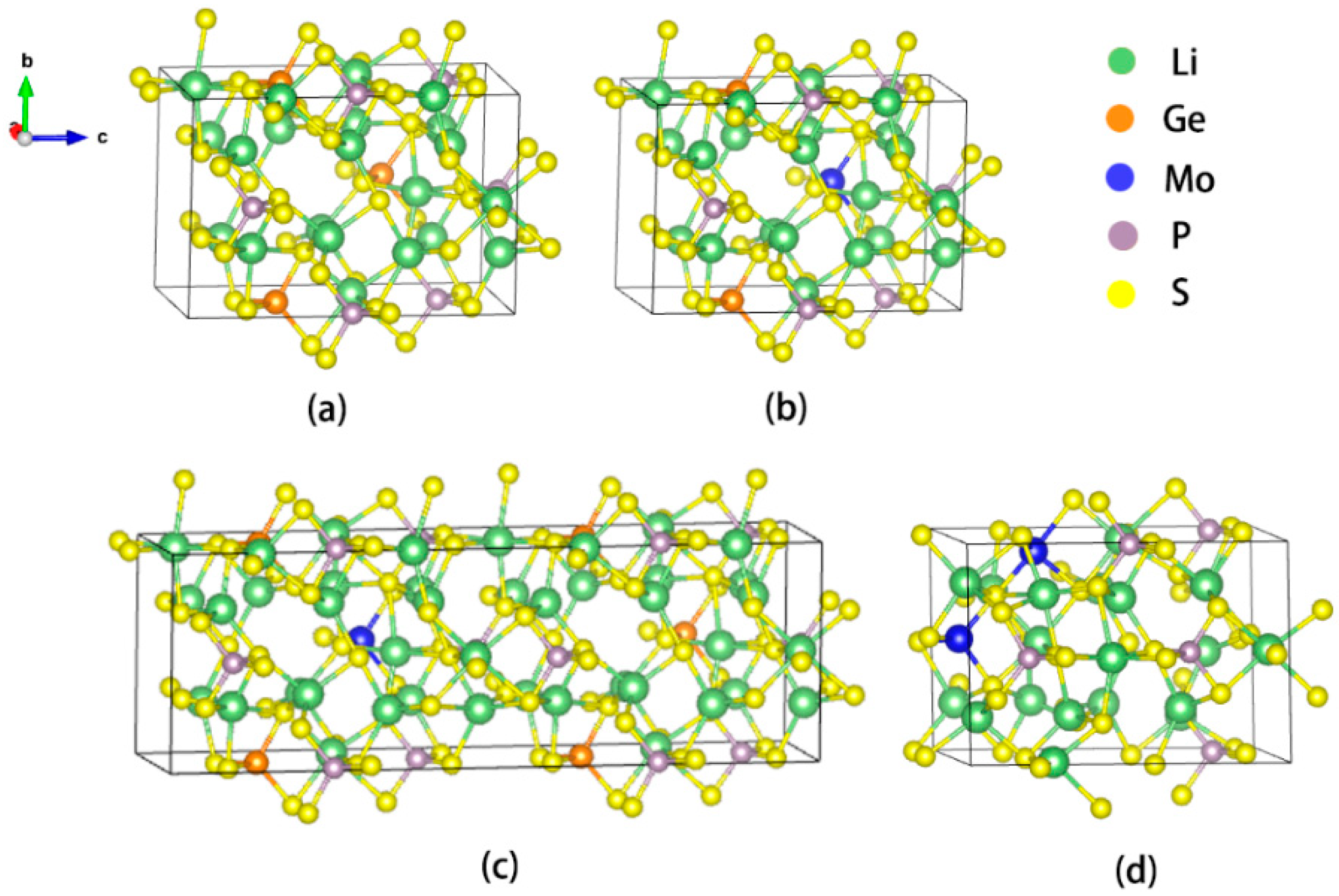

| Li20Ge2P4S24 | Li40Ge3MoP8S48 | Li20GeMoP4S24 | Li20Mo2P4S24 | |
|---|---|---|---|---|
| a (Å) | 8.6025 | 8.5905 | 8.5899 | 8.7922 |
| b (Å) | 8.6489 | 8.6606 | 8.6735 | 8.6187 |
| c (Å) | 12.8824 | 12.9232 | 12.9114 | 12.5916 |
| 89.1560 | 89.0088 | 88.9790 | 90.9771 | |
| 90.2020 | 90.2727 | 90.3518 | 90.5599 | |
| γ | 89.2361 | 89.1494 | 89.1528 | 89.6798 |
| V (Å3) | 958.2773 | 961.2006 | 961.6789 | 953.9658 |
| Li20Ge2P4S24 | Li40Ge3MoP8S48 | Li20GeMoP4S24 | Li20Mo2P4S24 | |
|---|---|---|---|---|
| binding energy (eV) | −4.29 | −4.34 | −4.39 | −4.50 |
| Li Ionic Diffusion Coefficients (cm2·s−1) | Conductivities of Lithium Ions (mS·cm−1) | Diffusion Activation Energies of Lithium Ions (eV) | |
|---|---|---|---|
| Li20Ge2P4S24 | 5.26 × 10−8 | 6.81 | 0.23 |
| Li40Ge3MoP8S48 | 8.66 × 10−9 | 1.12 | 0.37 |
| Li20GeMoP4S24 | 7.13 × 10−9 | 0.92 | 0.39 |
| Li20Mo2P4S24 | 6.65 × 10−10 | 0.09 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Chen, Y.; Chong, S. First Principles Study of the Phase Stability, the Li Ionic Diffusion, and the Conductivity of the Li10GexMo1−xP2S12 of Superionic Conductors. Batteries 2024, 10, 344. https://doi.org/10.3390/batteries10100344
Wu Y, Chen Y, Chong S. First Principles Study of the Phase Stability, the Li Ionic Diffusion, and the Conductivity of the Li10GexMo1−xP2S12 of Superionic Conductors. Batteries. 2024; 10(10):344. https://doi.org/10.3390/batteries10100344
Chicago/Turabian StyleWu, Yifang, Yuanzhen Chen, and Shaokun Chong. 2024. "First Principles Study of the Phase Stability, the Li Ionic Diffusion, and the Conductivity of the Li10GexMo1−xP2S12 of Superionic Conductors" Batteries 10, no. 10: 344. https://doi.org/10.3390/batteries10100344
APA StyleWu, Y., Chen, Y., & Chong, S. (2024). First Principles Study of the Phase Stability, the Li Ionic Diffusion, and the Conductivity of the Li10GexMo1−xP2S12 of Superionic Conductors. Batteries, 10(10), 344. https://doi.org/10.3390/batteries10100344







