Assessment of a Computational Protocol for Predicting Co-59 NMR Chemical Shift
Abstract
1. Introduction
2. Theoretical Methodology
2.1. NMR-DKH Basis Set Development for Co
2.2. Benchmarking the Computational Protocols
2.3. Validation of the Best Computational Protocol
3. Results and Discussion
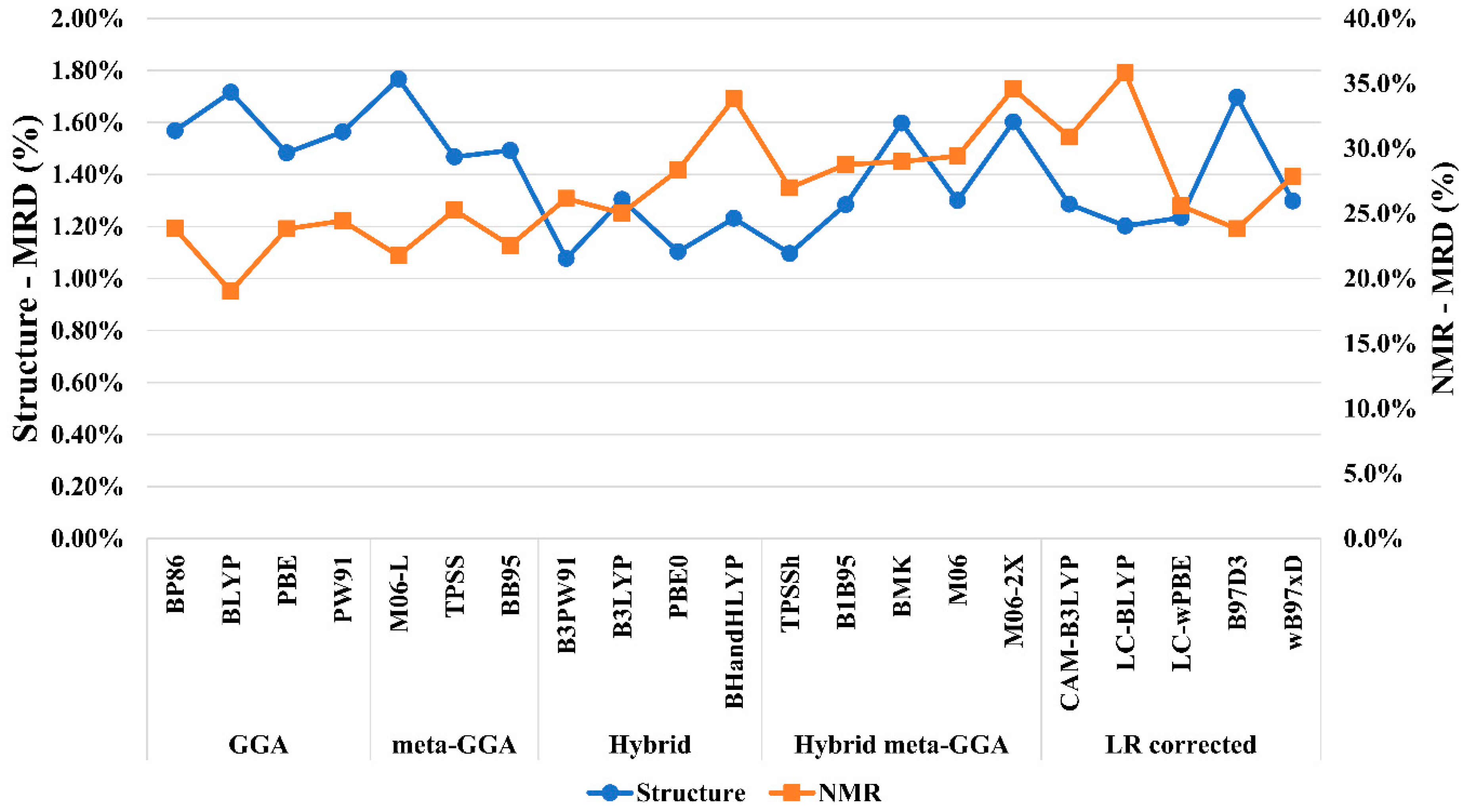
3.1. Benchmarking the Computational Protocols
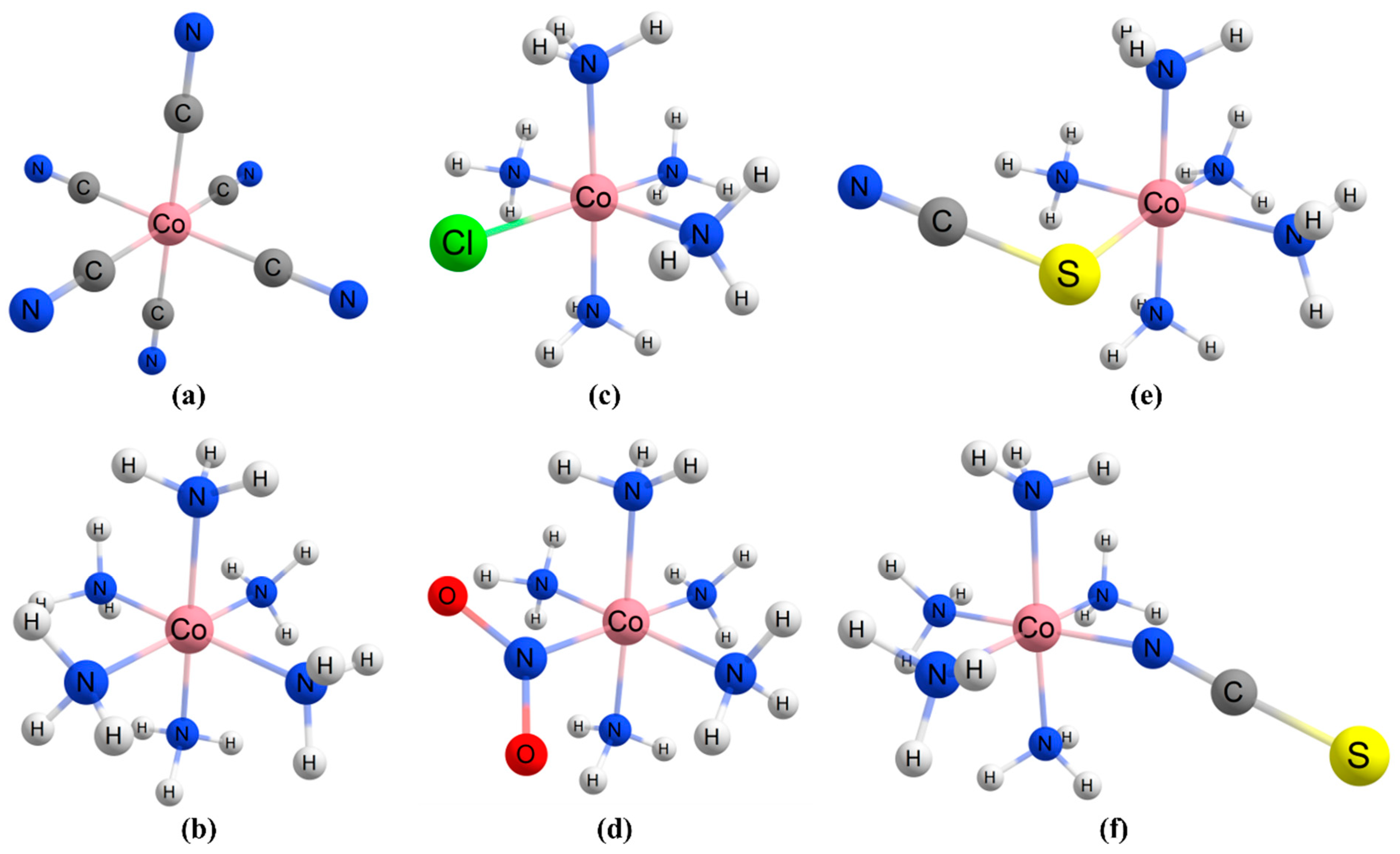
- (a)
- The structures of Co(III) complexes
- (b)
- Protocol for predicting the Co-59 NMR chemical shift (δ59Co)
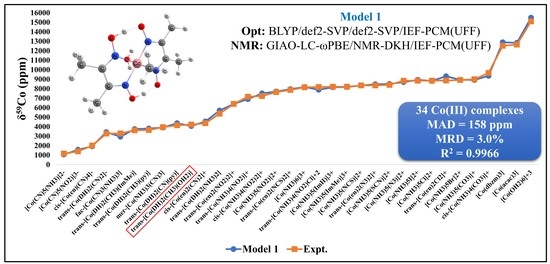
3.2. Validation of the Computational Protocol
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Delehanty, J.B.; Bongard, J.E.; Thach, D.C.; Knight, D.A.; Hickey, T.E.; Chang, E.L. Antiviral Properties of Cobalt(III)-Complexes. Bioorg. Med. Chem. 2008, 16, 830–837. [Google Scholar] [CrossRef] [PubMed]
- Mjos, K.D.; Orvig, C. Metallodrugs in Medicinal Inorganic Chemistry. Chem. Rev. 2014, 114, 4540–4563. [Google Scholar] [CrossRef]
- Anthony, E.J.; Bolitho, E.M.; Bridgewater, H.E.; Carter, O.W.L.; Donnelly, J.M.; Imberti, C.; Lant, E.C.; Lermyte, F.; Needham, R.J.; Palau, M.; et al. Metallodrugs Are Unique: Opportunities and Challenges of Discovery and Development. Chem. Sci. 2020, 11, 12888–12917. [Google Scholar] [CrossRef]
- Chang, E.L.; Simmers, C.; Knight, D.A. Cobalt Complexes as Antiviral and Antibacterial Agents. Pharmaceuticals 2010, 3, 1711–1728. [Google Scholar] [CrossRef] [PubMed]
- Heffern, M.C.; Yamamoto, N.; Holbrook, R.J.; Eckermann, A.L.; Meade, T.J. Cobalt Derivatives as Promising Therapeutic Agents. Curr. Opin. Chem. Biol. 2013, 17, 189–196. [Google Scholar] [CrossRef]
- Tsiliou, S.; Kefala, L.-A.; Hatzidimitriou, A.G.; Kessissoglou, D.P.; Perdih, F.; Papadopoulos, A.N.; Turel, I.; Psomas, G. Cobalt(II) Complexes with Non-Steroidal Anti-Inflammatory Drugs and α-Diimines. J. Inorg. Biochem. 2016, 160, 125–139. [Google Scholar] [CrossRef]
- Perontsis, S.; Dimitriou, A.; Fotiadou, P.; Hatzidimitriou, A.G.; Papadopoulos, A.N.; Psomas, G. Cobalt(II) Complexes with the Non-Steroidal Anti-Inflammatory Drug Diclofenac and Nitrogen-Donor Ligands. J. Inorg. Biochem. 2019, 196, 110688. [Google Scholar] [CrossRef]
- Khan, M.; Khan, N.; Ghazal, K.; Shoaib, S.; Ali, I.; Rauf, M.K.; Badshah, A.; Tahir, M.N.; Rehman, A.-U. Synthesis, Characterization, Crystal Structure, in-Vitro Cytotoxicity, Antibacterial, and Antifungal Activities of Nickel(II) and Cobalt(III) Complexes with Acylthioureas. J. Coord. Chem. 2020, 73, 1790–1805. [Google Scholar] [CrossRef]
- Sobiesiak, M.; Cieślak, M.; Królewska, K.; Kaźmierczak-Barańska, J.; Pasternak, B.; Budzisz, E. Thiosemicarbazone-Derived Copper(II), Cobalt(II) and Nickel(II) Complexes as Potential Anticancer Agents: Nuclease Activity, Cytotoxicity and Apoptosis Studies. New J. Chem. 2016, 40, 9761–9767. [Google Scholar] [CrossRef]
- Munteanu, C.R.; Suntharalingam, K. Advances in Cobalt Complexes as Anticancer Agents. Dalt. Trans. 2015, 44, 13796–13808. [Google Scholar] [CrossRef]
- King, A.P.; Gellineau, H.A.; Ahn, J.-E.; MacMillan, S.N.; Wilson, J.J. Bis(Thiosemicarbazone) Complexes of Cobalt(III). Synthesis, Characterization, and Anticancer Potential. Inorg. Chem. 2017, 56, 6609–6623. [Google Scholar] [CrossRef] [PubMed]
- Bühl, M. Chapter 3. DFT Computations of Transition-Metal Chemical Shifts. Annu. Rep. NMR Spectrosc. 2008, 64, 77–126. [Google Scholar] [CrossRef]
- Ronconi, L.; Sadler, P.J. Applications of Heteronuclear NMR Spectroscopy in Biological and Medicinal Inorganic Chemistry. Coord. Chem. Rev. 2008, 252, 2239–2277. [Google Scholar] [CrossRef] [PubMed]
- Zou, T.; Sadler, P.J. Speciation of Precious Metal Anti-Cancer Complexes by NMR Spectroscopy. Drug Discov. Today Technol. 2015, 16, 7–15. [Google Scholar] [CrossRef]
- Harris, R.K.; Becker, E.D.; Cabral de Menezes, S.M.; Goodfellow, R.; Granger, P. NMR Nomenclature: Nuclear Spin Properties and Conventions for Chemical Shifts. Solid State Nucl. Magn. Reson. 2002, 22, 458–483. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.C.C.; Au-Yeung, S.C.F. Cobalt-59 NMR Spectroscopy. Annu. Rep. NMR Spectrosc. 2000, 41, 1–54. [Google Scholar] [CrossRef]
- Yamasaki, A. Cobalt-59 Nuclear Magnetic Resonance Spectroscopy in Coordination Chemistry. J. Coord. Chem. 1991, 24, 211–260. [Google Scholar] [CrossRef]
- Yamasaki, A.; Yajima, F.; Fujiwara, S. Nuclear Magnetic Resonance Studies on Cobalt Complexes. I. Cobalt-59 Nuclear Magnetic Resonance Spectra of Cobalt(III) Complexes. Inorg. Chim. Acta 1968, 2, 39–42. [Google Scholar] [CrossRef]
- Barnard, I.; Koch, K.R. 59Co NMR, a Facile Tool to Demonstrate EEE, EEZ, EZZ and ZZZ Configurational Isomerism in Fac-[Co(L-ΚS,O)3] Complexes Derived from Asymmetrically Substituted N,N-Dialkyl-N′-Aroylthioureas. Inorg. Chim. Acta 2019, 495, 119019. [Google Scholar] [CrossRef]
- Rusakova, I.L. Quantum Chemical Approaches to the Calculation of NMR Parameters: From Fundamentals to Recent Advances. Magnetochemistry 2022, 8, 50. [Google Scholar] [CrossRef]
- Chan, J.C.C.; Au-Yeung, S.C.F.; Wilson, P.J.; Webb, G.A. SOS-DFPT-IGLO Calculations of 59Co NMR Shielding Parameters of Hexacoordinated Diamagnetic Co(III) Complexes. J. Mol. Struct. THEOCHEM 1996, 365, 125–130. [Google Scholar] [CrossRef]
- Chan, J.C.C.; Au-Yeung, S.C.F. A Comparative Study of the Calculation of 59Co NMR Shielding Constants of Hexacoordinated Diamagnetic Co(III) Complexes Using DFT-IGLO and DFT-GIAO Methods. J. Mol. Struct. THEOCHEM 1997, 393, 93–96. [Google Scholar] [CrossRef]
- Godbout, N.; Oldfield, E. Density Functional Study of Cobalt-59 Nuclear Magnetic Resonance Chemical Shifts and Shielding Tensor Elements in Co(III) Complexes. J. Am. Chem. Soc. 1997, 119, 8065–8069. [Google Scholar] [CrossRef]
- Bühl, M.; Grigoleit, S.; Kabrede, H.; Mauschick, F.T. Simulation of 59Co NMR Chemical Shifts in Aqueous Solution. Chem. A Eur. J. 2006, 12, 477–488. [Google Scholar] [CrossRef]
- Semenov, V.A.; Samultsev, D.O.; Krivdin, L.B. Four-Component Relativistic Computational NMR Study of Ferrous, Cobalt and Nickel Bisglycinates. Mendeleev Commun. 2020, 30, 476–478. [Google Scholar] [CrossRef]
- Samultsev, D.O.; Semenov, V.A.; Krivdin, L.B. Four-component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes. Part 1: Pentaammines of Cobalt, Rhodium, and Iridium. Magn. Reson. Chem. 2022, 60, 463–468. [Google Scholar] [CrossRef] [PubMed]
- Samultsev, D.O.; Semenov, V.A.; Rusakova, I.L.; Krivdin, L.B. Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 2: Nitrogen-Coordinated Complexes of Cobalt. Int. J. Mol. Sci. 2022, 23, 13178. [Google Scholar] [CrossRef]
- Samultsev, D.O.; Semenov, V.A.; Krivdin, L.B. Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 3: Fe, Co, Ni, Pd, and Pt Glycinates. Magnetochemistry 2023, 9, 83. [Google Scholar] [CrossRef]
- Paschoal, D.; Guerra, C.F.; de Oliveira, M.A.L.; Ramalho, T.C.; Dos Santos, H.F. Predicting Pt-195 NMR Chemical Shift Using New Relativistic All-Electron Basis Set. J. Comput. Chem. 2016, 37, 2360–2373. [Google Scholar] [CrossRef]
- Carvalho, J.; Paschoal, D.; Fonseca Guerra, C.; Dos Santos, H.F. Nonrelativistic Protocol for Calculating the 1J(195Pt-15N) Coupling Constant in Pt(II)-Complexes Using All-Electron Gaussian Basis-Set. Chem. Phys. Lett. 2020, 745, 137279. [Google Scholar] [CrossRef]
- E Silva, J.H.C.; Dos Santos, H.F.; Paschoal, D.F.S. Predicting Pt-195 Nmr Chemical Shift and 1J(195Pt-31P) Coupling Constant for Pt(0) Complexes Using the NMR-DKH Basis Sets. Magnetochemistry 2021, 7, 148. [Google Scholar] [CrossRef]
- de Andrade, T.F.C.B.; Dos Santos, H.F.; Fonseca Guerra, C.; Paschoal, D.F.S. Computational Prediction of Tc-99 NMR Chemical Shifts in Technetium Complexes with Radiopharmaceutical Applications. J. Phys. Chem. A 2022, 126, 5434–5448. [Google Scholar] [CrossRef] [PubMed]
- Paschoal, D.F.S.; Dos Santos, H.F. Predicting the Structure and NMR Coupling Constant 1J(129Xe-19F) of XeF6 Using Quantum Mechanics Methods. Phys. Chem. Chem. Phys. 2021, 23, 7240–7246. [Google Scholar] [CrossRef]
- Rolfes, J.D.; Neese, F.; Pantazis, D.A. All-electron Scalar Relativistic Basis Sets for the Elements Rb–Xe. J. Comput. Chem. 2020, 41, 1842–1849. [Google Scholar] [CrossRef] [PubMed]
- Aravena, D.; Neese, F.; Pantazis, D.A. Improved Segmented All-Electron Relativistically Contracted Basis Sets for the Lanthanides. J. Chem. Theory Comput. 2016, 12, 1148–1156. [Google Scholar] [CrossRef] [PubMed]
- Pantazis, D.A.; Neese, F. All-Electron Scalar Relativistic Basis Sets for the 6p Elements. Theor. Chem. Acc. 2012, 131, 1292. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Neese, F. All-Electron Scalar Relativistic Basis Sets for the Actinides. J. Chem. Theory Comput. 2011, 7, 677–684. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Neese, F. All-Electron Scalar Relativistic Basis Sets for the Lanthanides. J. Chem. Theory Comput. 2009, 5, 2229–2238. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Chen, X.-Y.; Landis, C.R.; Neese, F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef]
- Dyall, K.G.; Grant, I.P.; Johnson, C.T.; Parpia, F.A.; Plummer, E.P. GRASP: A General-Purpose Relativistic Atomic Structure Program. Comput. Phys. Commun. 1989, 55, 425–456. [Google Scholar] [CrossRef]
- Douglas, M.; Kroll, N.M. Quantum Electrodynamical Corrections to the Fine Structure of Helium. Ann. Phys. 1974, 82, 89–155. [Google Scholar] [CrossRef]
- Hess, B.A. Applicability of the No-Pair Equation with Free-Particle Projection Operators to Atomic and Molecular Structure Calculations. Phys. Rev. A 1985, 32, 756–763. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.A. Relativistic Electronic-Structure Calculations Employing a Two-Component No-Pair Formalism with External-Field Projection Operators. Phys. Rev. A 1986, 33, 3742–3748. [Google Scholar] [CrossRef] [PubMed]
- Jansen, G.; Hess, B.A. Revision of the Douglas-Kroll Transformation. Phys. Rev. A 1989, 39, 6016–6017. [Google Scholar] [CrossRef]
- Visscher, L.; Dyall, K.G. Dirac–Fock atomic electronic structure calculations using different nuclear charge distributions. At. Data Nucl. Data Tables 1997, 67, 207–224. [Google Scholar] [CrossRef]
- Barysz, M.; Sadlej, A.J. Two-Component Methods of Relativistic Quantum Chemistry: From the Douglas–Kroll Approximation to the Exact Two-Component Formalism. J. Mol. Struct. THEOCHEM 2001, 573, 181–200. [Google Scholar] [CrossRef]
- de Jong, W.A.; Harrison, R.J.; Dixon, D.A. Parallel Douglas–Kroll Energy and Gradients in NWChem: Estimating Scalar Relativistic Effects Using Douglas–Kroll Contracted Basis Sets. J. Chem. Phys. 2001, 114, 48. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Paschoal, D.; Costa, M.F.; Dos Santos, H.F. NLO-X (X = I-III): New Gaussian Basis Sets for Prediction of Linear and Nonlinear Electric Properties. Int. J. Quantum Chem. 2014, 114, 796–804. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef] [PubMed]
- Kruger, G.J.; Reynhardt, E.C. Hexaamminecobalt(III) Chloride. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1978, 34, 915–917. [Google Scholar] [CrossRef]
- Chan, J.C.C.; Au-Yeung, S.C.F. Interpretation of 59 Co NMR Shielding Using the Hard and Soft Acid–Base Concept. Insight into the Relative Magnitude of the Nephelauxetic and the Spectrochemical Effect. J. Chem. Soc. Faraday Trans. 1996, 92, 1121–1128. [Google Scholar] [CrossRef]
- Messmer, G.G.; Amma, E.L. Redetermination of the Crystal Structure of Chloropentamminecobalt(III) Dichloride. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1968, 24, 417–422. [Google Scholar] [CrossRef]
- Cotton, F.A.; Edwards, W.T. The Crystal and Molecular Structure of Nitropentamminocobalt(III) Bromide. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1968, 24, 474–477. [Google Scholar] [CrossRef]
- Snow, M.R.; Boomsma, R.F. The Crystal Structures and Isomerization of the Linkage Isomers Thiocyanato- and Isothiocyanato-Pentaamminecobalt(III) Dichloride, [Co(SCN)(NH3)5]Cl2.H2O, and [Co(NCS)(NH3)5]Cl2. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1972, 28, 1908–1913. [Google Scholar] [CrossRef]
- Iwata, M.; Saito, Y. The Crystal Structure of Hexamminecobalt(III) Hexacyanocobaltate(III): An Accurate Determination. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1973, 29, 822–832. [Google Scholar] [CrossRef]
- Scalmani, G.; Frisch, M.J. Continuous Surface Charge Polarizable Continuum Models of Solvation. I. General Formalism. J. Chem. Phys. 2010, 132, 114110. [Google Scholar] [CrossRef]
- London, F. Théorie Quantique Des Courants Interatomiques Dans Les Combinaisons Aromatiques. J. Phys. le Radium 1937, 8, 397–409. [Google Scholar] [CrossRef]
- McWeeny, R. Perturbation Theory for the Fock-Dirac Density Matrix. Phys. Rev. 1962, 126, 1028–1034. [Google Scholar] [CrossRef]
- Ditchfield, R. Self-Consistent Perturbation Theory of Diamagnetism. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Cheeseman, J.R.; Trucks, G.W.; Keith, T.A.; Frisch, M.J. A Comparison of Models for Calculating Nuclear Magnetic Resonance Shielding Tensors. J. Chem. Phys. 1996, 104, 5497–5509. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results Obtained with the Correlation Energy Density Functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized Gradient Approximation for the Exchange-Correlation Hole of a Many-Electron System. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865, Erratum in Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 1992, 46, 6671–6687, Erratum in Phys. Rev. B 1993, 48, 4978. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. A New Local Density Functional for Main-Group Thermochemistry, Transition Metal Bonding, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional Thermochemistry. IV. A New Dynamical Correlation Functional and Implications for Exact-exchange Mixing. J. Chem. Phys. 1996, 104, 1040–1046. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Becke, A.D. A New Mixing of Hartree–Fock and Local Density-functional Theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. J. Chem. Phys. 2003, 119, 12129, Erratum in J. Chem. Phys. 2004, 121, 11507. [Google Scholar] [CrossRef]
- Boese, A.D.; Martin, J.M.L. Development of Density Functionals for Thermochemical Kinetics. J. Chem. Phys. 2004, 121, 3405–3416. [Google Scholar] [CrossRef]
- Iikura, H.; Tsuneda, T.; Yanai, T.; Hirao, K. A Long-Range Correction Scheme for Generalized-Gradient-Approximation Exchange Functionals. J. Chem. Phys. 2001, 115, 3540–3544. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E. Assessment of a Long-Range Corrected Hybrid Functional. J. Chem. Phys. 2006, 125, 234109. [Google Scholar] [CrossRef] [PubMed]
- Vydrov, O.A.; Heyd, J.; Krukau, A.V.; Scuseria, G.E. Importance of Short-Range versus Long-Range Hartree-Fock Exchange for the Performance of Hybrid Density Functionals. J. Chem. Phys. 2006, 125, 074106. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E.; Perdew, J.P. Tests of Functionals for Systems with Fractional Electron Number. J. Chem. Phys. 2007, 126, 154109. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Kirby, C.W.; Puranda, C.M.; Power, W.P. Cobalt-59 Nuclear Magnetic Relaxation Studies of Aqueous Octahedral Cobalt(III) Complexes. J. Phys. Chem. 1996, 100, 14618–14624. [Google Scholar] [CrossRef]
- Medek, A.; Frydman, V.; Frydman, L. Solid and Liquid Phase 59Co NMR Studies of Cobalamins and Their Derivatives. Proc. Natl. Acad. Sci. USA 1997, 94, 14237–14242. [Google Scholar] [CrossRef]
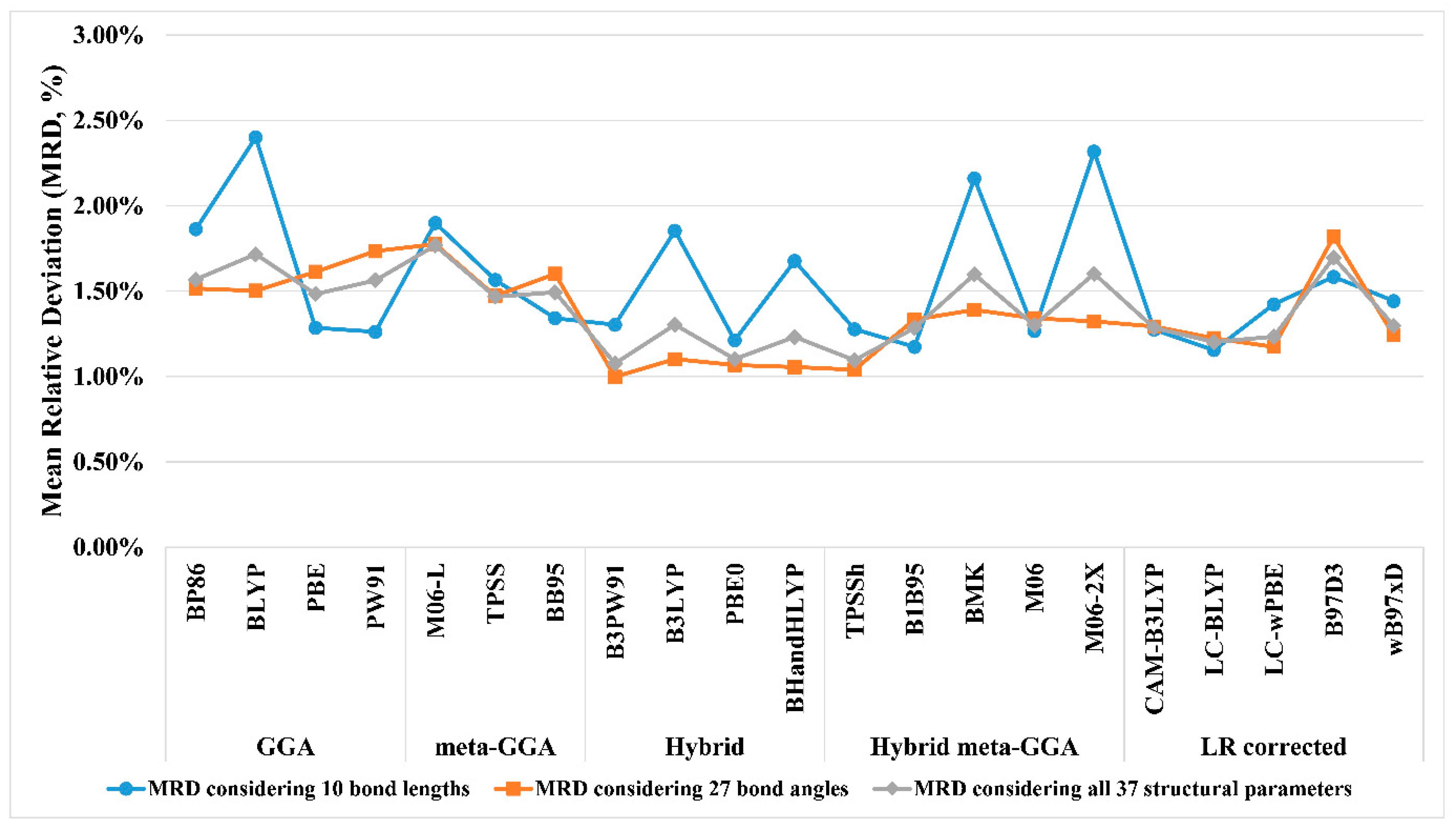

| DFT-Functional | Cpx01 | Cpx02 | Cpx03 | Cpx04 | Cpx05 | MAD | MRD | |
|---|---|---|---|---|---|---|---|---|
| GGA | BP86 | 6307 | 6689 | 5651 | 6352 | 6545 | 1973 | 23.8% |
| BLYP | 6673 | 7092 | 6041 | 6797 | 6941 | 1573 | 19.0% | |
| PBE | 6368 | 6703 | 5695 | 6218 | 6566 | 1972 | 23.8% | |
| PW91 | 6299 | 6643 | 5622 | 6242 | 6493 | 2022 | 24.4% | |
| meta-GGA | M06-L | 6476 | 6824 | 5888 | 6505 | 6707 | 1801 | 21.7% |
| TPSS | 6248 | 6567 | 5541 | 6191 | 6409 | 2090 | 25.3% | |
| BB95 | 6506 | 6684 | 5783 | 6400 | 6701 | 1867 | 22.5% | |
| Hybrid | B3PW91 | 6120 | 6501 | 5529 | 6127 | 6308 | 2164 | 26.1% |
| B3LYP | 6167 | 6605 | 5600 | 6288 | 6391 | 2071 | 25.0% | |
| PBE0 | 5946 | 6288 | 5368 | 5938 | 6139 | 2346 | 28.3% | |
| BHANDHLYP | 5463 | 5865 | 4874 | 5537 | 5683 | 2797 | 33.8% | |
| Hybrid meta-GGA | TPSSh | 6085 | 6443 | 5440 | 6070 | 6207 | 2232 | 27.0% |
| B1B95 | 5917 | 6280 | 5337 | 5870 | 6099 | 2381 | 28.8% | |
| BMK | 5815 | 6305 | 5264 | 5874 | 6158 | 2398 | 29.0% | |
| M06 | 5833 | 6207 | 5324 | 5827 | 6039 | 2435 | 29.4% | |
| M06-2X | 5421 | 5732 | 4798 | 5472 | 5680 | 2861 | 34.6% | |
| LR corrected | CAM-B3LYP | 5731 | 6097 | 5140 | 5732 | 5929 | 2556 | 30.9% |
| LC-BLYP | 5362 | 5666 | 4765 | 5267 | 5521 | 2965 | 35.8% | |
| LC-ωPBE | 5791 | 6085 | 7189 | 5635 | 5949 | 2152 | 25.6% | |
| B97D3 | 6318 | 6530 | 5811 | 6447 | 6423 | 1976 | 23.8% | |
| ωB97xD | 6030 | 6381 | 5391 | 5972 | 6111 | 2305 | 27.8% | |
| Experimental | 8152 | 8852 | 7643 | 8410 | 8350 | - | - | |
| DFT-Functional | Cpx01 | Cpx02 | Cpx03 | Cpx04 | Cpx05 | MAD | SD | MRD | |
|---|---|---|---|---|---|---|---|---|---|
| GGA | BP86 | 6467 | 6872 | 5871 | 6602 | 6736 | 1772 | 124 | 21.4% |
| BLYP | 6054 | 6387 | 5545 | 6149 | 6303 | 2194 | 154 | 26.5% | |
| PBE | 6673 | 7092 | 6041 | 6797 | 6941 | 1573 | 121 | 19.0% | |
| PW91 | 6522 | 6923 | 5934 | 6646 | 6780 | 1720 | 124 | 20.8% | |
| meta-GGA | M06-L | 4745 | 4941 | 4496 | 4759 | 4971 | 3499 | 261 | 42.2% |
| TPSS | 5439 | 5752 | 5066 | 5529 | 5663 | 2792 | 182 | 33.7% | |
| BB95 | 6617 | 7021 | 5971 | 6729 | 6912 | 1631 | 135 | 19.7% | |
| Hybrid | B3PW91 | 8335 | 9138 | 7822 | 8788 | 8759 | 287 | 96 | 3.4% |
| B3LYP | 7777 | 8337 | 7283 | 8058 | 8106 | 369 | 86 | 4.4% | |
| PBE0 | 9001 | 10,053 | 8978 | 10,013 | 9561 | 1240 | 244 | 15.0% | |
| BHANDHLYP | 10,828 | 12,847 | 10,784 | 12,360 | 11,767 | 3436 | 499 | 41.4% | |
| Hybrid meta-GGA | TPSSh | 6079 | 6546 | 5718 | 6317 | 6432 | 2063 | 141 | 24.9% |
| B1B95 | 9508 | 10,725 | 9634 | 10,483 | 10,179 | 1824 | 249 | 22.1% | |
| BMK | 13,132 | 15,018 | 12,739 | 14,850 | 14,068 | 5680 | 574 | 68.5% | |
| M06 | 14,199 | 15,839 | 13,529 | 15,201 | 15,079 | 6488 | 437 | 78.3% | |
| M06-2X | 25,260 | 29,621 | 23,322 | 29,962 | 28,460 | 19,044 | 2257 | 229.3% | |
| LR corrected | CAM-B3LYP | 8162 | 8732 | 7856 | 8377 | 8225 | 100 | 73 | 1.2% |
| LC-BLYP | 8382 | 8862 | 7749 | 8437 | 8283 | 88 | 78 | 1.1% | |
| LC-ωPBE | 8176 | 8826 | 7703 | 8505 | 8337 | 44 | 30 | 0.5% | |
| B97D3 | 6979 | 7426 | 6337 | 7141 | 7232 | 1258 | 107 | 15.2% | |
| ωB97xD | 8604 | 9255 | 8314 | 9001 | 8997 | 553 | 107 | 6.7% | |
| Experimental | 8152 | 8852 | 7643 | 8410 | 8350 | - | - | - | |
| Cpx | Structure | Solvent | Calc. | Expt. | Cpx | Structure | Solvent | Calc. | Expt. |
|---|---|---|---|---|---|---|---|---|---|
| 01 | 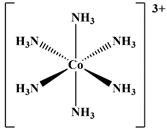 [Co(NH3)6]3+ | D2O | 8176 [9223.1] | 8152 a | 18 |  [Co(NH3)5(CO3)]+ | D2O | 8923 | 9000 b |
| 02 |  [Co(NH3)5Cl]2+ | D2O | 8826 [7685.5] | 8852 a | 19 | 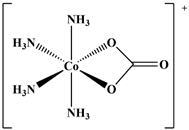 cis-[Co(NH3)4(CO3)]+ | D2O | 9360 | 9662 c |
| 03 | 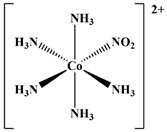 [Co(NH3)5(NO2)]2+ | D2O | 7703 [8409.0] | 7643 a | 20 |  [Co(CN)5(NO2)]3− | D2O | 1566 | 1400 b |
| 04 |  [Co(NH3)5(SCN)]2+ | D2O | 8505 | 8410 a | 21 |  [Co(NH3)(CN)5]2− | D2O | 1072 | 1162 b |
| 05 |  [Co(NH3)5(NCS)]2+ | D2O | 8337 | 8350 a | 22 | 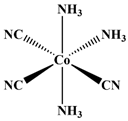 mer-[Co(CN)3(NH3)3] | D2O | 3917 | 3947 b |
| 06 | 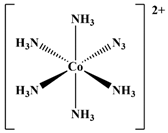 [Co(NH3)5(N3)]2+ | D2O | 8695 [9000.3] | 8842 a | 23 | 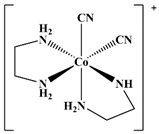 cis-[Co(CN)2(en)2]+ | D2O | 4545 | 4364 b |
| 07 | 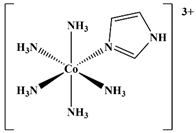 [Co(NH3)5(HIm)]3+ | MeOH | 8149 | 8208 a | 24 | 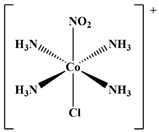 trans-[Co(NH3)4(NO2)Cl]+ | D2O | 7893 | 8180 b |
| 08 | 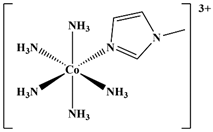 [Co(NH3)5(MeIm)]3+ | MeOH | 8182 | 8215 b | 25 | 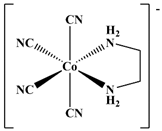 [Co(en)(CN)4]− | D2O | 1934 | 2006 b |
| 09 | 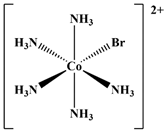 [CoBr(NH3)6]2+ | D2O | 8939 [9119.4] | 8919 b | 26 |  [Co(OH2)6]3+ | D2O | 15,485 | 15,100 b |
| 10 |  [Co(NH3)5I]2+ | D2O | 8935 [8639.2] | 8849 a | 27 |  trans-[Co(DH)2(CN)(py)] | DMSO | 4363 | 4150 d |
| 11 |  trans-[Co(en)2(N3)2]+ | DMSO | 8470 | 8350 a | 28 |  trans-[Co(DH)2(CN)2]− | DMSO | 3424 | 3270 d |
| 12 |  trans-[Co(en)2Cl2]+ | DMSO | 9313 | 8870 a | 29 |  trans-[Co(DH)2(CH3)(OH2)] | D2O | 4069 | 4220 d |
| 13 |  trans-[Co(en)2(NO2)2]+ | DMSO | 6396 | 6395 a | 30 | 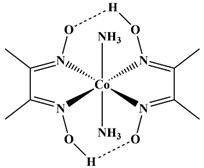 trans-[Co(DH)2(NH3)2] | D2O | 5704 | 5371 d |
| 14 |  trans-[Co(en)2(NCS)2]+ | MeOH | 7954 | 7870 a | 31 | 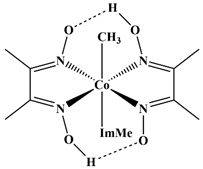 trans-[Co(DH)2(CH3)(MeIm)] | Acetone | 3744 | 3620 d |
| 15 |  trans-[Co(NH3)4(NO2)]+ | D2O | 6903 | 7157 c | 32 | 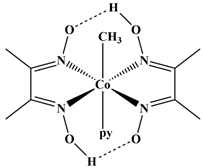 trans-[Co(DH)2(CH3)(py)] | Acetone | 3807 | 3645 d |
| 16 | 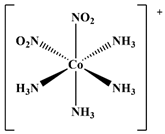 cis-[Co(NH3)4(NO2)2]+ | D2O | 7509 | 7227 c | 33 |  [Co(acac)3] | CHCl3 | 12,835 | 12,650 b |
| 17 |  fac-[Co(CN)3(NH3)3] | D2O | 2943 | 3289 c | 34 |  [Co(dbzm)3] | Benzene | 12,894 | 12,530 b |
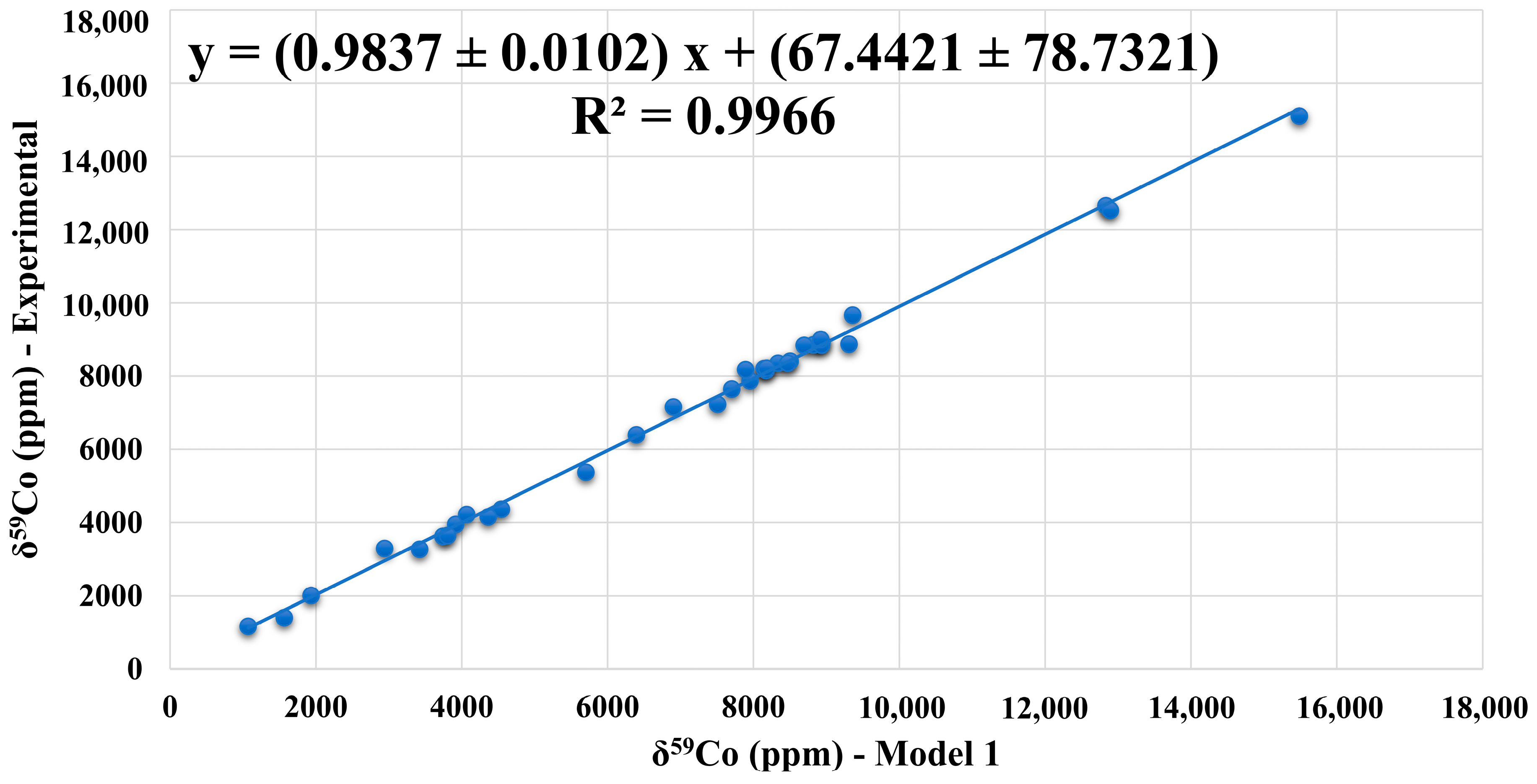
| 34 Co(III) complexes: MAD = 158 ppm/MRD = 3.0%/R2 = 0.9966 | |||||||||
| δ59Co (ppm) | ||||||
|---|---|---|---|---|---|---|
| Cpx | Co(III) Complexes | Solvent | Model 1 | Expt. | AD (ppm) | RD (%) |
| 07 | [Co(NH3)5(HIm)]3+ | D2O | 8132 | 8170 | 38 | 0.5% |
| MeOH | 8149 | 8208 | 59 | 0.7% | ||
| 08 | [Co(NH3)5(MeIm)]3+ | D2O | 8161 | 8178 | 17 | 0.2% |
| MeOH | 8182 | 8215 | 33 | 0.4% | ||
| 11 | trans-[Co(en)2(N3)2]+ | D2O | 8473 | 8359 | 114 | 1.4% |
| FA | 8471 | 8280 | 191 | 2.3% | ||
| DMSO | 8470 | 8350 | 120 | 1.4% | ||
| MeOH | 8468 | 8299 | 169 | 2.0% | ||
| 12 | trans-[Co(en)2Cl2]+ | D2O | 9331 | 8960 | 371 | 4.1% |
| DMSO | 9313 | 8870 | 443 | 5.0% | ||
| MeOH | 9296 | 8850 | 446 | 5.0% | ||
| 13 | trans-[Co(en)2(NO2)2]+ | D2O | 6396 | 6324 | 72 | 1.1% |
| DMSO | 6396 | 6395 | 1 | 0.0% | ||
| DMF | 6397 | 6400 | 3 | 0.0% | ||
| MeOH | 6397 | 6381 | 16 | 0.3% | ||
| MeCN | 6397 | 6366 | 31 | 0.5% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomes, M.G.R.; De Souza, A.L.F.; Dos Santos, H.F.; De Almeida, W.B.; Paschoal, D.F.S. Assessment of a Computational Protocol for Predicting Co-59 NMR Chemical Shift. Magnetochemistry 2023, 9, 172. https://doi.org/10.3390/magnetochemistry9070172
Gomes MGR, De Souza ALF, Dos Santos HF, De Almeida WB, Paschoal DFS. Assessment of a Computational Protocol for Predicting Co-59 NMR Chemical Shift. Magnetochemistry. 2023; 9(7):172. https://doi.org/10.3390/magnetochemistry9070172
Chicago/Turabian StyleGomes, Matheus G. R., Andréa L. F. De Souza, Hélio F. Dos Santos, Wagner B. De Almeida, and Diego F. S. Paschoal. 2023. "Assessment of a Computational Protocol for Predicting Co-59 NMR Chemical Shift" Magnetochemistry 9, no. 7: 172. https://doi.org/10.3390/magnetochemistry9070172
APA StyleGomes, M. G. R., De Souza, A. L. F., Dos Santos, H. F., De Almeida, W. B., & Paschoal, D. F. S. (2023). Assessment of a Computational Protocol for Predicting Co-59 NMR Chemical Shift. Magnetochemistry, 9(7), 172. https://doi.org/10.3390/magnetochemistry9070172