Abstract
Chemically altering molecules can have dramatic effects on the physical properties of a series of very similar molecular compounds. A good example of this is within the quasi-1D spin-Peierls system potassium TCNQ (TCNQ = 7,7,8,8-tetracyanoqunidimethane), where substitution of TCNQF for TCNQ has a dramatic effect on the 1D interactions, resulting in a drop in the corresponding spin-Peierls transition temperature. Within this work, we extend the investigation to potassium TCNQBr, where only two protons of TCNQ can be substituted with bromine atoms due to steric constraints. The new system exhibits evidence for a residual component of the magnetism when probed via magnetic susceptibility measurements and muon spin spectroscopy. The observations suggest that the system is dominated by short range, and potentially disordered, correlations within the bulk phase.
1. Introduction
There is a large interest in how to tune and drive molecular-based systems into different ground states to create a novel series of functional materials [1,2,3]. One way to achieve this is to use the application of pressure [4]; however, another option within molecular materials is to use chemical substitution [2], inducing different properties [5] or where ground states can be altered by using different ligands [6,7,8,9].
A simple, well known class of materials to use as a test bed for tuning magnetic interactions is spin-Peierls (SP) systems. The 1D nature of the chemical magnetic structure relies on anisotropic interactions, where the coupling of the structural and magnetic properties leads to a dimerisation of magnetic atoms, ions or molecules, where, in the case of magnetic materials, below the SP transition the system is dominated by singlet-triplet excitations.
A well-known molecular SP system is potassium TCNQ (KTCNQ, where TCNQ = 7,7,8,8-tetracyanoquinodimethane), where the TCNQ molecules form quasi-1D chains of anions that are dominated by – interactions [10,11,12], with TCNQ stacking along the a-axis of the crystal structure. At high temperatures, the TCNQ anions are evenly spaced within the crystal structure. Below the SP transition temperature (), at 396 K and identified by using magnetic susceptibility data, the TCNQ anions dimerise, with a strong intra-dimer exchange, , calculated to be approximately −1800 K [10]. This transition is mediated by electron–phonon coupling and one observes a change in the vibrational modes on going through [13].
Modern interest in these systems has arisen from the ability to be able to chemically tune their properties. Recent work by us [14] has shown that when replacing TCNQ with TCNQF (2,3,5,6-Tetrafluoro-7,7,8,8-tetracyanoquinodimethane), there is a dramatic shift in , from 396 K to 160 K, as indicated by the magnetic susceptibility, which is a result of the change in interaction strength between the magnetic dimers. Using muon spin relaxation (SR) [15,16], we were able to study the dynamics of the singlet-triplet excitations within the SP state, and the corresponding singlet–triplet gap was also shown to decrease from 0.20 eV to 0.11 eV on substitution of the fluorine atoms. Although the SP state is expected to be quasi-1D, the magnetic fluctuations follow the critical power-law expected for a 3D Heisenberg system; therefore, these types of systems exhibit strongly correlated 3D behaviour. Additionally, further work also illustrated that the highly concentrated defect states can separately order, where within KTCNQF, these states were suggestive of 2D ordering [17].
Within this work, we go a step further and replace TCNQ with TCNQBr (2,5-dibromo-7,7,8,8-tetracyanoquinodimethane), where the slightly bent structure and steric hindrance imposed by the larger bromine atoms on the TCNQ molecule present an interesting comparison. We show that the system, KTCNQBr, is a highly disordered, where the bulk behaviour of the magnetic susceptibility is dominated by paramagnetic defects. However, there is also a broad peak in the temperature-dependent magnetic susceptibility, which suggests the presence of quasi-1D chains with antiferromagnetic interactions that exist between spins residing on TCNQBr anions. Importantly, there is no convincing evidence that KTCNQBr undergoes an SP transition in the temperature range investigated in this work.
2. Materials and Methods
The TCNQBr, was synthesised using the route described by Wheland and Martin [18]. The KTCNQBr was then synthesised through a metathesis reaction of potassium iodide and TCNQBr in anhydrous acetonitrile, as described by Melby et al. [19]. As previously reported with KTCNQF, the crystallisation is extremely fast, and this creates an intrinsic level of disorder within the crystallites. UV-vis spectroscopy confirmed that the resulting blue/purple powder contained the reduced form of TCNQBr.
The magnetic susceptibility measurements were taken using a Quantum Design MPMS. SR data were collected on the ARGUS spectrometer at the RIKEN-RAL Muon Facility within the ISIS Neutron and Muon Source. Due to the small amount of sample, the measurements were performed using a mini cold-finger, helium flow cryostat in flypast, where a small sample holder is used that allows all muons that do not stop within the sample to “fly past” and not be detected. Further information on the technique can be found elsewhere [15,16].
3. Results and Discussions
The magnetic susceptibility was measured in both Zero-Field Cooled (ZFC) and Field Cooled (FC) within an applied field of 1 kG and is dominated by a Curie tail, indicative of the presence of paramagnetic defects. Figure 1A shows the magnetic susceptibility between base temperature and 130 K, where despite the presence of a Curie tail, there is a divergence of the ZFC and FC data sets at approximately 120 K that is outside of the error within the measurement. This behaviour suggests that there may be a hysteric effect in addition to the bulk paramagnetism. Plotting the FC data as vs. T (inset of Figure 1A) shows a gradual increase as the temperature is increased, with the dotted line at 120 K indicating a point of inflection. This provides evidence that there is a change in the type of magnetic interactions within this region, with the downturn in vs. T suggesting that these interactions may be antiferromagnetic.
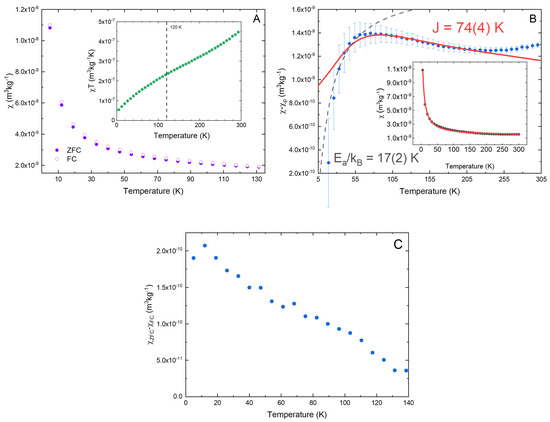
Figure 1.
Magnetic susceptibility data on KTCNQBr: (A) The zero-field cooled (ZFC) and field cooled (FC) magnetic susceptibility in 1 kG, where one can see the splitting of the curves at approximately 120 K, which is not accounted for by the error within the measurement (the error bars are smaller then the data points). The inset shows the FC data plotted as vs. T. (B) The residual FC magnetic susceptibility once the paramagnetic, Curie-tail has been subtracted, with the fit to Curie’s law shown in the inset. The solid line in the main figure is a fit to the Bonner–Fisher law and the dashed line a fit to Arrhenius behaviour. (C) Subtraction of the ZFC and FC magnetic susceptibilities highlighting the divergence of the two data sets.
In order to extract more information from these results, it is prudent to attempt to remove the Curie tail from the data. To do so, a fit was performed on the FC data set using the fitting function:
where C is the Curie constant and is the Weiss parameter. The parameter is an offset accounting for a temperature-independent contribution to the susceptibility, which was needed to obtain the best description of the data at high temperature. The general fit is shown in the inset of Figure 1B, with K, m kg K and m kg. On subtraction of the Curie tail from the data, one can see (Figure 1B) that there is a slight peak in the residual susceptibility at about 65 K. This is characteristic of a low-dimensional contribution to the bulk magnetic behaviour and is likely to be quasi-one-dimensional, being related to stacks of the TCNQBr anions forming a system where short-range magnetic correlations exist. To further extract information on this quasi-1D state, the Bonner–Fisher equation [20] with a constant background was fit to the data that describe the temperature dependence of antiferromagentic interactions along an chain. The fit, shown in Figure 1B, produces a exchange constant, K, with kg and a background value of the magnetic susceptibility of kg m. The value of , is consistent with the broad maxima within the data; however, intriguingly, the low value of N indicates that the 1D state does not account for the bulk of the sample. Additionally, in order to determine the size of a spin gap associated with a potential singlet–triplet excited state, the low temperature data were fitted to an Arrhenius function (see Figure 1B, dashed line) where an activation energy of 17(2) K (1.5 meV) was extracted. This result suggests that there may possibly be an SP transition occurring at the lowest temperatures investigated in this work, but one must be cautious with this interpretation; the Curie–Weiss law describing the defect paramagnetism may hold at higher temperatures but could break down at lower temperatures, within the region of interest, as other exchange pathways that are not governed by mean–field interactions may become dominant. In fact, the complexity of the defect paramagnetic response is highlighted by the underlying difference between the ZFC and FC curves, as shown in Figure 1C. There is a clear increase in the difference between the ZFC and FC magnetic susceptibilities as temperature is lowered, which is suggestive of a magnetically ordered component with remanence; however, this ordered state is not well defined and appears to have a slow onset as one cools the sample. This perhaps highlights the local and disordered nature of the underlying magnetism within the sample. It is also noteworthy that the number densities of each magnetic component derived from the data analyses are smaller then expected, and this may point to the predominance of itinerant electrons in the material, whilst the magnetic susceptibility measurements are dominated by the localised moments. Given the strong – interactions, it may not be surprising that electrons are able to delocalise across molecules or 1D stacks, and more work is needed to study this further.
In order to probe the evidence for a magnetic transition further, muon spin relaxation (SR) was used. SR is an exceptionally sensitive probe of weak magnetic order and dynamics on a local scale. The interaction between the muon, in this case , and the surrounding electronic and nuclear moments can provide information on both the static and dynamic parts of the magnetic susceptibility. The muon will respond to static magnetic fields that are transverse to its initial polarisation by precessing, where the precessional frequency can be related to the internal field through , MHz/T. Due to the small amount of sample, the measurements were performed using the fly-past set-up and this has to be optimised to collect the best quality data possible.
The SR data were collected in zero-field, and one measures the time dependence of the asymmetry in the decay of muon polarisation when the muon is implanted within the sample. All spectra were fit using an exponential function:
where is the relaxing asymmetry, is the muon spin relaxation rate and is the baseline. For the whole data set, the baseline was fixed at 16.4%. The temperature dependencies of other fitting parameters can be seen within Figure 2. The relaxation rate is sensitive to both static and dynamic magnetic behaviour, where in the fast fluctuating limit, , where is the correlation time and is the static field distribution. The gradual increase in within Figure 2 is a hallmark of a slowing down of dynamic electronic fluctuations, and this has been observed within other KTCNQ salts [14] as well as other TCNQ-based salts [21,22,23]. Key to this is the gradual increase in , where the slowing down of electronic fluctuations appears to be very broad and broader then that observed for other TCNQ-based SP systems [14,23,24], with the onset of this increase in being well above the drop observed in the magnetic susceptibility below 65 K, as shown in Figure 1B. The data are more indicative of a slowly evolving magnetic system, where there are a range of interactions, likely due to short-range order, that create local areas of magnetic order which drive the system into a quasi-static state. Such a magnetic state may be equivalent to that suggested by the magnetic susceptibility difference shown in Figure 1C. Accompanying this change in is a drop in the relaxing asymmetry, which can be indicative of the formation of static order with an internal field that pushes the precessional frequency beyond the experimental time resolution and is consistent with the rise in . An effective way to model the onset of a transition is to use an error function, a function describing the first derivative of a Gaussian distribution of transition temperatures, which has also been used elsewhere [25]. Using an error function to model the data within the inset of Figure 2, the midpoint of the curve is 167(9) K. Therefore, it is likely that this is not an SP transition, and instead, there is a build up of 1D correlations, where the electronic moments move into the experimental time scale and then become quasi-static. Below 50 K, the relaxing asymmetry increases, and this may be caused by a reduction in the internal field due to a rearrangement of the spin creating a weaker internal field, with the saturation of indicating that persistent dynamics are present. However, one cannot discount that the flattening out of could also be due to a quasi-static, disordered magnetic state, like a spin-glass [16]. Interestingly, this is the also the point at which the magnetic susceptibility shown within the Figure 1B turns over and so the two behaviours may be correlated.
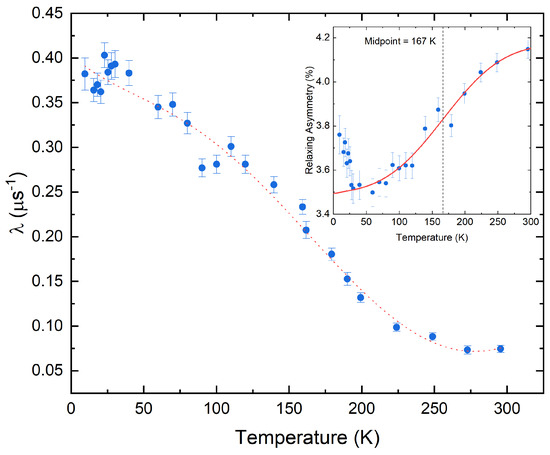
Figure 2.
The temperature dependence of the muon spin relaxation rate, in zero-field. The dotted line is a guide to the eye. The inset shows the temperature dependence of the relaxing asymmetry; the solid line is a fit to the data using an error function, with a midpoint of 167 K.
4. Conclusions
The substitution of TCNQ for TCNQBr within the simple spin-Peierls system KTCNQ has created a system where there is little evidence for a spin-Peierls transition as seen within similar molecular systems. The magnetic susceptibility data provide some evidence that there is a residual component that could be treated as showing 1D behaviour; however, it is worth nothing that the fits are merely suggestive and not conclusive on their own. Therefore, whilst one cannot discount that there is a change in behaviour below 65 K, there is evidence that the residual component undergoes a different transition or is dominated by a different type of interaction at higher temperatures. This is further highlighted by the difference between the ZFC and FC data sets. The SR data present complementary information, but the data are not consistent with an spin-Peierls system that would align with that from the magnetic susceptibility shown in Figure 1B. Instead, the SR measurements point to a system that has been driven into a state where short-range magnetic correlations dominate. The two different regions of behaviour within the SR certainly warrant more exploration, but the current data suggest that, on cooling, there is a build-up of magnetic correlations and these may order or enter a magnetic state where persistent dynamics are present. Given the planar nature of the TCNQ molecules, it makes sense that this system is also dominated by 1D interactions, but the bulky bromine atoms likely prevent the structural change needed for the system to dimerise and fall into the spin-Peierls ground state.
Author Contributions
Conceptualization, A.B.; Methodology, A.B. and I.T.; Formal analysis, A.B. and I.T.; Investigation, A.B., I.T. and M.S.; Data curation, A.B.; Writing—original draft, A.B.; Writing—review & editing, I.T. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the ISIS Neutron and Muon Source and RIKEN for access to the ARGUS spectrometer.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, C.; Liu, D.; Lin, W. Metal–Organic Frameworks as A Tunable Platform for Designing Functional Molecular Materials. J. Am. Chem. Soc. 2013, 135, 13222–13234. [Google Scholar] [CrossRef] [PubMed]
- Coronado, E. Molecular magnetism: From chemical design to spin control in molecules, materials and devices. Nat. Rev. Mater. 2020, 5, 87–104. [Google Scholar] [CrossRef]
- Reczyński, M.; Nakabayashi, K.; Ohkoshi, S.-I. Tuning the Optical Properties of Magnetic Materials. Eur. J. Inorg. Chem. 2020, 28, 2669–2678. [Google Scholar] [CrossRef]
- McMillan, P.F. New materials from high-pressure experiments. Nat. Mater. 2002, 1, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Coronado, E.; Martí-Gastaldo, C.; Navarro-Moratalla, E.; Ribera, A.; Blundell, S.J.; Baker, P.J. Coexistence of superconductivity and magnetism by chemical design. Nat. Chem. 2010, 2, 1031–1036. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Montigaud, V.; Cador, O.; Li, G.-P.; Guennic, B.L.; Tang, J.-K.; Wang, Y.-Y. Tuning the Magnetic Interactions in Dy(III)4 Single-Molecule Magnets. Inorg. Chem. 2018, 57, 8550–8557. [Google Scholar] [CrossRef]
- Yin, Z.; Zhou, Y.-L.; Zeng, M.-H.; Kurmoo, M. The concept of mixed organic ligands in metal–organic frameworks: Design, tuning and functions. Dalton Trans. 2015, 44, 5258–5275. [Google Scholar] [CrossRef]
- Xie, H.; Vignesh, K.R.; Zhang, X.; Dunbar, K.R. From spin-crossover to single molecule magnetism: Tuning magnetic properties of Co(II) bis-ferrocenylterpy cations via supramolecular interactions with organocyanide radical anion. J. Mater. Chem. C 2020, 8, 8135–8144. [Google Scholar] [CrossRef]
- Kurmoo, M. Magnetic metal–organic frameworks. Chem. Soc. Rev. 2009, 38, 1353–1379. [Google Scholar] [CrossRef]
- Vegter, J.G.; Hibma, T.; Kommandeur, J. New phase transitions in simple M-TCNQ-salts. Chem. Phys. Lett. 1969, 3, 427. [Google Scholar] [CrossRef]
- Lépine, Y.; Caillxex, A.; Larochelle, V. Potassium-tetracyanoquinodimethane (K-TCNQ): A spin-Peierls system. Phys. Rev. B 1978, 18, 3585. [Google Scholar] [CrossRef]
- Konno, M.; Ishii, T.; Saito, Y. The crystal structures of the low- and high-temperature modifications of potassium 7,7,8,8-tetracyanoquinodimethanide. Acta Cryst. 1977, B33, 7603–7770. [Google Scholar] [CrossRef]
- Tanner, D.B.; Jacobsen, C.S.; Bright, A.A.; Heeger, A.J. Infrared studies of the energy gap and electron-phonon interaction in potassium-tetracyanoquinodimethane (K-TCNQ). Phys. Rev. B 1977, 16, 3283. [Google Scholar] [CrossRef]
- Berlie, A.; Terry, I.; Szablewski, M.; Giblin, S.R. Tuneability and criticality in a three-dimensional stacked molecular system. Phys. Rev. B 2016, 93, 054422. [Google Scholar] [CrossRef]
- Hillier, A.D.; Blundell, S.J.; McKenzie, I.; Umegaki, I.; Shu, L.; Wright, J.A.; Prokscha, T.; Bert, F.; Shimomura, K.; Berlie, A.; et al. Muon Spin Spectroscopy. Nat. Rev. Methods Prim. 2022, 2, 4. [Google Scholar] [CrossRef]
- Blundell, S.J.; Renzi, R.D.; Lancaster, T.; Pratt, F.L. (Eds.) Muon Spectroscopy: An Introduction; Oxford University Press: Oxford, UK, 2022. [Google Scholar]
- Berlie, A.; Terry, I.; Cottrell, S.; Pratt, F.L.; Szablewski, M. Magnetic ordering of defects in a molecular spin-Peierls system. J. Phys. Condens. Matter 2017, 29, 025809. [Google Scholar] [CrossRef]
- Wheland, R.C.; Martin, E.L. Synthesis of Substituted 7,7,8,8-Tetracyanoquinodimethanes. J. Org. Chem. 1975, 40, 3101. [Google Scholar] [CrossRef]
- Melby, L.R.; Harder, R.J.; Hertler, W.R.; Mahler, W.; Benson, R.E.; Mochel, W.E. Substituted Quinodimethans. II. Anion-radical Derivatives and Complexes of 7,7,8,8-Tetracyanoquinodimethan. J. Am. Chem. Soc. 1962, 84, 3374–3387. [Google Scholar] [CrossRef]
- Bonner, J.C.; Fisher, M.E. Linear magentic chains with anisotropic coupling. Phys. Rev. 1964, 135, A640. [Google Scholar] [CrossRef]
- Berlie, A.; Terry, I.; Szablewski, M.; Giblin, S.R. Separating the ferromagnetic and glassy behavior within the metal-organic magnet Ni(TCNQ)2. Phys. Rev. B 2015, 92, 184431. [Google Scholar] [CrossRef]
- Blundell, S.J.; Lancaster, T.; Brooks, M.L.; Pratt, F.L.; Taliaferro, M.L.; Miller, J.S. A μSR study of the metamagnetic phase transition in the electron-transfer salt [Fe(Cp)2] [TCNQ]. Phys. B Condens. Matter 2006, 374–375, 114–117. [Google Scholar] [CrossRef]
- Berlie, A.; Terry, I.; Szablewski, M. A 3D antiferromagnetic ground state in a quasi-1D π-stacked charge-transfer system. J. Mater. Chem. C 2018, 6, 12468–12472. [Google Scholar] [CrossRef]
- Lovett, B.W.; Blundell, S.J.; Pratt, F.L.; Jestädt, T.; Hayes, W.; Tagaki, S.; Kurmoo, M. Spin fluctuations in the spin-Peierls compound MEM(TCNQ)2 studied using muon spin relaxation. Phys. Rev. B 2000, 61, 12241. [Google Scholar] [CrossRef]
- Frandsen, B.A.; Petersen, K.A.; Ducharme, N.A.; Shaw, A.G.; Gibson, E.J.; Winn, B.; Yan, J.; Zhang, J.; Manley, M.E.; Hermann, R.P. Spin dynamics and a nearly continuous magnetic phase transition in an entropy-stabilized oxide antiferromagnet. Phys. Rev. Mater. 2020, 4, 074405. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).