Spin-Topological Electronic Valve in Ni/hBN–Graphene–hBN/Ni Magnetic Junction
Abstract
1. Introduction
2. Computational Methods
3. Results and Discussion
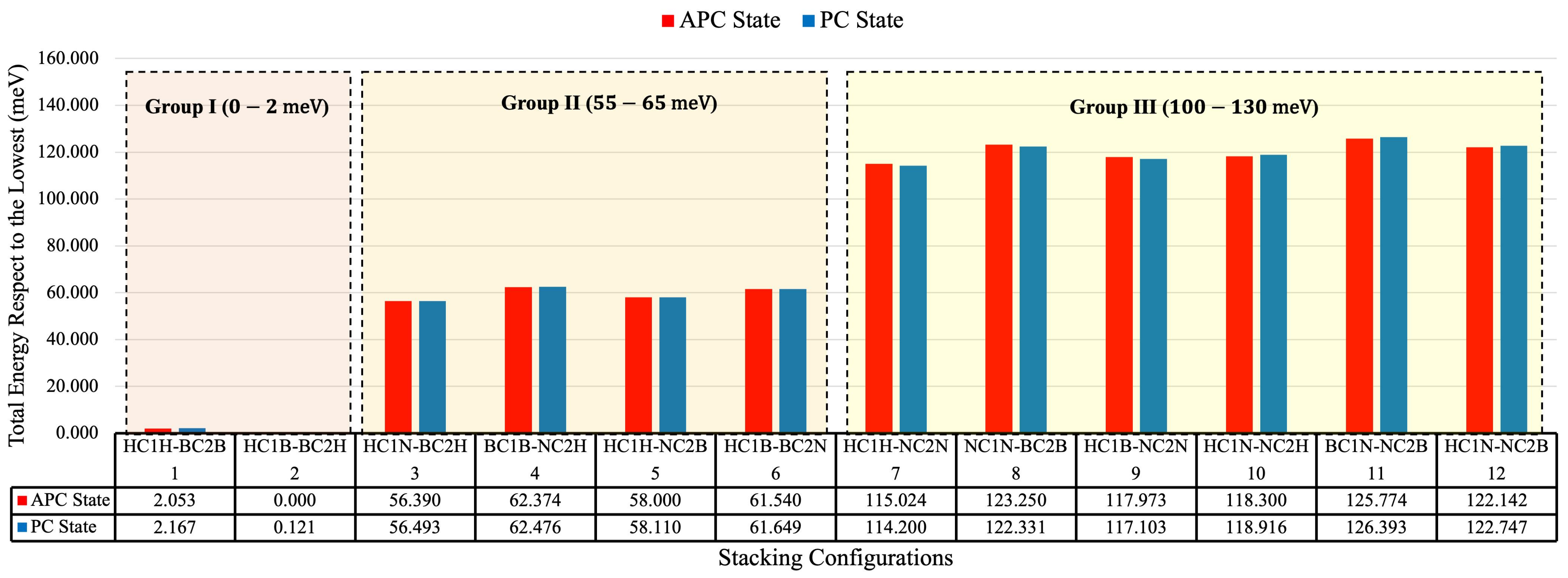
3.1. Total Energy and Its Correlation to Van Der Waals Interaction
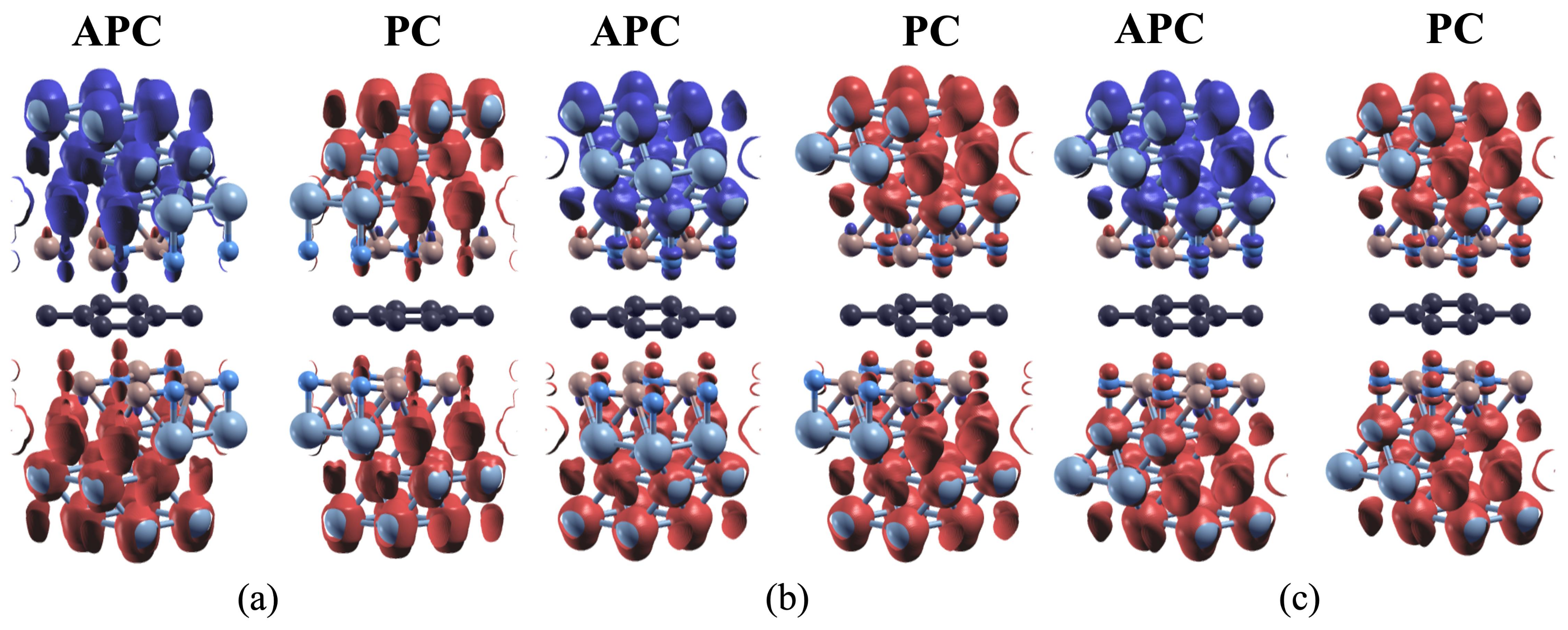
3.2. Magnetic Properties and Induced Magnetic Moments on Graphene
3.3. A Controllable Dirac Cone of Graphene due to a Tunable Pseudospin Term of Graphene
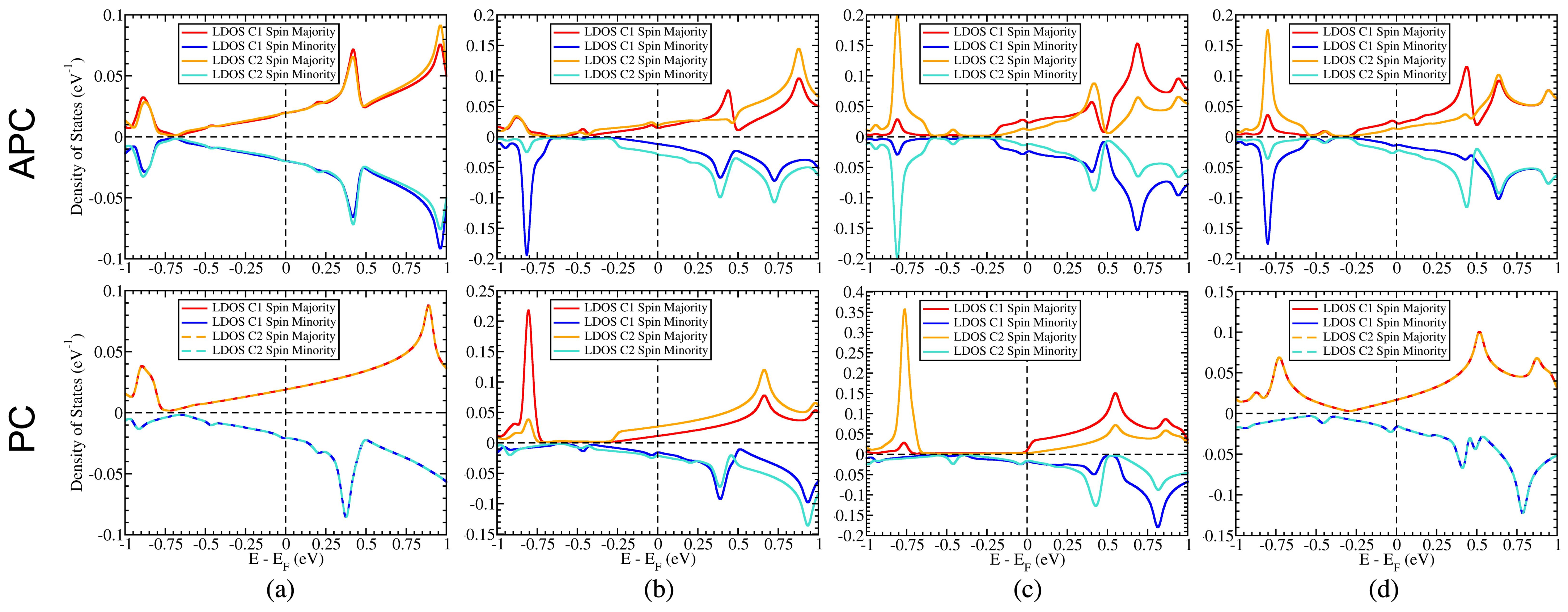
3.4. The Influence of the Surface State of Ni Works Directly on C Atoms in the Gapped Dirac Cone
3.5. Controllable Mass-Gapped Dirac Cone through the Ni Surface State Influence on C Atoms
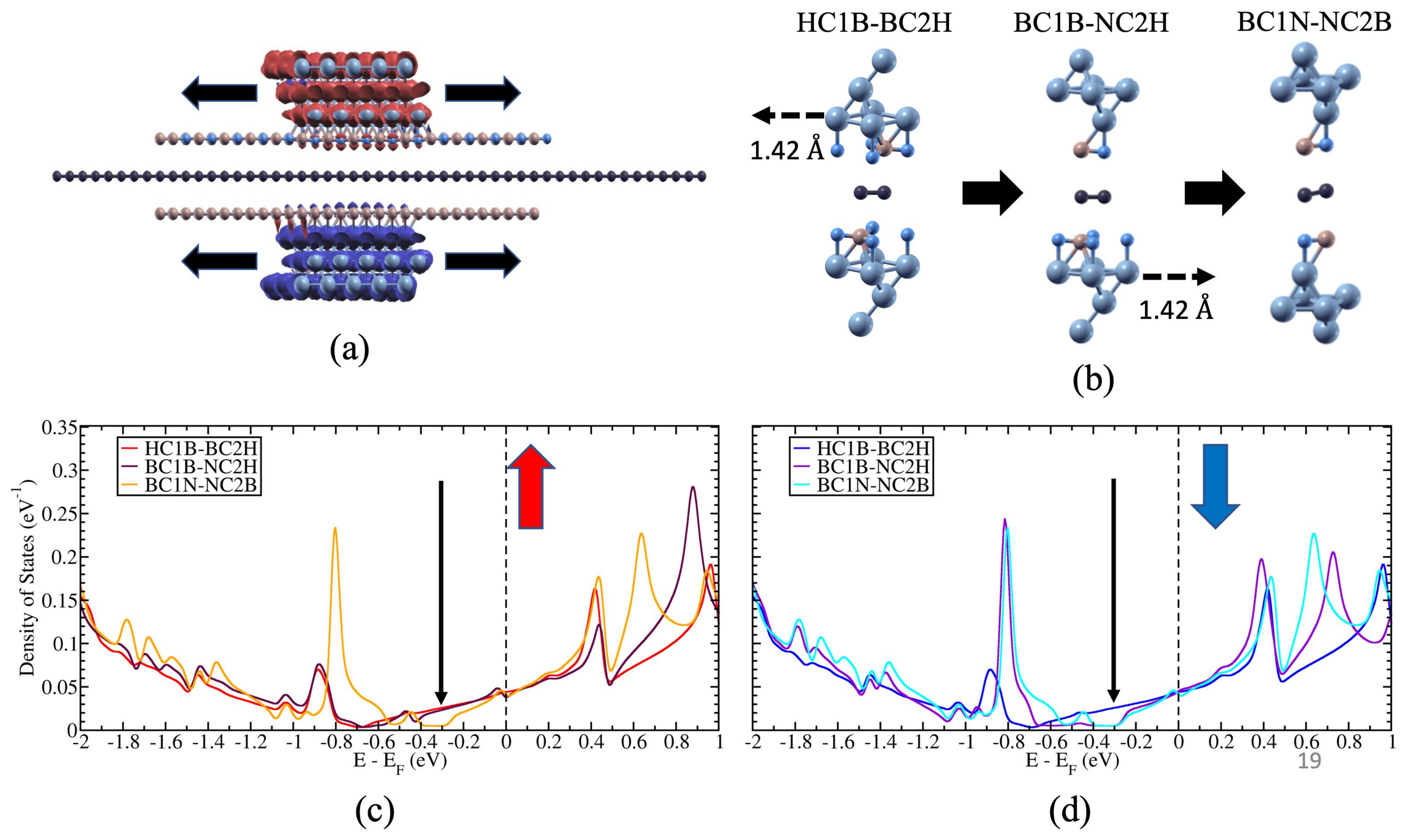
3.6. Possible Application on the Spin-Topological Electronic Valve
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Morozov, S.V.; Novoselov, K.S.; Katsnelson, M.I.; Schedin, F.; Elias, D.C.; Jaszczak, J.A.; Geim, A.K. Giant Intrinsic Carrier Mobilities in Graphene and Its Bilayer. Phys. Rev. Lett. 2008, 100, 016602. [Google Scholar] [CrossRef]
- Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef]
- Schultz, B.J.; Jaye, C.; Lysaght, P.S.; Fischer, D.A.; Prendergast, D.; Banerjee, S. On chemical bonding and electronic structure of graphene–metal contacts. Chem. Sci. 2013, 4, 494–502. [Google Scholar] [CrossRef]
- Abtew, T.; Shih, B.C.; Banerjee, S.; Zhang, P. Graphene–ferromagnet interfaces: Hybridization, magnetization and charge transfer. Nanoscale 2013, 5, 1902–1909. [Google Scholar] [CrossRef] [PubMed]
- Weser, M.; Rehder, Y.; Horn, K.; Sicot, M.; Fonin, M.; Preobrajenski, A.B.; Voloshina, E.N.; Goering, E.; Dedkov, Y.S. Induced magnetism of carbon atoms at the graphene/Ni(111) interface. Appl. Phys. Lett. 2010, 96, 012504. [Google Scholar] [CrossRef]
- Joshi, N.; Ballav, N.; Ghosh, P. Hydrogen-induced reversal of spin alignment in graphene supported on Ni(111) surface. Phys. Rev. B 2012, 86, 121411. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Morishita, N.; Sunnardianto, G.K.; Miyao, S.; Kusakabe, K. Theoretical Analysis of Pseudodegenerate Zero-Energy Modes in Vacancy-Centered Hexagonal Armchair Nanographene. J. Phys. Soc. Jpn. 2016, 85, 084703. [Google Scholar] [CrossRef]
- Dahal, A.; Batzill, M. Graphene–nickel interfaces: A review. Nanoscale 2014, 6, 2548–2562. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.; Choi, Y.C.; Kim, K.S. Graphene Spin-Valve Device Grown Epitaxially on the Ni(111) Substrate: A First Principles Study. J. Phys. Chem. C 2011, 115, 6019–6023. [Google Scholar] [CrossRef]
- Sato, R.; Hiraiwa, T.; Inoue, J.; Honda, S.; Itoh, H. Magnetoresistance in fcc Ni/graphene/fcc Ni(111) junctions. Phys. Rev. B 2012, 85, 094420. [Google Scholar] [CrossRef]
- Liu, H.; Kondo, H.; Ohno, T. Spintronic Transport in Armchair Graphene Nanoribbon with Ferromagnetic Electrodes: Half-Metallic Properties. Nanoscale Res. Lett. 2016, 11, 456. [Google Scholar] [CrossRef]
- Martin, M.B.; Dlubak, B.; Weatherup, R.S.; Piquemal-Banci, M.; Yang, H.; Blume, R.; Schloegl, R.; Collin, S.; Petroff, F.; Hofmann, S.; et al. Protecting nickel with graphene spin-filtering membranes: A single layer is enough. Appl. Phys. Lett. 2015, 107, 012408. [Google Scholar] [CrossRef]
- Asshoff, P.U.; Sambricio, J.L.; Rooney, A.P.; Slizovskiy, S.; Mishchenko, A.; Rakowski, A.M.; Hill, E.W.; Geim, A.K.; Haigh, S.J.; Fal’ko, V.I.; et al. Magnetoresistance of vertical Co-graphene-NiFe junctions controlled by charge transfer and proximity-induced spin splitting in graphene. 2D Mater. 2017, 4, 031004. [Google Scholar] [CrossRef]
- Entani, S.; Seki, T.; Sakuraba, Y.; Yamamoto, T.; Takahashi, S.; Naramoto, H.; Takanashi, K.; Sakai, S. Magnetoresistance effect in Fe20Ni80/graphene/Fe20Ni80 vertical spin valves. Appl. Phys. Lett. 2016, 109, 082406. [Google Scholar] [CrossRef]
- Mohiuddin, T.M.G.; Hill, E.; Elias, D.; Zhukov, A.; Novoselov, K.; Geim, A. Graphene in Multilayered CPP Spin Valves. IEEE Trans. Magn. 2008, 44, 2624–2627. [Google Scholar] [CrossRef]
- Iqbal, M.Z.; Iqbal, M.W.; Lee, J.H.; Kim, Y.S.; Chun, S.H.; Eom, J. Spin valve effect of NiFe/graphene/NiFe junctions. Nano Res. 2013, 6, 373–380. [Google Scholar] [CrossRef]
- Iqbal, M.Z.; Iqbal, M.W.; Jin, X.; Hwang, C.; Eom, J. Interlayer dependent polarity of magnetoresistance in graphene spin valves. J. Mater. Chem. C 2015, 3, 298–302. [Google Scholar] [CrossRef]
- Chen, J.J.; Meng, J.; Zhou, Y.B.; Wu, H.C.; Bie, Y.Q.; Liao, Z.M.; Yu, D.P. Layer-by-layer assembly of vertically conducting graphene devices. Nat. Commun. 2013, 4, 1921. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Li, T.; Guo, X. Vertical Graphene Spin Valves Based on La2/3Sr1/3MnO3 Electrodes. ACS Appl. Mater. Interfaces 2014, 6, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Xue, L.; Abruña, H.D.; Ralph, D.C. Magnetic tunnel junctions with single-layer-graphene tunnel barriers. Phys. Rev. B 2014, 89, 184418. [Google Scholar] [CrossRef]
- Mandal, S.; Saha, S.K. Ni/graphene/Ni nanostructures for spintronic applications. Nanoscale 2012, 4, 986–990. [Google Scholar] [CrossRef]
- Wicaksono, Y.; Teranishi, S.; Nishiguchi, K.; Kusakabe, K. Tunable induced magnetic moment and in-plane conductance of graphene in Ni/graphene/Ni nano-spin-valve-like structure: A first principles study. Carbon 2019, 143, 828–836. [Google Scholar] [CrossRef]
- Wicaksono, Y.; Harfah, H.; Sunnardianto, G.K.; Majidi, M.A.; Kusakabe, K. Colossal in-plane magnetoresistance ratio of graphene sandwiched with Ni nanostructures. RSC Adv. 2022, 12, 13985–13991. [Google Scholar] [CrossRef]
- Harfah, H.; Wicaksono, Y.; Sunnardianto, G.K.; Majidi, M.A.; Kusakabe, K. High magnetoresistance of a hexagonal boron nitride–graphene heterostructure-based MTJ through excited-electron transmission. Nanoscale Adv. 2022, 4, 117–124. [Google Scholar] [CrossRef]
- Pezo, A.; Zanolli, Z.; Wittemeier, N.; Ordejón, P.; Fazzio, A.; Roche, S.; Garcia, J.H. Manipulation of spin transport in graphene/transition metal dichalcogenide heterobilayers upon twisting. 2D Mater. 2021, 9, 015008. [Google Scholar] [CrossRef]
- Zollner, K.; Fabian, J. Engineering Proximity Exchange by Twisting: Reversal of Ferromagnetic and Emergence of Antiferromagnetic Dirac Bands in Graphene/Cr2Ge2Te6. Phys. Rev. Lett. 2022, 128, 106401. [Google Scholar] [CrossRef]
- Eliseev, E.A.; Morozovska, A.N.; Strikha, M.V. Strain Engineering of Ferromagnetic-Graphene-Ferroelectric Nanostructures. Phys. Rev. Appl. 2020, 14, 024081. [Google Scholar] [CrossRef]
- Harfah, H.; Wicaksono, Y.; Majidi, M.A.; Kusakabe, K. Spin-Current Control by Induced Electric Polarization Reversal in Ni/hBN/Ni: A Cross-Correlation Material. ACS Appl. Electron. Mater. 2020, 2, 1689–1699. [Google Scholar] [CrossRef]
- Wicaksono, Y. Theoretical Study of Gap Opening/Closing Control of Dirac Cone Using Spin-dependent Potentials in Graphene-based Magnetic Junctions. Ph.D. Thesis, Osaka University, Osaka, Japan, 2022. Available online: https://ir.library.osaka-u.ac.jp/repo/ouka/all/89505/32918_Dissertation.pdf (accessed on 21 March 2023).
- Sánchez-Portal, D.; Ordejón, P.; Artacho, E.; Soler, J.M. Density-functional method for very large systems with LCAO basis sets. Int. J. Quantum Chem. 1997, 65, 453–461. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Physics: Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar] [CrossRef]
- Sánchez-Portal, D.; Artacho, E.; Soler, J. Analysis of atomic orbital basis sets from the projection of plane-wave results. J. Phys. Condens. Matter 1996, 8, 3859–3880. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Ferri, N.; DiStasio, R.A.; Tkatchenko, A. Wavelike charge density fluctuations and van der Waals interactions at the nanoscale. Science 2016, 351, 1171–1176. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Silvestrelli, P.L.; Tkatchenko, A. Physical adsorption at the nanoscale: Towards controllable scaling of the substrate-adsorbate van der Waals interaction. Phys. Rev. B 2017, 95, 235417. [Google Scholar] [CrossRef]
- Dobson, J.F.; White, A.; Rubio, A. Asymptotics of the Dispersion Interaction: Analytic Benchmarks for van der Waals Energy Functionals. Phys. Rev. Lett. 2006, 96, 073201. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Silvestrelli, P.L. Hidden by graphene—Towards effective screening of interface van der Waals interactions via monolayer coating. Carbon 2018, 139, 486–491. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Silvestrelli, P.L. Faraday-like Screening by Two-Dimensional Nanomaterials: A Scale-Dependent Tunable Effect. J. Phys. Chem. Lett. 2019, 10, 2044–2050. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Reimers, J.R.; Dobson, J.F.; Gould, T. Faraday cage screening reveals intrinsic aspects of the van der Waals attraction. Proc. Natl. Acad. Sci. USA 2018, 115, E10295–E10302. [Google Scholar] [CrossRef] [PubMed]
- Ambrosetti, A.; Silvestrelli, P.L. Communication: Enhanced chemical reactivity of graphene on a Ni(111) substrate. J. Chem. Phys. 2016, 144, 111101. [Google Scholar] [CrossRef] [PubMed]
- Quhe, R.; Zheng, J.; Luo, G.; Liu, Q.; Qin, R.; Zhou, J.; Yu, D.; Nagase, S.; Mei, W.N.; Gao, Z.; et al. Tunable and sizable band gap of single-layer graphene sandwiched between hexagonal boron nitride. NPG Asia Mater. 2012, 4, e6. [Google Scholar] [CrossRef]
- Wasserman, E.; Murray, R.W.; Yager, W.A.; Trozzolo, A.M.; Smolinsky, G. Quintet ground states of m-dicarbene and m-dinitrene compounds. J. Am. Chem. Soc. 1967, 89, 5076–5078. [Google Scholar] [CrossRef]
- Ando, T. Exotic electronic and transport properties of graphene. Phys. Low-Dimens. Syst. Nanostruct. 2007, 40, 213–227. [Google Scholar] [CrossRef]
- Zhou, S.Y.; Gweon, G.H.; Fedorov, A.V.; First, P.N.; de Heer, W.A.; Lee, D.H.; Guinea, F.; Castro Neto, A.H.; Lanzara, A. Substrate-induced bandgap opening in epitaxial graphene. Nat. Mater. 2007, 6, 770–775. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.B.; Yin, J.; Tóvári, E.; Yang, Y.; Lin, L.; Holwill, M.; Birkbeck, J.; Perello, D.J.; Xu, S.; et al. Composite super-moirélattices in double-aligned graphene heterostructures. Sci. Adv. 2022, 5, eaay8897. [Google Scholar] [CrossRef] [PubMed]
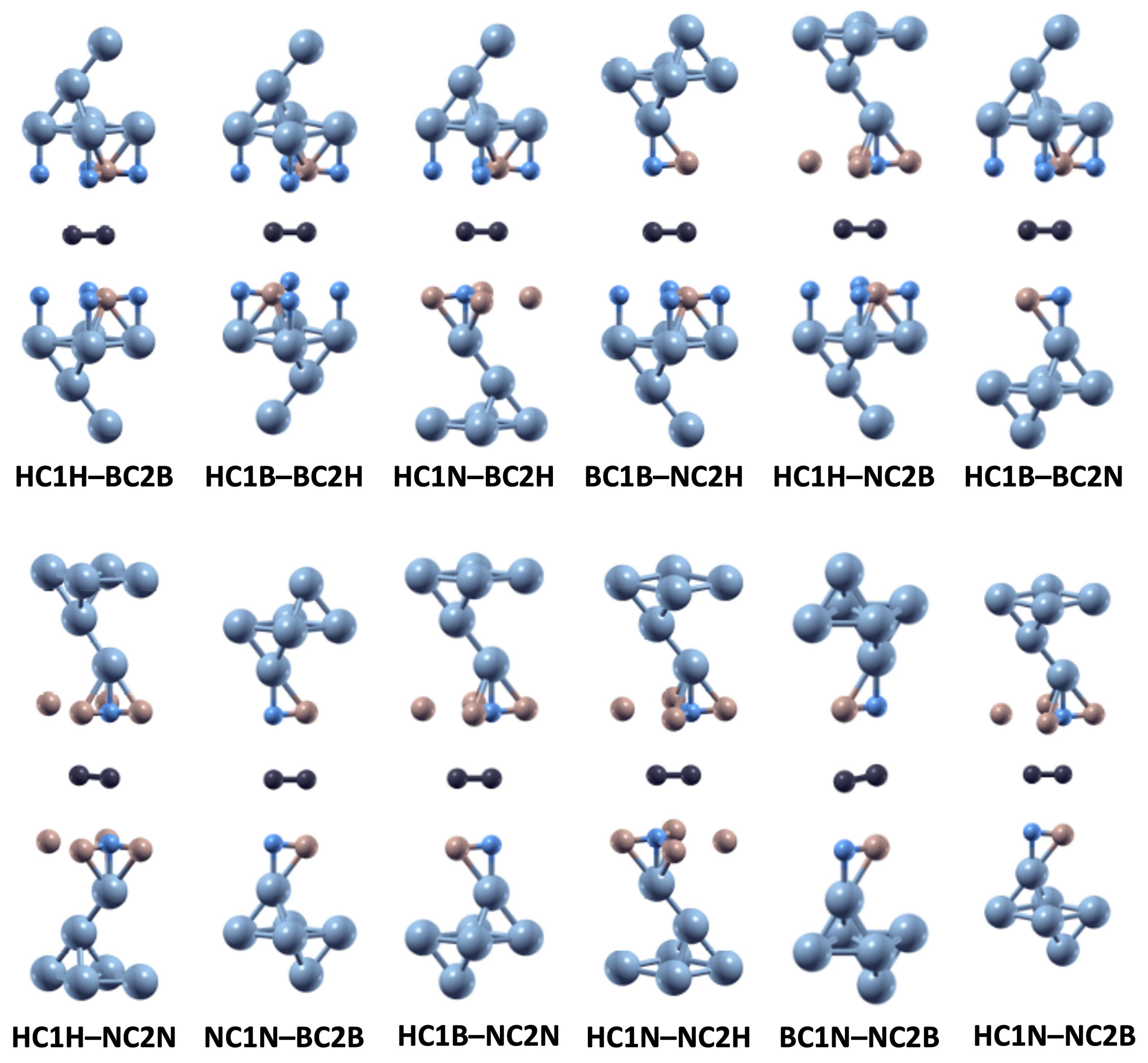


| No. | Stacking Arrangement Name | Interlayer Distance (Å) | |||
|---|---|---|---|---|---|
| N-Gr | B-Gr | ||||
| Upper | Lower | Upper | Lower | ||
| 1 | HC1H–BC2B | 2.71 | 2.71 | 2.85 | 2.85 |
| 2 | HC1B–BC2H | 2.71 | 2.71 | 2.85 | 2.85 |
| 3 | HC1N–BC2H | 2.74 | 2.76 | 2.88 | 2.90 |
| 4 | BC1B–NC2H | 2.77 | 2.76 | 2.91 | 2.89 |
| 5 | HC1H–NC2B | 2.76 | 2.75 | 2.90 | 2.88 |
| 6 | HC1B–BC2N | 2.76 | 2.78 | 2.89 | 2.92 |
| 7 | HC1H–NC2N | 2.79 | 2.79 | 2.93 | 2.93 |
| 8 | NC1N–BC2B | 2.81 | 2.81 | 2.95 | 2.95 |
| 9 | HC1B–NC2N | 2.80 | 2.81 | 2.94 | 2.94 |
| 10 | HC1N–NC2H | 2.80 | 2.80 | 2.94 | 2.94 |
| 11 | BC1N–NC2B | 2.83 | 2.83 | 2.96 | 2.96 |
| 12 | HC1N–NC2B | 2.81 | 2.82 | 2.95 | 2.95 |
| No. | Stacking Arrangement Name | Magnetic Moment () | |||
|---|---|---|---|---|---|
| APC | PC | ||||
| C1 | C2 | C1 | C2 | ||
| 1 | HC1H–BC2B | 0.000 | 0.000 | 0.002 | 0.003 |
| 2 | HC1B–BC2H | 0.001 | −0.001 | 0.002 | 0.002 |
| 3 | HC1N–BC2H | −0.006 | 0.005 | −0.004 | 0.006 |
| 4 | BC1B–NC2H | −0.005 | 0.006 | 0.006 | −0.003 |
| 5 | HC1H–NC2B | −0.004 | 0.005 | 0.007 | −0.002 |
| 6 | HC1B–BC2N | 0.004 | −0.004 | 0.007 | −0.002 |
| 7 | HC1H–NC2N | 0.000 | 0.000 | −0.011 | 0.015 |
| 8 | NC1N–BC2B | 0.000 | 0.000 | −0.014 | 0.015 |
| 9 | HC1B–NC2N | 0.000 | 0.001 | 0.015 | −0.012 |
| 10 | HC1N–NC2H | 0.012 | −0.012 | 0.002 | 0.002 |
| 11 | BC1N–NC2B | −0.010 | 0.010 | 0.003 | 0.003 |
| 12 | HC1N–NC2B | −0.011 | 0.011 | 0.002 | 0.002 |
| No. | Atom Name | Mulliken Partial Atomic Charge | |||
|---|---|---|---|---|---|
| HC1B–BC2H | BC1B–NC2H | ||||
| Spin UP | Spin DOWN | Spin UP | Spin DOWN | ||
| 1 | Upper B | 1.914 | 1.935 | 1.917 | 1.938 |
| 2 | Upper N | 2.193 | 2.169 | 2.187 | 2.161 |
| 3 | C1 | 1.981 | 1.979 | 1.997 | 1.991 |
| 4 | C2 | 1.981 | 1.979 | 1.969 | 1.972 |
| 5 | Lower N | 2.193 | 2.169 | 2.193 | 2.168 |
| 6 | Lower B | 1.914 | 1.935 | 1.915 | 1.936 |
| No. | Stacking Arrangement Name | Integrated SPIN-charge Density () of -Orbital | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APC | PC | ||||||||||||
| C1 | C2 | C1-C2 | C1 | C2 | C1-C2 | ||||||||
| ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | ||
| 1 | HC1H–BC2B | 0.456 | 0.456 | 0.460 | 0.460 | −0.004 | −0.004 | 0.457 | 0.456 | 0.461 | 0.461 | −0.004 | 0.003 |
| 2 | HC1B–BC2H | 0.458 | 0.459 | 0.459 | 0.458 | −0.001 | 0.001 | 0.459 | 0.458 | 0.459 | 0.459 | 0.000 | 0.000 |
| 3 | HC1N–BC2H | 0.451 | 0.457 | 0.468 | 0.463 | −0.017 | −0.006 | 0.453 | 0.456 | 0.468 | 0.463 | −0.015 | −0.007 |
| 4 | HC1H–NC2N | 0.449 | 0.449 | 0.474 | 0.474 | −0.025 | −0.025 | 0.443 | 0.454 | 0.482 | 0.467 | −0.039 | −0.013 |
| 5 | BC1N–NC2B | 0.455 | 0.464 | 0.464 | 0.455 | −0.009 | 0.009 | 0.461 | 0.459 | 0.460 | 0.459 | 0.001 | 0.000 |
| No. | Interchanging Stacking Configuration | In-Plane Conductance Difference Ratio |
|---|---|---|
| 1 | HC1B-BC2H ↔ BC1B-NC2H | 42% |
| 2 | BC1B-NC2H ↔ BC1N-NC2B | 66% |
| 3 | HC1B-BC2H ↔ BC1N-NC2B | 80% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wicaksono, Y.; Harfah, H.; Sunnardianto, G.K.; Majidi, M.A.; Kusakabe, K. Spin-Topological Electronic Valve in Ni/hBN–Graphene–hBN/Ni Magnetic Junction. Magnetochemistry 2023, 9, 113. https://doi.org/10.3390/magnetochemistry9050113
Wicaksono Y, Harfah H, Sunnardianto GK, Majidi MA, Kusakabe K. Spin-Topological Electronic Valve in Ni/hBN–Graphene–hBN/Ni Magnetic Junction. Magnetochemistry. 2023; 9(5):113. https://doi.org/10.3390/magnetochemistry9050113
Chicago/Turabian StyleWicaksono, Yusuf, Halimah Harfah, Gagus Ketut Sunnardianto, Muhammad Aziz Majidi, and Koichi Kusakabe. 2023. "Spin-Topological Electronic Valve in Ni/hBN–Graphene–hBN/Ni Magnetic Junction" Magnetochemistry 9, no. 5: 113. https://doi.org/10.3390/magnetochemistry9050113
APA StyleWicaksono, Y., Harfah, H., Sunnardianto, G. K., Majidi, M. A., & Kusakabe, K. (2023). Spin-Topological Electronic Valve in Ni/hBN–Graphene–hBN/Ni Magnetic Junction. Magnetochemistry, 9(5), 113. https://doi.org/10.3390/magnetochemistry9050113







