A Simulation Independent Analysis of Single- and Multi-Component cw ESR Spectra
Abstract
1. Introduction
2. Method
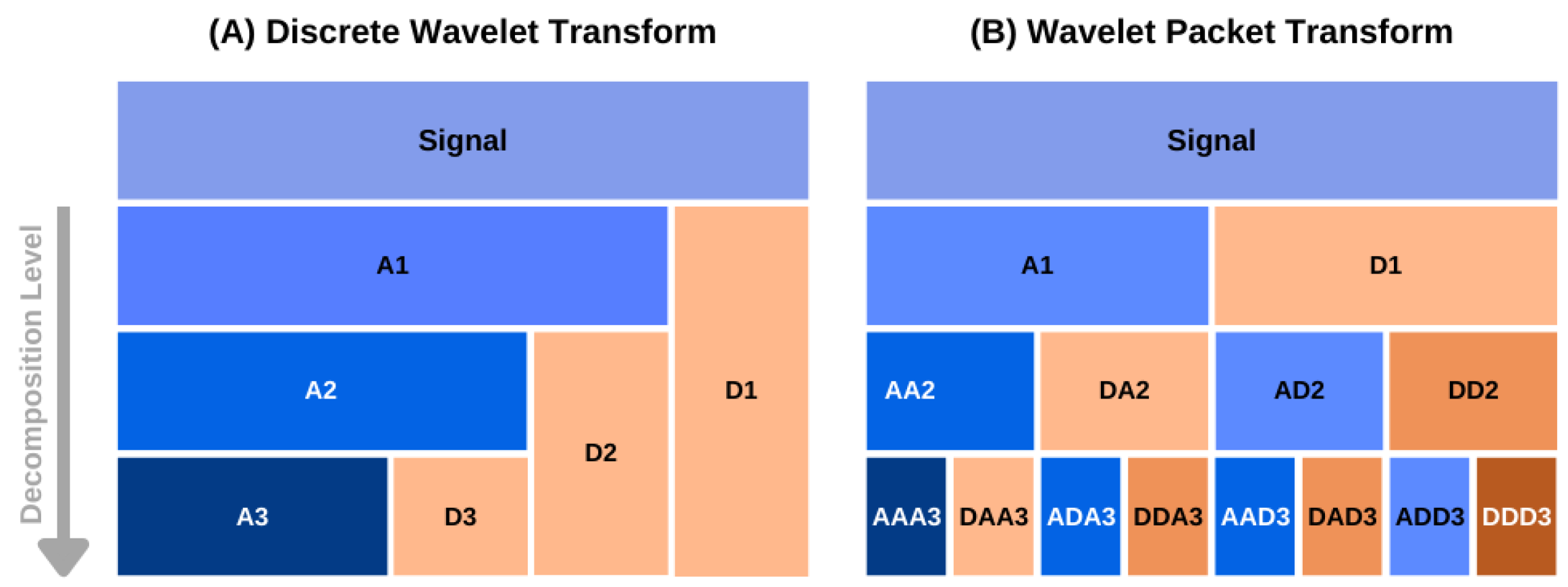
2.1. Overview of the Wavelet Packet Transform Theory
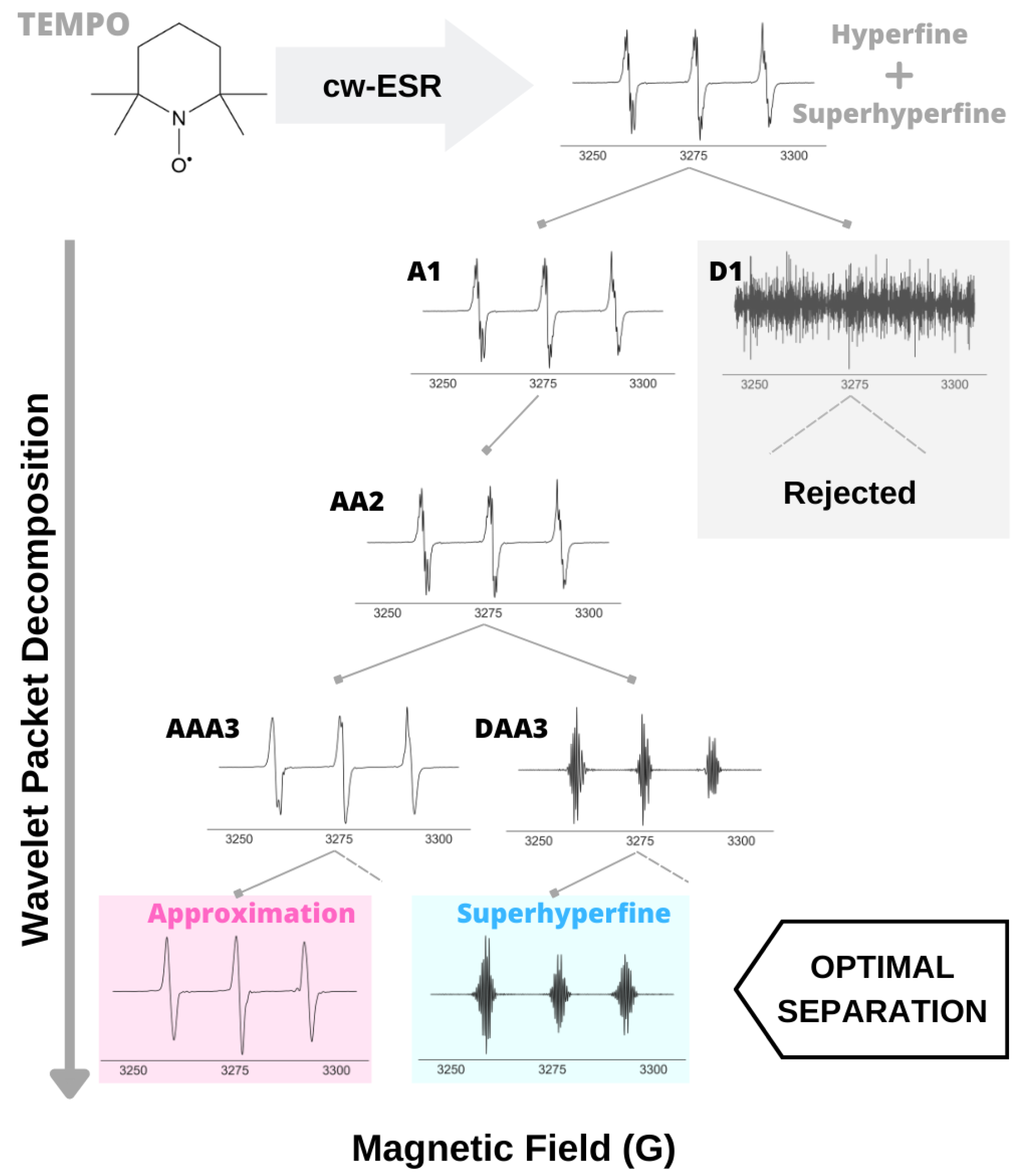
2.2. A Case Study: WPT Analysis of cw ESR Spectrum of Tempo
3. Materials
3.1. Experimental Section
Synthesis
3.2. ESR Experiments
3.3. ESR Spectral Mix
4. Results and Discussion
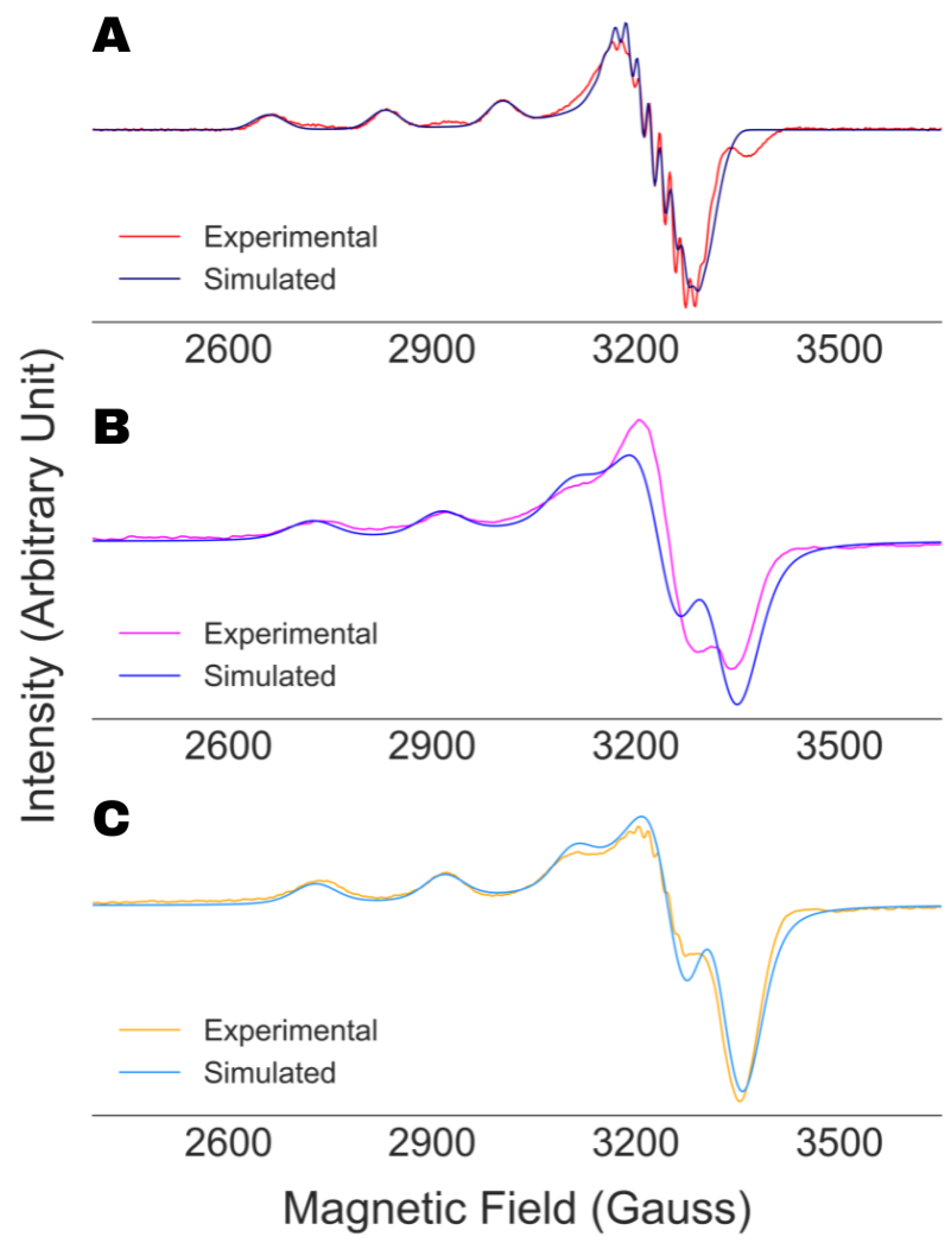
4.1. Validation of the Analysis
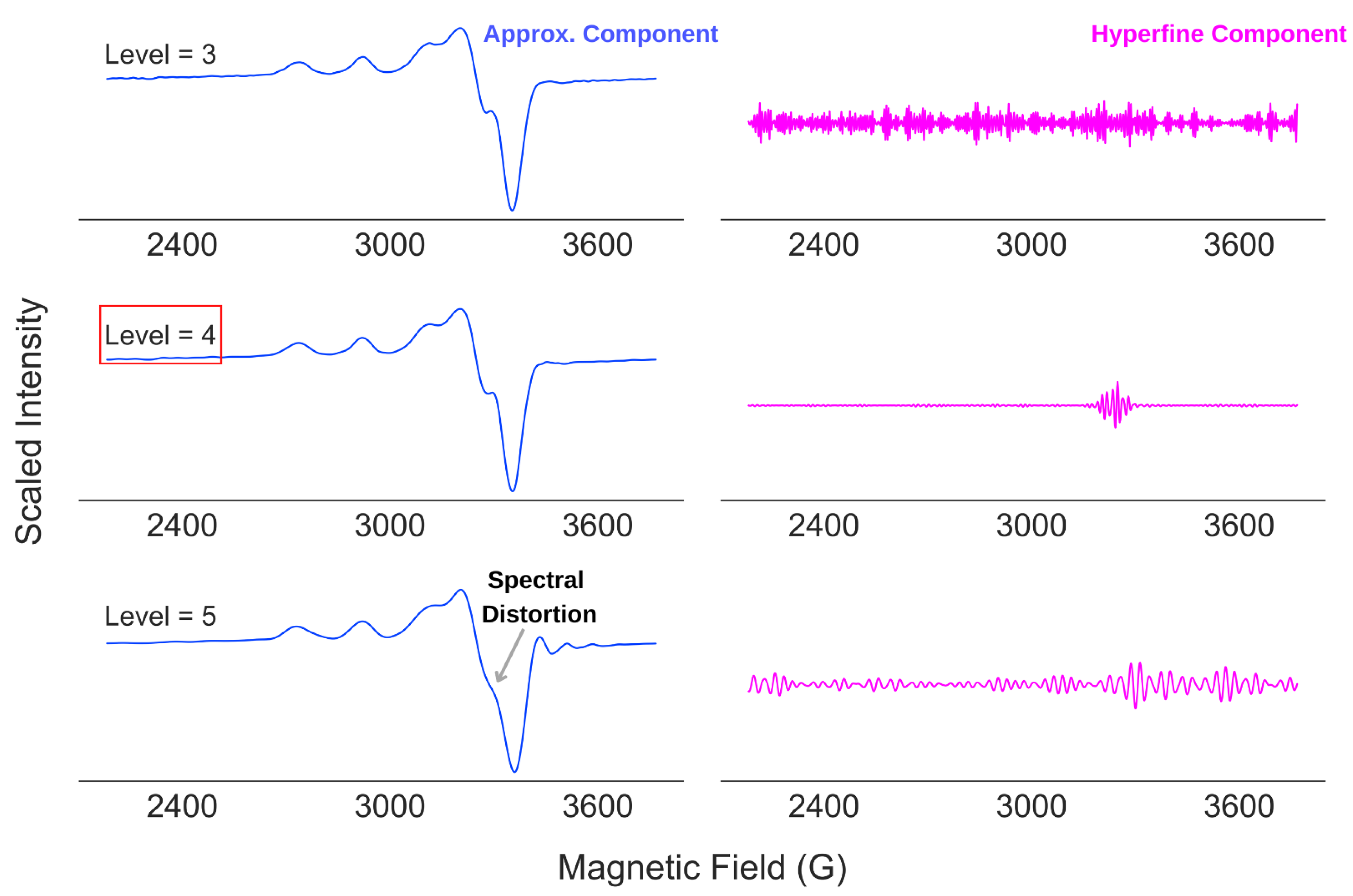
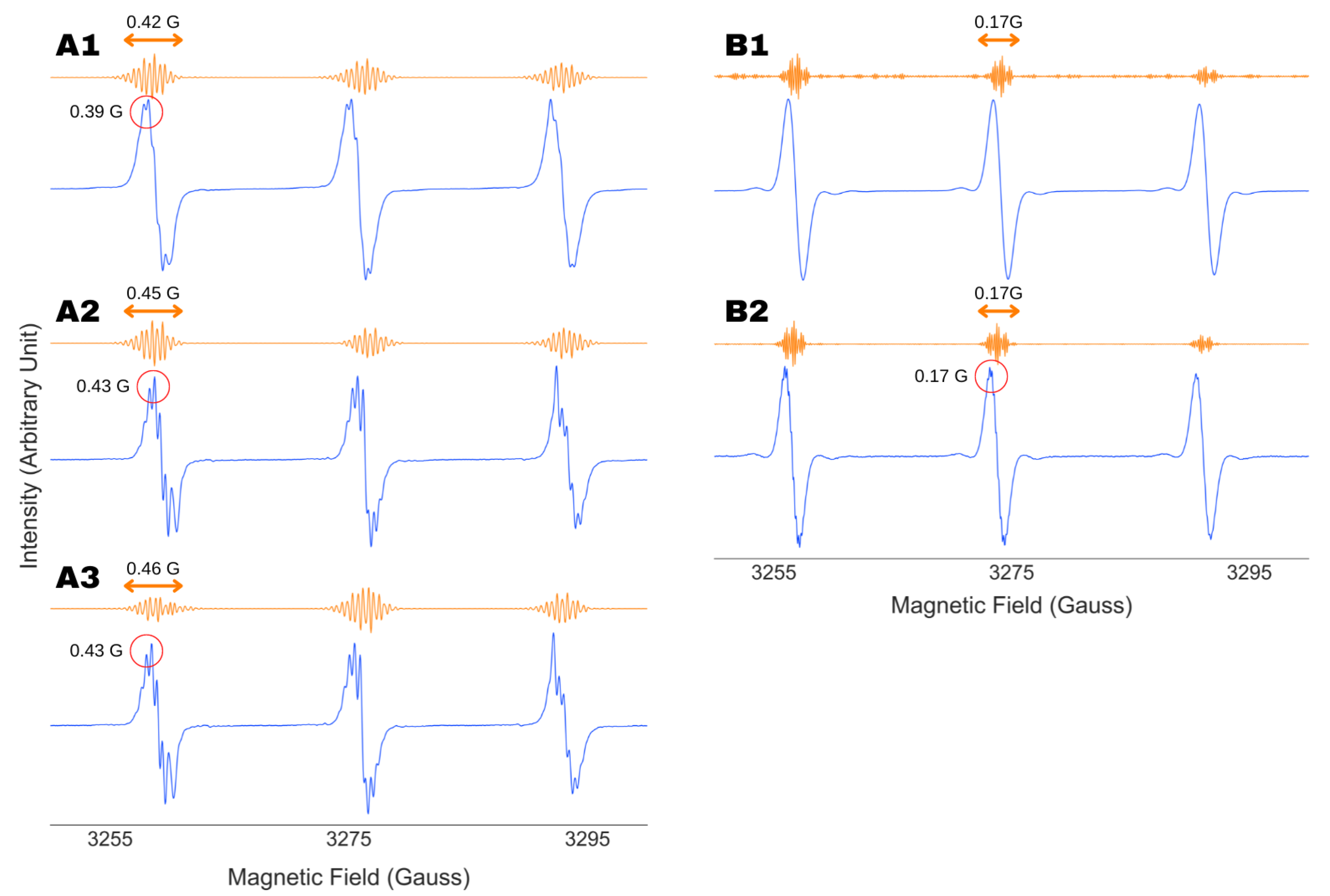
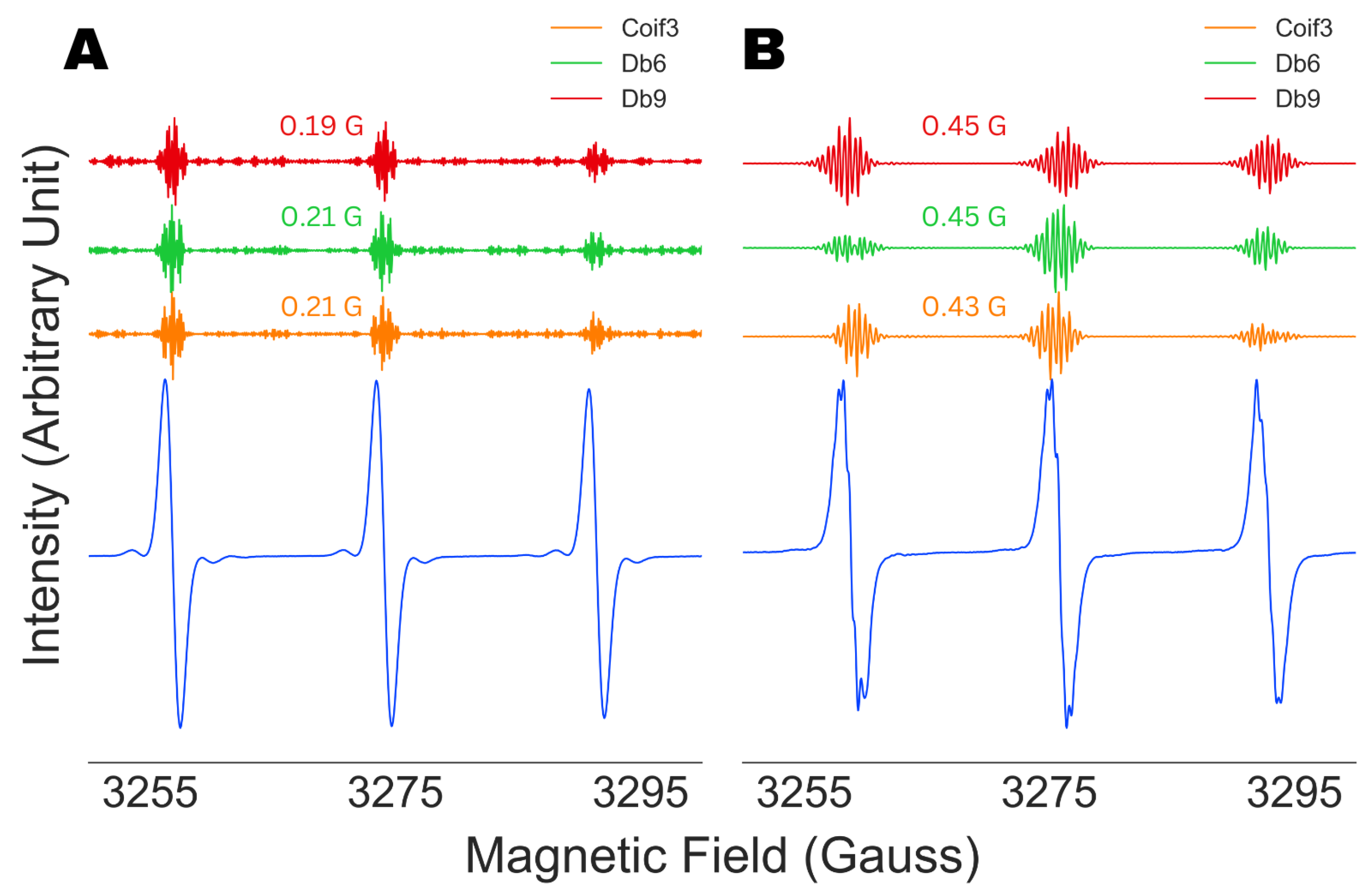
4.2. Robustness against Wavelet Selection
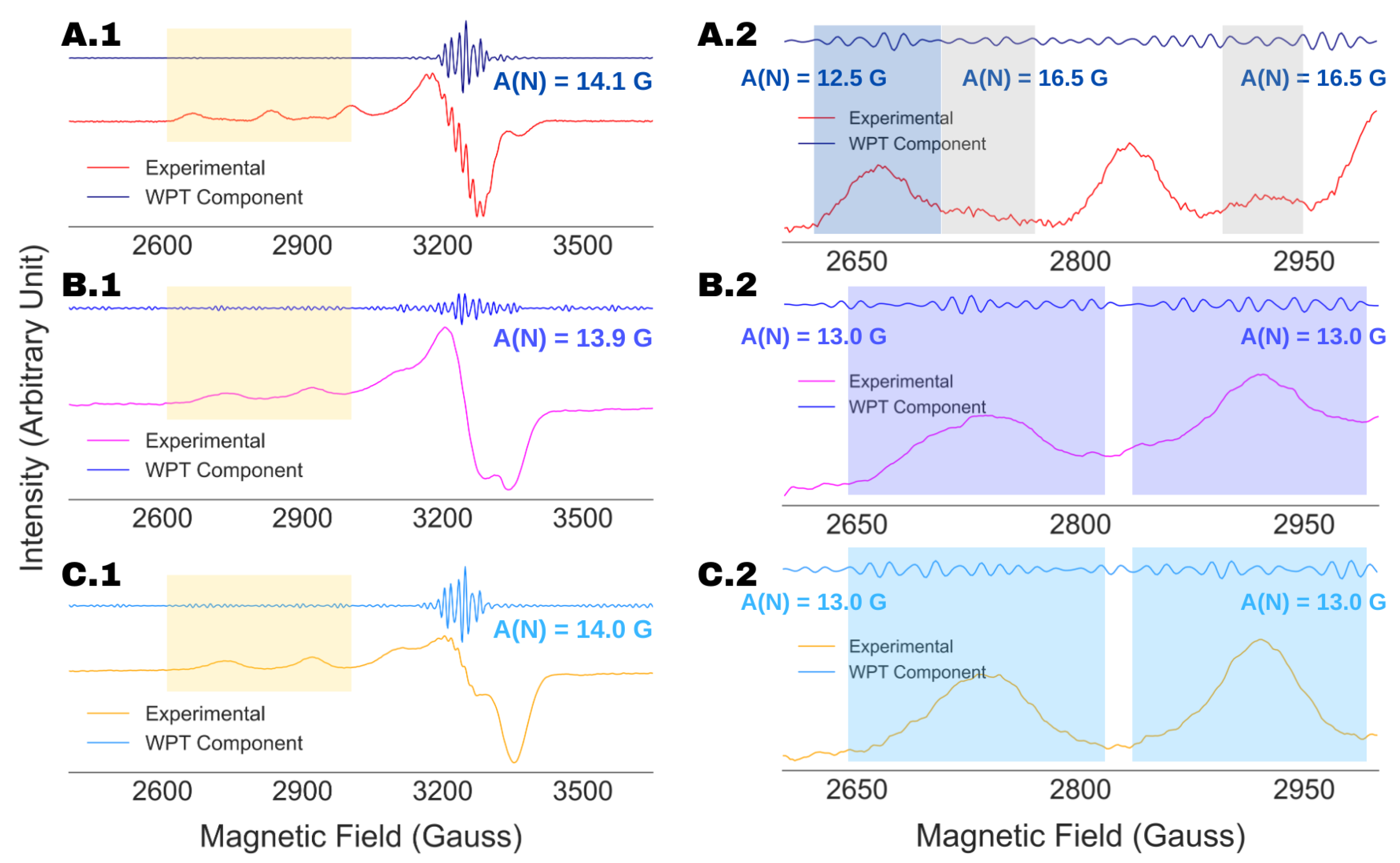
4.3. Spectral Analysis of Partially Resolved ESR Spectra
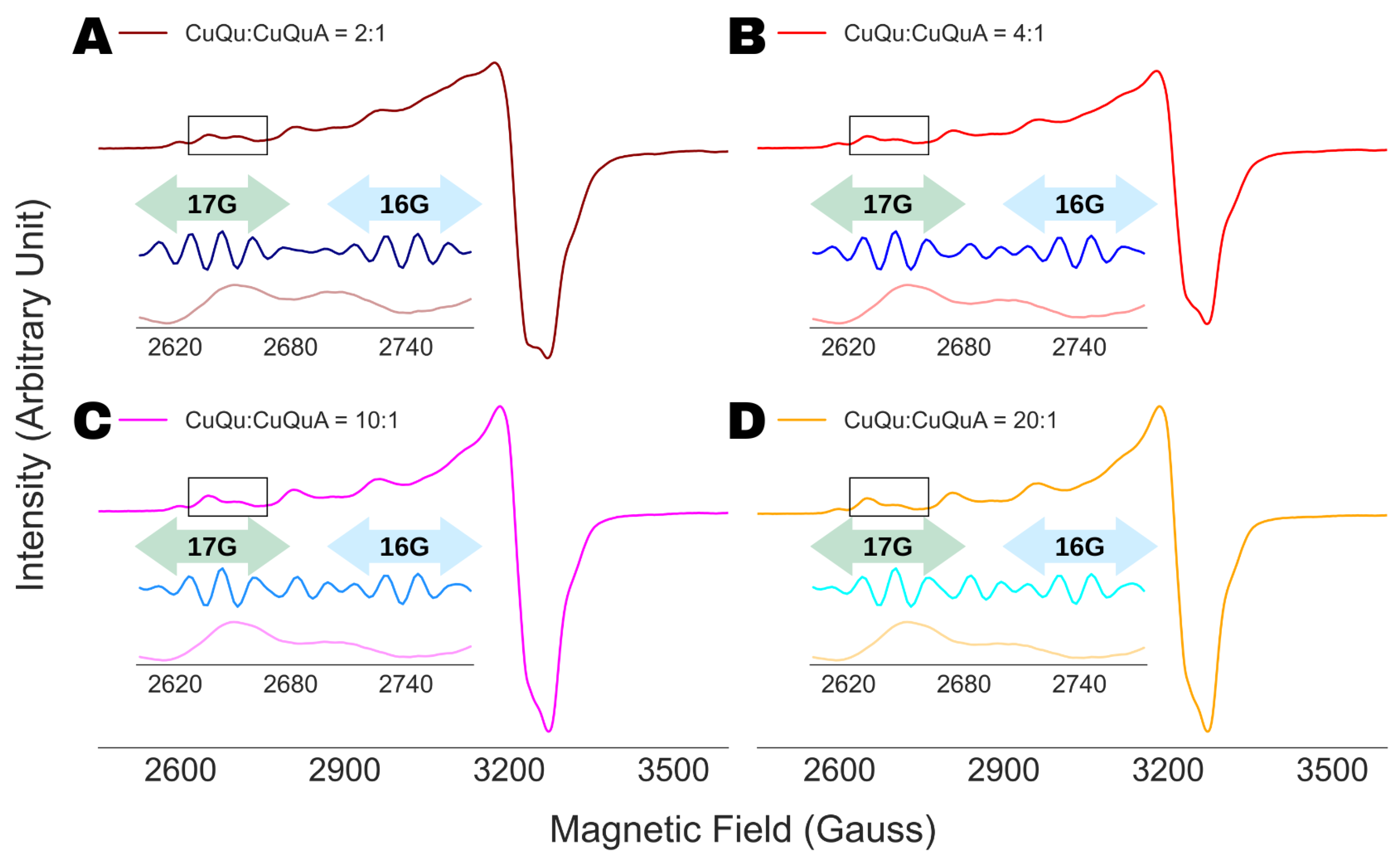
4.4. Analysis of Multi-Component ESR Spectra
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ESR | Electron spin resonance |
| WPT | Wavelet packet transform |
| NERD | Noise Elimination and Reduction via Denoising |
| SOD1 | Superoxide dismutase-1 |
Appendix A. Analysis of 100 K Cu-AHAHARA ESR Spectrum
Appendix A.1. Matlab Code for WPT Decomposition Shown in Figure A1
Appendix A.2. Spectral Analysis
References
- Mabbs, F.E.; Collison, D. Electron Paramagnetic Resonance of d Transition Metal Compounds; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Fukuzumi, S.; Ohkubo, K. Quantitative evaluation of Lewis acidity of metal ions derived from the g values of ESR spectra of superoxide: Metal ion complexes in relation to the promoting effects in electron transfer reactions. Chem.—A Eur. J. 2000, 6, 4532–4535. [Google Scholar] [CrossRef]
- Matsuda, K.; Takayama, K.; Irie, M. Photochromism of metal complexes composed of diarylethene ligands and Zn(II), Mn(II), and Cu(II) hexafluoroacetylacetonates. Inorg. Chem. 2004, 43, 482–489. [Google Scholar] [CrossRef] [PubMed]
- Raman, N.; Dhaveethu Raja, J.; Sakthivel, A. Synthesis, spectral characterization of Schiff base transition metal complexes: DNA cleavage and antimicrobial activity studies. J. Chem. Sci. 2007, 119, 303–310. [Google Scholar] [CrossRef]
- Lund, A.; Shiotani, M.; Shimada, S. Principles and Applications of ESR Spectroscopy; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Kohno, M. Applications of electron spin resonance spectrometry for reactive oxygen species and reactive nitrogen species research. J. Clin. Biochem. Nutr. 2010, 47, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Khramtsov, V.V.; Volodarsky, L.B. Use of imidazoline nitroxides in studies of chemical reactions ESR measurements of the concentration and reactivity of protons, thiols, and nitric oxide. In Biological Magnetic Resonance; Springer: Berlin/Heidelberg, Germany, 2002; pp. 109–180. [Google Scholar]
- Lazreg, F.; Nahra, F.; Cazin, C.S. Copper–NHC complexes in catalysis. Coord. Chem. Rev. 2015, 293, 48–79. [Google Scholar] [CrossRef]
- Ali, A.; Prakash, D.; Majumder, P.; Ghosh, S.; Dutta, A. Flexible Ligand in a Molecular Cu Electrocatalyst Unfurls Bidirectional O2/H2O Conversion in Water. ACS Catal. 2021, 11, 5934–5941. [Google Scholar] [CrossRef]
- Chen, Z.; Meyer, T.J. Copper (II) catalysis of water oxidation. Angew. Chem. Int. Ed. 2013, 52, 700–703. [Google Scholar] [CrossRef]
- Weng, Z.; Wu, Y.; Wang, M.; Jiang, J.; Yang, K.; Huo, S.; Wang, X.F.; Ma, Q.; Brudvig, G.W.; Batista, V.S.; et al. Active sites of copper-complex catalytic materials for electrochemical carbon dioxide reduction. Nat. Commun. 2018, 9, 415. [Google Scholar] [CrossRef]
- Bolm, C.; Martin, M.; Gescheidt, G.; Palivan, C.; Neshchadin, D.; Bertagnolli, H.; Feth, M.; Schweiger, A.; Mitrikas, G.; Harmer, J. Spectroscopic investigations of bis (sulfoximine) copper (II) complexes and their relevance in asymmetric catalysis. J. Am. Chem. Soc. 2003, 125, 6222–6227. [Google Scholar] [CrossRef]
- Bonke, S.A.; Risse, T.; Schnegg, A.; Brückner, A. In situ electron paramagnetic resonance spectroscopy for catalysis. Nat. Rev. Methods Prim. 2021, 1, 33. [Google Scholar] [CrossRef]
- Sánchez-Moreno, C. Methods used to evaluate the free radical scavenging activity in foods and biological systems. Food Sci. Technol. Int. 2002, 8, 121–137. [Google Scholar] [CrossRef]
- Okano, H. Effects of static magnetic fields in biology: Role of free radicals. Front. Biosci.-Landmark 2008, 13, 6106–6125. [Google Scholar] [CrossRef]
- Yin, H.; Xu, L.; Porter, N.A. Free radical lipid peroxidation: Mechanisms and analysis. Chem. Rev. 2011, 111, 5944–5972. [Google Scholar] [CrossRef]
- Eaton, G.R.; Eaton, S.S.; Barr, D.P.; Weber, R.T. Quantitative EPR; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Murphy, D.M.; Farley, R.D. Principles and applications of ENDOR spectroscopy for structure determination in solution and disordered matrices. Chem. Soc. Rev. 2006, 35, 249–268. [Google Scholar] [CrossRef] [PubMed]
- Golombek, A.P.; Hendrich, M.P. Quantitative analysis of dinuclear manganese (II) EPR spectra. J. Magn. Reson. 2003, 165, 33–48. [Google Scholar] [CrossRef] [PubMed]
- Drew, S.C.; Young, C.G.; Hanson, G.R. A density functional study of the electronic structure and spin hamiltonian parameters of mononuclear thiomolybdenyl complexes. Inorg. Chem. 2007, 46, 2388–2397. [Google Scholar] [CrossRef]
- Cox, N.; Jin, L.; Jaszewski, A.; Smith, P.J.; Krausz, E.; Rutherford, A.W.; Pace, R. The semiquinone-iron complex of photosystem II: Structural insights from ESR and theoretical simulation; evidence that the native ligand to the non-heme iron is carbonate. Biophys. J. 2009, 97, 2024–2033. [Google Scholar] [CrossRef]
- Trukhan, S.N.; Yakushkin, S.S.; Martyanov, O.N. Fine-tuning simulation of the ESR spectrum—Sensitive tool to identify the local environment of asphaltenes in situ. J. Phys. Chem. C 2022, 126, 10729–10741. [Google Scholar] [CrossRef]
- Stoll, S.; Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef]
- Khairy, K.; Budil, D.; Fajer, P. Nonlinear-least-squares analysis of slow motional regime EPR spectra. J. Magn. Reson. 2006, 183, 152–159. [Google Scholar] [CrossRef]
- Srivastava, M.; Dzikovski, B.; Freed, J.H. Extraction of Weak Spectroscopic Signals with High Fidelity: Examples from ESR. J. Phys. Chem. A 2021, 125, 4480–4487. [Google Scholar] [CrossRef]
- Roy, A.S.; Srivastava, M. Hyperfine Decoupling of ESR Spectra Using Wavelet Transform. Magnetochemistry 2022, 8, 32. [Google Scholar] [CrossRef]
- Sinha Roy, A.; Srivastava, M. Analysis of Small-Molecule Mixtures by Super-Resolved 1H NMR Spectroscopy. J. Phys. Chem. A 2022, 126, 9108–9113. [Google Scholar] [CrossRef]
- Sinha Roy, A.; Srivastava, M. Unsupervised Analysis of Small Molecule Mixtures by Wavelet-Based Super-Resolved NMR. Molecules 2023, 28, 792. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, M.; Anderson, C.L.; Freed, J.H. A New Wavelet Denoising Method for Selecting Decomposition Levels and Noise Thresholds. IEEE Access 2016, 4, 3862–3877. [Google Scholar] [CrossRef]
- Addison, P. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance, 2nd ed.; CRC Press: London, UK, 2016. [Google Scholar]
- Wang, Q.; Johnson, J.L.; Agar, N.Y.; Agar, J.N. Protein aggregation and protein instability govern familial amyotrophic lateral sclerosis patient survival. PLoS Biol. 2008, 6, e170. [Google Scholar] [CrossRef]
- Pratt, A.J.; Shin, D.S.; Merz, G.E.; Rambo, R.P.; Lancaster, W.A.; Dyer, K.N.; Borbat, P.P.; Poole, F.L.; Adams, M.W.; Freed, J.H.; et al. Aggregation propensities of superoxide dismutase G93 hotspot mutants mirror ALS clinical phenotypes. Proc. Natl. Acad. Sci. USA 2014, 111, E4568–E4576. [Google Scholar] [CrossRef] [PubMed]
- Makhlynets, O.V.; Gosavi, P.M.; Korendovych, I.V. Short Self-Assembling Peptides Are Able to Bind to Copper and Activate Oxygen. Angew. Chem. Int. Ed. 2016, 55, 9017–9020. [Google Scholar] [CrossRef] [PubMed]
- Merz, G.E.; Borbat, P.P.; Pratt, A.J.; Getzoff, E.D.; Freed, J.H.; Crane, B.R. Copper-based pulsed dipolar ESR spectroscopy as a probe of protein conformation linked to disease states. Biophys. J. 2014, 107, 1669–1674. [Google Scholar] [CrossRef]
- Ernst, R.; Anderson, W. Sensitivity enhancement in magnetic resonance. II. Investigation of intermediate passage conditions. Rev. Sci. Instrum. 1965, 36, 1696–1706. [Google Scholar] [CrossRef]
- Portis, A. Rapid passage effects in electron spin resonance. Phys. Rev. 1955, 100, 1219. [Google Scholar] [CrossRef]
- Noël, S.; Perez, F.; Pedersen, J.T.; Alies, B.; Ladeira, S.; Sayen, S.; Guillon, E.; Gras, E.; Hureau, C. A new water-soluble Cu(II) chelator that retrieves Cu from Cu (amyloid-β) species, stops associated ROS production and prevents Cu (II)-induced Aβ aggregation. J. Inorg. Biochem. 2012, 117, 322–325. [Google Scholar] [CrossRef] [PubMed]
- Bunda, S.; May, N.V.; Bonczidai-Kelemen, D.; Udvardy, A.; Ching, H.V.; Nys, K.; Samanipour, M.; Van Doorslaer, S.; Joo, F.; Lihi, N. Copper (II) complexes of sulfonated salan ligands: Thermodynamic and spectroscopic features and applications for catalysis of the Henry reaction. Inorg. Chem. 2021, 60, 11259–11272. [Google Scholar] [CrossRef] [PubMed]
| Molecule | Structure | ESR Frequency (GHz) |
|---|---|---|
| Tempo |  | 9.33 |
| Tempol |  | 9.33 |
| SOD1:H48Q | SOD1 mutant, histidine (48) replaced with glutamine | 9.26 |
| Cu-AHAHARA | A complex of Cu(II) and AHAHARA peptide: C-terminus as amide and N-terminus as acetyl group | 9.39 |
| CuQu |  | 9.316 |
| CuQuA |  | 9.316 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinha Roy, A.; Dzikovski, B.; Dolui, D.; Makhlynets, O.; Dutta, A.; Srivastava, M. A Simulation Independent Analysis of Single- and Multi-Component cw ESR Spectra. Magnetochemistry 2023, 9, 112. https://doi.org/10.3390/magnetochemistry9050112
Sinha Roy A, Dzikovski B, Dolui D, Makhlynets O, Dutta A, Srivastava M. A Simulation Independent Analysis of Single- and Multi-Component cw ESR Spectra. Magnetochemistry. 2023; 9(5):112. https://doi.org/10.3390/magnetochemistry9050112
Chicago/Turabian StyleSinha Roy, Aritro, Boris Dzikovski, Dependu Dolui, Olga Makhlynets, Arnab Dutta, and Madhur Srivastava. 2023. "A Simulation Independent Analysis of Single- and Multi-Component cw ESR Spectra" Magnetochemistry 9, no. 5: 112. https://doi.org/10.3390/magnetochemistry9050112
APA StyleSinha Roy, A., Dzikovski, B., Dolui, D., Makhlynets, O., Dutta, A., & Srivastava, M. (2023). A Simulation Independent Analysis of Single- and Multi-Component cw ESR Spectra. Magnetochemistry, 9(5), 112. https://doi.org/10.3390/magnetochemistry9050112






