Nonreciprocity of Optical Absorption in the Magnetoelectric Antiferromagnet CuB2O4
Abstract
1. Introduction
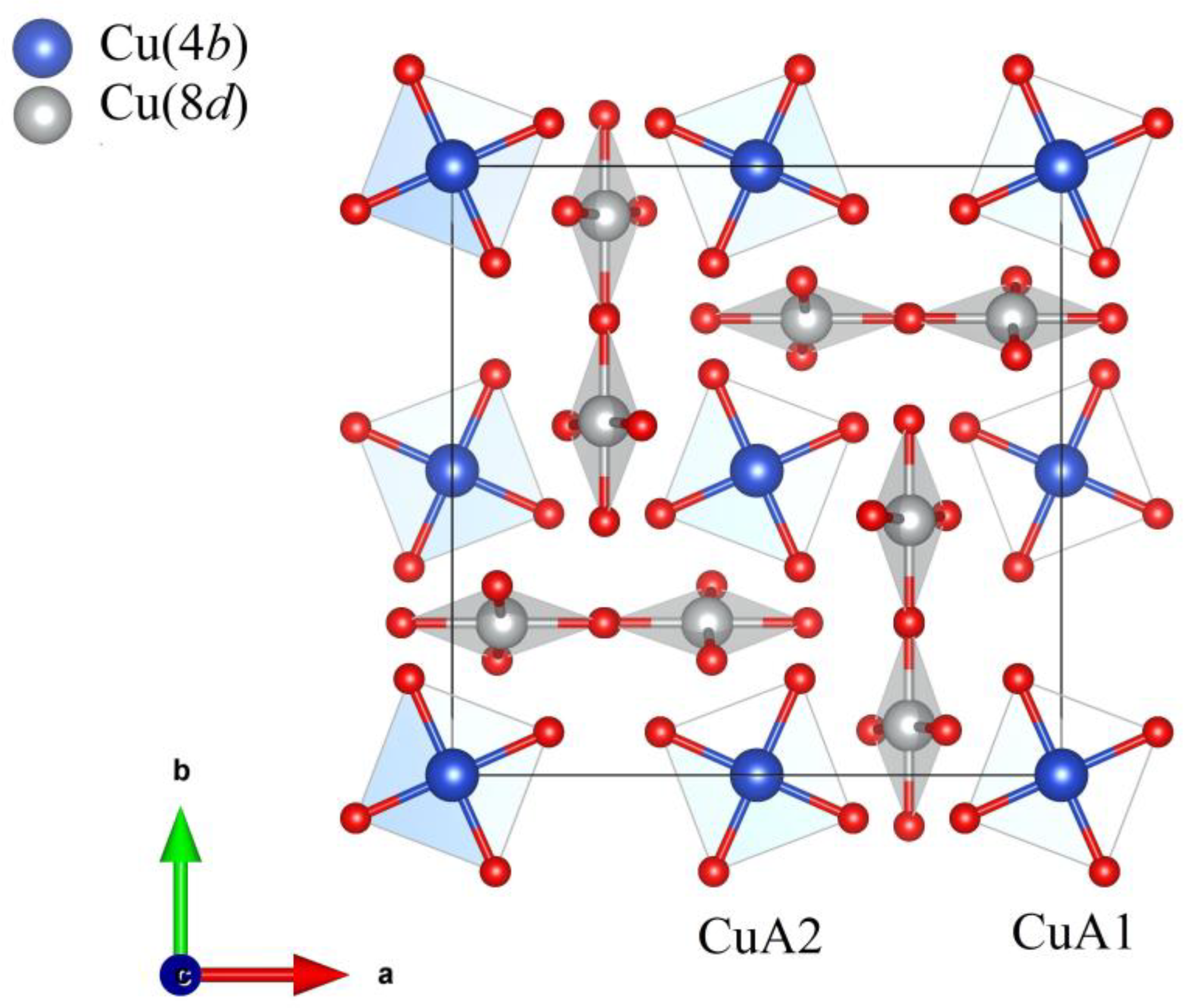
2. Crystal Structure, Magnetism, and Optical Properties of CuB2O4
3. Materials and Methods
4. Experimental Results
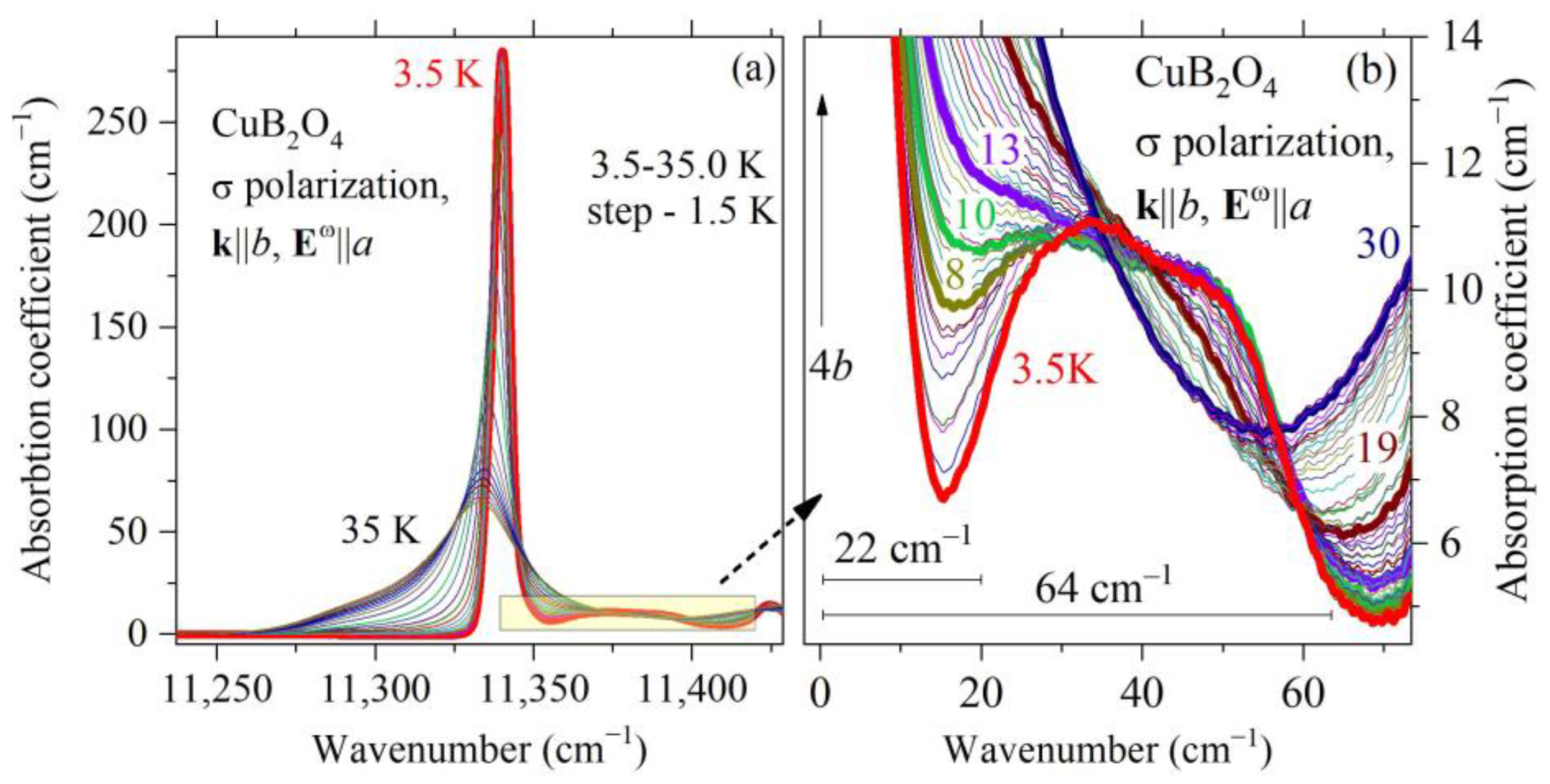
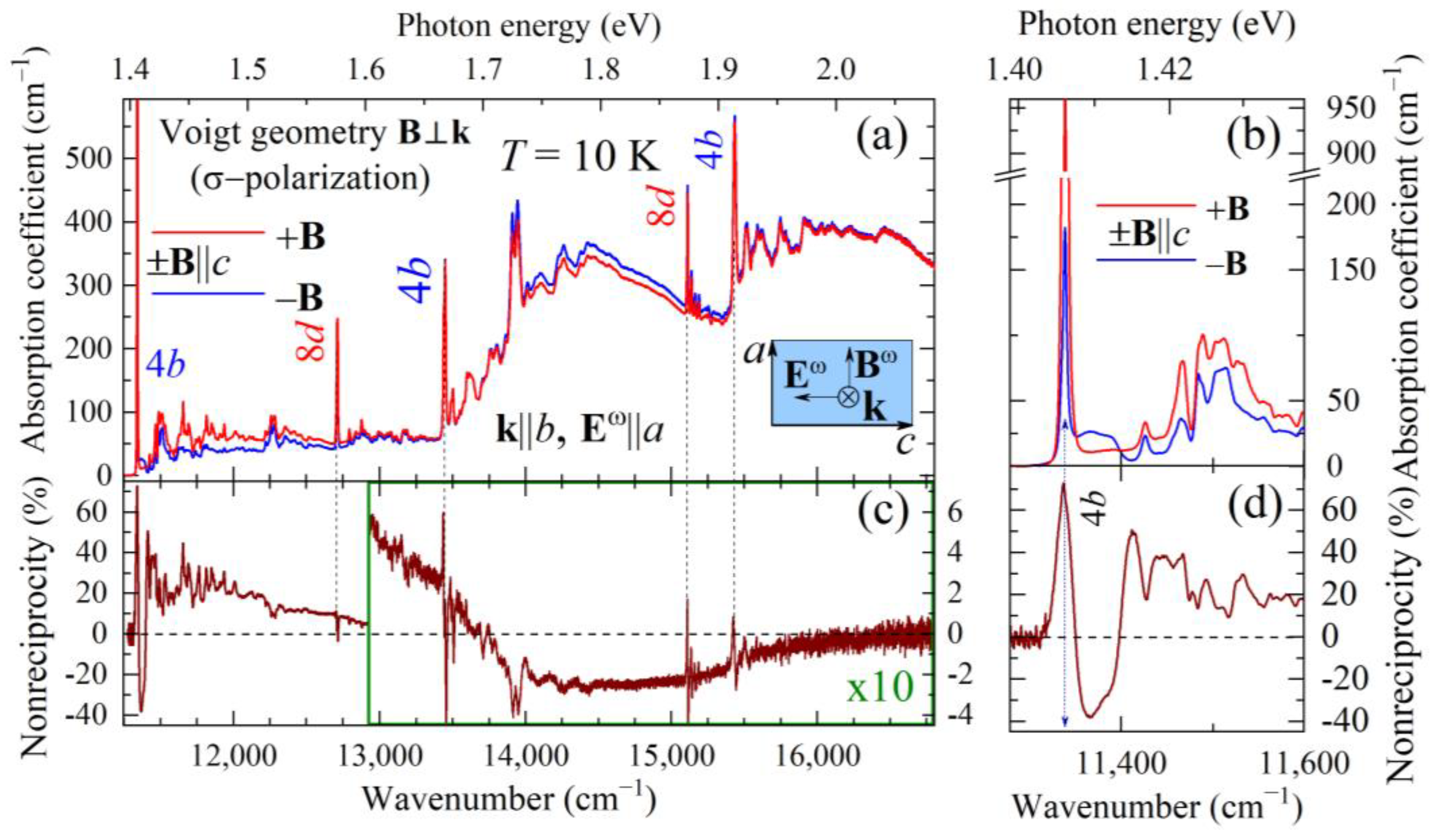
4.1. Polarized Absorption Spectra of CuB2O4 in Zero External Field
Iσ ~ |<daEωa + dbEωb + mcBωc>|2
Iπ ~ |<maBωa + mbBωb + dcEωc>|2,
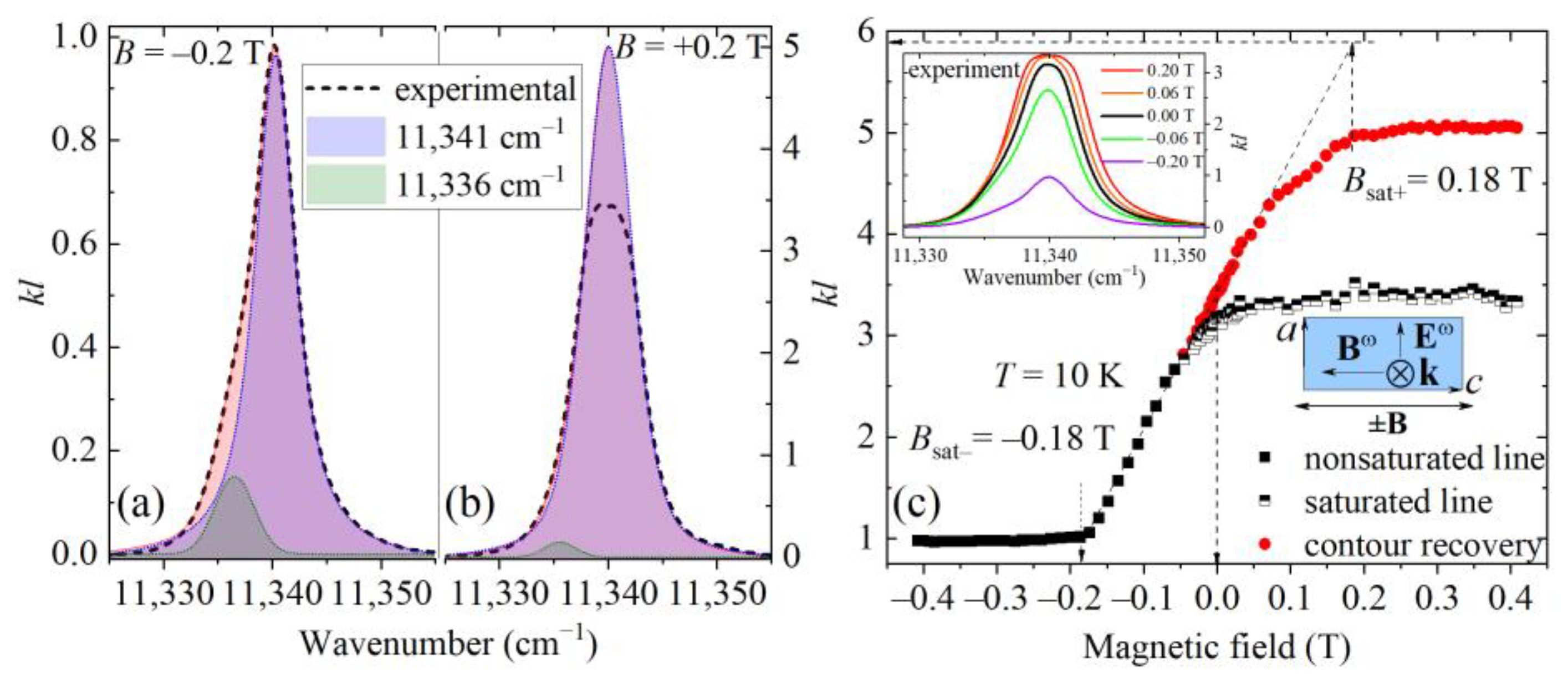
4.2. Absorption Nonreciprocity in an External Magnetic Field
5. Discussion of Results and Theoretical Analysis of Nonreciprocity within the Scenario of Interference of Magnetic and Electric Dipole Transitions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Wave Functions of the Ground and the First Excited Doublets
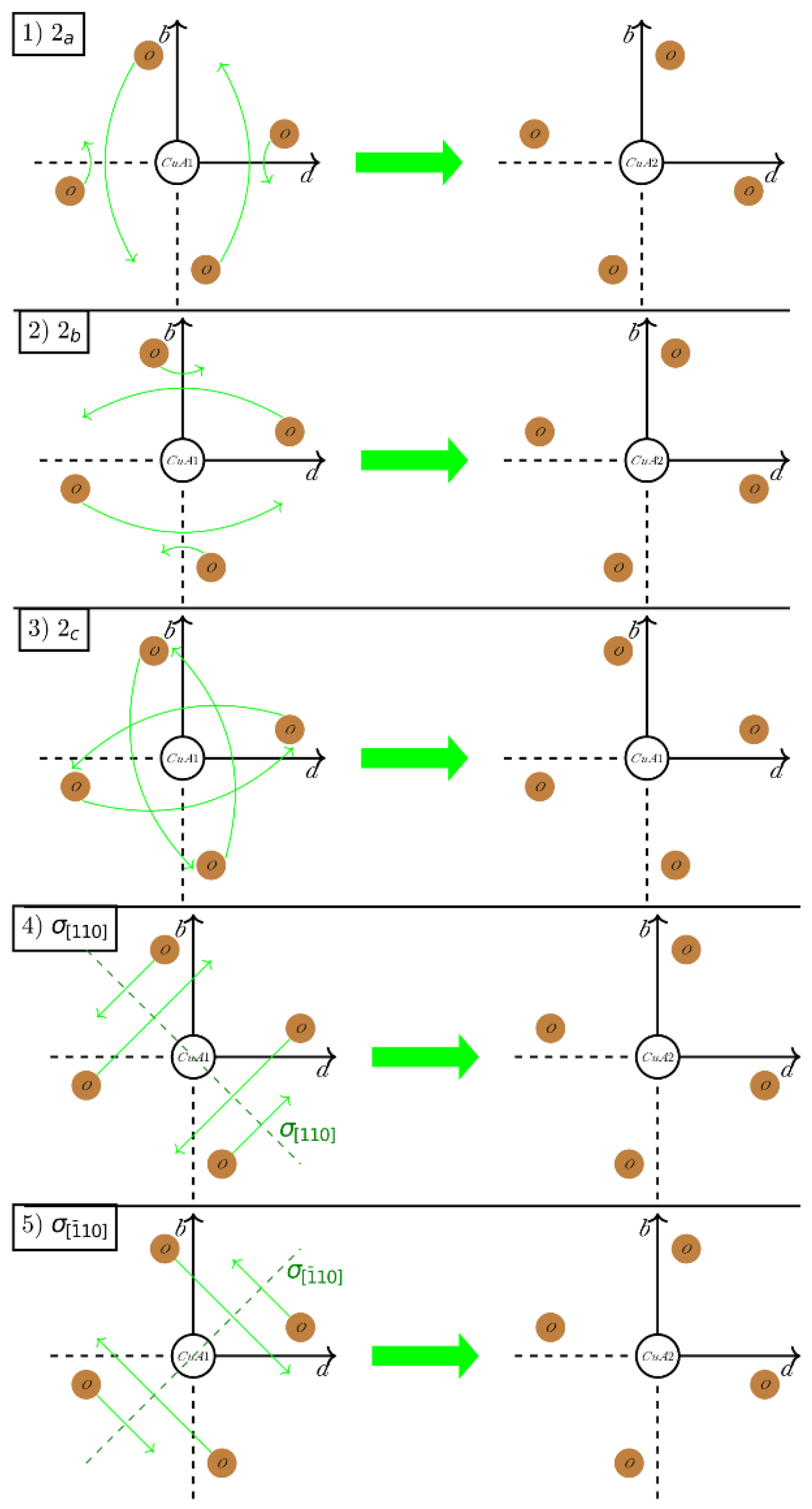
Appendix B. On the Difference between the Parameters of Electric Dipole Transitions for the Positions Cu(A1) and Cu(A2)
References
- Fujita, T.; Fujimoto, Y.; Mitsudo, S.; Idehara, T.; Inoue, K.; Kishine, J.; Kousaka, Y.; Yano, S.; Akimitsu, J.; Motokawa, M. High Field ESR Measurements on the Chiral Spin System CuB2O4. J. Phys. Conf. Ser. 2006, 51, 111–114. [Google Scholar] [CrossRef]
- Boehm, M.; Roessli, B.; Schefer, J.; Wills, A.S.; Ouladdiaf, B.; Lelièvre-Berna, E.; Staub, U.; Petrakovskii, G.A. Complex Magnetic Ground State of CuB2O4. Phys. Rev. B 2003, 68, 024405. [Google Scholar] [CrossRef]
- Pisarev, R.; Sänger, I.; Petrakovskii, G.; Fiebig, M. Magnetic-Field Induced Second Harmonic Generation in CuB2O4. Phys. Rev. Lett. 2004, 93, 037204. [Google Scholar] [CrossRef] [PubMed]
- Nénert, G.; Bezmaternykh, L.N.; Vasiliev, A.N.; Palstra, T.T.M. Magnetic, Structural, and Dielectric Properties of CuB2O4. Phys. Rev. B 2007, 76, 144401. [Google Scholar] [CrossRef]
- Khanh, N.D.; Abe, N.; Kubo, K.; Akaki, M.; Tokunaga, M.; Sasaki, T.; Arima, T. Magnetic Control of Electric Polarization in the Noncentrosymmetric Compound (Cu,Ni)B2O4. Phys. Rev. B 2013, 87, 184416. [Google Scholar] [CrossRef]
- Eremin, M.V.; Nurmukhametov, A.R. On the Magnetoelectric Coupling in (Ni, Cu)B2O4. JETP Lett. 2021, 114, 35–39. [Google Scholar] [CrossRef]
- Saito, M.; Taniguchi, K.; Arima, T. Gigantic Optical Magnetoelectric Effect in CuB2O4. J. Phys. Soc. Jpn. 2008, 77, 013705. [Google Scholar] [CrossRef]
- Saito, M.; Ishikawa, K.; Taniguchi, K.; Arima, T. Magnetic Control of Crystal Chirality and the Existence of a Large Magneto-Optical Dichroism Effect in CuB2O4. Phys. Rev. Lett. 2008, 101, 117402. [Google Scholar] [CrossRef]
- Boldyrev, K.N.; Pisarev, R.V.; Bezmaternykh, L.N.; Popova, M.N. Antiferromagnetic Dichroism in a Complex Multisublattice Magnetoelectric CuB2O4. Phys. Rev. Lett. 2015, 114, 247210. [Google Scholar] [CrossRef]
- Toyoda, S.; Abe, N.; Kimura, S.; Matsuda, Y.H.; Nomura, T.; Ikeda, A.; Takeyama, S.; Arima, T. One-Way Transparency of Light in Multiferroic CuB2O4. Phys. Rev. Lett. 2015, 115, 267207. [Google Scholar] [CrossRef]
- Lovesey, S.W.; Staub, U. Calculated Chiral and Magneto-Electric Dichroic Signals for Copper Metaborate (CuB2O4) in an Applied Magnetic Field. J. Phys. Condens. Matter 2009, 21, 142201. [Google Scholar] [CrossRef] [PubMed]
- Lovesey, S.W. Zeeman Spectrum, Magnetic Neutron Diffraction Pattern, and Dirac Multipoles for a Multiferroic Material CuB2O4. Phys. Rev. B 2016, 94, 094422. [Google Scholar] [CrossRef]
- Nikitchenko, A.I.; Pisarev, R.V. Magnetic and Antiferromagnetic Nonreciprocity of Light Propagation in Magnetoelectric CuB2O4. Phys. Rev. B 2021, 104, 184108. [Google Scholar] [CrossRef]
- Toyoda, S.; Abe, N.; Arima, T. Gigantic Directional Asymmetry of Luminescence in Multiferroic CuB2O4. Phys. Rev. B 2016, 93, 201109. [Google Scholar] [CrossRef]
- Nurmukhametov, A.R.; Eremin, M.V. On the Theory of the Dynamic Magnetoelectric Coupling in CuB2O4. J. Exp. Theor. Phys. 2022, 135, 339–346. [Google Scholar] [CrossRef]
- Martinez-Ripoll, M.; Martínez-Carrera, S.; García-Blanco, S. The Crystal Structure of Copper Metaborate, CuB2O4. Acta Crystallogr. B 1971, 27, 677–681. [Google Scholar] [CrossRef]
- Pisarev, R.V.; Boldyrev, K.N.; Popova, M.N.; Smirnov, A.N.; Davydov, V.Y.; Bezmaternykh, L.N.; Smirnov, M.B.; Kazimirov, V.Y. Lattice Dynamics of Piezoelectric Copper Metaborate CuB2O4. Phys. Rev. B 2013, 88, 024301. [Google Scholar] [CrossRef]
- Petrakovskii, G.; Velikanov, D.; Vorotinov, A.; Balaev, A.; Sablina, K.; Amato, A.; Roessli, B.; Schefer, J.; Staub, U. Weak Ferromagnetism in CuB2O4 Copper Metaborate. J. Magn. Magn. Mater. 1999, 205, 105–109. [Google Scholar] [CrossRef]
- Boehm, M.; Roessli, B.; Schefer, J.; Ouladdiaf, B.; Amato, A.; Baines, C.; Staub, U.; Petrakovskii, G.A. A Neutron Scattering and ΜSR Investigation of the Magnetic Phase Transitions of CuB2O4. Phys. B Condens. Matter 2002, 318, 277–281. [Google Scholar] [CrossRef]
- Roessli, B.; Schefer, J.; Petrakovskii, G.A.; Ouladdiaf, B.; Boehm, M.; Staub, U.; Vorotinov, A.; Bezmaternikh, L. Formation of a Magnetic Soliton Lattice in Copper Metaborate. Phys. Rev. Lett. 2001, 86, 1885–1888. [Google Scholar] [CrossRef]
- Martynov, S.; Petrakovskii, G.; Roessli, B. Quasi-One-Dimensional Excitations of Copper Metaborate in the Commensurate Phase. J. Magn. Magn. Mater. 2004, 269, 106–112. [Google Scholar] [CrossRef]
- Molchanova, A.D.; Boldyrev, K.N. High-Resolution Spectroscopy of Low-Temperature Phase Transitions in Copper Metaborate CuB2O4. Opt. Spectrosc. 2019, 127, 33–35. [Google Scholar] [CrossRef]
- Pankrats, A.I.; Petrakovskii, G.A.; Popov, M.A.; Sablina, K.A.; Prozorova, L.A.; Sosin, S.S.; Szimczak, G.; Szimczak, R.; Baran, M. New Magnetic States in Copper Metaborate CuB2O4. J. Exp. Theor. Phys. Lett. 2003, 78, 569–573. [Google Scholar] [CrossRef]
- Pankrats, A.; Petrakovskii, G.; Tugarinov, V.; Sablina, K.; Bezmaternykh, L.; Szymczak, R.; Baran, M.; Kundys, B.; Nabialek, A. Magnetic Phase Diagram of Copper Metaborate in Magnetic Field Parallel to C-Axis. J. Magn. Magn. Mater. 2006, 300, e388–e391. [Google Scholar] [CrossRef]
- Petrova, A.E.; Pankrats, A.I. Copper Metaborate CuB2O4 Phase Diagrams Based on the Results of Measuring the Magnetic Moment. J. Exp. Theor. Phys. 2018, 126, 506–513. [Google Scholar] [CrossRef]
- Pisarev, R.V.; Kalashnikova, A.M.; Schöps, O.; Bezmaternykh, L.N. Electronic Transitions and Genuine Crystal-Field Parameters in Copper Metaborate CuB2O4. Phys. Rev. B 2011, 84, 075160. [Google Scholar] [CrossRef]
- Aleksandrov, K.S.; Sorokin, B.P.; Glushkov, D.A.; Bezmaternykh, L.N.; Burkov, S.I.; Belushchenko, S.V. Electromechanical Properties and Anisotropy of Acoustic Wave Propagation in CuB2O4 Copper Metaborate. Phys. Solid State 2003, 45, 41–45. [Google Scholar] [CrossRef]
- Martynov, S.; Petrakovskii, G.; Boehm, M.; Roessli, B.; Kulda, J. Spin-Wave Spectrum of Copper Metaborate in the Incommensurate Phase. J. Magn. Magn. Mater. 2006, 299, 75–81. [Google Scholar] [CrossRef]
- Kopteva, N.E.; Kudlacik, D.; Yakovlev, D.R.; Eremin, M.V.; Nurmukhametov, A.R.; Bayer, M.; Pisarev, R.V. Zeeman and Davydov Splitting of Frenkel Excitons in the Antiferromagnet CuB2O4. Phys. Rev. B 2022, 105, 024421. [Google Scholar] [CrossRef]
- Abragam, A.; Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; Oxford Classic Texts in the Physical Sciences; Oxford University Press: Oxford, UK, 2012; ISBN 978-0-19-965152-8. [Google Scholar]
- Eremin, M.V. On the Theory of Magnetoelectric Coupling in LiCu2O2. J. Exp. Theor. Phys. 2019, 129, 990–997. [Google Scholar] [CrossRef]
- Eremin, M.V. Coupling of Spins with an Electric Field in FeV2O4. Phys. Rev. B 2019, 100, 140404. [Google Scholar] [CrossRef]
- Shuai, D.; Jun-Ming, L.; Sang-Wook, C.; Zhifeng, R. Multiferroic materials and magnetoelectric physics: Symmetry, entanglement, excitation, and topology. Adv. Phys. 2015, 64, 519–626. [Google Scholar] [CrossRef]
- Takahashi, Y.; Shimano, R.; Kaneko, Y.; Murakawa, H.; Tokura, Y. Magnetoelectric resonance with electromagnons in a perovskite helimagnet. Nat. Phys. 2012, 8, 121–125. [Google Scholar] [CrossRef]
- Kida, N.; Ikebe, Y.; Takahashi, Y.; He, J.P.; Kaneko, Y.; Yamasaki, Y.; Shimano, R.; Arima, T.; Nagaosa, N.; Tokura, Y. Electrically driven spin excitation in a ferroelectric magnet DyMnO3. Phys. Rev. B 2008, 78, 104414. [Google Scholar] [CrossRef]

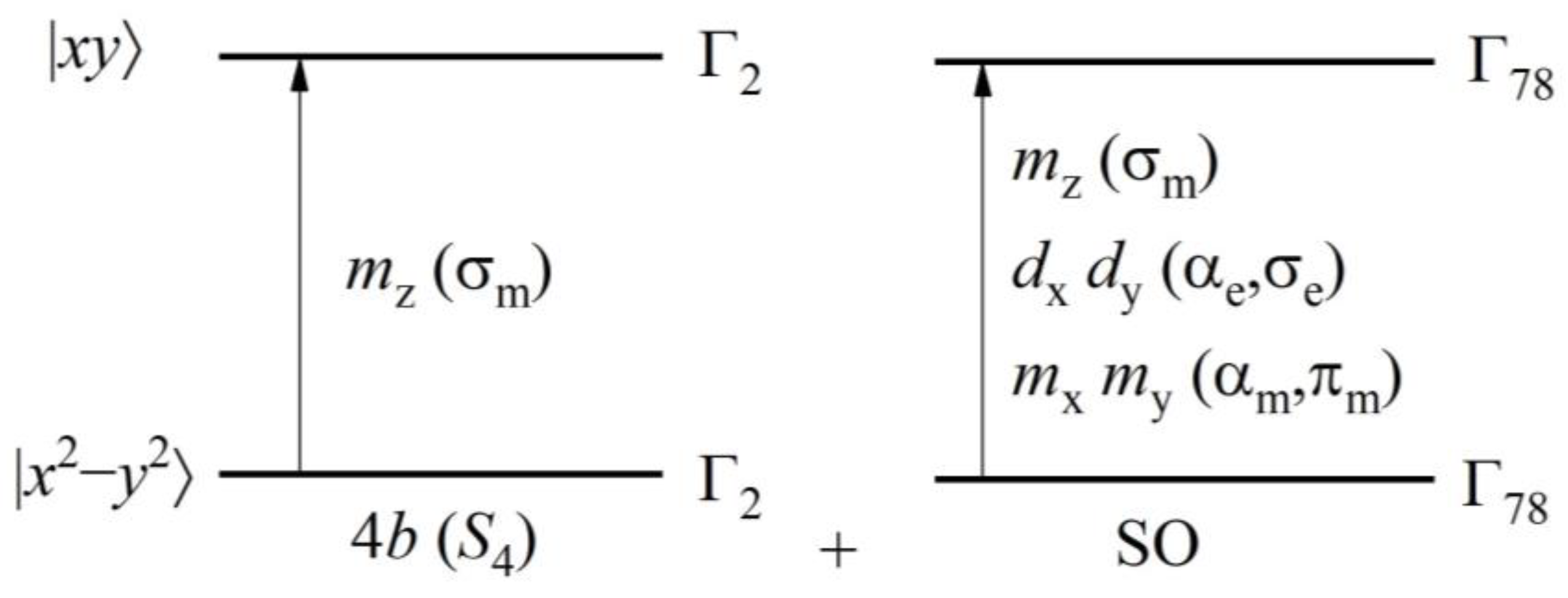
| Iα (k∥c) | Iσ (k∥b, Eω∥a) | Iπ (k∥b, Eω∥c) | |
|---|---|---|---|
| 1st 4b line (1.405 eV) | 1497 | 4830 | 84 |
| Geometry of the Experiment | |||||
|---|---|---|---|---|---|
| Exp. | Theor. | Exp. | Theor. | ||
| Voigt σ, , k ∥ [010] | - | 76 | - | 222 | |
| - | 76 | - | 1040 | ||
| Voigt σ, , k ∥ [010] | 25 | 76 | 953 (1094) | 1040 | |
| 26 | 76 | 189 | 222 | ||
| Voigt π, , k ∥ [010] | 8 | 4 | 8 | 4 | |
| 5 | 4 | 11 | 4 | ||
| Voigt σ, , k ∥ [010] | 166 | 151 | 542 | 556 | |
| 154 | 151 | 554 | 556 | ||
| Voigt π, , k ∥ [010] | 15 | 0 | 0 | 7 | |
| 14 | 0 | 1 | 7 | ||
| Faraday σ, , k ∥ [010] | 0 | 1 | 127 | 127 | |
| 0 | 0 | 1071 (1141) | 1286 | ||
| Faraday π, , k ∥ [010] | 7 | 7 | 9 | 0 | |
| 7 | 7 | 9 | 0 | ||
| CuA1 | CuA2 | |||
|---|---|---|---|---|
| da | −1230i | −1102 | −1100i | −1232 |
| db | −1100i | 1232 | −1230i | 1102 |
| dc | 0 | 0 | 0 | 0 |
| ma | 258 | 258i | −258 | −258i |
| mb | 258 | −258i | −258 | 258i |
| mc | 0 | −3168 | 0 | −3168 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boldyrev, K.N.; Molchanova, A.D.; Nurmukhametov, A.R.; Eremin, M.V.; Pisarev, R.V.; Popova, M.N. Nonreciprocity of Optical Absorption in the Magnetoelectric Antiferromagnet CuB2O4. Magnetochemistry 2023, 9, 95. https://doi.org/10.3390/magnetochemistry9040095
Boldyrev KN, Molchanova AD, Nurmukhametov AR, Eremin MV, Pisarev RV, Popova MN. Nonreciprocity of Optical Absorption in the Magnetoelectric Antiferromagnet CuB2O4. Magnetochemistry. 2023; 9(4):95. https://doi.org/10.3390/magnetochemistry9040095
Chicago/Turabian StyleBoldyrev, Kirill N., Anastasiia D. Molchanova, Alexey R. Nurmukhametov, Mikhail V. Eremin, Roman V. Pisarev, and Marina N. Popova. 2023. "Nonreciprocity of Optical Absorption in the Magnetoelectric Antiferromagnet CuB2O4" Magnetochemistry 9, no. 4: 95. https://doi.org/10.3390/magnetochemistry9040095
APA StyleBoldyrev, K. N., Molchanova, A. D., Nurmukhametov, A. R., Eremin, M. V., Pisarev, R. V., & Popova, M. N. (2023). Nonreciprocity of Optical Absorption in the Magnetoelectric Antiferromagnet CuB2O4. Magnetochemistry, 9(4), 95. https://doi.org/10.3390/magnetochemistry9040095







