Origin of Multiferroism of β-NaFeO₂

Abstract

The multiferroic $\beta$-NaFeO${}_2$ is theoretically investigated for the first time using a microscopic model and Green’s function technique. A small room-temperature ferromagnetism is observed, which could be explained by canting of the antiferromagnetic sublattices. The ferromagnetic behaviour can be applied to applications in spintronic devices. We have investigated the temperature and magnetic field dependence of the spontaneous polarization $P_s$, as calculated from the transverse Ising model and the spin-assisted polarization $\Delta P$ due to magnetostriction and antisymmetric Dzyaloshinsky–Moriya interactions. The influence of external magnetic fields along the y and z axis is discussed. This is indirect evidence for the multiferroic behaviour of NaFeO${}_2$. The temperature dependence of the relative dielectric permittivity is calculated.

1. Introduction

Materials that are both ferroelectric and magnetic—multiferroics—are rare in nature. Most multiferroic materials have simultaneous magnetic and ferroelectric orders at low temperatures. Howwever, for their applications, the materials have to show ferroelectricity and ferromagnetism at room temperature. An example of a room-temperature multiferroic is $\beta$-NaFeO${}_2$ ($\beta$-NFO), which shows a weak ferromagnetism (WFM) with a Curie temperature $T_C^{FM}$∼723 K [1,2]. This makes it a potentially promising material for applications in spintronic devices. The origin of WFM of $\beta$-NFO can be attributed to the presence of the Dzyaloshinsky–Moriya (DM) interactions in this compound. NFO can crystallize in different phases—$\alpha ,\beta ,\gamma$: the first exists at low, the second at middle, and the third at high temperatures [3]. Only the $\alpha$ and $\beta$ phases show ferroelectricity [1,4]. The $\gamma$ phase is paraelectric [1]. The ferroelectric phase transition temperature $T_C^{FE}$ of $\beta$-NFO is found at around 1373 K [1], which is much higher than its $T_C^{FM}$ of 723 K. The recently magnetic properties of $\beta$-NFO nanoparticles are reported [5,6], which makes them applicable to the treatment of cancer via hyperthermia [7,8].

Unfortunately, there are no theoretical works to explain the multiferroicity of $\beta$-NFO. The main aim of this study is to observe the magnetoelectric effect in $\beta$-NFO using a microscopic model.

2. The Model

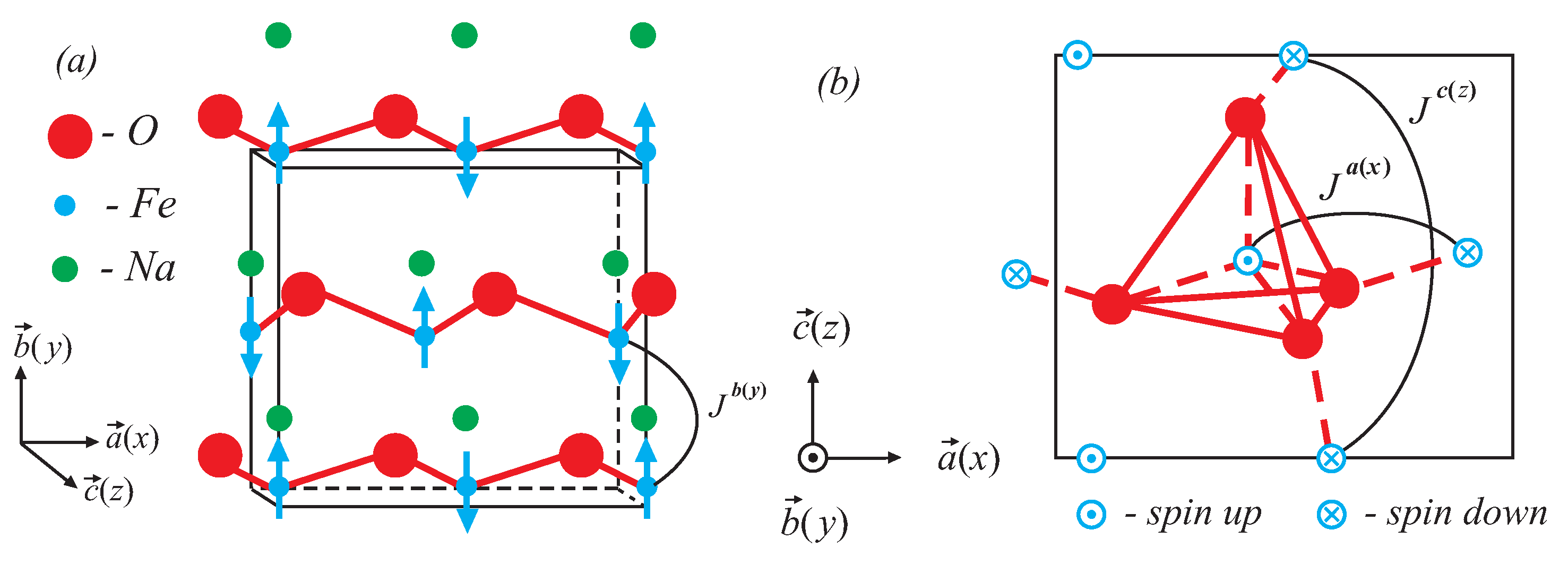
$\beta$-NFO crystallizes in a non-centrosymmetric orthorhombic structure Pn2${}_1$a (see Figure 1) with lattice parameters a = 5.6793 $\dot{A}$, b = 7.1243 $\dot{A}$ and c = 5.3784 $\dot{A}$ [1]. The Fe${}^{3+}$ ions form a monoclinic lattice, where each magnetic ion has four nearest neighbors. The basic magnetic interaction is a super-exchange one Fe-O-Fe with an angle 113$°$–126$°$[2], which is not optimal for antiferromagnetic ordering. Neutronographic studies have shown that the magnetic moments of Fe${}^{3+}$ are arranged in a G-type antiferromagnetic structure along the $b\left(y\right)$ axis with a phase transition temperature of $T_C^{FM}$ = 723 K [1]. Magnetic measurements indicate the presence of a weak ferromagnetism with a spontaneous magnetic value of about $5.{10}^{-4}{\mathrm{\mu }}_{\mathrm{B}}$/cell at room temperature with a deviation from the antiferromagnetic arrangement of 0.003$°$[1]. This behavior is a consequence of the presence of an antisymmetric DM exchange interaction. For symmetric reasons, it is clear that if the antiferromagnetic order is along the $b\left(y\right)$ axis, the appearance of the WFM is along the $c\left(z\right)$ axis as the DM vector has the form $\mathbf{D}$ = $\mathbf{d}(\pm 1;0;\pm 1)$. The sign and direction of the DM vector provides the relationship between the coordinates of the Fe ions in the elementary cell for each Fe-O-Fe bond [9]. Following the peculiarities of the crystalline structure, it is clear that the symmetric operators n and a do not impose any restriction on the polarization vector. The operator $2_1$ (determining a rotation of 180$°$ around the $b\left(y\right)$ axis) changes the atomic positions from $(x,y,z)$ in $(-x,y,-z)$. This means that the polarization will only have a component along the $b\left(y\right)$ axis [10].

The magnetic properties of $\beta$-NFO are described by a modified Heisenberg Hamiltonian $H_m$:

$$\begin{array}{ccc}\hfill H_m& =& -\sum _{ij}\frac{1}{2}{J}_{ij}^z{S}_i^z{S}_j^z-\sum _{ij}\frac{1}{2}{J}_{ij}^x{S}_i^x{S}_j^x-\sum _{ij}\frac{1}{2}{J}_{ij}^y{S}_i^y{S}_j^y\hfill \\ & -& \sum _{ij}{\mathbf{D}}_{ij}·({\mathbf{S}}_i\times {\mathbf{S}}_j)-\sum _i{K}_i{\left(S_i^y\right)}^2-g{\mu }_B\mathbf{h}·\sum _i{\mathbf{S}}_i,\hfill \end{array}$$

(1)

where ${\mathbf{S}}_i$ is the Heisenberg spin operator of the Fe ion at the site i. J is the symmetric exchange interaction, K is the constant of the single-ion magnetic anisotropy, g is the gyromagnetic factor, and ${\mu }_B$ is the Bohr magneton. The first three terms in (1) describe the isotropic super-exchange interactions in the magnetic system as: $J^z>0$ (see Figure 1b). This determines a ferromagnetic arrangement along the z axis, $J^x<0$ (see Figure 1b) and $J^y<0$ (see Figure 1a) determines an antiferromagnetic arrangement along the x and y axis, respectively. The fourth term includes the antisymmetric exchange DM interaction type and is responsible for the appearance of a weak ferromagnetism along the z axis. The fifth term in (1) defines the y-axis as the easy axis of the magnetization, i.e., $K_i>0$. $\mathbf{h}$ is an external magnetic field.

Since the crystal lattice of $\beta$-NFO is non-centrosymmetric, the spontaneous polarization appears at temperatures higher than $T_C^{FM}$. At temperatures above $T_C^{FE}$ = 1373 K $\beta$-NFO is in a paraelectric state, where the lattice symmetry is tetragonal (the so-called $\gamma$-NFO). This means that, at $T_C^{FE}$ = 1373 K, there is a structural phase transition from a paraelectric P4${}_1$2${}_1$2 centrosymmetric tetragonal phase into a non-centrosymmetric orthorhombic structure Pn2${}_1$a [1]. This is a phase transition of a displacive type. The polarization properties can be described using the pseudo-spin formalism and the transverse Ising model (TIM) $H_f$, considering that, from a symmetrical point of view, the polarization is on the y axis:

$$H_f=-\mathrm{\Omega }\sum _i{B}_i^z-\frac{1}{2}\sum _{ij}{J}_{ij}^{\prime }{B}_i^y{B}_j^y.$$

(2)

The pseudo-spin operator $B_i^y$ characterizes the two positions of the ferroelectric unit at the lattice point i. $J_{ij}^{\prime }$ denotes the nearest-neighbor pseudo-spin interaction. The dynamics of the ferroelectric part are realized by the first term with the flipping rate $\mathrm{\Omega }$ and the operator $B_i^z$. The TIM was proposed by Blinc and de Gennes, describing order–disorder and displacive type ferroelectrics [11,12].

For $\beta$-NFO the Fe${}^{3+}$, ions are involved in the formation of the polar state through their displacements, together with those of the Na${}^{+}$ ions relative to the oxygen matrix. Moreover, the same iron ions, due to super-exchange interactions, are responsible for the appearance of a G-type magnetic ordering and a weak ferromagnetism. This means that these compounds must be defined as multiferroics, in which an additional, spin-assisted polarization $\Delta P$ is also observed. From a theoretical perspective, the appearance of the magnetoelectric terms in the Hamiltonian $H_{mf}$ is a consequence of the modulation of the symmetric and antisymmetric exchange interactions between the Fe${}^{3+}$ spins from the polar lattice displacements $u_{ij}$. Considering that $P_s=e^{*}\langle u\rangle$, where $e^{*}$ is the Born charge, $H_{mf}$ can be written as:

$$\begin{array}{ccc}\hfill H_{mf}& =& -{\gamma }_1\sum _{ij}\mid {\mathbf{P}}_s\mid ({\mathbf{S}}_i·{\mathbf{S}}_j)-{\gamma }_2\sum _{ij}{\left({\mathbf{P}}_s\right)}^2({\mathbf{S}}_i·{\mathbf{S}}_j)\hfill \\ & -& \lambda \sum _{ij}({\mathbf{P}}_s\times {\mathbf{e}}_{ij})·({\mathbf{S}}_i\times {\mathbf{S}}_j).\hfill \end{array}$$

(3)

${\gamma }_1$ and $\lambda$ are the first derivatives of the exchange interaction J and of the DM vector on the polar displacements $u_{ij}$, respectively, and ${\gamma }_2$ is the second derivative of J on $u_{ij}$. The terms in (3) are formally similar to the Peierls-type spin–phonon interactions. Note that $P_s$ is responsible for the change in the hybridization of the magnetic Fe-O-Fe and Fe-O-O-Fe bonds, i.e., under $T_C^{FM}$, the magnetic arrangement is influenced by the spontaneous polarization.

Finally, the total Hamiltonian for the description of the multiferroic properties of $\beta$-NFO takes the form:

$$H=H_m+H_f+H_{mf}.$$

(4)

Comparing the third term in Equation (3) with the fourth one in (1), it can be concluded that the spontaneous polarization induces a DM interaction with a vector ${\mathbf{D}}_{ij}^{ind}=\lambda ({\mathbf{P}}_s\times {\mathbf{e}}_{ij})$. This leads to an effective temperature-dependent DM vector:

$${\mathbf{D}}_{ij}^{eff}={\mathbf{D}}_{ij}+{\mathbf{D}}_{ij}^{ind},$$

(5)

which, below $T_C^{FM}$ increases, with decreases in temperature.

Analogically, the first and second terms in Equation (3) mean that the isotropic exchange interaction J is also temperature-dependent:

$$J^{eff}=J+{\gamma }_1\mid P_s\mid +{\gamma }_2\mid P_s{\mid }^2.$$

(6)

Qualitatively, Equations (5) and (6) define a kind of a feedback connection between the two subsystems. The spontaneous polarization changes the nature of the symmetric and antisymmetric exchange interactions. However, below the ferromagnetic phase transition temperature $T_C^{FM}$, due to the magnetic ordering, the spontaneous polarization will be changed and “controlled” through renormalization of the pseudo-spin interaction and the tunneling rate by applying a magnetic field and the appearance of a spin-assisted additive polarization $\Delta P_{tot}$.

Let us emphasize that a strong spin–phonon interaction is reported in ABO${}_2$ compounds (A = Cu, Ag, Na, Li and B = Fe, Cr) [13]. Therefore, a further polarization may be a consequence of magnetostriction (MS) effects:

$$\Delta P_{ss}\sim \sum _{ij}\langle ({\mathbf{S}}_i·{\mathbf{S}}_j)\rangle$$

(7)

or (and) inverse DM mechanism [14]:

$${(\Delta P_{IDM})}^d\sim \sum _{ij}{\langle {\mathbf{e}}_{ij}\times ({\mathbf{S}}_i\times {\mathbf{S}}_j)\rangle }^d,d=(x,y,z),$$

(8)

where d are the components of $\Delta P$. The second mechanism is characteristic for compounds in which non-collinear magnetic structures (commensurate and non-commensurate spirals) are observed, and for crystals, which have a two fold axis perpendicular to ${\mathbf{e}}_{ij}$, or a mirror plane of symmetry containing ${\mathbf{e}}_{ij}$. In our opinion, this is not the case in $\beta$-NFO. As Kaplan et al. [10] have shown, in the absence of such elements of symmetry, an additional polarization resulting from the DM interaction will appear:

$$\Delta P_{as}^d\sim \sum _{ij}{\langle ({\mathbf{S}}_i\times {\mathbf{S}}_j)\rangle }^d,d=(x,y,z).$$

(9)

Therefore the spin-assisted polarization is calculated from the following equation:

$$\Delta P_{tot}=\Delta P_{ss}+\Delta P_{as}.$$

(10)

From Equation (2), it can be seen that the ferroelectric ordered phase is characterized by non-zero mean values of $\langle B^y\rangle$ and $\langle B^z\rangle$. In order to obtain, below the ferroelectric phase-transition temperature $T_C^{FE}$, one order of parameter that determines spontaneous polarization, the coordinate system is rotated around the x axis at about an angle of $\theta$, which is the angle locked between the direction of the pseudo-spin vector and the positive direction of the y-axis. $\theta$ is determined from the requirements of $\langle B^{z^{\prime }}\rangle =0$ in the new coordinate system:

$$\langle B_i^y\rangle =\frac{1}{2}tanh\left(\frac{E_i}{2k_{B}T}\right)cos{\theta }_i.$$

(11)

$E_i$ is the pseudo-spin wave energy observed from the poles of the Green’s function $G_{ij}=\langle \langle B_i^{+};B_j^{-}\rangle \rangle$.

From the 3 × 3 matrix Green’s function $g_{ij}=\langle \langle S_i^{+,-,z};S_j^{-,+,z}\rangle \rangle$, the expression for the magnetization $M_c$ is calculated as follows:

$$M_c=\frac{1}{N}\sum _i\langle S_i^z\rangle =\frac{1}{N}\sum _i\left[(S+0.5)coth\left(\frac{(S+0.5){\omega }_i}{k_{B}T}\right)-0.5coth\left(\frac{0.5{\omega }_i}{k_{B}T}\right)\right],$$

(12)

where ${\omega }_i$ is the spin-wave energy.

For the spin-assisted additive polarizations, we have observed:

$$\Delta P_{ss}\sim \frac{2}{N}\sum _{ij}\left(\langle S_i^{-}{S}_j^{+}\rangle +\langle S_i^z{S}_j^z\rangle \right),$$

(13)

$$\Delta P_{as}\sim \frac{1}{2N}\sum _{ij}\left(\langle S_i^z{S}_j^{-}\rangle +\langle S_i^z{S}_j^{+}\rangle \right).$$

(14)

The correlation functions are obtained using the Spectral theorem.

3. Numerical Results and Discussion

For the numerical calculations of the properties of $\beta$-NFO, we will use the following model parameters for the magnetic subsystem: $J^x$ = −61.94 K, $J^z$ = 17.27 K, $J^y$ = −9.84 K, d = 0.26 K, K = 0.034 K, S = 5/2, $T_C^{FM}$ = 723 K. For the ferroelectric subsystem, we use the following: $J^{\prime }$ = 1472.28 K, $\mathrm{\Omega }$ = 16.47 K, s = 1/2, $T_C^{FE}$ = 1373 K.

We will provide a short description of the calculation of some model parameters. From Figure 1b, it can be seen that, along the a axis, the spins are ordered antiferromagnetically, with type Fe-O-Fe. Along the c axis, the spins are ordered ferromagnetically, with type Fe-O-O-Fe (next nearest neighbors) (Figure 1b), which leads to a smaller interaction compared to that along the a axis. The exchange interaction $J^x$ along the x axis in the $ac$ plane is approximately observed from the expression in the mean field approximation $J^x=3k_B{T}_C^{FM}/\left(zS(S+1)\right)$, where $k_B$ is the Boltzmann constant, z = 4 is the number of nearest neighbors, S = 5/2 is the spin value, and $T_C^{FM}$ is the magnetic critical temperature. The above expression for $J^x$ determines the magnitude of the exchange interaction value while the magnetic configuration is its sign. There is an antiferromagnetic arrangement along the x-axis (see Figure 1b). This means that the sign of $J^x$ is negative. Finally, we find that $J^x$ = −61.94 K. It must be noted that the units for all exchange interactions are shown in Kelvin [K] as $1J=0.724\times {10}^{23}$ K [15]. $J^z$ along the z axis is calculated, considering the dependence of the magnetic exchange interaction constant on the distance r between two neighbouring spins, $J\sim 1/r^2$, as follows: $J^z\sim -{(a/2c)}^2{J}^x$ = 17.27 K. Using the same assumption, we observe for $J^y\sim {(a/2b)}^2{J}^x$ = −9.84 K. Following [16], we can observe the DM constant from the relation between the canting angle $\tau$ and the value of the DM vector D: $sin\tau =-D/\left(2J^x\right)=-d/\left(\sqrt{2}{J}^x\right)$. With $\tau$ = 0.003$°$[1], i.e., $sin\tau \sim \tau$, we can observe $d=-\sqrt{2}\tau J^x$ = 0.26 K. The model parameters for the ferroelectric subsystem $J^{\prime }$ and $\mathrm{\Omega }$ are calculated from the following expressions: $2\mathrm{\Omega }/J^{\prime }=tanh\left(0.5{\beta }_c\mathrm{\Omega }\right)$, ${\beta }_c=1/\left(k_B{T}_C^{FE}\right)$, below $T_C^{FE}$ and $2\mathrm{\Omega }$ ≈ $E_i$ with $E_i\approx$ 40–45 K (the energies of the ferroelectric system assumed within our model) at very high temperatures [11].

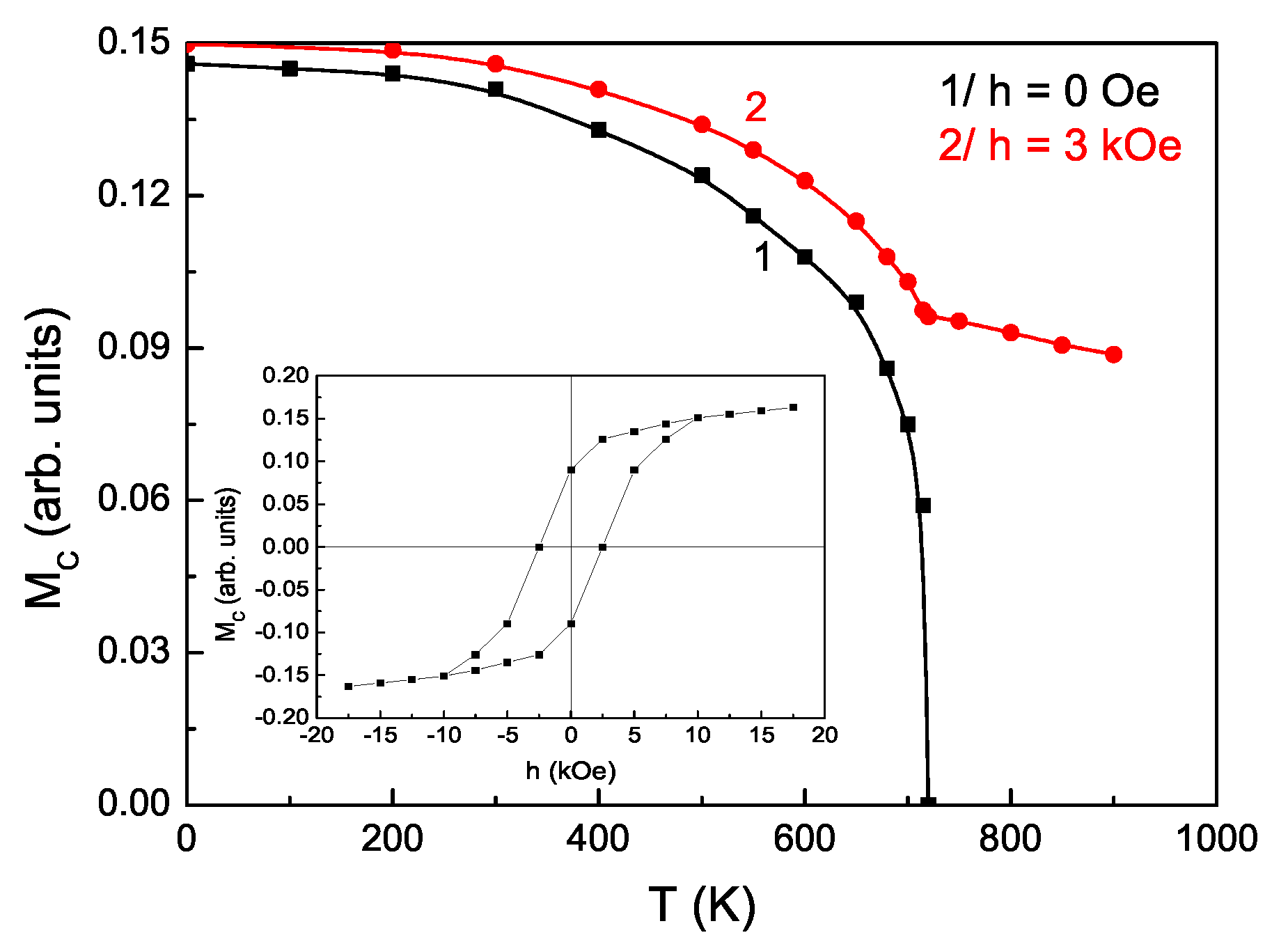
Firstly, we will study the magnetic field and temperature dependence of the magnetization of $\beta$-NFO. The results are presented in Figure 2. We observe that $\beta$-NFO exhibits a WFM, a magnetization $M_c$ along the c axis, which is in agreement with the experimental data of Viret et al. [1] and Watanabe et al. [2]. The WFM decreases with increasing temperature and vanishes for a magnetic field h = 0 at a critical temperature $T_C^{FM}$ = 723 K. We also investigated the influence of an external magnetic field h in the c direction on the magnetization $M_c$. The hysteresis is shown as being inset in Figure 2. It can be seen that this shows a typical ferromagnetic behavior. This behavior could be due to the spin-canted Fe moments, to the competition between antiferromagnetic super-exchange and ferromagnetic interactions, or to the antisymmetric DM interactions. It should be mentioned that the latter could also depend on the coupling between local spins and electrical polarization. Let us emphasize that the DM interaction, which is the main origin of the WFM, leads to its increase. For D = 0, there is not a WFM, the magnetization $M_c$ is zero.

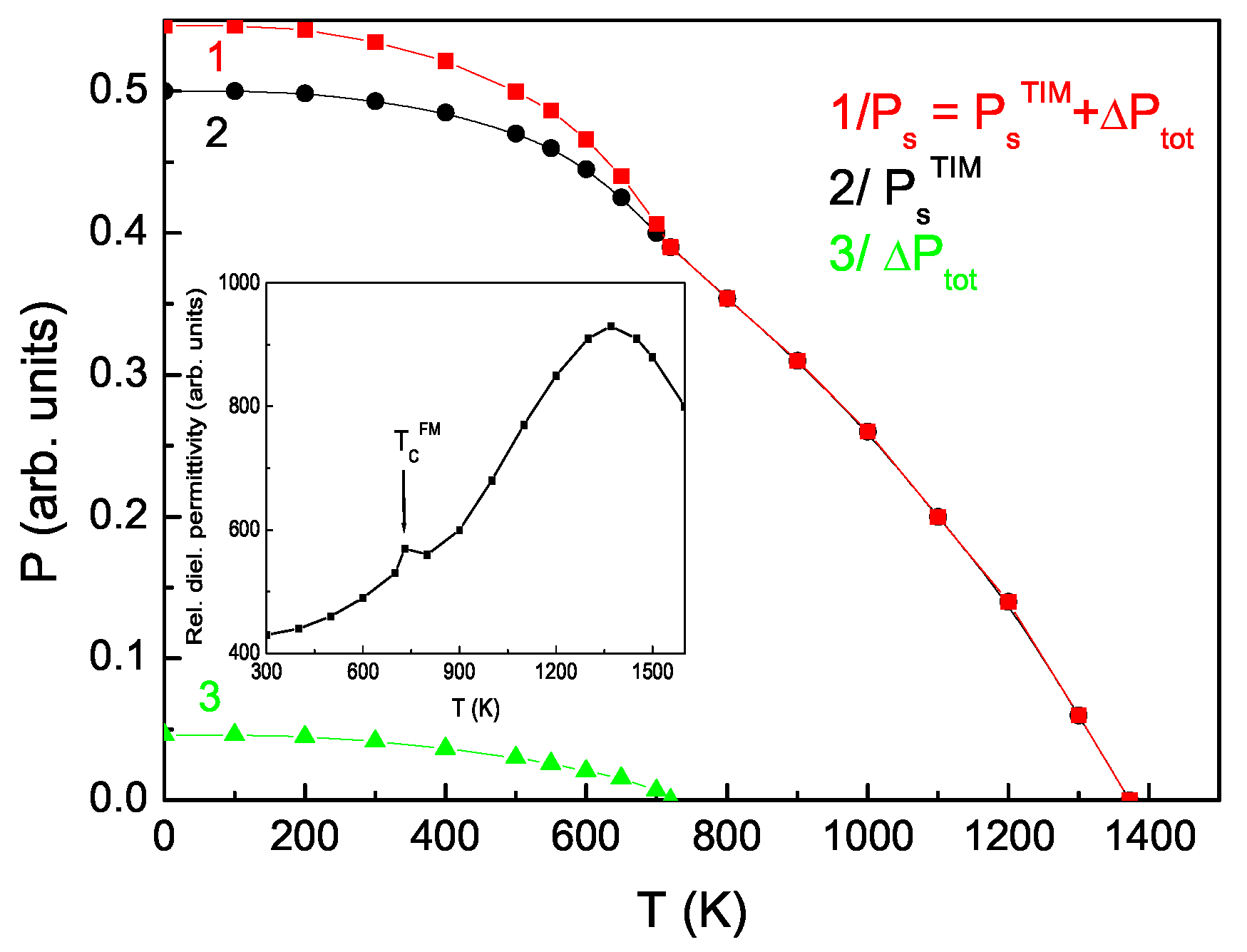
Figure 3 shows the temperature dependence of the spontaneous polarization $P_s$ along the b axis, which vanishes at $T_C^{FE}$ = 1373 K, a phase transformation from the orthorhombic to tetragonal phase. The hysteresis of $P_s$ is reported by Viret et al. [1]. In $P_s$, there are two contributions: curve 2 describes the spontaneous polarization observed from the TIM $P_s^{TIM}$, whereas curve 1 describes the behavior of $P_s$, also considering the ME interactions in $\beta$-NFO. At $T_C^{FM}$ = 723 K, a “kink” is observed (see curve 1). The additional contribution in $P_s$ is due to the appearance under $T_C^{FM}$ of an additional spin-dependent polarization $\Delta P_{tot}$ (curve 3), which is due to the MS and the antisymmetric DM interaction. In the “inset”, the temperature dependence of the relative dielectric permittivity $ϵ$ is presented, where a peak is observed at the magnetic-phase transition temperature $T_C^{FM}$. This is evidence of the presence of ME interactions in $\beta$-NFO. The appearance of the additional polarization $\Delta P_{tot}$, which is spin-dependent, determines the possibility of controlling $P_s$ in this compound within an external magnetic field h at room temperature.

The relative dielectric permittivity $ϵ$ is calculated from equation [17]:

$$({(\mathrm{\Lambda }/(ϵ(\mathbf{k},E)-1))}_{\alpha \beta }+\mathrm{\Lambda }\frac{k_{\alpha }{k}_{\beta }}{k^2})G^{\beta \gamma }(\mathbf{k},E)={\delta }_{\alpha \gamma };\mathrm{\Lambda }=4\pi Z^2/v,$$

(15)

where $\mathbf{k}$ is wave vector, E is energy or frequency, the indices $\alpha ,\beta ,\gamma$ are the components of the related spins, $\delta$ is the delta function, Z is the electron charge and v is the volume. To study the relative dielectric permittivity $ϵ(\mathbf{k},E)$, we need the Green’s function $G^{xx}(\mathbf{k},E)$:

$$G^{xx}(\mathbf{k},E)=\frac{2P_s({ϵ}_{11}-{ϵ}_{12})}{E^2-E_k^2+2iE{\gamma }_{11}},$$

(16)

$E_k$ and ${\gamma }_{11}$ are the transverse pseudo-spin wave energy and its damping.

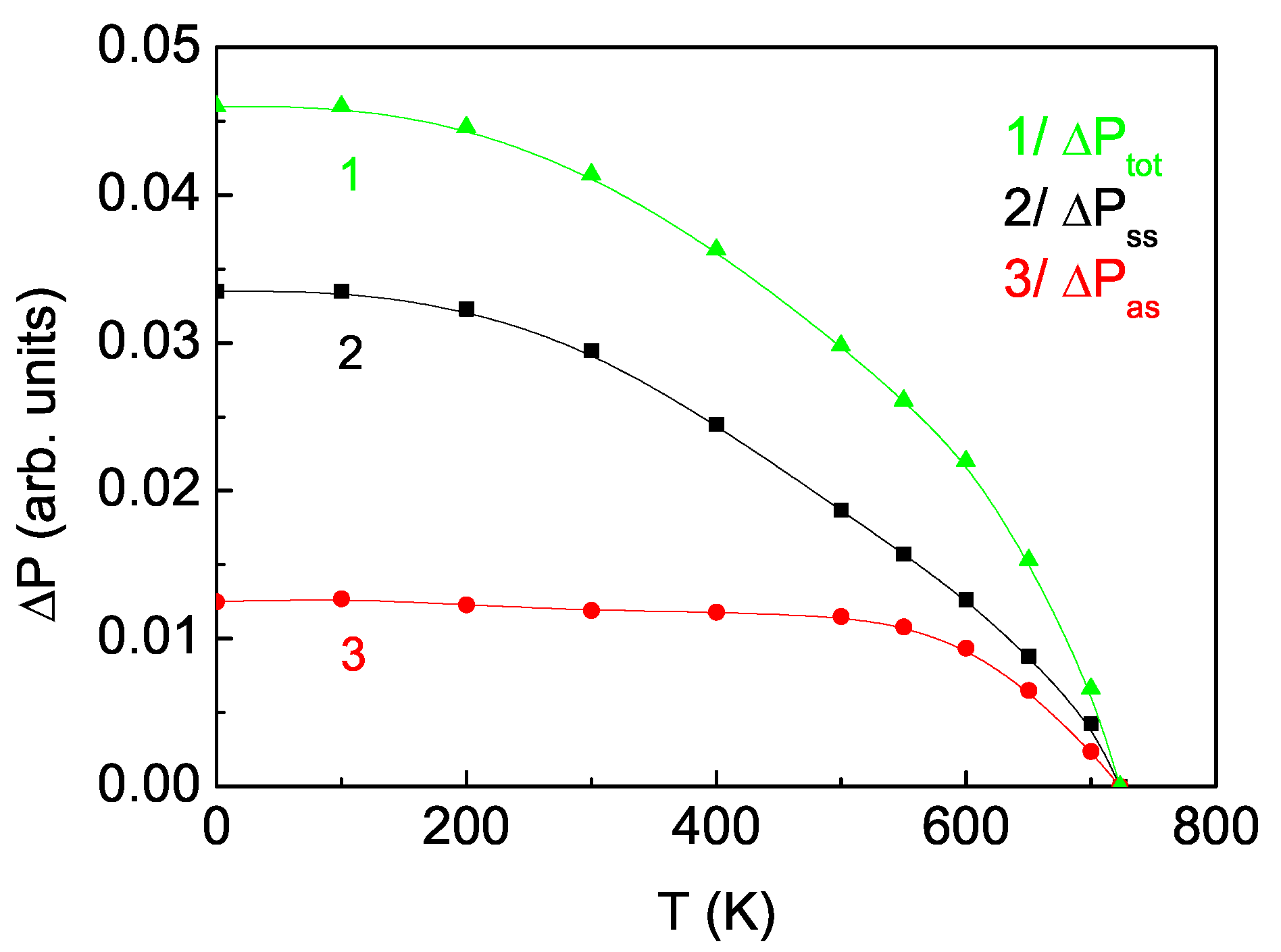
The contributions of each of the mechanisms to $\Delta P_{tot}$ are presented in the next Figure. From the temperature dependence of $\Delta P_{tot}$ (see Figure 4, curve 1), this can be seen to disappear at the magnetic-phase transition temperature $T_C^{FM}$. Curves 2 and 3 determine the contributions of the two mechanisms to the additional polarization, $\Delta P_{ss}$ and $\Delta P_{as}$, due to the MS and the antisymmetric DM interaction, respectively. It is clear that the additional polarization associated with the MS (curve 2) prevails over that due to the DM-related interaction (curve 3).

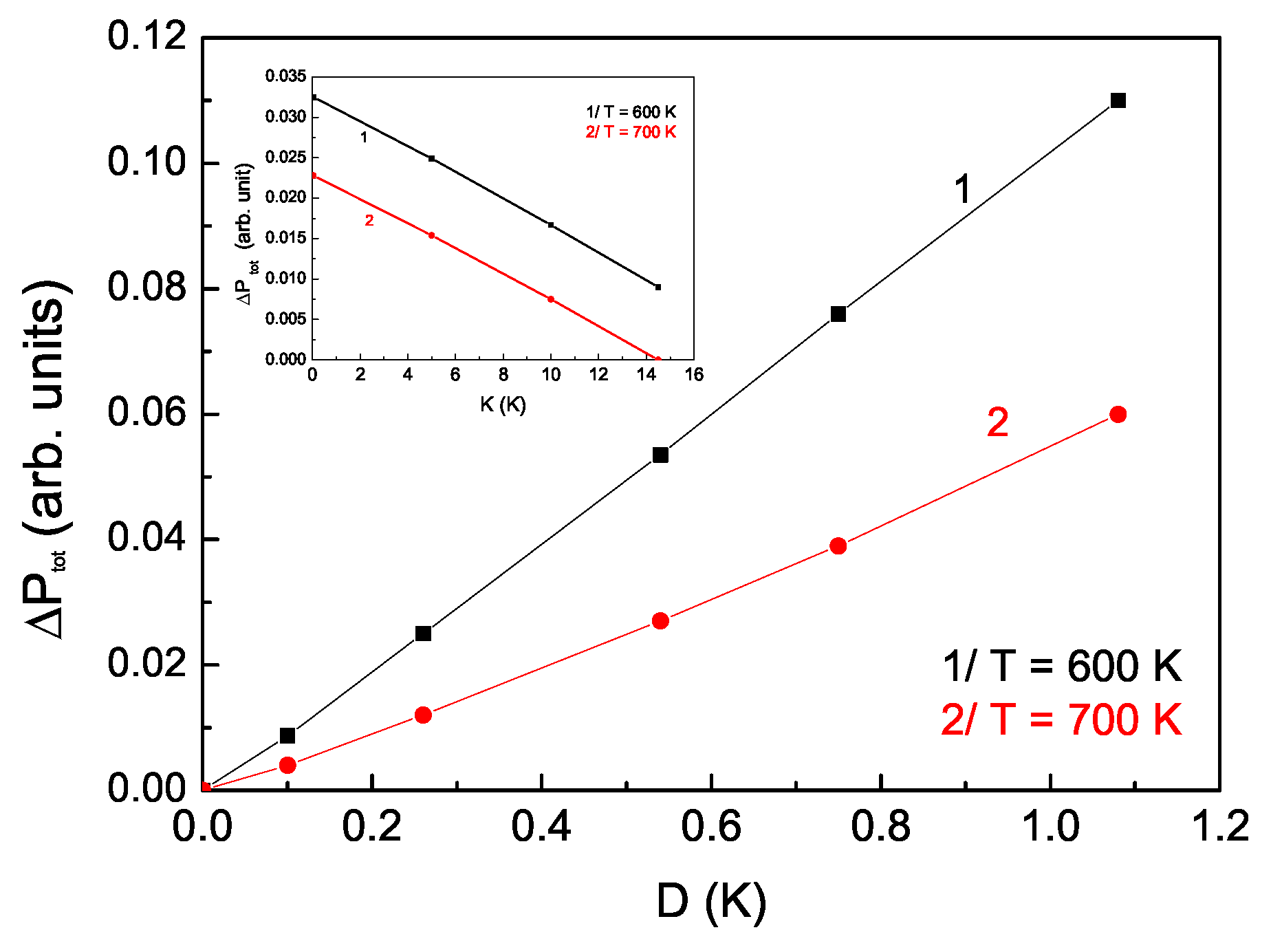
Figure 5 presents the dependence of the spin-dependent polarization $\Delta P_{tot}$ on the DM vector D, whereas the inset shows the dependence on the magnetic anisotropy constant K for different temperature values (curves 1 and 2). As D increases, the value of the additional polarization increases, while as K grows, it decreases. These results are expected because the antisymmetric magnetic interaction (the intensity of which depends on the size of the DM vector D) determines the presence of a magnetoelectric (ME) mechanism (see the third term in Equation (3)) for the occurrence of the additional polarisation $\Delta P_{as}$ (see Equation (9)). As D grows, the “canting” angle and WFM will increase, leading to an increase in the contribution of $\Delta P_{as}$. However, enhancing K will lead to stabilization of the antiferromagnetic G-structure, a decrease in the “canting” angle, and the WFM. The contribution of $\Delta P_{as}$ due to the antisymmetric DM interaction decreases; therefore, $\Delta P_{tot}$ also decreases.

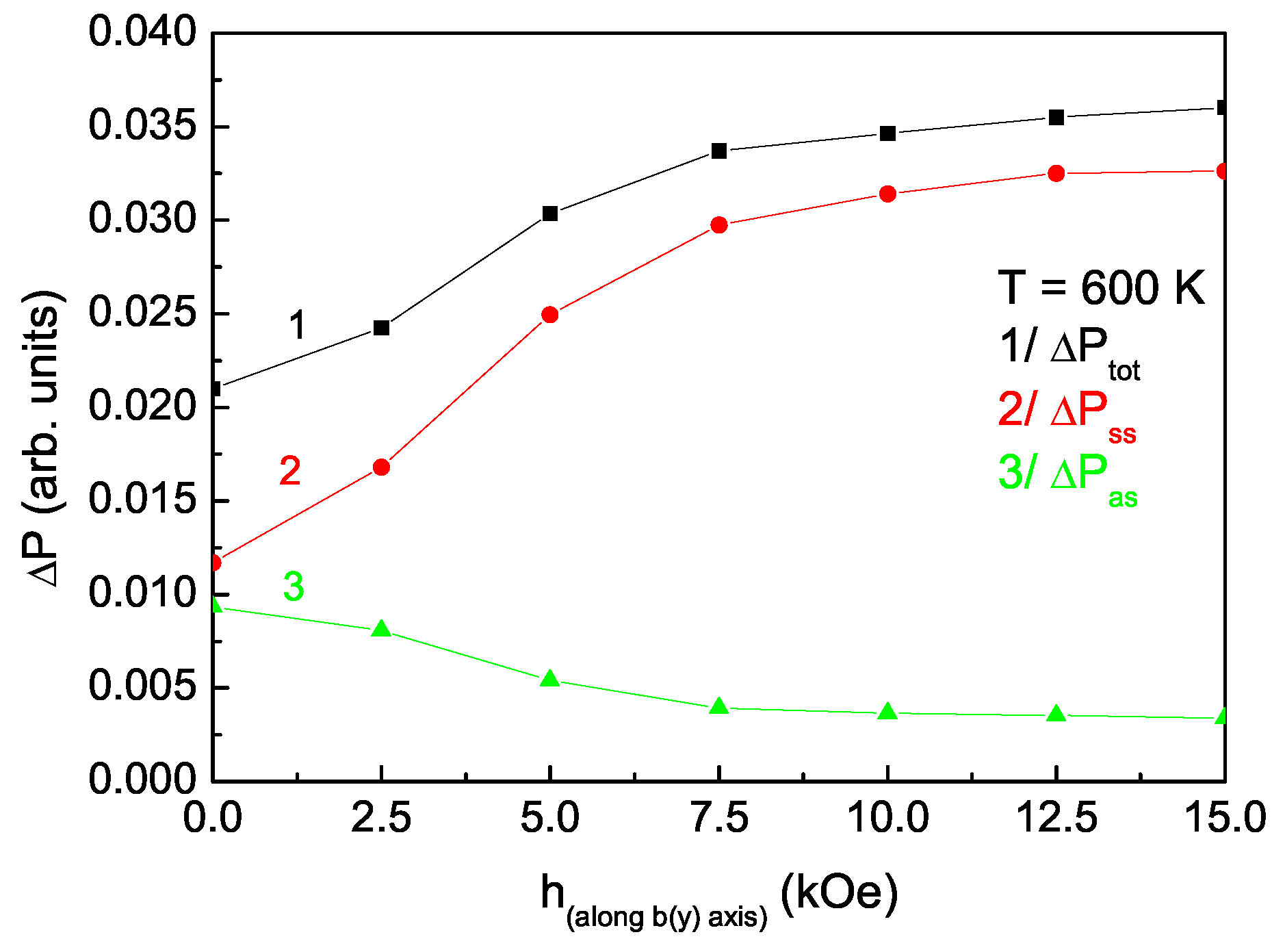
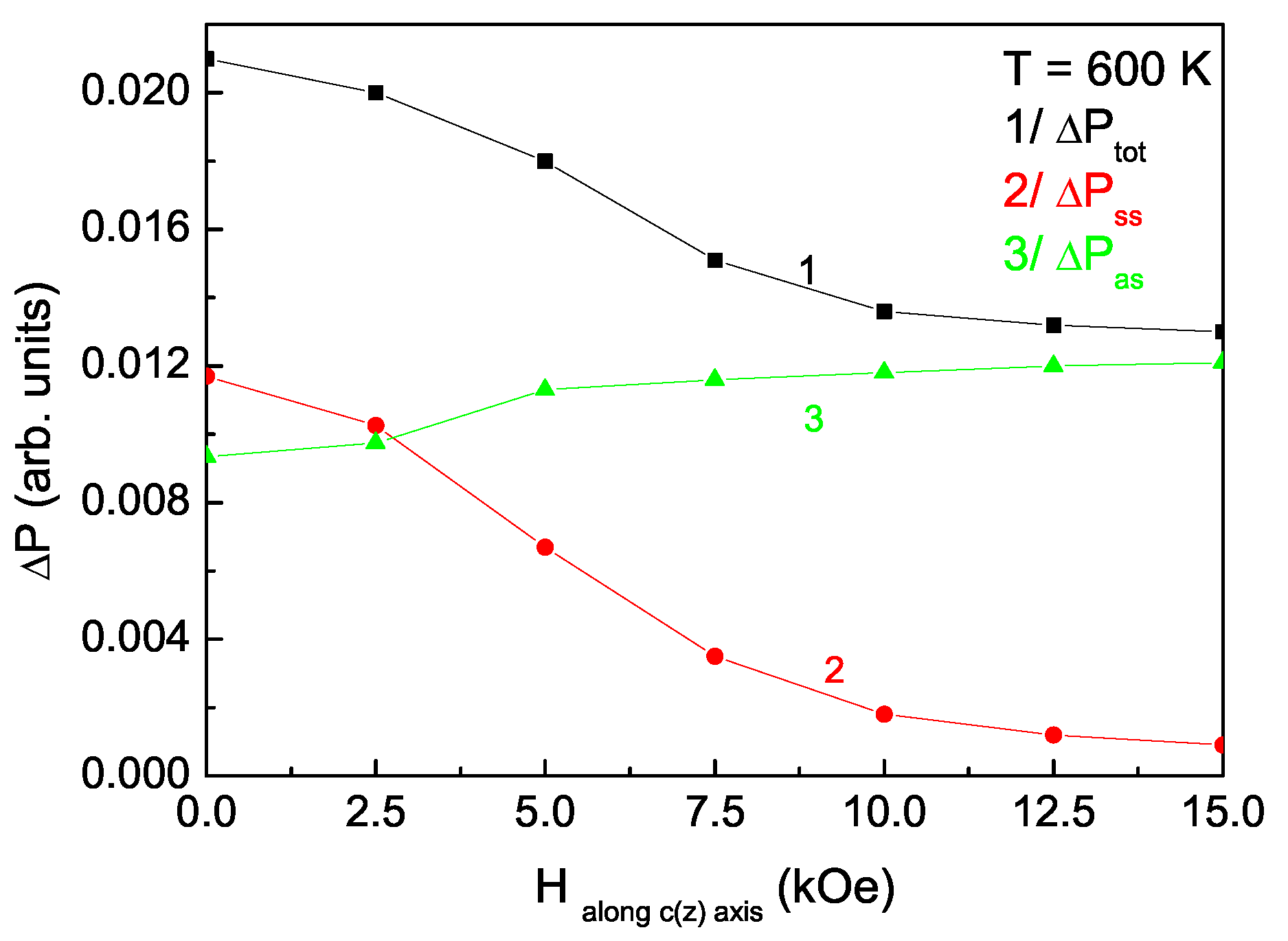
Figure 6 shows the dependence of the additional spin-dependent polarisation as a function of an external magnetic field applied in the y direction at a fixed temperature below $T_C^{FM}$. As the field increases, the influence of the spin-dependent polarization increases (curve 1). However, the components of $\Delta P_{tot}$ with the field are different. Using the MS mechanism, $\Delta P_{ss}$ increases as the magnetic field increases (curve 2), while $\Delta P_{as}$ decreases (curve 3). In contrast, when the applied magnetic field is along the z axis (see Figure 7) the influence of the spin-assisted polarization decreases when the magnetic field increases (curve 1), as $\Delta P_{ss}$ decreases with the field (curve 2), whereas $\Delta P_{as}$ increases (curve 3). This means that there is competition between the two mechanisms and, when the field increases, depending on its direction, the two mechanisms will always have different behaviors (if one mechanism leads to an increase in the polarization $P_s$, the other will lead to its reduction). As a result, in an external magnetic field applied in the y direction, the spontaneous polarization $P_s$ of the system will increase as the field increases, while, if h is in the z direction, $P_s$ will decrease. The dynamics in the change in the spontaneous polarization is mainly determined by the MS mechanism (this is more sensitive to changes in the value of the field compared to those due to DM interactions).

From a theoretical perspective, the reason for the dependence of the spontaneous polarization on the direction and size of the field below $T_C^{FM}$ is, in our opinion, due to the influence of the ME mechanisms on the basic microscopic parameters of the pseudo-spin system, namely, on the flipping rate $\mathrm{\Omega }$ and pseudo-spin interchange interaction $J^{{}^{\prime }}$. Below the magnetic phase transition temperature, they are renormalized and spin-dependent. Theoretical calculations lead to the following expressions: $J_{ij}^{{}^{\prime }eff}=J_{ij}^{{}^{\prime }}+2{\gamma }_2(\langle S_i^{-}{S}_j^{+}\rangle +\langle S_i^z{S}_j^z\rangle )$ and ${\mathrm{\Omega }}_{eff}=\mathrm{\Omega }+2[d_{eff}+\lambda {\sum }_{ij}(\langle S_i^z{S}_j^{-}\rangle +\langle S_i^z{S}_j^{+}\rangle )]$ where $d_{eff}=d+\lambda \mid {\mathbf{P}}_s\mid$. From these expressions, it is clear that the ME interaction due to the MS renormalizes the pseudo-spin exchange interaction $J_{ij}^{\prime }$, whereas the ME interaction connected with the DM interaction renormalizes the flipping rate $\mathrm{\Omega }$. The numerical calculations show that, with a constant temperature and increasing magnetic field along the y axis, ${\mathrm{\Omega }}_{eff}$ increases, which, according to the TIM, will decrease $P_s$, i.e., the antisymmetric ME interaction $-\lambda {\sum }_{ij}({\mathbf{P}}_s\times {\mathbf{e}}_{ij})·({\mathbf{S}}_i\times {\mathbf{S}}_j)$ destabilizes the ferroelectric phase. Under the same conditions, the calculations show that $J_{ij}^{{}^{\prime }eff}$ would increase, which, according to the TIM, means that $P_s$ would also increase, i.e., the ME interaction connected with the MS $-{\gamma }_1{\sum }_{ij}\mid {\mathbf{P}}_s\mid ({\mathbf{S}}_i·{\mathbf{S}}_j)-{\gamma }_2{\sum }_{ij}{\left({\mathbf{P}}_s\right)}^2({\mathbf{S}}_i·{\mathbf{S}}_j)$ stabilizes the ferroelectric phase. However, for h in the direction of the z axis at a constant temperature, the numerical calculations indicate that ${\mathrm{\Omega }}_{eff}$ decreases with increasing h, which means that following the TIM, $P_s$ would increase, i.e., the antisymmetric ME interaction will stabilize the ferroelectric phase. Under the same conditions, the calculations show that $J_{ij}^{{}^{\prime }eff}$ would decrease, which, within the TIM, means that $P_s$ would also be reduced, i.e., the ME interaction associated with the MS would destabilize the ferroelectric phase. The magnetic field dependence of the polarization is evidence for the multiferroic behavior of $\beta$-NFO. Unfortunately, to our knowledge, there are no experimental data for the the temperature and magnetic field dependence of the polarization $P(T,h)$.

4. Conclusions

In conclusion, we have theoretically investigated the multiferroic properties of $\beta$-NFO for the first time. We have observed a small ferromagnetism along the c axis, which makes $\beta$-NFO a promising material for applications in spintronic devices.

Moreover, we have calculated the spontaneous polarization $P_s$ along the b axis, as well as the spin-assisted polarization $\Delta P$, due to the ME interactions, including the MS and the DM interaction. The temperature dependence of the relative dielectric permittivity is also observed, which shows a kink at $T_C^{FM}$.

The study presents interesting results regarding the influence of an external magnetic field along the y and z axis on $\Delta P$. The latter is evidence for the MF behaviour of $\beta$-NFO. Further experimental and theoretical studies are clearly needed to explain the multiferroic behaviour of $\beta$-NFO.