Abstract
The magnetic nanoparticles (MNPs) with decreasing heating efficiency (characterized by specific loss power, SLP) with temperature increase, especially around the Curie temperature (TC), are expected to realize the self-regulated temperature hyperthermia of the tumor. However, the actual decrease of the SLP is gradual, resulting in the deviation of self-regulated temperatures from the measured TC. So far, no method is available for evaluating the heating performances of those MNPs. Here, by simulating the temperature-dependent SLP, the heating performances of MNPs are evaluated from three clinically concerning aspects: the capacity for effective heating, the temperature uniformity in the tumor, and the temperature stability under environmental changes such as MNP loss or tumor progression. The developed methods were applied to ZnCoCrFeO, Fe3O4, and γ-Fe2O3 MNPs. It was found that the uniform temperature distribution relies on lowering the heating power in the inner regions of the tumor, and the stable control of temperature depends on the dynamic adaptation of the heating power to the tumor temperature change. The proposed method may be used to predict the heating ability of MNPs and help the selection of MNPs for hyperthermia.
1. Introduction
After being introduced to tumors, magnetic nanoparticles (MNPs) can heat and cure tumors under an alternating magnetic field (AMF) with few side effects. The efficiency of the therapy has been verified in several clinical trials [1,2,3,4]. For further improving the therapeutic effects, the MNPs with suitable Curie temperature (TC) attracted attention for better temperature control [5]. The TC is the critical temperature at which the MNPs transform from ferromagnetic to paramagnetic and lose heating abilities under AMF. By selecting the MNPs with proper TC, the temperature in the tumor can be self-regulated at preferred temperature ranges of different therapies, removing the burdens of thermometers and cooling systems [5]. In addition, these MNPs can produce uniform temperature distribution all over the tumor and lead to consistent therapeutic outcomes [6,7]. By now, MNPs with TC of 37–93 °C have been manufactured. Their ability to self-regulate temperatures has been verified both in vitro [8,9,10] and in vivo [11,12,13,14].
In previous work, we reported ZnCoCrFeO MNPs with TC of 29–103 °C [10]. The ZnCoCrFeO MNPs with TC of 61 °C could self-regulate temperatures at 43–44 °C in vivo [14]. The MnZnFeO ferrite MNPs with TC of 89.6 °C raised the temperature of tumors in nude mice to 42.8 °C [11]. However, the ZnCoCrFeO MNPs with TC of 37.5 °C elevated the water temperature to 43.8 °C [10]. Similarly, the FeCuZnMgO ferromagnetic MNPs with TC of 43 °C achieved 45 °C in vivo [13]. The ZnFeO MNPs with TC of 93 °C obtained 41.5 °C in cellular magnetic heating experiments [9]. Clearly, the deviations exist between TC and self-regulated temperature, suggesting the insufficiency of using TC to predict the heating performances of MNPs. Theoretically, the ideal MNPs should have high heating efficiency (represented by specific loss power, SLP) below TC, and the SLP instantly drops to zero at TC. Thus, the temperature can be controlled at TC. However, the actual decline of SLP around TC is usually gradual, leaving residual SLP and extra heating abilities over TC [14]. It seems necessary to consider the temperature-dependent SLP for predicting the heating abilities, rather than just relying on the TC and a single SLP value. However, no such evaluation standard can be found yet.
In this paper, a tumor simulation model considering the temperature-dependent SLP was established to predict the heating capacity of MNPs in hyperthermia and their performances in forming a uniform and stable temperature distribution in the tumor. The method was applied to 46 °C hyperthermia of ZnCoCrFeO [14], Fe3O4 [15,16] and γ-Fe2O3 MNPs [17]. It was found that the MNPs with a steeper decrease of heat source power densities within 37–46 °C can reduce the heating power in the inner tumor regions and automatically adjust the heating power to the tumor temperature changes, possessing better uniformities and stabilities.
2. Materials and Methods
2.1. Temperature-Dependent SLP Measurements
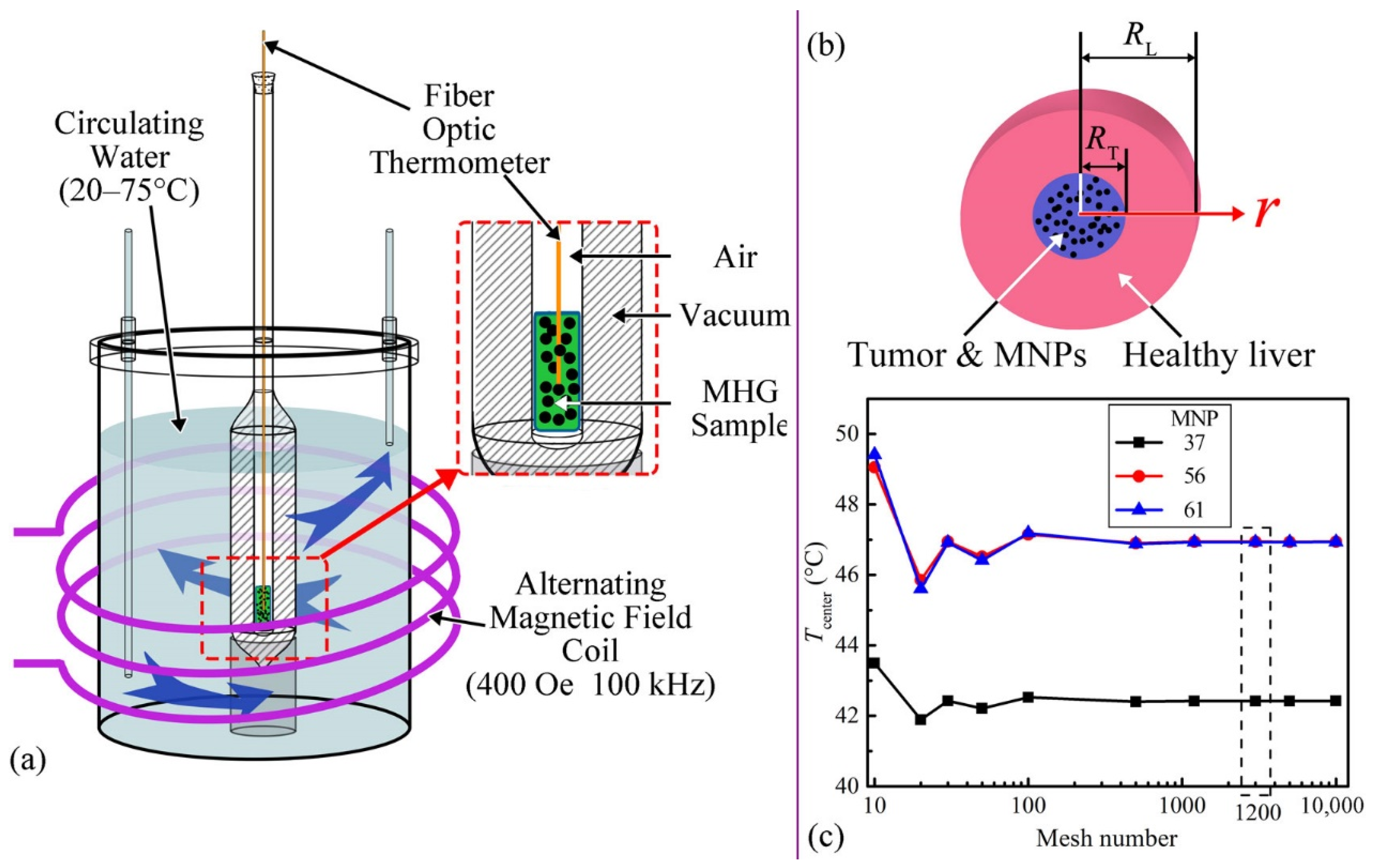
The MNPs were manufactured by the methods used in previous studies [10,14]. The Zn0.54Co0.46Cr0.7Fe1.3O4, Zn0.54Co0.46Cr0.65Fe1.35O4 and Zn0.54Co0.46Cr0.6Fe1.4O4 MNPs with TC of 37.5 °C, 56.0 °C and 61.0 °C are signed as MNP37, MNP56, and MNP61. The SLP data were calculated, based on the temperature-time (T-t) data from the calorimetry experiments. The experimental setup (Figure 1a) is as follows. The MNPs were fixed by hydrogel in a tube as magnetic hydrogel (MHG) for uniform and stable dispersion [14]. The tube was placed in a Dewar vacuum flask for reducing heat dissipation. Then, they were surrounded by circulating water with controllable temperature. The fiber optic thermometer (Fotemp-Trafo FTT-0100, Optocon, Dresden, Germany) monitored the central temperature of 2 mL MHG of 80 mg/mL (MNPs mass/hydrogel volume) in the tube. Before calorimetry measurements, the inner startup temperatures were monitored by the fiber optic thermometer and controlled by adjusting the circulating water temperature. When the startup temperatures were stable, the AMF generator (GUF-30T, Shenqiu Yongda High Frequency Equipment Co., Ltd., Zhoukou, China) heated the MNPs at 400 ± 5 Oe and 100 ± 5 kHz for 3 min to obtain the T-t curves. The startup temperatures were set from 20 °C to 75 °C with a 5 °C interval. The measurement was repeated four times for each kind of MNPs at each startup temperature. The mean values of T-t curves were used for the calculations of SLP data.
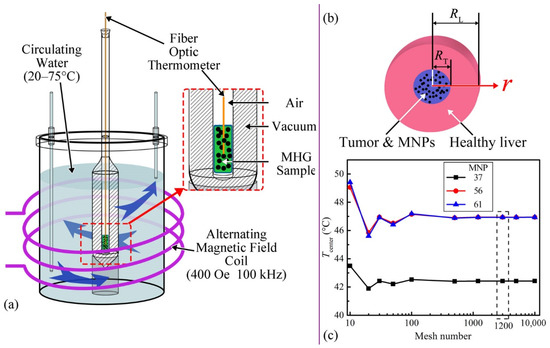
Figure 1.
(a) Experimental setup of calorimetry experiments; (b) Tissue model of the thermal simulations, RT is the radius of the sphere tumor, RL is the radius of the healthy liver tissue; (c) Convergence analysis of mesh number about the final temperatures of tumor center (Tcenter), with 1200 as the chosen mesh number.
The SLP describes the heat, converted from the energy of AMF, per unit time and unit MNP mass, as Equation (1) [18].
where, cMHG is the specific heat capacity of MHG (2.30 ± 0.18 J/(g·°C)) [14]; T is the temperature (°C); t is the time (s); dT/dt is the initial slope of the T-t curve (the linear fragment at 10–20 s of temperature rising), provided the temperature distribution within the sample is homogeneous and the initial thermal losses are negligible [19,20]; mMHG is the mass of MHG (mg); mMNP is the mass of MNPs (mg). The T-t data and SLP data of MNP61 were cited from reference [14].
2.2. Heating Performance Simulations
The model is shown in Figure 1b, i.e., a sphere tumor (15 mm radius) surrounded by healthy liver tissue (90 mm radius). The MNPs were assumed to be evenly distributed in the tumor without displacement and loss. Two Pennes bioheat transfer equations for simulating the temperature changes in tumor and healthy tissue are as Equations (2) and (3) [21].
The initial condition is as Equation (4).
At the interface of the tumor and healthy tissue, the temperature and heat flow are continuous. In addition, the inner and outer boundary conditions are as Equations (5) and (6).
where, T is the temperature (°C); r is the radius from the center (m); RT is the radius of the tumor (15 mm); RL is the radius of healthy liver tissue (90 mm); ρ is the density (kg/m3); c is the specific heat capacity (J/(kg·°C)); k is the thermal conductivity (W/(m·°C)); Qm is the power density of metabolic heat generation (W/m3); Qb is the power density of heat dissipation by blood perfusion effect (W/m3); PDP is the power density of MNPs [7], i.e., the power dissipation of MNPs per unit of volume (W/m3); the subscript T represents the tumor; the subscript L represents the healthy liver tissue; the subscript TP represents the tumor region with evenly distributed MNPs. The ρ, c, and k of the tumor region change with the MNP concentration as Equation (7) [22,23].
where, the subscript P represents MNPs; ϕ is the volume fraction of MNPs in the tumor, which can be calculated through ϕ = C/ρP; and the C is the concentration of MNPs in the tumor (kg/m3 or mg/mL, MNP mass/tumor volume).
The Qm and Qb rely on the body temperature change. The Qm (W/m3) is as Equation (8) [24].
where, Qm0 is the Qm when the tissue is at 37 °C (W/m3).
The Qb (W/m3) is as Equation (9) [25].
where, the subscript b represents blood; wb is the blood perfusion rate (1/s); Tα is the temperature of arterial blood (°C), here assumed as 37 °C.
The physical parameters used for tissues and MNPs are shown in Table 1.

Table 1.
Physical parameters of tissues and MNPs.
The PDP(T) is calculated as Equation (10) [27].
where, SLP(T) is the specific loss power of MNPs (W/kg), obtained in the experiments; C is the MNP concentration (kg/m3, MNP mass/tumor volume).
The Pennes bioheat transfer equations were solved by the PDEPE function in MATLAB. The mesh numbers of time and spatial dimensions were equal. The convergence of mesh numbers was analyzed by comparing the final temperatures of the tumor center at different mesh numbers in Figure 1c. The MNP concentration in the convergence analysis was 35 mg/mL. The mesh number of 1200 was selected.
3. Results and Discussion
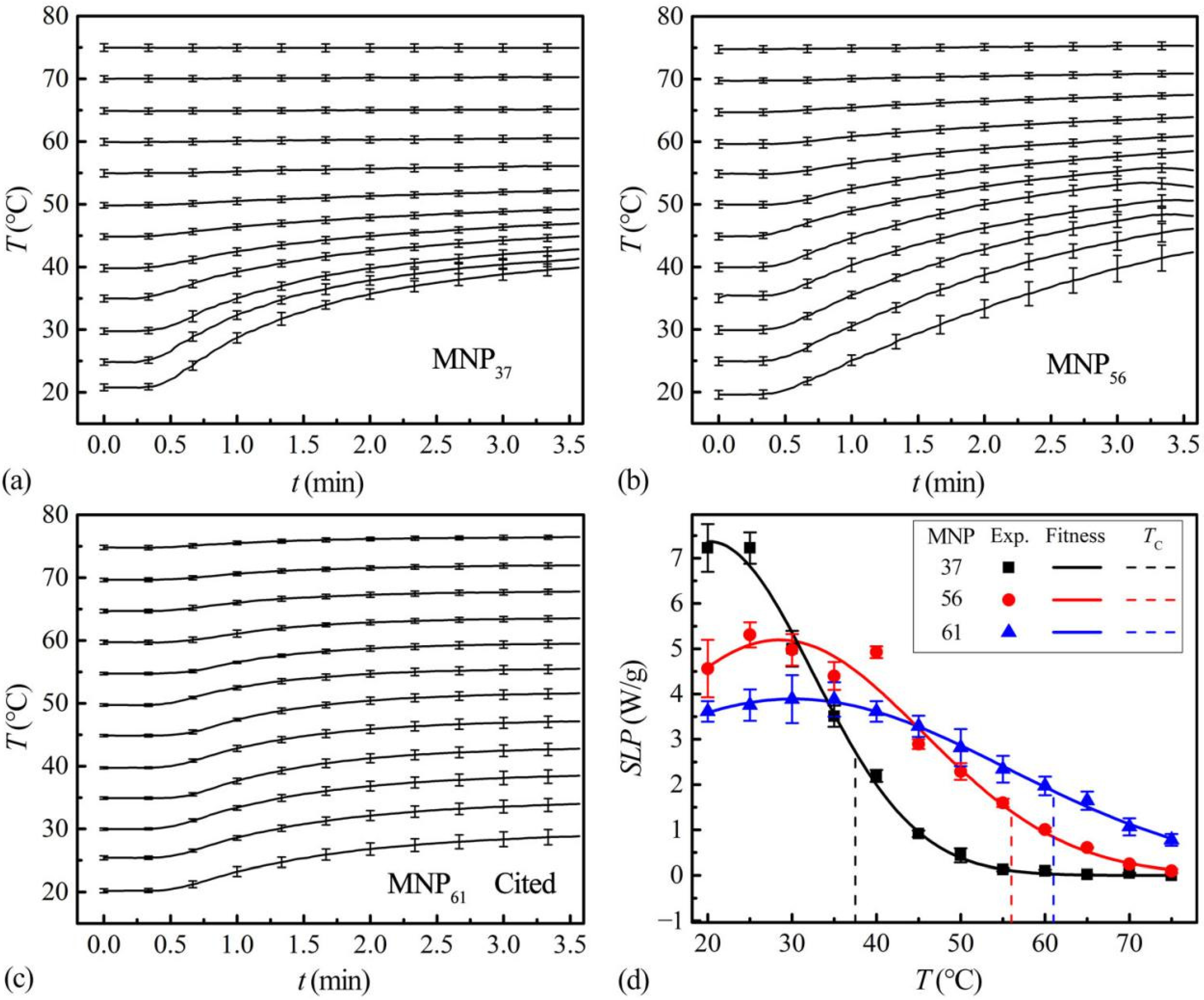
3.1. SLP-T Relationships
The temperature-time (T-t) curves of the MHG of ZnCoCrFeO MNPs are shown in Figure 2a–c. As the startup temperature increases, the temperature rising amplitude gradually decreases to zero, indicating that the MNPs have self-regulating temperatures. However, the elevated temperatures can exceed the TC, indicating that the MNPs have residual heating abilities over TC. The initial slopes of the T-t curves are extracted for SLP calculations (Equation (1)). In addition, the SLPs at different temperatures are shown in Figure 2d. With the increase of temperature, the SLP decreases gradually around the TC, ranging for dozens of degrees. Above the TC, considerable residual SLP exists, possibly resulting from the underestimated TC by measurement methods. The TC is normally determined by locating the maximum first derivatives of the thermogravimetric mass-temperature curves [10,14] or the minimum first derivatives of the magnetization-temperature curves [8]. So, the obtained TC value represents the majority of the MNPs. While the MNPs, in fact, always have a wide range of TC (some over 100 °C [10,14]). The measurement methods are practical for determining the representative TC but may result in inaccurate prediction of heating performances. For accurate predictions, the SLPs at different temperatures should be considered. The SLP-T data were fitted with Gaussian curves to provide the heat source in simulations with continuous coupling relationships. The fitting equation is as Equation (11).
where, a, b and c are the fitting parameters, summarized in Table 2.
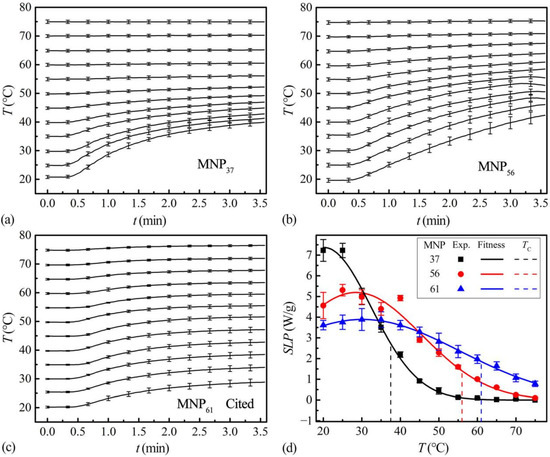
Figure 2.
The T-t data of the MNP37 (a), MNP56 (b), and MNP61 from reference [14] (c) at different initial temperatures (20–75 °C, 5 °C intervals); n = 4 for each line, data: mean value and standard uncertainty. (d) Experimental SLP data and fitted SLP-T curves of MNP37, MNP56 and MNP61; the SLP data of MNP61 were from reference [14]; n = 4 for each point, data: mean value and standard uncertainty.

Table 2.
Gaussian fitting parameters of SLP-T curves for ZnCoCrFeO MNPs.
3.2. Heating Performances
3.2.1. Temperature Rises and Distributions
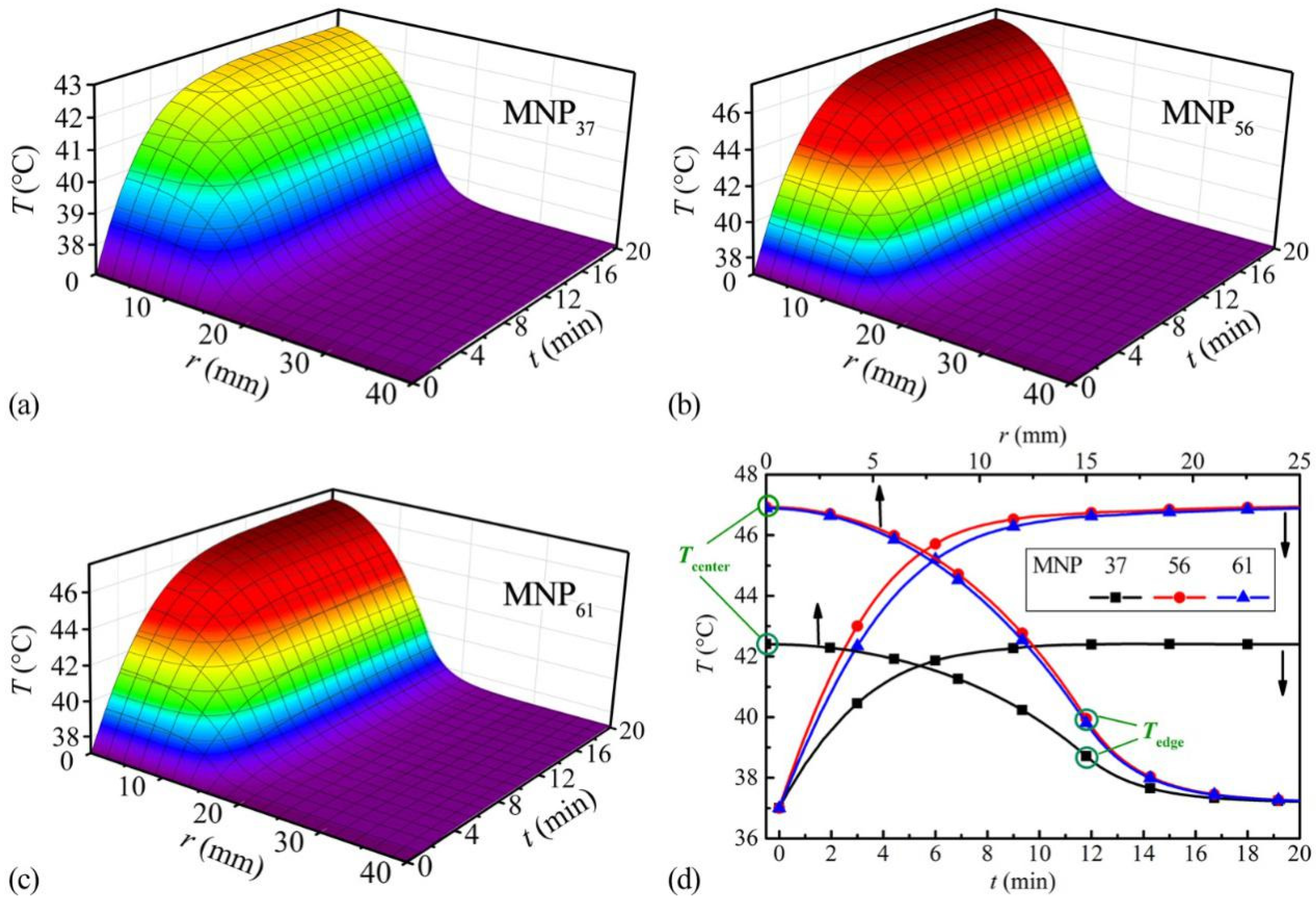
The temperature changes in time and spatial dimensions of the three ZnCoCrFeO MNPs are shown in Figure 3a–c. In addition, the corresponding temperature rises of tumor centers and the final temperature distributions are summarized in Figure 3d. The temperatures rise from 37 °C (body temperature). So, the SLP over 37 °C (Figure 2d) contributes to the heating processes and should be focused on. The temperature increase in the tumor stops after about 10 min, which can be seen from the central temperatures in Figure 3d (lower abscissa). Furthermore, the final temperature distributions, in Figure 3d (upper abscissa), would last for another 50 min in the one-hour clinical hyperthermia treatment, mainly determining the curing effects [1,2,3,4]. Thus, in the following heating performance evaluations, the final temperature distributions would be focused on. In the tumor, the maximum and minimum temperatures appear at the center and the edge, marked in Figure 3d. So, the final temperatures at the center (Tcenter) and the edge (Tedge) would be used to represent the final temperature range within the tumor in the simulations hereafter.
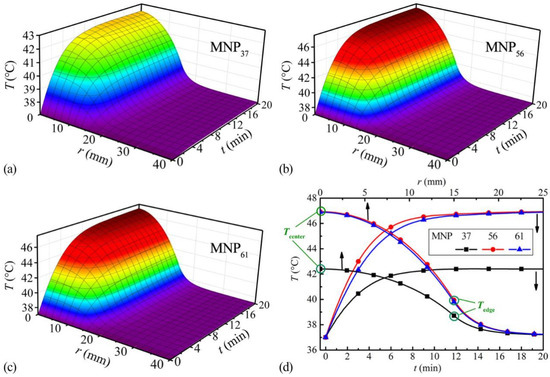
Figure 3.
The time and spatial temperature changes in the tissue model of MNP37 (a), MNP56 (b) and MNP61 (c), at 35 mg/mL MNP concentration; (d) The corresponding temperature rises of tumor centers (lower abscissa) and the final temperature distributions (upper abscissa).
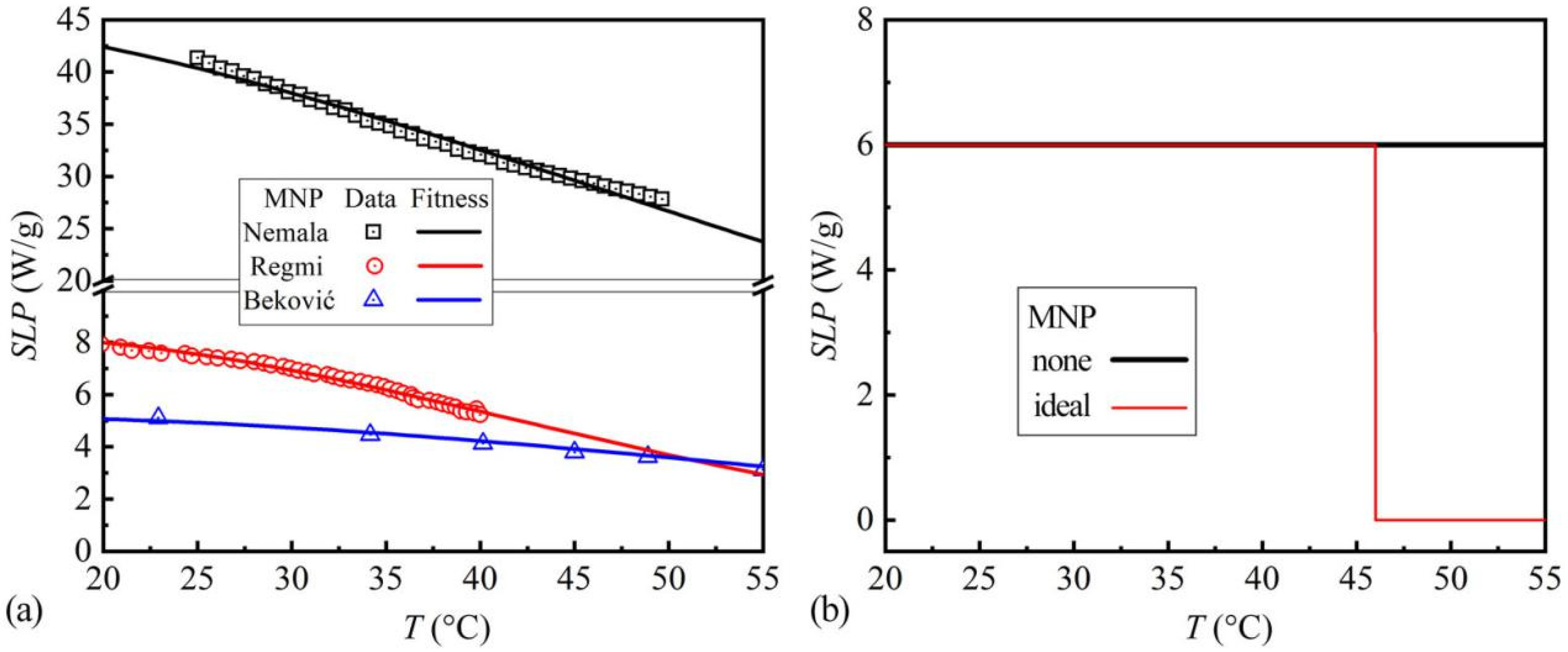
In the following simulations of heating performances, three kinds of MNPs in references with temperature-dependent SLP (TC unknown) are also included. They are signed after the authors’ names as MNPNemala (Fe3O4) [15], MNPRegmi (Fe3O4) [16], and MNPBeković (γ-Fe2O3) [17]. The SLP data, extracted from references [15,16,17], are shown in Figure 4a. They are fitted by Equation (11) for the curves in Figure 4a. Furthermore, the fitting parameters are shown in Table 3. In addition, two assumed MNPs are also simulated, in order to exhibit the improvements and limitations in heating performances of the actual MNPs. They are the MNPs without TC (MNPnone) with the SLP of 6 W/g at any temperature, and the ideal MNPs (TC 46 °C, MNPideal) with the SLP of 6 W/g under TC and 0 W/g above TC. The chosen 6 W/g is within the 5–7 W/g of MNP56 and MNP37. For convergence consideration, the SLP decrease of MNPideal was set as a linear drop from 6 W/g at 45.99 °C to 0 W/g at 46.00 °C. Their SLP-T curves are shown in Figure 4b.
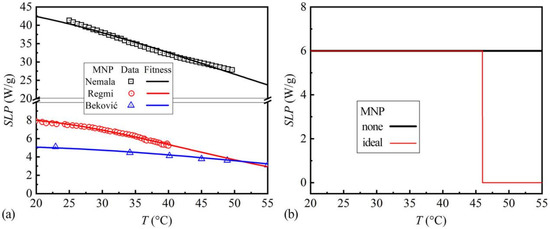
Figure 4.
(a) The SLP data and fitted SLP-T curves of MNPNemala, MNPRegmi, and MNPBeković; the SLP data are obtained from the references [15,16,17]; (b) The SLP-T curves of MNPnone and MNPideal.

Table 3.
Gaussian fitting parameters of SLP-T curves for the MNPs from references.
3.2.2. Capacities
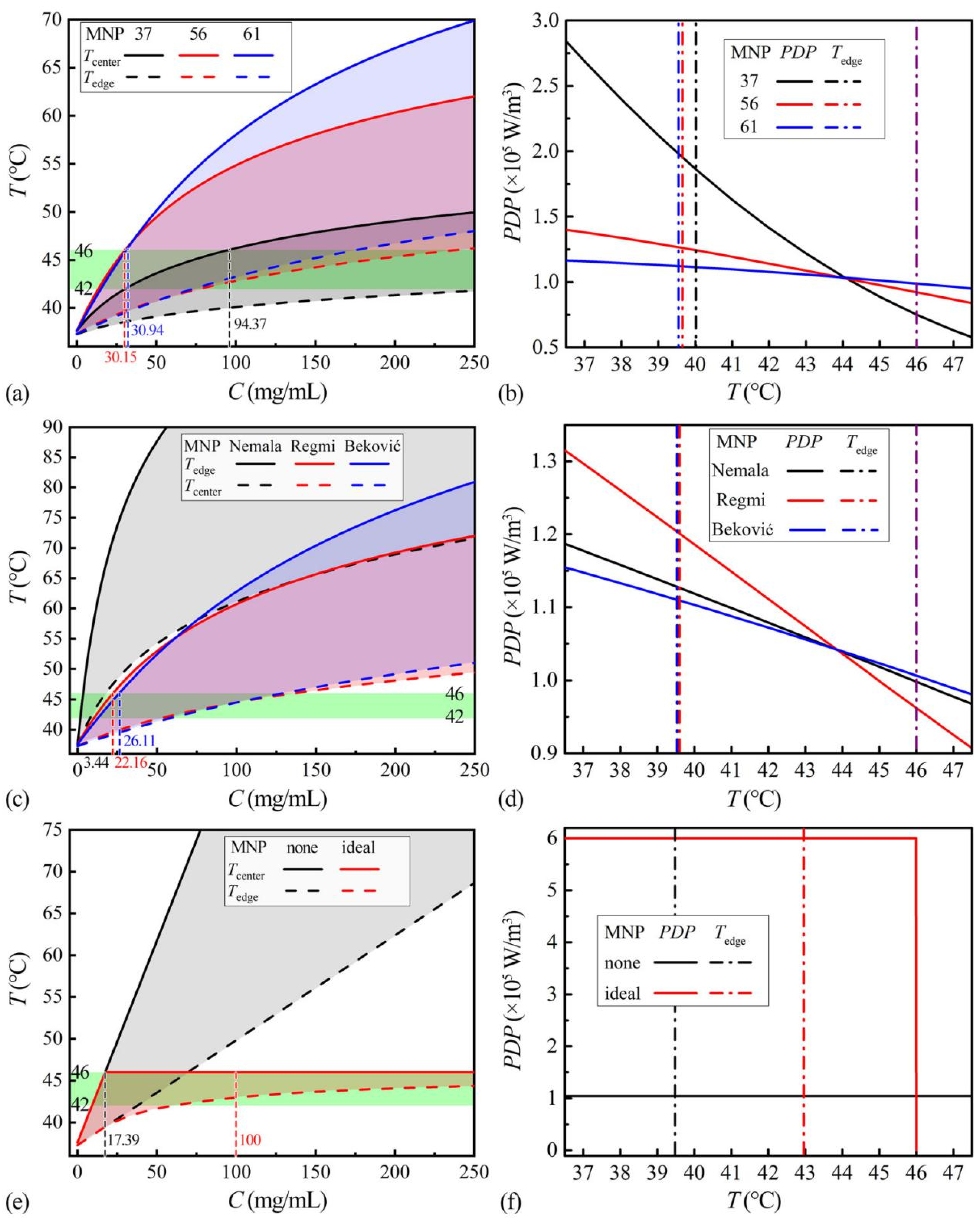
For heating capability evaluation, the proper MNP concentration for heating the tumor center to 46 °C is searched for each kind of MNP. The Tcenters and Tedges at different MNP concentrations (Cs) are shown in Figure 5a,c,e marked as envelope curves. The MNPnone and MNPideal in Figure 5e have the same temperature distributions below 17.39 mg/mL. Over this concentration, the temperatures of the MNPnone increase linearly, while the Tcenter of MNPideal self-regulates at 46 °C. The exceeded concentration only elevates the Tedge of MNPideal, indicating the whole tumor approaches 46 °C and the temperature distribution may be more uniform. The temperature-concentration curves of the actual MNPs, in Figure 5a,c, show upper convex shapes, indicating they have part of the self-regulating abilities. At extortionate concentrations, the Tcenter of ZnCoCrFeO MNPs with lower TC, in Figure 5a, is closer to 46 °C, suggesting better self-regulating abilities. For the sake of comparing the heating performances of the different MNPs, the proper concentrations, providing the Tcenter of 46 °C, are chosen in Figure 5a,c and will be used in the following analysis. Since the MNPideal has a large range of concentrations for Tcenter of 46 °C, a high concentration of 100 mg/mL is selected, which can increase the Tedge over 42 °C. At the proper concentrations, the PDP-T curves are calculated by Equation (10) and shown in Figure 5b,d,f.
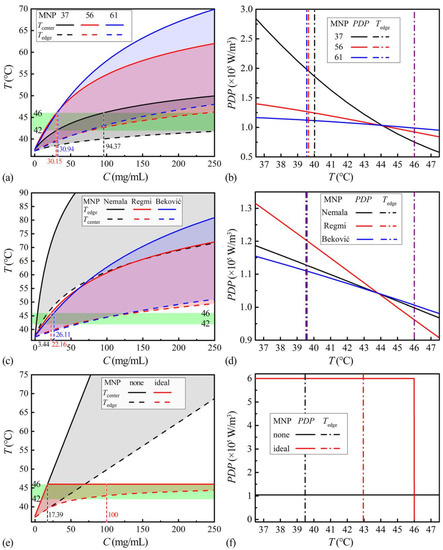
Figure 5.
The temperature range (Tcenter-Tedge) at different MNP concentrations of MNP37, MNP56 and MNP61 (a); of MNPNemala, MNPRegmi and MNPBeković (c); of MNPnone and MNPideal (e). The PDP-T curves at proper concentrations for Tcenter 46 °C of MNP37, MNP56 and MNP61 (b); of MNPNemala, MNPRegmi and MNPBeković (d); of MNPnone and MNPideal (f).
After confirming their abilities to heat the tumor to 46 °C, whether the corresponding AMF conditions and concentrations are safe still needs to be investigated. High AMF intensity or frequency may cause pain [1]. Normally, the safe criteria for AMF are “intensity (H) × frequency (f) < 5 × 109 A/(m·s)” [28]. High MNP concentrations may lead to cytotoxicity [14]. The maximum ever applied MNP concentration, recorded in clinical trials, is 280 mg/mL [29]. With regards to the ZnCoCrFeO MNPs, the AMF conditions of 100 kHz and 400 Oe (32 kA/m) in calorimetry experiments and the chosen MNP concentrations of 30–95 mg/mL in Figure 5a may be acceptable. For the MNPs in Figure 5c, the chosen AMF conditions of MNPNemala (375 kHz, 11.28 kA/m) [15], MNPRegmi (395 kHz, 5.6 kA/m) [16], and MNPBeković (100 kHz, 15 kA/m) [17], as well as the MNP concentrations of 3–27 mg/mL in Figure 5c may also be acceptable. So, these MNPs may be capable of hyperthermia. Noticeably, the safe AMF criteria depend on the body diameter exposed to the AMF, and the acceptable MNP concentration relates to the MNP composition, the biocompatibility of the surface coating, and so on. So, the capability of the specific MNPs will need detailed evaluations in clinical applications. Overall, by simulating the temperature-dependent heating efficiencies, the required concentration of MNPs can be determined, and the safety can be discussed.
In clinical hyperthermia applications, the AMF conditions and concentrations can be adjusted according to patient tolerance. If the patient is more sensitive to the pain, the AMF intensity needs to be reduced [1]. Consequently, the MNP concentration requires elevation for ensuring effective heating. The balance of the AMF and MNP concentration values refers to Equation (10). In Equation (10), the PDP(T) equals SLP(T) × C, where the SLP is proportional to the square of AMF intensity (H2), and correlates to the AMF frequency (f), according to Rosensweig’s model [30]. Thus, multiple combinations of H, f and C values can lead to the same PDP-T curves in Figure 5b,d, which result in effective heating. In addition, the combination with lower overall side effects can be selected among them. For instance, if the MNPs have excellent biocompatibility, raising the concentration to four times and reducing the H to half will lower the pain risk of high AMF but still maintain the Tcenter at 46 °C.
3.2.3. Uniformities
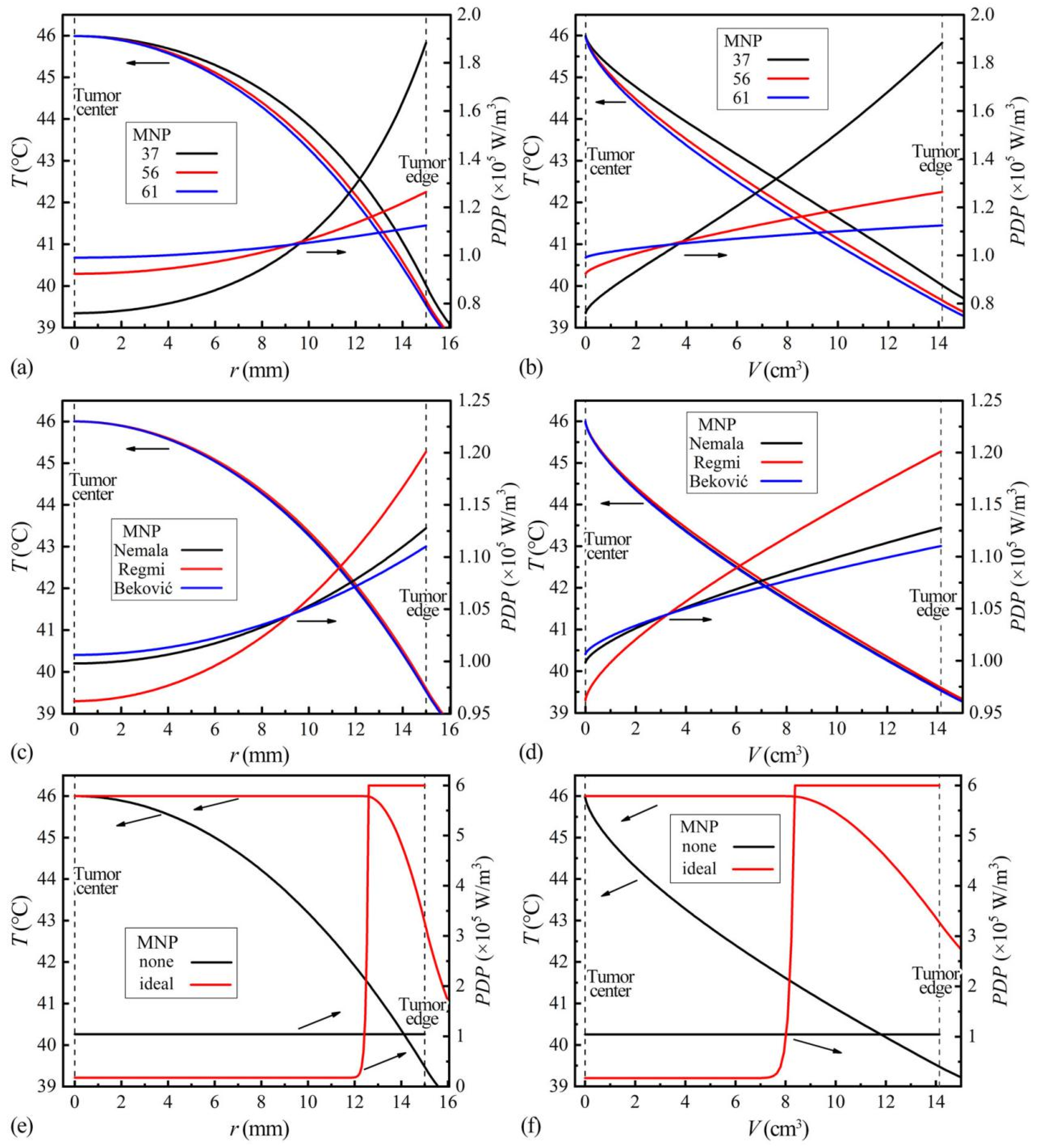
The temperature distributions in the tumor model are shown by the radius in Figure 6a,c,e (left ordinate), and by the volume in Figure 6b,d,f (left ordinate). Along the radial direction, the temperature decreases from the center to edge. The actual MNPs (Figure 6a–d) have higher temperatures all over the tumor than the MNPnone (Figure 6e,f), indicating more uniform temperature distributions. In addition, the MNP37 has the best uniformities among the investigated actual MNPs. However, they cannot provide a temperature distribution like the MNPideal, which forms 46 °C in over half of the tumor in Figure 6f.
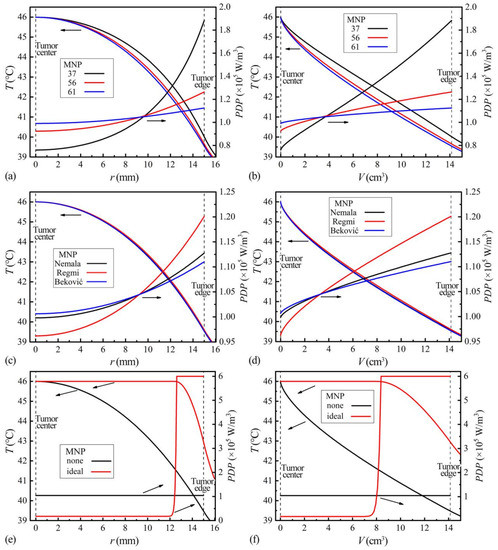
Figure 6.
Temperature distributions (left ordinate) and PDP distributions (right ordinate) in the tumor of the ZnCoCrFeO MNPs by radius (a), by volume (b); of the MNPs from references by radius (c), by volume (d); and of the MNPideal and MNPnone by radius (e), by volume (f).
In clinical trials, the final temperatures at the tumor center (Tcenter) and the tumor edge (Tedge), as well as the exceeded temperatures in 20% volume (T20), 50% volume (T50), 90% volume (T90) of the tumor are concerned [29]. To quantitatively evaluate the uniformities, the dimensionless parameter Ui is defined, shown in Equations (12) and (13).
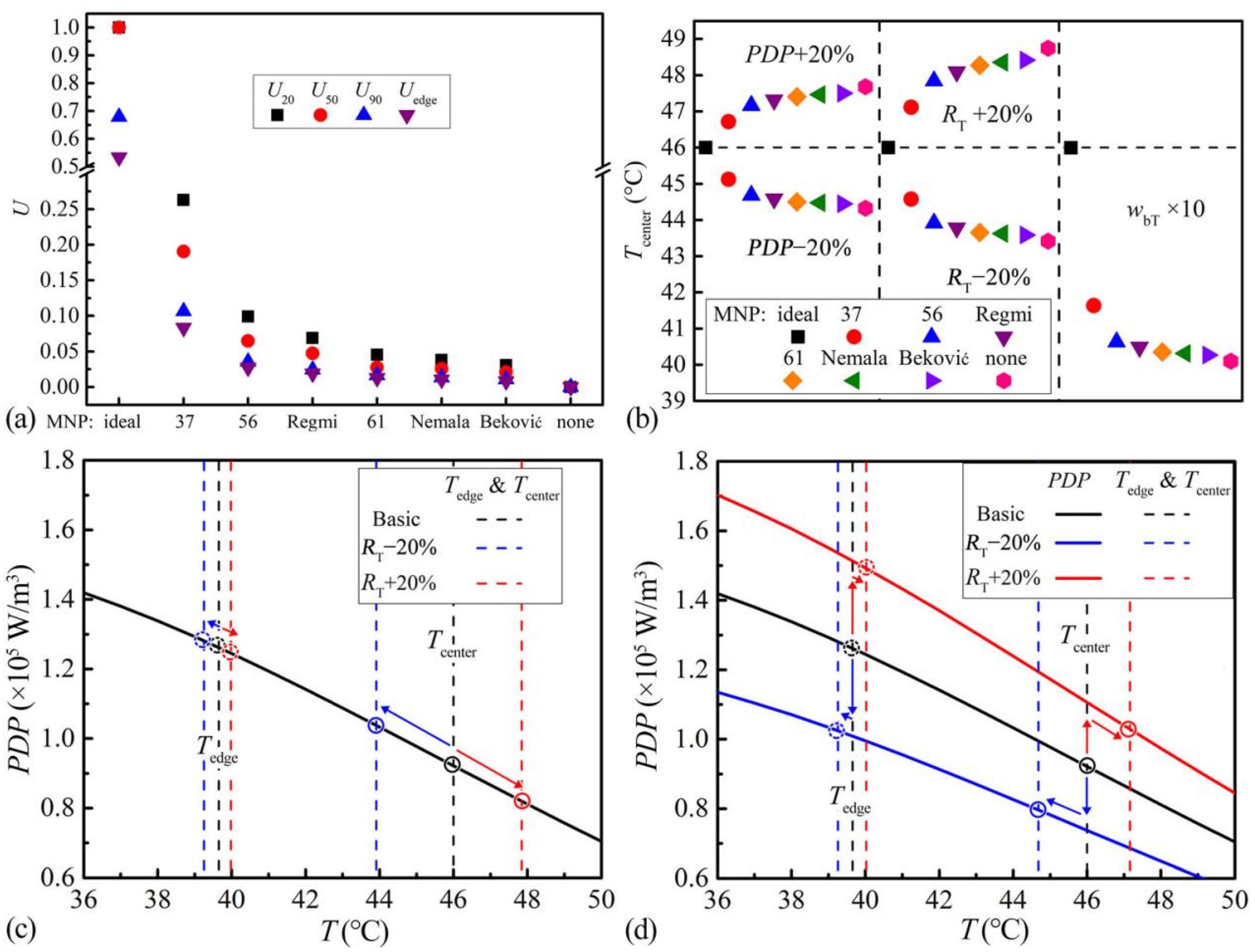
where, the subscript i can be 20, 50, 90 and edge, representing 20% volume, 50% volume, 90% volume of the tumor, and the tumor edge; the superscript 0 represents the values obtained from the MNPnone (Figure 6f). The temperature distribution of the MNPnone is taken as the baseline, corresponding to Ui = 0. Higher Ui means the temperature is closer to Tcenter. Ui = 1 means extremely uniform. The uniformity indexes of corresponding MNPs are shown in Figure 7a. The results suggest that the ZnCoCrFeO MNPs with lower TC have higher uniformity at each position. The MNPideal and MNPnone present the upper and lower limits of uniformities. Among the actual MNPs, the MNP37 has the highest U90, indicating the best therapeutic outcome [29,31].
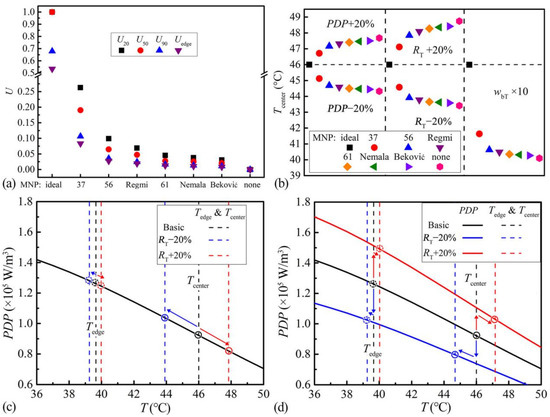
Figure 7.
(a) Temperature uniformities (U) of the ZnCoCrFeO MNPs, the MNPs from references, MNPideal and MNPnone. (b) Stabilities (Tcenter changes) under PDP, RT and wbT fluctuations of the ZnCoCrFeO MNPs, the MNPs from references, MNPideal and MNPnone; (c) Changes of temperature ranges of the MNP56 under RT fluctuations; (d) Changes of temperature ranges and PDP-T curves of the MNP56 under PDP fluctuations.
The improvements in uniformity result from the equalized absorbed energies (for temperature rise) within the tumor. Before interpreting the contribution of the decreased PDPs with increased temperatures in this process, the reason for the temperature distribution of “inner higher, outer lower” needs to be explained first. Taking the MNPnone with constant SLP as an example, when a small amount of MNPs is placed in a tumor as a unit and starts to generate heat, part of the generated heat will elevate the temperature of the local tissue, and the rest will be transferred to the ambient tissues. If three equidistant units are arranged in a line around the tumor center, the central part will receive most of the energy for temperature rise, thus higher temperature at the center. So, when the sphere tumor is uniformly filled with such units of MNPnone, the temperature decreases from the tumor center to the edge, as seen in Figure 6e,f. Once the SLP of MNPs decreases with the increased temperatures, the powers of the inner hot units are restricted automatically, reducing the central and overall temperatures. To maintain the same Tcenter, a higher concentration is needed. In addition, compensatory elevations in outer units’ powers present as higher PDPs in outer regions. The phenomenon can be seen through the PDP-T curves of the actual MNPs and MNPideal in Figure 6 (right ordinate). Thus, the MNPs with steeper PDP-T curves form more uneven PDP distributions with higher values around the tumor center, helping to equalize the absorbed energies in different regions and leading to better temperature uniformity.
The uniformity improvement can also be accomplished by distributing more MNPs around the tumor center, regardless of the TC. Bagaria, et al. simulated different secondary polynomial MNPs’ radial distributions [32]. Liangruksa, et al. compared the homogenous, exponential, and Gaussian MNP distributions [33]. Zhang, et al. divided the tumor into multi regions with different MNP concentrations [34]. They all proved that, by distributing more MNPs around the tumor center patterns, the PDP at the center is higher, leading to more uniform temperature distributions. So, the temperature uniformities of the MNPs with low TC can be further improved by optimizing the distribution of the MNPs in the tumor.
3.2.4. Stabilities
In hyperthermia of MNPs, the reasons for temperature instabilities can be summed up as the changes of heat sources (heat generation) and the tumor properties (heat dissipation). (a) For heat sources, the AMF and the concentration influence heat generation. In clinical trials, the applied AMF intensity and frequency may fluctuate, influencing the SLP of MNPs [1,29]. Furthermore, the concentrations of MNPs may change in the subsequent therapeutic procedure. For instance, in a tumor mouse model, only 3/4 of the applied MNPs can be detected after 24 h [35]. Thus, the PDP of the heat source may be affected by the SLP and concentration (Equation (10)), altering the temperature distribution in the tumor. (b) For tumor properties, the tumor itself may progress or recover, affecting the heating process. The alteration of tumor size (RT) affects the heat dissipation efficiency from tumor to peripheral tissue. Larger RT provides a smaller surface area over volume ratio, leading to more heat retention and higher temperatures in the tumor. Besides, the blood perfusion rate in tumors (wbT), which relates to heat dissipation along blood vessels, varies with the tumor stages and also impacts the temperature distribution significantly [36]. So, the varying PDP, RT and wbT mainly contribute to the instability of hyperthermia.
For evaluating the stabilities of MNPs, the simulations with the Tcenter of 46 °C in Figure 5 are taken as the base. The PDP, RT in Equation (2) and wbT in Equation (9) are separately changed in the simulations and the resultant changes in Tcenter are compared as stability evaluations, as shown in Figure 7b. For the influences of heat source change, 20% increase and decrease of PDP are simulated. For the impact of tumor progression or recovery, 20% increase and decrease of RT are simulated. For the effect of tumor blood system recovery, 10 times of wbT is simulated in reference to the wbT range of liver (0.000833–0.02289 s−1) [26]. In the results, less change in Tcenter (closer to 46 °C) represents better stability. The increases of PDP and RT cause overheating. The decreases of PDP and RT, as well as the elevation of wbT, lead to insufficient heating. The changes of Tcenter are less for the ZnCoCrFeO MNPs with lower TC, indicating higher stabilities. The actual MNPs are better than the MNPnone. The MNPideal can self-regulate the Tcenter at 46 °C for all situations.
The improvements of stabilities result from the automatic adaptation of PDPs to the thermal parameter fluctuations. However, the PDP behaviors for alleviating the fluctuations from the environment and the heat source are different. (a) For the fluctuations in the heat dissipation environment, the RT and wbT alterations are included. Taking RT fluctuations of MNP56 as examples, the PDP-T curve and original temperature range (Tcenter and Tedge) are drawn in Figure 7c. When the temperature decreases, the temperature range in Figure 7c shifts lower (blue dash lines), while the PDP-T curve remains unchanged (black solid line). At this time, the PDPs of all units in the tumor increase with the shifted temperature range, causing an elevation of the overall PDP in the tumor (blue circles), thus alleviating the effect of the environmental changes and exhibiting self-regulating behaviors. (b) For the fluctuations in the heat source, the PDP alteration is included. Taking the MNP56 as an example, the PDP-T curve and original temperature range are drawn in Figure 7d. When the PDPs of all units decrease (blue solid line), the temperature ranges also decrease (blue dash lines), elevating the units’ PDPs back a little bit (blue circles). Thus, for both situations, although the mechanisms are different, a steeper PDP-T curve always leads to better stabilities. In addition, the MNP37 has the steepest PDP-T curve and the best stabilities among the actual MNPs.
The simulation methods on stability established here can quantitatively evaluate the MNPs’ abilities of self-regulating temperatures. Unlike the uniformities, stability superiority cannot be achieved by properly distributing the MNPs but may be approached by monitoring the temperatures in the tumor and adjusting the intensity and frequency of AMF. Besides, sifting the MNPs with the same TC helps to gather the MNPs with the same SLP decrease temperature and may offer the MNPs steeper PDP-T curves, thus improving the stabilities. The evaluation methods, proposed in this paper, are applicable to other kinds of tumors with different shapes, as well as hyperthermia with different temperature ranges, such as 46–60 °C.
4. Conclusions
A simulation method for quantitatively evaluating the heating performances of MNPs is established here. By simulating the temperature-dependent SLP of MNPs, evaluations on the heating capacity, uniformity, and stability can be performed. Through the applications of the method on the ZnCoCrFeO, Fe3O4 and γ-Fe2O3 MNPs, it can be seen that, with proper concentrations, these MNPs are capable of 46 °C hyperthermia for the proposed tumor model. Moreover, the MNPs with steeper PDP-T curves within 37–46 °C have better uniformities and stabilities, relying on restricting the PDP around the tumor center and automatically regulating the PDP under temperature change.
Author Contributions
Conceptualization, S.-W.D., C.-W.W. and W. Z.; methodology, S.-W.D.; software, S.-W.D.; validation, C.D. formal analysis, S.-W.D.; investigation, S.-W.D.; resources, S.-W.D.; data curation, S.-W.D. and C.D.; writing—original draft, S.-W.D.; writing—review & editing, X.-G.Y., W.Z. and J.-P.G.; visualization, S.-W.D.; supervision, C.-W.W. and W.Z.; project administration, W.Z.; funding acquisition, W.Z.. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Project of China (2018YFA0704103, 2018YFA0704104), National Natural Science Foundation China (12172083, U1908233), and Fundamental Research Funds for the Central Universities (DUT21TD105).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| AMF | alternating magnetic field |
| TC | Curie temperature (°C) |
| MHG | magnetic hydrogel |
| MNP | magnetic nanoparticles |
| MNP37, MNP56, MNP61 | ZnCoCrFeO MNPs with TC of 37.5 °C, 56.0 °C and 61.0 °C |
| MNPNemala | MNPs by Nemala et al. |
| MNPRegmi | MNPs by Regmi et al. |
| MNPBeković | MNPs by Beković et al. |
| MNPideal | assumed ideal MNPs with TC of 46 °C (heating efficiency is constant below TC and zero above TC) |
| MNPnone | assumed MNPs without TC (heating efficiency does not change with temperature) |
| b (subscript) | of blood |
| L (subscript) | of healthy liver tissue |
| MHG (subscript) | of MHG |
| MNP (subscript) | of MNPs |
| T (subscript) | of tumor |
| TP (subscript) | of tumor and MNPs |
| T (°C) | temperature |
| t (s) | time |
| Tcenter (°C) | temperature at the center of the tumor |
| T20, T50, T90 (°C) | temperatures exceeded in 20%, 50% or 90% volume of the tumor |
| Tedge (°C) | temperature at the edge between tumor and healthy tissue |
| Tα (°C) | the temperature of arterial blood (37 °C) |
| U20, U50, U90, Uedge (dimensionless) | uniformities within 20%, 50%, 90% or 100% volume of the tumor |
| SLP (W/g) | specific loss power |
| PDP (W/m3) | power dissipation of MNPs per unit of tumor volume |
| c (J/(kg·°C)) | specific heat capacity |
| C (kg/m3 or mg/mL) | MNP concentration in tumor region (MNP mass/tumor volume) |
| RT, RL (mm) | radiuses of tumor region and overall healthy liver region |
| r (mm) | radius from the tumor center |
| ρ (kg/m3) | density |
| k (W/(m·°C)) | thermal conductivity |
| Qm (W/m3) | power density of metabolic heat generation |
| Qm0 (W/m3) | power density of metabolic heat generation at body temperature (37 °C) |
| Qb (W/m3) | power density of heat dissipation by blood perfusion effect |
| wb (1/s) | blood perfusion rate |
| ϕ | volume fraction of MNPs in the tumor |
References
- Johannsen, M.; Gneveckow, U.; Eckelt, L.; Feussner, A.; Waldöfner, N.; Scholz, R.; Deger, S.; Wust, P.; Loening, S.A.; Jordan, A. Clinical hyperthermia of prostate cancer using magnetic nanoparticles: Presentation of a new interstitial technique. Int. J. Hyperth. 2005, 21, 637–647. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wust, P.; Gneveckow, U.; Johannsen, M.; Böhmer, D.; Henkel, T.; Kahmann, F.; Sehouli, J.; Felix, R.; Ricke, J.; Jordan, A. Magnetic nanoparticles for interstitial thermotherapy-feasibility, tolerance and achieved temperatures. Int. J. Hyperth. 2006, 22, 673–685. [Google Scholar] [CrossRef] [PubMed]
- Maier-Hauff, K.; Ulrich, F.; Nestler, D.; Niehoff, H.; Wust, P.; Thiesen, B.; Orawa, H.; Budach, V.; Jordan, A. Efficacy and safety of intratumoral thermotherapy using magnetic iron-oxide nanoparticles combined with external beam radiotherapy on patients with recurrent glioblastoma multiforme. J. Neuro-Oncol. 2011, 103, 317–324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grauer, O.; Jaber, M.; Hess, K.; Weckesser, M.; Schwindt, W.; Maring, S.; Wölfer, J.; Stummer, W. Combined intracavitary thermotherapy with iron oxide nanoparticles and radiotherapy as local treatment modality in recurrent glioblastoma patients. J. Neuro-Oncol. 2019, 141, 83–94. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Ding, S.; Yang, R.; Wu, C.; Zhang, W. Research progress on magnetic nanoparticles for magnetic induction hyperthermia of malignant tumor. Ceram. Int. 2021, 47, 5909–5917. [Google Scholar] [CrossRef]
- Astefanoaei, I.; Dumitru, I.; Chiriac, H.; Stancu, A. Controlling temperature in magnetic hyperthermia with low Curie temperature particles. J. Appl. Phys. 2014, 115, 17B531. [Google Scholar] [CrossRef]
- Tang, Y.-D.; Flesch, R.; Jin, T. Numerical analysis of temperature field improvement with nanoparticles designed to achieve critical power dissipation in magnetic hyperthermia. J. Appl. Phys. 2017, 122, 034702. [Google Scholar] [CrossRef]
- Prasad, N.K.; Rathinasamy, K.; Panda, D.; Bahadur, D. TC-tuned biocompatible suspension of La0.73Sr0.27MnO3 for magnetic hyperthermia. J. Biomed. Mater. Res. B 2008, 85B, 409–416. [Google Scholar] [CrossRef]
- Hanini, A.; Lartigue, L.; Gavard, J.; Kacem, K.; Wilhelm, C.; Gazeau, F.; Chau, F.; Ammar, S. Zinc substituted ferrite nanoparticles with Zn0.9Fe2.1O4 formula used as heating agents for in vitro hyperthermia assay on glioma cells. J. Magn. Magn. Mater. 2016, 416, 315–320. [Google Scholar] [CrossRef]
- Yu, X.; Yang, R.; Wu, C.; Zhang, W. Effect of chromium ion substitution of ZnCo ferrites on magnetic induction heating. J. Alloys Compd. 2020, 830, 154724. [Google Scholar] [CrossRef]
- Tang, Q.; Zhang, D.; Cong, X.; Wan, M.; Jin, L. Using thermal energy produced by irradiation of Mn-Zn ferrite magnetic nanoparticles (MZF-NPs) for heat-inducible gene expression. Biomaterials 2008, 29, 2673–2679. [Google Scholar] [CrossRef]
- Saito, H.; Mitobe, K.; Ito, A.; Sugawara, Y.; Maruyama, K.; Minamiya, Y.; Motoyama, S.; Yoshimura, N.; Ogawa, J. Self-regulating hyperthermia induced using thermosensitive ferromagnetic material with a low Curie temperature. Cancer Sci. 2008, 99, 805–809. [Google Scholar] [CrossRef] [PubMed]
- Ito, A.; Saito, H.; Mitobe, K.; Minamiya, Y.; Takahashi, N.; Maruyama, K.; Motoyama, S.; Katayose, Y.; Ogawa, J.-I. Inhibition of heat shock protein 90 sensitizes melanoma cells to thermosensitive ferromagnetic particle-mediated hyperthermia with low Curie temperature. Cancer Sci. 2009, 100, 558–564. [Google Scholar] [CrossRef] [PubMed]
- Ding, S.; Wu, C.-W.; Yu, X.-G.; Li, H.; Yu, L.; Zhang, Y.-X.; Yang, R.-P.; Zhang, W. Magnetic hydrogel with long in situ retention time for self-regulating temperature hyperthermia. Int. J. Hyperth. 2021, 38, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Nemala, H.; Thakur, J.S.; Naik, V.M.; Vaishnava, P.P.; Lawes, G.; Naik, R. Investigation of magnetic properties of Fe3O4 nanoparticles using temperature dependent magnetic hyperthermia in ferrofluids. J. Appl. Phys. 2014, 116, 034309. [Google Scholar] [CrossRef] [Green Version]
- Regmi, R.; Naik, A.; Thakur, J.S.; Vaishnava, P.P.; Lawes, G. Temperature dependent dissipation in magnetic nanoparticles. J. Appl. Phys. 2014, 115, 17B301. [Google Scholar] [CrossRef]
- Beković, M.; Trlep, M.; Jesenik, M.; Goričan, V.; Hamler, A. An experimental study of magnetic-field and temperature dependence on magnetic fluid’s heating power. J. Magn. Magn. Mater. 2013, 331, 264–268. [Google Scholar] [CrossRef]
- Hilger, I.; Frühauf, K.; Andrä, W.; Hiergeist, R.; Hergt, R.; Kaiser, W.A. Heating potential of iron oxides for therapeutic purposes in interventional radiology. Acad. Radiol. 2002, 9, 198–202. [Google Scholar] [CrossRef]
- Bordelon, D.E.; Cornejo, C.; Grüttner, C.; Westphal, F.; DeWeese, T.L.; Ivkov, R. Magnetic nanoparticle heating efficiency reveals magneto-structural differences when characterized with wide ranging and high amplitude alternating magnetic fields. J. Appl. Phys. 2011, 109, 124904. [Google Scholar] [CrossRef]
- Wildeboer, R.R.; Southern, P.; Pankhurst, Q.A. On the reliable measurement of specific absorption rates and intrinsic loss parameters in magnetic hyperthermia materials. J. Phys. D Appl. Phys. 2014, 47, 495003. [Google Scholar] [CrossRef]
- Ebrahimi, M. On the temperature control in self-controlling hyperthermia therapy. J. Magn. Magn. Mater. 2016, 416, 134–140. [Google Scholar] [CrossRef]
- Astefanoaei, I.; Dumitru, I.; Chiriac, H.; Stancu, A. Thermo-fluid analysis in magnetic hyperthermia using low Curie temperature particles. IEEE Trans. Magn. 2016, 52, 1–5. [Google Scholar] [CrossRef]
- Wang, Q.; Deng, Z.S.; Liu, J. Theoretical evaluations of magnetic nanoparticle-enhanced heating on tumor embedded with large blood vessels during hyperthermia. J. Nanopart Res. 2012, 14, 974. [Google Scholar] [CrossRef]
- Gupta, P.K.; Singh, J.; Rai, K.N. Numerical simulation for heat transfer in tissues during thermal therapy. J. Therm. Biol. 2010, 35, 295–301. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Hasgall, P.A.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues, Version 4.0; IT’IS Foundation: Zurich, Switzerland, 2018. [Google Scholar]
- Raouf, I.; Khalid, S.; Khan, A.; Lee, J.; Kim, H.S.; Kim, M.-H. A review on numerical modeling for magnetic nanoparticle hyperthermia: Progress and challenges. J. Therm. Biol. 2020, 91, 102644. [Google Scholar] [CrossRef]
- Hergt, R.; Dutz, S. Magnetic particle hyperthermia-biophysical limitations of a visionary tumour therapy. J. Magn. Magn. Mater. 2007, 311, 187–192. [Google Scholar] [CrossRef]
- Johannsen, M.; Gneveckow, U.; Thiesen, B.; Taymoorian, K.; Cho, C.H.; Waldöfner, N.; Scholz, R.; Jordan, A.; Loening, S.A.; Wust, P. Thermotherapy of prostate cancer using magnetic nanoparticles: Feasibility, imaging, and three-dimensional temperature distribution. Eur. Urol. 2006, 52, 1653–1662. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Thrall, D.E.; Rosner, G.L.; Azuma, C.; LaRue, S.M.; Case, B.C.; Samulski, T.; Dewhirst, M.W. Using units of CEM 43 °C T90, local hyperthermia thermal dose can be delivered as prescribed. Int. J. Hyperth. 2000, 16, 415–428. [Google Scholar] [CrossRef]
- Bagaria, H.G.; Johnson, D.T. Transient solution to the bioheat equation and optimization for magnetic fluid hyperthermia treatment. Int. J. Hyperth. 2005, 21, 57–75. [Google Scholar] [CrossRef] [PubMed]
- Liangruksa, M.; Ganguly, R.; Puri, I.K. Parametric investigation of heating due to magnetic fluid hyperthermia in a tumor with blood perfusion. J. Magn. Magn. Mater. 2011, 323, 708–716. [Google Scholar] [CrossRef]
- Zhang, C.; Johnson, D.T.; Brazel, C.S. Numerical study on the multi-region bio-heat equation to model magnetic fluid hyperthermia (MFH) using low Curie temperature nanoparticles. IEEE Trans. Nanobiosci. 2008, 7, 267–275. [Google Scholar] [CrossRef]
- Richter, H.; Kettering, M.; Wiekhorst, F.; Steinhoff, U.; Hilger, I.; Trahms, L. Magnetorelaxometry for localization and quantification of magnetic nanoparticles for thermal ablation studies. Phys. Med. Biol. 2010, 55, 623–633. [Google Scholar] [CrossRef] [PubMed]
- Rast, L.; Harrison, J.G. Computational modeling of electromagnetically induced heating of magnetic nanoparticle materials for hyperthermic cancer treatment. PIERS Online 2010, 6, 5. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).