Mononuclear Heptacoordinated 3d-Metal Helicates as a New Family of Single Ion Magnets
Abstract
1. Introduction
2. Results and Discussion
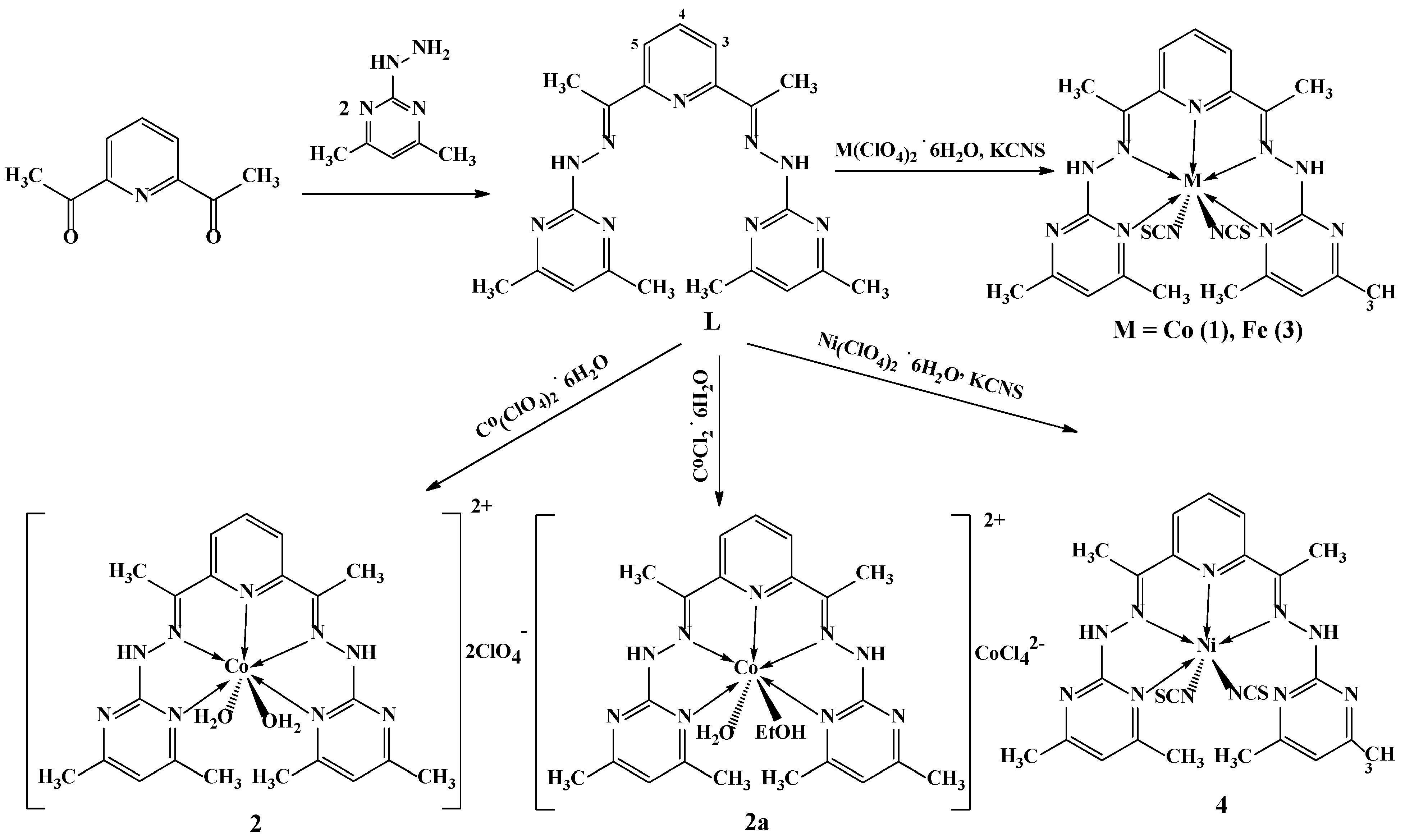
2.1. Synthesis
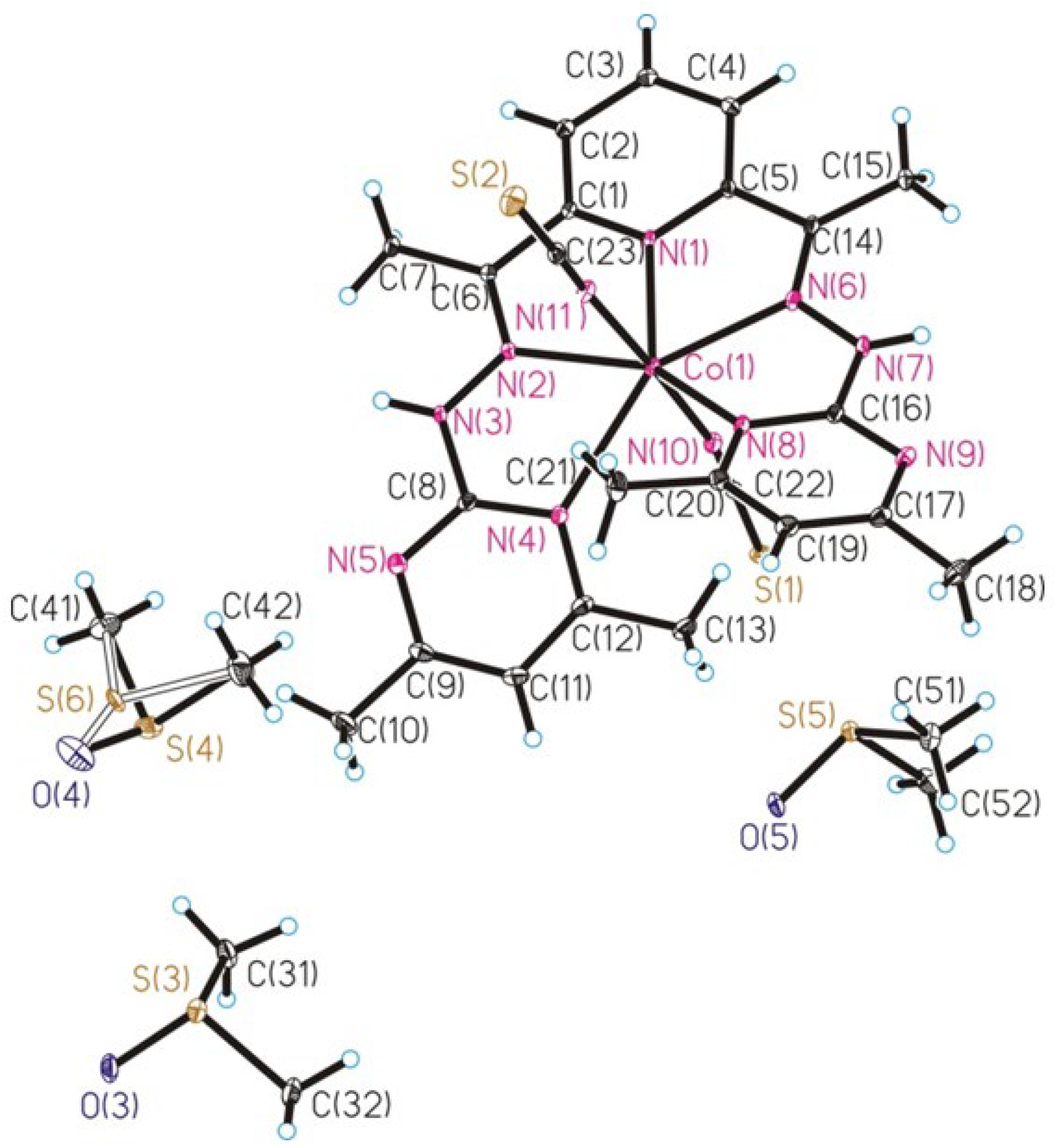
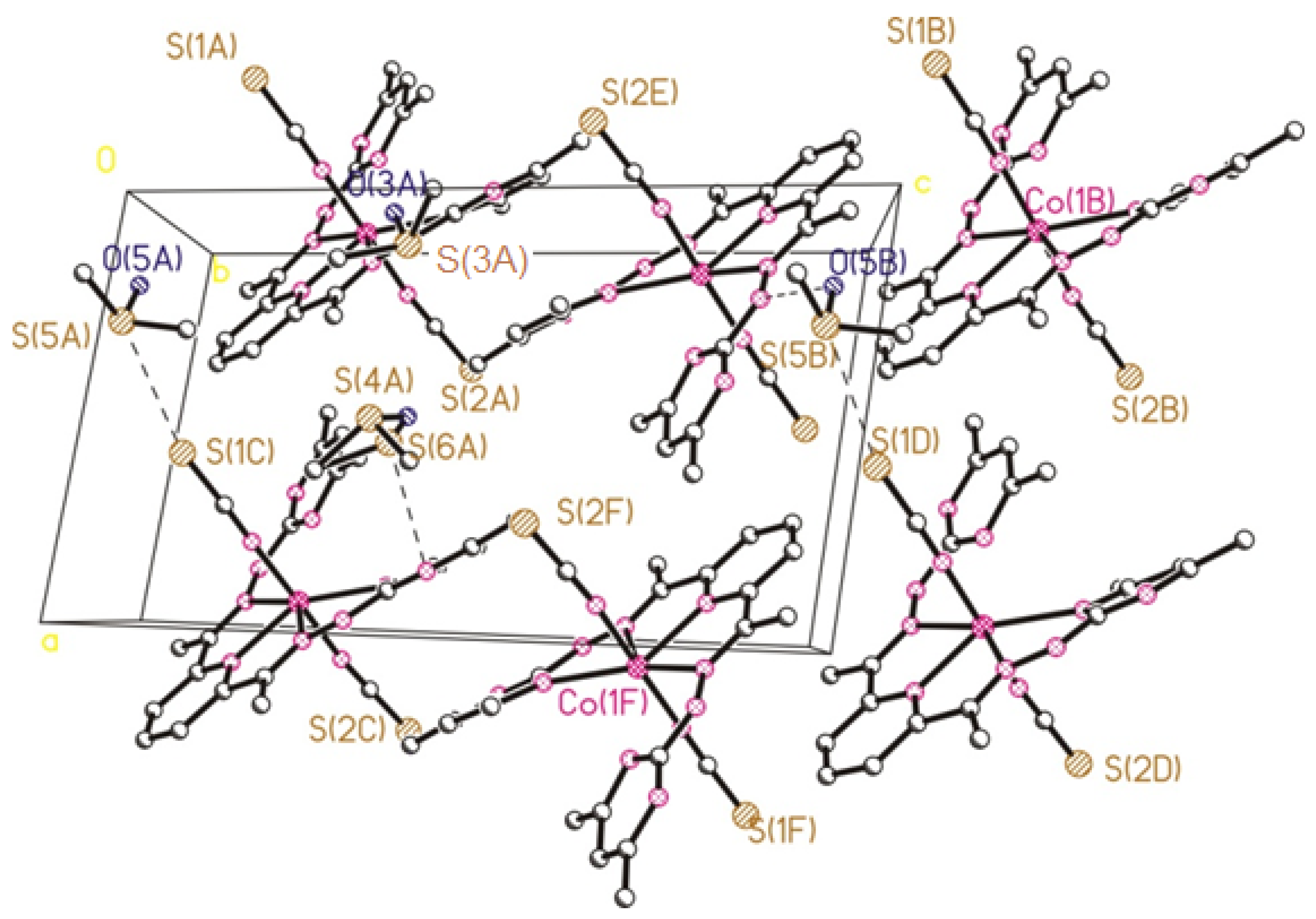
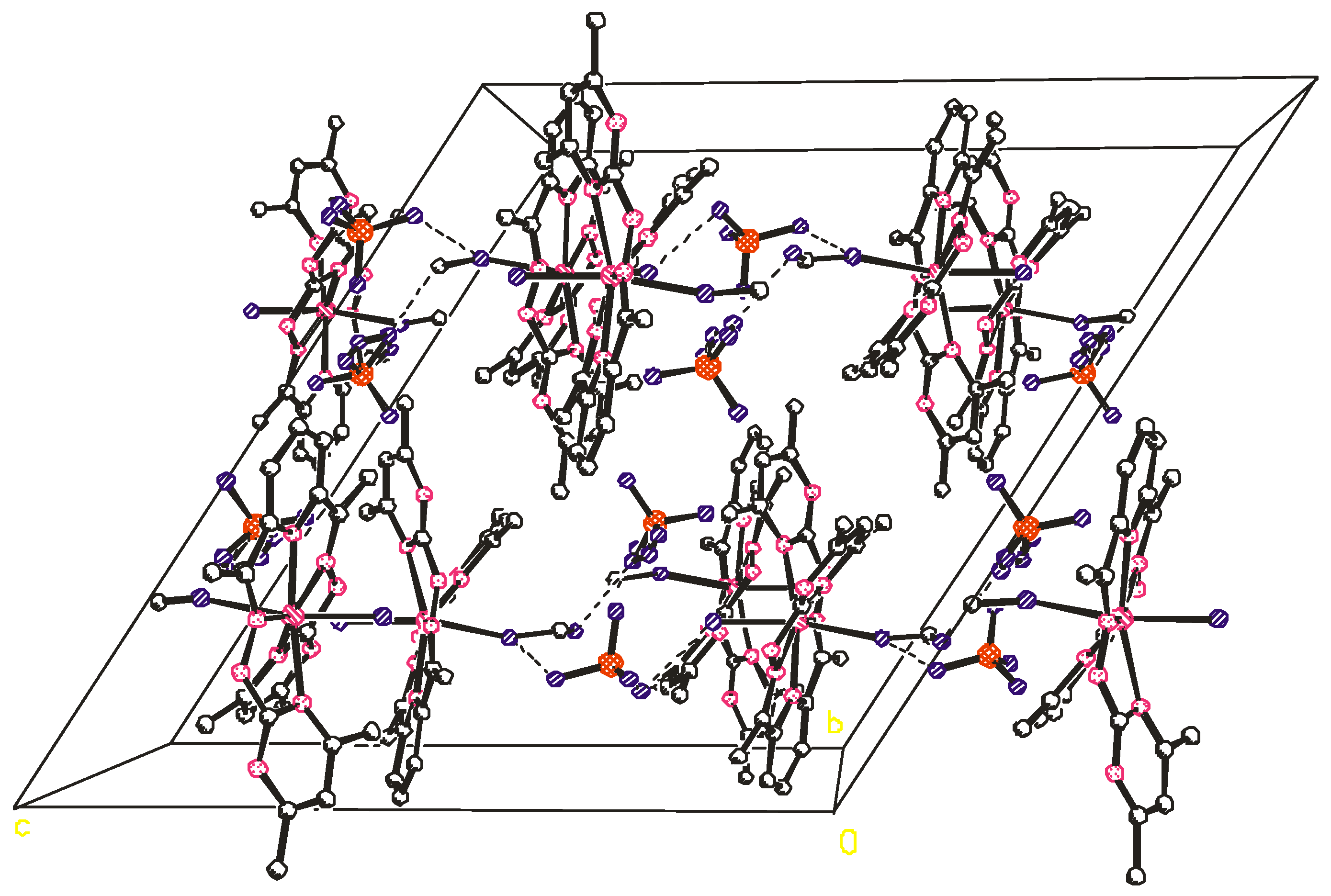
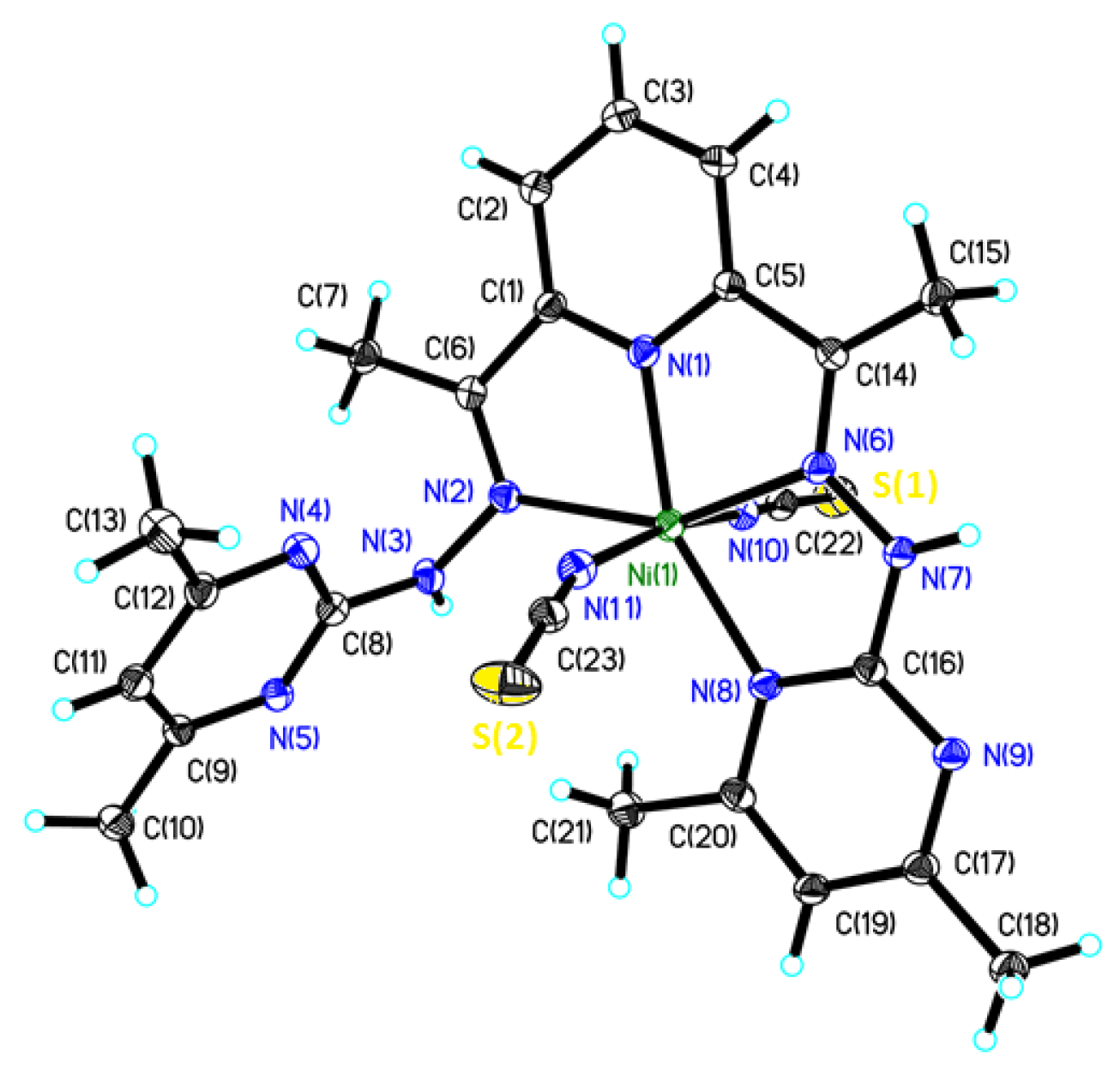
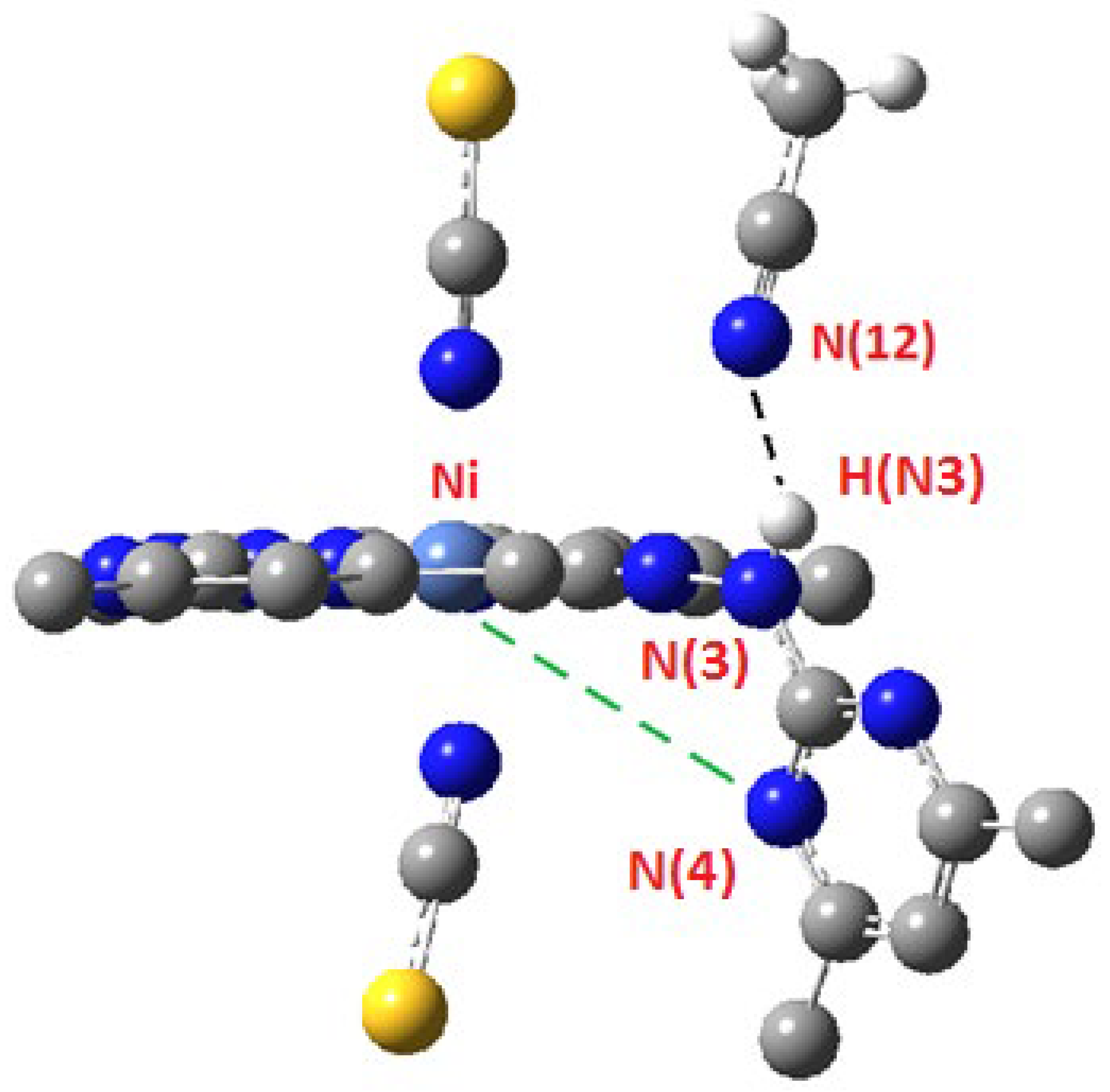
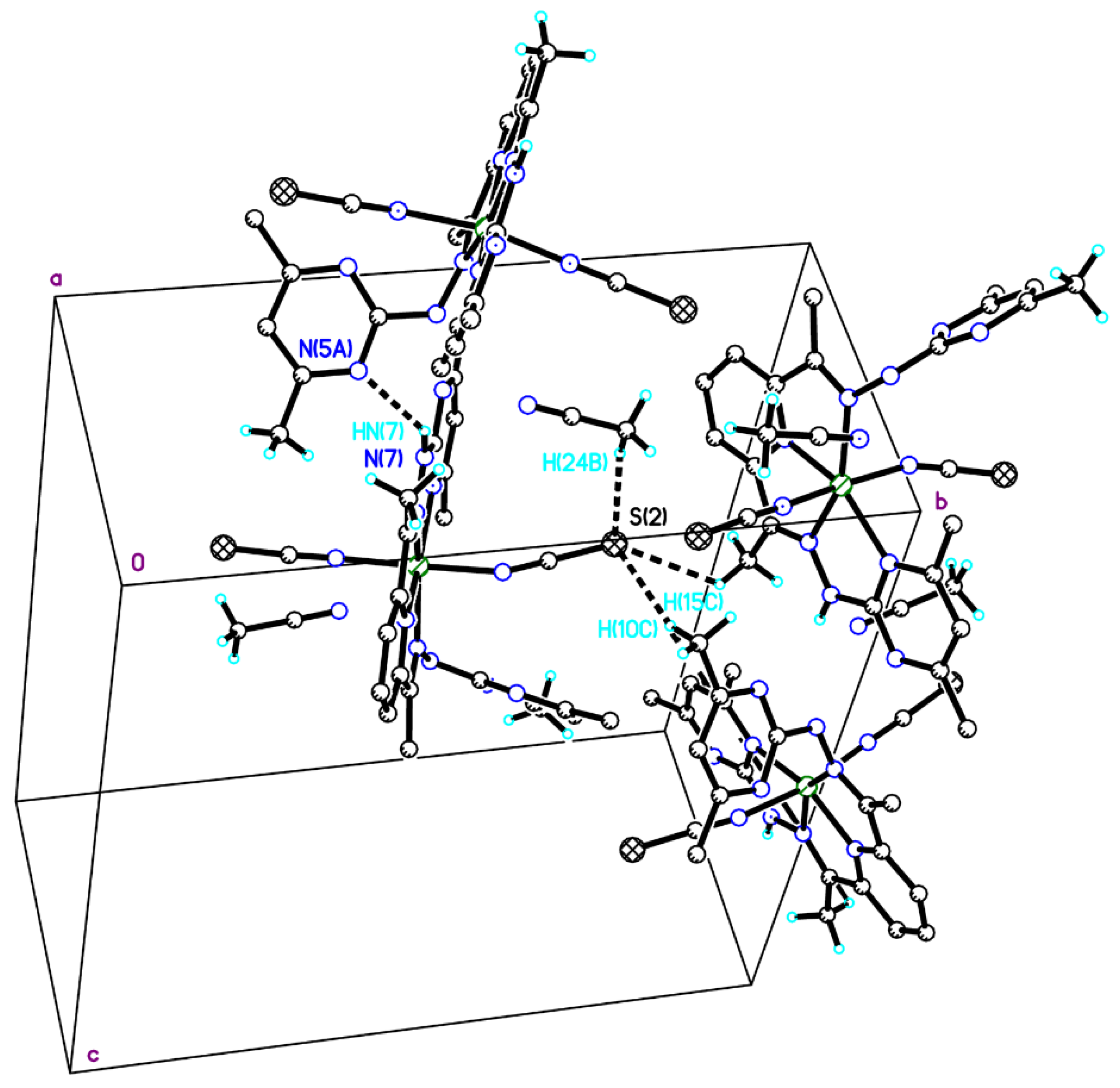
2.2. Crystal Structure
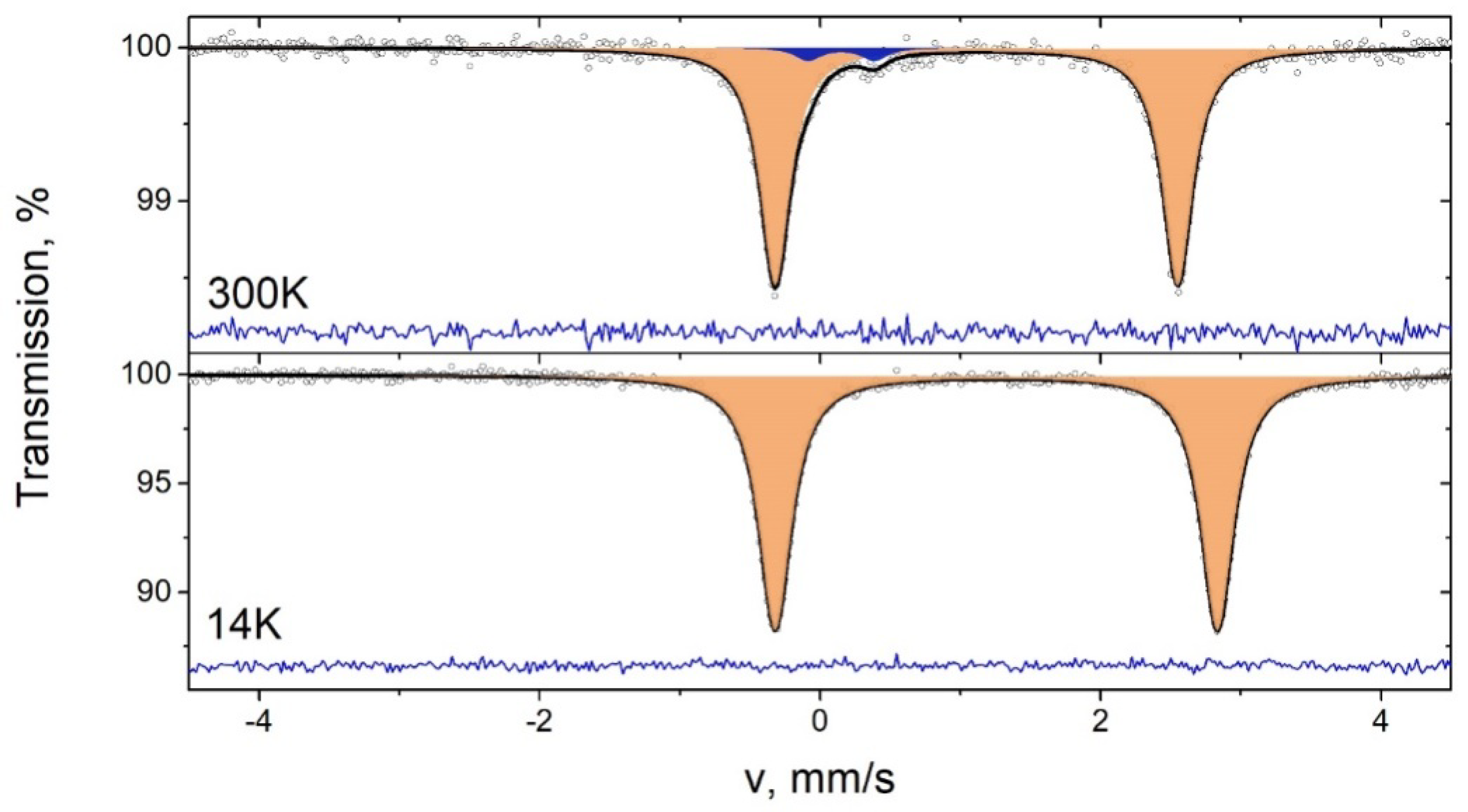
2.3. Mössbauer Spectroscopy of 3
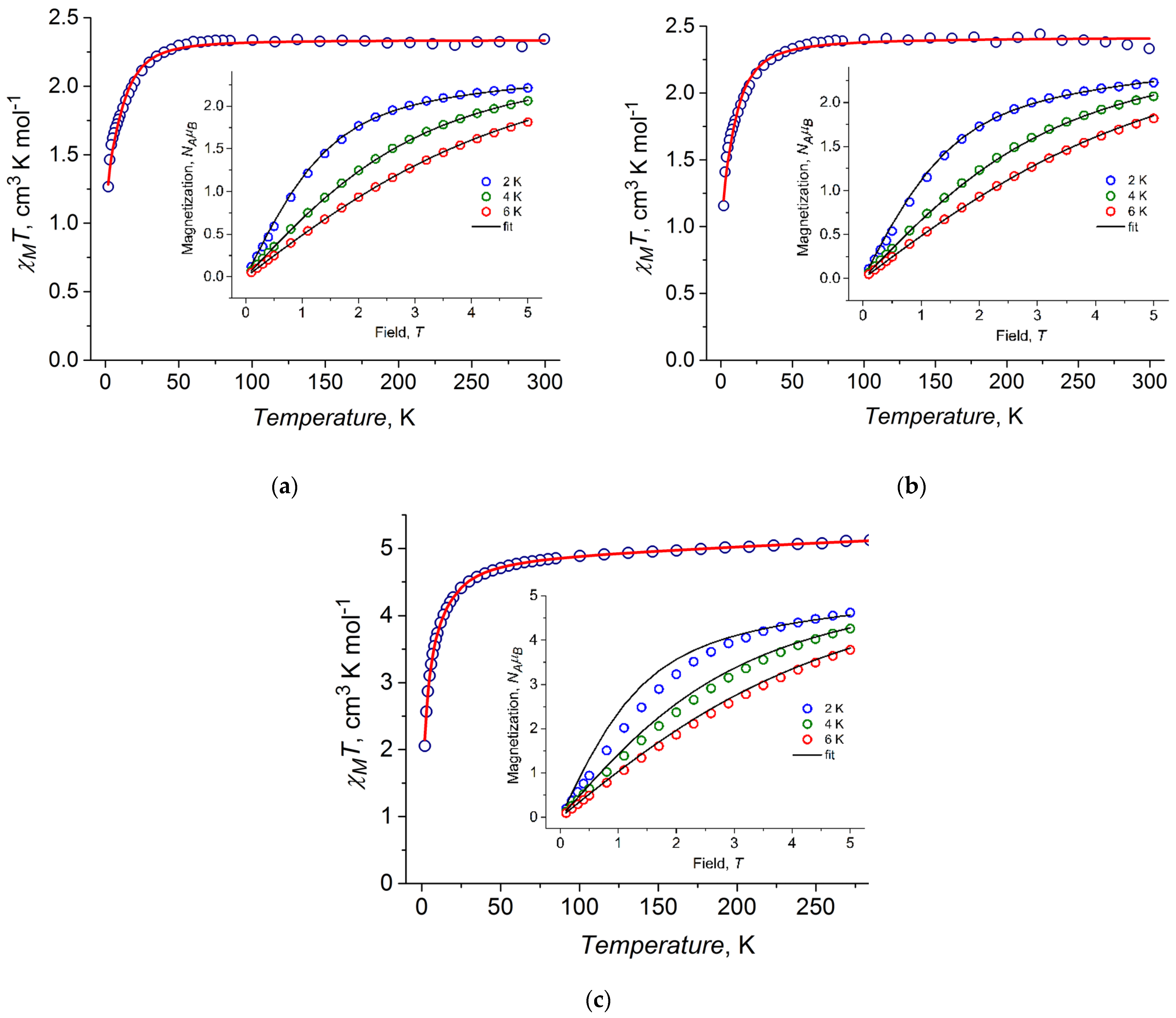
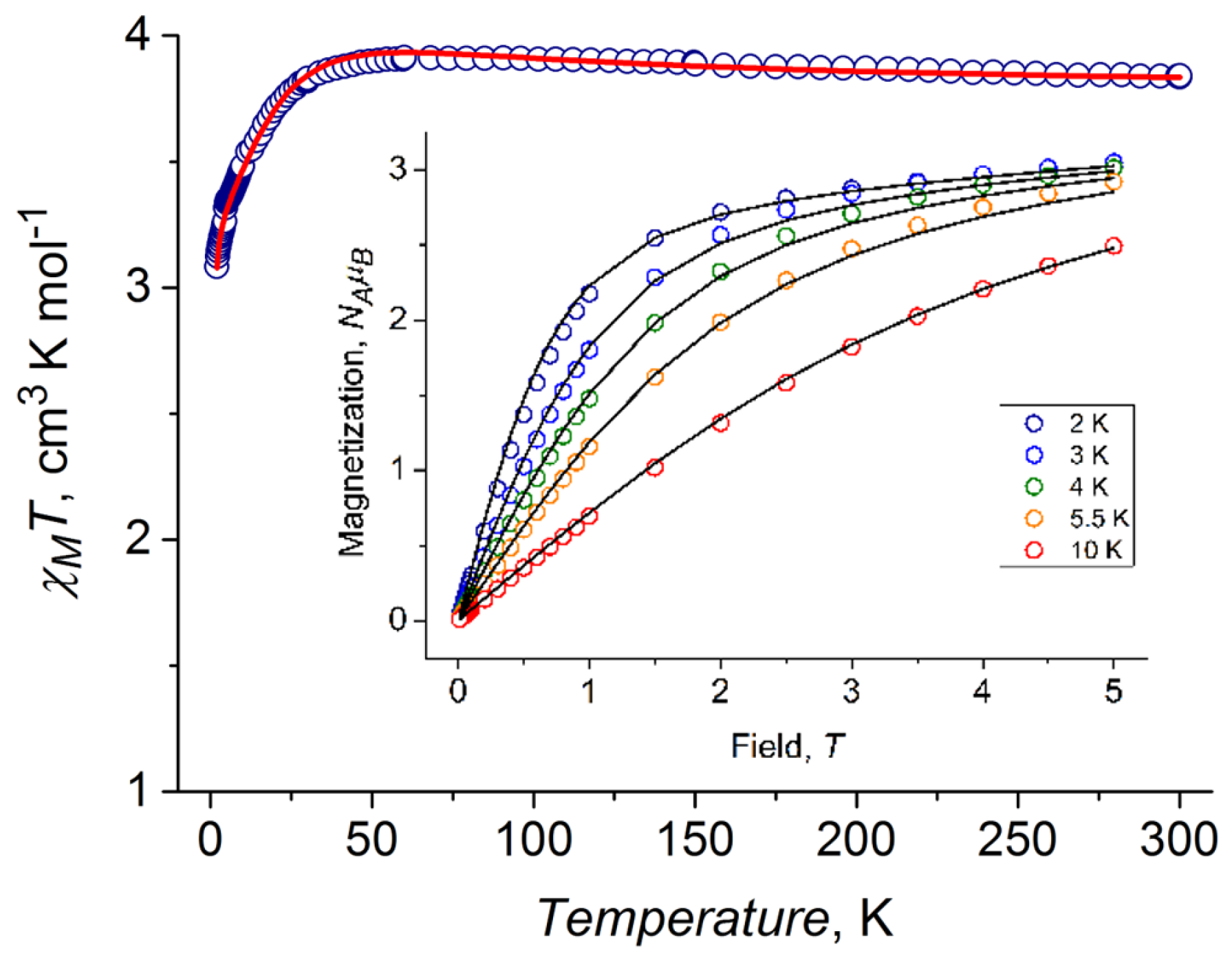
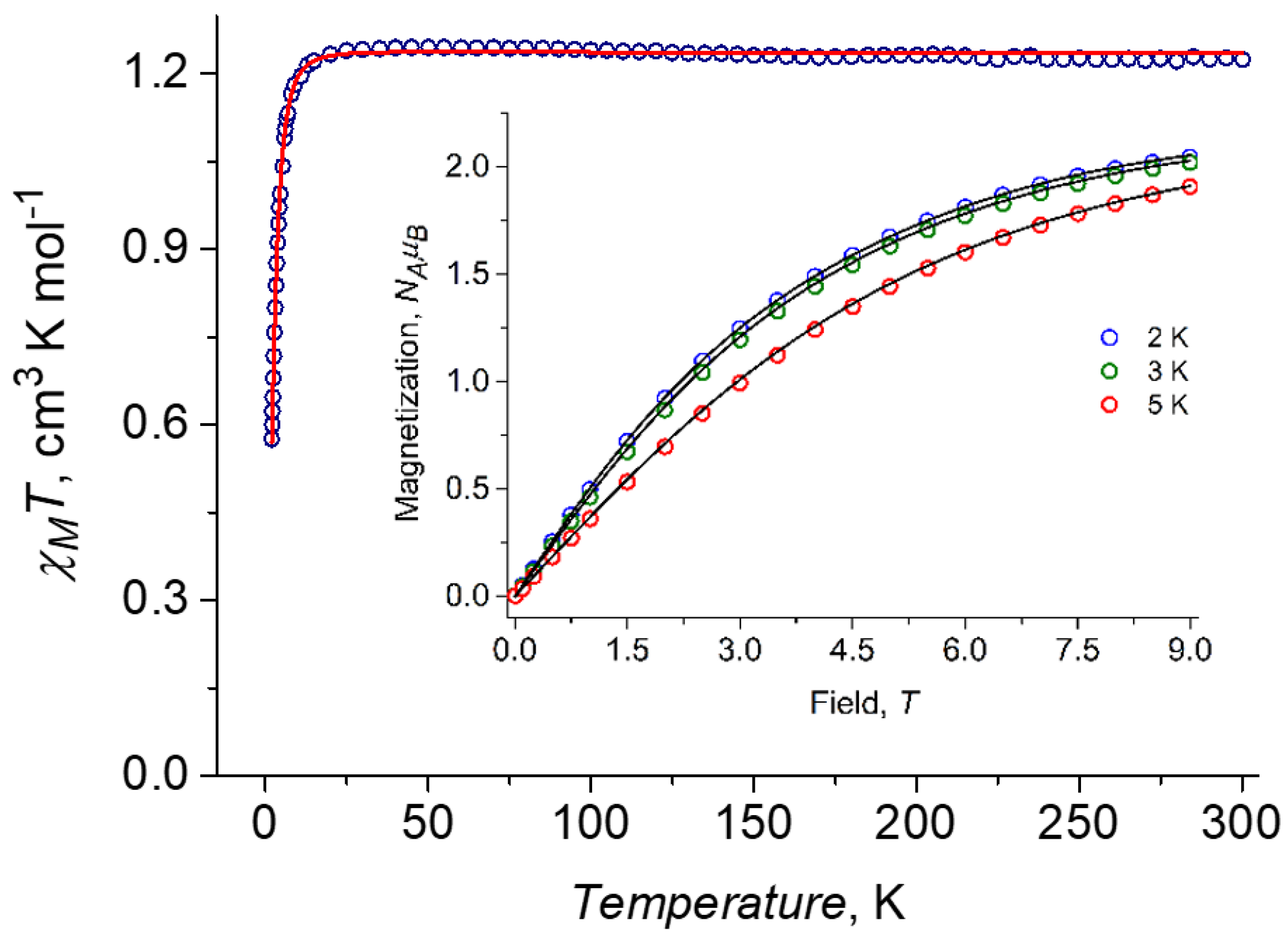
2.4. DC Magnetic Properties
2.5. Computational Results
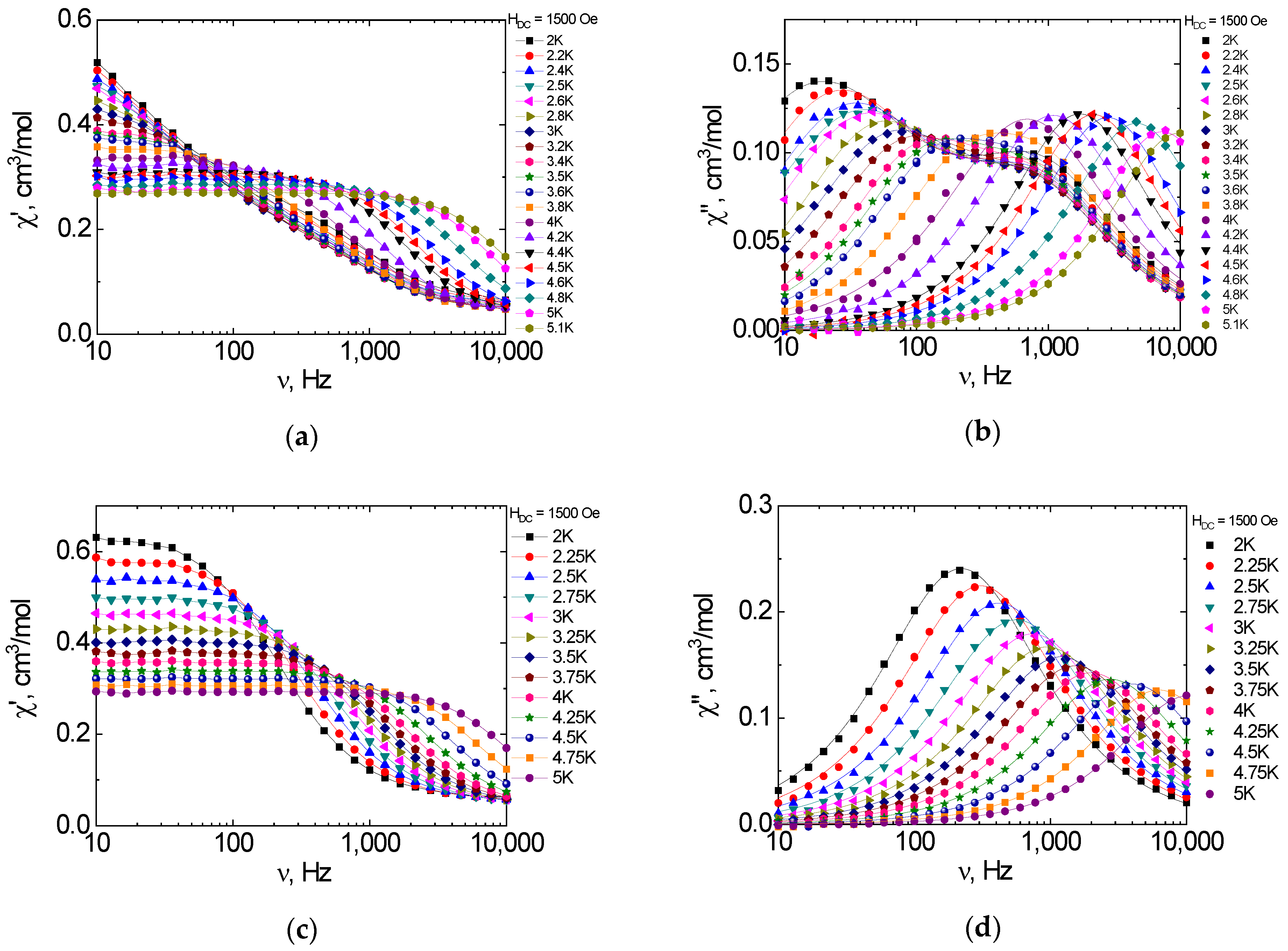
2.6. Dynamic Magnetic Properties (AC Susceptibility)
3. Materials and Methods
3.1. Synthesis of 2,6-bis(1-(2-(4,6-dimethylpyrimidin-2-yl)hydrazineylidene)ethyl)pyridine (L)
3.2. Synthesis of [CoL(NCS)2]·3DMSO (1)
3.3. Synthesis of [CoL(H2O)2](ClO4)2·H2O (2)
3.4. Synthesis of [CoL(H2O)(C2H5OH)][CoCl4]·2H2O (2a)
3.5. Synthesis of [FeL(NCS)2]·DMSO (3)
3.6. Synthesis of [NiL(NCS)2]·CH3CN (4)
3.7. Single-Crystal X-ray Diffraction Study
3.8. Magnetic Measurements
3.9. Computational Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gomez-Coca, S.; Cremades, E.; Aliaga-Alcalde, N.; Ruiz, E. Mononuclear Single-Molecule Magnets: Tailoring the Magnetic Anisotropy of First-Row Transition-Metal Complexes. J. Am. Chem. Soc. 2013, 135, 7010–7018. [Google Scholar] [CrossRef] [PubMed]
- Ruamps, R.; Batchelor, L.J.; Maurice, R.; Gogoi, N.; Jiménez-Lozano, P.; Guihéry, N.; de Graaf, C.; Barra, A.-L.; Sutter, J.-P.; Mallah, T. Origin of the Magnetic Anisotropy in Heptacoordinate NiII and CoII Complexes. Chem. Eur. J. 2013, 19, 950–956. [Google Scholar] [CrossRef] [PubMed]
- Darmanović, D.; Shcherbakov, I.N.; Duboc, C.; Spasojević, V.; Hanžel, D.; Anđelković, K.; Radanović, D.; Turel, I.; Milenković, M.; Gruden, M.; et al. Combined Experimental and Theoretical Investigation of the Origin of Magnetic Anisotropy in Pentagonal Bipyramidal Isothiocyanato Co(II), Ni(II), and Fe(III) Complexes with Quaternary-Ammonium-Functionalized 2,6-Diacetylpyridine Bisacylhydrazone. J. Phys. Chem. C 2019, 123, 31142–31155. [Google Scholar] [CrossRef]
- Gatteschi, D. Single molecule magnets: A new class of magnetic materials. J. Alloys Compd. 2001, 317–318, 8–12. [Google Scholar] [CrossRef]
- Gatteschi, D.; Bogani, L.; Cornia, A.; Mannini, M.; Sorace, L.; Sessoli, R. Molecular magnetism, status and perspectives. Solid State Sci. 2008, 10, 1701–1709. [Google Scholar] [CrossRef]
- Caneschi, A.; Gatteschi, D.; Sessoli, R.; Barra, A.L.; Brunel, L.C.; Guillot, M. Alternating current susceptibility, high field magnetization, and millimeter band EPR evidence for a ground S = 10 state in [Mn12O12(Ch3COO)16(H2O)4].2CH3COOH.4H2O. J. Am. Chem. Soc. 1991, 113, 5873–5874. [Google Scholar] [CrossRef]
- Kahn, O. Molecular Magnetism; VCH Publishers: New York, NY, USA, 1993; p. 396. [Google Scholar]
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Miller, J.S.; Gatteschi, D. Molecule-based magnets. Chem. Soc. Rev. 2011, 40, 3065–3066. [Google Scholar] [CrossRef]
- Ferrando-Soria, J.; Vallejo, J.; Castellano, M.; Martínez-Lillo, J.; Pardo, E.; Cano, J.; Castro, I.; Lloret, F.; Ruiz-García, R.; Julve, M. Molecular magnetism, quo vadis? A historical perspective from a coordination chemist viewpoint. Coord. Chem. Rev. 2017, 339, 17–103. [Google Scholar] [CrossRef]
- Lukov, V.V.; Kogan, V.A.; Levchenkov, S.I.; Shcherbakov, I.N.; Popov, L.D. Modern studies in the area of molecular magnets: State, problems, and prospects. Russ. J. Coord. Chem. 2015, 41, 1–15. [Google Scholar] [CrossRef]
- Gatteschi, D.; Cornia, A.; Mannini, M.; Sessoli, R. Organizing and Addressing Magnetic Molecules. Inorg. Chem. 2009, 48, 3408–3419. [Google Scholar] [CrossRef] [PubMed]
- Ritter, S.K. Single-Molecule Magnets Evolve. Chem. Eng. News Arch. 2004, 82, 29–32. [Google Scholar] [CrossRef]
- Sanvito, S. Molecular spintronics. Chem. Soc. Rev. 2011, 40, 3336–3355. [Google Scholar] [CrossRef] [PubMed]
- Bogani, L. Experiments on Molecular Magnets for Molecular Spintronics. In Molecular Nanomagnets and Related Phenomena; Gao, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 331–381. [Google Scholar]
- Winpenny, R.E.P. Quantum Information Processing Using Molecular Nanomagnets as Qubits. Angew. Chem Int. Ed. 2008, 47, 7992–7994. [Google Scholar] [CrossRef] [PubMed]
- Troiani, F.; Affronte, M. Molecular spins for quantum information technologies. Chem. Soc. Rev. 2011, 40, 3119–3129. [Google Scholar] [CrossRef]
- Leuenberger, M.N.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Cornia, A.; Mannini, M.; Sainctavit, P.; Sessoli, R. Chemical strategies and characterization tools for the organization of single molecule magnets on surfaces. Chem. Soc. Rev. 2011, 40, 3076–3091. [Google Scholar] [CrossRef]
- Miller, J.S. Magnetically ordered molecule-based materials. Chem. Soc. Rev. 2011, 40, 3266–3296. [Google Scholar] [CrossRef]
- Jeon, I.-R.; Clerac, R. Controlled association of single-molecule magnets (SMMs) into coordination networks: Towards a new generation of magnetic materials. Dalton Trans. 2012, 41, 9569–9586. [Google Scholar] [CrossRef]
- Coronado, E. Molecular magnetism: From chemical design to spin control in molecules, materials and devices. Nat. Rev. Mater. 2020, 5, 87–104. [Google Scholar] [CrossRef]
- Frost, J.M.; Harriman, K.L.M.; Murugesu, M. The rise of 3-d single-ion magnets in molecular magnetism: Towards materials from molecules? Chem. Sci. 2016, 7, 2470–2491. [Google Scholar] [CrossRef] [PubMed]
- Craig, G.A.; Murrie, M. 3d single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef] [PubMed]
- Cirera, J.; Ruiz, E.; Alvarez, S.; Neese, F.; Kortus, J. How to Build Molecules with Large Magnetic Anisotropy. Chem. Eur. J. 2009, 15, 4078–4087. [Google Scholar] [CrossRef]
- Saber, M.R.; Singh, M.K.; Dunbar, K.R. Geometrical control of the magnetic anisotropy in six coordinate cobalt complexes. Chem. Commun. 2020, 56, 8492–8495. [Google Scholar] [CrossRef] [PubMed]
- Meng, Y.-S.; Jiang, S.-D.; Wang, B.-W.; Gao, S. Understanding the Magnetic Anisotropy toward Single-Ion Magnets. Acc. Chem. Res. 2016, 49, 2381–2389. [Google Scholar] [CrossRef]
- Bar, A.K.; Pichon, C.; Sutter, J.-P. Magnetic anisotropy in two- to eight-coordinated transition–metal complexes: Recent developments in molecular magnetism. Coord. Chem. Rev. 2016, 308, 346–380. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B 2016, 72, 171–179. [Google Scholar] [CrossRef]
- Drahoš, B.; Císařová, I.; Laguta, O.; Santana, V.T.; Neugebauer, P.; Herchel, R. Structural, magnetic, redox and theoretical characterization of seven-coordinate first-row transition metal complexes with a macrocyclic ligand containing two benzimidazolyl N-pendant arms. Dalton Trans. 2020, 49, 4425–4440. [Google Scholar] [CrossRef]
- Antal, P.; Drahoš, B.; Herchel, R.; Trávníček, Z. Late First-Row Transition-Metal Complexes Containing a 2-Pyridylmethyl Pendant-Armed 15-Membered Macrocyclic Ligand. Field-Induced Slow Magnetic Relaxation in a Seven-Coordinate Cobalt(II) Compound. Inorg. Chem. 2016, 55, 5957–5972. [Google Scholar] [CrossRef]
- Sutter, J.-P.; Béreau, V.; Jubault, V.; Bretosh, K.; Pichon, C.; Duhayon, C. Magnetic anisotropy of transition metal and lanthanide ions in pentagonal bipyramidal geometry. Chem. Soc. Rev. 2022, 51, 3280–3313. [Google Scholar] [CrossRef]
- Huang, X.-C.; Zhou, C.; Shao, D.; Wang, X.-Y. Field-Induced Slow Magnetic Relaxation in Cobalt(II) Compounds with Pentagonal Bipyramid Geometry. Inorg. Chem. 2014, 53, 12671–12673. [Google Scholar] [CrossRef] [PubMed]
- Shao, D.; Zhang, S.-L.; Shi, L.; Zhang, Y.-Q.; Wang, X.-Y. Probing the Effect of Axial Ligands on Easy-Plane Anisotropy of Pentagonal-Bipyramidal Cobalt(II) Single-Ion Magnets. Inorg. Chem. 2016, 55, 10859–10869. [Google Scholar] [CrossRef] [PubMed]
- Yi, G.; Cui, H.; Zhang, C.; Zhao, W.; Chen, L.; Zhang, Y.-Q.; Chen, X.-T.; Song, Y.; Yuan, A. A capped trigonal prismatic cobalt(ii) complex as a structural archetype for single-ion magnets. Dalton Trans. 2020, 49, 2063–2067. [Google Scholar] [CrossRef] [PubMed]
- Yi, G.; Zhang, C.; Zhao, W.; Cui, H.; Chen, L.; Wang, Z.; Chen, X.-T.; Yuan, A.; Liu, Y.-Z.; Ouyang, Z.-W. Structure, magnetic anisotropy and relaxation behavior of seven-coordinate Co(ii) single-ion magnets perturbed by counter-anions. Dalton Trans. 2020, 49, 7620–7627. [Google Scholar] [CrossRef] [PubMed]
- Regueiro-Figueroa, M.; Lima, L.M.P.; Blanco, V.; Esteban-Gómez, D.; de Blas, A.; Rodríguez-Blas, T.; Delgado, R.; Platas-Iglesias, C. Reasons behind the Relative Abundances of Heptacoordinate Complexes along the Late First-Row Transition Metal Series. Inorg. Chem. 2014, 53, 12859–12869. [Google Scholar] [CrossRef]
- Alvarez, S.; Alemany, P.; Casanova, D.; Cirera, J.; Llunell, M.; Avnir, D. Shape maps and polyhedral interconversion paths in transition metal chemistry. Coord. Chem. Rev. 2005, 249, 1693–1708. [Google Scholar] [CrossRef]
- Llunell, M.; Casanova, D.; Cirera, J.; Alemany, P.; Alvarez, S. SHAPE (2.1); Universitat de Barcelona: Barcelona, Spain, 2013. [Google Scholar]
- Varga, F.; Rajnák, C.; Titiš, J.; Moncoľ, J.; Boča, R. Slow magnetic relaxation in a Co(ii) octahedral–tetrahedral system formed of a [CoL3]2+ core with L = bis(diphenylphosphanoxido) methane and tetrahedral [CoBr4]2− counter anions. Dalton Trans. 2017, 46, 4148–4151. [Google Scholar] [CrossRef]
- Rajnák, C.; Titiš, J.; Moncoľ, J.; Renz, F.; Boča, R. Field-Supported Slow Magnetic Relaxation in Hexacoordinate CoII Complexes with Easy Plane Anisotropy. Eur. J. Inorg. Chem. 2017, 2017, 1520–1525. [Google Scholar] [CrossRef]
- Titiš, J.; Rajnák, C.; Valigura, D.; Boča, R. Field influence on the slow magnetic relaxation of nickel-based single ion magnets. Dalton Trans. 2018, 47, 7879–7882. [Google Scholar] [CrossRef]
- Mandal, S.; Mondal, S.; Rajnák, C.; Titiš, J.; Boča, R.; Mohanta, S. Syntheses, crystal structures and magnetic properties of two mixed-valence Co(iii)Co(ii) compounds derived from Schiff base ligands: Field-supported single-ion-magnet behavior with easy-plane anisotropy. Dalton Trans. 2017, 46, 13135–13144. [Google Scholar] [CrossRef]
- Tupolova, Y.P.; Shcherbakov, I.N.; Popov, L.D.; Lebedev, V.E.; Tkachev, V.V.; Zakharov, K.V.; Vasiliev, A.N.; Korchagin, D.V.; Palii, A.V.; Aldoshin, S.M. Field-induced single-ion magnet behaviour of a hexacoordinated Co(II) complex with easy-axis-type magnetic anisotropy. Dalton Trans. 2019, 48, 6960–6970. [Google Scholar] [CrossRef] [PubMed]
- Tupolova, Y.P.; Shcherbakov, I.N.; Korchagin, D.V.; Tkachev, V.V.; Lebedev, V.E.; Popov, L.D.; Zakharov, K.V.; Vasiliev, A.N.; Palii, A.V.; Aldoshin, S.M. Fine-Tuning of Uniaxial Anisotropy and Slow Relaxation of Magnetization in the Hexacoordinate Co(II) Complexes with Acidoligands. J. Phys. Chem. C 2020, 124, 25957–25966. [Google Scholar] [CrossRef]
- Kosolapoff, G.M.; Roy, C.H. Synthesis of Some Pyrimidylphosphonates. J. Org. Chem. 1961, 26, 1895–1898. [Google Scholar] [CrossRef]
- Matsnev, M.E.; Rusakov, V.S. SpectrRelax: An application for Mössbauer spectra modeling and fitting. AIP Conf. Proc. 2012, 1489, 178–185. [Google Scholar] [CrossRef]
- Agilent. CrysAlis PRO, version 171.35.19; Agilent Technologies UK Ltd.: Yarnton, UK, 2011.
- Sheldrick, G.M. G.M. Sheldrick (8/06/2000). SHELXTL v. 6.14, Structure Determination Software Suite, Bruker AXS: Madison, WI, USA, 2000.
- Lazarenko, V.A.; Dorovatovskii, P.V.; Zubavichus, Y.V.; Burlov, A.S.; Koshchienko, Y.V.; Vlasenko, V.G.; Khrustalev, V.N. High-Throughput Small-Molecule Crystallography at the ‘Belok’ Beamline of the Kurchatov Synchrotron Radiation Source: Transition Metal Complexes with Azomethine Ligands as a Case Study. Crystals 2017, 7, 325. [Google Scholar] [CrossRef]
- Svetogorov, R.D.; Dorovatovskii, P.V.; Lazarenko, V.A. Belok/XSA Diffraction Beamline for Studying Crystalline Samples at Kurchatov Synchrotron Radiation Source. Cryst. Res. Technol. 2020, 55, 1900184. [Google Scholar] [CrossRef]
- Kabsch, W. XDS. Acta Crystallogr. Sect. D 2010, 66, 125–132. [Google Scholar] [CrossRef]
- Sheldrick, G. SHELXT-Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Roos, B.O.; Taylor, P.R.; Si≐gbahn, P.E.M. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
- Per, S.; Anders, H.; Björn, R.; Bernard, L. A Comparison of the Super-CI and the Newton-Raphson Scheme in the Complete Active Space SCF Method. Phys. Scr. 1980, 21, 323. [Google Scholar]
- Siegbahn, P.E.M.; Almlöf, J.; Heiberg, A.; Roos, B.O. The complete active space SCF (CASSCF) method in a Newton–Raphson formulation with application to the HNO molecule. J. Chem. Phys. 1981, 74, 2384–2396. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.P. Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.-P. N-electron valence state perturbation theory: A fast implementation of the strongly contracted variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R. Multireference perturbation configuration interaction V. Third-order energy contributions in the Møller–Plesset and Epstein–Nesbet partitions. Theor. Chem. Acc. 2002, 107, 313–317. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.-P. n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants. J. Chem. Phys. 2002, 117, 9138–9153. [Google Scholar] [CrossRef]
- Hess, B.A. Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators. Phys. Rev. A 1986, 33, 3742–3748. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Chen, X.Y.; Landis, C.R.; Neese, F. All-electron scalar relativistic basis sets for third-row transition metal atoms. J. Chem. Theory Comput. 2008, 4, 908. [Google Scholar] [CrossRef]
- Schafer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Schafer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. An improvement of the resolution of the identity approximation for the formation of the Coulomb matrix. J. Comput. Chem. 2003, 24, 1740–1747. [Google Scholar] [CrossRef] [PubMed]
- Ganyushin, D.; Neese, F. First-principles calculations of zero-field splitting parameters. J. Chem. Phys. 2006, 125, 024103. [Google Scholar] [CrossRef] [PubMed]


| Comp. | M–N(1) | M–N(2) | M–N(4) | M–N(6) | M–N(8) | M–N(10) | M–N(11) |
|---|---|---|---|---|---|---|---|
| 1 | 2.178(3) | 2.271(3) | 2.492(3) | 2.215(3) | 2.336(3) | 2.095(3) | 2.085(3) |
| 2 | 2.139(3) | 2.143(3) | 2.223(3) | 2.157(3) | 2.238(3) | - | - |
| 2a | 2.155(2) | 2.172(2) | 2.230(2) | 2.171(2) | 2.325(2) | 2.157(2) O(H2O) 1 | 2.184(2) O(EtOH) 1 |
| 3 | 2.240(3) | 2.318(2) | 2.481(2) | 2.318(2) | 2.481(2) | 2.095(2) | 2.095(2) |
| M … M(1)# | # | |
|---|---|---|
| 1 | 7.886 | 2 − x, −y, −z |
| 2 | 8.522 8.783 | −x, 1 − y, 1 − z 1/2 − x, 1/2 + y, 3/2 − z |
| 2a | 7.0735(5) | To Co ion of [CoCl4]2− unit |
| 3 | 7.795 7.838 | x, y, −1 + z 2 − x, 1 + x − y, 1/3 + z |
| Compound | M | N(4) | M | N(8) | N(10)–M–N(11) (for 1, 3, 4) O(1)–M–O(2) (for 2, 2a) |
|---|---|---|---|---|---|
| 1 | Co | −0.665 | −0.132 | 0.561 | 177.4 |
| 2 | Co | 0.812 | −0.007 | −0.876 | 166.3 |
| 2a | Co | 0.753 | −0.005 | −0.761 | 167.0 |
| 3 | Fe | 0.599 | 0.000 | −0.599 | 173.7 |
| 4 | Ni | 2.388 | 0.059 | 0.09 | 168.9 |
| T, K | Component | δ ± 0.01, mm/s | Δ ± 0.01, mm/s | A ± 1, % | G ± 0.01, mm/s | χ2 |
|---|---|---|---|---|---|---|
| 300 | D1 | 1.12 | 2.86 | 96 | 0.26 | 0.939 |
| D2 | 0.15 | 0.48 | 4 | 0.23 | ||
| 14 | D1 | 1.26 | 3.16 | 100 | 0.29 | 1.014 |
| Parameter | 1 | 2 | 2a | 3 | 4 | |
|---|---|---|---|---|---|---|
| Value | ||||||
| gx | 2.24(1) a | 2.44(1) | 2.29(2) b | 2.38(1) c | 2.00(1) | 2.22(1) a |
| gy | - | 2.34(2) | 2.15(1) | |||
| gz | 2.22(1) | 2.02(1) | 2.11(4) | 2.54(2) | ||
| D, cm−1 | 13.7(1) | 11.5(1) | 20(1) | 5.3(3) | −14.5(1) | 6.0(1) |
| E, cm−1 | 2.5(1) | 2.0(1) | - | - | 0.7(1) | 0 |
| zJ, cm−1 | −0.04(1) | −0.05(1) | −0.07 | - | - | |
| Parameter | 1 | 2 | 2a | 3 | 4 |
|---|---|---|---|---|---|
| Value | |||||
| gx | 2.276/2.280 | 2.351/2.254 | 2.330/2.257 | 1.975/2.414 | 2.233/2.175 |
| gy | 2.348/2.326 | 2.328/2.271 | 2.368/2.286 | 2.043/2.054 | 2.310/2.233 |
| gz | 2.427/2.213 | 2.126/2.099 | 2.127/2.099 | 2.476/1.991 | 2.319/2.238 |
| D, cm−1 | 12.61/11.28 | 22.2/18.7 | 23.5/19.9 | −22.10/−18.04 | 11.53/8.10 |
| E, cm−1 | 2.83/1.76 | 1.33/1.08 | 1.73/1.35 | 0.43/0.54 | 0.07/0.40 |
| 23.4 | 37.5 | 40.2 | |||
| Complex | 1 | 2 |
|---|---|---|
| Δeff/kB, K | 65(1) | 60(1) |
| τ0, s | 5.0(5) × 10−11 | 1.5(1) × 10−10 |
| C, s−1K−n | 14.8(4) | 182(3) |
| n | 2.92(3) | 2.93(2) |
| R2 | 0.999 | 0.999 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tupolova, Y.P.; Korchagin, D.V.; Andreeva, A.S.; Tkachev, V.V.; Shilov, G.V.; Lazarenko, V.A.; Popov, L.D.; Babeshkin, K.A.; Efimov, N.N.; Morgunov, R.B.; et al. Mononuclear Heptacoordinated 3d-Metal Helicates as a New Family of Single Ion Magnets. Magnetochemistry 2022, 8, 153. https://doi.org/10.3390/magnetochemistry8110153
Tupolova YP, Korchagin DV, Andreeva AS, Tkachev VV, Shilov GV, Lazarenko VA, Popov LD, Babeshkin KA, Efimov NN, Morgunov RB, et al. Mononuclear Heptacoordinated 3d-Metal Helicates as a New Family of Single Ion Magnets. Magnetochemistry. 2022; 8(11):153. https://doi.org/10.3390/magnetochemistry8110153
Chicago/Turabian StyleTupolova, Yulia P., Denis V. Korchagin, Anastasya S. Andreeva, Valery V. Tkachev, Gennadii V. Shilov, Vladimir A. Lazarenko, Leonid D. Popov, Konstantin A. Babeshkin, Nikolay N. Efimov, Roman B. Morgunov, and et al. 2022. "Mononuclear Heptacoordinated 3d-Metal Helicates as a New Family of Single Ion Magnets" Magnetochemistry 8, no. 11: 153. https://doi.org/10.3390/magnetochemistry8110153
APA StyleTupolova, Y. P., Korchagin, D. V., Andreeva, A. S., Tkachev, V. V., Shilov, G. V., Lazarenko, V. A., Popov, L. D., Babeshkin, K. A., Efimov, N. N., Morgunov, R. B., Palii, A. V., Kubrin, S. P., Shcherbakov, I. N., & Aldoshin, S. M. (2022). Mononuclear Heptacoordinated 3d-Metal Helicates as a New Family of Single Ion Magnets. Magnetochemistry, 8(11), 153. https://doi.org/10.3390/magnetochemistry8110153