Effect of External Pressure on the Metal–Insulator Transition of the Organic Quasi-Two-Dimensional Metal κ-(BEDT-TTF)₂Hg(SCN)₂Br ^†

Abstract

The metal–insulator transition in the organic quasi-two-dimensional metal κ-(BEDT-TTF)₂Hg(SCN)₂Br at T_MI ≈ 90 K has been investigated. The crystal structure changes during this transition from monoclinic above T_MI to triclinic below T_MI. A theoretical study suggested that this phase transition should be of the metal-to-metal type and brings about a substantial change of the Fermi surface. Apparently, the electronic system in the triclinic phase is unstable toward a Mott insulating state, leading to the growth of the resistance when the temperature drops below T_MI ≈ 90 K. The application of external pressure suppresses the Mott transition and restores the metallic electronic structure of the triclinic phase. The observed quantum oscillations of the magnetoresistance are in good agreement with the calculated Fermi surface for the triclinic phase, providing a plausible explanation for the puzzling behavior of κ-(BEDT-TTF)₂Hg(SCN)₂Br as a function of temperature and pressure around 100 K. The present study points out interesting differences in the structural and physical behaviors of the two room temperature isostructural salts of κ-(BEDT-TTF)₂Hg(SCN)₂X with X = Br, Cl.

1. Introduction

The organic metal κ-(BEDT-TTF)₂Hg(SCN)₂Br belongs to the family of quasi-two-dimensional metallic conductors where the cation–radical layers of a molecule such as BEDT-TTF (bis(ethylenedithio)tetrathiafulvalene) alternate with inorganic anion layers. The holes created in the donor layers provide metallic conductivity inside these layers that is several orders of magnitude higher than the conductivity between the layers [1]. Quasi-two-dimensional molecular conductors have aroused a large amount of interest, primarily due to the abundance of exotic quantum states occurring at low-temperatures. In particular, for κ-(BEDT-TTF)₂Hg(SCN)₂Br, evidence has been found concerning the realization of dipole liquid, spin liquid, and spin glass states; the formation of ferromagnetic polarons; and as a consequence the formation of weak ferromagnetism [2,3,4,5,6,7].

The main reason for this wealth in physical states resides in the crystalline and electronic structure of the conducting donor layers. In organic metals with the general chemical formula of (BEDT-TTF)₂X, the conduction band is one-quarter-filled. However, in metals with κ-type packing, the donor molecules form dimers and the conduction band formally splits into fully filled and half-filled sub-bands [8]; that is, the significant units concerning the electron transfer are the donor dimers. Taking into account that the conduction band in organic metals is quite narrow, of the order of 1000 K [9], the possibility arises for such dimerized metals to have an instability toward a Mott insulating state when decreasing the temperature. Such instability is likely when the condition U/W > 1 is fulfilled (U is the Coulomb repulsion energy on one dimer and W is the kinetic energy of an electron in the conduction band). In that case, below the transition temperature the electrons are generally localized within the dimers, forming an ordered antiferromagnetic system.

A metal–insulator transition was detected in κ-(BEDT-TTF)₂Hg(SCN)₂Br at a temperature of ≈90 K [2]. However, since the dimers form a triangular frustrated lattice, once an electronic localized state below the transition is reached, the long-range spin order is destroyed, leading to the formation at low-temperatures of a spin liquid and other quantum states. The nature of these exotic states was the main object of most of the previous work on this salt. However, the nature of the insulating transition itself, which is the source of the low-temperature exotic states, is not fully understood. In particular, in a previous study [3], a hysteresis was found in the temperature dependence of the susceptibility, suggesting that a first-order transition may take place. At the same time, the absence of changes in the crystal structure during the transition was noted in [2]. In this paper, we provide new information related to the nature of the ≈90 K transition in κ-(BEDT-TTF)₂Hg(SCN)₂Br. In particular, we present the results of X-ray diffraction studies providing evidence for a structural change at the transition temperature. We also report on the electronic structure above and below the transition calculated on the basis of this new information, as well as an analysis of the magnetoresistance behavior, which is in good agreement with the theoretical results.

2. Crystal Structure of κ-(BEDT-TTF)₂Hg(SCN)₂Br before and after the Phase Transition

The κ-(BEDT-TTF)₂Hg(SCN)₂Br crystals were previously studied by our group using an X-ray diffraction analysis [10,11]. The structure was determined and refined in a monoclinic cell with the space group C2/c. Our new conductivity measurements showed that a phase transition occurs below 100 K and that the conductivity regime varies from metallic to semiconducting. In the present work, we determined the crystal structure before and after the ≈90 K transition in order to gain an understanding of the nature of the transition. From 300 K to 100 K, the crystal structure did not experience any change. At temperatures below 100 K, additional weak superstructure reflections appeared in the diffraction field. Above the phase transition temperature, the crystal belongs to the monoclinic system and below it to the triclinic one. The crystal structure of the high-temperature phase can be described in the space group C2/c and the low-temperature phase in P-1. 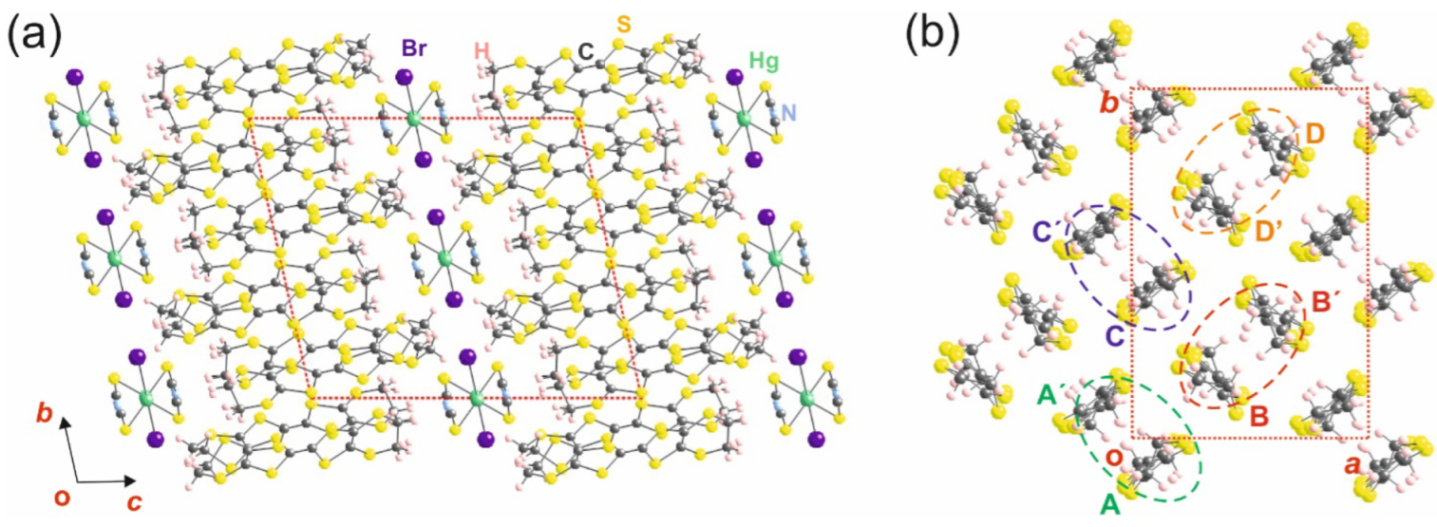The monoclinic cell at 150 K has parameters of a = 36.7651 (19) Å, b = 8.2240 (5) Å, c = 11.6716 (5) Å, α = 90⁰, β = 90.163 (4)⁰, γ = 90⁰, V = 3529.0 (3) ų, Z = 4, and Goof = 1.046, with final R indices of [I > 2σ (I)] R1 = 0.0375, wR2 = 0.0817. The crystal structure of the low-temperature P-1 triclinic cell at 80 K (Figure 1a) can be described with the following parameters: a = 11.6613 (6) Å, b = 16.3444 (6) Å, c = 18.7804 (9) Å, α = 102.592 (4)⁰, β = 90.113 (4)⁰, γ = 90.005 (3)⁰, V = 3493.4 (3) ų, Z = 4. The crystal structure below the transition was determined using the direct method and refined using the least squares method in space group P-1, with Goof = 1.011 and final R indices of [I > 2σ (I)] R1 = 0.0336, wR2 = 0.0747. In this case, the number of symmetry-independent BEDT-TTF molecules is four and the unit cell contains eight of them (Figure 1b). The monoclinic cell is related to the triclinic cell of the high-temperature structure by the transition matrix (0 0 -1  0 -2 0   -0.5 0.5 0). Using this transformation, the cell parameters of the 80 K structure lead to the cell parameters a = 36.6575 (17) Å, b = 8.1722 (3) Å, c = 11.6613 (6) Å, α = 90⁰, β = 90.117 (6)⁰, γ = 90⁰ for a monoclinic cell. An attempt was made to determine the low-temperature structure in the space group P1 within the same unit cell. However, this led to a deterioration of the refinement results. In addition, whereas the band structure calculations with the P-1 structure led to results that were easily understandable in terms of the folding of the high-temperature donor layer structure and were in good agreement with the experimental data (see below), those based on the P1 structure led to unreasonable results.

Note that although not shown in Figure 1, half of the ethylidenedithio groups of BEDT-TTF (i.e., those not facing the Br atoms, which strongly interact with the hydrogen atoms of the donor) exhibit disorder in both the high- and low-temperature structures. The disorder degree is not very influenced by the transition if we take into account the effect of the thermal contraction (58/42% at 150 K and 68/31% at 80 K). The internal structure of the anions is not substantially altered by the distortion, except for the decrease in symmetry. A slight change of the Hg-N distance from 2.754 (150 K) to 2.739/2.728 Å (80 K) as well as variations in the C-N (from 1.154 (150 K) to 1.114 Å (80 K) and C-S (from 1.667 (150 K) to 1.701 Å (80 K) bonds of the SCN group are the more significant changes detected.

The main structural features controlling the different transport properties of the high- and low-temperature structures concern the internal structure of the donor layers. The high-temperature crystal structure contains two symmetry-equivalent donor layers [10,11], but as shown in Figure 1a, there is only one after the phase transition. This layer (Figure 1b) is simply the usual one for κ-phases but is doubled along the b-direction. The repeat unit of the layer contains eight donors making four dimers (AA’, BB’, CC’, and DD’, shown with different colors in Figure 1b), although only three of them are different, AA’, CC’, and BB’= DD’ (see

Table 1. Central C = C bond lengths for the different BEDT-TTF donors in the low- and high-temperature structures of κ-(BEDT-TTF)₂Hg(SCN)₂Br (in Å) (see Figure 1b for the labeling).

Donor Molecule	Low-Temperature Structure (80 K)	High-Temperature Structure (150 K)
A	1.357	1.357
A’	1.357	1.357
C	1.386	1.357 (CC’ = AA’)
C’	1.386	1.357 (CC’ = AA’)
B	1.358	1.357
B’	1.367	1.357
D	1.358	1.357 (DD’ = BB’)
D’	1.367	1.357 (DD’ = BB’)

). In the usual κ-phases, the repeat unit of the layer contains only two dimers, which can be equivalent or not. The central C = C bond lengths of the four donor molecules (see Figure 1b for the labeling) are reported in Table 1, together with those for the high-temperature structure. Note that in the high-temperature structure, the two dimers are equivalent and contain just one type of donor, while as mentioned above, in the low-temperature structure there are three different types of dimers. One of the dimers in the high-temperature structure becomes a dimer containing two different donors in the low-temperature structure (for instance, BB’). There are two equivalent dimers of this type (i.e., BB’ = DD’). In addition, the other dimer of the high-temperature structure leads to two different symmetrical dimers with equivalent donors (AA’ and CC’) in the low-temperature structure. The short S…S intra-dimer contacts for the three different dimers of the 80 K structure are very similar; in all dimers there are two contacts of ~3.68 Å and two of ~3.87 Å. Thus, according to the crystal structure analysis, the structural changes brought about by the transition seem to be mostly located in the donor layers (i.e., the inner C = C bond lengths of the donors). The non-equivalence between symmetrical dimers (AA’ and CC’) or between the two donors of an unsymmetrical dimer (BB’ = DD’) leads to the opening of gaps in the electronic structure, which are at the origin of the difference transport properties.

3. Resistance and Magnetoresistance

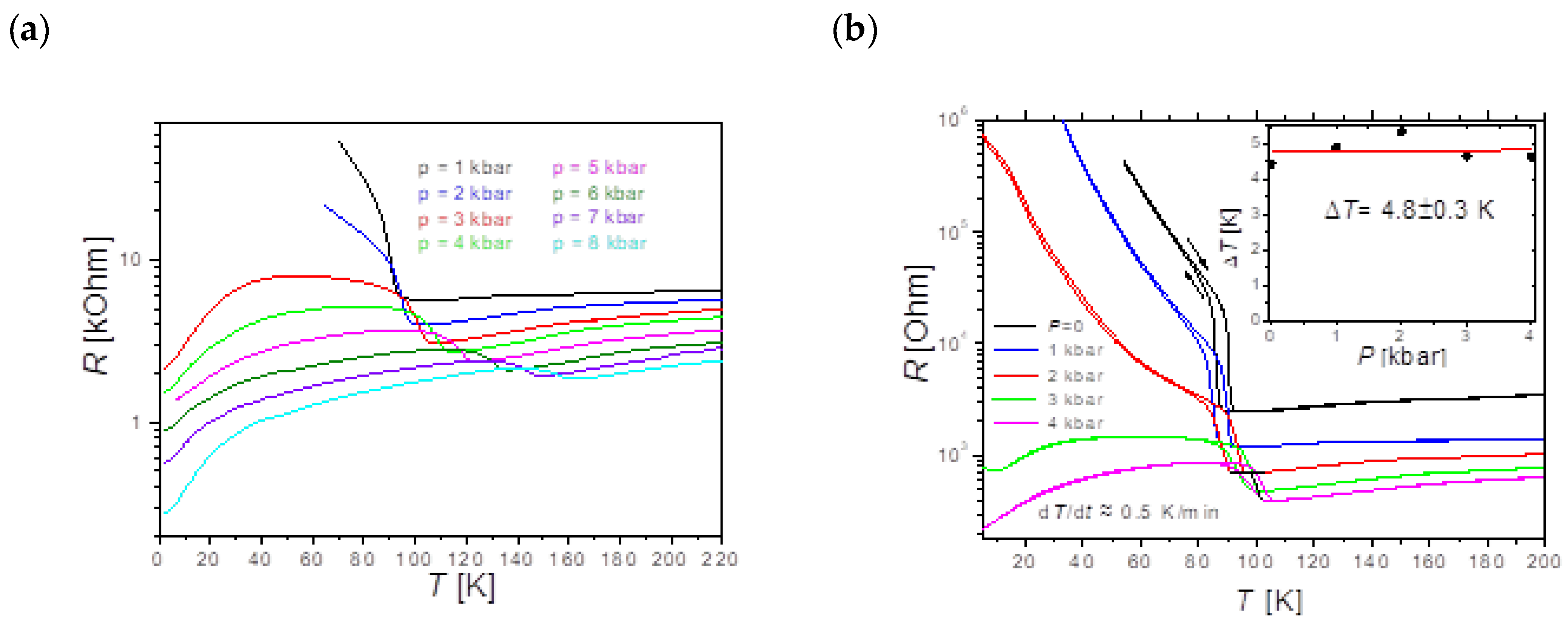
Figure 2a,b show the temperature dependences of the interlayer resistance in κ-(BEDT-TTF)₂Hg(SCN)₂Br at different pressures for two different samples. At ambient pressure and T_MI ≈ 90 K, a pronounced metal–insulator transition is observed. It can be clearly seen (Figure 2b) that the transition occurs with a noticeable hysteresis with a width ΔT = (4.8 ± 0.3) K, which is almost pressure-independent. 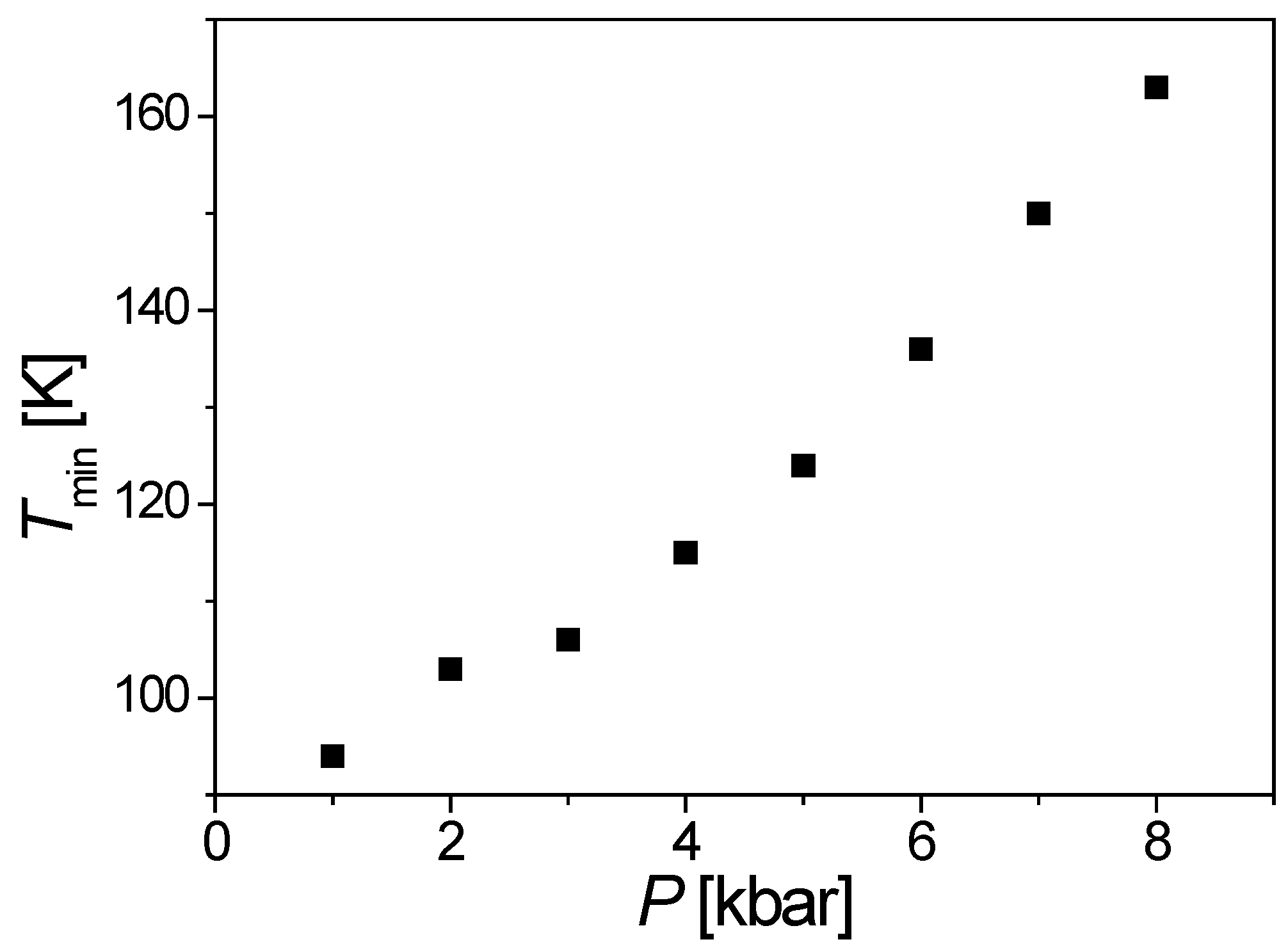The onset of the transition, defined as the temperature of the minimum on the temperature dependence, shifts with increasing pressure toward high temperatures and does not disappear completely up to the maximum available pressure of p = 8 kbar. The dependence of the shift of the beginning of the transition with the pressure in the cooling mode is reported in Figure 3. At the same time, the increase in resistance upon cooling below the transition temperature is suppressed by pressure in such a way that even at a pressure of p = 3 kbar, the “metallic” behavior of the resistance at low temperatures is quite pronounced. A further increase in pressure enhances this behavior.

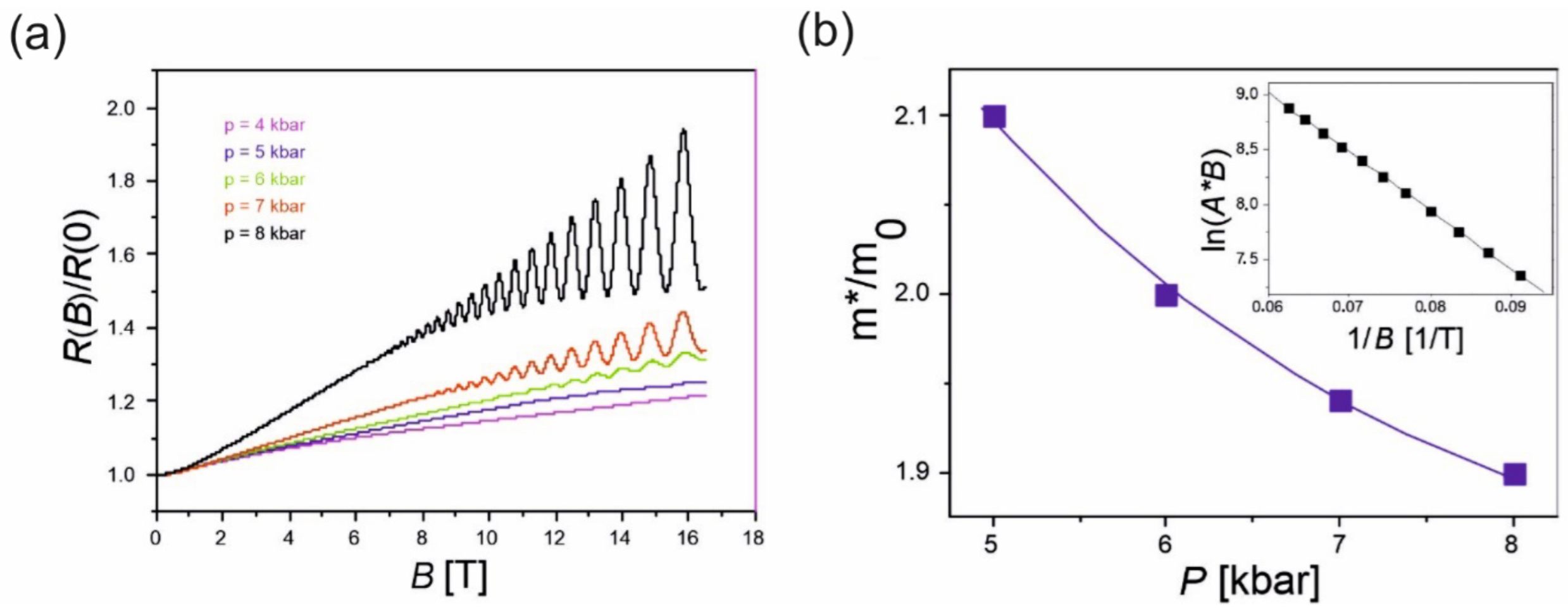
Figure 4a shows the field dependences of the magnetoresistance R(B)/R(0) in κ-(BEDT-TTF)₂Hg(SCN)₂Br at various pressures. At pressures above 4 kbar, Shubnikov–de Haas oscillations were observed with a frequency F ≈ 240 T, which hardly change with increasing pressure. At the same time, the value of the non-oscillating part of the magnetoresistance and the amplitude of the oscillations showed noticeable increases with pressure. The pressure dependence of the cyclotron mass associated with the observed oscillations is shown in Figure 4b. The cyclotron mass decreases by about 10% when the pressure changes from 5 to 8 kbar. The inset to the figure shows the dependence of the oscillation amplitude on the magnetic field (Dingle plot) in the coordinates that make it possible to estimate the Dingle temperature (T_D ≈ 1.5 K at p = 8 kbar). It should be noted that the dependence presented does not deviate from the Lifshitz–Kosevich model for fields up to 16.5 T, and the Dingle temperature within good accuracy does not depend on the pressure.

4. Band Structure Calculations

The calculated band structure for the donor lattice in the low-temperature structure of κ-(BEDT-TTF)₂Hg(SCN)₂Br is shown in Figure 5a. The eight bands are mostly built from the HOMO (highest occupied molecular orbital) of BEDT-TTF, and because of the stoichiometry, two of these bands should be empty. Since the second and third bands from the top overlap, the salt is predicted to be metallic below the phase transition (see below). The calculated Fermi surface (FS) is reported in Figure 5b and contains two contributions: first, elongated bone-like electron pockets with a cross-sectional area of 9.4% of the Brillouin zone (BZ); second, two boomerang-like hole pockets with a cross sectional area of 4.6% for each of them, which either touch or very slightly superpose at the M point. Strictly speaking, these two pockets very slightly interact, leading to a pocket with an area of 9.2% and another very small one at M with an area of 0.2%. However, as it is clear from Figure 5b (see lines Γ-M and Γ-S), a minute change in the structure could suppress the overlap and lead to a single hole pocket with an area of 9.4%. This FS can be described as resulting from the superposition and hybridization of a series of ellipses centered at the Y point. This is a surprising result because the FS of the κ-phases usually results from the superposition and hybridization of a series of pseudo-circles centered at the Γ point.

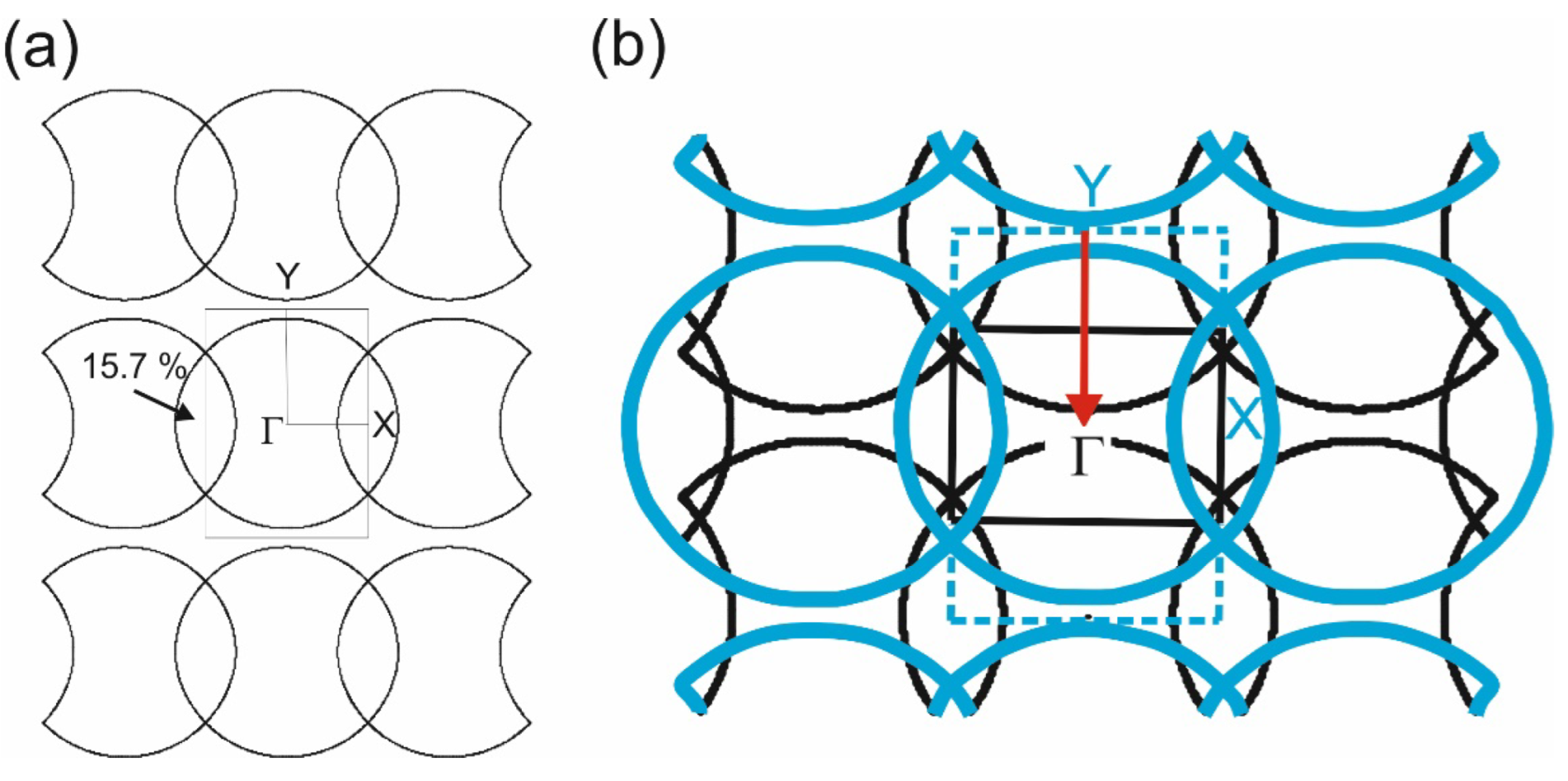
In order to understand this unusual shape, we also calculated the FS for the high-temperature structure (see Figure 6a). This FS is the expected one for the κ-phase; it results from the superposition of a series of circles centered at the Γ point with a cross-sectional area of 100% of the BZ. Because of the superposition, closed pockets with a cross-section of 15.7% around the X point are generated. Note that the a- and c-directions are interchanged with respect to those in the low-temperature structure, but we keep the same labelling for the high- and low-temperature structures in order to facilitate the comparison. The FSs for the donor layers of the high- (Figure 6a) and low-temperature (Figure 5b) structures can be easily related if it is taken into account that the b parameter of the crystal structure practically doubles when going from the high- to the low-temperature structures. Thus, the FS of the low-temperature structure should simply result from a folding of the high-temperature one. This process is schematically illustrated in Figure 6b. The FS of the high-temperature structure and the BZ are shown in blue. Because the new BZ of the low-temperature structure is only half the size, half of the high-temperature FS must be translated within the new smaller BZ. Since the b parameter doubles, the folding must be carried out along the b*-direction and consequently the Y point of the original BZ is translated into the Γ point of the new BZ, as schematized by the red arrow in Figure 6b, and the black lines are generated. In that way, the approximate FS of the low-temperature structure is generated (i.e., the black and blue lines of Figure 6b). Finally, because of the lack of symmetry (except for the trivial symmetry of the inversion center), small gaps are opened at the crossing points and the FS of Figure 5b is generated. Thus, because of the doubling of the repeat unit of the donor layers as a result of the dimer differentiation, the FS changes from a superposition of circles to a superposition of ellipses and finally contains closed orbits differing in area and nature before and after the transition.

5. Discussion

The present X-ray diffraction study has shown that when a single crystal of κ-(BEDT-TTF)₂Hg(SCN)₂Br is cooled at a temperature T ≈ 90 K, a structural phase transition occurs, with a change in the crystal structure from monoclinic at T > T_MI to triclinic at T < T_MI. According to our theoretical calculations, the electronic structures of the monoclinic and triclinic lattices are different, but in both cases the system is predicted to be metallic. Thus, the structural transition at T_MI ≈ 90 K should not be accompanied by a change toward an activated conductivity regime and a metal-to-metal transition should indeed occur. The electronic structures of the different types of κ-type salts are consistently well described by the types of calculations employed here [12]. In addition, the overlap between the second and third bands from the top in Figure 5a is substantial. We, thus, believe that it is unlikely that an intrinsic band gap separating the top two bands in Figure 5a from the lower ones opens below the transition. Measurements of the temperature dependence of the resistance confirm the occurrence of a transition, and based on the observation of hysteresis, we propose that this is a first-order transition. However, at temperatures below T_MI and ambient pressure, κ-(BEDT-TTF)₂Hg(SCN)₂Br turns out to be an insulator that is at odds with the results of the band structure calculations (but remember that these are one-electron band structure calculations).

Since the BEDT-TTF molecules in the triclinic phase are still combined into dimers, and consequently the band is formally half-filled, it can be assumed that the U/W ratio can subtly change from <1 to >1 around T < T_MI, so that a Mott transition can interfere with the structural transition. A Mott insulating state is usually suppressed under external pressure, essentially because of a change in W caused by the decrease in the unit cell size. Indeed, as shown in Figure 2a, the behavior of the resistance as a function of temperature below the transition temperature strongly depends on the external pressure. The resistance increase upon cooling at low pressures is gradually suppressed when the pressure increases. At the same time, the transition temperature increases with the pressure. Thus, it seems that at all pressures, at least up to 8 kbar, free and localized electrons may coexist, and the fraction of free electrons increases with increasing pressure.

At 0.5 K and starting from a pressure of p = 5 kbar, magnetoresistance oscillations can be observed (see Figure 4a). The oscillation frequency is F ≈ 240 T, which corresponds to an orbit with a cross-section of approximately 10% of the area of the first BZ in the conducting plane. This is in good agreement with the calculated FS of the low-temperature triclinic cell (see Figure 5b). The increases in magnetoresistance and amplitude of oscillations with increasing pressure (Figure 4a) may indicate an increase in the concentration of free carriers with increasing pressure because of the increase in HOMO–HOMO interactions. Thus, one can probably think of a partial delocalization of electrons and the restoration of the FS of the triclinic phase due to pressure.

The oscillation frequency practically does not change with increasing pressure. An estimate of the cyclotron mass of the electrons associated with quantum oscillations at a pressure of 5 kbar gives a value of m* ≈ 2.1 m₀ (m₀ is the mass of a free electron), which decreases by approximately 10% as the pressure increases to 8 kbar (Figure 4b). Such behavior is typical in the vicinity of the M-I transition and could be due to the mass renormalization by many-body interactions [13]. The decrease could be due to an increase in the concentration of free carriers, and as a consequence a weakening of the electron correlations [13]. The field dependences of the oscillation amplitude in Dingle coordinates for two-dimensional systems (see the example in the inset in Figure 4b) makes it possible to calculate the Dingle temperature. In the present case, T_D ≈ 1.5 K and does not change with pressure. This fact excludes the influence of a change in scattering under pressure over the amplitude of the magnetoresistance oscillations. In addition, a good agreement between the field dependence of the amplitude and the Lifshitz–Kosevich model (Figure 4b) indicates the absence, at least in our range of fields, of the contribution of the incoherent interlayer transfer to the oscillations [14].

Finally, let us note that the suppression of the dielectric state when localized and delocalized electrons coexist at each pressure looks rather unusual. In particular, in the isostructural metal κ-(BEDT-TTF)₂Hg(SCN)₂Cl, the Mott-type transition at T ≈ 30 K shifts under pressure towards lower temperatures and is completely suppressed even at a pressure of 0.7 kbar, where the initial metallic state is completely restored [15,16]. However, in contrast with the present system, the transition is not accompanied by a change in the structure. It is possible that for a more accurate description of the process of stabilization of the metallic state in κ-(BEDT-TTF)₂Hg(SCN)₂Br, it will be necessary to take into account the low-temperature state of the localized electrons in the absence of pressure, called a dipole liquid, characterized by charge distribution fluctuations inside the dimer [5].

6. Methods

6.1. Synthesis

The crystals of κ-(BEDT-TTF)₂Hg(SCN)₂Br were prepared using a technique similar to that described in [17] via the electrocrystallization of BEDT-TTF in the presence of Hg(SCN)₂, [Me₄N]SCN∙1.5 KBr, and dibenzo-18-crown-6 in 1,1,2-trichloroethane at a temperature of 40 °C and a constant current of 0.3 μA [17].

6.2. X-ray Structure Determination

The X-ray diffraction studies of κ-(BEDT-TTF)₂Hg(SCN)₂Br crystals were carried out on an Agilent XCalibur single-crystal diffractometer with an EOS CCD detector in the temperature range of 80–300 K. From 300 to 100 K, the crystal structure did not experience any changes. At temperatures below 100 K, additional weak superstructure reflections appeared in the diffraction field. In the X-ray experiment carried out at 80 K, the diffraction field was limited to a hemisphere. In this way, we avoided the loss of reflections for any choice of unit cell. The hydrogen atoms of ethylene groups were calculated geometrically. All calculations were performed using the SHELXTL software package [18].

6.3. Conductivity Measurements

The resistance and magnetoresistance were measured using the standard four-contact method using a synchronous detector on single-crystal samples with characteristic dimensions of 0.5 × 0.3 × 0.03 mm³. A measuring current with a frequency of 20 Hz, the value of which did not exceed 10 µA, was directed perpendicularly to the conductive layers of the crystal. The sample was mounted in a high-pressure chamber filled with a silicon oil as a pressure medium, which ensured the operation under quasi-hydrostatic conditions up to a pressure of p = 8 kbar at low temperatures. The pressure was controlled through the resistance of the manganin sensor. The measurements were carried out in an insert with ³He pumping, which made it possible to operate in the temperature range from room temperature to 0.5 K. A magnetic field up to 17 T created by a superconducting solenoid was used and was directed normal to the conducting layers along the current direction.

6.4. Band Structure Calculations

The tight-binding band structure calculations were of the extended Hückel type [19]. A modified Wolfsberg–Helmholtz formula was used to calculate the non-diagonal H_μν values [20]. All valence electrons were taken into account in the calculations and the basis set consisted of Slater-type orbitals of double-ζ quality for C 2s and 2p and S 3s and 3p, and of single-ζ quality for H 1s. The ionization potentials, contraction coefficients, and exponents were taken from previous work [21].

7. Concluding Remarks

The crystal structure of the organic quasi-two-dimensional metal κ-(BEDT-TTF)₂Hg(SCN)₂Br was studied before and after the metal-to-insulator transition at T_MI ≈ 90 K, and the evolution of the FS was calculated based on the new data. The behaviors of the resistance and magnetoresistance as a function of both the magnetic field and temperature under external pressures of up to 8 kbar were studied. The main conclusions of this study are as follows:

(1) The κ-(BEDT-TTF)₂Hg(SCN)₂Br undergoes a first-order phase transition at T_MI ≈ 90 K, where the crystal structure changes from monoclinic above T_MI to triclinic below T_MI. The repeat unit of the donor layer below the transition contains twice the number of dimers and the internal structure of these dimers changes;

(2) Band structure calculations have shown that this phase transition can be described on the basis of a folding model that rearranges the FS and suggests a metal–metal transition;

(3) In contrast with the monoclinic high-temperature phase, the metallic state of the triclinic phase is probably unstable to the transition toward a Mott insulating state, which leads to the growth of the resistance when the temperature drops below T_MI ≈ 90 K;

(4) The application of external pressure suppresses the Mott transition and restores the metallic state of the triclinic phase. The frequency of the detected quantum oscillations of the magnetoresistance is in good agreement with the calculated FS for the triclinic phase.

These results provide interesting differences with respect to the physical behavior of the room temperature isostructural κ-(BEDT-TTF)₂Hg(SCN)₂Cl salt.