Dynamic Bloch Chirality and Enhanced Velocities from Spin-Orbit Torque Driven Domain Wall Motion in Thick Magnetic Films
Abstract
1. Introduction
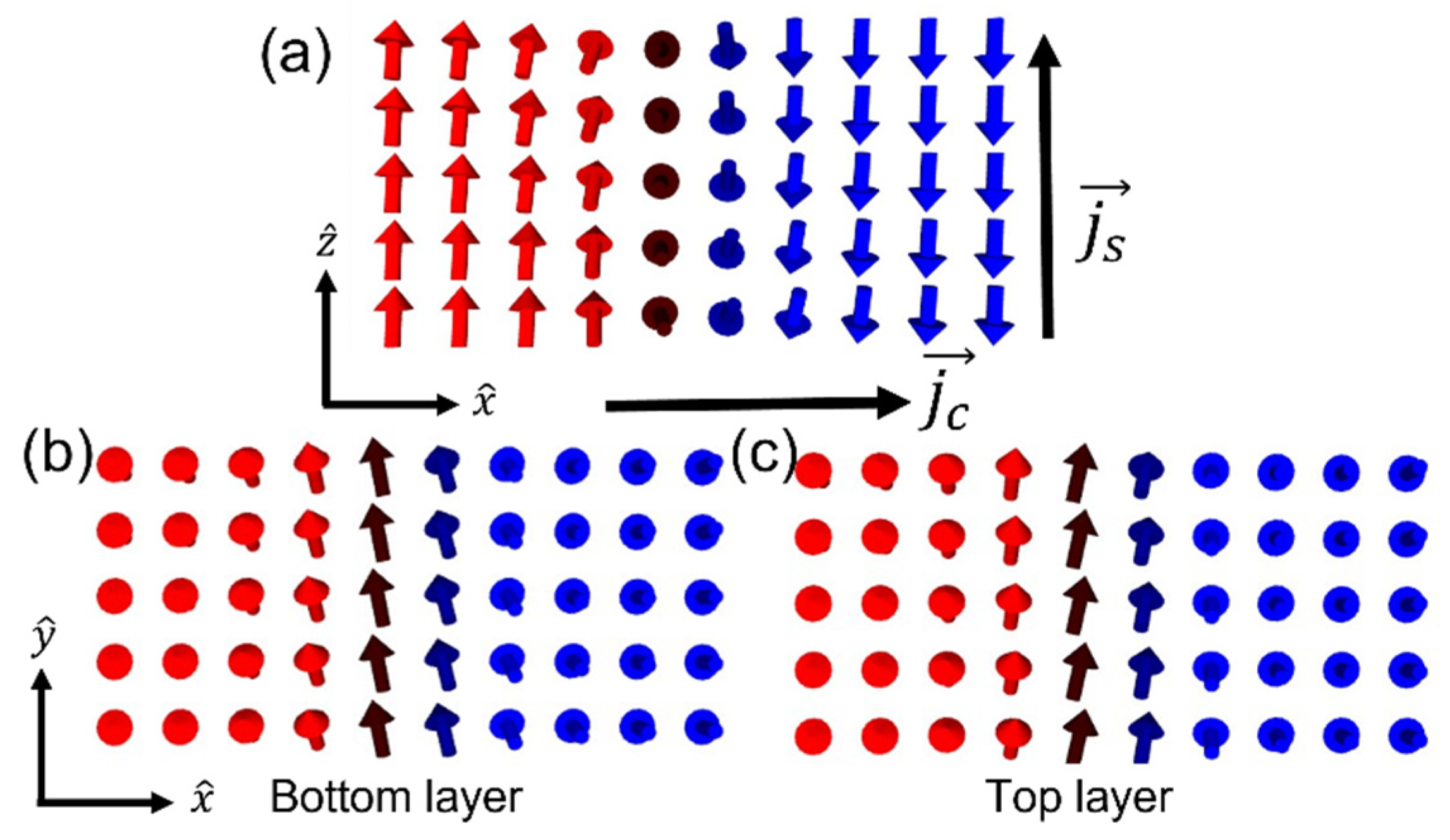
2. Methods
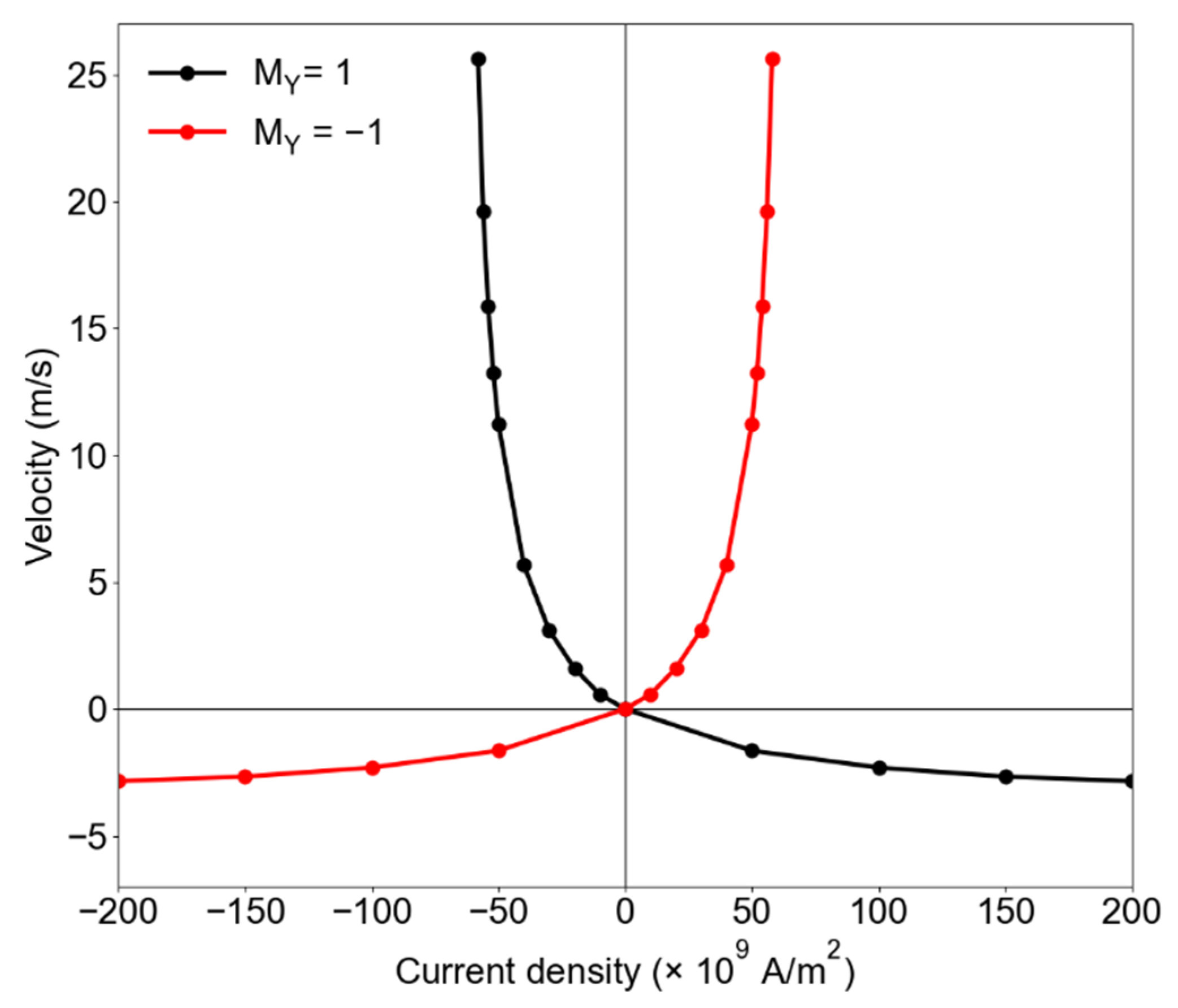
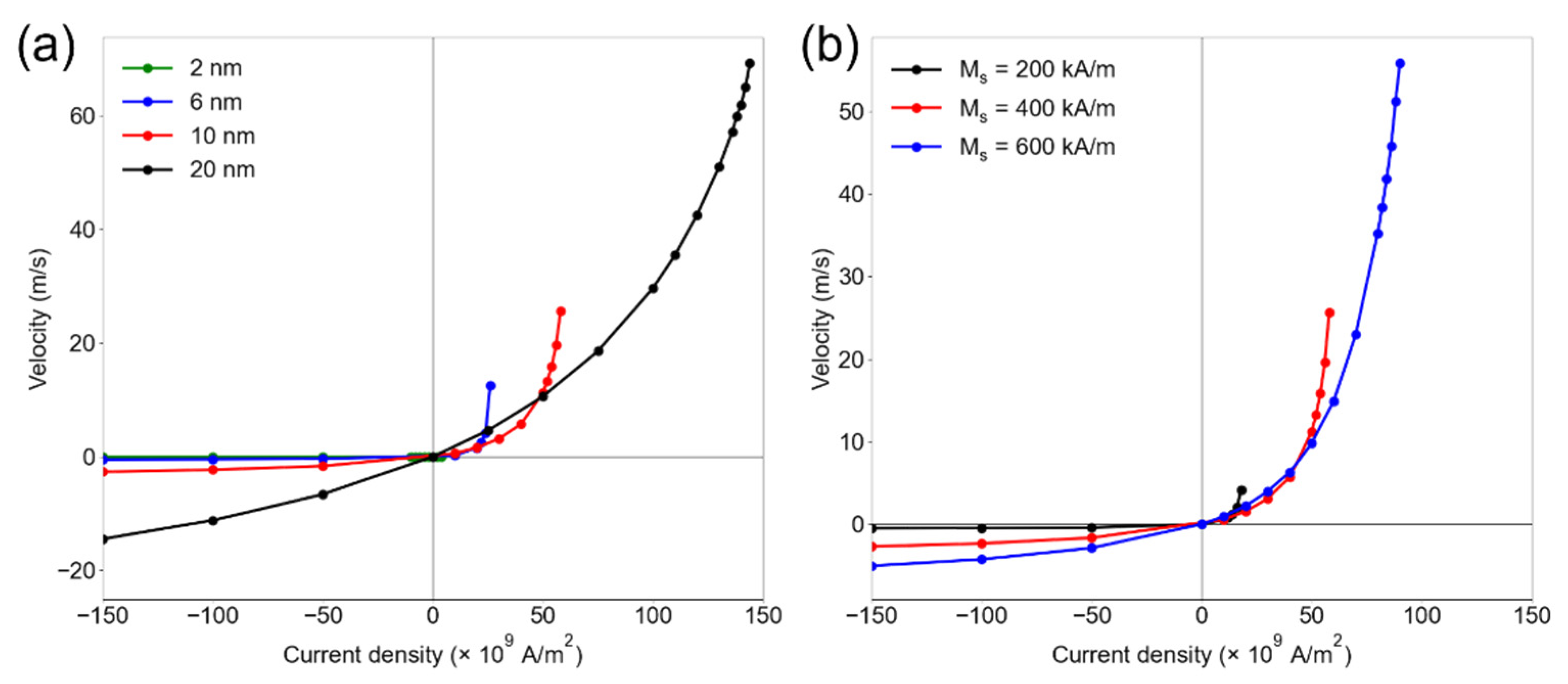
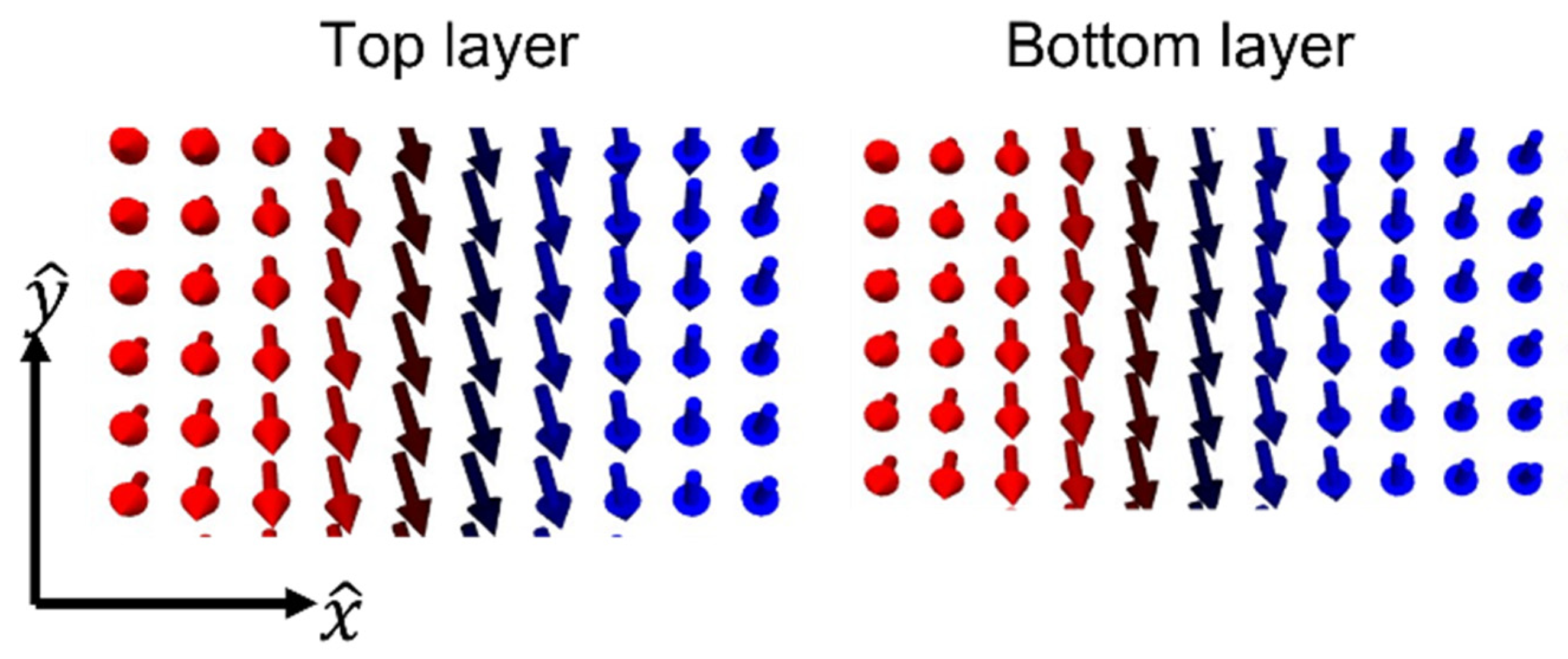
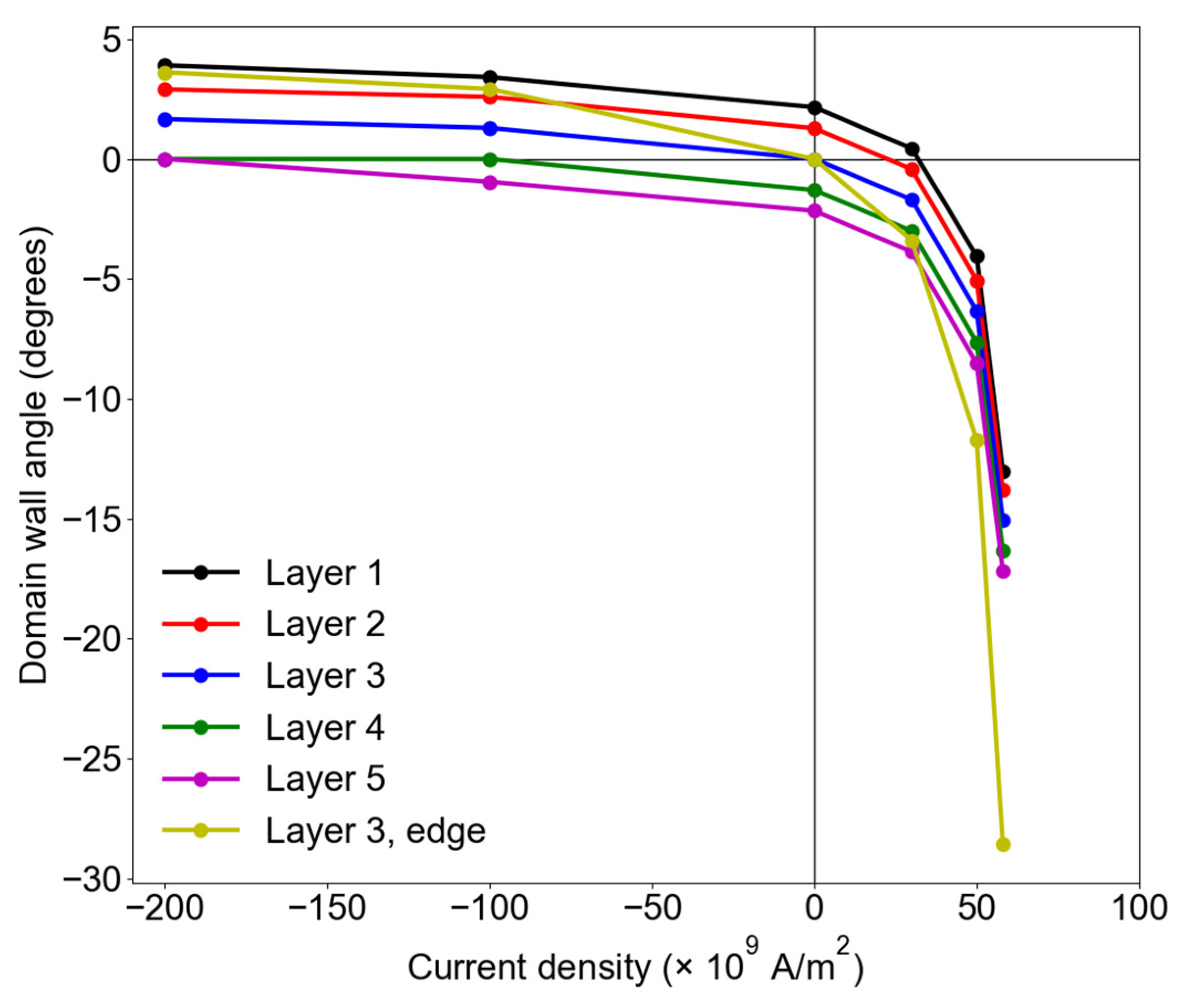
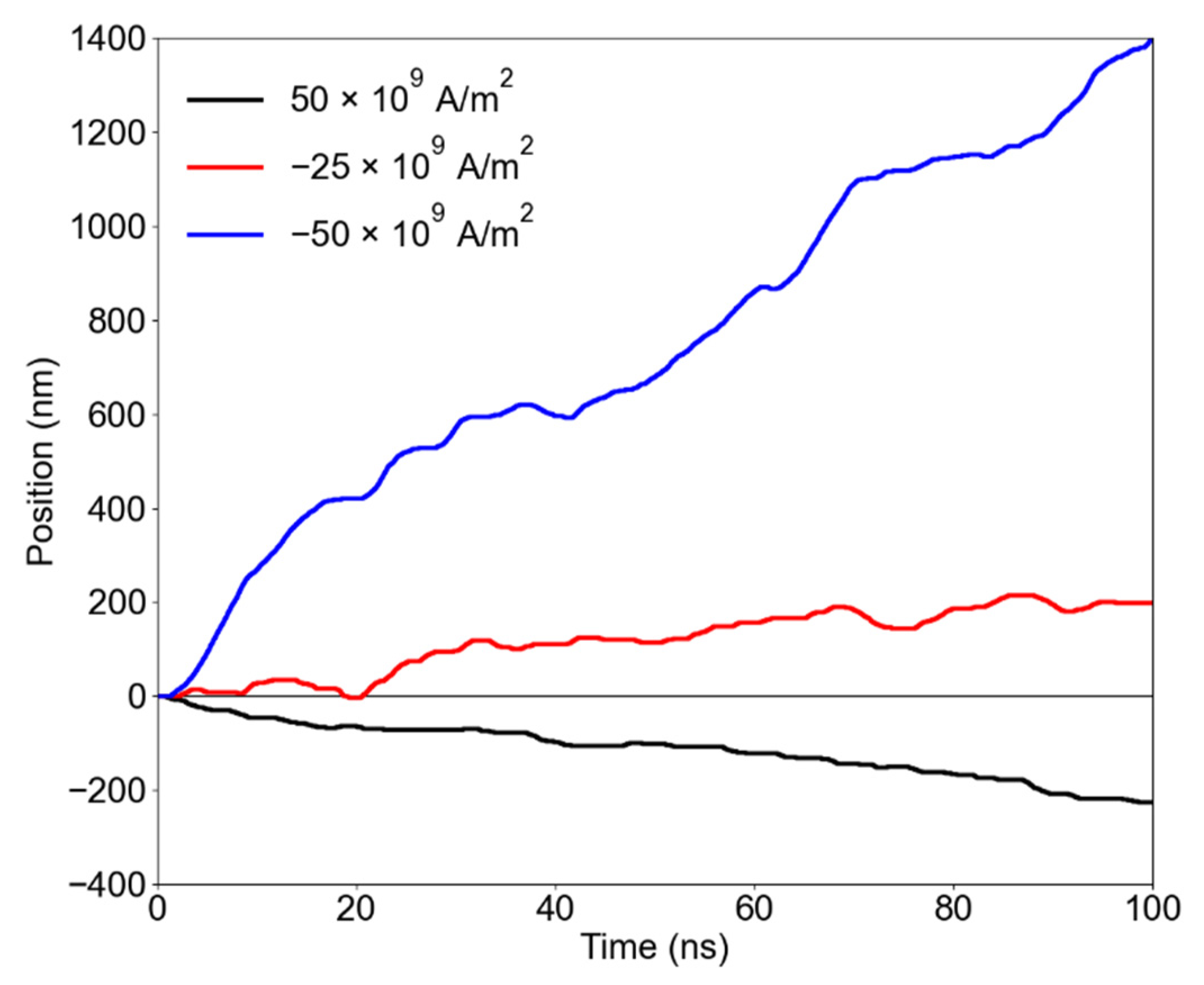
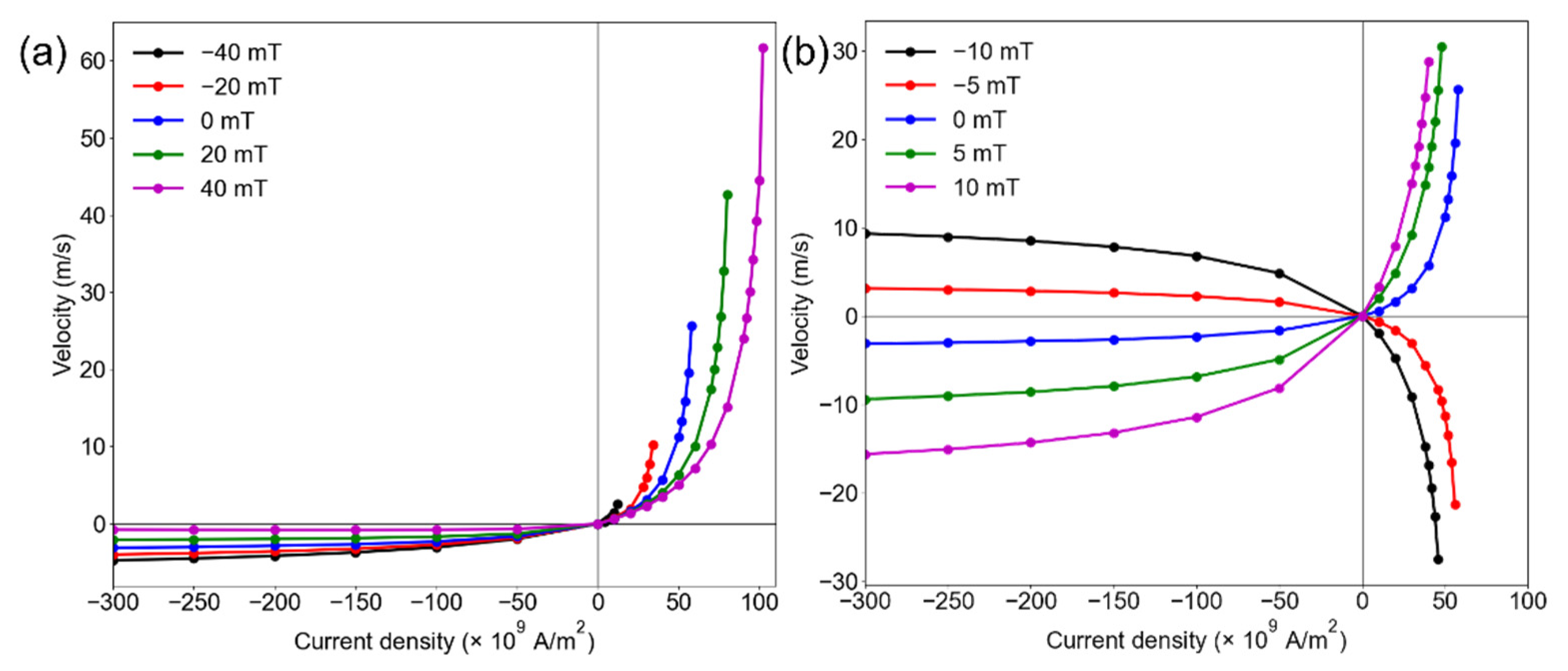
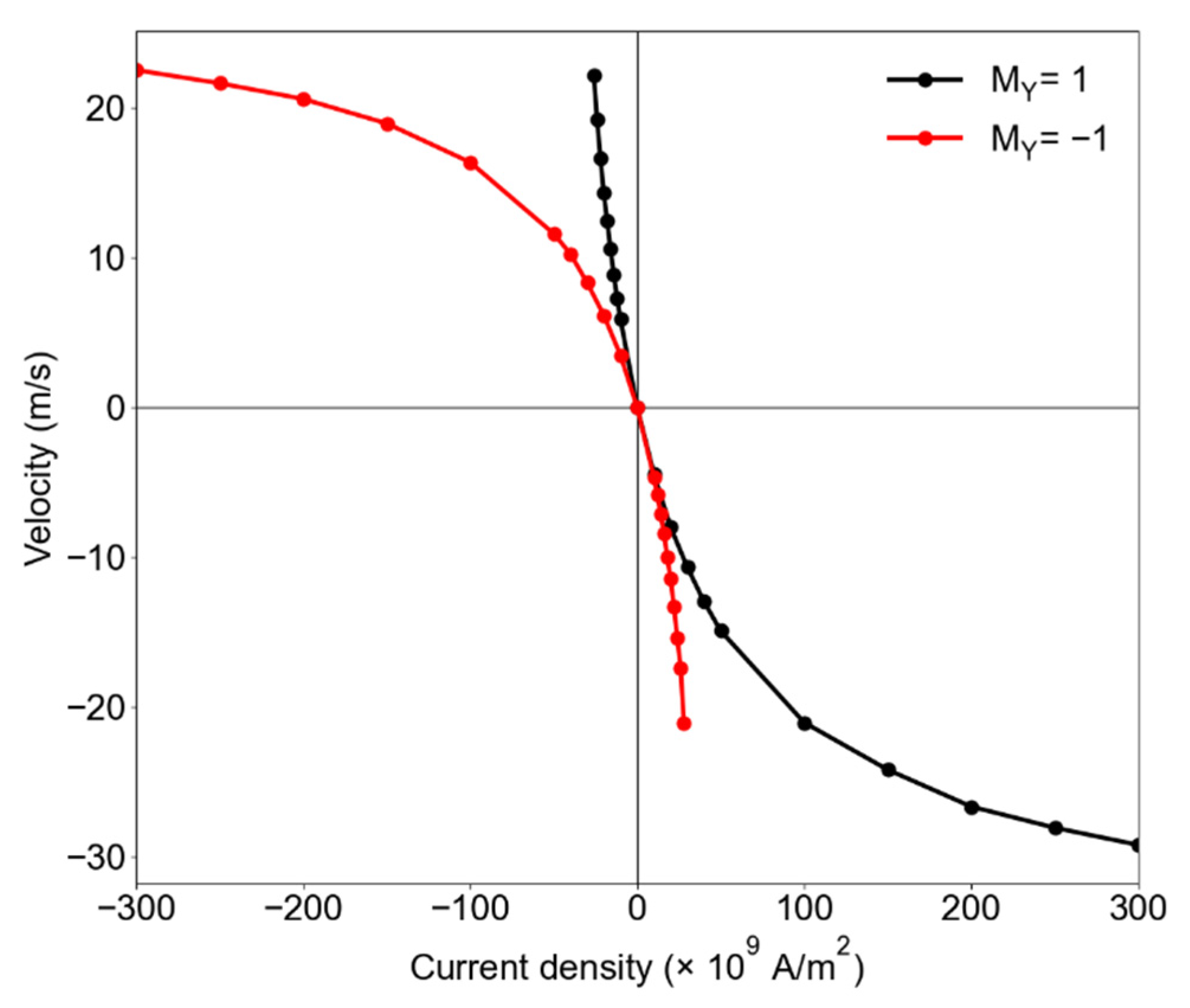
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- You, L.; Sousa, R.C.; Bandiera, S.; Rodmacq, B.; Dieny, B. Co/Ni Multilayers with Perpendicular Anisotropy for Spintronic Device Applications. Appl. Phys. Lett. 2012, 100, 172411. [Google Scholar] [CrossRef]
- Pribiag, V.S.; Krivorotov, I.N.; Fuchs, G.D.; Braganca, P.M.; Ozatay, O.; Sankey, J.C.; Ralph, D.C.; Buhrman, R.A. Magnetic Vortex Oscillator Driven by d.c. Spin-Polarized Current. Nat. Phys. 2007, 3, 498–503. [Google Scholar] [CrossRef]
- Moriyama, T.; Zhou, W.; Seki, T.; Takanashi, K.; Ono, T. Spin-Orbit-Torque Memory Operation of Synthetic Antiferromagnets. Phys. Rev. Lett. 2018, 121, 167202. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Han, X.; Zhao, X.; Dong, Y.; Chen, Y.; Bai, L.; Yan, S.; Tian, Y. Programmable Spin-Orbit Torque Multistate Memory and Spin Logic Cell. ACS Nano 2022, 16, 6878–6885. [Google Scholar] [CrossRef] [PubMed]
- Sato, N.; Xue, F.; White, R.M.; Bi, C.; Wang, S.X. Two-Terminal Spin–Orbit Torque Magnetoresistive Random Access Memory. Nat. Electron. 2018, 1, 508–511. [Google Scholar] [CrossRef]
- Kim, Y.; Fong, X.; Kwon, K.W.; Chen, M.C.; Roy, K. Multilevel Spin-Orbit Torque MRAMs. IEEE Trans. Electron. Devices 2015, 62, 561–568. [Google Scholar] [CrossRef]
- De Orio, R.L.; Ender, J.; Fiorentini, S.; Goes, W.; Selberherr, S.; Sverdlov, V. Optimization of a Spin-Orbit Torque Switching Scheme Based on Micromagnetic Simulations and Reinforcement Learning. Micromachines 2021, 12, 443. [Google Scholar] [CrossRef]
- Yang, S.; Tan, M.; Yu, T.; Li, X.; Wang, X.; Zhang, J. Hybrid Reduced Graphene Oxide with Special Magnetoresistance for Wireless Magnetic Field Sensor. Nanomicro Lett. 2020, 12, 69. [Google Scholar] [CrossRef] [PubMed]
- Woo, S.; Song, K.M.; Zhang, X.; Zhou, Y.; Ezawa, M.; Finizio, S.; Raabe, J.; Choi, J.W.; Min, B.-C.; Koo, H.C.; et al. Current-Driven Dynamics and Inhibition of the Skyrmion Hall Effect of Ferrimagnetic Skyrmions in GdFeCo Films. Nat. Commun. 2018, 9, 959. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Zhang, X.; Yu, G.; Zhang, W.; Jungfleisch, M.B.; Pearson, J.E.; Heinonen, O.; Wang, K.L.; Zhou, Y.; Hoffmann, A.; et al. Direct Observation of the Skyrmion Hall Effect. Nat. Phys. 2016, 13, 162. [Google Scholar] [CrossRef]
- Kanazawa, N.; Kubota, M.; Tsukazaki, A.; Kozuka, Y.; Takahashi, K.S.; Kawasaki, M.; Ichikawa, M.; Kagawa, F.; Tokura, Y. Discretized Topological Hall Effect Emerging from Skyrmions in Constricted Geometry. Phys. Rev. B 2015, 91, 041122. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, D.; Wu, Y.; Yang, Y.; Yu, J.; Ramaswamy, R.; Mishra, R.; Shi, S.; Elyasi, M.; Teo, K.-L.; et al. Room Temperature Magnetization Switching in Topological Insulator-Ferromagnet Heterostructures by Spin-Orbit Torques. Nat. Commun. 2017, 8, 1364. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhu, D.; Yang, Y.; Lee, K.; Mishra, R.; Go, G.; Oh, S.; Kim, D.; Cai, K.; Liu, E.; et al. Magnetization Switching by Magnon-Mediated Spin Torque through an Antiferromagnetic Insulator. Science 2019, 366, 1125–1128. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Bang, D.; Mishra, R.; Ramaswamy, R.; Oh, J.H.; Park, H.-J.; Jeong, Y.; van Thach, P.; Lee, D.-K.; Go, G.; et al. Long Spin Coherence Length and Bulk-like Spin–Orbit Torque in Ferrimagnetic Multilayers. Nat. Mater. 2019, 18, 29–34. [Google Scholar] [CrossRef]
- Benitez, M.J.; Hrabec, A.; Mihai, P.; Moore, T.; Burnell, G.; McGrouther, D.; Marrows, C.H.; McVitie, S. Magnetic Microscopy and Topological Stability of Homochiral Néel Domain Walls in a Pt/Co/AlOx Trilayer. Nat. Commun. 2015, 6, 8957. [Google Scholar] [CrossRef] [PubMed]
- Hrabec, A.; Porter, N.A.; Wells, A.; Benitez, M.J.; Burnell, G.; McVitie, S.; McGrouther, D.; Moore, T.A.; Marrows, C.H. Measuring and Tailoring the Dzyaloshinskii-Moriya Interaction in Perpendicularly Magnetized Thin Films. Phys. Rev. B 2014, 90, 020402. [Google Scholar] [CrossRef]
- Yoshimura, Y.; Kim, K.J.; Taniguchi, T.; Tono, T.; Ueda, K.; Hiramatsu, R.; Moriyama, T.; Yamada, K.; Nakatani, Y.; Ono, T. Soliton-like Magnetic Domain Wall Motion Induced by the Interfacial Dzyaloshinskii–Moriya Interaction. Nat. Phys. 2015, 12, 157–161. [Google Scholar] [CrossRef]
- Thiaville, A.; Rohart, S.; Jué, É.; Cros, V.; Fert, A. Dynamics of Dzyaloshinskii Domain Walls in Ultrathin Magnetic Films. Europhys. Lett. 2012, 100, 57002. [Google Scholar] [CrossRef]
- Liu, L.; Lee, O.J.; Gudmundsen, T.J.; Ralph, D.C.; Buhrman, R.A. Current-Induced Switching of Perpendicularly Magnetized Magnetic Layers Using Spin Torque from the Spin Hall Effect. Phys. Rev. Lett. 2012, 109, 096602. [Google Scholar] [CrossRef]
- Miron, I.M.; Garello, K.; Gaudin, G.; Zermatten, P.J.; Costache, M.; Auffret, S.; Bandiera, S.; Rodmacq, B.; Schuhl, A.; Gambardella, P. Perpendicular Switching of a Single Ferromagnetic Layer Induced by In-Plane Current Injection. Nature 2011, 476, 189–193. [Google Scholar] [CrossRef]
- Liu, L.; Pai, C.F.; Li, Y.; Tseng, H.W.; Ralph, D.C.; Buhrman, R.A. Spin-Torque Switching with the Giant Spin Hall Effect of Tantalum. Science 2012, 336, 555–558. [Google Scholar] [CrossRef] [PubMed]
- Estevez, G.; Cui, B.; Zhu, Z.; Wu, C.; Guo, X.; Nie, Z.; Wu, H.; Guo, T.; Chen, P.; Zheng, D.; et al. Comprehensive Study of the Current-Induced Spin-Orbit Torque Perpendicular Effective Field in Asymmetric Multilayers. Nanomaterials 2022, 12, 1887. [Google Scholar] [CrossRef]
- Montoya, S.A.; Couture, S.; Chess, J.J.; Lee, J.C.T.; Kent, N.; Im, M.Y.; Kevan, S.D.; Fischer, P.; McMorran, B.J.; Roy, S.; et al. Resonant Properties of Dipole Skyrmions in Amorphous Fe/Gd Multilayers. Phys. Rev. B 2017, 95, 224405. [Google Scholar] [CrossRef]
- Montoya, S.A.; Couture, S.; Chess, J.J.; Lee, J.C.T.; Kent, N.; Henze, D.; Sinha, S.K.; Im, M.-Y.; Kevan, S.D.; Fischer, P.; et al. Tailoring Magnetic Energies to Form Dipole Skyrmions and Skyrmion Lattices. Phys. Rev. B 2017, 95, 024415. [Google Scholar] [CrossRef]
- Legrand, W.; Chauleau, J.-Y.; Maccariello, D.; Reyren, N.; Collin, S.; Bouzehouane, K.; Jaouen, N.; Cros, V.; Fert, A. Hybrid Chiral Domain Walls and Skyrmions in Magnetic Multilayers. Sci. Adv. 2018, 4, eaat0415. [Google Scholar] [CrossRef]
- Garlow, J.A.; Pollard, S.D.; Beleggia, M.; Dutta, T.; Yang, H.; Zhu, Y. Quantification of Mixed Bloch-Néel Topological Spin Textures Stabilized by the Dzyaloshinskii-Moriya Interaction in Co/Pd Multilayers. Phys. Rev. Lett. 2019, 122, 237201. [Google Scholar] [CrossRef]
- Banerjee, C.; Gruszecki, P.; Klos, J.W.; Hellwig, O.; Krawczyk, M.; Barman, A. Magnonic Band Structure in a Co/Pd Stripe Domain System Investigated by Brillouin Light Scattering and Micromagnetic Simulations. Phys. Rev. B 2017, 96, 024421. [Google Scholar] [CrossRef]
- Chauleau, J.-Y.; Legrand, W.; Reyren, N.; Maccariello, D.; Collin, S.; Popescu, H.; Bouzehouane, K.; Cros, V.; Jaouen, N.; Fert, A. Chirality in Magnetic Multilayers Probed by the Symmetry and the Amplitude of Dichroism in X-Ray Resonant Magnetic Scattering. Phys. Rev. Lett. 2018, 120, 037202. [Google Scholar] [CrossRef]
- Pollard, S.D.; Garlow, J.A.; Kim, K.W.; Cheng, S.; Cai, K.; Zhu, Y.; Yang, H. Bloch Chirality Induced by an Interlayer Dzyaloshinskii-Moriya Interaction in Ferromagnetic Multilayers. Phys. Rev. Lett. 2020, 125, 227203. [Google Scholar] [CrossRef]
- Yoon, J.; Lee, S.W.; Kwon, J.H.; Lee, J.M.; Son, J.; Qiu, X.; Lee, K.J.; Yang, H. Anomalous Spin-Orbit Torque Switching Due to Field-like Torque–Assisted Domain Wall Reflection. Sci. Adv. 2017, 3, e1603099. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; van Waeyenberge, B. The Design and Verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; de Wiele, B. van MUMAX: A New High-Performance Micromagnetic Simulation Tool. J. Magn. Magn. Mater. 2011, 323, 2585–2591. [Google Scholar] [CrossRef]
- Kim, D.H.; Haruta, M.; Ko, H.W.; Go, G.; Park, H.J.; Nishimura, T.; Kim, D.Y.; Okuno, T.; Hirata, Y.; Futakawa, Y.; et al. Bulk Dzyaloshinskii–Moriya Interaction in Amorphous Ferrimagnetic Alloys. Nat. Mater. 2019, 18, 685–690. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, Y.; Lopez-Dominguez, V.; Sánchez-Tejerina, L.; Shi, J.; Feng, X.; Chen, L.; Wang, Z.; Zhang, Z.; Zhang, K.; et al. Field-Free Spin-Orbit Torque-Induced Switching of Perpendicular Magnetization in a Ferrimagnetic Layer with a Vertical Composition Gradient. Nat. Commun. 2021, 12, 4555. [Google Scholar] [CrossRef]
- Xie, X.; Zhao, X.; Dong, Y.; Qu, X.; Zheng, K.; Han, X.; Han, X.; Fan, Y.; Bai, L.; Chen, Y.; et al. Controllable Field-Free Switching of Perpendicular Magnetization through Bulk Spin-Orbit Torque in Symmetry-Broken Ferromagnetic Films. Nat. Commun. 2021, 12, 2473. [Google Scholar] [CrossRef] [PubMed]
- Jamali, M.; Narayanapillai, K.; Qiu, X.; Loong, L.M.; Manchon, A.; Yang, H. Spin-Orbit Torques in Co/Pd Multilayer Nanowires. Phys. Rev. Lett. 2013, 111, 246602. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Liang, J.; Bi, K.; Zhao, L.; Bai, H.; Cui, Q.; Zhou, H.A.; Bai, H.; Feng, H.; Song, W.; et al. Quantifying the Dzyaloshinskii-Moriya Interaction Induced by the Bulk Magnetic Asymmetry. Phys. Rev. Lett. 2022, 128, 167202. [Google Scholar] [CrossRef]
- Brown, W.F. Thermal Fluctuations of a Single-Domain Particle. J. Appl. Phys. 2004, 34, 1319. [Google Scholar] [CrossRef]
- Oh, Y.-W.; Chris Baek, S.; Kim, Y.M.; Lee, H.Y.; Lee, K.-D.; Yang, C.-G.; Park, E.-S.; Lee, K.-S.; Kim, K.-W.; Go, G.; et al. Field-Free Switching of Perpendicular Magnetization through Spin–Orbit Torque in Antiferromagnet/Ferromagnet/Oxide Structures. Nat. Nanotechnol. 2016, 11, 878–884. [Google Scholar] [CrossRef] [PubMed]
- Ryu, K.-S.; Thomas, L.; Yang, S.-H.; Parkin, S. Chiral Spin Torque at Magnetic Domain Walls. Nat. Nanotechnol. 2013, 8, 527–533. [Google Scholar] [CrossRef] [PubMed]
- Litzius, K.; Leliaert, J.; Bassirian, P.; Rodrigues, D.; Kromin, S.; Lemesh, I.; Zazvorka, J.; Lee, K.J.; Mulkers, J.; Kerber, N.; et al. The Role of Temperature and Drive Current in Skyrmion Dynamics. Nat. Electron. 2020, 3, 30–36. [Google Scholar] [CrossRef]
- Ngo, D.T.; Ikeda, K.; Awano, H. Direct Observation of Domain Wall Motion Induced by Low-Current Density in TbFeCo Wires. Appl. Phys. Express 2011, 4, 093002. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staggers, T.L.; Pollard, S.D. Dynamic Bloch Chirality and Enhanced Velocities from Spin-Orbit Torque Driven Domain Wall Motion in Thick Magnetic Films. Magnetochemistry 2022, 8, 119. https://doi.org/10.3390/magnetochemistry8100119
Staggers TL, Pollard SD. Dynamic Bloch Chirality and Enhanced Velocities from Spin-Orbit Torque Driven Domain Wall Motion in Thick Magnetic Films. Magnetochemistry. 2022; 8(10):119. https://doi.org/10.3390/magnetochemistry8100119
Chicago/Turabian StyleStaggers, Trae Lawrence, and Shawn David Pollard. 2022. "Dynamic Bloch Chirality and Enhanced Velocities from Spin-Orbit Torque Driven Domain Wall Motion in Thick Magnetic Films" Magnetochemistry 8, no. 10: 119. https://doi.org/10.3390/magnetochemistry8100119
APA StyleStaggers, T. L., & Pollard, S. D. (2022). Dynamic Bloch Chirality and Enhanced Velocities from Spin-Orbit Torque Driven Domain Wall Motion in Thick Magnetic Films. Magnetochemistry, 8(10), 119. https://doi.org/10.3390/magnetochemistry8100119





