Manipulation of Time- and Frequency-Domain Dynamics by Magnon-Magnon Coupling in Synthetic Antiferromagnets
Abstract
:1. Introduction
2. Simulation Model
3. Results and Discussion
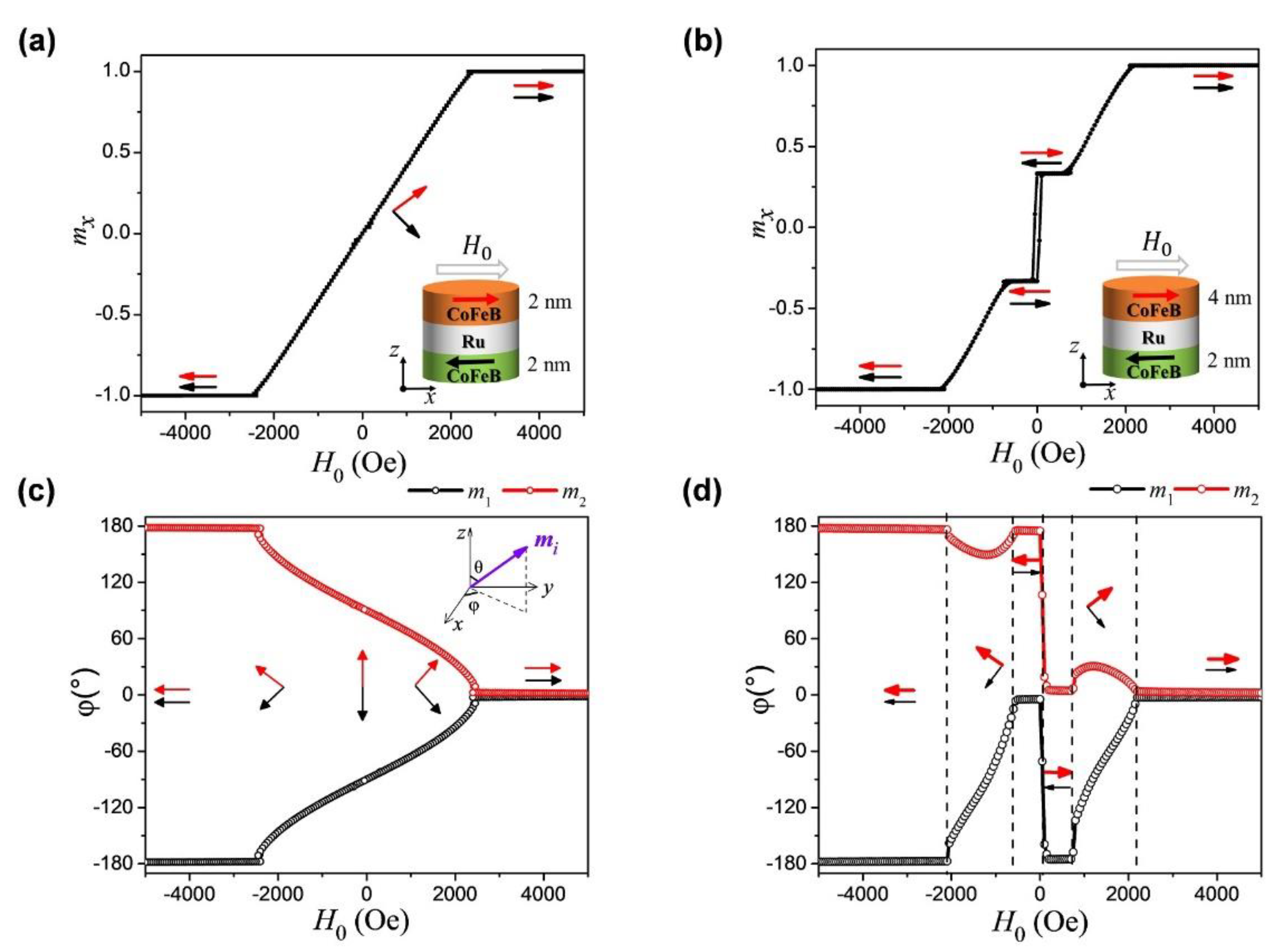
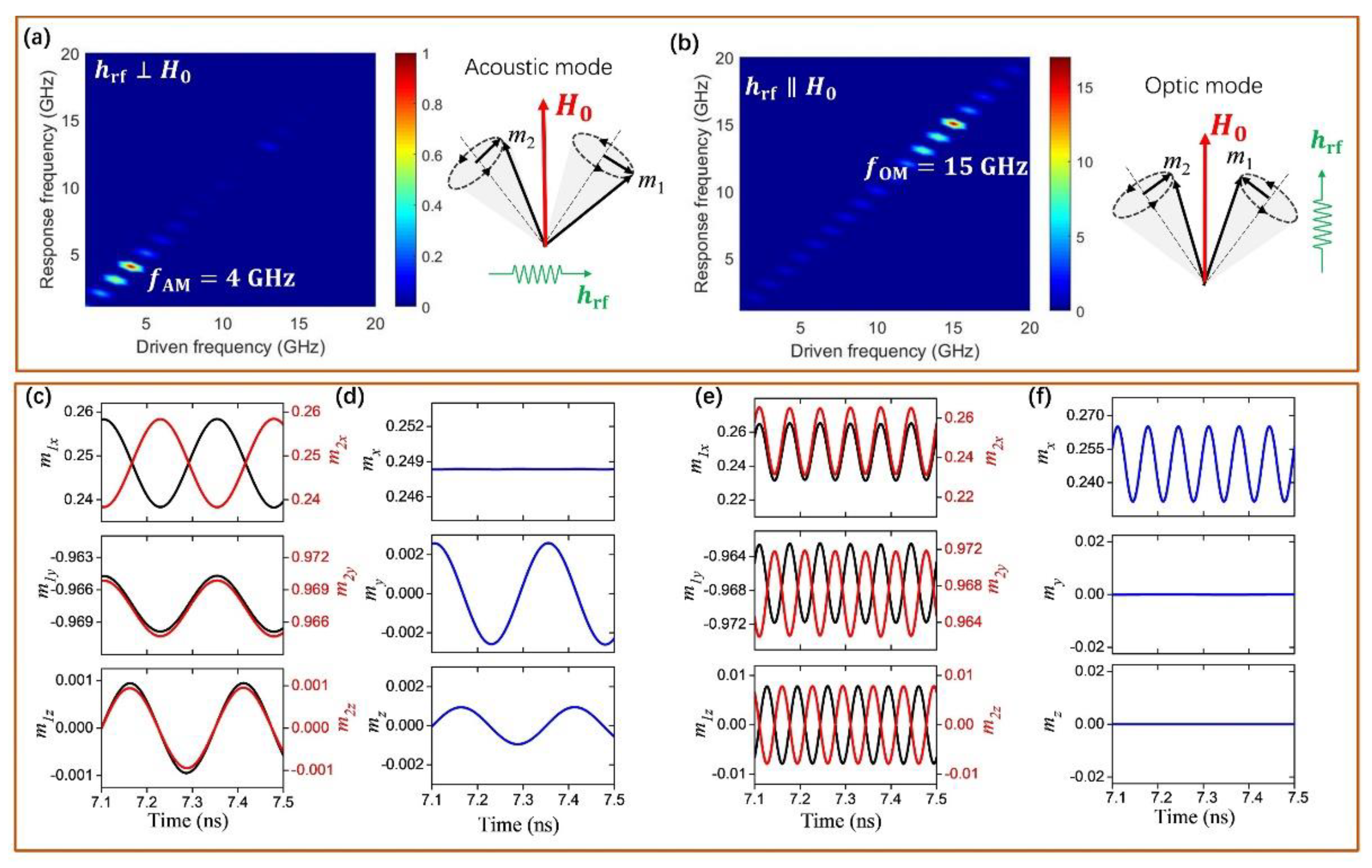
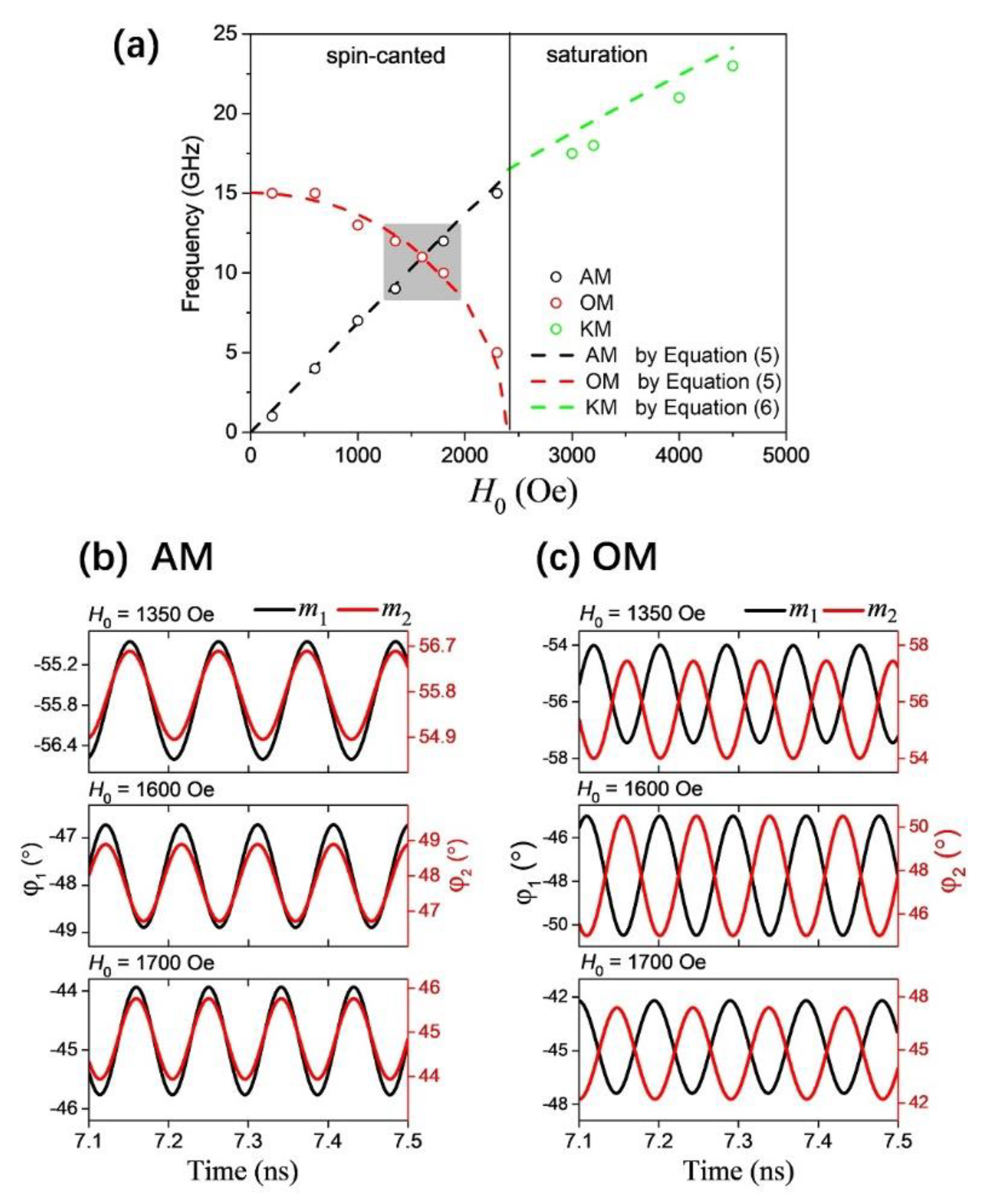
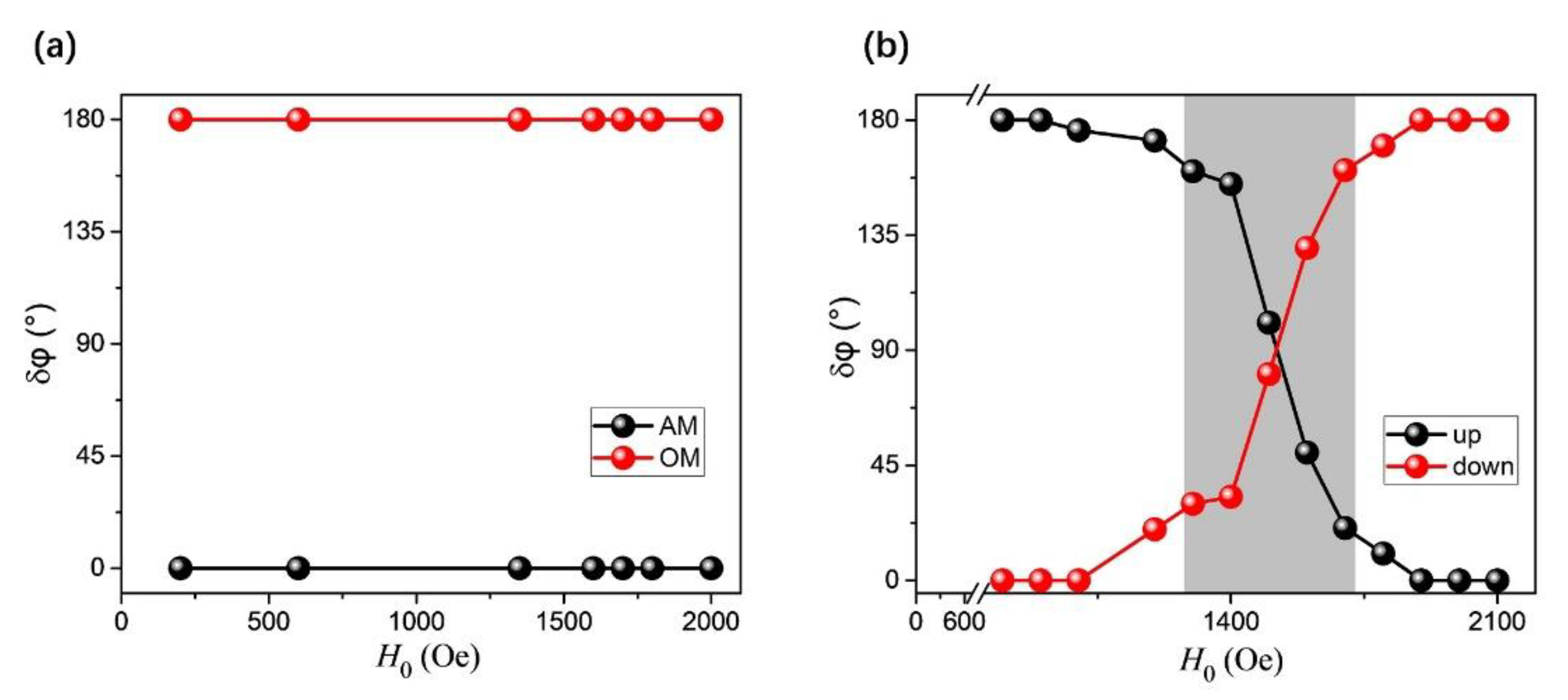
3.1. Dynamic Resonance Properties of Symmetrical SAF
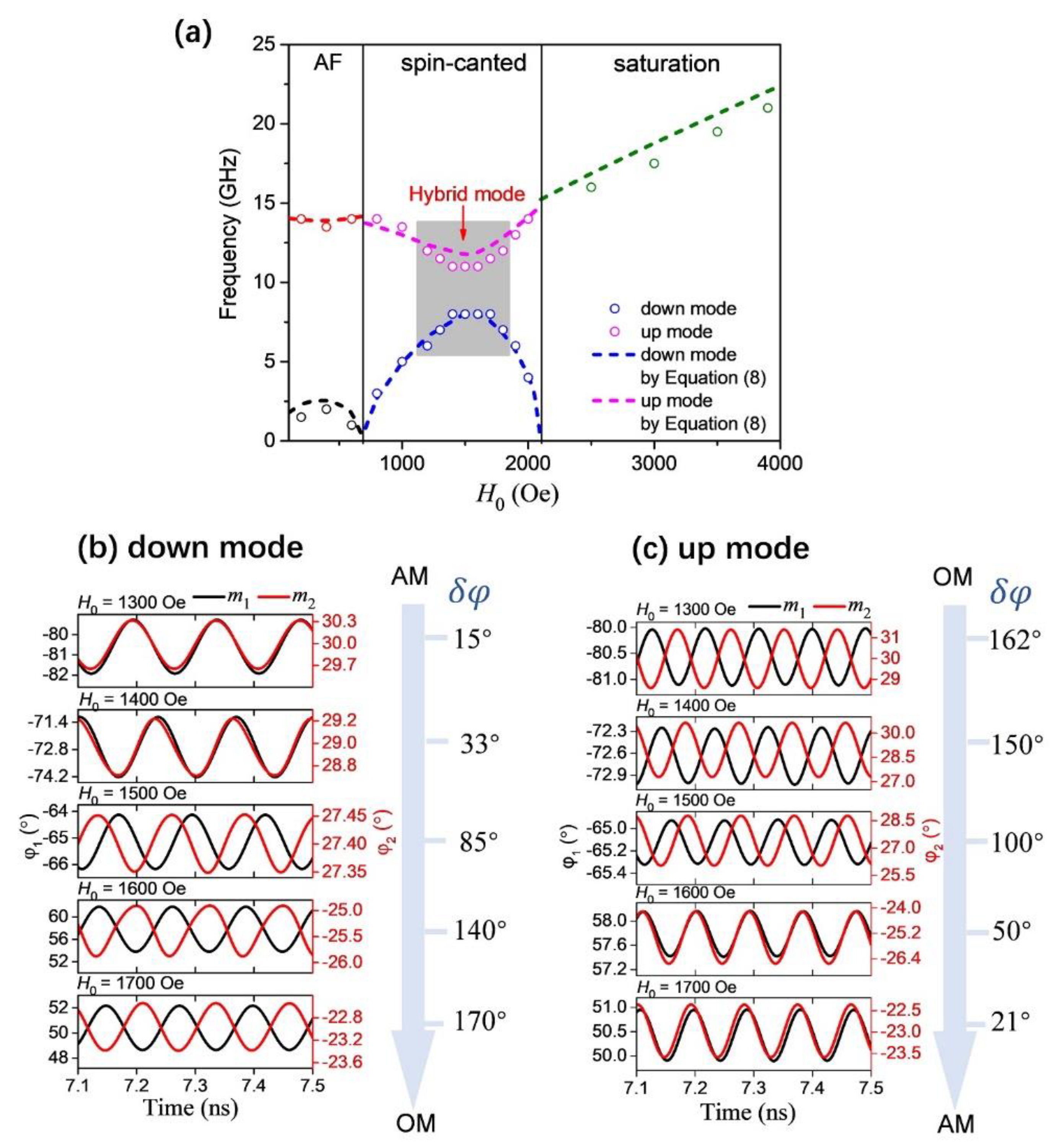
3.2. Dynamic Resonance Properties of Asymmetrical SAF
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chumak, A.V.; Vasyuchka, V.I.; Serga, A.A.; Hillebrands, B. Magnon spintronics. Nat. Phys. 2015, 11, 453. [Google Scholar] [CrossRef]
- Yu, H.; Xiao, J.; Schultheiss, H. Magnetic texture based magnonics. Phys. Rep. 2021, 905, 1. [Google Scholar] [CrossRef]
- Cheng, R.; Xiao, J.; Niu, Q.; Brataas, A. Spin Pumping and Spin-Transfer Torques in Antiferromagnets. Phys. Rev. Lett. 2014, 113, 057601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baltz, V.; Manchon, A.; Tsoi, M.; Moriyama, T.; Ono, T.; Tserkovnyak, Y. Antiferromagnetic spintronics. Rev. Mod. Phys. 2018, 90, 015005. [Google Scholar] [CrossRef] [Green Version]
- Rezende, S.M.; Azevedo, A.; Rodríguez-Suárez, R.L. Introduction to antiferromagnetic magnons. J. Appl. Phys. 2019, 126, 151101. [Google Scholar] [CrossRef] [Green Version]
- Cheng, R.; Xiao, D.; Brataas, A. Terahertz Antiferromagnetic Spin Hall Nano-Oscillator. Phys. Rev. Lett. 2016, 116, 207603. [Google Scholar] [CrossRef]
- Vaidya, P.; Morley, S.A.; van Tol, J.; Liu, Y.; Cheng, R.; Brataas, A.; Lederman, D.; del Barco, E. Subterahertz spin pumping from an insulating antiferromagnet. Science 2020, 368, 160. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wilson, C.B.; Cheng, R.; Lohmann, M.; Kavand, M.; Yuan, W.; Aldosary, M.; Agladze, N.; Wei, P.; Sherwin, M.S.; et al. Spin current from sub-terahertz-generated antiferromagnetic magnons. Nature 2020, 578, 70. [Google Scholar] [CrossRef]
- MacNeill, D.; Hou, J.T.; Klein, D.R.; Zhang, P.; Jarillo-Herrero, P.; Liu, L. Gigahertz Frequency Antiferromagnetic Resonance and Strong Magnon-Magnon Coupling in the Layered Crystal CrCl3. Phys. Rev. Lett. 2019, 123, 047204. [Google Scholar] [CrossRef] [Green Version]
- Sklenar, J.; Zhang, W. Self-Hybridization and Tunable Magnon-Magnon Coupling in van der Waals Synthetic Magnets. Phys. Rev. Appl. 2021, 15, 044008. [Google Scholar] [CrossRef]
- Liensberger, L.; Kamra, A.; Maier-Flaig, H.; Geprags, S.; Erb, A.; Goennenwein, S.T.B.; Gross, R.; Belzig, W.; Huebl, H.; Weiler, M. Exchange-Enhanced Ultrastrong Magnon-Magnon Coupling in a Compensated Ferrimagnet. Phys. Rev. Lett. 2019, 123, 117204. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Cao, W.; Amin, V.P.; Zhang, Z.; Gibbons, J.; Sklenar, J.; Pearson, J.; Haney, P.M.; Stiles, M.D.; Bailey, W.E.; et al. Coherent Spin Pumping in a Strongly Coupled Magnon-Magnon Hybrid System. Phys. Rev. Lett. 2020, 124, 117202. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Liu, C.; Liu, T.; Xiao, Y.; Xia, K.; Bauer, G.E.W.; Wu, M.; Yu, H. Strong Interlayer Magnon-Magnon Coupling in Magnetic Metal-Insulator Hybrid Nanostructures. Phys. Rev. Lett. 2018, 120, 217202. [Google Scholar] [CrossRef] [Green Version]
- Parkin, S.S.P.; More, N.; Roche, K.P. Oscillations in exchange coupling and magnetoresistance in metallic superlattice structures: Co/Ru, Co/Cr, and Fe/Cr. Phys. Rev. Lett. 1990, 64, 2304. [Google Scholar] [CrossRef]
- Grunberg, P.; Schreiber, R.; Pang, Y.; Brodsky, M.B.; Sowers, H. Layered magnetic structures: Evidence for antiferromagnetic coupling of Fe layers across Cr interlayers. Phys. Rev. Lett. 1986, 57, 2442. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, L.; Wigen, P.E.; Ounadjela, K. Angular dependence of ferromagnetic resonance in exchange-coupled Co/Ru/Co trilayer structures. Phys. Rev. B 1994, 50, 6094. [Google Scholar] [CrossRef] [PubMed]
- Rezende, S.M.; Chesman, C.; Lucena, M.A.; Azevedo, A.; de Aguiar, F.M.; Parkin, S.S.P. Studies of coupled metallic magnetic thin-film trilayers. J. Appl. Phys. 1998, 84, 958. [Google Scholar] [CrossRef]
- Belmeguenai, M.; Martin, T.; Woltersdorf, G.; Maier, M.; Bayreuther, G. Frequency- and time-domain investigation of the dynamic properties of interlayer-exchange-coupled Ni81Fe19/Ru/Ni81Fe19 thin films. Phys. Rev. B 2007, 76, 104414. [Google Scholar] [CrossRef] [Green Version]
- Waring, H.J.; Johansson, N.A.B.; Vera-Marun, I.J.; Thomson, T. Zero-field Optic Mode Beyond 20 GHz in a Synthetic Antiferromagnet. Phys. Rev. Appl. 2020, 13, 034035. [Google Scholar] [CrossRef] [Green Version]
- Sud, A.; Zollitsch, C.W.; Kamimaki, A.; Dion, T.; Khan, S.; Iihama, S.; Mizukami, S.; Kurebayashi, H. Tunable magnon-magnon coupling in synthetic antiferromagnets. Phys. Rev. B 2020, 102, 100403. [Google Scholar] [CrossRef]
- Dai, C.; Ma, F. Strong magnon–magnon coupling in synthetic antiferromagnets. Appl. Phys. Lett. 2021, 118, 112405. [Google Scholar] [CrossRef]
- Shiota, Y.; Taniguchi, T.; Ishibashi, M.; Moriyama, T.; Ono, T. Tunable Magnon-Magnon Coupling Mediated by Dynamic Dipolar Interaction in Synthetic Antiferromagnets. Phys. Rev. Lett. 2020, 125, 017203. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Xie, Z.K.; Sun, R.; Yang, M.; Li, Y.; Zhao, X.-T.; Liu, W.; Zhang, Z.D.; Cai, J.-W.; Cheng, Z.-H.; et al. Anisotropic Magnon–Magnon Coupling in Synthetic Antiferromagnets. Chin. Phys. Lett. 2021, 38, 057502. [Google Scholar] [CrossRef]
- Donahue, M.J.; Porter, D.G. OOMMF User’s Guide; Interagency Report NISTIR 6376; NIST: Gaithersburg, MD, USA, 1999. Available online: http://math.nist.gov/oommf (accessed on 10 October 2021).
- Kanai, S.; Yamanouchi, M.; Ikeda, S.; Nakatani, Y.; Matsukura, F.; Ohno, H. Electric field-induced magnetization reversal in a perpendicular-anisotropy CoFeB-MgO magnetic tunnel junction. Appl. Phys. Lett. 2012, 101, 122403. [Google Scholar] [CrossRef]
- Devolder, T.; Bianchini, L.; Miura, K.; Ito, K.; Kim, J.-V.; Crozat, P.; Morin, V.; Helmer, A.; Chappert, C.; Ikeda, S.; et al. Spin-torque switching window, thermal stability, and material parameters of MgO tunnel junctions. Appl. Phys. Lett. 2011, 98, 162502. [Google Scholar] [CrossRef] [Green Version]
- Sorokin, S.; Gallardo, R.A.; Fowley, C.; Lenz, K.; Titova, A.; Atcheson, G.Y.P.; Dennehy, G.; Rode, K.; Fassbender, J.; Lindner, J.; et al. Magnetization dynamics in synthetic antiferromagnets: Role of dynamical energy and mutual spin pumping. Phys. Rev. B 2020, 101, 144410. [Google Scholar] [CrossRef]
- Kittel, C. On the Theory of Ferromagnetic Resonance Absorption. Phys. Rev. 1948, 73, 155. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, C.; Zhang, Y.; Zhou, S.; Liu, Y.; Zhang, Z. Identification and manipulation of spin wave polarizations in perpendicularly magnetized synthetic antiferromagnets. New J. Phys. 2021, 23, 113029. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, C.; Zhou, S.; Liu, Y.; Zhang, Z. Ferromagnetic resonance modes of a synthetic antiferromagnet at low magnetic fields. J. Phys. Condens. Matt. 2021, 34, 015802. [Google Scholar] [CrossRef]
- Li, M.; Lu, J.; He, W. Symmetry breaking induced magnon-magnon coupling in synthetic antiferromagnets. Phys. Rev. B 2021, 103, 064429. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Zheng, C.; Zhou, S.; Liu, Y.; Zhang, Z. Manipulation of Time- and Frequency-Domain Dynamics by Magnon-Magnon Coupling in Synthetic Antiferromagnets. Magnetochemistry 2022, 8, 7. https://doi.org/10.3390/magnetochemistry8010007
Chen X, Zheng C, Zhou S, Liu Y, Zhang Z. Manipulation of Time- and Frequency-Domain Dynamics by Magnon-Magnon Coupling in Synthetic Antiferromagnets. Magnetochemistry. 2022; 8(1):7. https://doi.org/10.3390/magnetochemistry8010007
Chicago/Turabian StyleChen, Xing, Cuixiu Zheng, Sai Zhou, Yaowen Liu, and Zongzhi Zhang. 2022. "Manipulation of Time- and Frequency-Domain Dynamics by Magnon-Magnon Coupling in Synthetic Antiferromagnets" Magnetochemistry 8, no. 1: 7. https://doi.org/10.3390/magnetochemistry8010007
APA StyleChen, X., Zheng, C., Zhou, S., Liu, Y., & Zhang, Z. (2022). Manipulation of Time- and Frequency-Domain Dynamics by Magnon-Magnon Coupling in Synthetic Antiferromagnets. Magnetochemistry, 8(1), 7. https://doi.org/10.3390/magnetochemistry8010007




