Abstract
The study of magnetic relaxations in Mn-stearate single-molecule magnets deposited on the surface of spherical silica nanoparticles was performed. For such a purpose, the investigation of AC magnetic susceptibility dependence on the frequency and temperature was performed. Based on the Argand plots obtained for different temperatures and temperature dependencies of susceptibility, obtained for different frequencies of AC field, the corresponding relaxation times were derived. Fitting to the Arrhenius law revealed the values of an effective energy barrier and a mean relaxation time, which were consistent for both measuring techniques ( 50 K and 10 s) and similar to the corresponding values for the analogous bulk compounds. Additionally, the obtained relaxation parameters for the Mn-stearate molecules on the spherical silica surface were compared with corresponding values for the Mn-based single-molecule magnets deposited upon other types of nanostructured silica surface.
1. Introduction
Nowadays, significant effort is being dedicated to the design and manufacture of new nanosized materials with specific magnetic properties. Very attractive from such a point of view seems to be the single-molecule magnets (SMMs)—low dimensional molecules consisting of coupled paramagnetic metal ions, possessing unique magnetic properties (magnetic hysteresis, slow magnetic relaxations, quantum tunneling effects) available at the molecular level [1,2]. Due to such magnetic characteristics, SMMs have high applicative potential in the fields of molecular spintronics, quantum computers and dense magnetic memory devices [3]. However, to have the possibility of manipulating individual molecules for the realization of nanoelectronic devices, it is necessary to deposit and separate SMMs on the solid surface [4]. In this aim, different techniques and methods, as well as different types of SMMs and solid substrate materials were applied and described in the literature. A gold surface was the substrate of choice in the earliest investigations of SMM surface deposition [5]. A variety of complexes of the most commonly used families of SMMs, Mn and Fe, have been specifically designed for direct deposition on gold substrate [6,7,8,9]. Furthermore, in numerous studies, the described approaches were extended to more technologically relevant substrates (carbon, metal oxides, silicon) as well as other SMM complexes [4,10]. However, despite the successful efforts for the organization of such SMMs on the surface and using sensitive measurement techniques, the fact that SMMs retain magnetic hysteresis and slow relaxation behavior when anchored to surfaces is not always evident.
In our previous studies, the possibility of the successful deposition of Mn-stearate (Mn-st) SMMs on the surface of silica nanoparticles was shown [11,12]. The nanostructured silica substrate seems to be the ideal material for the deposition of such molecules providing the preservation of their inner structure and magnetic properties [13,14]. Furthermore, the application of the substrate with a developed surface allows for a very detailed analysis of the separated SMMs. In our case, considering the weight of the measured sample—0.1 g—the corresponding surface area was close to 1.3 m [11]. Such a property gives the possibility for a very detailed analysis of the behavior of the SMMs distributed on this surface. The detailed study of magnetic relaxation in surface-deposited SMMs could reveal new interesting features of such structures, important for the practical applications of similar magnetic systems. The sensitive instrument for the characterization of magnetic materials that allows for obtaining additional information on the mechanism of slow relaxation in SMMs is the dynamic magnetic susceptibility technique, also called AC susceptibility, [15]. Therefore, in the current study, the detailed analysis of magnetic relaxation in Mn-st SMMs deposited on the surface of spherical silica was performed with the use of AC susceptibility measurements. Furthermore, obtained data were compared to the results of magnetic relaxations in similar magnetic materials.
2. Materials and Methods
The experimental material was a nanocomposite developed by our team: silica spheres with a diameter of approximately 300 nm containing Mn-st single-molecule magnets anchored at the surface with assumed concentration, as depicted in Figure 1. The control of the distribution was realized by means of the spacer units and anchoring groups, as we reported earlier [12]. In this case, the material containing six spacer molecules per single anchored SMM was chosen. Such a material presented the most interesting magnetic properties [14], and in our opinion, is worthy of further analysis. The synthesis procedure was described in our previous work [12]. The investigated sample was denoted as SilS–Mn.
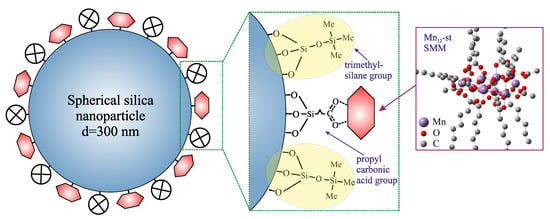
Figure 1.
Schematic representation of the investigated material—spherical silica nanoparticles containing deposited Mn-st SMMs with controlled distance between molecules. Trimethyl silane units play the role of spacers/separators between SMMs, maintaining the assumed distances between them. The number of spacers per single magnetic molecules determines the distribution of Mn-st at the silica’s surface.
Magnetic measurements were carried out with the Quantum Design Magnetic Property Measurement System (MPMS) magnetometer on the sample in a powder form. The mass of the sample was 0.1 g, which includes the mass of the silica nanoparticles with deposited Mn-st magnetic molecules. The measurements of the phase-sensitive AC susceptibility were based on the measurement of in-phase and out-of-phase components of dependence on the temperature. The oscillating magnetic fields of T f = 10 Hz and f = 120 Hz were used in the temperature range from 2.0 K to 8.0 K. The frequency dependence of susceptibility was measured in the temperature range 3.0 K–5.0 K with the amplitude of the oscillating field of 3 Oe and frequencies changing from 0.1 Hz to 1 kHz.
3. Results and Discussion
The frequency dependence of the and signals are a consequence of one or more relaxation processes with characteristic relaxation time constants. A common way to determine the relaxation time is the so-called Cole–Cole plot [16], known in magnetism as the Argand plot [17], where versus is plotted for a given temperature and different angular frequencies . If the relaxation process is characterized by a distribution of relaxation times, then the Cole–Cole expression is modified to the so-called extended Debye model [16]:
where is isothermal susceptibility, is adiabatic susceptibility and is a measure of the distribution of the relaxation times. The latter parameter can be derived by the experimental AC data in the Argand plot because the semicircle becomes an arc of a circle with a central angle equal to . The angular frequency at which the magnetic absorption reaches its maximum determines the relaxation time of the relevant relaxation process as . As a result, by performing such an analysis for the sample at different temperatures, it is possible to obtain the temperature dependence of the relaxation time . In order to obtain information about the relaxation process for the case of surface-deposited SMMs at the sample SilS-Mn, the AC susceptibility studies were performed. Firstly, dynamic magnetic properties were studied with frequency-dependent AC susceptibilities in the zero-applied DC field for the frequency range 0.1–1000 Hz. The corresponding Cole–Cole plots for the temperatures from 3.0 K to 5.0 K with a driving AC field amplitude of 3 Oe are presented in Figure 2.
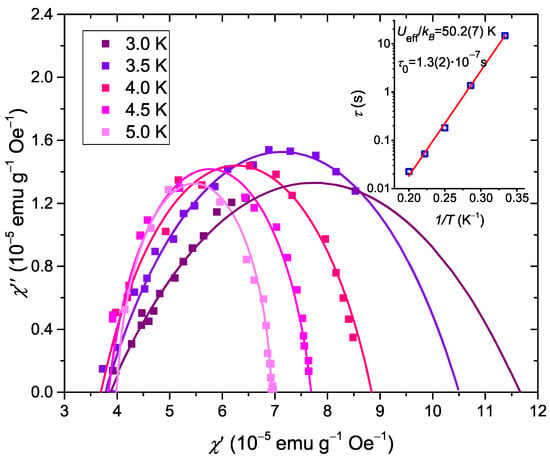
Figure 2.
Argand plots for the sample SilS-Mn measured in the frequency range of 0.1 Hz–1000 Hz with an oscillating magnetic field amplitude of = 3 Oe for different temperatures (solid lines represent the best fit to Equation (1)) (inset: corresponding data of temperature dependence of the relaxation time on a log scale (solid line stands for the best fit to the Arrhenius function (2))).
As can be seen, the obtained experimental data for each temperature differ considerably from perfect semicircles and form arcs of size . Moreover, for each temperature, most of the data lie in little flattened semi-circles. Such a behavior is typical of a wide distribution of relaxation times [18]. The obtained results can be analyzed using the extended Debye model by fitting AC susceptibility data to Equation (1). All of the parameters corresponding to the best fits are summarized in Table 1. The fit reveals that parameter , which gives information about the distribution of the relaxation, is temperature dependent and continuously decreases up to the highest temperature of 5.0 K. The fitting determines that for a temperature of 5.0 K, the parameter , which indicates that the system reverts to the Debye form of a single relaxation time, while with the decreasing temperature, a wide distribution of relaxation times is observed. The average distribution of relaxation times is equal to approximately 0.3. This result is consistent with similar studies performed on other Mn complexes [19,20,21] and probably results from a distribution of effective energy barriers, as a consequence of the distribution of environments of the molecules in a sample in powder form [19]. Furthermore, the relaxation time increases with the decreasing temperature.

Table 1.
Fit parameters obtained from AC susceptibility data for sample SilS-Mn using the extended Debye model.
In addition to the parameters, the effective time constants can be obtained for each temperature from the reciprocal angular frequency at maximum absorption. The zero-field relaxation times are the function of inverse temperature collected in the inset of Figure 2. In the temperature range 3.0 K–5.0 K, the relaxation times can be approximated by an Arrhenius law:
where is the relaxation time at the high temperature limit, the is effective energy barrier and is Boltzmann constant. The fit of Equation (2) yielded / = 50.2(7) K and s. These results slightly differ from the values obtained from the AC susceptibility measurements of bulk Mn complexes ( 60 K, s) [1,22], but the order of magnitude remains the same.
The next step was the measurement of temperature dependence of the in-phase and out-of-phase components of the magnetic susceptibility for the sample SilS-Mn. The study was performed for three different values of frequencies f = 1 Hz, f = 10 Hz and f = 120 Hz in the temperature range from 2.0 K to 8.0 K with the amplitude of an oscillating magnetic field 3 Oe. As it can be seen from Figure 3, of such a sample shows strong dependence on frequency. Upon decreasing temperature, reaches the frequency-dependent maximum, and when the moments cannot follow the oscillating field, start to decrease. From the other side, the out-of-phase signal shows the shifting of peaks to a higher temperature on the increasing frequency. This indicates that the relaxation rate increases with temperature. Such a frequency-dependent shift in the temperature of the maxima of can be analyzed by the Mydosh parameter [23]:
where is the temperature of the maximum of , is the difference between the peaks corresponding to the extremes of and f is the frequency. The obtained value for the SilS-Mn sample is equal to 0.21(1), which is close to the reported value = 0.19 for bulk Mn-ac [24]. This confirms the superparamagnetic character of the compound. From the frequency dependence of peaks, it is also possible to estimate the temperature dependence of the relaxation time at the zero applied field. By taking the temperature positions of the maxima for corresponding frequency, the relaxation time can be plotted as the function of inverse temperature (see the inset of Figure 3). Such a dependence can then be fitted to the Arrhenius law (2). As a result of the fitting, we obtained / = 51(1) K and = 4.7(4) × 10 s. These results are consistent with those obtained earlier from the Argand plots and are close to the data reported in the literature [1,22].
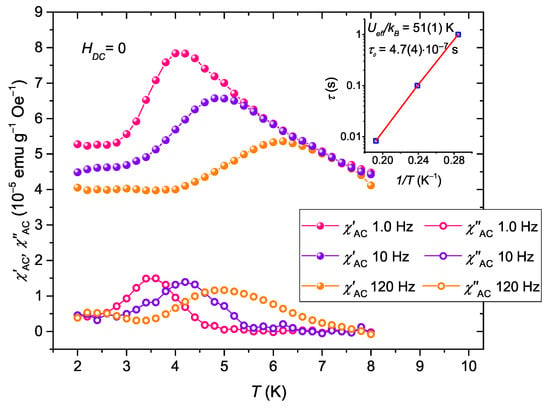
Figure 3.
Temperature dependence of in-phase and out-of-phase susceptibility at various frequencies in the zero static field for the sample SilS-Mn (lines are a guide for eyes) (inset: corresponding relaxation times in function of inverse temperature (solid line stands for the best fit to the Arrhenius function (2))).
We can also compare the results of relaxation time dependence on the reciprocal temperature for both used approaches, as shown in Figure 4. Additionally, the relaxation dynamics of Mn-st SMMs deposited into spherical nanoparticles can be compared with the corresponding results for analogous molecules incorporated into mesoporous silica matrix SBA-15 (corresponding sample is denoted as SBA-Mn in Figure 4). As it was reported [25], Mn-st molecules incorporated into mesoporous silica show strong frequency-dependent susceptibility with a wide distribution of relaxation times. The relaxation vs. reciprocal temperature dependence of such a sample shows quite good consistency with the results of the data for Mn-st molecules on the spherical silica substrate. The values of an effective energy barrier and mean relaxation time, derived from AC susceptibility measurements, are similar for both silica substrates.
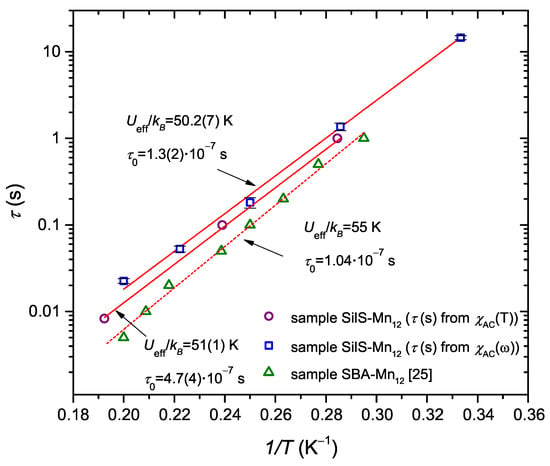
Figure 4.
Relaxation times in function of inverse temperature for sample SilS-Mn in comparison to the SBA-Mn sample (solid lines stand for the best fit to the Arrhenius function (2) for each measurement).
It should be noted that using nanostructured silica as a substrate for the deposition of Mn derivatives was described in the literature and mostly based on applying incorporation inside various mesoporous silica structures using different chemical strategies (see Table 2). The silica matrices SBA-15 and MCM-41 belong to the most common type of host material for such a purpose [26,27]. Numerous studies show the preservation of the slow magnetic relaxation of deposited SMMs; however, very often, the simple impregnation of a mesoporous matrix cannot guarantee the SMMs’ separation and regular distribution of functionalities inside silica pores. Any practical applications of such nanocomposites require the controlled organization and separation of SMMs in different dimensions to allow for easy read-and-write processes. Furthermore, a nanostructuration process should provide the preservation of chemical integrity and unique magnetic properties of deposited molecules. Unfortunately, the control of the inter-molecular distances between individual SMMs inside the channels of mesoporous silicas was not yet achieved [28]. From such a point of view, spherical silica as a substrate provides not only the successful deposition of molecules, but also the possibility of the horizontal distribution of deposited SMMs. As described in our previous studies [13], the use of spacer units creates the possibility of the regular organization of SMMs on the spherical silica surface. Such observation could be of great importance for the nanotechnological applications of surface-deposited SMMs.

Table 2.
Relaxation parameters derived from AC susceptibility measurements for Mn-based SMMs organized on different nanostructured silica substrates.
The important thing that should also be taken into consideration is the analysis of magnetic relaxation by an AC susceptibility study along with magnetic relaxation obtained from DC studies. As shown in previous studies for the analogous sample [14], the values of an effective energy barrier and mean relaxation time, obtained from time-dependent magnetization measurements, were slightly different to those obtained by AC susceptibility measurements (for DC measurements: / = 33.6(9) K and = 4.6(3) × 10 s; for AC measurements: 50 K and 10 s), which can be seen in Figure 5. It can be explained by considering the different temperature range of each measurement. At relatively low temperatures, below the blocking temperature, magnetic relaxation in the sample is enhanced by the quantum tunneling of magnetization (QTM), as can be concluded from the typical shape of the curve at zero field (see Figure 3a at [14]). Moreover, the time decay of the magnetization study revealed that the relaxation rate significantly changes with the temperature. Such a behavior indicates that quantum tunneling is thermally assisted and becomes more important as the temperature is lowered. This relaxation mechanism is well-known for Mn complexes [24,30] and results in the reduced value of an effective energy barrier and accelerates the relaxations. In contrast to AC measurements, at a higher measuring frequency (and temperature), the shortcuts due to tunneling in the middle of the energy barrier lose their importance, the apparent energy barrier is larger and approaches the value of 10 s. Nevertheless, there is a possibility of correlating the relaxation data obtained from the AC and DC measurements in order to evaluate the average relaxation parameters for the sample in the whole temperature region (see Figure 5). This resulted in the fit to the Arrhenius law revealing the following values: / = 45.2(7) K and = 3.4(9) × 10 s.
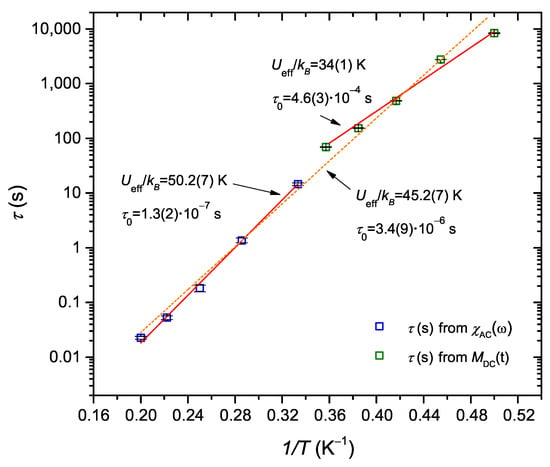
Figure 5.
Relaxation times in function of the inverse temperature for sample SilS-Mn, derived from the AC susceptibility measurements and DC magnetization measurements (solid lines stand for the best fit to the Arrhenius function (2) for each measurement and the dashed line represents the best fit to such a function for both the DC and AC relaxation data).
4. Conclusions
In this work, we analyzed magnetic relaxation in Mn-stearate single-molecule magnets deposited on the surface of spherical silica with assumed distribution. As we can conclude, the obtained results of the AC susceptibility study of magnetic relaxations confirm that molecular magnets in sample SilS-Mn exhibit considerable magnetic anisotropy and slow magnetic relaxations, which remain almost intact after the surface deposition. Obtained values of the effective energy barrier and relaxation time show full consistency for both applied techniques (frequency dependence of AC susceptibility and temperature dependence of ) and are similar to the corresponding values for analogous bulk compounds. Obtained data could be useful for further analysis of SMMs’ surface behavior and the investigation of similar nanocomposite structures.
Author Contributions
Conceptualization: O.P., M.L. and Ł.L.; methodology, O.P. and P.K.; investigation, O.P. and P.K.; resources, M.L. and Ł.L.; data curation, O.P.; writing—original draft preparation, O.P. and Ł.L.; writing—review and editing, M.L., Ł.L. and P.K.; visualization, O.P.; project administration, O.P., M.L. and Ł.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the resources of the National Centre of Science (Grant-No: 2017/26/E/ST5/00162 (Ł.L.)).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Christou, G.; Gatteschi, D.; Hendrickson, D.N.; Sessoli, R. Single-molecule magnets. MRS Bull. 2000, 25, 66–71. [Google Scholar] [CrossRef]
- Bartolome, S.J.; Luis, F.; Fernández, J.F. Molecular Magnets: Physics and Applications; Springer: Berlin/Heidelberg, Germany, 2014; p. 395. [Google Scholar]
- Cornia, A.; Mannini, M.; Sainctavit, P.; Sessoli, R. Chemical strategies and characterization tools for the organization of single molecule magnets on surfaces. Chem. Soc. Rev. 2011, 40, 3076–3091. [Google Scholar] [CrossRef] [PubMed]
- Cornia, A.; Fabretti, A.C.; Pacchioni, M.; Zobbi, L.; Bonacchi, D.; Caneschi, A.; Gatteschi, D.; Biagi, R.; Del Pennino, U.; De Renzi, V.; et al. Direct observation of single-molecule magnets organized on gold surfaces. Angew. Chem. Int. Ed. 2003, 42, 1645–1648. [Google Scholar] [CrossRef]
- Mannini, M.; Pineider, F.; Sainctavit, P.; Danieli, C.; Otero, E.; Sciancalepore, C.; Talarico, A.M.; Arrio, M.A.; Cornia, A.; Gatteschi, D.; et al. Magnetic memory of a single-molecule quantum magnet wired to a gold surface. Nat. Mater. 2009, 8, 194–197. [Google Scholar] [CrossRef] [PubMed]
- Voss, S.; Burgert, M.; Fonin, M.; Groth, U.; Rüdiger, U. A comparative study on the deposition of Mn 12 single molecule magnets on the Au (111) surface. Dalton Trans. 2008, 499–505. [Google Scholar] [CrossRef] [Green Version]
- Zobbi, L.; Mannini, M.; Pacchioni, M.; Chastanet, G.; Bonacchi, D.; Zanardi, C.; Biagi, R.; Del Pennino, U.; Gatteschi, D.; Cornia, A.; et al. Isolated single-molecule magnets on native gold. Chem. Commun. 2005, 12, 1640–1642. [Google Scholar] [CrossRef]
- Mannini, M.; Pineider, F.; Danieli, C.; Totti, F.; Sorace, L.; Sainctavit, P.; Arrio, M.A.; Otero, E.; Joly, L.; Cezar, J.C.; et al. Quantum tunnelling of the magnetization in a monolayer of oriented single-molecule magnets. Nature 2010, 468, 417–421. [Google Scholar] [CrossRef] [PubMed]
- Cornia, A.; Mannini, M. Single-Molecule Magnets on Surfaces. In Molecular Nanomagnets and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 2014; pp. 293–331. [Google Scholar]
- Laskowski, L.; Kityk, I.; Konieczny, P.; Pastukh, O.; Schabikowski, M.; Laskowska, M. The Separation of the Mn12 Single-Molecule Magnets onto Spherical Silica Nanoparticles. Nanomaterials 2019, 9, 764. [Google Scholar] [CrossRef] [Green Version]
- Laskowska, M.; Pastukh, O.; Kuźma, D.; Laskowski, Ł. How to Control the Distribution of Anchored, Mn12–Stearate, Single-Molecule Magnets. Nanomaterials 2019, 9, 1730. [Google Scholar] [CrossRef] [Green Version]
- Laskowska, M.; Pastukh, O.; Konieczny, P.; Dulski, M.; Zalsiński, M.; Laskowski, L. Magnetic behaviour of Mn12-stearate single-molecule magnets immobilized on the surface of 300 nm spherical silica nanoparticles. Materials 2020, 13, 2624. [Google Scholar] [CrossRef]
- Pastukh, O.; Konieczny, P.; Czernia, D.; Laskowska, M.; Dulski, M.; Laskowski, Ł. Aging effect on the magnetic properties of Mn12-stearate single-molecule magnets anchored onto the surface of spherical silica nanoparticles. Mater. Sci. Eng. B 2020, 261, 114670. [Google Scholar] [CrossRef]
- Balanda, M. AC susceptibility studies of phase transitions and magnetic relaxation: Conventional, molecular and low-dimensional magnets. Acta Phys. Pol. A 2013, 124, 964–976. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef] [Green Version]
- Dekker, C.; Arts, A.; De Wijn, H.; Van Duyneveldt, A.; Mydosh, J. Activated dynamics in a two-dimensional Ising spin glass: Rb 2 Cu1-xCox F4. Phys. Rev. B 1989, 40, 11243. [Google Scholar] [CrossRef] [Green Version]
- Evangelisti, M.; Bartolomé, J. Secondary magnetic relaxations in Mn12 complexes. J. Magn. Magn. Mater. 2000, 221, 99–102. [Google Scholar] [CrossRef]
- Chakov, N.E.; Soler, M.; Wernsdorfer, W.; Abboud, K.A.; Christou, G. Single-molecule magnets: Structural characterization, magnetic properties, and 19F NMR spectroscopy of a Mn12 family spanning three oxidation levels. Inorg. Chem. 2005, 44, 5304–5321. [Google Scholar] [CrossRef] [PubMed]
- Boskovic, C.; Brechin, E.K.; Streib, W.E.; Folting, K.; Bollinger, J.C.; Hendrickson, D.N.; Christou, G. Single-molecule magnets: A new family of Mn12 clusters of formula [Mn12O8X4 (O2CPh)8L6]. J. Am. Chem. Soc. 2002, 124, 3725–3736. [Google Scholar] [CrossRef] [PubMed]
- Bałanda, M.; Pełka, R.; Fitta, M.; Laskowski, Ł.; Laskowska, M. Relaxation and magnetocaloric effect in the Mn 12 molecular nanomagnet incorporated into mesoporous silica: A comparative study. RSC Adv. 2016, 6, 49179–49186. [Google Scholar] [CrossRef]
- Bagai, R.; Christou, G. The drosophila of single-molecule magnetism:[Mn12O12(O2CR)16(H2O)4]. Chem. Soc. Rev. 2009, 38, 1011–1026. [Google Scholar] [CrossRef]
- Mydosh, J.A. Spin Glasses: An Experimental Introduction; Taylor and Francis: Abingdon, UK, 1993. [Google Scholar]
- Novak, M.; Folly, W.; Sinnecker, J.; Soriano, S. Relaxation in magnetic nanostructures. J. Magn. Magn. Mater. 2005, 294, 133–140. [Google Scholar] [CrossRef]
- Laskowska, M.; Bałanda, M.; Fitta, M.; Dulski, M.; Zubko, M.; Pawlik, P.; Laskowski, Ł. Magnetic behaviour of Mn12-stearate single-molecule magnets immobilized inside SBA-15 mesoporous silica matrix. J. Magn. Magn. Mater. 2019, 478, 20–27. [Google Scholar] [CrossRef]
- Willemin, S.; Arrachart, G.; Lecren, L.; Larionova, J.; Coradin, T.; Clérac, R.; Mallah, T.; Guérin, C.; Sanchez, C. Immobilisation of single molecule magnets in mesoporous silica hosts. New J. Chem. 2003, 27, 1533–1539. [Google Scholar] [CrossRef]
- Clemente-León, M.; Coronado, E.; Forment-Aliaga, A.; Amorós, P.; Ramírez-Castellanos, J.; González-Calbet, J.M. Incorporation of Mn12 single molecule magnets into mesoporous silica. J. Mater. Chem. 2003, 13, 3089–3095. [Google Scholar] [CrossRef]
- Aulakh, D.; Bilan, H.K.; Wriedt, M. Porous substrates as platforms for the nanostructuring of molecular magnets. CrystEngComm 2018, 20, 1011–1030. [Google Scholar] [CrossRef]
- Coradin, T.; Larionova, J.; Smith, A.A.; Rogez, G.; Clérac, R.; Guérin, C.; Blondin, G.; Winpenny, R.E.; Sanchez, C.; Mallah, T. Magnetic nanocomposites built by controlled incorporation of magnetic clusters into mesoporous silicates. Adv. Mater. 2002, 14, 896–898. [Google Scholar] [CrossRef]
- Friedman, J.R.; Sarachik, M.; Tejada, J.; Ziolo, R. Macroscopic measurement of resonant magnetization tunneling in high-spin molecules. Phys. Rev. Lett. 1996, 76, 3830. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).