AC Susceptibility Studies under DC Fields in Superspinglass Nanomaghemite-Multiwall Carbon Nanotube Hybrid
Abstract
1. Introduction
2. Results and Discussions
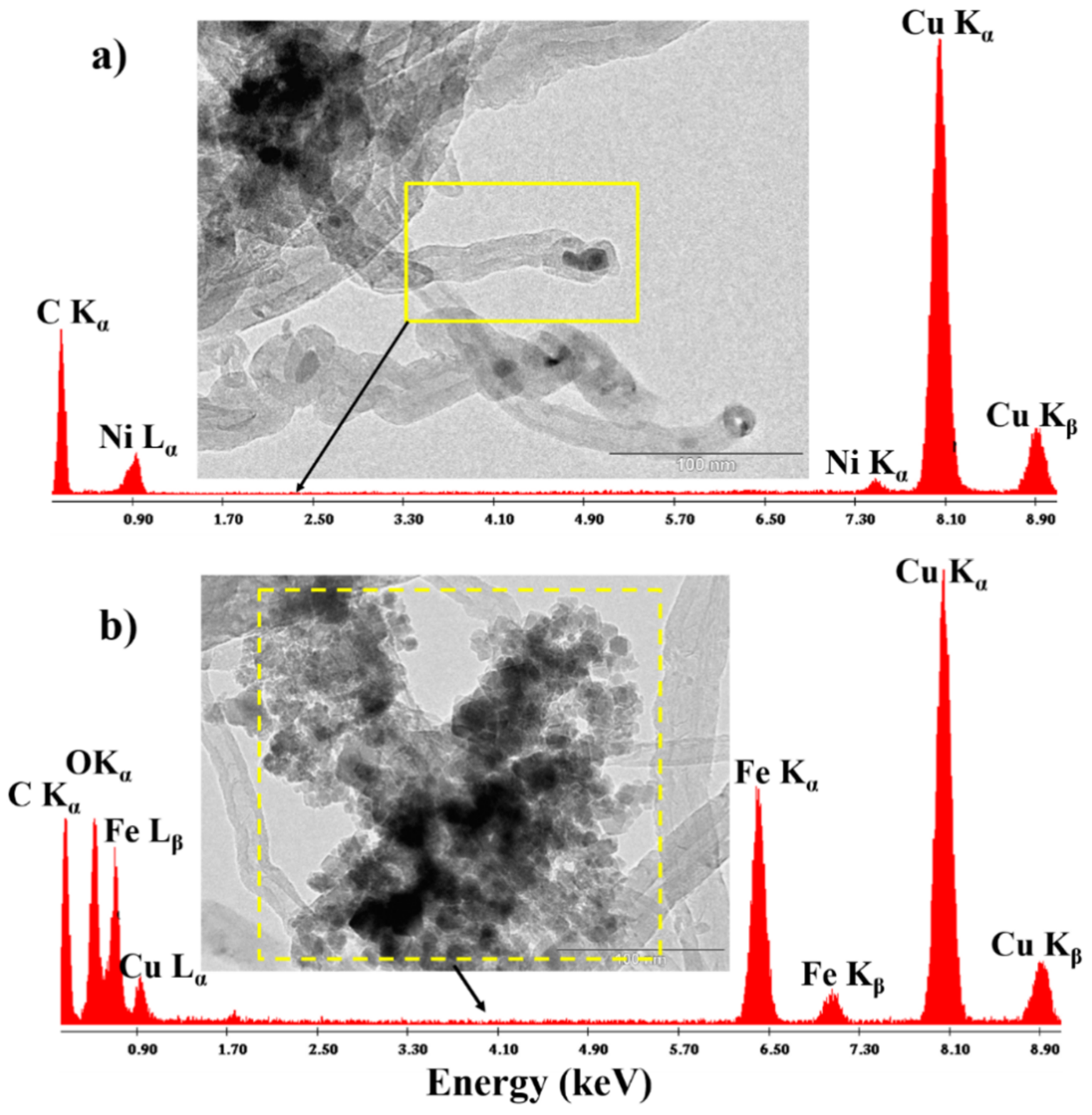
2.1. Transmission Electron Microscopy (TEM) and Energy Dispersive X-ray (EDX) Analysis
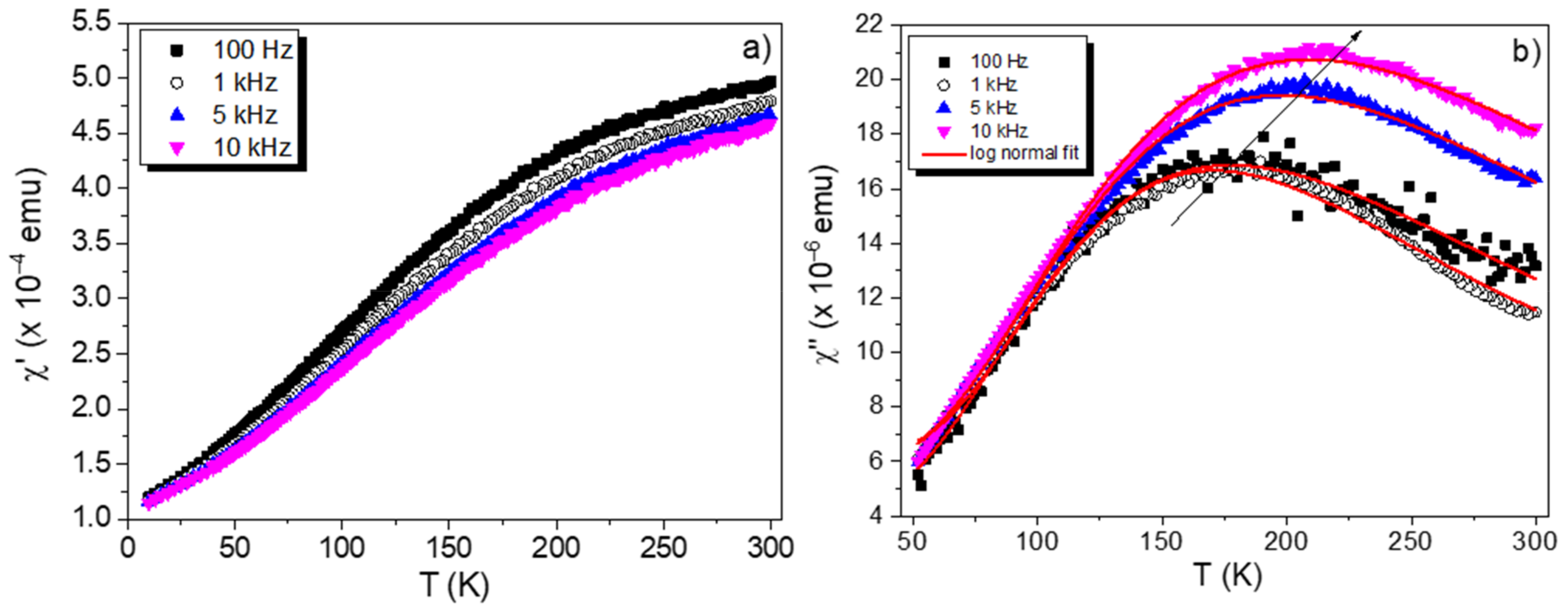
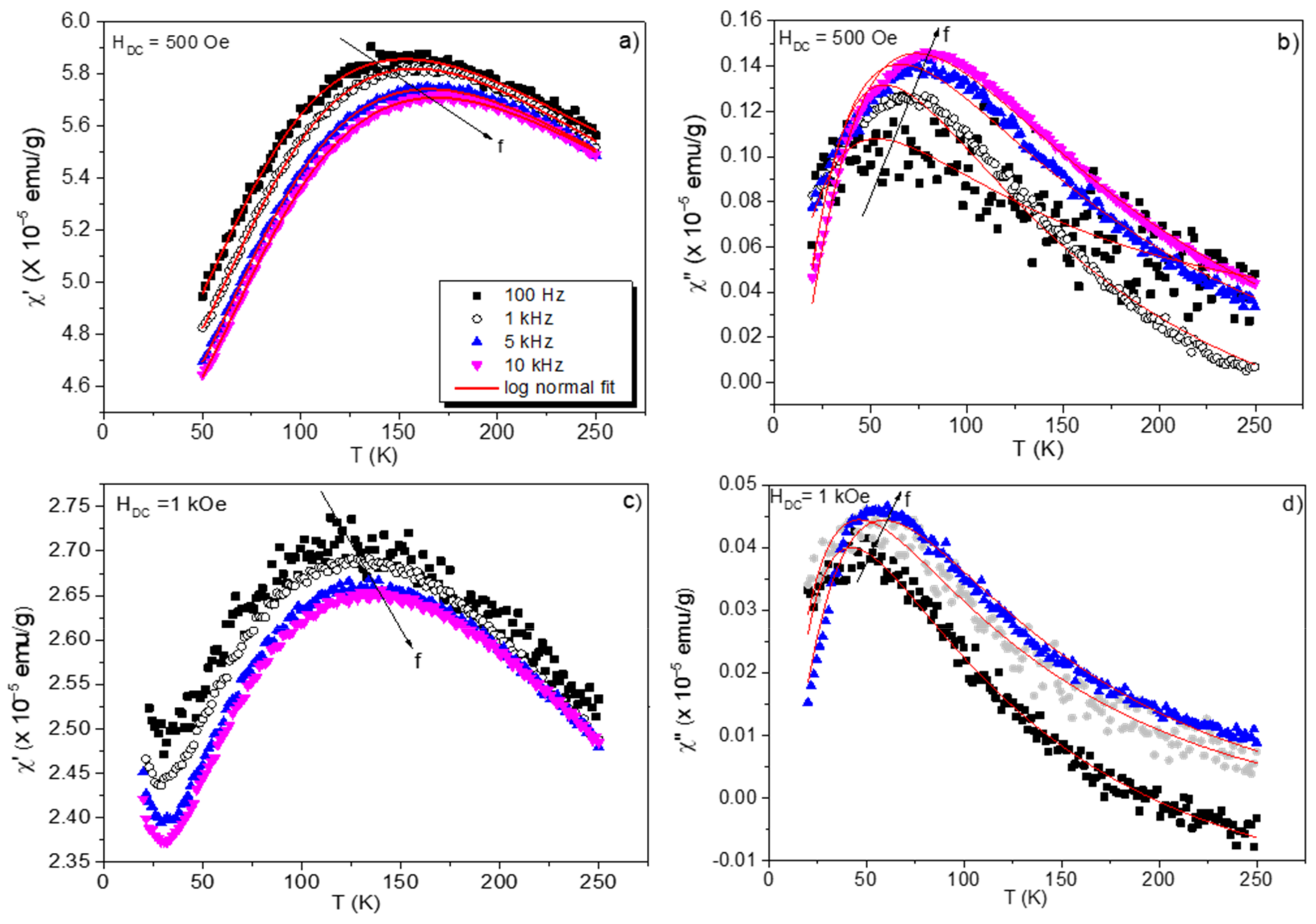
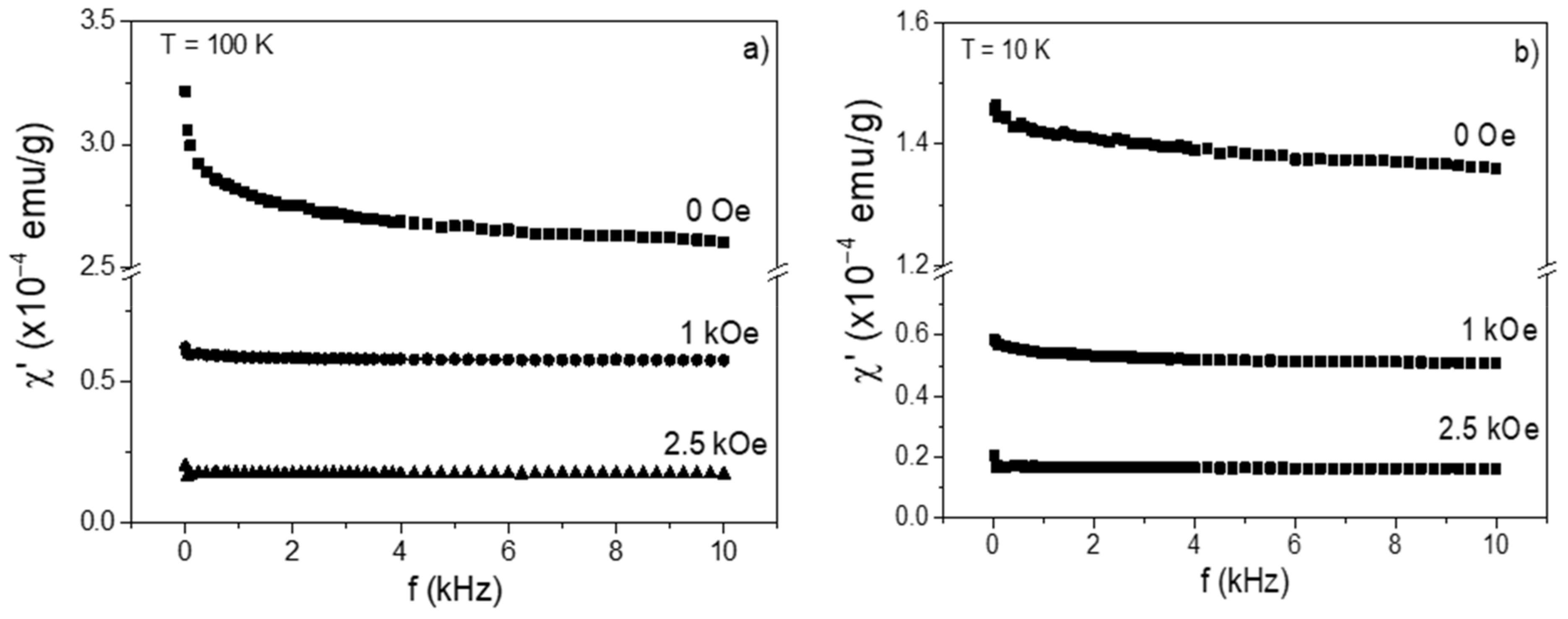
2.2. Superspinglass Phase Analysis
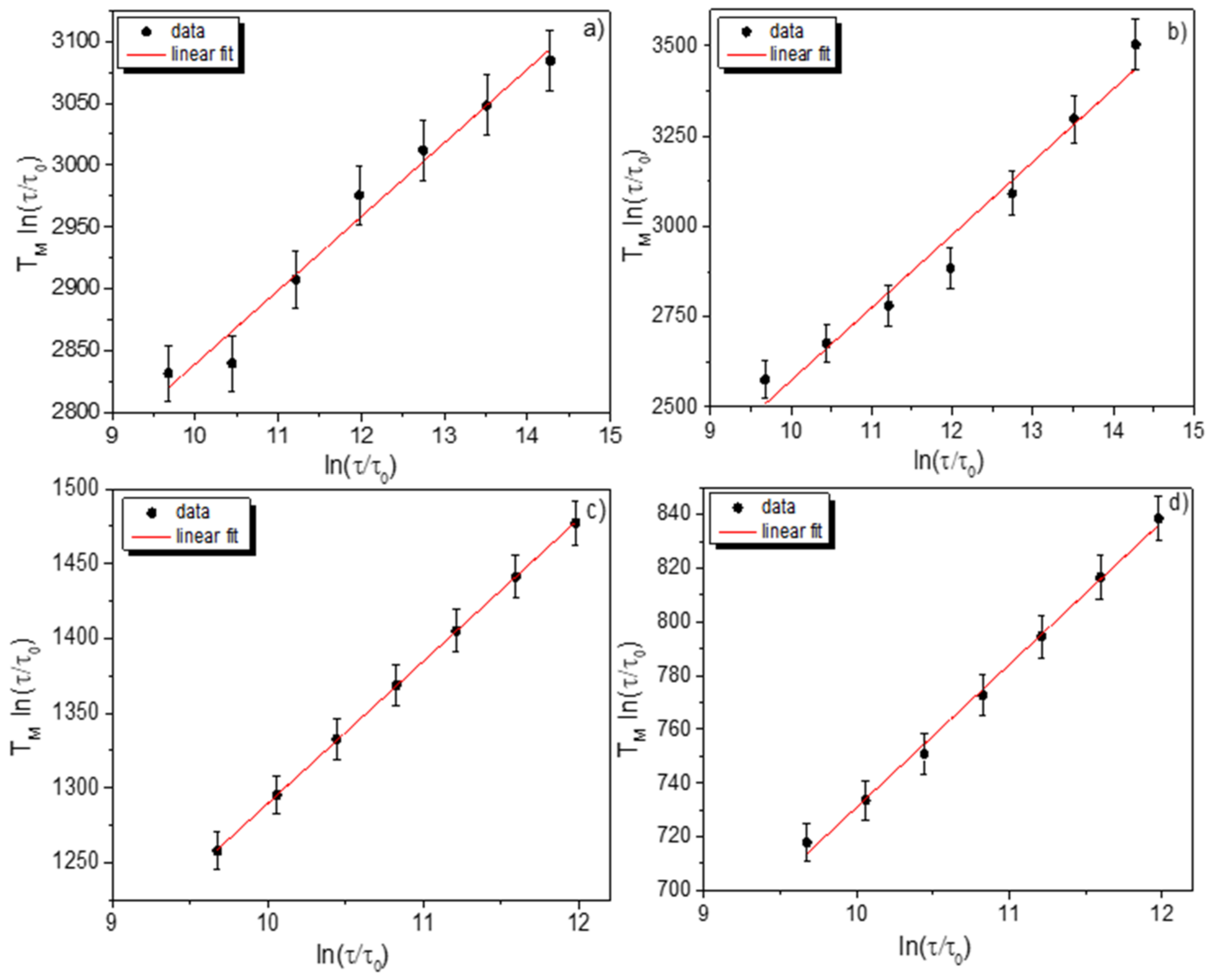
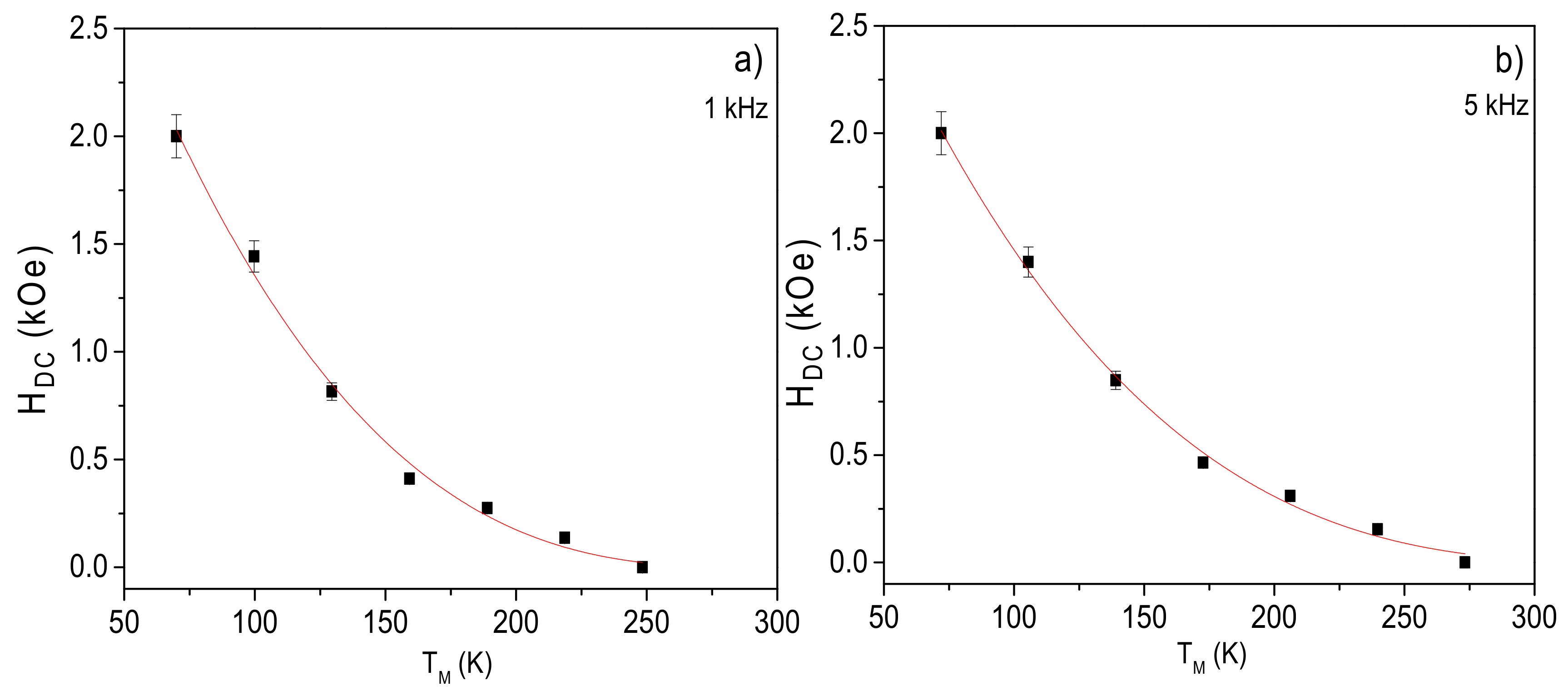
2.3. Almeida-Thouless Plot
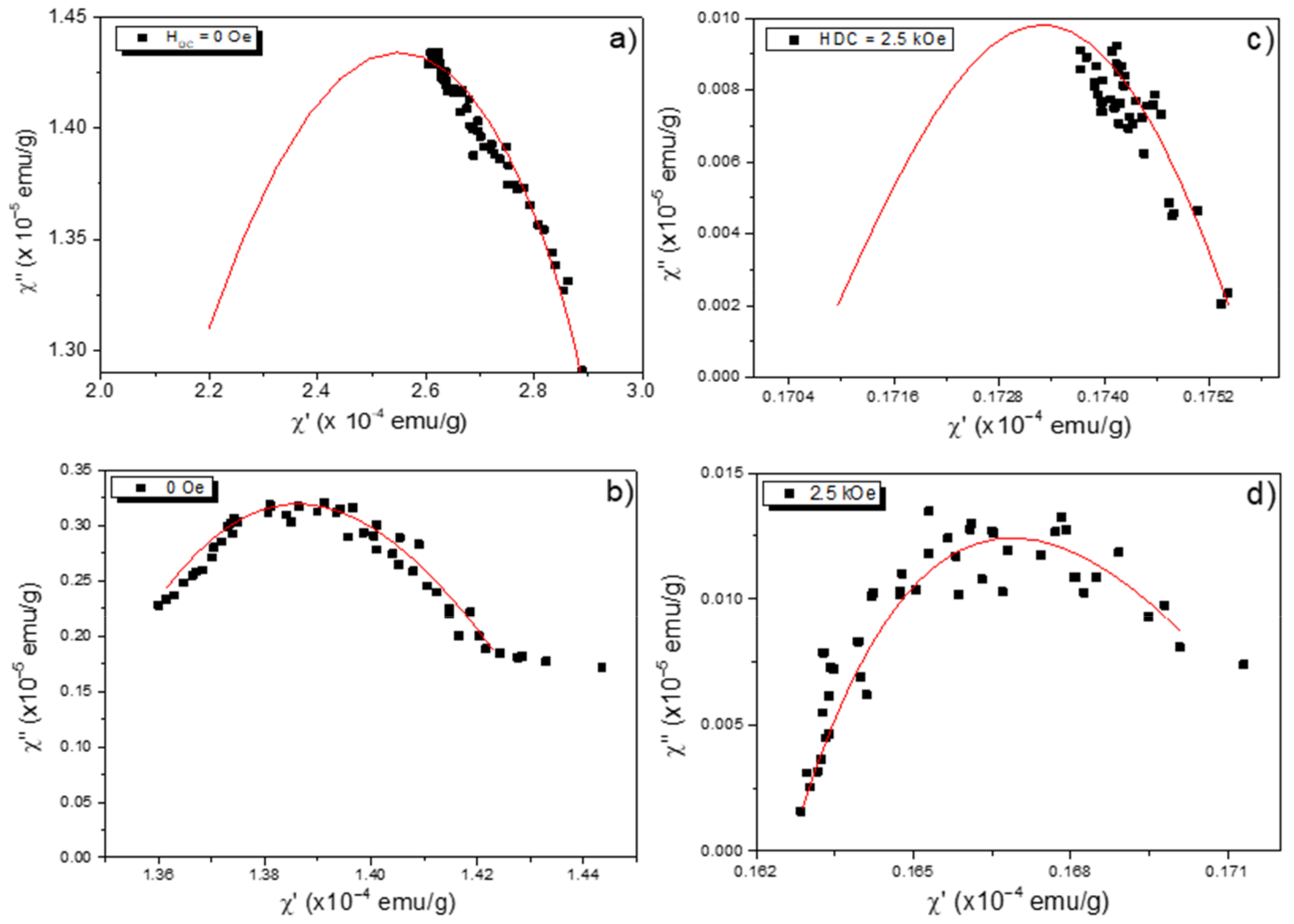
2.4. Argand Diagrams
3. Materials and Methods
Synthesis and Magnetic Characterization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kheirkhah, P.; Denyer, S.; Bhimani, A.D.; Arnone1, G.D.; Esfahani, D.R.; Aguilar, T.; Zakrzewski, J.; Venugopal, I.; Habib, N.; Gallia, G.L.; et al. Magnetic Drug Targeting: A Novel Treatment for Intramedullary Spinal Cord Tumors. Sci. Rep. 2018, 8, 11417. [Google Scholar] [CrossRef]
- Saleem, H.; Zaidi, S.J. Recent Developments in the Application of Nanomaterials in Agroecosystems. Nanomaterials 2020, 10, 2411. [Google Scholar] [CrossRef]
- Khan, F.S.A.; Mubarak, N.M.; Khalid, M.; Walvekar, R.; Abdullah, E.C.; Mazari, S.A.; Nizamuddin, S.; Karri, R.R. Magnetic nanoadsorbents’potential route for heavy metals removal—A review. Environ. Sci. Pollut. Res. 2020, 27, 24342–24356. [Google Scholar] [CrossRef]
- Guivar, J.A.R.; Sadrollahi, E.; Menzel, D.; Fernandes, E.G.R.; López, E.O.; Torres, M.M.; Arsuaga, J.M.; Arencibia, A.; Litterst, F.J. Magnetic, structural and surface properties of functionalized maghemite nanoparticles for copper and lead adsorption. RSC Adv. 2017, 7, 28763. [Google Scholar] [CrossRef]
- Guivar, J.A.R.; Bustamante, A.; Gonzalez, J.C.; Sanches, E.A.; Morales, M.A.; Raez, J.M.; López-Muñoz, M.J.; Arencibia, A. Adsorption of arsenite and arsenate on binary and ternary magnetic nanocomposites with high iron oxide content. Appl. Surf. Sci. 2018, 454, 87–100. [Google Scholar] [CrossRef]
- Ramos-Guivar, J.A.; Taipe, K.; Schettino Jr, M.A.; Silva, E.; Torres, M.A.M.; Passamani, E.C.; Litterst, F.J. Improved removal capacity and equilibrium time of maghemite nanoparticles growth in zeolite type 5A for Pb(II) adsorption. Nanomaterials 2020, 10, 1668. [Google Scholar] [CrossRef]
- Morales, M.P.; Veintemillas-Verdaguer, S.; Monteo, M.I.; Serna, C.J.; Roig, A.; Casas, L.L.; Martínez, B.; Sandiumenge, F. Surface Internal spin canting in γ-Fe2O3 nanoparticles. Chem. Mater. 1999, 11, 3058–3064. [Google Scholar] [CrossRef]
- Ramos-Guivar, J.A.; López, E.O.; Greneche, J.M.; Litterst, F.J.; Passamani, E.C. Effect of EDTA organic coating on the spin canting behavior of maghemite nanoparticles for lead (II) adsorption. Appl. Surf. Sci. 2021, 538, 148021. [Google Scholar] [CrossRef]
- Phan, M.-H.; Alonso, J.; Khurshid, H.; Lampen-Kelley, P.; Chandra, S.; Repa, K.S.; Nemati, Z.; Das, R.; Iglesias, O.; Srikanth, H. Exchange Bias Effects in Iron Oxide-Based Nanoparticle Systems. Nanomaterials 2016, 6, 221. [Google Scholar] [CrossRef]
- Bedanta, S.; Kleemann, W. Superparamagnetism. J. Phys. D Appl. Phys. 2009, 42, 013001. [Google Scholar] [CrossRef]
- Ramos-Guivar, J.A.; Krohling, A.C.; López, E.O.; Litterst, F.J.; Passamani, E.C. Superspinglass behavior of maghemite nanoparticles dispersed in mesoporous silica. J. Magn. Magn. Mater. 2019, 485, 142–150. [Google Scholar] [CrossRef]
- Akhter, S.; Hakim, M.A.; Hoque, S.M.; Das, H.N. Disorder magnetic behavior of Zn-substituted Cu1-xZnxFe2O4 spinel ferrites. Solid State Commun. 2021, 326, 114181. [Google Scholar] [CrossRef]
- Zhang, X.X.; Wen, G.H.; Xiao, G.; Sun, S. Magnetic relaxation of diluted and self-assembled cobalt nanocrystals. J. Magn. Magn. Mater. 2003, 261, 21–28. [Google Scholar] [CrossRef]
- Balanda, M. AC susceptibility studies of phase transitions and magnetic relaxation: Conventional, Molecular and Low-Dimensional Magnets. Acta Phys. Pol. A 2013, 124, 964–976. [Google Scholar] [CrossRef]
- Gonzalez, J.F. Isotopic Enrichments of Lanthanide Based Single Molecule Magnets. Ph.D. Thesis, Université Rennes 1, Rennes, France, 2019. [Google Scholar]
- Peng, H.-X. Multifunctional Polymer Nanocomposites, Chapter 8: Polyurethane Nanocomposite Coatings for Aeronautical Applications; CRC Press: Cleveland, OH, USA, 2011; p. 361. ISBN 978-1-4398-1682-0. [Google Scholar]
- Cunha, C.; Panseri, S.; Iannazzo, D.; Piperno, A.; Pistone, A.; Fazio, M.; Russo, A.; Marcacci, M.; Galvagno, S. Hybrid composites made of multiwalled carbon nanotubes functionalized with Fe3O4 nanoparticles for tissue engineering applications. Nanotechnology 2012, 23, 465102. [Google Scholar] [CrossRef]
- Demir, A.; Baykal, A.; Sözeri, H.; Topkaya, R. Low temperature magnetic investigation of Fe3O4 nanoparticles filled into multiwalled carbon nanotubes. Synth. Met. 2014, 187, 75–80. [Google Scholar] [CrossRef]
- Hua, M.; Zhang, S.; Pan, B.; Zhang, W.; Lv, L.; Zhang, Q. Heavy metal removal from water/waste water by nanosized metal oxides: A review. J. Hazard. Mater. 2012, 211–212, 317–331. [Google Scholar] [CrossRef]
- Muniz, E.P.; de Assuncao, L.S.D.; de Souza, L.M.; Ribeiro, J.J.K.; Marques, W.P.; Pereira, R.D.; Porto, P.S.S.; Proveti, J.R.C.; Passamani, E.C. On cobalto ferrite production by sol-gel from orange fruit residue by three related procedures and its application in oil removal. J. Clean. Prod. 2020, 265, 121712. [Google Scholar] [CrossRef]
- Fossati, A.; Alho, M.M.; Jacobo, S.E. Covalent functionalized magnetic nanoparticles for crude oil recovery. Mater. Chem. Phys. 2019, 238, 121910. [Google Scholar] [CrossRef]
- Zhang, J.; Shao, Y.; Hsieh, C.-T.; Chen, Y.F.; Su, T.-C.; Hsu, J.-P.; Juang, R.-S. Synthesis of magnetic iron oxide nanoparticles onto fluorinated carbon fabrics for contaminant removal and oil-water separation. Sep. Purif. Technol. 2017, 174, 312–319. [Google Scholar] [CrossRef]
- Ramos-Guivar, J.A.; Gonzalez-Gonzalez, J.C.; Litterst, F.J.; Passamani, E.C. Rietveld refinement, μ-Raman, XPS, and Mössbauer studies of metal oxide—Nanoparticles growth on multiwall carbon nanotubes and graphene oxide. Cryst. Growth Des. 2021. [Google Scholar] [CrossRef]
- Aslibeiki, B.; Kameli, P.; Salamati, H.; Eshraghi, M.; Tahmasebi, T. Superspin glass state in MnFe2O4 nanoparticles. J. Magn. Magn. Mater. 2010, 322, 2929–2934. [Google Scholar] [CrossRef]
- Bruvera, I.J.; Zélis, P.M.; Calatayud, M.P.; Goya, G.F.; Sánchez, F.H. Determination of the blocking temperature of magnetic nanoparticles: The good, the bad, and the ugly. J. Appl. Phys. 2015, 118, 184304. [Google Scholar] [CrossRef]
- Shtrikman, S.; Wohlfarth, E.P. The theory of the Vogel-Fulcher law of spin glasses. Phys. Lett. A 1981, 85, 467–470. [Google Scholar] [CrossRef]
- Dormann, J.I.; Bessais, L.; Fiorani, D. A dynamic study of small interacting particles: Superparamagnetic model and spin-glass laws. J. Phys. C Solid State Phys. 1988, 21, 2015–2034. [Google Scholar] [CrossRef]
- Khurshid, H.; Lampen-Kelley, P.; Iglesias, O.; Alonso, J.; Phan, M.; Sun, C.-J.; Saboungi, M.-L.; Srikanth, H. Spin-glass-like freezing of inner and outer surface layers in hollow γ-Fe2O3 nanoparticles. Sci. Rep. 2015, 5, 15054. [Google Scholar] [CrossRef]
- Fertman, E.; Dolya, S.; Desnenko, V.; Beznosov, A.; Kajňaková, M.; Fecher, A. Cluster glass magnetism in the phase-separated Nd2/3Ca1/3MnO3 perovskite. J. Magn. Magn. Mater. 2012, 324, 3213–3217. [Google Scholar] [CrossRef][Green Version]
- Balanda, M.; Tomkowicz, Z.; Haase, W.; Rams, M. Single-chain magnet features in 1D [MnR4TPP][TCNE] compounds. J. Phys. Conf. Ser. 2011, 303, 012036. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Budnick, J.I.; Hines, W.A.; Chien, C.L.; Xiao, J.Q. Effect of magnetic field on the superparamagnetic relaxation in granular Co-Ag samples. Appl. Phys. Lett. 1998, 72, 2053. [Google Scholar] [CrossRef]
- Suzuki, M.; Fullem, S.I.; Suzuki, I.S.; Wang, L.; Zhong, C.-H. Observation of superspin-glass behavior in Fe3O4 nanoparticles. Phys. Rev. B 2009, 79, 024418. [Google Scholar] [CrossRef]
- Ramos-Guivar, J.A.; Passamani, E.C.; Litterst, J. Superspinglass state in functionalized zeolite 5A-maghemite nanoparticles. AIP Adv. 2021, 11, 035223. [Google Scholar] [CrossRef]
| HDC (Oe) | T0 (K) | (K) |
|---|---|---|
| 0 | 59.5 (4) | 2244 (5) |
| 500 | 202 (5) | 556 (5) |
| 1000 | 95 (3) | 338 (4) |
| 2000 | 53 (1) | 199 (4) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos-Guivar, J.A.; Litterst, F.J.; Passamani, E.C. AC Susceptibility Studies under DC Fields in Superspinglass Nanomaghemite-Multiwall Carbon Nanotube Hybrid. Magnetochemistry 2021, 7, 52. https://doi.org/10.3390/magnetochemistry7040052
Ramos-Guivar JA, Litterst FJ, Passamani EC. AC Susceptibility Studies under DC Fields in Superspinglass Nanomaghemite-Multiwall Carbon Nanotube Hybrid. Magnetochemistry. 2021; 7(4):52. https://doi.org/10.3390/magnetochemistry7040052
Chicago/Turabian StyleRamos-Guivar, Juan A., F. Jochen Litterst, and Edson C. Passamani. 2021. "AC Susceptibility Studies under DC Fields in Superspinglass Nanomaghemite-Multiwall Carbon Nanotube Hybrid" Magnetochemistry 7, no. 4: 52. https://doi.org/10.3390/magnetochemistry7040052
APA StyleRamos-Guivar, J. A., Litterst, F. J., & Passamani, E. C. (2021). AC Susceptibility Studies under DC Fields in Superspinglass Nanomaghemite-Multiwall Carbon Nanotube Hybrid. Magnetochemistry, 7(4), 52. https://doi.org/10.3390/magnetochemistry7040052







