Thermodynamics of General Heisenberg Spin Tetramers Composed of Coupled Quantum Dimers
Abstract
1. Introduction
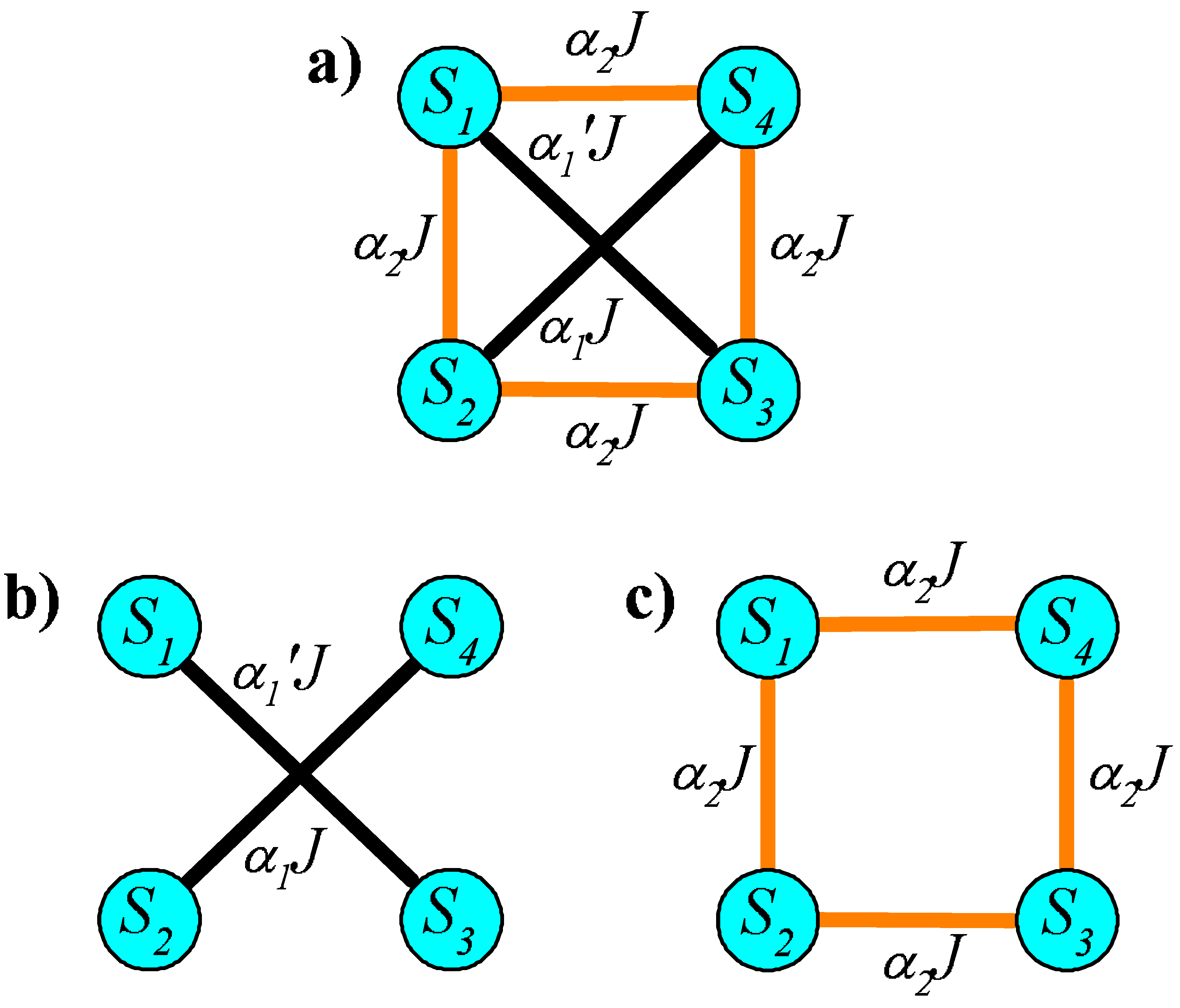
2. The Quantum Spin Tetramer Representation
3. General Quantum Spin Tetramer
4. Ground-State Energy Levels and Heat Capacities
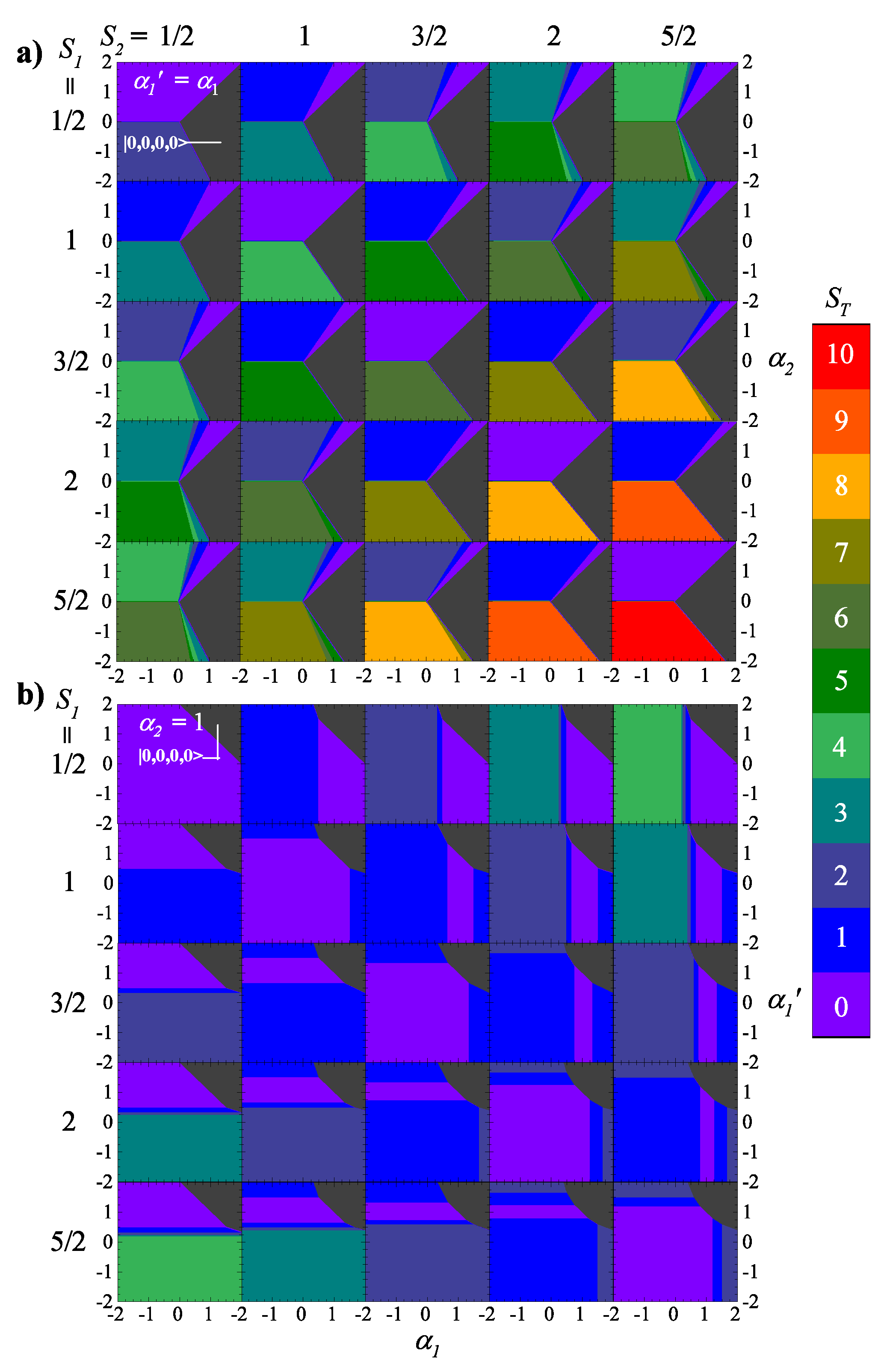
4.1. Zero-Field Ground-State Energies and Heat Capacities
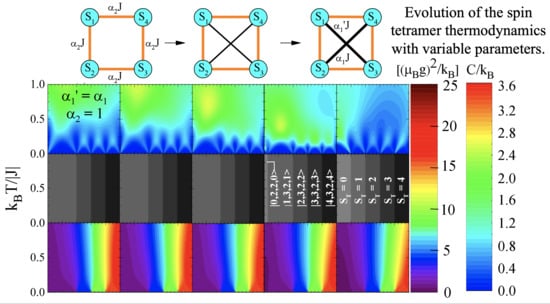
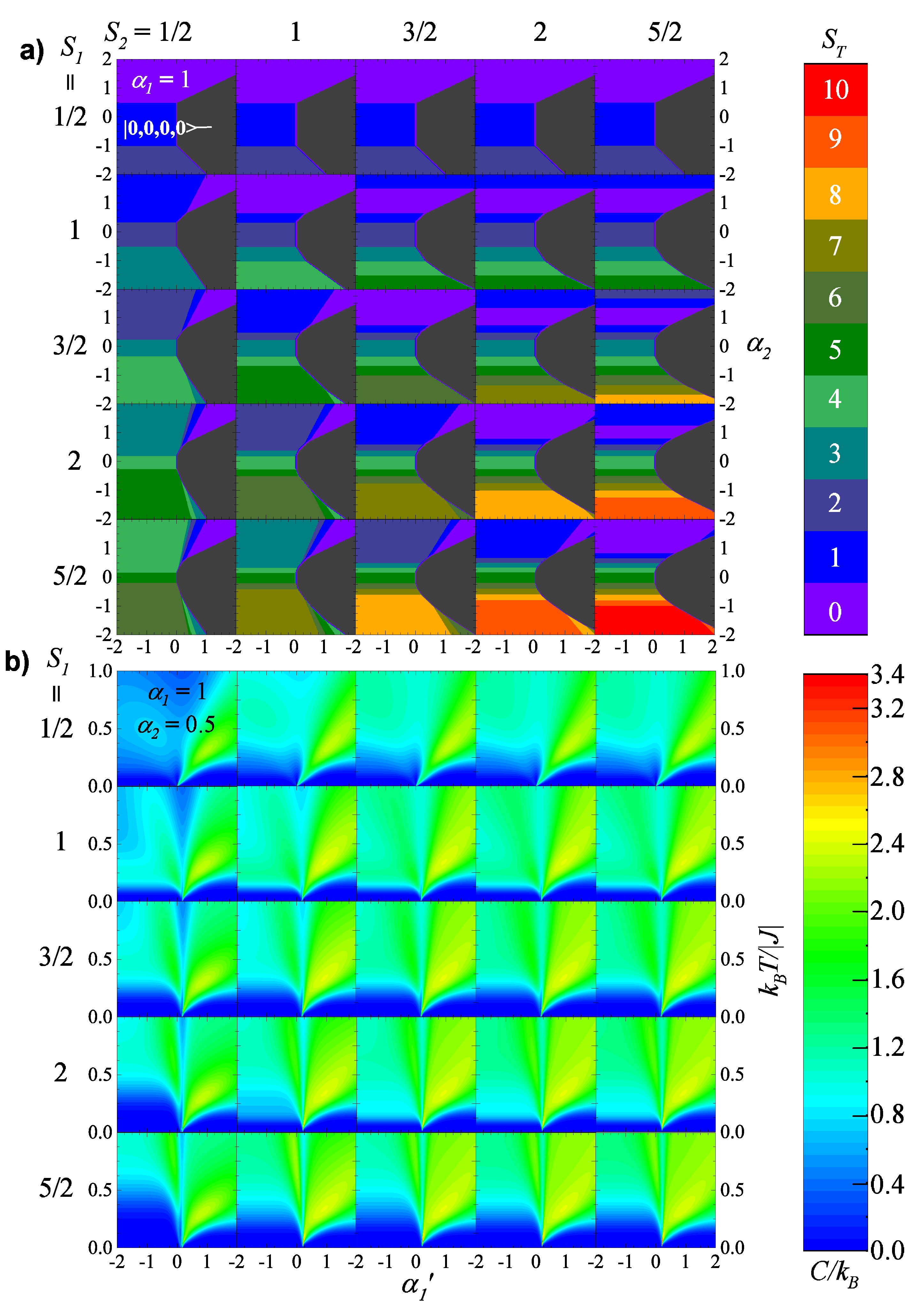
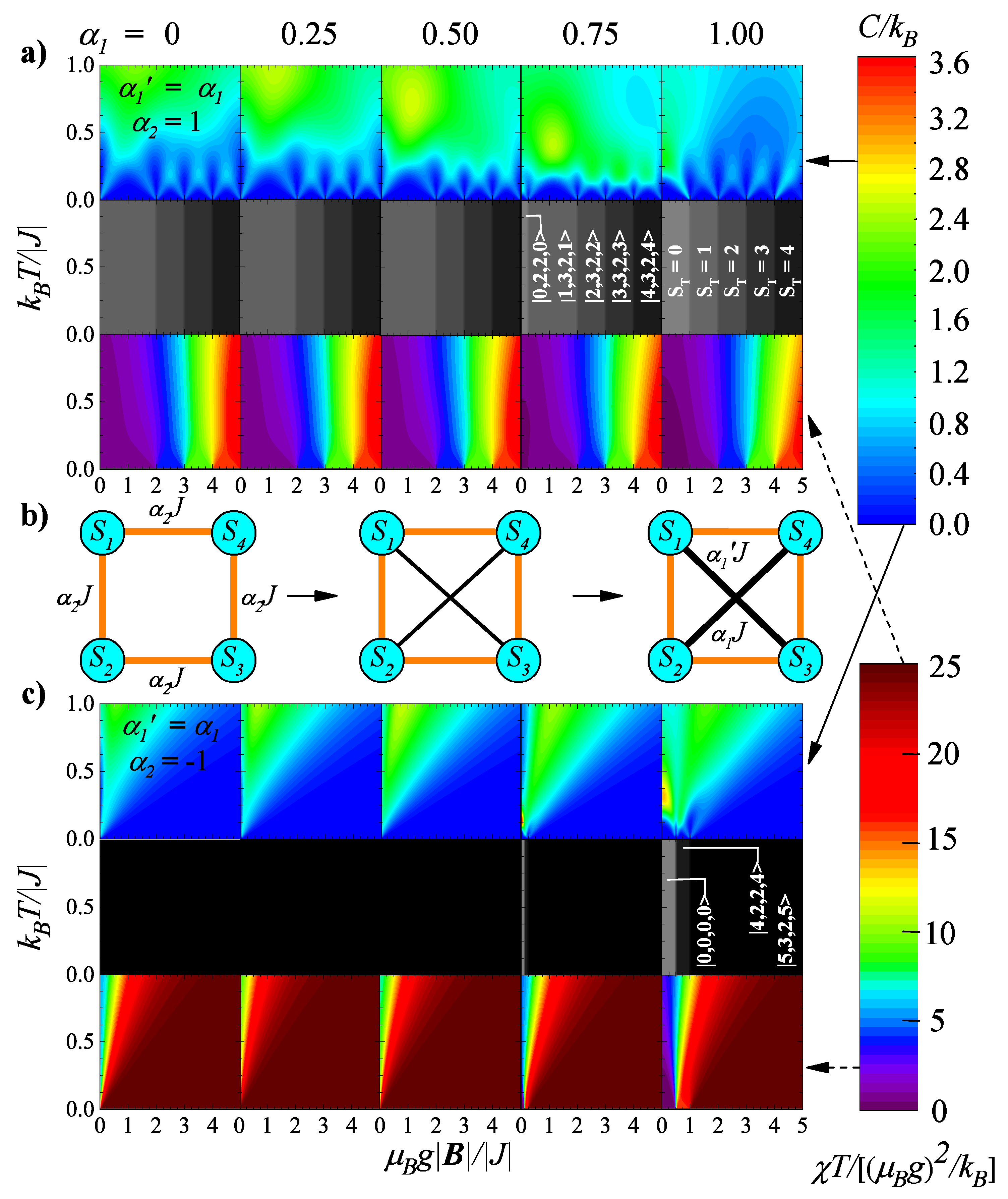
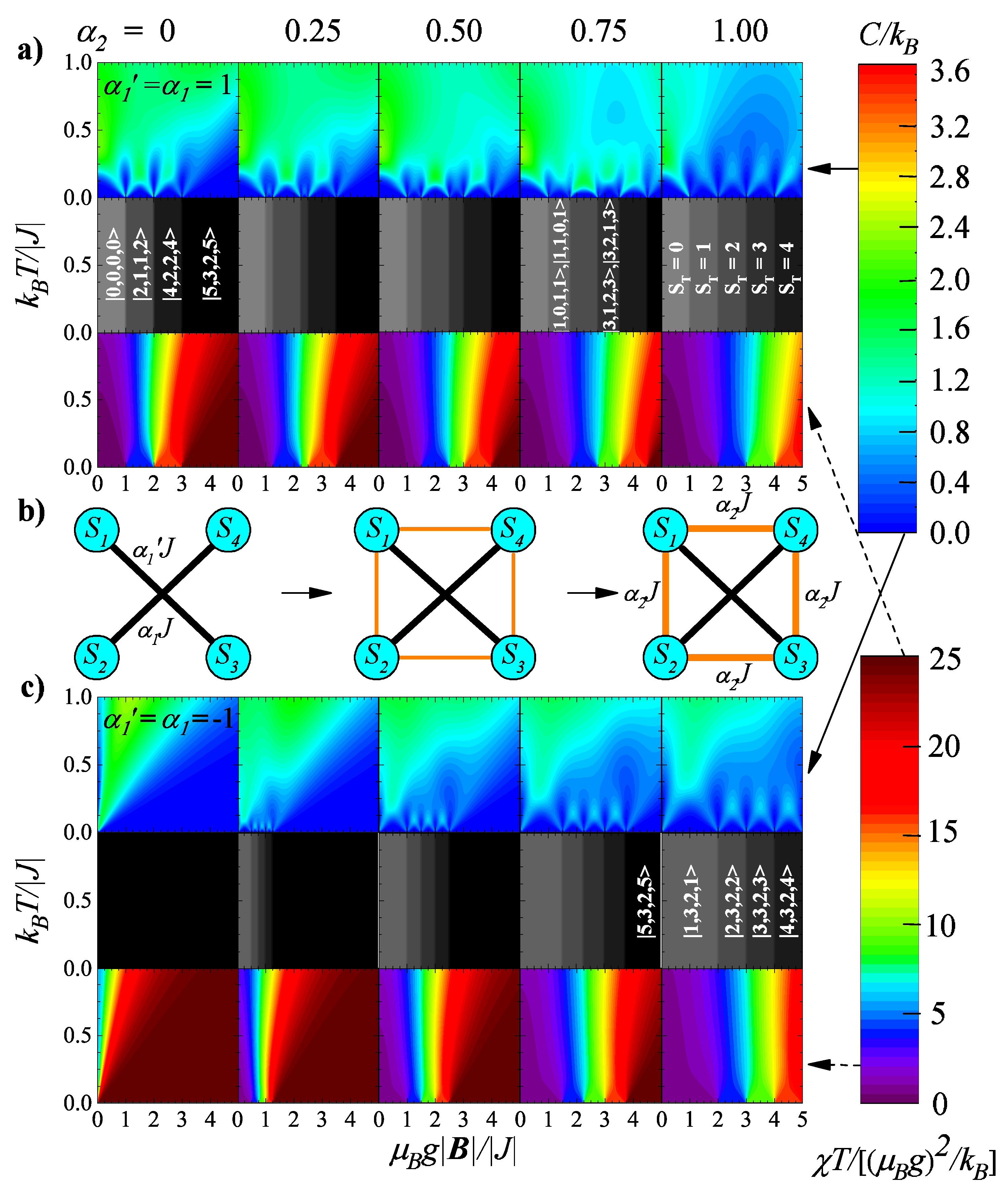
4.2. Heat Capacities in the Presence of a Magnetic Field
5. Magnetic Susceptibility
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meier, F.; Levy, J.; Loss, D. Quantum computing with antiferromagnetic spin clusters. Phys. Rev. B 2003, 68, 134417. [Google Scholar] [CrossRef]
- Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120–126. [Google Scholar] [CrossRef]
- Mironov, V.S.; Chibotaru, L.F.; Ceulemans, A. Mechanism of a Strongly Anisotropic MoIII-CN-MnII Spin-Spin Coupling in Molecular Magnets Based on the [Mo(CN)7]4-Heptacyanometalate: A New Strategy for Single-Molecule Magnets with High Blocking Temperatures. J. Am. Chem. Soc. 2003, 125, 9750–9760. [Google Scholar] [CrossRef]
- Pederson, M.R.; Porezag, D.V.; Kortus, J. Theoretical calculations of magnetic order and anisotropy energies in molecular magnets. J. Appl. Phys. 2000, 87, 5487. [Google Scholar] [CrossRef]
- Barra, A.L.; Caneschi, A.; Cornia, A.; Fabrizi de Biani, F.; Gatteschi, D.; Sangregorio, C.; Sessoli, R.; Sorace, L. Single-Molecule Magnet Behavior of a Tetranuclear Iron(III) Complex. The Origin of Slow Magnetic Relaxation in Iron(III) Clusters. J. Am. Chem. Soc. 1999, 121, 5302–5310. [Google Scholar] [CrossRef]
- DiVincenzo, D.P.; Loss, D. Quantum computers and quantum coherence. J. Magn. Magn. Mater. 1999, 200, 202–218. [Google Scholar] [CrossRef]
- Cornia, A.; Sessoli, R.; Sorace, L.; Gatteschi, D.; Barra, A.L.; Daiguebonne, C. Origin of Second-Order Transverse Magnetic Anisotropy in Mn12-Acetate. Phys. Rev. Lett. 2002, 89, 257201. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wu, B.; Fu, L.; Diener, R.B.; Niu, Q. Quantum step heights in hysteresis loops of molecular magnets. Phys. Rev. B 2002, 65, 224401. [Google Scholar] [CrossRef]
- Leuenberger, M.N.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Houchins, G.; Haraldsen, J.T. Generalization of polarized spin excitations for asymmetric dimeric systems. Phys. Rev. B 2015, 91, 014422. [Google Scholar] [CrossRef]
- Meier, F.; Levy, J.; Loss, D. Quantum Computing with Spin Cluster Qubits. Phys. Rev. Lett. 2003, 90, 047901. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A.; Chuang, I.; Grover, L.K. Quantum Computation and Quantum Information. Am. J. Phys. 2002, 70, 558. [Google Scholar] [CrossRef]
- Tyagi, P. Molecular spin devices: Current understanding and new territories. Nano 2009, 4, 325–338. [Google Scholar] [CrossRef]
- Ardavan, A.; Rival, O.; Morton, J.J.L.; Blundell, S.J.; Tyryshkin, A.M.; Timco, G.A.; Winpenny, R.E.P. Will Spin-Relaxation Times in Molecular Magnets Permit Quantum Information Processing? Phys. Rev. Lett. 2007, 98, 057201. [Google Scholar] [CrossRef]
- Bogani, L.; Wernsdorfer, W. Molecular Spintronics Using Single-Molecule Magnets; Nanoscience and Technology, Macmillan Publishers Ltd.: London, UK, 2009; pp. 194–201. [Google Scholar]
- Ardavan, A.; Blundell, S.J. Storing quantum information in chemically engineered nanoscale magnets. J. Mater. Chem. 2009, 19, 1754–1760. [Google Scholar] [CrossRef]
- Haraldsen, J.T.; Barnes, T.; Musfeldt, J.L. Neutron scattering and magnetic observables for S = 1/2 spin clusters and molecular magnets. Phys. Rev. B 2005, 71, 064403. [Google Scholar] [CrossRef]
- Bose, I.; Tribedi, A. Thermal entanglement properties of small spin clusters. Phys. Rev. A 2005, 72, 022314. [Google Scholar] [CrossRef]
- Brumfield, A.; Haraldsen, J.T. Thermodynamics and Magnetic Excitations in Quantum Spin Trimers: Applications for the Understanding of Molecular Magnets. Crystals 2019, 9, 93. [Google Scholar] [CrossRef]
- Roxburgh, A.; Haraldsen, J.T. Thermodynamics and spin mapping of quantum excitations in a Heisenberg spin heptamer. Phys. Rev. B 2018, 98, 214434. [Google Scholar] [CrossRef]
- Haraldsen, J.T. Heisenberg Pentamer: Insights into Inelastic Neutron Scattering on Magnetic Clusters. Phys. Rev. Lett. 2011, 107, 037205. [Google Scholar] [CrossRef]
- Haraldsen, J.T. Evolution of thermodynamic properties and inelastic neutron scattering intensities for spin-12 antiferromagnetic quantum rings. Phys. Rev. B 2016, 94, 054436. [Google Scholar] [CrossRef]
- Dagotto, E.; Rice, T.M. Surprises on the Way from One- to Two-Dimensional Quantum Magnets: The Ladder Materials. Science 1996, 271, 618. [Google Scholar] [CrossRef]
- Goswami, S.; Mondal, A.K.; Konar, S. Nanoscopic molecular magnets. Inorg. Chem. Front. 2015, 2, 687–712. [Google Scholar] [CrossRef]
- Darradi, R.; Derzhko, O.; Zinke, R.; Schulenburg, J.; Krüger, S.E.; Richter, J. Ground state phases of the spin-1/2 J1--J2 Heisenberg antiferromagnet on the square lattice: A high-order coupled cluster treatment. Phys. Rev. B 2008, 78, 214415. [Google Scholar] [CrossRef]
- Clemente, J.M.; Andres, H.; Aebersold, M.; Borrás-Almenar, J.J.; Coronado, E.; Güdel, H.U.; Büttner, H.; Kearly, G. Magnetic Excitations in Tetrameric Clusters of Polyoxometalates Observed by Inelastic Neutron Scattering. Evidence for Anisotropic Exchange Interactions in Cobalt(II) Clusters. Inorg. Chem. 1997, 36, 2244–2245. [Google Scholar] [CrossRef] [PubMed]
- Hase, M.; Nakajima, K.; Ohira-Kawamura, S.; Kawakita, Y.; Kikuchi, T.; Matsumoto, M. Magnetic excitations in the spin-12 tetramer substance Cu2114Cd11B2O6 obtained by inelastic neutron scattering experiments. Phys. Rev. B 2015, 92, 184412. [Google Scholar] [CrossRef]
- Haraldsen, J.T.; Stone, M.B.; Lumsden, M.D.; Barnes, T.; Jin, R.; Taylor, J.W.; Fernandez-Alonso, F. Spin-lozenge thermodynamics and magnetic excitations in Na3RuO4. J. Phys. Condens. Matter 2009, 21, 506003. [Google Scholar] [CrossRef] [PubMed]
- Andres, H.; Clemente-Juan, J.M.; Aebersold, M.; Güdel, H.U.; Coronado, E.; Büttner, H.; Kearly, G.; Melero, J.; Burriel, R. Magnetic Excitations in Polyoxometalate Clusters Observed by Inelastic Neutron Scattering: Evidence for Anisotropic Ferromagnetic Exchange Interactions in the Tetrameric Cobalt(II) Cluster [Co4(H2O)2(PW9O34)2]10-. Comparison with the Magnetic and Specific Heat Properties. J. Am. Chem. Soc. 1999, 121, 10028–10034. [Google Scholar] [CrossRef]
- Bodnar, S.Y.; Šmejkal, L.; Turek, I.; Jungwirth, T.; Gomonay, O.; Sinova, J.; Sapozhnik, A.A.; Elmers, H.J.; Kläui, M.; Jourdan, M. Writing and reading antiferromagnetic Mn2Au by Néel spin-orbit torques and large anisotropic magnetoresistance. Nat. Commun. 2018, 9, 348. [Google Scholar] [CrossRef]
- Gatteschi, D.; Caneschi, A.; Pardi, L.; Sessoli, R. Large Clusters of Metal Ions: The Transition from Molecular to Bulk Magnets. Science 1994, 265, 1054. [Google Scholar] [CrossRef]
- Szaĺowski, K.; Kowalewska, P. Magnetocaloric Effect in Cu5-NIPA Molecular Magnet: A Theoretical Study. Materials 2020, 13, 485. [Google Scholar] [CrossRef]
- Szalowski, K. Low-Temperature Magnetocaloric Properties of V12 Polyoxovanadate Molecular Magnet: A Theoretical Study. Materials 2020, 13, 4399. [Google Scholar] [CrossRef]
- Čenčariková, H.; Strečka, J. Unconventional strengthening of the bipartite entanglement of a mixed spin-(1/2,1) Heisenberg dimer achieved through Zeeman splitting. Phys. Rev. B 2020, 102, 184419. [Google Scholar] [CrossRef]
- Torrico, J.; Plascak, J.A. Ground state and thermodynamic properties of spin-1/2 isosceles Heisenberg triangles for V6-like magnetic molecules. Phys. Rev. E 2020, 102, 062116. [Google Scholar] [CrossRef]
- Kowalewska, P.; Szaĺ‚owski, K. Magnetocaloric properties of V6 molecular magnet. J. Magn. Magn. Mater. 2020, 496, 165933. [Google Scholar] [CrossRef]
- KarǏová, K.; Strečka, J.; Richter, J. Enhanced magnetocaloric effect in the proximity of magnetization steps and jumps of spin-1/2 XXZ Heisenberg regular polyhedra. J. Phys. Condens. Matter 2017, 29, 125802. [Google Scholar] [CrossRef] [PubMed]
- Karlóvá, K.; Strečka, J.; Hanis, J.; Hagiwara, M. Insights into Nature of Magnetization Plateaus of a Nickel Complex [Ni4(μ-CO3)2(aetpy)8](ClO4)4 from a Spin-1 Heisenberg Diamond Cluster. Magnetochemistry 2020, 6, 59. [Google Scholar] [CrossRef]
- Karľová, K.; Strečka, J.; Madaras, T. The Schottky-type specific heat as an indicator of relative degeneracy between ground and first-excited states: The case study of regular Ising polyhedra. Phys. B Condens. Matter 2016, 488, 49–56. [Google Scholar] [CrossRef]
- MacKay, H.B.; Woolf, L.D.; Maple, M.B.; Johnson, D.C. Specific-Heat Anomalies at the Lower Critical Temperature in Reentrant Ferromagnetic Superconductors. Phys. Rev. Lett. 1979, 42, 918–921. [Google Scholar] [CrossRef]
- Pathak, A.K.; Paudyal, D.; Mudryk, Y.; Gschneidner, K.A.; Pecharsky, V.K. Anomalous Schottky Specific Heat and Structural Distortion in Ferromagnetic PrAl2. Phys. Rev. Lett. 2013, 110, 186405. [Google Scholar] [CrossRef]
- Blundell, S.; Blundell, K. Concepts in Thermal Physics; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Yamase, T.; Ishikawa, E.; Fukaya, K.; Nojiri, H.; Taniguchi, T.; Atake, T. Spin-Frustrated (VO)36+-Triangle-Sandwiching Octadecatungstates as a New Class of Molecular Magnets. Inorg. Chem. 2004, 43, 8150–8157. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Fu, Y.S.; Ji, S.H.; Zhang, T.; Cheng, P.; Ma, X.C.; Zou, X.L.; Duan, W.H.; Jia, J.F.; Xue, Q.K. Probing Superexchange Interaction in Molecular Magnets by Spin-Flip Spectroscopy and Microscopy. Phys. Rev. Lett. 2008, 101, 197208. [Google Scholar] [CrossRef] [PubMed]
- Leger, J.M.; Loriers-Susse, C.; Vodar, B. Pressure Effect on the Curie Temperatures of Transition Metals and Alloys. Phys. Rev. B 1972, 6, 4250–4261. [Google Scholar] [CrossRef]
- Strečka, J.; Karľová, K.; Madaras, T. Giant magnetocaloric effect, magnetization plateaux and jumps of the regular Ising polyhedra. Phys. B Condens. Matter 2015, 466–467, 76–85. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dyszel, P.; Haraldsen, J.T. Thermodynamics of General Heisenberg Spin Tetramers Composed of Coupled Quantum Dimers. Magnetochemistry 2021, 7, 29. https://doi.org/10.3390/magnetochemistry7020029
Dyszel P, Haraldsen JT. Thermodynamics of General Heisenberg Spin Tetramers Composed of Coupled Quantum Dimers. Magnetochemistry. 2021; 7(2):29. https://doi.org/10.3390/magnetochemistry7020029
Chicago/Turabian StyleDyszel, Peter, and Jason T. Haraldsen. 2021. "Thermodynamics of General Heisenberg Spin Tetramers Composed of Coupled Quantum Dimers" Magnetochemistry 7, no. 2: 29. https://doi.org/10.3390/magnetochemistry7020029
APA StyleDyszel, P., & Haraldsen, J. T. (2021). Thermodynamics of General Heisenberg Spin Tetramers Composed of Coupled Quantum Dimers. Magnetochemistry, 7(2), 29. https://doi.org/10.3390/magnetochemistry7020029