Next Article in Journal
Microstructure and Magnetic Properties of Ce14Fe78Co2B6 Nanopowders Prepared by Ball Milling at Low Temperature
Previous Article in Journal
Polarized Neutron Diffraction: An Excellent Tool to Evidence the Magnetic Anisotropy—Structural Relationships in Molecules
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 7
Issue 12
10.3390/magnetochemistry7120159
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Structural, Electronic and Magnetic Properties of Mn2Co1-xVxZ (Z = Ga, Al) Heusler Alloys: An Insight from DFT Study

by
Fatima Abuova
1,*,
Talgat Inerbaev
1,2,
Aisulu Abuova
1,
Nurpeis Merali
1,
Nurgul Soltanbek
1,
Gulbanu Kaptagay
3,
Marina Seredina
4 and
Vladimir Khovaylo
4
1
Department of Technical Physics, International Department of Nuclear Physics, New Materials and Technologies, L.N.Gumilyov Eurasian National University, Nur-Sultan 010000, Kazakhstan
2
Laboratory of Phase Transitions and Diagrams of the Earth’s Matter under High Pressure, Sobolev Institute of Geology and Mineralogy, 630058 Novosibirsk, Russia
3
Physics Department, Kazakh National Women’s Teacher Training University, Almaty 050000, Kazakhstan
4
Department of Functional Nanosystems and High-Temperature Materials, National University of Science and Technology “MISIS”, 119049 Moscow, Russia
*
Author to whom correspondence should be addressed.
Magnetochemistry 2021, 7(12), 159; https://doi.org/10.3390/magnetochemistry7120159
Submission received: 25 October 2021 / Revised: 3 December 2021 / Accepted: 3 December 2021 / Published: 8 December 2021
(This article belongs to the Section Spin Crossover and Spintronics)
Browse Figures
Review Reports Versions Notes

Abstract

:
Structural, electronic, and magnetic properties of Mn2Co1-xVxZ (Z = Ga, Al, x = 0, 0.25, 0.5, 0.75, 1) Heusler alloys were theoretically investigated for the case of L21 (space group Fm 3 ¯ m), L21b (L21 structure with partial disordering between Co and Mn atoms) and XA (space group F 4 ¯ 3m) structures. It was found that the XA structure is more stable at low V concentrations, while the L21 structure is energetically favorable at high V concentrations. A transition from L21 to XA ordering occurs near x = 0.5, which qualitatively agrees with the experimental results. Comparison of the energies of the L21b and XA structures leads to the fact that the phase transition between these structures occurs at x = 0.25, which is in excellent agreement with the experimental data. The lattice parameters linearly change as x grows. For the L21 structure, a slight decrease in the lattice constant a was observed, while for the XA structure, an increase in a was found. The experimentally observed nonlinear behavior of the lattice parameters with a change in the V content is most likely a manifestation of the presence of a mixture of phases. Almost complete compensation of the magnetic moment was achieved for the Mn2Co1-xVxZ alloy (Z = Ga, Al) at x = 0.5 for XA ordering. In the case of the L21 ordering, it is necessary to consider a partial disorder of atoms in the Mn and Co sublattices in order to achieve compensation of the magnetic moment.

1. Introduction

In recent years, Heusler alloys have been studied extensively because of their diverse magnetic phenomena [1]. Among them, Mn-based Heusler alloys have attracted much attention due to their unique properties and potential applications in many technological areas. One of the essential applications of Mn-based Heusler alloys is their use in the field of spintronics—the field of electronics where the transfer of energy and information is carried out not by an electric current but by a current of spins. Until now, it has been reported that quite a few Mn-based Heusler alloys are half-metals or spin-gapless semiconductors (SGS) [2,3,4,5,6]. Half-metallic materials exhibit high spin polarization reaching 100% near the Fermi level (EF). These properties allow us to consider them as materials for magnetic sensors or non-volatile random-access memory devices [7]. Thus, their use in devices significantly reduces the energy loss [8].
The SGS are an intermediate state between the well-known half-metallic ferromagnets and gapless semiconductors. In SGS, one spin channel has an open bandgap near EF, like a half-metal, and the other spin channel has a zero bandgap, like in a gapless semiconductor. Thus, conducting electrons or holes are not only 100% spin-polarized but can easily be transferred to an excited state. Among these Mn-based Heusler alloys, Mn2CoZ (Z = Al, Ga) are of particular interest since they are not only theoretically predicted as half-metals/SGS but can also be realized experimentally [2,3,9,10,11].
Heusler alloys X2YZ (X, Y are transition metals, Z is a chemical element from the main group) crystallize in a cubic structure of the Cu2MnAl-type (L21 structure, space group Fm 3 ¯ m), which has four interpenetrating fcc sublattices, namely A, B, C, and D with X, Y, and Z atoms occupying Wyckoff positions 8c (0.25.0.25.0.25), 4b (0.5.0.5.0.5), and 4a (0, 0, 0), respectively. The X atoms are equally occupied in the A and C sublattices. The Y and Z atoms occupy B and D sublattices, respectively. Apart from the usual Cu2MnAl structure, Heusler alloys also crystallize in a structure of the Hg2CuTi-type, commonly known as the inverse Heusler structure (XA structure, space group F 4 ¯ 3m). The main difference of this structure from the conventional L21 structure is the interchange between X atoms in the C sublattice and Y atoms in the B sublattice. These structural models are shown in Figure 1 for the case of X = Mn and Y = Co.
It was shown [12], that the Heusler alloy Mn2CoAl has the electronic structure of SGS that is stable against tetragonal lattice distortions. However, it transforms into a semi-metallic state with an excess of Co or atomic swaps even between sites with different local symmetry. In the case of Mn2CoAl, the doping decreases the bandgap while an increase in the bandgap is noticed for Mn2CoGa. The half-metallicity is destroyed in both cases when the doping level is beyond a certain degree [12]. Despite numerous studies devoted to the electronic structure and magnetic properties of Heusler alloys, this problem remains not fully disclosed.
Recently, the existence of several fully compensated ferrimagnets in the Mn-Co-V-Al, Mn-Co-V-Si, and Mn-Co-V-Ga systems was predicted theoretically [13,14]. Some of the predicted half-metallic ferrimagnets Mn2-xCoxVAl were synthesized and studied [15,16]. The main drawback of these alloys is a low Curie temperature, which is an obstacle to the use of alloys in spintronics. For example, for the composition MnCoVAl, the Curie temperature TC is 105 K [17,18]. More suitable for the use as a spintronic material is Mn1.5FeV0.5Al with a Curie temperature TC = 355 K and almost 100% spin polarization [19]. The highest Curie temperatures were achieved for the Mn-Co-V-Ga system, exceeding 690 K for the Mn2V1-xCoxGa compositions (x = 0; 0.25; 0.5; 0.75; 1). The reported values of TC are the highest among the Mn2V-based fully compensated ferrimagnets. Compensation of the magnetic moment without a significant decrease in TC indicates that the substitution of Co for V does not weaken the exchange interaction in the Mn2VGa alloys [19]. On the other hand, substitution of Co for Mn leads to a decrease in the Curie temperature in Mn2-xCoxVGa alloys (x = 0.5; 0.75; 1) up to 171 K for MnCoVGa composition. In the mean-field approximation, it was found that the antiferromagnetic Mn-V exchange interaction is the strongest interaction and makes a larger contribution to the Curie temperature than ferromagnetic Mn-Mn and V-V exchange interaction [20]. In the Mn2-xCoxVGa alloys, the Curie temperature correlates with the total magnetic moment. With an increase in cobalt concentration, the total magnetic moment per formula unit decreases, which is accompanied by a decrease in TC. Consequently, the Curie temperature for Co2VGa is almost 300 K lower than that for Mn2VGa. [21] Such a low magnetic ordering temperature of Co2VGa as compared to that of Mn2VGa is a consequence of a weak ferromagnetic interaction between Co and V atoms as compared to the strong antiferromagnetic interaction between Mn and V.
Combined study by neutron diffraction measurements and ab initio calculations revealed the crystal structure and magnetic configuration of the Mn2Co1-xVxZ (Z = Al, Ga) alloy. The neutron diffraction data and detailed ab initio studies confirmed the L21 structure for Mn2VGa and the XA structure for Mn2CoGa. It was found that alloys with a high V concentration have the L21 structure. When the Co concentration reaches 75%, a transition from L21 to XA was observed [22]. When the content of Co in the substance is higher than 75%, the lattice constants change nonlinearly. With an equal Co and V atoms content, almost complete compensation of the magnetic moment (0.1 μB/f.u.) was found due to the ferrimagnetic coupling of Mn with V and Co [23].
Powder neutron diffraction experiments suggested that in Heusler Mn2CoGa the atomic arrangement can be described by the so-called L21b-type structure rather than by the XA structure [24]. The L21b-type structure is equivalent to the L21-type structure, where a partial disorder exists between Co and Mn atoms. In this case, the atomic configuration becomes “(Mn, Co), Mn, (Mn, Co), and Z.” The magnetic moments obtained experimentally were in good agreement with the theoretical values in the model of the L21b structure. At the same time, the calculations showed that the L21b structure is metastable with respect to the XA structure [24].
In present work, we theoretically investigate the effect of substitution of Co for V on structural, magnetic, and electronic properties of Mn2Co1-xVxZ (Z = Al, Ga) Heusler alloy for the case of L21 and XA structures.

2. Materials and Methods

Computation Details

Mn2Co1-xVxZ (Z = Al, Ga) Heusler alloy for the case of L21, L21b, and XA structures density functional theory (DFT) with periodic boundary conditions using projector-augmented wave (PAW) [25] method and Perdew-Burke-Ernzerhof (PBE) functional [26] were performed using the ab initio total energy and molecular dynamics program VASP (Vienna Ab initio Simulation Package) [27,28,29]. All calculations were performed with the 4 × 4 × 4 Monkhorst–Pack k-points sampling and 500 eV cut-off energy. The convergence tolerance for the calculations was chosen as the difference in total energy within 10−6 eV/atom. The following electronic configurations were used for the pseudopotentials: Mn (3p63d54s2), Co (3d74s2), V (3s23p63d34s2), Ga (3s23p13d10), Al (3s23p1), respectively. All calculations were performed using 2 × 2 × 2 supercells of the XA and L21 structures, consisting of 128 atoms. Magnetic moments were computed using DDEC6 formalism [30,31].

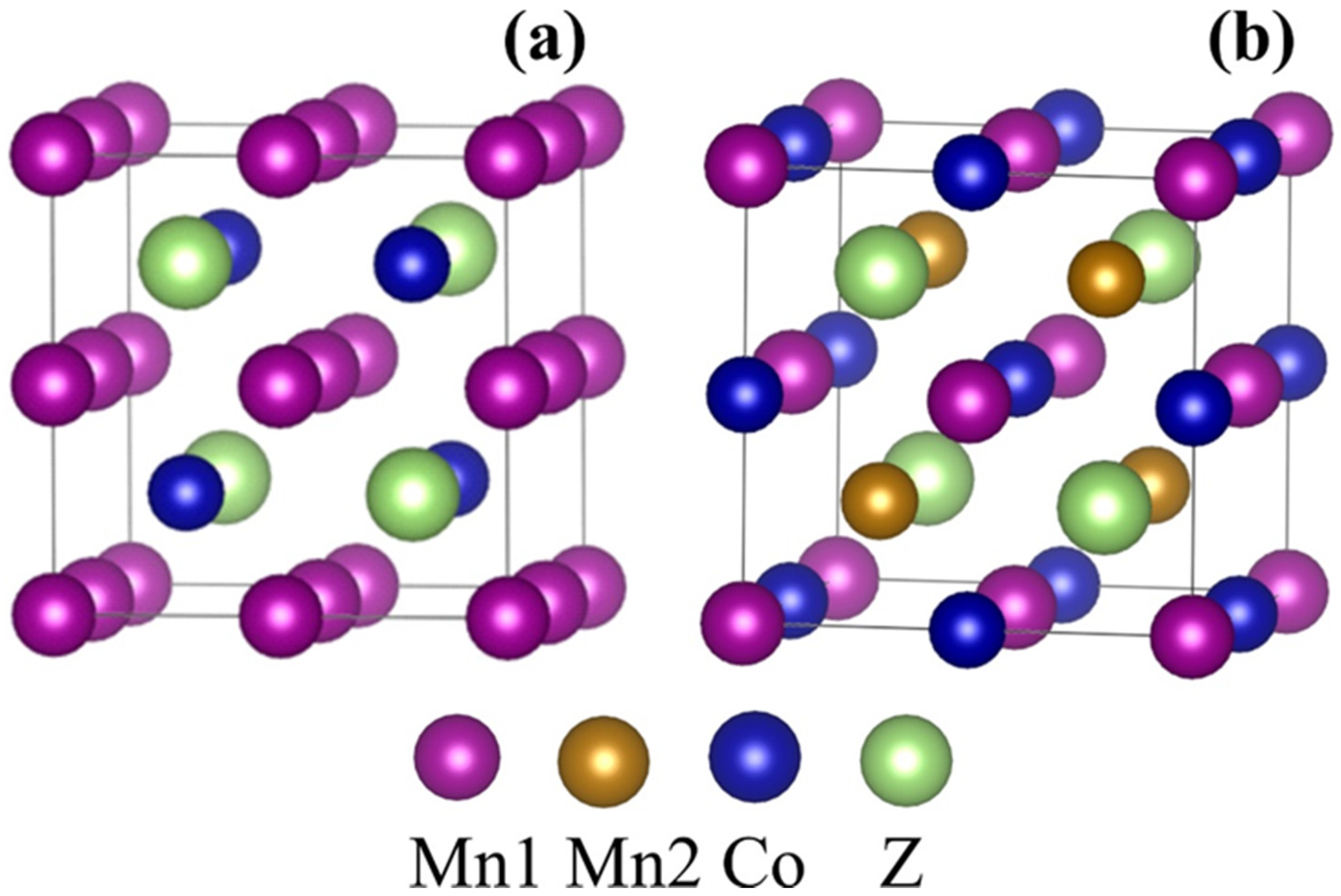
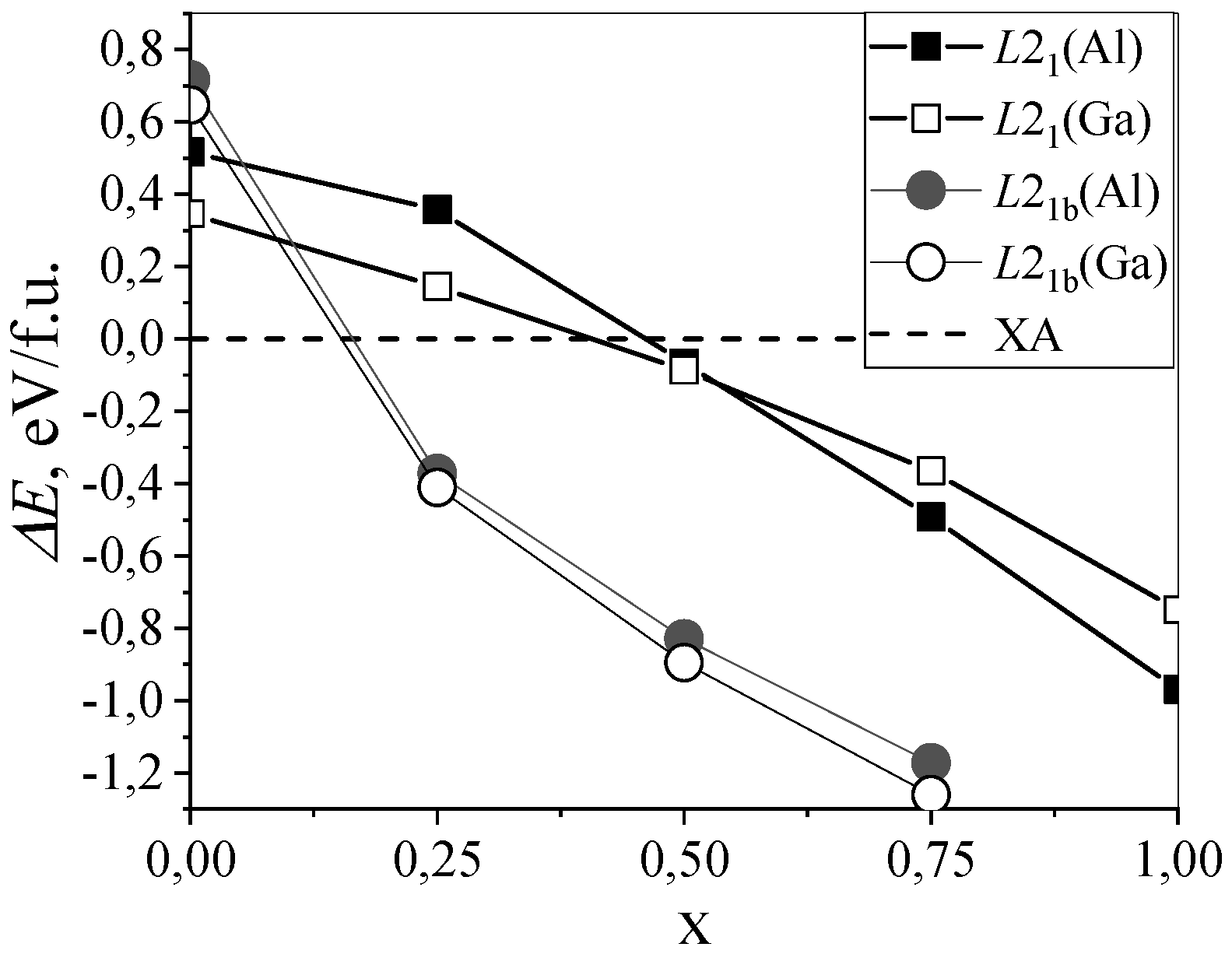
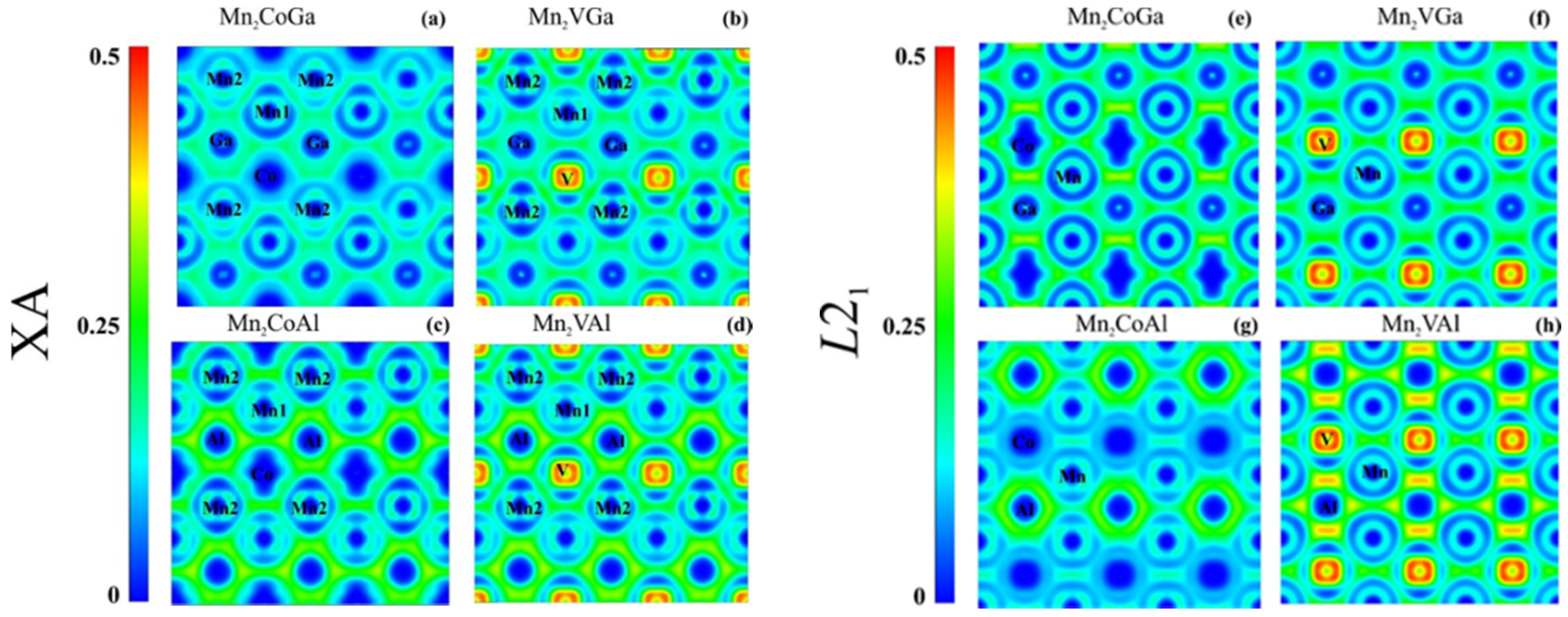
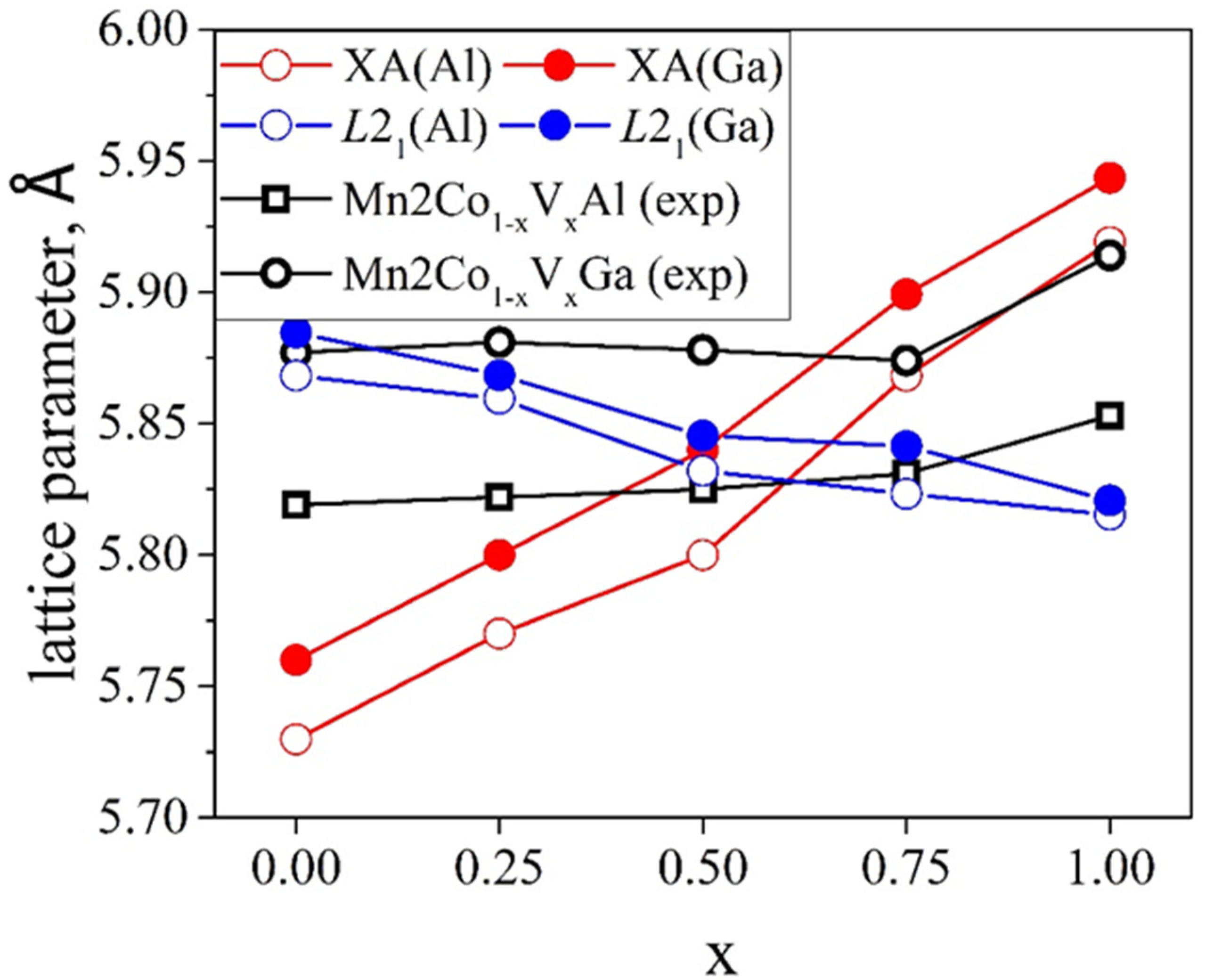
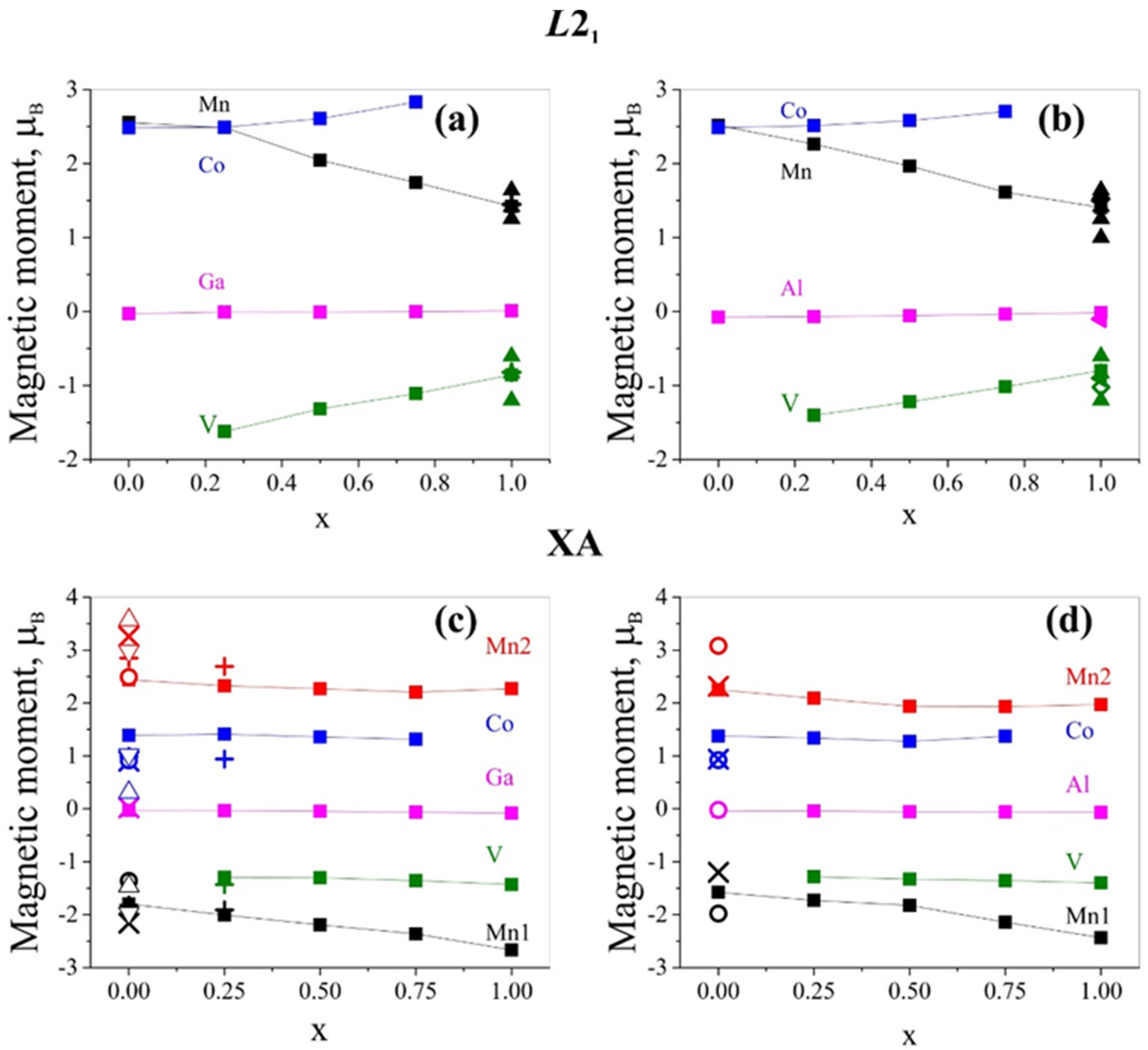
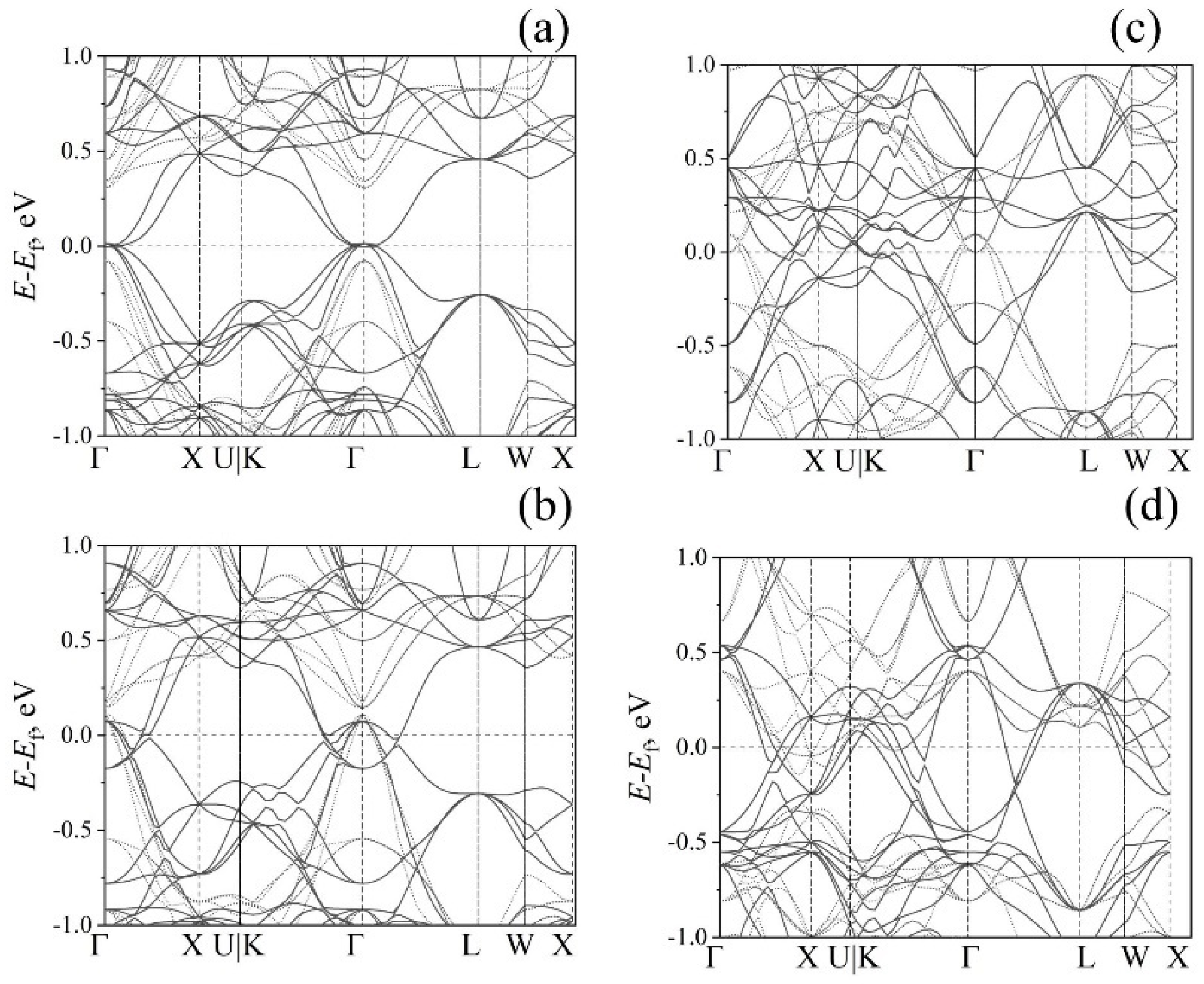
3. Results and Discussion

Structure. In total, the unit cell of X2YZ contains four structural units. In this case, the XA symmetry cell contains two symmetrically nonequivalent atoms X (Mn), which we further denote as Mn1 (Mn2). These atoms differ in their nearest environment. Mn1 atoms are surrounded by 4 Mn2 and 4 Z atoms, while Mn2 atoms are neighbored by 4 Mn1 atoms and 4 Y atoms. Y atoms have 4 Z and 4 Mn1 atoms in the first coordination shell, and Z atoms are surrounded by 4Mn1 and 4Y atoms. This difference in the local environment determines the difference in the physical properties of the Mn1 and Mn2 atoms. In the L21 symmetry lattice, the X atoms are equivalent and are surrounded by 4 Y and 4 Z atoms.
We simulated the properties of Mn2Co1-xVxZ alloys when V atoms replace Co. Preliminary calculations have showed that when replacing Co atoms with V, it is energetically more favorable to arrange them at the most distant distances from each other. For this reason, the replacement of atoms was carried out randomly so that the average distance between the replacement atoms was maximized.
The interatomic distance maximization was achieved by arranging the V atoms so that, if possible, they did not occupy positions at the sites corresponding to the minimum distance between the pairs of Co-Co atoms at x = 0, equal to approximately 4A. Note that each Co atom is surrounded by 12 of the same type at the indicated distance. These characteristics are the same for both considered types of crystal lattices. When x is not equal to 0, the number of V-V pairs can be considered a characteristic of the local order in substituting Co atoms. In the case of uniform substitution of V for Co atoms, it can be expected that the number of pairs of V-V atoms will vary in proportion to their concentration. At x = 0.25, 0.5 and 0.75, there will be 3, 6, and 9 of such pairs, respectively. However, in the systems we studied, the number of these pairs of atoms was 1.5 (x = 0.25), 5.875 (x = 0.5), and 8.75 (x = 0.75). In this case, the average distance between all possible pairs of V-V atoms varied from approximately 6.4 Å (x = 0.25) to 5.9 Å (x = 1).
Comparison of the ground state energies ΔE = E(L21) – E(XA) of the considered crystalline modifications of the Mn2Co1-xVxZ compound (Figure 2) showed the presence of a phase transition near x = 0.5. At low x, the XA structure is more energetically favorable, while the L21 is more stable at high V concentrations. This result is in good agreement with the experimental data [22].
In addition to filling either B or C with the Co/V mixture, we also distribute V randomly on B and half of remaining Co atoms randomly on A and C sites (structure L21b). Calculations have shown that considering the L21 structure, the total energy of the systems decreases, and the L21 structure turns out to be more favorable. In the case of the XA structure, introducing such additional disorder leads to an increase in energy. As a result of comparing the energies of the L21b and XA structures, the theoretical structural phase transition should occur at x = 0.25 (Figure 2), which is in excellent agreement with the experimental data [22].
The transition from one to another structure is explained by the difference in the energies of crystal formation (Eform) for modifications of the crystal structure. For the Heusler X2YZ alloys the Eform values were calculated by the formula
Eform(X2YZ) = Etot − (2E(X) + E(Y) + E(Z))
The data obtained for the end cases x = 0 and x = 1, of the Mn2Co1-xVxZ compounds are shown in Table 1. It can be seen that Co-containing alloys are more stable in the crystalline modification of the XA type, while the V-containing ones are more stable in the crystalline modification of the L21 type.
To explain this trend, we calculated an electron-localization function (ELF) to study the change in the nature of chemical bonds when replacing Co with V. The ELF is a ground-state property that is useful to visualize and distinguish between different bonding interactions in solids [32].
In regions with higher ELF values, the electrons tend to become paired, which indicates the covalent character of the bonding between the nearest-neighbor atoms in this intermetallic compound [33,34]. Figure 3 shows the ELF projections in the (110) plane for the Heusler alloys Mn2Co1-xVxZ (Z = Ga, Al) for x = 0 and x = 1 in the case of XA (Figure 3, left) and L21 (Figure 3, right) structures.
Replacing Co with V leads to an increase in ELF, which means an increase in the covalent nature of the chemical bond between the elements (compare Figure 3a and Figure 3b; Figure 3c and Figure 3d; Figure 3e and Figure 3f; Figure 3g and Figure 3h). Strengthening the covalent bond should lead to an increase in the stability of the compounds. A competing effect leading to the destabilization of alloys is an increase in the degree of polarity of the covalent bond. An effect of this kind was found in the Mn2CoGa alloy when the Ga atoms were replaced by Ti, V, Cr, and Ni [34]. The relatively high ELF values around atoms serve as an indicator of an increase in the polarity of the covalent bond [34]. In our case, high ELF values were found near V atoms. Thus, on the one hand, the substitution of V for Co atoms leads to an increase in the degree of covalence of chemical bonds in Heusler alloys, stabilizing the crystal lattices. On the other hand, the strong polarity of the covalent bond of V atoms with neighboring atoms leads to the destabilization of the crystal lattices. The crystal structures realized are the result of a compromise between these two trends.
The lattice parameters of the L21 and XA structures of the Mn2Co1-xVxZ compound behave differently depending on the V concentration (Figure 4).
It can be seen that the XA structure is characterized by a linear increase in the lattice constants with increasing x. In the L21 structure, an increase in the V concentration leads to a slight decrease in the lattice parameters. A nonlinear dependence of the lattice constants was observed experimentally [20]. In experiment, the XA structure was detected at x ≥ 0.25 [22]. The authors of [22] point out the difficulties in identifying the crystal structure associated with determining the arrangement of atoms in the lattices. In addition, the samples can represent a mixture of the L21 and XA structures, one of which can be metastable. From the point of view of theory, it is also necessary to take into account the possibility of considering not only the disorder at the Co-V sites but also the other types of disorder.
Magnetic properties. The results of calculating the average values of the magnetic moment on atoms of various types in the Heusler alloys Mn2Co1-xVxZ (Z = Ga, Al) for the case of the L21 and XA structures are shown in Figure 5. The magnetic moment values at x = 0, 0.25, and 1 are in good agreement with the known literature data.
In the case of the L21 ordering, as Co is replaced by V, the absolute values of the magnetic moments on the Mn and V atoms decrease, which is accompanied by an increase in the magnetic moments on the remaining Co atoms (Figure 5a,b). The values of the magnetic moments on the Mn and V atoms at x = 0 are almost 2 times larger than the corresponding values for x = 1. On the Mn and Co atoms, the direction of the magnetic moments is the same, while the moments on the V atoms have the opposite direction.
As compared with the L21 structure, the values of the magnetic moments on the atoms in the XA structure change more weakly with the increase in V content. The magnetic moments at the Mn1 atoms undergo the most remarkable change. The absolute value of the magnetic moment increases at x = 1 by approximately 0.8 μB in the x = 1 composition as compared to the corresponding value in the x = 0 composition. In this case, the magnetic moments on the Mn1 and V atoms are parallel, and the moments on the Mn2 and Co atoms are antiparallel (Figure 5c,d).
The presence of two types of Mn atoms in the XA-type lattice, which have the opposite direction of the magnetic moment, determines the difference in the magnetic properties of these crystalline modifications. The calculated values of the total magnetic moment of the XA and L21 structures are shown in Table 2.
The most significant changes in the values of the magnetic moments are observed for Mn and V atoms in the case of Heusler alloys with the L21 structure. A decrease in the absolute values of the magnetic moments of atoms occurs here with an increase in the concentration of V atoms in the first coordination sphere of Mn atoms. For the Heusler alloy of the XA structure, the Mn1 and V atoms are located at the sites of the second coordination sphere of each other. In this case, the increase in the absolute value of the magnetic moment at the Mn1 atoms is determined by the number of V atoms at the next-nearest neighbors Mn1 positions.
The value of the total magnetic moment in the XA ordering obeys the Slater-Pauling rule (S-P rule) [35]. According to this rule, the total magnetic moment in half-metallic Heusler alloys can be found by the formula Mt = Zt − 24, where Zt is the total number of valence electrons per unit cell, and Mt is the total magnetic moment per formula unit. The value of the total magnetic moment of the L21-type lattices does not obey this rule due to the ferromagnetic coupling of the Mn and Co atoms, except the case x = 1. The decrease in the value of the total magnetic moment with increasing x occurs due to the contribution of the antiferromagnetically coupled spins of the V atoms. In contrast to the L21 structure, the spins of Mn1-V and Mn2-Co atom pairs in the XA structure have the opposite direction. In order to make the Mn2Co1-xVxZ compositions obeying the S-P rule in the L21 structure, it is necessary to take into account the disordering of pairs of Mn-Co atoms, i.e., to consider the structure L21 [24,38]. Taking this kind of disorder into account is beyond the scope of this work.
Electronic properties.Figure 6 shows the calculated electronic densities of states for the Heusler alloys Mn2Co1-xVxZ (Z = Ga, Al) of the XA structure for various x values.
Since our theoretical consideration indicated that in the L21 type ordering there is no compensation of the magnetic moment required for practical applications, we did not investigate the dependence of the electronic structure of these compounds for the case of L21 ordering. The electronic structure of Mn2VAl and Mn2VGa for the case of L21 ordering was studied in References [2,38], respectively.
According to our calculations (Figure 6), Mn2CoGa is a half-metal, while Mn2CoAl is SGS, which is consistent with previous studies [10,11,12,39]. As in the case of replacement of the Z element by Fe or Cr [12], the replacement of Co by V destroys the SGS state of Mn2CoAl and its electronic structure becomes half-metallic. As x increases to 0.5, the density of states of spin-up electrons near the Fermi level increases and is formed due to the electronic states on Mn1, Mn2, and V atoms. In this case, the fraction of states near EF on the V atoms increases.
In the Mn2CoGa compound, the replacement of Co by V leads to a change in the electronic structure towards an enhancement of the half-metallic properties. However, the obtained electronic structure does not fully correspond to the standard definition of half-metal, where there must be an energy gap at the Fermi level for spin-minority states. Instead, spin-minority states exhibit properties characteristic of semi-metals rather. As a result, the electronic DOS, in this case, is characterized by a high density of states for spin-majority states and a low density of states (by about two orders of magnitude) for spin-minority states. For this reason, we will further call compounds with such an electronic structure as semi-half-metals. As x grows, the DOS minimum at x = 0 near the Fermi level is gradually replaced by a peak. DOS near the Fermi level for the spin-up states, as in the case of Mn2CoAl, is formed by the states on Mn1, Mn2, and V atoms with an increase in the fraction of states on V atoms as x increases. In all the cases considered, the energy gap for spin-down states when Co atoms are replaced by V is filled with d-states on Mn1 and V.
In order to examine details of the electronic structure near the Fermi level, one has to examine the band structure around the Ef since band crossing is not always easily distinguished in usual DOS calculations. The results obtained for ordered alloys of the XA structure are shown in Figure 7. For the Mn2CoAl alloy, the data obtained are in complete agreement with the results of [12]. The rest of the compounds exhibit semi-half-metallic behavior. In this case, the energy levels for spin-down states intersect the Fermi level, which indicates that their DOS near Ef is not precisely equal to zero.

4. Conclusions

This paper presents the results of DFT studies of the structural, electronic, and magnetic properties of Heusler alloys Mn2Co1-xVxZ (Z = Ga, Al, x = 0, 0.25, 0.5, 0.75, 1) for the case of L21 and XA structures. It is shown that for x = 0, the XA structure is more stable, while for x = 1 the L21 structure is stable. A transition from one to another type of ordering occurs near x = 0.5. The inclusion of additional atomic disorder through consideration of the lattices of the L21b structure improves the agreement between theory and experiment, and the phase transition occurs at a vanadium concentration x = 0.25. Depending on the degree of Co substitution for V, the lattice constants of the L21 and XA structures change in different ways, explaining the experimentally observed trends of the lattice constants. Almost complete compensation of the magnetic moment was achieved in the Mn2Co0.5V0.5Z (Z = Al, Ga) composition for the case of the XA structure. The compensated magnetic moment for these alloys is 0.06 μB/f.u. The calculated values of the magnetic moments of the alloys with XA ordering correspond to the values calculated according to the S-P rule. In order to achieve agreement with the S-P rule for the L21 structure, it is necessary to take into consideration other types of the atomic disorder, such as swap between Co and Mn atoms. Substitution of V for Co atoms leads to a change in the electronic structure of the alloy from SGS to a semi-half-metallic state. At the same time, the bandgap for spin-minority states disappears, and a pseudogap state is formed with DOS 2 orders of magnitude smaller than the same value for spin-majority states.

Author Contributions

Author contributions F.A. and T.I. conceived the study, designed the theoretical calculations and wrote the manuscript. A.A. performed most of the calculations. N.M. performed the theoretical calculations. N.S. and G.K. analyzed simulation data. M.S. and V.K. contributed to DFT simulations. All authors contributed to manuscript revision. All authors have read and agreed to the published version of the manuscript.

Funding

This work was carried out within the framework of grant from the Ministry of Education and Science of the Republic of Kazakhstan (project AP08957176 “First-principles design of fully compensated ferrimagnetic materials for spintronic applications”).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The work of T.I. was performed under the state assignment of IGM SB RAS. T.I. also thanks the Center for Computational Materials Science (IMR, Tohoku University) for access to the supercomputing system to perform the simulations. Th calculations were partially performed at the Cherry supercomputer cluster provided by the Materials Modeling and Development Laboratory at NUST “MISIS” (supported via the Grant from the Ministry of Education and Science of the Russian Federation No. 14.Y26.31.0005).

Conflicts of Interest

There are no conflicts to declare.

References

  1. Graf, T.; Felser, C.; Stuart, S.P. Parkin Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1. [Google Scholar] [CrossRef]
  2. Weht, R.; Pickett, W.E. Half-metallic ferrimagnetism in Mn2VAl. Phys. Rev. B 1999, 60, 13006. [Google Scholar] [CrossRef] [Green Version]
  3. Liu, G.D.; Dai, X.F.; Liu, H.Y.; Chen, J.L.; Li, Y.X.; Xiao, G.; Wu, G.H. Mn2CoZ (Z = Al, Ga, In, Si, Ge, Sn, Sb) compounds: Structural, electronic, and magnetic properties. Phys. Rev. B 2008, 77, 014424. [Google Scholar] [CrossRef] [Green Version]
  4. Ouardi, S.; Fecher, G.H.; Felser, C. Realization of Spin Gapless Semiconductors: The Heusler Compound Mn2CoAl. Phys. Rev. Lett. 2013, 110, 100401. [Google Scholar] [CrossRef] [Green Version]
  5. Chen, X.R.; Zhong, M.M.; Feng, Y.; Zhou, Y.; Yuan, H.K.; Chen, H. Structural, electronic, elastic, and thermodynamic properties of the spin-gapless semiconducting Mn2CoAl inverse Heusler alloy under pressure. Phys. Status Solidi B 2015, 252, 2830. [Google Scholar] [CrossRef]
  6. Luo, H.Z.; Liu, G.D.; Meng, F.B.; Wang, L.L.; Liu, E.K.; Wu, G.H.; Zhu, X.X.; Jiang, C.B. Slater–Pauling behavior and half-metallicity in Heusler alloys Mn2CuZ (Z = Ge and Sb). Comput. Mater. Sci. 2011, 50, 3119. [Google Scholar] [CrossRef]
  7. Abada, A.; Amara, K.; Hiadsi, S.; Amrani, B. First principles study of a new half-metallic ferrimagnets Mn2-based full Heusler compounds: Mn2ZrSi and Mn2ZrGe. J. Magn. Magn. Mater. 2015, 388, 59. [Google Scholar] [CrossRef]
  8. Palmstrom, C.J. Heusler compounds and spintronics. Prog. Cryst. Growth Charact. Mater. 2016, 62, 371. [Google Scholar] [CrossRef] [Green Version]
  9. Marti, X.; Fina, I.; Frontera, C.; Liu, J.; Wadley, P.; He, Q.; Paull, R.J.; Clarkson, J.D.; Kudrnovsky, J.; Tirek, I.; et al. Room-temperature antiferromagnetic memory resistor. Nat. Mater. 2014, 13, 367. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  10. Jamer, M.E.; Assaf, B.A.; Devakul, T.; Heiman, D. Magnetic and transport properties of Mn2CoAl oriented films. Appl. Phys. Lett. 2013, 103, 142403. [Google Scholar] [CrossRef] [Green Version]
  11. Seredina, M.; Gavrikov, I.; Gorshenkov, M.; Taskaev, S.; Dyakonov, A.; Komissarov, A.; Chatterjee, R.; Novosad, V.; Khovaylo, V. Magnetic and transport properties of Mn2CoGa. J. Magn. Magn. Mater. 2019, 470, 55. [Google Scholar] [CrossRef]
  12. Galanakis, I.; Özdoğan, K.; Şaşioğlu, E.; Blügel, S. Conditions for spin-gapless semiconducting behavior in Mn2CoAl inverse Heusler compound. J. Appl. Phys. 2014, 115, 093908. [Google Scholar] [CrossRef] [Green Version]
  13. Dhakal, R.; Nepal, S.; Ray, R.B.; Paudel, R.; Kaphle, G.C. Effect of doping on SGS and weak half-metallic properties of inverse Heusler Alloys. J. Magn. Magn. Mater. 2020, 503, 166588. [Google Scholar] [CrossRef]
  14. Galanakis, I.; Ozdogan, K.; Sasioglu, E.; Aktas, B. Doping of Mn2VAl and Mn2VSi Heusler alloys as a route to half-metallic antiferromagnetism. Phys. Rev. B 2007, 75, 092407. [Google Scholar] [CrossRef] [Green Version]
  15. Li, Q.F.; Zhao, H.F.; Zhong, X.; Su, J.L. Co doping effects on structural, electronic and magnetic properties in Mn2VGa. J. Magn. Magn. Mater. 2012, 324, 1463. [Google Scholar] [CrossRef]
  16. Meinert, M.; Schmalhorst, J.-M.; Reiss, G.; Arenholz, E. Ferrimagnetism and disorder epitaxial Mn2-xCoxVAl Heusler compound thin films. J. Phys. D Appl. Phys. 2011, 44, 215003. [Google Scholar] [CrossRef] [Green Version]
  17. Jiang, C.; Venkatesan, M.; Coey, J.M.D. Transport and magnetic properties of Mn2VAl: Search for half-metallicity. Solid State Commun. 2001, 118, 513. [Google Scholar] [CrossRef]
  18. Deka, B.; Srinivasan, A.; Singh, R.K.; Varaprasad, B.S.D.C.S.; Takahashi, Y.K.; Hono, K. Effect of Co substitution for Mn on spin polarization and magnetic properties of ferrimagnetic Mn2VAl. J. Alloys Compd. 2016, 662, 510–515. [Google Scholar] [CrossRef]
  19. Stinshoff, R.; Nayak, A.K.; Fecher, G.H.; Balke, B.; Ouardi, S.; Skourski, Y.; Nakamura, T.; Felser, C. Completely compensated ferrimagnetism and sublattice spin crossing in the half-metallic Heusler compound Mn1.5FeV0.5Al. Phys. Rev. B 2017, 95, 060410. [Google Scholar] [CrossRef] [Green Version]
  20. Midhunlal, P.V.; Arout Chelvane, J.; Arjun Krishnan, U.M.; Prabhu, D.; Gopalan, R.; Harish Kumar, N. Near total magnetic moment compensation with high Curie temperature in Mn2V0.5Co0.5Z (Z = Ga, Al) Heusler alloys. J. Phys. D Appl. Phys. 2018, 51, 075002. [Google Scholar] [CrossRef]
  21. Ramesh Kumar, K.; Arout Chelvane, J.; Markandeyulu, G.; Malik, S.K.; Harish Kumar, N. Effect of Co substitution on the magnetic and transport properties of the half-metalc ferrimagnet Mn2VGa. Solid State Commun. 2010, 150, 70. [Google Scholar] [CrossRef]
  22. Midhunlal, P.V.; Venkatesh, C.; Chelvane, J.A.; Babu, P.D.; Kumar, N.H. Neutron diffraction and ab initio studies on the fully compensated ferrimagnetic characteristics of Mn2V1-xCoxGa Heusler alloys. arXiv 2001, arXiv:2001.00707v1. [Google Scholar]
  23. Midhunlal, P.V.; Venkatesh, C.; Arout Chelvane, J.; Babu, P.D.; Harish Kumar, N. Mn2V0.5Co0.5Z (Z= Ga, Al) Heusler alloys: High TC compensated P-type ferrimagnetism in arc melted bulk and N-type ferrimagnetism in melt-spun ribbons. J. Magn. Magn. Mater. 2019, 489, 165298. [Google Scholar] [CrossRef]
  24. Umetsu, R.Y.; Tsujikawa, M.; Saito, K.; Ono, K.; Ishigaki, T.; Kainuma, R.; Shirai, M. Atomic ordering, magnetic properties, and electronic structure of Mn2CoGa Heusler alloy. J. Phys. Condens. Matter 2019, 31, 065801. [Google Scholar] [CrossRef]
  25. Blöchl, P.E. Projector augmented−wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [Green Version]
  26. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalize gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  27. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15. [Google Scholar] [CrossRef]
  28. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
  29. Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
  30. Manz, T.A.; Limas, N.G. Introducing DDEC6 atomic population analysis: Part 1. Charge partitioning theory and methodology. RSC Adv. 2016, 53, 47771. [Google Scholar] [CrossRef] [Green Version]
  31. Clark, A.; Davidson, E.R. Population Analyses That Utilize Projection Operators. Int. J. Quantum Chem. 2003, 93, 384. [Google Scholar] [CrossRef]
  32. Savin, A.; Nesper, R.; Wengert, S.; Fässler, T.F. ELF: The Electron Localization Function. Angew. Chem. Int. Ed. 1997, 36, 1808. [Google Scholar] [CrossRef]
  33. Liu, E.K.; Wang, W.H.; Feng, L.; Zhu, W.; Li, G.J.; Chen, J.L.; Zhang, H.W.; Wu, G.H.; Jiang, C.B.; Xu, H.B.; et al. Stable magnetostructural coupling with tunable magnetoresponsive effects in hexagonal ferromagnets. Nat. Commun. 2012, 3, 873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  34. Offernes, L.; Ravindran, P.; Kjekshus, A. Electronic structure and chemical bonding in half-Heusler phases. J. Alloys Compd. 2007, 439, 37. [Google Scholar] [CrossRef]
  35. Galanakis, I.; Dederichs, P.H.; Papanikolaou, N. Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys. Phys. Rev. B 2002, 66, 174429. [Google Scholar] [CrossRef] [Green Version]
  36. Sasioglu, E.; Sandratskii, L.M.; Bruno, P. Stability of ferromagnetism in the half-metallic pnictides and similar compounds: A first-principles study. J. Phys. Condens. Matter 2005, 17, 995. [Google Scholar] [CrossRef] [Green Version]
  37. Ramesh Kumar, K.; Harish Kumar, N.; Babu, P.D.; Venkatesh, S.; Ramakrishnan, S. Investigation of atomic anti-site disorder and ferrimagnetic order in the half-metallic Heusler alloy Mn2VGa. J. Phys. Condens. Matter 2012, 24, 336007. [Google Scholar] [CrossRef]
  38. Xin, Y.; Hao, H.; Ma, Y.; Luo, H.; Meng, F.; Liu, H.; Liu, E.; Wu, G. Competition of XA and L21B ordering in Heusler alloys Mn2CoZ (Z = Al, Ga, Si, Ge and Sb) and its influence on electronic structure. Intermetallics 2017, 80, 10. [Google Scholar] [CrossRef]
  39. Galanakis, I.; Özdoğan, K.; Aktaş, B.; Şaşıoğlu, E. Effect of doping and disorder on the half metallicity of full Heusler alloys. Appl. Phys. Lett. 2006, 89, 042502. [Google Scholar] [CrossRef] [Green Version]
Magnetochemistry 07 00159 g001 550
Figure 1. Unit cells of the Heusler alloys Mn2CoZ of structure (a) L21 and (b) XA.
Figure 1. Unit cells of the Heusler alloys Mn2CoZ of structure (a) L21 and (b) XA.
Magnetochemistry 07 00159 g001
Magnetochemistry 07 00159 g002 550
Figure 2. The ground state energies for the XA, L21 and L21b structures in the Mn2Co1-xVxZ compositions as a function of V concentration x.
Figure 2. The ground state energies for the XA, L21 and L21b structures in the Mn2Co1-xVxZ compositions as a function of V concentration x.
Magnetochemistry 07 00159 g002
Magnetochemistry 07 00159 g003 550
Figure 3. Calculated ELF in the (110) plane of (a) Mn2CoGa, (b) Mn2VGa, (c) Mn2CoAl, and (d) Mn2VAl of XA and (e) Mn2CoGa, (f) Mn2VGa, (g) Mn2CoAl, and (h) Mn2VAl of L21 structures.
Figure 3. Calculated ELF in the (110) plane of (a) Mn2CoGa, (b) Mn2VGa, (c) Mn2CoAl, and (d) Mn2VAl of XA and (e) Mn2CoGa, (f) Mn2VGa, (g) Mn2CoAl, and (h) Mn2VAl of L21 structures.
Magnetochemistry 07 00159 g003
Magnetochemistry 07 00159 g004 550
Figure 4. The calculated values of the lattice constants of the Mn2Co1-xVxZ (Z = Ga, Al) compounds for the case of the L21 and XA structures. Experimental data are adopted from Reference [20].
Figure 4. The calculated values of the lattice constants of the Mn2Co1-xVxZ (Z = Ga, Al) compounds for the case of the L21 and XA structures. Experimental data are adopted from Reference [20].
Magnetochemistry 07 00159 g004
Magnetochemistry 07 00159 g005 550
Figure 5. Average values of magnetic moment on atoms calculated by the DDEC6 method on atoms of the Heusler alloy Mn2Co1-xVxZ of the L21 structure (a) Z = Ga, (b) Z = Al and XA structure (c) Z = Ga, (d) Z = Al. Literature data are given for comparison: ×—Ref. [2], ○—Ref. [13], +—Ref. [22], Δ—Ref. [24] (theory), ∇—Ref. [24] (experiment). ◄ [2], ● [35], ◊—[36], ▲—[37].
Figure 5. Average values of magnetic moment on atoms calculated by the DDEC6 method on atoms of the Heusler alloy Mn2Co1-xVxZ of the L21 structure (a) Z = Ga, (b) Z = Al and XA structure (c) Z = Ga, (d) Z = Al. Literature data are given for comparison: ×—Ref. [2], ○—Ref. [13], +—Ref. [22], Δ—Ref. [24] (theory), ∇—Ref. [24] (experiment). ◄ [2], ● [35], ◊—[36], ▲—[37].
Magnetochemistry 07 00159 g005
Magnetochemistry 07 00159 g006 550
Figure 6. Electronic DOS of the Mn2Co1-xVxZ (Z = Ga, Al) Heusler alloys for the case of the XA structure. Panels (a,c,e,g,i) correspond to Mn2Co1-xVxGa alloys at x = 0, 0.25, 0.5, 0.75 and 1, respectively. Panels (b,d,f,h,j) correspond to Mn2Co1-xVAl alloys at x = 0, 0.25, 0.5, 0.75 and 1, respectively.
Figure 6. Electronic DOS of the Mn2Co1-xVxZ (Z = Ga, Al) Heusler alloys for the case of the XA structure. Panels (a,c,e,g,i) correspond to Mn2Co1-xVxGa alloys at x = 0, 0.25, 0.5, 0.75 and 1, respectively. Panels (b,d,f,h,j) correspond to Mn2Co1-xVAl alloys at x = 0, 0.25, 0.5, 0.75 and 1, respectively.
Magnetochemistry 07 00159 g006
Magnetochemistry 07 00159 g007 550
Figure 7. Spin-resolved band structures of ordered (a) Mn2CoAl, (b) Mn2CoGa, (c) Mn2VAl, (d) Mn2VGa Heusler alloys for the case of the XA structure (solid lines represent spin-up states; dotted lines correspond to spin-down states).
Figure 7. Spin-resolved band structures of ordered (a) Mn2CoAl, (b) Mn2CoGa, (c) Mn2VAl, (d) Mn2VGa Heusler alloys for the case of the XA structure (solid lines represent spin-up states; dotted lines correspond to spin-down states).
Magnetochemistry 07 00159 g007
Table
Table 1. Energies of crystal formation.
Table 1. Energies of crystal formation.
CompoundEform, eV/atomReference
XAL21
Mn2CoGa−0.211
−0.192		−0.127Present work
[11]
Mn2CoAl−0.319
−0.286		−0.190Present work
[11]
Mn2VGa−0.080−0.267Present work
Mn2VAl−0.117−0.358Present work
Table
Table 2. Total magnetic moment calculated for the L21 and XA structures of the Mn2Co1-xVxZ (Z = Al, Ga) Heusler alloy.
Table 2. Total magnetic moment calculated for the L21 and XA structures of the Mn2Co1-xVxZ (Z = Al, Ga) Heusler alloy.
ZxTotal Magnetic Moment Per Formula Unit, μB/f.u.
XA StructureL21 Structure
Ga02.00 (a), 2.05 (b), 2 (c), 1.99 (d)7.71 (a), 7.68 (d)
0.251.00 (a), 1.11 (b), 1 (c)6.43 (a)
0.50.06 (a), 0.1 (b), 0 (c)4.73 (a)
0.751.05 (a), 0.97 (b), 1 (c)3.36 (a)
12.01 (a), 1.8 (b), 2 (c)1.98 (a)
Al02.00 (a), 2.06 (b), 2 (c)7.44 (a)
0.251.00 (a), 1.09 (b), 1 (c)5.99 (a)
0.50.06 (a), 0.06 (b), 0 (c)4.56 (a)
0.750.93 (a), 0.99 (b), 1 (c)3.11 (a)
11.94 (a), 1.863 (b), 2 (c)2.00 (a)
(a)—Present work, (b)—Experimental data from Ref. [12], (c)—S-P rule, (d)—Theoretical data from Ref. [24].
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Abuova, F.; Inerbaev, T.; Abuova, A.; Merali, N.; Soltanbek, N.; Kaptagay, G.; Seredina, M.; Khovaylo, V. Structural, Electronic and Magnetic Properties of Mn2Co1-xVxZ (Z = Ga, Al) Heusler Alloys: An Insight from DFT Study. Magnetochemistry 2021, 7, 159. https://doi.org/10.3390/magnetochemistry7120159

AMA Style

Abuova F, Inerbaev T, Abuova A, Merali N, Soltanbek N, Kaptagay G, Seredina M, Khovaylo V. Structural, Electronic and Magnetic Properties of Mn2Co1-xVxZ (Z = Ga, Al) Heusler Alloys: An Insight from DFT Study. Magnetochemistry. 2021; 7(12):159. https://doi.org/10.3390/magnetochemistry7120159

Chicago/Turabian Style

Abuova, Fatima, Talgat Inerbaev, Aisulu Abuova, Nurpeis Merali, Nurgul Soltanbek, Gulbanu Kaptagay, Marina Seredina, and Vladimir Khovaylo. 2021. "Structural, Electronic and Magnetic Properties of Mn2Co1-xVxZ (Z = Ga, Al) Heusler Alloys: An Insight from DFT Study" Magnetochemistry 7, no. 12: 159. https://doi.org/10.3390/magnetochemistry7120159

APA Style

Abuova, F., Inerbaev, T., Abuova, A., Merali, N., Soltanbek, N., Kaptagay, G., Seredina, M., & Khovaylo, V. (2021). Structural, Electronic and Magnetic Properties of Mn2Co1-xVxZ (Z = Ga, Al) Heusler Alloys: An Insight from DFT Study. Magnetochemistry, 7(12), 159. https://doi.org/10.3390/magnetochemistry7120159

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop