Abstract
Electrocaloric is a novel emerging not-in-kind cooling technology based on solid-state materials exhibiting the electrocaloric effect, i.e., the property of changing their temperature because of an adiabatic change in the intensity of the electric field applied. This technology has only attracted the interests of the scientific community in the last two decades, even though it has the main feature of being based on eco-friendly materials that, because of their solid-state nature, do not provide a direct contribution in global warming. Even if some steps have already been taken, the research fields connected to electrocaloric cooling are still open: The identification of the most appropriated thermodynamic cycle, electrocaloric refrigerants, as well as the development of efficient cooling systems. To this purpose, this review paper provides a snapshot of the electrocaloric world and compares the progress made by the inherent scientific community in all the connected fields: the thermodynamic cycles, materials, experimental devices, numerical models, energy performances and prospective cooling applications.
Keywords:
electrocaloric; effect; thermodynamic; cycles; AER; materials; experimental; device; prototype; numerical model 1. Introduction
The road to cooling and air-conditioning in a way other than vapor compression, among the various innovative eco-friendly possibilities, certainly passes through the solid-state technologies based on the so-called caloric effects [1,2]. The caloric class belongs to the not-in kind technologies [3] with the main characteristic of being eco-friendly because of the employment of caloric effect materials that, due to their solid-state nature, do not present any global warming potential (GWP) [4], i.e., they do not provide a direct contribution to global warming, unlike the refrigerant fluids on which vapor compression is based [5,6,7,8] as well as transcritical alternatives to HFCs [9].
A caloric effect is the response by a solid-state material that is sensitive to a variation of an external field applied to it. The nature of the material’s reaction could be magnetic, electrical, or mechanical, depending on the characteristics of the material and the nature of the field, and can manifest itself as a variation in temperature or entropy, giving rise to the magnetocaloric, electro-caloric, or mechanocaloric effect [10,11,12,13,14]. The electrocaloric effect (ECE), as well as the other caloric phenomena, occurs consequently to a re-arrangement of the inner structure of the electrocaloric materials; specifically, if the transformation is adiabatic, a decrease in the material’s entropy ensues, thus giving an increase in the temperature of the material itself [11]. The electrocaloric effect, observed for the first time by Kobeko and Kurtschatov in 1930 in Rochelle salt [15] and quantitatively measured by Hautzenlaub in 1943 [16], is a reversible phenomenon, hence, the opposite behaviour (a decrease in the temperature of the material) befalls following the remotion of the electric field, adiabatically. The cyclic application and remotion of the electric field, interspersed with heat transfer to or from the electrocaloric material, gives life to thermodynamic cycles at the base of electrocaloric cooling (or heat pumping).
Electrocaloric refrigeration is a relatively young technique among the caloric ones, since the scientific community has been significantly attracted toward it only in the last decade, especially with reference to applications at room temperature [11] because of its potentialities and the environmentally friendly nature of its refrigerants [17]. Truthfully, the turning point was the discovery [18] of the giant electrocaloric effect in the PZT (Pb[Zr0.95Ti0.05]O3), that resulted in an adiabatic temperature change much larger than the ECE exhibited by the other materials studied until then. This breakthrough opened the opportunity for the exploitation of electrocaloric effect materials for cooling applications in the room temperature range. The consequence deriving from this recent interest is a large number of studies on electrocaloric materials [19,20,21,22] (employable as solid-state refrigerants), with respect to a more limited quantity of numerical or experimental researches [23,24,25] focused on the development of systems for electrocaloric refrigeration. In short, there are still many efforts to be made to take this technology towards reaching relevant breakthrough points. The purpose of this review paper is to provide a snapshot of the situation and to compare the progresses made by the electrocaloric community in terms of thermodynamic cycles, materials, experimental devices, numerical studies, energy performances, and perspective cooling applications.
In the following sections, the paper is organized as follows:
- Section 2 is devoted to the thermodynamics of the electrocaloric effect and to the possible thermodynamic cycles that an electrocaloric device for cooling or heat pumping could be based on.
- In Section 3, a wide overview of the materials showing an electrocaloric effect is provided. The electrocaloric materials are discussed and reviewed based on multiple possibilities of classification.
- Section 4 aims to underline the importance of numerical modelling to opportunely tune the working conditions to operate with optimized device, in terms of energy performances.
- Section 5 provides a review of the experimental prototypes of electrocaloric coolers built up to now.
- In Section 6, the main conclusions are drawn and an analysis of the future perspectives for the electrocaloric research is done.
2. Thermodynamics and Cycles
This section aims to introduce the theory and the fundamental relations [11] connected to the electrocaloric effect and to provide a general scenario of the possible thermodynamic cycles employable in an electrocaloric system for cooling or heat pumping.
2.1. Thermodynamics of the Electrocaloric Effect
The electric field (E) is a field of forces generated in space by the presence of one or more electric charges and the relation that connects it to its conjugated fields (electric displacement D and polarization P) is:
Under the hypothesis of linear and homogeneous material, Equation (1) becomes:
Considering a reversible thermodynamic process, with no pressure or volume work in the electrocaloric material, the internal energy of an electrocaloric material could be written as:
and, as reported in Equation (4), the specific entropy of a dielectric material at a constant electric field and temperature, is formed by three contributions: One due to lattice vibrations (), one due to electrons agitation (), and one due to the interaction with an electric field ().
Consequently:
By relating the internal energy and Equation (5) the following relations can be obtained:
Thus:
Indeed, the application of the external electric field to an electrocaloric material generates the ordering of the electric dipoles of the material according to the field direction. If the isothermal conditions are kept during the field application, and do not change whereas decreases; thus, a negative change in the total entropy (−) occurs. If the transformation is adiabatic, the total entropy of the material does not change while decreases; consequently, and must increase generating a positive temperature change () in the electrocaloric material. Dually, an isothermal remotion of the electric field implies a positive change in total entropy ; whereas a negative variation of the temperature of the material (−) is observed if the intensity of the field varies adiabatically. and constitutes the quantities that measure the entity of the electrocaloric effect in a material.
Based on the above relations, the isothermal change of the total entropy, due to electrocaloric effect, is given by:
The adiabatic change of temperature, due to electrocaloric effect, could be written as:
2.2. Thermodynamic Cycles
A certain number of thermodynamic cycles could be applied to electrocaloric refrigeration. These cycles are already known for having been used with respect to other cooling technologies (vapor compression or magnetic refrigeration) [26]. Before presenting them singularly, to facilitate the reader, the generalities of the working principles of an electrocaloric system for cooling or heat pumping are introduced briefly.
The scheme of principle of an electrocaloric system operating in cooling mode sees the electrocaloric material (refrigerant) vehiculating the heat from the cold to the hot environment through the cyclical repetition of four (or more) processes [27]. Indeed, after the reiteration of each cycle, the load will result in being cooled. An electrocaloric cooler exploits the manifesting of the electrocaloric effect to achieve this goal. Specifically, in an electrocaloric-based thermodynamic cycle, the processes of isothermal and adiabatic polarization (where, respectively, ECE manifests itself as an entropy and a temperature variation) can be opportunely combined giving rise to the specific cycle on which the electrocaloric system founds itself.
The components that typically form an electrocaloric system are a system for generating/removing the electric field, the solid-state electrocaloric material realizable in different shape configurations, two heat exchangers connected with the cold and the hot environments, and a heat transfer mechanism (that could involve an auxiliary fluid or another solid-state material) to opportunely vehiculate the heat flux for subtracting heat from the cooling load.
2.2.1. Carnot Cycle
The electrocaloric Carnot cycle consists of two adiabatic and two isothermal processes, applied to an electrocaloric refrigerant, as shown in Figure 1. In process 1 → 2, the intensity of the electric field is adiabatically increased; indeed, the material is partially polarized (process 1–2) and it adiabatically increases its temperature from T1 to T2 because of the electrocaloric effect. In 2 → 3, an isothermal polarization occurs: While the temperature of the material is constant, its total entropy is reduced up to s3 (due to ECE) and the heat is released to the hot environment. The adiabatic depolarization (3 → 4) decreases the temperature of the electrocaloric material up to T4, thus, in the consequential isothermal depolarization (4 → 1), it absorbs heat from the cold environment, recuperating the energy lost during the previous process. The area drawn by the points 1, 2, 3, and 4 represents the work w required by the system to transfer heat from the cold to hot environment; whereas the area 4,1,a,b accounts for the cooling heat removed from the cold environment. The coefficient of performance (COP) of the Carnot cycle that quantifies the desired effect (qc) on the work made (w) and that represents the concept of perfect refrigeration as well as the upper limit achievable by a refrigeration system, is:
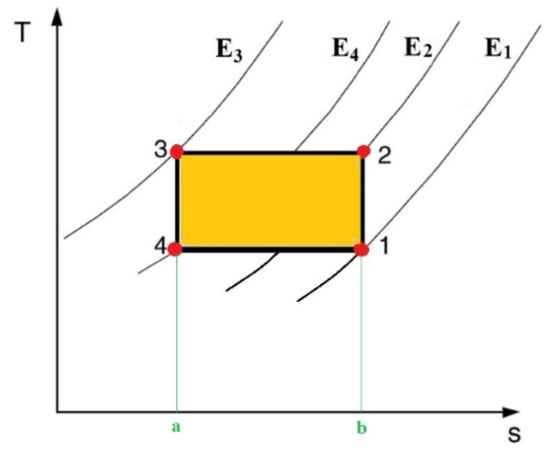
Figure 1.
The four processes of the Carnot cycle for electrocaloric cooling.
The disadvantage related to the employment of the Carnot cycle is the need for the operation with four different intensities of electric field. Moreover, another limit is that the temperature interval between the hot and could source is limited by the adiabatic temperature change of the electrocaloric material achievable during the isentropic polarization and depolarization; indeed, this could limit its applicability when larger temperature differences are required.
2.2.2. Brayton Cycle
The Brayton cycle consists of two adiabatic and two isofield processes as shown in Figure 2a. The first process (1 → 2) is the adiabatic polarization (the electric field increases from E1 to E2) that leads to an increment (ΔTad,12) in the temperature of the solid-state refrigerant. With the field kept constant at E2, in the isofield process (2 → 3), the heat is transferred from the refrigerant to the hot environment. During the adiabatic depolarization (3 → 4) the intensity of the electric field falls from E2 to E1, thus in the electrocaloric material, a negative change of its temperature (ΔTad,34), due to ECE, occurs. The isofield (E1) process (4 → 1) allows the heat subtraction from the cold environment.
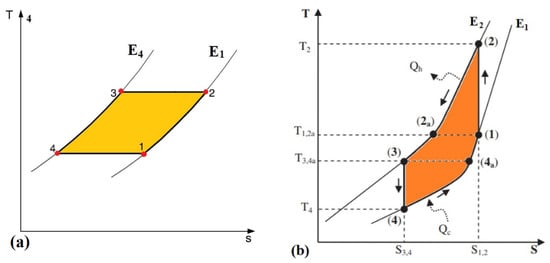
Figure 2.
The four processes of the Brayton cycle for electrocaloric cooling: (a) Without and (b) with regeneration.
Even if the Brayton cycle could not achieve the Carnot COP, the Brayton cycle can exhibit optimal performances as well as the electrocaloric refrigerants has parallel T-S curves and it presents the additional advantage to require only two levels of electric field intensity. The heat transfer in the Brayton cycle arises in a different way from the Carnot cycle one, since in the former, the heat transfer occurs while the electric field intensity remains constant; conditions that favor the heat exchange. Anyhow, to further enhance the performances of the Brayton cycle, the concept of regeneration could be introduced, as Figure 2b exhibits. The adiabatic polarization (1 → 2) provokes the temperature rising to T2, due to ECE. Then, the electrocaloric material releases heat to the hot environment, thus the temperature falls to T2a; subsequently, an additional cooling at the constant electric field occurs thanks to the presence of the regenerator up to T3. The adiabatic depolarization lowers the temperature further to T4 (due to ECE). Then, Qc is the heat subtracted from the cold environment and absorbed by the electrocaloric materials that consequently rises its temperature up to T4a. A dual operation of regeneration transfers further heat to the electrocaloric materials causing it to reach T1 and closing the cycle. Indeed, the main difference of the cycle described in Figure 2b with respect to the cycle without regeneration (Figure 2a) is that, in the cycle with regeneration, after the adiabatic polarization process, thanks to the presence of the regenerator, there is an additional cooling (2 → 2a), as well as an additional heating provided in process (4 → 4a). Indeed, the regenerator recovers the heat fluxes.
2.2.3. Ericsson Cycle
Next to the Brayton cycle, the Ericsson is a thermodynamic cycle with regeneration, too. The difference is the presence of two isothermal processes instead of the two adiabatic ones. Indeed, the Ericsson cycle consists of two isothermal and two isofield processes and it requires the heat regeneration. With reference to Figure 3, where the processes of the Ericsson cycle are shown, during the isoelectric step (1 → 2), thanks to regeneration, the heat is absorbed by the electrocaloric material; during the isothermal polarization (2 → 3) it is released to the hot source. Another regeneration process happens during 3 → 4, to prepare the electrocaloric material to absorb the heat from the cold source while an isothermal depolarization occurs (4 → 1).
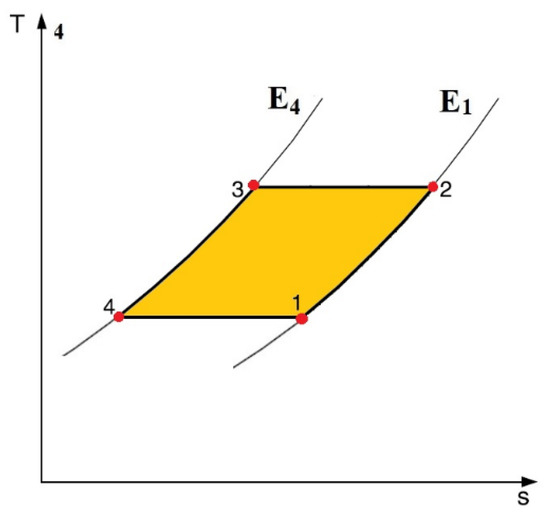
Figure 3.
The four processes of the Ericsson cycle for electrocaloric cooling.
In an ideal transformation, the amount of heat transferred into the regenerator in the regeneration process (1 → 2) must correspond to the one rejected out by the regenerator during the other regeneration process (3 → 4) but, through the Ericsson cycle, it never happens. The reason lies in the fact that the specific heat capacity at constant electric field, as demonstrated by He et al. [28], is a function of both the temperature and the electric field. Indeed:
Undeniably, the amount of heat absorbed and released will never be equal quantities. Indeed, the cycle is characterized by irreversible processes and, therefore, by a decrease in the efficiency of the Ericsson machine [27,28]. Consequently, the Ericsson cycle cannot achieve the condition of ideal regeneration and its COP is always smaller than that of the reversible Carnot refrigeration cycle, on an equal temperature range.
2.2.4. Stirling Cycle
The Stirling cycle is a regenerative cycle very similar to the Ericsson one, but with the difference of being characterized by two isothermal and two iso-polarization processes (instead of the two Ericsson’s isofield processes) as shown in Figure 4. He et al. showed mathematically [28] that the specific heat at constant polarization just depends on the temperature. This allows the Stirling cycle to be able to achieve the conditions of perfect regeneration through the utilization of a reversible regenerator. Consequently, the upper limit of its coefficient of performance coincides with the one of a reversible Carnot refrigeration cycle, operating in the same temperature range. In conclusion, the Stirling cycle becomes more competitive as is its regeneration process is closer to ideality.
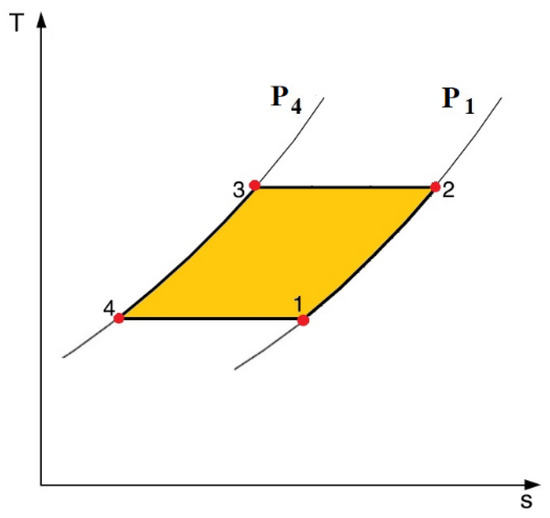
Figure 4.
The four processes of the Stirling cycle for electrocaloric cooling.
2.3. The Concept of Active Regeneration and the Active Electrocaloric Regenerative Refrigeration (AER) Cycle
As shown in the previous sections, the choice of the regenerator is very influent with respect to the performances of an electrocaloric system for cooling. There are three types of regenerators: External, internal, and active. The external regenerator exchanges heat with the refrigerant by means of an auxiliary heat transfer fluid that flows both within the electrocaloric material and in the regenerator that it is externally placed. With the solution of internal regenerator, the electrocaloric refrigerant is placed into the regenerator together with the regenerator material and heat is transferred directly between themselves. If the regenerator is active, the electrocaloric material itself plays the double role of refrigerant and regenerator and the auxiliary fluid only flows to exchange heat with the heat exchangers connected to the hot and cold environments. The latter choice leads two advantages: Both the irreversibility losses, due to the auxiliary fluid, and the losses related to the regenerating fluid mixing at different temperatures, are reduced. With reference to the electrocaloric cooling, the active electrocaloric regenerator, where the electrocaloric material is both refrigerant and regenerator, was developed. An auxiliary fluid is used to move the heat from the cold to the hot end of the regenerator.
Based on the concept of active regeneration, the active electrocaloric regenerative refrigeration (AER) cycle is introduced here.
The AER is a regenerative Brayton-based cycle, and it is characterized by four processes shown in Figure 5. The step (I) is the adiabatic polarization that occurs in the absence of the passage of the secondary fluid: An electric field is applied to the electro-caloric solid that heats up because of the electrocaloric effect. The second phase (II) is called cold-to-hot heat transfer: As the name suggests, a secondary fluid flows from the cold to the hot environment, while the electric field is constant at the maximum value. The fluid cools the EC material, because the temperature of the former when it enters the electrocaloric regenerator is equal to that of the cold environment, which is lower than the material one. Thus, while crossing the regenerator, the secondary fluid heats up whereas the regenerator is cooled down; the former reaches a temperature higher than the hot environment one, so it releases heat once it approaches the hot heat exchanger. The third phase (III) is called adiabatic depolarization: While the auxiliary fluid is not moving, the intensity of the electric field is reduced adiabatically up to the minimum value and a lowering of the temperature of the electrocaloric material, due to electrocaloric effect, is registered. In the hot-to-cold heat transfer (IV), the auxiliary fluid cools down because it crosses the regenerator from the hot to the cold environment, thus heating the electrocaloric material. The cold fluid then goes into the cold heat exchanger, where it absorbs the heat, and it realizes the useful effect of the cycle.
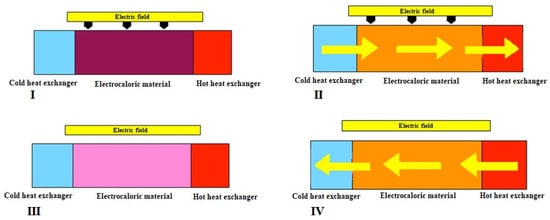
Figure 5.
The four processes of the active electrocaloric regenerative refrigeration cycle.
The above-described processes refer to an electrocaloric material not showing thermal hysteresis. As a matter of fact, this undesired phenomenon modifies the regenerative Brayton cycle on which the AER found its operation; as a consequence, the steps (I) and (III) are not characterized by constant entropy anymore (since there are non-zero aliquots of generated entropy). Indeed, the AER cycle with hysteresis is modified as shown in Figure 6, where thermal and electrical hysteresis occur [29].
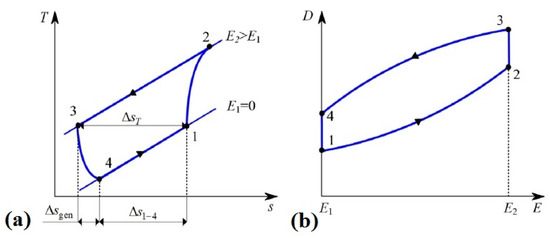
Figure 6.
Active electrocaloric regenerative (AER) thermodynamical cycle, property of a hysteretic material, on (a) T-s; (b) D-E diagram [29].
During the evolution of the four steps of the cycle, the temperature in the electrocaloric material is not constant, but a different temperature profile is triggered instant by instant. Substantially, every section of the regenerator experiments its own AER cycle, according to the local working temperature. The main advantage in using this system is that, through an AER, one can appreciate a larger temperature span between the sides of the regenerator than in a Brayton cycle without regeneration. On the other side, the main disadvantage is the limitation in operating with high frequencies of the AER cycle due to the upper limits in time required for fluid flowing and heat exchanging.
Lastly, with reference to all the above-introduced cycles, in a real application, the performances could be significantly affected by the irreversibilities of both the material (thermal and electrical hysteresis) and the process (i.e., Joule heating, leakage currents etc.). The former could make it difficult to get isentropic processes of polarization and depolarization whereas the latter could degrade the energy performances in terms of COP.
2.4. Thermal Diodes-Based Electrocaloric Cooler
An electrocaloric application for cooling that allows operation with higher frequencies is based on thermal-diodes (or thermal switches), where the vehiculation of the heat fluxes is ensured by solid-state materials, with variable thermal conductivity, independent of the variation of the electric field. Indeed, the auxiliary fluid is not utilized anymore, but the combination of slices of electrocaloric materials interspersed with materials whose thermal conductivity is controlled by the intensity and the direction of the electric field. In this way, it is possible to switch the direction of the heat flow in sync with the temperature variation of the electrocaloric material. In Figure 7a, the transformations on the T-S diagram of the electrocaloric cycle based on thermal diodes are reported, with reference to the scheme of principle of the system formed by one slices of electrocaloric material sandwiched between two thermal switches (single-stage system) visible in Figure 7b. In the first process (1 → 2), the electrocaloric material is adiabatically polarized while the thermal conductivity of the two thermal diodes would be 0 W m−1 K−1 in an ideal concept of thermal switch but, realistically, one can state that the thermal conductivity falls significantly. There is an increase in temperature due to the electrocaloric effect. In (2 → 3), there is the passage of the heat flow towards the hot environment since the thermal diode A is conducting. The third process (3 → 4) is the adiabatic depolarization: While the thermal diodes act as insulators (kA = kB = 0), a reduction in the temperature of the electrocaloric material due to the electrocaloric effect is registered. In the fourth phase (4 → 1), the heat flux flows from the cold environment toward the electrocaloric material since: The diode A is a thermal insulator, the diode B is a thermal conductor, and the temperature of the electrocaloric element is lower than that of the cold environment.
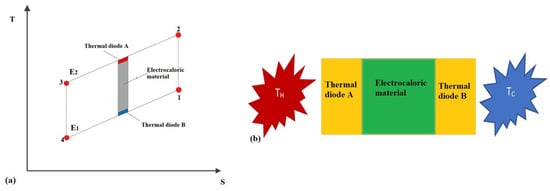
Figure 7.
(a) The electrocaloric thermal diode cycle on T-S diagram; (b) scheme of principles of the electrocaloric thermal-diode system for cooling.
The one described above is a single-stage system; therefore, the achievable temperature spans are limited by the peak of adiabatic temperature change of the electrocaloric material. To overcome this limit, it is possible to design a multi-stage electrocaloric thermal diode system where multiple blocks of thermal-diode/electrocaloric-material/thermal-diode are cascaded. As visible in Figure 8, with this solution, the temperature difference is increased.
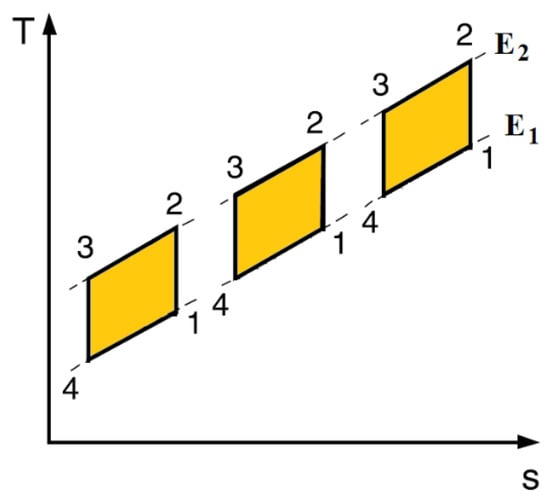
Figure 8.
An example of cascaded multi-stage thermal diode cycle on T-S diagram.
Furthermore, for thermal diodes-based thermodynamic cycles, it is useful to discuss the concept of heat recovery: Plaznik et al. [30] highlighted the work done by an electrocaloric system based on the Brayton cycle. They suggested that a special electric circuit should be employed to recover part of it. Anyhow, the irreversibilities lying in the material and the system (thermal hysteresis as well as Joule heating) can degrade the rate of the successfully recovered work. Defay et al. [31] showed that it is possible to artificially recover the electrical work expended: It could be done by charging the electrocaloric capacitor (formed by the thermal diode sandwiched between two ECE elements) to cause heating, when needed. Dually, the inverse operation of capacitor discharge provokes a cooling of the ECE material. In their work, they demonstrated that it is possible to recover up to 70–80% of the electrical work done to drive the electrocaloric effect through the utilization of inductors. The final benefit is a significant increase of the coefficient of performance of the electrocaloric system. Further applications of heat recovering in electrocaloric devices can be found in [32,33,34,35].
Anyhow, the systems based on thermal switches work efficiently when the frequency of the thermodynamic cycle per unit of time is very high. The performances of the caloric materials working as refrigerants in high-frequency applications, in turn, depend on the nature of the material, the amplitude of their electrocaloric effect, and their phase transition. Previous inherent scientific studies [36,37] evidenced that the materials with second-order phase transitions perform much better than those of first order. All these concepts on the electrocaloric materials will be introduced in the following section.
3. Materials
As mentioned in previous sections, in addition to the choice of the most appropriate thermodynamic cycle, the performance of a refrigeration device is closely linked to the refrigerant used. Indeed, with reference to the application to electrocaloric systems for cooling ad heat pumping, the conditions to find the most suitable electrocaloric materials are [38,39,40]:
- The detection of a pronounced electrocaloric effect at room temperature, under relatively small intensities of the electric field;
- To be toxic-free and chemically stable;
- To present low economic costs;
- The resistance to corrosion (by the heat transfer fluid or by the contact with other materials);
- The easiness to be reproduced (in terms of the number of composing elements, the compatibility with large-scale production);
- To show slight thermal hysteresis;
- To present little values of specific heat to enhance the adiabatic temperature changes as well as a rapid response, in terms of electrocaloric effect, to the electric field variations;
- The possibility of being polarized by high electric fields (indeed electrical robustness to avoid the breakdown phenomenon);
- Small electrical conductivity to prevent the instauration of leakage currents that provoke the undesired heating (due to Joule heating), which could conflict with the cooling phases of the cycle and high thermal conductivity to efficiently manage heat fluxes as fast as possible [41].
Many are the possibilities to classify the electrocaloric materials. The purpose of the following sections is to provide to the reader all the elements to classify and categorize them, in order to assist them in the selection of an electrocaloric material to be used as a refrigerant.
3.1. Order of Phase Transition
All the materials showing the electrocaloric effect could be categorized based on their phase change between the ferroelectric to the paraelectric state: First- and Second-Order Transition, i.e., FOT and SOT. In both cases, the electrocaloric material changes its state from ferroelectric to paraelectric in correspondence with a specific temperature called the Curie point. The Curie is also the temperature where the electrocaloric effect is the most pronounced in terms of both isothermal entropy change and adiabatic variation of temperature [11,38].
The transition is defined as first order if a discontinuity in the first-order derivative of the Gibbs free energy (Gfe) function is observed, i.e., the polarization function with respect to the temperature shows a discontinuity, since it is the first-order derivative of Gfe with the electric field strength. This kind of transition is not instantaneous because of the co-existence of two phases in equilibrium and the consequent presence of latent heat. Indeed, applying an electric field to a FOT material can result in both the state transition from paraelectric or antiferroelectric to a ferroelectric, and the structural variation or a significant phase volume discontinuity but without showing a clear crystallographic modification. The latter two phenomena produce a displacement of the atoms that occurs in a non-infinitesimal time. The consequence is the non-immediate electrocaloric effect response to the stimulus of the intensity variation of the electric field. Furthermore, the presence of latent heat, during this phase transition, implies a heat dissipation during the polarization process that influences the final temperature that the electrocaloric material will reach at the end of the process. This results in the presence of thermal hysteresis in FOT materials. On the other side, in the FOT material, the co-existence of two phases in equilibrium could carry to the detection of a Giant electrocaloric effect that is the product of two phenomena: The conventional electric-field entropy-driven process (electric entropy variation ) and the difference in the entropies of the two crystallographic modifications (structural entropy variation ). Indeed, the first-order transition materials present very large (giant) peaks of adiabatic temperature changes (around the Curie point), but the presence of ECE is concentrated in a narrow temperature range.
The second-order phase transition in an electrocaloric material occurs if the Gfe first-order derivative is a continuous function while the discontinuity appears in the second-order derivative; indeed, the electric susceptibility that is the derivative of the electric polarization is discontinuous. The continuity in the polarization and the absence of latent heat in the phase transition ensure that SOT materials do not present hysteresis, thus, the adiabatic temperature change is close to instantaneousness as well as SOTs do no manifest volume changes. On the contrary, the electrocaloric effect shown by second-order materials has smaller peaks than FOT (on equal intensity change of the electric field) but it spreads over a broad temperature range. [18,38,42].
3.2. Structural Composition and Shape Classification
Based on their structural composition, and according to other specific reviews on electrocaloric materials already published in the scientific literature [11,19], the electrocaloric materials belong to three macro-groups:
- Monocrystals;
- Ceramics;
- Polymers.
The above three groups could be further divided, based on their shape and thickness, in:
- Bulk samples;
- Thick films;
- Thin films.
Other similar classifications are proposed in the literature, like the division among inorganic and organic electrocaloric materials by Shi et al. [24], or the categorizing of ferroelectric and antiferroelectric materials introduced by Lu et al. [20] or dividing them in relaxer ferroelectric-based materials, multilayer capacitors, and polymers [43].
In the present section, we decided to follow the classification based on structural composition [11,19] where, within each category, a further differentiation among the shape and the thickness will be done. Indeed, we do not intend to review all the materials already present in [11,19] from the beginning but we intend to take these two reviews [11,19] as a starting point for our section on the electrocaloric materials and, to complete them, we will only add the recently developed materials and therefore not included in [11,19]. Moreover, we focus prevalently on room temperature range rather than cryogenics.
3.2.1. Monocrystals
Monocrystals, also called single crystals, are the structural composition of the electrocaloric materials that could be employed only as bulk samples because of the relatively small mechanical robustness with respect to the solicitation with big electric field changes. Due to the crystallographic structure, the main limitation is the easiness of fracture due to the electric field stress. Therefore, to the bulk materials, only smaller electric field changes can be applied, if compared with thin films. Consequently, the resulting variations in terms of entropy and temperature changes due to the electrocaloric effect are moderate.
In Table 1, to the best of our knowledge, all the monocrystals introduced in the literature showing the electrocaloric effect are listed. Most of them were previously classified in other review papers; for them, we report the reference to the review in which they already appeared. As already mentioned above, the electrocaloric single crystals show very slight electrocaloric effect answers in terms of adiabatic temperature changes and isothermal entropy variation. As reviewed by Valant [19], up to 2014, the highest ΔTad (2.7 K) was exhibited by 0.72Pb(Mg1/3Nb2/3)O3-0.28PbTiO3 under ΔE = 1.2 MV m−1, but this value is quite far from the possibility of considering such electrocaloric single-crystals employable for cooling applications, considering also that its Curie temperature is quite far from the room temperature range. As a matter of fact, most of the electrocaloric single crystals reported in Table 1 show the peak of the electrocaloric effect at temperature to be not suitable for applications at room temperature with the exception of a small number of them whose electro-caloric effects in terms of ΔTad do not exceed, however, 1 K. Anyhow, worthy of special mention is MDABCO](NH4)I3 that is a single crystal belonging to the family of the ferroelectric metal-free perovskites, studied by Wang et al. [44], that exhibits an extraordinary giant electrocaloric effect (16 K) at relatively moderated electric field intensity (2 MV m−1), if compared with the other materials listed in Table 1. Anyhow, the main limitation is that the electrocaloric answer to this perovskite is limited to a small temperature range around the peak (450 K).

Table 1.
Monocrystals materials and their electrocaloric properties.
In conclusion, the group of electrocaloric monocrystals is characterized by small peaks of adiabatic temperature change (apart from the metal-free perovskites [MDABCO](NH4)I3 characterized by a giant electrocaloric effect) and isothermal entropy variation also due to the limited electric field that could be applied to bulk materials.
3.2.2. Ceramics
The ceramics with electrocaloric properties are inorganic materials that could be organized in bulk, thick, and thin films. Higher electric fields could be applied to a thick (thickness 10 μm as order of magnitude) or thin (thickness minor than 1 μm) film rather than the bulk version (thickness greater than 100 μm), even if the material has the same composition. Another advantage is that the ceramics have high thermal conductivity and small electrical conductivity: It fully satisfies the criteria that an electrocaloric material must show to be considered a good solid-state refrigerant.
Table 2 reports as comprehensive a list as possible of ceramic materials together with the electrocaloric effect shown, while they are arranged as bulk or thick/thin films. As a general comment, there are much more ceramic materials showing a promising electrocaloric effect rather than the single-crystal ones. The class of PLZT thin films exhibit enhanced adiabatic temperature changes and various temperature ranges of applicability. Specifically, worthy of mention is the Pb1-3x/2LaxZr0.85Ti0.15O3 (PLZT 11/85/15) [57] that seems suitable for cooling and heat pumping applications: It exhibits 12 K as ΔTad due to an electrocaloric effect under ΔE = 90 MV m−1. Through the increase or the decrease of the La content in 8–14% range, giant ECEs in terms of peaks of ΔTad could be detected: 28 K and 20 K (ΔE = 90 MV m−1) for the upgraded and downgraded versions, respectively. The thin film of ceramic ferroelectric Pb0.8Ba0.2ZrO3 [54] ensures 45.3 K at 290 K as response to the electric field change of 0.6 MV m−1. Further, in the class of the antiferroelectric ceramics, the thick-film Pb0.97La0.02(Zr0.75Sn0.18Ti0.07)O3 [56] emerges due to the extraordinary ECE shown around 278 K, with resulting ΔTad = 54 K for ΔE = 90 MV m−1.

Table 2.
Ceramic materials and their electrocaloric properties.
3.2.3. Polymers
At the best of our knowledge, the polymers showing an electrocaloric effect are all based on the PolyVinyliDene-Fluoride P(VDF) copolymers that, without the presence of an electric field, are crystallized in a non-polar form, to which is associated the lowest energy configuration. During the polymerization process, some defects could be voluntarily added in form of the following monomers: ChloroTriFluoroEthylene (CTFE), TriFluoroEthylene (TrFE), Vinylidene DiFluoride (VDF), and Chlorofluoroethylene (CFE). Different electrocaloric answers could be observed, depending on the type and the quantity of the defects introduced, and the polymers are all arranged in thick or thin films. Table 3 schedules the main polymers showing electrocaloric properties. Worthy of mention is the class of P(VDF-TrFE-CFE)/BSTs polymer nanocomposites, obtained from the terpolymer P(VDF-TrFE-CFE) 62.3/29.9/7.8 doped with different alloys of the ferroelectric ceramics (BaxSr1−xTiO3). The result is a reduction of both the ferroelectric domain and the energy bandgap occurring for ferroelectric/paraelectric phase transition. This phenomenon carries a larger electrocaloric effect at moderate electric field changes.

Table 3.
Ferroelectric polymers and their electrocaloric properties.
In conclusion, there are many possibilities of the electrocaloric materials to be employed as solid-state refrigerants, but no single one would completely satisfy all the criteria specified at the beginning of this section. The research of a fair compromise between pros and cons in the choice of an electrocaloric refrigerant is suggested with reference to the specific application.
4. Numerical Models
As underlined in the previous section, a basic requirement is to find the most appropriate electrocaloric refrigerant with the purpose of operating with energy-efficient electrocaloric systems. This condition is necessary but not sufficient, since, next to it, the working conditions must also be set opportunely. Indeed, it is necessary to design an electrocaloric device (AER or thermal-diodes-based) that is ensured to work with operating conditions such as to guarantee the highest energy performance. A quality optimization process can only be guaranteed by extensive operations of numerical modeling.
Even though electro-caloric refrigeration has been in the spotlight for 15 years now, the number of developed models and numerical studies presented in the literature is still small. Table 4 reports all the numerical models of electrocaloric systems for cooling, developed and introduced in the literature: Up to now, there are only five AER-based models, four thermal-diode systems, and a recent model of an electrocaloric multilayer capacitor.

Table 4.
Numerical models of electrocaloric devices introduced in the literature up to now.
Regardless of whether the model is one-, two-, or three-dimensional, the mathematical model that regulates an electrocaloric system based on the AER cycle is defined by the following equations:
The above is the most general and complete form of proposing the AER equations to describe, at the same time, both phases of adiabatic variation of the electric field and both regenerative steps of fluid flowing. The term , a power density that accounts for the electrocaloric effect, is positive during the polarization, negative during depolarization, and zero during the regenerative fluid flow processes. Dually, while the electric field changes adiabatically, the auxiliary fluid is not moving, is null, and the AER is regulated only by the energy Equations (18) and (19).
Among the AER numerical models proposed in the literature, there are different ways to build the term; indeed, the modalities of considering the electrocaloric effect shown by the solid-state refrigerant are different. They will be illustrated following the introduction of the various models.
To the best of our knowledge, the first model of an active electrocaloric refrigerator was presented in 2014 by Guo et al. [35] belonging to the research group of the Carnegie Mellon University, Pittsburgh (USA). They modelled a 3D microscale regenerator (7 mm × 1.25 mm × 125 µm) composed of five parallel plates of P(VDF–TrFE–CFE) terpolymer [11,19], as electrocaloric solid-state refrigerant, each one with a thickness of 10 μm. The auxiliary fluid, flowing in the channels, formed between the plates is HT-70 whose fundamental properties is to be an electric insulator, so that the electrical insulation of the plates is not required. The model is solved through finite-element method (FEM) but, mathematically, it obeys the Equations (16)–(19) and the term, modelling the electrocaloric effect of P(VDF–TrFE–CFE), was built as follows:
where the relationship between the entropy and the electric field for the P(VDF–TrFE–CFE) terpolymer has been obtained by experimental data [71] and formalized as:
with
The numerical model was employed to explore the energy performances of the above-introduced active electrocaloric regenerative refrigerator, under the following working conditions:
- The frequency of the electrocaloric cycle that varies from 0 to 30 Hz;
- The electric field that was varies between 0–150 MV m−1;
- The hot source temperature was set at 300.15 K;
- The temperature span was varied from 0 to 30 K.
The cooling power density and the coefficient of performance were evaluated, and an extract of their results is reported in Figure 9a–d [35]. In Figure 9a,b, the cooling power density and COP vs. frequency trends, estimated with ΔE = 100 MV m−1 in correspondence of a temperature span of 5 K, show that the cooling power density saturates around 30 Hz and that the maximum COP is 8.5 at 15 Hz. Furthermore, in Figure 9c,d, one can observe that the AER working with 15 K as temperature span is able to produce 3 W cm−2 as cooling power density, whereas the corresponding COP of the Carnot one is 31%.
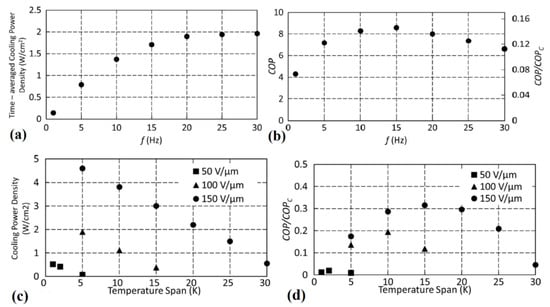
Figure 9.
An extract of the results on cooling power density and coefficient of performance introduced by Guo et al. (reprinted with permission from [35], Elsevier, 2014).
Recently, in 2020, this group introduced [64] a thermodynamic level-device model that includes the contact thermal resistance and dielectric loss heating, that are non-ideality factors. The electrocaloric effect, in terms of adiabatic temperature change, was modelled through three different methods:
(a) the Curie–Weiss law:
(b) the Landau–Devonshire theory:
and (c) a new Gaussian fit method introduced by the authors [64]. The Curie–Weiss law gives an explicit expression for the EC temperature change as a function of the material properties, electric field, and temperature, but it is appliable only to materials whose behavior is paraelectric (i.e., electrocaloric materials working upon the Curie point). The Landau–Devonshire theory covers a wider temperature range, but the agreement with the experimental data, detected by the authors, is not satisfactory. The authors found the Gaussian fit method as the most affordable in predicting results close to the experimental data that they used for comparison [64]. The electrocaloric materials under testing are the P(VDF-TrFE) 55/45 mol % copolymer [11,19] and the P(VDF-TrFE-CFE) 59.2/33.6/7.2 mol % terpolymer [10,18]. They studied the influence of the operating frequency (0.2 Hz; 0.5 Hz, and 0.8 Hz) on the COP and they found that [64]:
- The wider temperature range over which the COP remains large was noticed for P(VDF-TrFE-CFE);
- 0.2 Hz is the frequency ensuring the larger COPs;
- Due to heat losses, the best COP calculated is only 60% of the Carnot COP and it was detected in the copolymer P(VDF-TrFE).
In the same year of the presentation of the first model by the above-introduced research group (2014), the Slovenian research group of the Ljubljana University studied the behavior of one of the, up to then, most promising relaxer ceramics at room temperature [68], through a 1D Matlab tool of an AER regenerator. The Equations (16) and (17), projected on one-dimension, are coupled with the explicit forms of the energy equations of the fluid and the solid, modelled as follows:
where:
The was calculated according to the thermal conductivities and the volume fractions (ψ) of both the electrocaloric material and the electrodes as:
The electrocaloric effect on the solid temperature occurring during the variation of the electrical field intensity (adiabatic polarization and depolarization processes) is modelled as:
The model was run under the following operative conditions:
- Hot side temperature = 293 K;
- The temperature span varied in 5–15 K;
- The fluid flow rate changes in 0.003–0.2 kg s−1,
- The investigated frequencies of the AER are: 0.25, 0.5, 1, 2 and 3 Hz.
The results carried out were published and compared to the ones carried out by an active magnetocaloric refrigerator based on the same mathematical model architecture [72] and operating under the same above conditions. The magnetocaloric refrigerant is gadolinium and the energy performances were evaluated in terms of specific cooling power and COP vs. AER cycle frequency. They observed that for low intensities of electric field (39.2 MV m−1), the AER gives smaller specific cooling powers but larger COP than the active magnetocaloric regenerator (subjected to ΔB = 1 T). Under greater ΔE (77.4 MV m−1), the electrocaloric regenerator gives both better specific cooling powers and COPs. The maximum values shown by the AER mounting PST as solid-state refrigerant, were COP = 28 and 1300 W kg−1 as specific cooling power.
One year later, in 2015, this research group provided an updated version of the model [69]: A two-dimensional one where, subsequently [29], the hysteresis was also accounted for. The model is based on a parallel plate regenerator, the electrocaloric refrigerant is the bulk ceramic PMN-0.1PT [19,69] whereas the auxiliary fluid is silicone oil chosen because of its dielectric nature (bad electrical conductor). The regenerator is made of three stacks, each one assembled with 10 plates of bulk ceramic with a length of 20 mm (thus achieving a total length of 60 mm).
Equations (16) and (17) were projected two-dimensionally and the energy Equations (26) and (27) were replaced by Equations (31) and (32):
where and are the power densities associated to the heat transfer from the ambient to the solid and the fluid part of the AER (heat gains). The specific entropy generated because of the hysteresis of the EC material and the specific entropy of the EC material at a constant temperature ( and ) were calculated through:
With reference to [29] (in Figure 3 of [29]), the authors plot the maximum specific cooling power and the COP vs. frequency. Worthy of notation is the influence of the hysteresis in the energy performances of the AER since one can observe the energy performances while the system operates with and without accounting the hysteresis intrinsic in the electrocaloric material. Specifically, the influence of the hysteresis on the specific cooling power become noticeable from 1.0 Hz onwards, whereas the COP is strongly affected by this undesired effect also for lower frequencies. On equal frequency, the medium difference between COPs with and without hysteresis is 1.
The behavior of both ferroelectric polymers and ceramics as solid-state refrigerants was tested also, in 2016, by Aprea et al. [38] in their comparative numerical study of the energy performances of an AER system. As a matter of fact, the Italian group (University of Salerno and University of Naples Federico II) proposed a 2D FEM parallel-plate AER model, experimentally validated [73,74], through which a wide evaluation of the energy performances of the most promising electrocaloric materials, showing an ECE at room temperature, was carried out. The regenerator (longitudinal section: 20 mm × 45 mm) was proposed in two different configurations:
- (1)
- 27 plates of 0.5 mm thick;
- (2)
- 54 plates of 0.25 mm thick.
Both of them are separated by channels dedicated to the flowing of unionized water to transfer heat between the cold and the hot environments. Given that this tool is also regulated by Equations (16)–(19), the peculiarity is the way in which the electrocaloric effect was implemented, i.e., the is a function of temperature and ΔE, and it was modelled as:
where Δt is the duration of the polarization/depolarization process.
Indeed, in their investigation [38], each electrocaloric material under test has different Q functions built utilizing experimental data on available in the scientific literature. Indeed, by the help of a mathematical function finder software, that allows to transform a table function in a mathematical expression, the mathematical expression for each Q has been extracted both for polarization and depolarization processes [38].
Many electrocaloric materials were analyzed: Relaxer ceramics and ferroelectric polymers in thick/thin films whose electrocaloric properties are reported in Figure 1 of reference [38] in terms of ΔTad. The figure shows the ferroelectric terpolymer P(VDF–TrFE–CFE) tested both as thin film and as a matrix in which bulky chlorine atoms were added as random defects to reduce the ferroelectric domain size and the energy barrier to phase transition (BaxSr1−xTiO3 has been selected as the filler) [69]. Moreover, a number of relaxer ceramics were considered: To the relaxer PbMg2/3Nb1/3O3 (PMN), a certain amount of the ferroelectric perovskite PbTiO3 (PT) was added. In the group of ceramics, the family of Pb1−3/2xLaxZr0.85Ti0.15O3 (PLZT) antiferroelectric (AFE) thick films was also tested both in single composition of PLZT 11/85/15 and in two compositionally graded structures: The “up-graded” one, by varying the La content from 8 mol % at the substrate interface to 14 mol % at the top surface; and the “down-graded” one, obtained through the opposite mol % gradient [38].
Below, the operating conditions of their investigation are reported:
- The frequency of the electrocaloric cycle was fixed at 1.25 Hz;
- The fluid flow rate was varied in 0.03–0.06 kg s−1;
- The temperatures of the hot and cold source were set at 300 K and 292 K, respectively;
- The electric field was changed adiabatically according to the literature data of each electrocaloric material [38].
In Figure 10, the temperature span, the cooling power density, and the COP of the AER mounting 27 and 54 parallel plates are shown. The 54-slice configuration globally confers better energy performances than the 27-plate one. The explanation is that 54 parallel plates ensure a larger heat exchange area for the convective heat transfer between the fluid and the electrocaloric material. Moreover, Aprea et al. observed that the best energy performances are given by the compositionally graded structures of PLZT ceramics; specifically, through the upgraded configurations, the maximum values of temperature span of 23 K, cooling power density of 135 W cm−2, and coefficient of performance of 11.2 are registered.
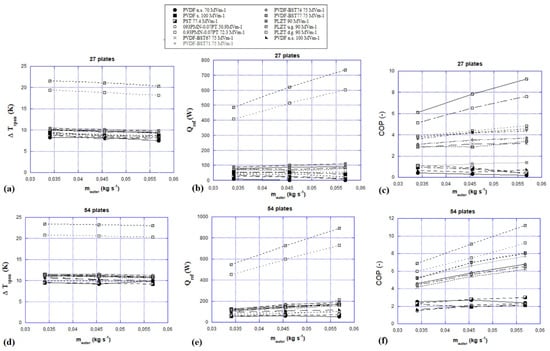
Figure 10.
The energy performances of the AER, in terms of temperature span, cooling power density, and COP, carried out while the regenerator is formed by: 27 (a,c,e) and 54 (b,d,f) parallel plates (reproduced from [38], Elsevier, 2016).
Subsequently, the Italian research group, based on the same numerical model, in a following work [39], integrated this investigation with two more ECE materials: The thin films of Pb0.8Ba0.2ZrO3 and Pb0.97La0.02(Zr0.75Sn0.18Ti0.07)O3. They compared them with other caloric effect materials and asserted that the class of electrocaloric PLZT materials gives higher energy performances than the other caloric-effect materials. Specifically, Pb0.97La0.02(Zr0.75Sn0.18Ti0.07)O3 ensures a temperature span higher than 40 K, with a cooling power that ranged between 1010 W and 1800 W, concluding that an electrocaloric refrigerator working with this material can be employed for a broader scope of commercial cooling applications [39]. Furthermore, if the Pb0.97La0.02(Zr0.75Sn0.18Ti0.07)O3 is employed is an AER system operating as a heat pump, because of the largest hot–cold temperature range required by this application, a consistent electrical power affects the coefficients of performance [40].
The latest novelty among the models based on the AER cycle is represented by the rotary electrocaloric refrigeration system, introduced by the Institute of Refrigeration and Cryogenics of the Shanghai Jiao Tong University [66], whose design allows thee continuous solid/fluid heat transfer. Specifically, the device is composed of 12 working parts of the electrocaloric material P(VDF–TrFE–CFE) [11,19] integrated on a rotating cylinder, whereas HT-70 is the heat transfer fluid that continuously guarantees the convective heat exchange and to which the heat recovery process is entrusted to. The mathematical model was based on Equations (16)–(19), the Q term was built according to Equation (20), and the device is designed as quasi-3D since the EC materials are designed as 2D rotational solids and the heat transfer fluid flows in out-of-plane direction. A sensitive parametric analysis was performed to improve the energy performances of the device; it was initially tested with 298 K and 308 K as the temperature of the cold and hot sides and the cyclic period is 64 s, whereas ΔE = 145 MV m−1. Under these conditions, the model can provide 290.6 W and 5.5, respectively, as cooling power and COP. Subsequently, they opportunely tuned the cycle-time and they found that with shorter cyclic periods, the cooling power increases; if the time of the AER cycle is 10 s, the system guarantees a cooling power of 1730 W [66].
Next to the AER cycle-based models, as already introduced, the alternative is to design solid-to-solid electrocaloric systems, founded on the concept of thermal-diodes: Solid-state materials to which the heat transfer role is entrusted, given their property of changing the thermal conductivity independent of the electric field applied. Indeed, since the auxiliary fluid is not required for such applications, the mathematical model of electrocaloric thermal diode systems is described only by the energy equations of the two solid materials, that are reported in the implicit form as:
After their AER model, in 2016, Feng et al., i.e., the research group of the Carnegie Mellon University, were the first in also developing a 3D model of an electrocaloric thermal diodes-based system [65]. Specifically, through a collaboration with Pennsylvania State University, they introduced and employed the model in a robust and comprehensive study: The system is a hybrid thermoelectric/electrocaloric heat pump with the purpose of being used for the cooling of electronics. The device is a proof of concept made of nine blocks placed on a substrate: Each block is composed of a slice of the electrocaloric material BZT [50], sandwiched between two Bi2Te3 thermoelectric elements. The mathematical model of their numerical tool is described by Equations (36) and (37). In Equation (37), a heat source is added to consider the power density associated to the heat generated in the TE elements by the Joule heating effect. On the other side, the following contributions were neglected: The heat losses between the blocks and the environment as well as the energy losses during the electric field changes, the contact thermal resistance between the electrocaloric and the thermoelectric blocks, and the heat transfer due to convection and radiation. The model is solved through the finite element method under a wide number of working conditions; an extract of the results presented by them are reported in Figure 11. By the analysis, the authors concluded that large electric currents, to be provided to the thermoelectric elements, are needed to obtain high cooling capacity but, with respect to the COP, there is an optimum point over which, due to Joule Heating and the reliability of TE element, a further current increment only carries to a reduction of it [65].
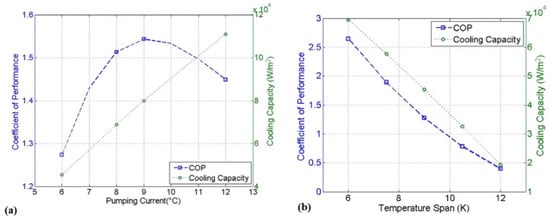
Figure 11.
(a) Coefficient of performance (COP) and cooling capacity vs. pumping current; (b) COP and cooling capacity vs. temperature span at 6 °C as electric pumping current applied (reprinted with permission from [65], The American Society of Mechanical Engineers, 2016).
In 2018, another electrocaloric model based on thermal switches was introduced by a research group belonging to the Kobe University [67]. They studied the effect of the thickness of electrocaloric materials, as well as the optimum number of plates and the time for thermal switching by varying cold-hot temperature difference and the frequency of the system operation. The electrocaloric material employed is a thin film of BaTiO3 [49]. The equations mathematically describing the numerical model are the one-dimensional projections of Equations (36) and (37). Moreover, in this model, the heat transfer between the boundaries of the materials and the environment was considered: Indeed, an additional power density (QB-term) was added to each equation to consider the leakage of both the electrocaloric and the thermoelectric materials.
The simulations were performed on many consecutive layers of the TE-EC-TE sandwiches, under 100 Hz as frequency of the TD-cycle and 20 K as cold-hot side temperature differences. In the evaluation of the energy performances of the system, particularly interesting is the effect of the thickness of the electrocaloric material on the average heat transfer efficiency and average specific cooling power generated in the system. The latter parameter increases according to the thickness of the electrocaloric material, but the average heat transfer efficiency decreases due to the ineffectiveness in thermal conduction heat transfer in the electrocaloric material. Therefore, the average heat flux transferred from the cold side of the system is maximum at 70 µm. Furthermore, 100 µm is the optimized thickness for the thermal diode. In the execution of their investigation, the authors observed that the heat transfer efficiency is maximum with the system mounting two layers of the electrocaloric material [67].
In 2020, the Luxembourg Institute of Science and Technology, in collaboration with the University of Cambridge, proposed [70] a three-dimensional FEM model of an electrocaloric multilayer capacitor system formed by 19 multilayer PMN capacitors (38 μm as global thickness) sequentially placed and devoted to Pd inner electrodes.
The model based on Equations (36) and (37) and is forced into the active layers for a short period of time using a Dirac-delta function whose values have been experimentally determined during the investigation. In Figure 12, an extract of the results they collected in the study is reported. In Figure 12a, the authors also report a comparison with experimental data (ΔTd) and good agreement was found. As shown in Figure 12b, the simulations started with all the system at the uniform temperature Ts and under with ΔE = 210 kV cm−1; after the steady state is reached, depending on the value of the starting temperature (298 K), a certain temperature difference is detected.
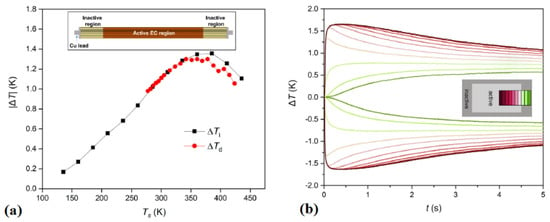
Figure 12.
(a) Experimental and numerical comparison under ΔE = 130 kV cm−1. (b) Temperature profile across the electrocaloric system under ΔE = 210 kV cm−1, up to reaching steady state with a starting temperature of 298 K [70].
Worthy of mention is the methodological approach recently developed (in 2019) by Blumenthal and Raatz [75], it is based on a V-Model for identifying optimized geometrical and operating parameters of an electrocaloric cooling device, since it integrates various tools like classification of device types, influencing factors, and methods of numerical simulation. They applied the methodology to a small-scale demonstrator that was tested for 2000 h, under ΔE of 210 kV mm−1 it was able to provide a temperature span of 1.1 K.
In this section, by reviewing all the models of electrocaloric devices presented to the scientific community up to now, our intent was to show the importance of numerical modelling as a fundamental instrument to predict the performances of the electrocaloric devices. Indeed, a consistent model can drive the road to correctly choose the parameters for pursuing a quality optimization process. Furthermore, it is noticeable as, step by step, the models become closer and closer to reality with the possibility of considering real irreversibility (like Joule heating or thermal hysteresis) in the electrocaloric refrigerant. Moreover, the numerical model is, in our opinion, the preliminary step for the design and realization of a performant experimental device since, to ferry the electrocaloric cooling technology towards reaching breakthrough points, it is necessary to realize optimized prototypes. As a matter of fact, is not so important to register an immediate increase in the number of developed prototypes, as it is essential that the new devices would be optimized.
5. Experimental Devices
In this section, a general overview of the experimental prototypes of the electrocaloric coolers will be presented. Greco et al. [25] exhaustively reviewed all the prototypes of caloric processes realized and introduced to the scientific community up to 2019. Indeed, an extract of the section they dedicated to the electrocaloric devices is reported below, additionally, the latest prototypes developed after the publication of their review will be faithfully added.
Even if the interest toward electrocaloric cooling has grown in the last two decades, literature accounts for the first developed prototype in 1979. Specifically, Radebaugh et al. developed [76] a proof-of-concept cryogenic heat-switches-based electrocaloric systems. In the study, the refrigeration was proven with two different switches: A multiple-leaf contact and a magnetothermal switch of single-crystal beryllium, whereas the electrocaloric material is the glass ceramics SrTiO3 [11]. The range of application was 4–15 K, and the device provided 0.3 K as temperature span under ∆E = 0.2 MV m−1.
In 1989, Sinyavsky et al. [77] realized the first prototype based on the AER cycle where multilayers of PST [11] were employed as refrigerant. The multilayer ceramics of PST were realized as cascading materials whose peak temperature is decreased according to the direction of the temperature gradient. The auxiliary fluid is a pentane liquid with dielectric behavior.
In a subsequent investigation, Sinyavsky and Brodyansky tested [78] the prototype under the following working conditions:
- 300 K is the hot side temperature;
- 5 Hz is the AER frequencies;
- 0.6 MV m−1 is the electric field change applied to the material.
and they noticed [78] that it could reach 5 K as maximum temperature span.
In 2005, Lawless, belonging to CeramPhysics, Inc. company (USA), designed and patented [79] an electrocaloric device whose applicability refers to the room temperature working range. The electrocaloric material is a multilayer of the ceramic family x(PbMg0.33Nb0.67O3) + y(PbSc0.5Nb0.5O3) or x(PbMg0.33Nb0.67O3) + y(PbTiO3) + z(SrTiO3). X, y, and z are the coefficients that should be opportunely varied to enhance the applicability range up to [−10; +50] °C. In the patent, the author hypothesizes, but does not bind, the housing of the electrocaloric material in parallel-plates separated by channels where a heat transfer fluid flows with the purpose to direction the heat flux. from the thermal load to the thermal sink. Anyhow, the patented device is suitable for a wide range of applications and opened for many design solutions.
After almost a decade of silence, in 2014, a novel electrocaloric device was developed and introduced [80] to scientific community by Plaznik et al. (the research group of University of Ljubljana): it is a small-scale cooling system based on the AER cycle. The regenerator is composed of 30 parallel-plates of bulk relaxor ferroelectric ceramics of PMN-0.1PT [69]; each one has a thickness of 0.2 mm and exchanges heat with the silicon oil that has the role of heat transfer medium.
The highest detected temperature spans are 2.3 K and 3.3 K under 2.5 MV m−1 and 5 MV m−1, respectively, with the device working at the operating frequency of 0.75 Hz. In 2019, an upgraded version of the device was presented: The AER is made of five stacks of bulk ceramic material (1 − x)Pb(Mg1/3Nb2/3)O3 − xPbTiO3 (PMN-100xPT) [29] where each one is formed by nine parallel plates. The tests revealed a peak in the temperature span of 3.3 K under f = 0.65 Hz, ∆E = 0.57 MV m−1 and TH = 296 K; the maximum specific cooling power is 16 W kg−1 but in correspondence with 1 K as temperature span.
PMN-PT is the electrocaloric material on which the device built in 2016 by the German group made of scientists of Leibniz Universitat Hannover and Fraunhofer Institute for Ceramic Technologies and Systems is also based [81]. Specifically, the electrocaloric material PMN-PT was conceived in two versions: As bulk samples and as multilayer structures, housed in two stacks of electrocaloric elements in series. The regenerator is contained in a wrapper of 36 × 8 × 5 mm3 and the electrocaloric material occupies 47% of the total volume of the AER. Each element of PMN-PT has a thickness of 0.8 mm, whereas 0.4 mm is the space stacked by two elements where the fluid (silicon-oil) flows. Blumenthal et al. noticed that the multilayer structures guarantee larger dielectric strength (10 kV mm−1) than the bulk samples (7 kV mm−1) of the same material; as well as smaller is the minimum thickness employable for each element. By their campaign of tests, they observed that the device could confer a maximum temperature span of 0.17 K with ∆E = 1 kV mm−1 and f = 1 Hz [81].
Next to the AER-based prototypes, the literature also accounts of an exiguous number of thermal-diode-based electrocaloric systems. Next to the above-mentioned pioneering device developed by Radebaugh et al. in 1979 [76] that was oriented to cryogenic applications, the first thermal-diode device dedicated to room-temperature range was realized in 2013 by the research group of Pennsylvania State University [82]. The device was called Electrocaloric Oscillatory Refrigeration and it is formed by 24 layers of the electrocaloric irradiated P(VDF-TrFE 68/32) copolymer [11,19] whose thickness is 8 µm per layer with four stainless-steel regenerators. The preliminary tests conducted on the device revealed that it can provide a maximum temperature span of 6 K under ∆E = 100 MV m−1 and 0.5 Hz frequency [82].
In 2017, the same research group proposed [83] an electrocaloric device with direct solid-to-solid regeneration, composed by two rings where the electrocaloric Y5V multilayer capacitor was installed. Each block is formed by 20 electrocaloric elements for a global thickness of 0.2 mm. The innovation is in the layout, but the energy performances are not so satisfactory since 2 K as ∆Tspan,max, under ∆E = 16.6 MV m−1, was observed.
As always in USA, by Parc, a Xerox company, was developed the latest electrocaloric prototype that was announced [84] during the Thermag 2018 conference. It is a self-regenerating electrocaloric cooler, made of two layers of alternating rows of electrocaloric and insulating material; in preliminary results [84], it achieved a ∆Tspan,max = 2.5 K under ∆E = 30.8 MV m−1. More details were declared in 2020 by Wang et al. [85] and some picture of the device are reported in Figure 13. The electrocaloric material is a multilayer structure of PbSc0.5Ta0.5O3 formed by 39 elements. The authors observed a temperature span of 5.2 °C (among the highest detected for TD-based systems) and a maximum heat flux of 135 mW cm−2 that is more than four times higher than the other values found in literature on similar devices [85].

Figure 13.
The electrocaloric device of Parc, a Xerox company: (A) The assembly of the EC elements; (B) the housing structure; (C) the 3-D model; (D) the realized architecture (reprinted with permission from [85], Science 2020).
A recent and promising concept at the basis of electrocaloric devices development is the electrostatic actuation. This type of electrocaloric system does not need either an auxiliary fluid or to sandwich the electrocaloric material between two thermal diodes: The electrostatic actuation quickly moves a flexible electrocaloric polymer between a heat source and a heat sink. Ma et al. [86] in 2017 reported on their electrostatic actuation-based electrocaloric device. It is smart (7 cm × 3 cm × 0.6 cm), flexible, and it is appliable to cool a small battery. The electrocaloric material employed is P(VDF-TrFE-CFE) because of its mechanical flexibility and for showing a relevant electrocaloric effect at room temperature in two laminated sheets. Each laminate sheet consists of a double-sided Kapton tape, a polyimide film, and a silver-nanowire percolation network layer inserted in between. The best energy performances provided by the system are 13 as COP (that corresponds to 0.061 of the Carnot COP), 1.4 K as maximum temperature span between the heat source and sink and a specific cooling power of 2.8 W g−1. In 2020 the same research group proposed a novel version [87] of the electrocaloric prototype based on electrostatic actuation where multiple units of electrocaloric sheets, to enhance the achievable maximum temperature span and to allow the heat flux to flow continuously from the heat source to the heat sink. The device formed by four cascaded layers of electrocaloric elements reaches 8.7 K as maximum temperature span under no load condition, whereas 9 is the COP calculated under 2.4 as ΔT and 10.4 at zero temperature span.
In the end, Deafay et al. in 2018 introduced a solid-to-solid prototype with energy recovery [31]. The device is formed by 12 multilayer capacitors where the electrocaloric element is BaTiO3. The charge transfer took place via an inductor, with series diodes to prevent resonance. The prototype was able to recover 65% of the work done without reducing the average heat Q pumped; this led to an increase of the COP up to 2.9 on equal temperature span with respect to the case without energy recovering.
A summary of al the prototypes is reported in Table 5.

Table 5.
The experimental electrocaloric devices introduced in literature up to now.
6. Conclusions
This paper aimed to review as widest as possible the background, the state of the art and the research directions of the electrocaloric technology for cooling application. Aside from some pioneering achievements, this technology is of recent interest; indeed, it is still in an evolutionary phase in which some important results have been achieved, but the goal for the marketing of its products is still far away. The fundamentals for obtaining satisfactory results are to have a system based on optimum thermodynamic cycle and electrocaloric refrigerants with reference to its intended use and its field of application. The emerging data from this review is that many progresses have been made both in thermodynamic cycles and in novel materials development. There are many promising electrocaloric materials both in the ceramic group because of their giant electrocaloric effect shown and both among polymers and polymer nanocomposites also due to their capability of being flexible. This last property could lead to the development of revolutionary prototypes completely based on new conceptions like the one proposed by Ma et al. [86] and Meng et al. [87]. In our opinion, their idea could be the way to develop competitive systems able to cool the electronic circuits or the batteries. Anyhow, the general hope is that scientific research will orient its efforts in this direction with the development of more efficient devices that can represent a turning point on the market for innovative refrigeration systems.
Author Contributions
All the authors contributed in the same manner. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Roman symbols | |
| A | area, m2 |
| B | magnetic field induction, T |
| c | specific heat capacity, J kg−1 K−1 |
| D | electric displacement, C m−2 |
| d | diameter, |
| E | electric field, V m−1 |
| f | frequency, Hz |
| h | heat transfer coefficient, W m−2 |
| k | thermal conductivity, W m−1 K−1 |
| identity vector | |
| flow rate, kg s−1 | |
| P | electric polarization, C m−2 |
| p | pressure, Pa |
| Q | power, W |
| power density, w m−3 | |
| s | entropy, J kg−1 K−1 |
| T | temperature, K |
| t | time, s |
| velocity vector, m s−1 | |
| Greek symbols | |
| β | temperature derivative of the reciprocal permittivity, m F−1 K−1 |
| electric permittivity, F m−1 | |
| µ | dynamic viscosity, Pa s |
| ρ | density, kg m−3 |
| porosity, - | |
| Curie constant, K A T−1. m−1 | |
| χ | electric susceptibility, - |
| ψ | volume fraction, - |
| Subscripts | |
| 0 | vacuum |
| ab | absorbed |
| ad | adiabatic |
| Curie | at the Curie point |
| E | constant electric field |
| e | due to interactions with an electric field |
| ECM | ElectroCaloric Material |
| eff | effective |
| el | due to electrons agitation |
| electrodes | electrodes |
| f | fluid |
| fin | final |
| fr | frontal |
| gen | generated |
| h | hydraulic |
| ht | heat transfer |
| i | initial |
| irr | irreversible |
| JH | Joule Heating |
| l | due to lattice vibrations |
| max | maximum |
| P | constant polarization |
| r | proper of the material |
| s | solid |
| st | structural |
| T | constant temperature |
| TDM | Thermal Diode Material |
| x | x-axes component |
References
- Kitanovski, A.; Plaznik, U.; Tomc, U.; Poredoš, A. Present and future caloric refrigeration and heat-pump technologies. Int. J. Refrig. 2015, 57, 288–298. [Google Scholar] [CrossRef]
- Fähler, S. Caloric effects in ferroic materials: New concepts for cooling. Energy Technol. 2018, 6, 1394–1396. [Google Scholar] [CrossRef]
- Qian, S.; Nasuta, D.; Rhoads, A.; Wang, Y.; Geng, Y.; Hwang, Y.; Radermacher, R.; Takeuchi, I. Not-in-kind cooling technologies: A quantitative comparison of refrigerants and system performance. Int. J. Refrig. 2016, 62, 177–192. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. The environmental impact of solid-state materials working in an active caloric refrigerator compared to a vapor compression cooler. Int. J. Heat Technol. 2018, 36, 1155–1162. [Google Scholar] [CrossRef]
- Greco, A.; Vanoli, G.P. Experimental two-phase pressure gradients during evaporation of pure and mixed refrigerants in a smooth horizontal tube. Comparison with correlations. Heat Mass Transf. 2006, 42, 709–725. [Google Scholar] [CrossRef]
- Greco, A.; Vanoli, G.P. Flow boiling heat transfer with HFC mixtures in a smooth horizontal tube. Part II: Assessment of predictive methods. Exp. Therm. Fluid Sci. 2005, 29, 199–208. [Google Scholar] [CrossRef]
- Greco, A.; Mastrullo, R.; Palombo, A. R407C as an alternative to R22 in vapour compression plant: An experimental study. Int. J. Energy Res. 1997, 21, 1087–1098. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. The drop-in of HFC134a with HFO1234ze in a household refrigerator. Int. J. Therm. Sci. 2018, 127, 117–125. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A. The application of a desiccant wheel to increase the energetic performances of a transcritical cycle. Energy Convers. Manag. 2015, 89, 222–230. [Google Scholar] [CrossRef]
- Moya, X.; Kar-Narayan, S.; Mathur, N.D. Caloric materials near ferroic phase transitions. Nat. Mater. 2014, 13, 439–450. [Google Scholar] [CrossRef]
- Ožbolt, M.; Kitanovski, A.; Tušek, J.; Poredoš, A. Electrocaloric refrigeration: Thermodynamics, state of the art and future perspectives. Int. J. Refrig. 2014, 40, 174–188. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. The use of barocaloric effect for energy saving in a domestic refrigerator with ethylene-glycol based nanofluids: A numerical analysis and a comparison with a vapor compression cooler. Energy 2020, 190, 116404. [Google Scholar] [CrossRef]
- Qian, S.; Yuan, L.; Yu, J.; Yan, G. Numerical modeling of an active elastocaloric regenerator refrigerator with phase transformation kinetics and the matching principle for materials selection. Energy 2017, 141, 744–756. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. Analyzing the energetic performances of AMR regenerator working with different magnetocaloric materials: Investigations and viewpoints. Int. J. Heat Technol. 2017, 35, S383–S390. [Google Scholar] [CrossRef]
- Kobeko, P.; Kurtschatov, J. Dielektrische eigenschaften der seignettesalzkristalle. Z. Phys. 1930, 66, 192–205. [Google Scholar] [CrossRef]
- Hautzenlaub, J.F. Electric and Dielectric Behavior Potassium Dihydrogen Phosphate. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1943. [Google Scholar]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. Electrocaloric refrigeration: An innovative, emerging, eco-friendly refrigeration technique. J. Phys. Conf. Ser. 2017, 796, 012019. [Google Scholar] [CrossRef]
- Mischenko, A.S.; Zhang, Q.; Scott, J.F.; Whatmore, R.W.; Mathur, N.D. Giant electrocaloric effect in thin-film PbZr0.95Ti0.05O3. Science 2006, 311, 1270–1271. [Google Scholar] [CrossRef]
- Valant, M. Electrocaloric materials for future solid-state refrigeration technologies. Prog. Mater. Sci. 2012, 57, 980–1009. [Google Scholar] [CrossRef]
- Lu, S.G.; Zhang, Q. Electrocaloric materials for solid-state refrigeration. Adv. Mater. 2009, 21, 1983–1987. [Google Scholar] [CrossRef]
- Scott, J.F. Electrocaloric materials. Annu. Rev. Mater. Res. 2011, 41, 229–240. [Google Scholar] [CrossRef]
- Kar-Narayan, S.; Mathur, N.D. Electrocaloric materials for cooling applications. Ferroelectrics 2012, 433, 107–110. [Google Scholar] [CrossRef]
- Crossley, S. Electrocaloric Materials and Devices. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2013. [Google Scholar]
- Shi, J.; Han, D.; Li, Z.; Yang, L.; Lu, S.G.; Zhong, Z.; Chen, J.; Zhang, Q.M.; Qian, X. Electrocaloric cooling materials and devices for zero-global-warming-potential, high-efficiency refrigeration. Joule 2019, 3, 1200–1225. [Google Scholar] [CrossRef]
- Greco, A.; Aprea, C.; Maiorino, A.; Masselli, C. A review of the state of the art of solid-state caloric cooling processes at room-temperature before 2019. Int. J. Refrig. 2019, 106, 66–88. [Google Scholar] [CrossRef]
- Kitanovski, A.; Egolf, P.W. Thermodynamics of magnetic refrigeration. Int. J. Refrig. 2006, 29, 3–21. [Google Scholar] [CrossRef]
- Gómez, J.R.; Garcia, R.F.; Catoira, A.D.M.; Gómez, M.R. Magnetocaloric effect: A review of the thermodynamic cycles in magnetic refrigeration. Renew. Sustain. Energy Rev. 2013, 17, 74–82. [Google Scholar] [CrossRef]
- He, J.; Chen, J.; Zhou, Y.; Wang, J.T. Regenerative characteristics of electrocaloric Stirling or Ericsson refrigeration cycles. Energy Convers. Manag. 2002, 43, 2319–2327. [Google Scholar] [CrossRef]
- Plaznik, U.; Vrabelj, M.; Kutnjak, Z.; Malič, B.; Rožič, B.; Poredoš, A.; Kitanovski, A. Numerical modelling and experimental validation of a regenerative electrocaloric cooler. Int. J. Refrig. 2019, 98, 139–149. [Google Scholar] [CrossRef]
- Plaznik, U.; Vrabelj, M.; Kutnjak, Z.; Malič, B.; Poredoš, A.; Kitanovski, A. Electrocaloric cooling: The importance of electric-energy recovery and heat regeneration. Europhys. Lett. 2015, 111, 57009. [Google Scholar] [CrossRef]
- Defay, E.; Faye, R.; Despesse, G.; Strozyk, H.; Sette, D.; Crossley, S.; Moya, X.; Mathur, N.D. Enhanced electrocaloric efficiency via energy recovery. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef]
- Gu, H.; Craven, B.; Qian, X.; Li, X.; Cheng, A.; Zhang, Q.M. Simulation of chip-size electrocaloric refrigerator with high cooling-power density. Appl. Phys. Lett. 2013, 102, 112901. [Google Scholar] [CrossRef]
- Gu, H.; Qian, X.S.; Ye, H.J.; Zhang, Q.M. An electrocaloric refrigerator without external regenerator. Appl. Phys. Lett. 2014, 105, 162905. [Google Scholar] [CrossRef]
- Epstein, R.I.; Malloy, K.J. Electrocaloric devices based on thin-film heat switches. J. Appl. Phys. 2009, 106, 064509. [Google Scholar] [CrossRef]
- Guo, D.; Gao, J.; Yu, Y.J.; Santhanam, S.; Slippey, A.; Fedder, G.K.; McGaughey, A.J.H.; Yao, S.C. Design and modeling of a fluid-based micro-scale electrocaloric refrigeration system. Int. J. Heat Mass Transf. 2014, 72, 559–564. [Google Scholar] [CrossRef]
- Kitanovski, A.; Egolf, P.W. Innovative ideas for future research on magnetocaloric technologies. Int. J. Refrig. 2010, 33, 449–464. [Google Scholar] [CrossRef]
- Tishin, A.M.; Spichkin, Y.I. The Magnetocaloric Effect and Its Applications; Series in Condensed Matter Physics; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. A comparison between different materials in an active electrocaloric regenerative cycle with a 2D numerical model. Int. J. Refrig. 2016, 69, 369–382. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. Solid-state refrigeration: A comparison of the energy performances of caloric materials operating in an active caloric regenerator. Energy 2018, 165, 439–455. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. The employment of caloric-effect materials for solid-state heat pumping. Int. J. Refrig. 2020, 109, 1–11. [Google Scholar] [CrossRef]
- Zhang, G.; Weng, L.; Hu, Z.; Liu, Y.; Bao, R.; Zhao, P.; Feng, H.; Yang, N.; Li, M.Y.; Zhang, S.; et al. Nanoconfinement-Induced Giant Electrocaloric Effect in Ferroelectric Polymer Nanowire Array Integrated with Aluminum Oxide Membrane to Exhibit Record Cooling Power Density. Adv. Mater. 2019, 31, 1806642. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. A comparison between rare earth and transition metals working as magnetic materials in an AMR refrigerator in the room temperature range. Appl. Therm. Eng. 2015, 91, 767–777. [Google Scholar] [CrossRef]
- Correia, T.; Zhang, Q. Electrocaloric Materials: New Generation of Coolers; Springer: Berlin/Heidelberg, Germany, 2014; Volume 34. [Google Scholar]
- Wang, J.J.; Fortino, D.; Wang, B.; Zhao, X.; Chen, L.Q. Extraordinarily Large Electrocaloric Strength of Metal-Free Perovskites. Adv. Mater. 2020, 32, 1906224. [Google Scholar] [CrossRef]
- Huang, F.; Tian, H.; Meng, X.; Tan, P.; Cao, X.; Bai, Y.; Hu, C.; Zhou, Z. Large room temperature electrocaloric effect in KTa1−xNbxO3 single crystal. Phys. Status Solidi RRL Rapid Res. Lett. 2019, 13, 1800515. [Google Scholar] [CrossRef]
- Jankowska-Sumara, I.; Gwizd, P.; Majchrowski, A.; Soszyński, A. Electrocaloric effect in pure and Cr doped lead germanate single crystals. Mater. Chem. Phys. 2020, 242, 122494. [Google Scholar] [CrossRef]
- Zhang, T.F.; Tang, X.G.; Ge, P.Z.; Liu, Q.X.; Jiang, Y.P. Orientation related electrocaloric effect and dielectric phase transitions of relaxor PMN-PT single crystals. Ceram. Int. 2017, 43, 16300–16305. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, L.; Wang, H.; Guo, M.; Lou, X.; Wang, D. Composition-driven inverse-to-conventional transformation of electrocaloric effect and large energy storage density in strontium modified Ba (Zr0.1Ti0.9) O3 thin films. J. Mater. Chem. C 2020, 8, 1366–1373. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X.; Huang, H.; Wang, J.; Li, Q.; Chen, L.Q.; Wang, Q. Toward wearable cooling devices: Highly flexible electrocaloric Ba0.67Sr0.33TiO3 nanowire arrays. Adv. Mater. 2016, 28, 4811–4816. [Google Scholar] [CrossRef]
- Bai, Y.; Zheng, G.P.; Ding, K.; Qiao, L.; Shi, S.Q.; Guo, D. The giant electrocaloric effect and high effective cooling power near room temperature for BaTiO3 thick film. J. Appl. Phys. 2011, 110, 094103. [Google Scholar]
- Qian, X.S.; Ye, H.J.; Zhang, Y.T.; Gu, H.; Li, X.; Randall, C.A.; Zhang, Q.M. Giant electrocaloric response over a broad temperature range in modified BaTiO3 ceramics. Adv. Funct. Mater. 2014, 24, 1300–1305. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, C.; Zheng, T.; Wu, J. Large electrocaloric effect in (Bi0.5Na0.5) TiO3-based relaxor ferroelectrics. ACS Appl. Mater. Interfaces 2020, 12, 33934–33940. [Google Scholar] [CrossRef]
- Shirsath, S.E.; Cazorla, C.; Lu, T.; Zhang, L.; Tay, Y.Y.; Lou, X.; Liu, Y.; Li, S.; Wang, D. Interface-charge induced giant electrocaloric effect in lead free ferroelectric thin-film bilayers. Nano Lett. 2019, 20, 1262–1271. [Google Scholar] [CrossRef]
- Peng, B.; Fan, H.; Zhang, Q. A giant electrocaloric effect in nanoscale antiferroelectric and ferroelectric phases coexisting in a relaxor Pb0.8Ba0.2ZrO3 thin film at room temperature. Adv. Funct. Mater. 2013, 23, 2987–2992. [Google Scholar] [CrossRef]
- Shen, B.Z.; Li, Y.; Hao, X. Multifunctional all-inorganic flexible capacitor for energy storage and electrocaloric refrigeration over a broad temperature range based on PLZT 9/65/35 thick films. ACS Appl. Mater. Interfaces 2019, 11, 34117–34127. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Hao, X.; Zhang, Q. A giant electrocaloric effect of a Pb0.97La0.02(Zr0.75Sn0.18Ti0.07)O3 antiferroelectric thick film at room temperature. J. Mater. Chem. C 2015, 3, 1694–1699. [Google Scholar] [CrossRef]
- Zhao, Y.; Hao, X.; Zhang, Q. Enhanced energy-storage performance and electrocaloric effect in compositionally graded Pb (1− 3x/2) LaxZr0.85Ti0.15O3 antiferroelectric thick films. Ceram. Int. 2016, 42, 1679–1687. [Google Scholar] [CrossRef][Green Version]
- Correia, T.M.; Young, J.S.; Whatmore, R.W.; Scott, J.F.; Mathur, N.D.; Zhang, Q. Investigation of the electrocaloric effect in a PbMg2/3Nb1/3 O3-PbTiO3 relaxor thin film. Appl. Phys. Lett. 2009, 95, 182904. [Google Scholar] [CrossRef]
- Hamad, M.A. Theoretical investigations on electrocaloric properties of relaxor ferroelectric 0.9PbMg1/3Nb2/3O3–0.1PbTiO3 thin film. J. Comput. Electron. 2012, 11, 344–348. [Google Scholar] [CrossRef]
- Rožič, B.; Kosec, M.; Uršič, H.; Holc, J.; Malič, B.; Zhang, Q.M.; Blinc, R.; Pirc, R.; Kutnjak, Z. Influence of the critical point on the electrocaloric response of relaxor ferroelectrics. J. Appl. Phys. 2011, 110, 064118. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, G.; Zhang, X.; Jiang, S.; Zeng, Y.; Wang, Q. Relaxor ferroelectric-based electrocaloric polymer nanocomposites with a broad operating temperature range and high cooling energy. Adv. Mater. 2015, 27, 2236–2241. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Zhang, X.; Yang, T.; Li, Q.; Chen, L.Q.; Jiang, S.; Wang, Q. Colossal room-temperature electrocaloric effect in ferroelectric polymer nanocomposites using nanostructured barium strontium titanates. ACS Nano 2015, 9, 7164–7174. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Li, Q.; Gu, H.; Jiang, S.; Han, K.; Gadinski, M.R.; Haque, M.A.; Zhang, Q.; Wang, Q. Ferroelectric polymer nanocomposites for room-temperature electrocaloric refrigeration. Adv. Mater. 2015, 27, 1450–1454. [Google Scholar] [CrossRef] [PubMed]
- Gong, J.; McGaughey, A.J. Device-level thermodynamic model for an electrocaloric cooler. Int. J. Energy Res. 2020, 44, 5343–5359. [Google Scholar] [CrossRef]
- Feng, D.; Yao, S.C.; Zhang, T.; Zhang, Q. Modeling of a smart heat pump made of laminated thermoelectric and electrocaloric materials. J. Electron. Packag. 2016, 138. [Google Scholar] [CrossRef]
- Shi, J.; Li, Q.; Gao, T.; Han, D.; Li, Y.; Chen, J.; Qian, X. Numerical evaluation of a kilowatt-level rotary electrocaloric refrigeration system. Int. J. Refrig. 2020, in press. [Google Scholar] [CrossRef]
- Hirasawa, S.; Kawanami, T.; Shirai, K. Electrocaloric Refrigeration using Multi-Layers of Electrocaloric Material Films and Thermal Switches. Heat Transf. Eng. 2018, 39, 1091–1099. [Google Scholar] [CrossRef]
- Ožbolt, M.; Kitanovski, A.; Tušek, J.; Poredoš, A. Electrocaloric vs. magnetocaloric energy conversion. Int. J. Refrig. 2014, 37, 162–167. [Google Scholar] [CrossRef]
- Plaznik, U.; Kitanovski, A.; Rožič, B.; Malič, B.; Uršič, H.; Drnovšek, S.; Cilenšek, J.; Vrabelj, M.; Poredoš, A.; Kutnjak, Z. Bulk relaxor ferroelectric ceramics as a working body for an electrocaloric cooling device. Appl. Phys. Lett. 2015, 106, 043903. [Google Scholar] [CrossRef]
- Faye, R.; Usui, T.; Torello, A.; Dkhil, B.; Moya, X.; Mathur, N.D.; Hirose, S.; Defay, E. Heat flow in electrocaloric multilayer capacitors. J. Alloy. Compd. 2020, 834, 155042. [Google Scholar] [CrossRef]
- Li, X.; Qian, X.S.; Lu, S.G.; Cheng, J.; Fang, Z.; Zhang, Q.M. Tunable temperature dependence of electrocaloric effect in ferroelectric relaxor poly(vinylidene fluoride-trifluoroethylene-chlorofluoroethylene terpolymer. Appl. Phys. Lett. 2011, 99, 052907. [Google Scholar] [CrossRef]
- Tušek, J.; Kitanovski, A.; Prebil, I.; Poredoš, A. Dynamic operation of an active magnetic regenerator (AMR): Numerical optimization of a packed-bed AMR. Int. J. Refrig. 2011, 34, 1507–1517. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. Energy performances and numerical investigation of solid-state magnetocaloric materials used as refrigerant in an active magnetic regenerator. Therm. Sci. Eng. Prog. 2018, 6, 370–379. [Google Scholar] [CrossRef]
- Aprea, C.; Cardillo, G.; Greco, A.; Maiorino, A.; Masselli, C. A rotary permanent magnet magnetic refrigerator based on AMR cycle. Appl. Therm. Eng. 2016, 101, 699–703. [Google Scholar] [CrossRef]
- Blumenthal, P.; Raatz, A. Design Methodology for Electrocaloric Cooling Systems. Energy Technol. 2018, 6, 1560–1566. [Google Scholar] [CrossRef]
- Radebaugh, R.; Lawless, W.N.; Siegwarth, J.D.; Morrow, A.J. Feasibility of electrocaloric refrigeration for the 4–15 K temperature range. Cryogenics 1979, 19, 187–208. [Google Scholar] [CrossRef]
- Sinyavsky, Y.V.; Pashkov, N.D.; Gorovoy, Y.M.; Lugansky, G.E.; Shebanov, L. The optical ferroelectric ceramic as working body for electrocaloric refrigeration. Ferroelectrics 1989, 90, 213–217. [Google Scholar] [CrossRef]
- Sinyavsky, Y.V.; Brodyansky, V.M. Experimental testing of electrocaloric cooling with transparent ferroelectric ceramic as a working body. Ferroelectrics 1992, 131, 321–325. [Google Scholar] [CrossRef]
- Lawless, W.N. Electrocaloric Device and Thermal Transfer Systems Employing the Same. U.S. Patent No. 6,877,325, 12 March 2005. [Google Scholar]
- Plaznik, U.; Kitanovski, A.; Malič, B.; Kutnjak, Z.; Poredoš, A. Small scale electrocaloric cooling device with an active heat regenerator. In Proceedings of the Thermag VI, 6th IIR/IIF International Conference on Magnetic Refrigeration 2014, Victoria, BC, Canada, 7–10 September 2014; International Institute of Refrigeration: Paris, France, 2014. [Google Scholar]
- Blumenthal, P.; Molin, C.; Gebhardt, S.; Raatz, A. Active electrocaloric demonstrator for direct comparison of PMN-PT bulk and multilayer samples. Ferroelectrics 2016, 497, 1–8. [Google Scholar] [CrossRef]
- Gu, H.; Qian, X.; Li, X.; Craven, B.; Zhu, W.; Cheng, A.; Yao, S.C.; Zhang, Q.M. A chip scale electrocaloric effect based cooling device. Appl. Phys. Lett. 2013, 102, 122904. [Google Scholar] [CrossRef]
- Zhang, T.; Qian, X.S.; Gu, H.; Hou, Y.; Zhang, Q.M. An electrocaloric refrigerator with direct solid to solid regeneration. Appl. Phys. Lett. 2017, 110, 243503. [Google Scholar] [CrossRef]
- Wang, Y.; Schwartz, D.; Kalb, J.; Lee, J. A self-regenerating electrocaloric cooler. In Proceedings of the Thermag VIII, 8th IIR/IIF International Conference on Caloric Cooling, Darmstadt, Germany, 16–20 September 2018; International Institute of Refrigeration: Paris, France, 2018. [Google Scholar]
- Wang, Y.; Zhang, Z.; Usui, T.; Benedict, M.; Hirose, S.; Lee, J.; Kalb, J.; Schwartz, D. A high-performance solid-state electrocaloric cooling system. Science 2020, 370, 129–133. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, Z.; Tong, K.; Huber, D.; Kornbluh, R.; Ju, Y.S.; Pei, Q. Highly efficient electrocaloric cooling with electrostatic actuation. Science 2017, 357, 1130–1134. [Google Scholar] [CrossRef]
- Meng, Y.; Zhang, Z.; Wu, H.; Wu, R.; Wu, J.; Wang, H.; Pei, Q. A cascade electrocaloric cooling device for large temperature lift. Nat. Energy 2020, 10. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).