Abstract
The assembly of [Co2III(μ-2,5-dpp)(CN)8]2− anions and [MII(CH3OH)2(DMSO)2]2+ cations resulted into the formation of two heterobimetallic 1D coordination polymers of formula [MII(CH3OH)2(DMSO)2(μ-NC)2Co2III(μ-2,5-dpp)(CN)6]n·4nCH3OH [M = CoII (1)/FeII (2) and 2,5-dpp = 2,5-bis(2-pyridyl)pyrazine. The [Co2III(μ-2,5-dpp)(CN)8]2− metalloligand coordinates the paramagnetic [MII(CH3OH)2(DMSO)2]2+ complex cations, in a bis-monodentate fashion, to give rise to neutral heterobimetallic chains. Cryomagnetic dc (1.9–300 K) and ac (2.0–13 K) magnetic measurements for 1 and 2 show the presence of Co(II)HS (1) and Fe(II)HS (2) ions (HS – high-spin), respectively, with D values of +53.7(5) (1) and −5.1(3) cm−1 (2) and slow magnetic relaxation for 1, this compound being a new example of SIM with transversal magnetic anisotropy. Low-temperature Q-band EPR study of 1 confirms that D value is positive, which reveals the occurrence of a strong asymmetry in the g-tensors and allows a rough estimation of the E/D ratio, whereas 2 is EPR silent. Theoretical calculations by CASSCF/NEVPT2 on 1 and 2 support the results from magnetometry and EPR. The analysis of the ac magnetic measurements of 1 shows that the relaxation of M takes place in the ground state under external magnetic dc fields through dominant Raman and direct spin-phonon processes.
1. Introduction
The design of heterometallic coordination polymers (CPs) is of high interest due to their potential applications as molecular magnets and luminescent or multifunctional materials [1,2,3,4,5,6,7,8,9,10,11,12,13]. For constructing CPs with various dimensionalities and network topologies, the node-and-spacer approach was proved to be very efficient [14,15,16,17]. The spacers can be represented by organic molecules [18,19] or diamagnetic/paramagnetic metalloligands [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39], while the nodes are a species with complementary chemical and physical properties (as Lewis acidity, charge, shape, etc.). Cyanido-bearing metalloligands are commonly used spacers due to their ability to bridge metal ions. Aiming at the preparation of polynuclear complexes, homoleptic cyanide complexes such as [M(CN)6]3− [MIII = Fe, Cr, Mn, and Co] and [M(CN)8]3− [MV = Mo and W] were largely exploited [20,21,22,23,24,25,26,27] as opposed to the heteroleptic ones with a diversity of capping ligands, e.g., [MIII(AA)(CN)4]− [AA = 2,2′-bipyridine (bpy), 1,10-phenantroline (phen), 2,2′-bipyrimidine (bpym) and derivatives; MIII = Fe, Cr, and Co], [MIII{HB(pz)3}(CN)3]−, [HB(pz)3− = tris(pyrazolyl)borate ion] and [WV/IV(bpy)(CN)6]−/2− [28,29,30,31,32,33,34,35,36,37,38,39]. Moreover, in comparison with the homoleptic analogues, the capping ligands reduce the number of potential bridges, favoring the achievement of low-dimensional CPs.
Single-ion and single-molecule magnets (SIMs and SMMs) are highly anisotropic discrete motifs showing slow relaxation of the magnetization [40,41,42,43,44]. Most of them are complexes of trivalent rare-earth cations (for instance DyIII, NdIII, etc.) [45,46,47,48,49,50,51], while examples concerning 3d metal ions such as CoII, FeII, MnIII or NiII are comparatively fewer [43,52,53,54,55,56,57,58,59]. Recent studies evidenced the influence of the coordination environment around the metal ion on the magnitude of the magnetic anisotropy [60,61,62,63,64,65]. Coordinative and supramolecular architectures enclosing magnetically isolated SIMs and SMMs moieties are very appealing considering their potential use in molecular electronics [66,67]. Mostly, these networks consist of organic diamagnetic spacers that connect the spin centers [68,69,70,71,72,73,74,75,76,77,78,79,80,81]. Large axial magnetic anisotropy values were determined for chains of cobalt(II) SIMs such as [CoII(tpyt)2(HCOO)2(H2O)]n [tpyt = 2,4,6-tris(4-pyridyl)-1,3,5-triazine] [82] and [Co(btm)2(SCN)2·H2O]n, [btm = bis(1H-1,2,4-triazol-1-yl)methane] [83] or 2D networks, {[Co(3,3′-Hbpt)2(SCN)2]·2H2O}n [Hbpt = 1H-3-(3-pyridyl)-5-(3′-pyridyl)-1,2,4-triazole] [84] and [Co(bpeb)2(NCS)2]·nG [bpeb = 1,4-bis(pyridine-4-ylethynyl)benzene and: G = ortho-dichlorobenzene, thianthrene, toluene, and pyrrole] [85]. Diamagnetic cyanido-bearing building blocks such as the homo- [CoIII(CN)6]3− and [MIV(CN)8]4− (MIV = Mo and W) or the heteroleptic [WIV(bipy)(CN)6]2− complex anions were less employed as metalloligands to prepare extended structures of molecule-based nanomagnets [86,87,88,89,90]. The 2D networks of SMMs built from [WIV(bipy)(CN)6]2− spacers and {NiIIDyIII} nodes are illustrative examples of this strategy [86].
Recently, we reported the use of diamagnetic mononuclear cyanide-bearing cobalt(III) complexes to obtain 1D {CoIIIMnIII} CPs showing slow relaxation of the magnetization because of the presence in them of the magnetically non-interacting {MnIII(salen)} fragment [H2salen = N,N′-ethylenebis(salicylimine)] [87]. Based on our previous results, we start a systematic study of the use of the diamagnetic dicobalt(III) compound [Co2III(μ-2,5-dpp)(CN)8]2− [2,5-dpp = 2,5-bis(2-pyridyl)pyrazine] as a metalloligand against fully solvated transition metal ions. Our first results dealt with two isostructural neutral chains of formula [MII(CH3OH)2(DMSO)2(μ-NC)2Co2III(μ-2,5-dpp)(CN)6]n·4nCH3OH [M = Co (1) and Fe (2)]. Their synthesis, X-ray structure and cryomagnetic investigation are discussed herein.
2. Results and Discussion
2.1. Synthesis, IR Spectroscopy and Thermal Study
In previous work, we have shown that the use as a metalloligand of the [Co2III(μ-2,5-dpp)(CN)8]2− complex anion towards the preformed complex of formula [MnII(MAC)(H2O)2]Cl2 · 4H2O (MAC = 2,13-dimethyl-3,6,9,12,18-pentaazabicyclo-[12.3.1]-octadeca-(18),2,12,14,16-pentaene] afforded a neutral {CoIII2MnII} chain exhibiting a Curie law behavior because of the occurrence of intrachain magnetically isolated {MnII(MAC)} units whose trans-positioned coordinated water molecules were replaced by two cyanide groups from two 2,5-dpp-bridged dicobalt(III) entities [91]. Based on this result, we decided to explore the complexing ability of this diamagnetic dicobalt(III) building block, against anisotropic 3d cations such as cobalt(II) and iron(II) cations. The reaction of [Co2III(μ-2,5-dpp)(CN)8]2– with fully solvated cobalt(II) and iron(II) cations in DMSO:MeOH solvent mixtures yielded the two isostructural heterobimetallic chains of formula [MII(CH3OH)2(DMSO)2(μ-NC)2Co2III(μ-2,5-dpp)(CN)6]n·4nCH3OH [M = Co (1) and Fe (2)]. They consist of chains with regular alternating [Co2(μ-2,5-dpp)(CN)8]2– spacers and [MII(CH3OH)2(DMSO)2]2+ nodes.
The FTIR spectra of 1 and 2 (see Figures S1(1) and S2(2) in Supplementary Materials) show bands at 2140 (1 and 2), 2171 (1) and 2165 cm−1 (2) corresponding to the stretching vibrations of the terminal and bridging cyanide ligands. As expected, these bands occur at higher frequencies compared to that of the free dicobalt(III) metalloligand (about 2130 cm−1) but close to those for the similar {Co2IIIMnII} zig-zag chain (ca. 2140 and 2160 cm−1) [91]. The 2,5-dpp ligand exhibits absorption bands at 1632 (1 and 2), 1443 (1) and 1437 cm−1 (2), which correspond to the υ(C=N) and υ(C=C) stretching vibrations, respectively. The strong absorption peaks at 1028 (1) and 1020 cm−1 (2) are tentatively attributed to the S=O stretching vibration of the DMSO ligands. Finally, the medium intensity peaks at 429 (1)/420 cm−1 (2) are most likely due to the vibrations of the CoII-O/FeII-O bonds. The FTIR spectroscopic characteristics of 1 and 2 are consistent with the single-crystal X-ray results (see below).
The TG curves of 1 [Figure S3a] and 2 [Figure S3b] are similar, as expected. The first step between 25 and 150 °C is the result of several endothermic processes, and it can be assigned to the loss of the methanol molecules. These molecules are slowly released, starting from room temperature under the measurement conditions, as indicated by the slope of the step in the TG curve, the crystal lattice being subjected to rearrangements. The mass loss which occurs in the temperature range 145–400 °C is attributed to the release of the DMSO and cyanide ligands and to the combustion of the organic residues. Finally, a small step can be observed for 1 close to 900 °C (associated with the endothermic DSC, Tpeak = 894 °C) that indicates the transformation of Co3O4 into CoO. Most likely, a mixture of cobalt and iron oxides is formed in the case of 2.
2.2. Description of the Structures
1 and 2 crystallize in the triclinic system, spatial group P–1, and their structures are made up of neutral zig-zag chains of formula [MII(CH3OH)2(DMSO)2(μ-NC)2Co2III(μ-2,5-dpp)(CN)6]n·4nCH3OH, M = Co (1) and Fe (2) [see Figure 1 (1) and Figure S4(2)]. Since 1 and 2 are isostructural compounds, only the structure of 1 will be discussed in detail hereafter, and we will refer to the other one when needed. The asymmetric unit is made up from half of the structure—the crystallographic inversion center generates the second half—and two non-coordinated methanol molecules. Each [Co2III(μ-2,5-dpp)(CN)8]2- complex anion acts as a linker, connecting the [CoII(CH3OH)2(DMSO)2]2+ unit through two trans-positioned cyanido ligands. Selected bond lengths and angles for 1 and 2 are listed in Table 1.
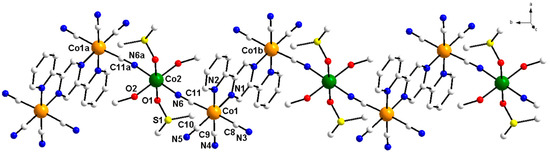
Figure 1.
View of a part of the neutral chain of 1 along with the atom numbering of the chromophores. Free methanol molecules were not represented for the sake of clarity [symmetry code: (a) = 1 − x, −1 − y, 3 − z; (b) = x, −1 + y, z]. The same atom numbering was used for 2.

Table 1.
Bond lengths (Å) and angles (deg) of the cobalt(II/III) (1) and cobalt(III) and iron(II) (2) coordination environments.
The two Co(III) ions from 1 and 2 are each hexacoordinated to one pyrazine- and one pyridine-N of 2,5-dpp ligand and four C atoms of cyanide ligands, in a distorted octahedral geometry. Two N2,5-dpp and two Ccyanide atoms (N1N2C9C10 set of atoms) are placed in the equatorial positions of a distorted octahedron, whereas the apical sites are occupied by the other two CN- ligands (C11N6 and C8N3). The reduced bite angle of the 2,5-dpp molecule [N1-Co1-N2 = 82.5(2) (1) 82.05(17)° (2)] is the source of the primary distortion of the octahedral environment. The Co1-C bond distances range between 1.873(7)-1.928(7) (1) and 1.871(6)-1.918(6) Å (2). These values are slightly inferior to the Co-N bond lengths [Co1-N1 = 1.969(5) (1) and 1.965(4) Å (2) and Co1-N2 = 1.986(6) (1) and 1.961(4) Å (2)]. All structural parameters (bond lengths and angles) of the cobalt(III) environment in 1 and 2 correspond well to previously reported cyanido-based/bridged CoIII complexes, [CoIII(AA)(CN)4]− [AA = bidentate ligand], the dicobalt(III) complex (PPh4)2[Co2III(-2,5-dpp)(CN)8] · 2H2O (PPh4+ = tetraphenylphosphonium cation) and the chain {[MnIII(salen)(-NC)2CoIII(4,4′-dmbpy)(CN)2] · H2O}n (4,4′-dmbpy = 4,4′-dimethyl-2,2′-bipyridine) [87,91,92]. The Co-C-Ncyanide angles in 1 are almost linear, their values ranging from 177.0(6) to 179.1(6)° [176.8(5)-178.6(5)o (2)]. The values of the CoIII···CoIII separation through the 2,5-dpp spacer are 6.68 (1) and 6.67 Å (2).
Each MII ion [M = Co2 (1) and Fe1 (2)] is placed in a centrosymmetric octahedral surrounding. Two trans-positioned nitrogen atoms from two cyanide bridges and two methanol molecules build the equatorial plane, and two O atoms from two DMSO molecules fill the apical coordination sites. An almost ideal octahedral geometry at the cobalt(II) (1) and iron(II) (2) ions was estimated through the SHAPE 2.1 program (0.212 (1) and 0.202 (2) for OC-6, being zero for the ideal octahedron; see Table S1 in Supplementary Materials†) [93,94]. The value of the equatorial M1-N6 bond length (2.104(7) (1) and 2.155(5) Å (2)) is slightly longer than the other equatorial M2–O2 interaction (2.096(5) (1) and 2.134(4) Å (2)), the axial M2-O1 bond distance being the shorter one (2.081(6) (1) and 2.083(4) Å (2)).
The values of the CoIII···MII separation across the bridging cyanide are ca. 5.13 (1) and 5.17 Å (2). The shortest intrachain MII···MII distances are 11.74 (1) and 11.77 Å (2), values which are somewhat shorter than the interchain ones (13.35 (1) and 13.51 Å (2)). The metal ions are placed in an almost intrachain right angle, through the bridging cyanido and 2,5-dpp ligand (Co1b-Co1-M2 = 84.82 (1) and 84.51° (2)), and linear angle through the cyanido-bridge (Co1-M2-Co1a = 180° (1 and 2)).
Intrachain H-bonds involve the methanol molecules of crystallization and the coordinated methanol and peripheral cyanido ligands (see Figure 2 (1) and Figure S5(2) and Table 2 (1 and 2)). The O2 atom of the coordinated methanol molecule acts as a hydrogen donor towards the O3 atom from a crystallization methanol molecule (O2···O3 = 2.603(10) (1) and 2.614(7) Å (2)), which in turn is a hydrogen acceptor towards the other crystallographically independent O4 water molecule (O3···O4 = 2.800(19) (1) and 2.715(9) Å for (2)). The latter one is also connected to the N3cyanide atom through a hydrogen bond (O4···N3 = 2.802(15) (1) and 2.836(8) Å (2)), the whole leading to an 18-gon (octadecagon) heteronuclear ring which is sectioned by a pyrazine ring.
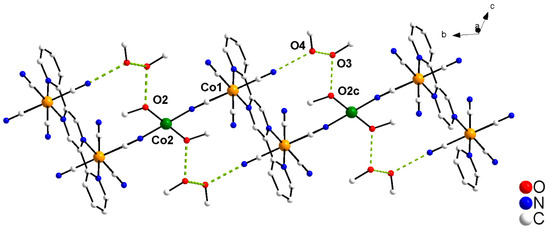
Figure 2.
A view of the hydrogen bonds pattern (dashed lines) in 1. The DMSO molecules were not represented for the sake of clarity (Symmetry code: (c) = x, –1+y, z).

Table 2.
Hydrogen bonds in 1 and 2 (compound 1/compound 2).
2.3. Static (dc) Magnetic Properties of 1 and 2
Static (dc) magnetic properties of 1, represented as the thermal dependence of the χMT product, is depicted in Figure 3 (χM is the magnetic susceptibility per CoIII2CoII unit). At room temperature, the value of χMT is 2.97 cm3 mol−1 K and is an expected value for magnetically diluted CoHSII single-ion (CoIII ion is diamagnetic) with a significant orbital angular momentum [95]. The χMT vs. T plot is continuously decreasing upon cooling process to reach a value of 1.68 cm3 mol−1 K at 1.9 K. No maximum of the magnetic susceptibility is observed in the χM vs. T plot. Two main factors could cause the decrease of χMT vs. T curve: the thermal depopulation of the higher Kramer doublets of the CoHSII ions and, also, AF interactions between the CoHSII paramagnetic centers. However, this last possibility is discarded due to the large cobalt(II)–cobalt(II) separation (shortest intra- and intrachain values of ca. 11.7 and 13.4 Å, respectively).
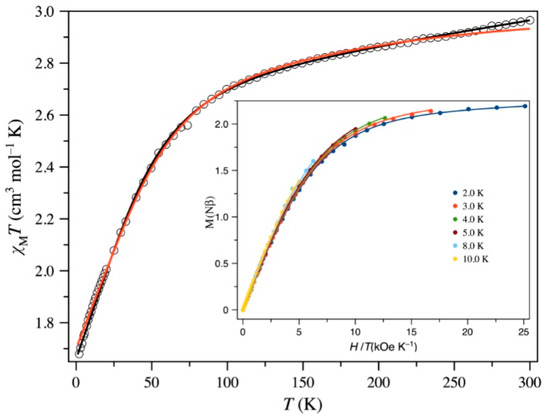
Figure 3.
MT vs. T and the reduced M vs. H plots (inset) for 1: (empty and filled circles) experimental; (solid lines) best-fit curves to the experimental data by using the parameters reported in the text for the 1st order SOC (black) and zfs (red) approaches.
Consequently, the magnetic data of 1 were analyzed through the Hamiltonian of Equation (1):
in which the three parameters α, λ and ∆, have the same meaning as in our previous papers [72,96]. It deserves to be highlighted that considering the isomorphism of T and P terms L(T1g = −AL(P) [97], one can use L = 1 and S = 3/2, αλ-being the coupling parameter. The following best-fit parameters and a well-match of the experimental data of 1, in the 300-2 K temperature range, were obtained through the VPMAG package [98]: λλ=−136.1(5) cm−1, α =1.431(4), ∆ = 699(8) cm−1 and TIP = 997(25) × 10−6 cm3 mol−1 with F = 2.7 × 10−6 (F is the agreement factor defined as Σ[Pexp − Pcalcd]2/Σ[Pexp]2 where P is the physical property under study). The values of λ, α and ∆ are close to those resulted for other examples of six-coordinate high-spin cobalt(II) complexes [64,72,97,99,100,101].
H = −αλLCoSCo + ∆[Lz,CoSCo − L(L+1)/3 ] + βH(geSCo − LCo),
An alternative phenomenological approach to spin-orbit coupling (SOC) Hamiltonian, introduced through the T-P isomorphism, to analyze the magnetic data in 1, is based on the zero-field splitting (zfs) of an S = 3/2 and is expressed in Equation (2):
where S, D and E are the ground spin state and axial and transverse anisotropies, respectively, β is the Bohr magneton and H is the applied dc field. If E = 0, 2D for 1 corresponds to the energy gap between the ±1/2 and ±3/2 doublets arising from the 2nd order spin-orbit coupling of the quartet ground state of the distorted octahedral cobalt(II) ion. In this respect, the fact that the M vs. H/T curves for 1 in the temperature range 2.0–10 K quasi collapse (see inset of Figure 3), is indicative of a large value of D. The simultaneous analysis of the variable-temperature magnetic susceptibility measurements and the magnetization data under different applied dc fields and temperatures of 1 through the VPMAG package [98] led to the following set of best-fit parameters: D = +53.7(5) cm−1, E/|D| = 0.012(9), g// = 2.007(4), g⊥ = 2.524(6) and TIP = −1010(30) × 10−6 cm3 mol−1 with F = 2.4 × 10−5. The calculated curves well-fitted the experimental ones in the whole investigated temperature range. Moreover, when starting with a negative value of D gave no reasonable results. Then, this system can be considered as a doublet at low temperatures. Both approaches used in the analysis of the magnetic data in 1 were validated by the similar values for the energy gap between the ground and the first excited Kramers doublets (ca. 124.9 and 107.4 cm−1 for SOC and zfs approaches, respectively).
Hzfs+Zeeman = D[Sz2 − S(S+1)] + E(Sx2 − Sy2) + βH[g//|Sz + g⊥(Sx + Sy)]
Figure 4 shows the χMT vs. T plot for 2 (χM is the magnetic susceptibility per CoIII2FeII unit). At room temperature, χMT is 3.29 cm3 mol−1 K, a value which is in agreement with the presence of a high-spin iron(II) ion (SFe = 2 with a gFe value largely above that for the free electron in this compound), the cobalt(III) being diamagnetic. Upon cooling, although this value slightly decreases, it remains practically constant until ca. 40 K and it further decreases to 2.14 cm3 mol−1 K at 1.9 K. No maximum of the magnetic susceptibility is observed in the whole temperature range explored. The decrease of χMT in the low temperatures domain can be due to first-order spin-orbit coupling (SOC) or zero-field splitting (zfs) effects together with intra-/interchain magnetic interactions. Because of the large iron···iron separation (shortest intra- and interchain distances of ca. 11.8 and 13.5 Å, respectively), these last interactions are ruled out.
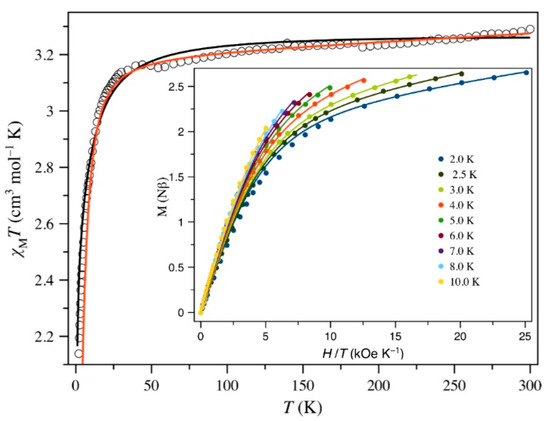
Figure 4.
χMT vs. T and the reduced M vs. H plots (inset) for 2: (empty and filled circles) experimental; (solid lines) best-fit curves to the experimental data by using the parameters reported in the text for the 1st order SOC (black) and zfs (red) approaches.
Since the magnetic properties of magnetically isolated six-coordinate high-spin iron(II) complexes are usually controlled by a 1st order SOC, the use of the SOC Hamiltonian introduced through the T-P isomorphism is an appropriate option to analyze its magnetic properties. The presence of a 5T2g term that does not mix with the other ones validates this approach. Consequently, the magnetic susceptibility data of 2 were treated through the Hamiltonian of Equation (3):
H = −κλLFeSFe + ∆[Lz,Fe − L(L+1)/3] +E(Lx2 − Ly2)+ βH(−κLFe + geSFe)
In this Hamiltonian, λ is the spin-orbit coupling, κ stands for the reduction of the orbital momentum (L) caused by the delocalization of the unpaired electrons, and ∆ is the energy gap between the 5B2g and 5Eg levels arising from the splitting of the 5T2g ground state through an axial distortion of the Oh symmetry. The E parameter accounts for the splitting of the 5Eg level caused by the molecular low-symmetry bound to the rhombicity of the coordination sphere. Although this additional parameter can lead to an overparameterization, it will be still essential in the present case, as shown below by the theoretical study. The inclusion of the magnetic rhombicity (E) slightly improves the results and affects mainly to the ∆ value, which in any case is large and positive. Least-squares best-fit parameters though the VPMAG package [98] on the magnetic susceptibility are the following for the whole model: κ = 0.997(6), λ = −109(3) cm−1, ∆ = +1660(30) cm−1, E/∆ = 0.1109(4), TIP = 126(7) × 10−6 cm3 mol−1 and F = 1.2 × 10−5. The values of κ and λ do not reveal the presence of an important covalent reduction, despite it being a common feature in complexes with 3d transition metal ions. However, these two values lie in the range of those previously reported for mononuclear high-spin six-coordinate iron(II) complexes [52,102]. Moreover, the large value of ∆ and a non-negligible rhombicity (E/∆ ≈ 0.11) agree with the different electronic nature of the ligands building the six-coordination at the iron(II) ion.
Owing to the unquenched angular momentum in the ground state of the high-spin iron(II) complexes by the ligand field, the resulting “in state” SOC can lead to a sizable axial zfs parameter D.32 In this respect, the large value of ∆ supports a strong splitting of the 5T2g ground state into the 5B2g and 5Eg levels. In fact, the M vs. H/T curves for 2 in the temperature range 2.0–10 K does not collapse (see inset of Figure 4), a feature that rules out a null or a very large value of D, indicating instead a relatively moderate zero-field splitting. Besides, the different nature of the ligands in the equatorial plane at the metal center (two cyanide-nitrogen atoms and two methanol molecules) allows describing a rhombic distortion through two different directions from the trans arrangement of these ligands, leading to a splitting of the low-lying 2Eg level. Given that this splitting is large enough, the three states arising from the 5T2g ground state are well separated from each other, and they do not present any orbital momentum. CASSCF/NEVPT2 calculations (see below) show that the two excited levels are 1600 and 1966 cm−1 above the ground level. Having this in mind, a phenomenological zfs approach summarized in the Hamiltonian of Equation (2) should be appropriate.
Consequently, the simultaneous analysis of the magnetization at different applied dc fields and temperatures and the variable-temperature magnetic susceptibility data of 2 through this approach led to the following best-fit parameters: D = −5.1(3) cm−1, E/|D| = 0.227(7), g// = 2.193(3), g⊥ = 2.045(5) with F = 3.8 × 10−5. A positive D value should lead to a vanishing of the χMT product at a very low temperature, but the observed trend to reach a value close to 2.0 cm3 mol−1 at 0 K agrees with an easy-axis of the magnetization (D < 0). This negative sign is also supported by the EPR spectroscopy and partially by the ab initio CASSCF/NEVPT2 calculations on the real geometry of 2 (see discussion below). The uniaxial anisotropy is thus confirmed for the iron(II) ion in 2 and its magnitude is comparable with those of previous magneto-structural reports on six-coordinate iron(II) complexes [52,103,104,105].
2.4. EPR Spectroscopy and Theoretical Calculations of 1 and 2
The Q-band EPR spectra on a crushed sample of 1 in the temperature range 4.0–20 K exhibits an increase of the intensity of the signals as far as the temperature decreases unambiguously supporting a positive value of D (Figure 5). Due to the large value of D in this compound, only the low-lying Kramers doublet will be thermally populated at low temperatures, and its EPR spectra will correspond only to this low-lying Kramers doublet.
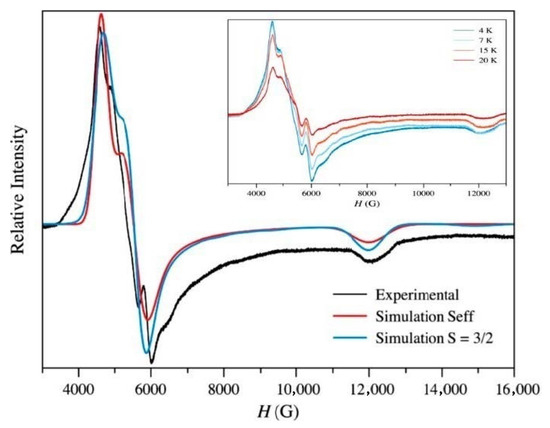
Figure 5.
Q-band EPR spectrum of a crushed sample of 1 at 4.0 K (black trace). The grey and black traces correspond to the best simulations for an effective spin Seff = ½ and an anisotropic spin S = 3/2 respectively (see text). Inset: The thermal evolution of the EPR spectra from 20 (red) to 4.0 K (blue).
So, considering a Seff = ½, the simulation of the EPR spectra of 1 was achieved with the following parameters: g1 = 5.25, g2 = 4.35 and g3 = 2.02. This set of values of the Landé factor agree with a positive value of the D parameter after the Bencini’s study on EPR spectroscopy of cobalt(II) complexes [106], such as those obtained through the simultaneous fit of the magnetic susceptibility and reduced magnetization data. These values for 1 also indicate a significant rhombicity, a feature which is corroborated by the occurrence of multiple peaks. The analysis of the EPR spectra of 1 through an S = 3/2 model could be achieved only with D > 0 and a small value of E/D quotient: g// = 2.04, g⊥ = 2.40 and E/D = 0.06. The great value of D and the slight deviation of the octahedral geometry of the cobalt(II) environment in 1 accounts for the small value of the E/D quotient for this compound.
Compound 2 is EPR silent, a feature which is as expected because of the relatively large and negative value of D for the high-spin iron(II) complex of this compound.
To further confirm the validity of the experimental results of 1 and 2, we carried out theoretical calculations by CASSCF/NEVPT2 (Tables S2(1) and S3(2)). These calculations support the experimental results found for 1 and 2. The absolute values of D for both compounds (+68.1 (1) and +6.9 cm−1 (2)) agree with those obtained by magnetometry. According to the octahedral environment of the six-coordinate cobalt(II) ion in 1, D is positive, and the values of the g-factors of the ground quartet (gx = 2.717, gy = 2.427 and gz = 1.985; g⊥ = 2.597 and g// = 1.99) and Kramers doublet states (g’x = 6.597, g’y = 3.508 and g’z = 1.988) agree with those from magnetometry and EPR spectroscopy. The moderate rhombicity observed in the EPR study of 1 (E/D = 0.06) is more pronounced in the theoretical result (E/D = 0.18), but the greatest difficulty to estimate it in an accurate and quantitative way from quantum chemical methods is well-known. The origin of the axial anisotropy in 1 mainly lies on the contributions from the low-lying quintet states (DQ = +56.6 cm−1) and particularly from the first two ones (+51.9 cm−1), which together with the ground state make up the 4T1g ground term in an ideal octahedral geometry. The remaining excited states are well above in energy (≥7900 cm−1) and therefore, their contribution to D is much lower or negligible.
In the case of 2, the origin of the uniaxial anisotropy mainly comes from the contributions of the low-lying quintet states (DQ = +5.7 cm−1), those from the triplet states being practically negligible (DT = +1.3 cm−1). Among the states that contribute to the D parameter in 2, those arising from the 5T2g term are the dominant ones (see Table S3). Although apparently there is in 2 an inconsistency in the sign of D obtained from the theoretical calculations and the absence of signals in the EPR spectrum, this is not real since the high rhombicity found both from magnetometry (E/D = 0.227) and theoretical calculations (0.29 and 0.33 from effective and 2nd-order SOC Hamiltonians, respectively), which are close to 1/3, prevent setting unambiguously the sign of D. Therefore, a negative value of D is reasonable for 2, and it would justify both the experimental and theoretical results. Anyway, an analysis of the NEVPT2 energies found for the first fifteen Mj levels (0.0, 2.4, 14.3, 29.0, 30.6, 1561.8, 1563.9, 1634.2, 1653.7, 1671.2, 2021,9, 2023.6, 2061.3, 2102.1 and 2106.8 cm−1) can provide information on the parameters that define the 1st-order SOC. The splitting of some Kramers doublets supports the inclusion of the rhombicity into the model through the E parameter. Considering the standard deviation, while D and E were determined with precision, this was not possible for the remaining parameters. However, all of them (κ = 0.987, λ = −108.4 cm−1, ∆ = 1784 cm−1 and E/∆ = 0.098) agree with those obtained from the temperature dependence of magnetic susceptibility.
2.5. Dynamic (ac) Magnetic Properties of 1 and 2
Alternating current (ac) magnetic susceptibility measurements were performed for 1 and 2 below 12 K to probe their magnetization dynamics. Interestingly, even though the relatively large and negative value of D in 2 indicates an intrinsic spin-reversal energy barrier of Ueff = S2|D| = 20.4 cm−1, no out-of-phase signals (χM”) were observed for this compound down to 2.0 K, either in the lack or in the presence of non-zero applied dc magnetic fields. It deserves to be noted that in a previous report concerning the first example of a mononuclear six-coordinate high-spin iron(II) complex with an FeO6 chromophore behaving as SIM [52], blocking temperatures below 4.0 K were observed under the explored applied dc fields, the value of D being −11.7 cm−1. In the present example with a FeO4N2 chromophore having a smaller value of D (ca. −5.1cm−1), out-of-phase signals might be possible at very low temperatures which are not accessible in our susceptometer. In the case of 1, the incipient frequency-dependent of χM” below 12 K under a 0 G static field turned into maxima under Hdc = 1000 (Figure S6) and 2500 G (Figure 6).
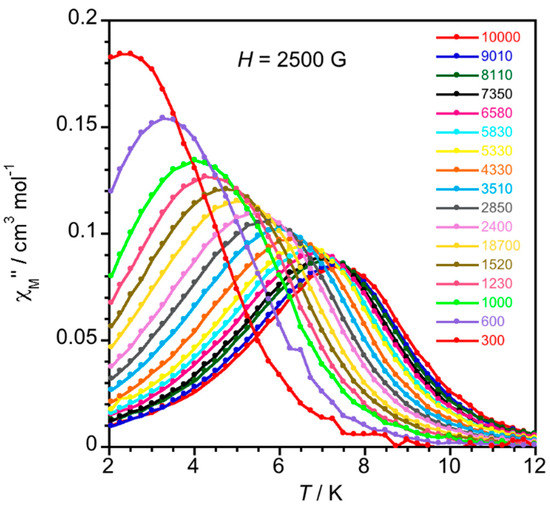
Figure 6.
Thermal dependence of χM” (bottom) for 1 under an applied static field of Hdc = 2500 G with a ±5 G oscillating field at frequencies in the range 0.30–10 kHz.
The Cole–Cole plots of 1 in the temperature range 2.0–7.0 K under applied dc fields of 1000 (Figure S7) and 2500 G (Figure 7) give almost perfect semicircles which can be fitted by the generalized Debye model. The values of α (the parameter which is related to the width of the distribution of the relaxation times and that takes values between 1 (pure spin-glass) and 0 (single relaxation process)) vary between ca. 0.08 (at 6.5 K) and 0.11 (at 3.5 K) under both 1000 and 2500 G (see Table S4), most likely because of the arising of additional relaxation processes.
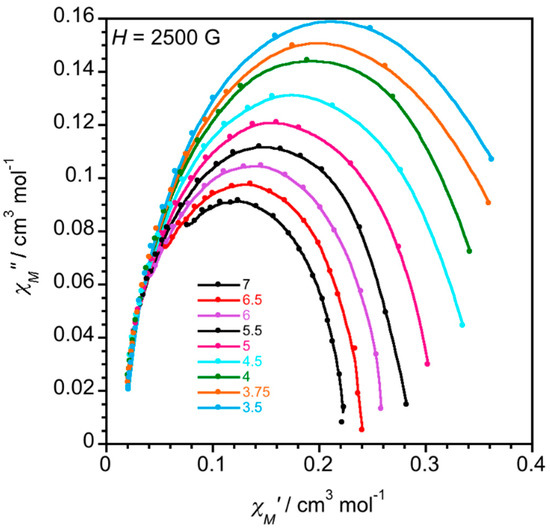
Figure 7.
Cole–Cole plots in the temperature range 3.5–7.0 K for 1 under an applied static field Hdc = 2500 G. The solid lines are the best-fit curves.
The values of the relaxation time for 1 were calculated from the maximum of χM” at a given frequency (χM” vs. T, τ−1 = 2πν) and the corresponding Arrhenius plots were built on the basis of these data (see Figure 8 (Hdc = 2500 G) and Figure S8 (Hdc = 1000 G)). Among the approaches used to analyze the Arrhenius plots (for example Orbach, Raman, direct and quantum-tunneling processes), our experimental data are best described through a combination of direct and Raman (Equation (4)) as shown in Figure 8 and Figure S8.
τ−1 = AT + BTn
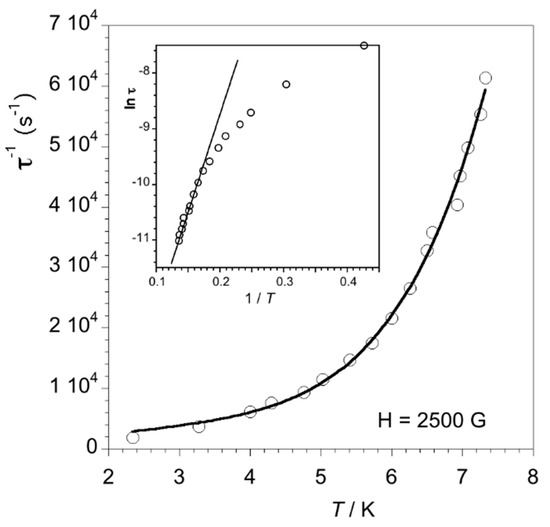
Figure 8.
Temperature dependence of τ−1 (o) for 1 under Hdc = 2500 G showing the best-fit (solid line) to the combination of a direct and one Raman approach. The inset is the Arrhenius plot (o) showing the best-fit (solid line) to one Orbach process.
The best-fit parameters through Equation (4) for 1 are A = 185 K−1 s−1, B = 0.160 K−n s−1 and n = 5.9 (Hdc = 1000 G) and A = 1200 K−1 s−1, B = 0.240 K−n s−1 and n = 6.2 (Hdc = 2500 G). Although values for n covering the range 1–8 can be considered reasonable, the common ones for a Raman process would take values between 6 and 8. Alternatively, the insets of Figure 8 and Figure S8 show how the calculated values of τ for 1 in the high-temperature range follow the Arrhenius law characteristic of a thermally activated Orbach process, τ−1 = τ0−1 exp(−Ea/kT). The deviation of the linearity observed at low temperatures is probably due to other relaxation processes. The values of τ0 and Ea are 7.70 × 10−8 s and 33.19 cm−1 (Hdc = 1000 G) and 1.89 × 10−7 s and 23.0 cm−1 (Hdc = 2500 G), given that the values of Ea are well below that of a possible energy barrier 2D (ca. 107 cm−1 with E = 0) assuming a negative value of D. But, as D > 0 for 1, any energy barrier associated to the zfs is prevented. In such a case, a relaxation of the magnetization obeying a single Orbach process should be ruled out. Then, the combination of a direct and one Raman process seems to be the more appropriate analysis for the dynamic magnetic behavior of 1.
3. Experimental
3.1. Materials and General Methods
All reagents and solvents were purchased from commercial suppliers and used without further purification. The organic 2,5-dpp ligand and the (PPh4)2[Co2(μ-2,5-dpp)(CN)8]·2H2O complex were prepared according to the literature [91,107]. Elemental analyses (C, H, N) were performed with a Perkin Elmer 2400 analyzer. IR spectra were carried out with a FTIR Bruker Tensor V-37 spectrophotometer using KBr pellets in the range 4000–400 cm−1. Thermal measurements were done on a Netzsch STA 449 F1 Jupiter Simultaneous Thermal Analyzer in dynamic air (30 mL/min) with a heating rate of 5 °C min−1 spanning the temperature range 25–1000 °C and using alumina crucibles covered with pierced alumina lids.
Caution! The high toxicity of the cyanides implies great caution when using them. The syntheses were carried out at mmol scale, in a well-ventilated hood. The waste was treated with solutions of NaClO and NaOH to transform the cyanide into cyanate.
3.2. Preparation of the Complexes
3.2.1. Synthesis of [CoII(CH3OH)2(DMSO)2(μ-NC)2Co2III(μ-2,5-dpp)(CN)6]n·4nCH3OH (1)
A DMSO solution (15 mL) of (PPh4)2[Co2(μ-2,5-dpp)(CN)8]·2H2O (127 mg, 0.1 mmol) was layered on a methanolic solution (10 mL) of Co(NO3)2·6H2O (51 mg, 0.4 mmol), in a test tube of 2.5 cm diameter and 20 cm height. X-ray quality crystals of 1 were obtained after one week on standing under ambient conditions. Yield: ca. 50%. Anal. calcd. for C32H46Co3N12O8S2 (1): C, 39.72; H, 4.79; N, 17.37. Found: C, 39.64; H, 4.76; N, 17.34%. IR (KBr/cm−1): 3404(vs), 2923(w), 2171(m), 2140(s), 1632(m), 1443(s), 1195(s), 1028(s), 782(s).
3.2.2. Synthesis of [FeII(CH3OH)2(DMSO)2(μ-NC)2Co2III(μ-2,5-dpp)(CN)6]n·2nCH3OH (2)
The same procedure was used for the synthesis of 2, replacing Co(NO3)2·6H2O by Fe(BF4)2·4H2O. X-ray quality crystals of 1 were obtained after several days. Yield: ca. 60%. Anal. calcd. for C32H46Co2FeN12O8S2 (2): C, 39.84; H, 4.80; N, 17.42. Found: C, 39.79; H, 4.77; N, 17.38%. IR (KBr/cm−1): 3334(s), 2922(s), 2167(m), 2136(m), 1640(w), 1469(s), 1029(s), 795(w).
3.3. Physical Measurements
Direct current (dc) magnetic susceptibility measurements (1.9–300 K) under applied dc magnetic fields of 5000 G (T ≥ 50 K) and 100 G (1.9 ≤ T ≤ 50 K) and variable-field (0–5 T) magnetization measurements (2.0–10 K) on crushed crystals of 1 and 2 (mixed with grease to avoid the crystallite orientation) were carried out with a Quantum Design SQUID magnetometer. Variable-temperature (2.0–12 K) alternating current (ac) magnetic susceptibility measurements under different applied dc magnetic fields in the range 0–2500 G were performed for 1 and 2 by using a Quantum Design Physical Property Measurement System (PPMS). The magnetic susceptibility data of both compounds were corrected for the diamagnetism of the constituent atoms and the sample holder (a plastic bag). Q-band EPR spectra (4.0–20 K) on powdered samples of 1 and 2 were carried out with a Bruker ER 200 spectrometer equipped with a helium continuous-flow cryostat. The EPR spectra were fitted through the version 5.2 of the EasySpin software [108]. Powder X-ray diffraction (XPRD) measurements were done on a PANalytical Empyrean X-ray diffractometer using Cu-Kα radiation (α = 1.5418 Å), in which the X-ray tube was operated at 40 kV and 30 mA ranging from 5 to 30°.
3.4. Computational Details
To evaluate the parameters which determine the axial (D) and rhombic zfs, calculations based on the second order N-electron valence state perturbation theory (CASSCF/NEVPT2) applied on the wave function, which was previously obtained from complete active space (CAS) calculation, were carried out on the real cobalt(II) and iron(II) environments in 1 and 2, respectively. The calculations were performed with the version 4.0 of the ORCA program [109] using the TZVP basis set proposed by Ahlrichs [64,99,100,101,110] and the auxiliary TZV/C Coulomb fitting basis sets [111,112,113,114]. The contributions to zfs from ten quartet and twenty doublet excited states [Co(II) in 1] and from five quintets and thirty triplet excited states [Fe(II) in 2] generated from an active space with seven [Co(II) (1)] and six electrons [Fe(II) (2)] in five d orbitals were included using an effective Hamiltonian. The g-tensors were calculated for the ground Kramers pair [Co(II)] using Multireference Configuration Interaction (MRCI) wavefunctions with a first-order perturbation theory on the SOC matrix [115]. The RIJCOSX method was used combining resolution of the identity (RI) and “chain of spheres” COSX approximations for the Coulomb and exchange terms, respectively [116,117].
3.5. X-ray Data Collection and Structure Refinement
X-ray quality single crystals of 1 and 2 were measured on an Oxford Diffraction XCALIBUR E CCD diffractometer equipped with graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å). The crystals were positioned 40 mm from the CCD detector. The determination of the unit cell and data integration were performed by using the CrysAlis package of Oxford Diffraction [118]. The structures were solved by direct methods using Olex2 software [119] with the SHELXS-2014 structure solution program and refined by full-matrix least-squares on F2 with SHELXL-2014 [120] with anisotropic displacement parameters for the non-hydrogen atoms. All hydrogen atoms attached to carbon were introduced in idealized positions (dC-H = 0.96 Å) using the riding model with their isotropic displacement parameters fixed at 120% of the riding atom. The structural images were obtained with the Diamond 4 program [121]. The unit cell parameters and refinement conditions for 1 and 2 are given in Table 3. CCDC- 2042057 (1), 2042058 (2).

Table 3.
Crystal data and structure refinement for 1 and 2.
4. Conclusions
We recently reported a new cyanido-based binuclear complex, [Co2III(μ-2,5-dpp)(CN)8]2−, and investigated its ability to act as a metalloligand [91]. Based on these results, we employed this diamagnetic species as a node in order to design low-dimensional complexes with specific magnetic properties. The exploration of its binding ability toward the anisotropic fully solvated high-spin cobalt(II) and iron(II) cations afforded the corresponding heterobimetallic chains CoIII2CoII (1) and CoIII2FeII (2) where the six-coordinate divalent metal ions are magnetically non-interacting. Static (dc) and dynamic (ac) magnetic measurements show that 1 is a new example of SIM with transversal anisotropy, the positive sign of D being confirmed by Q-band EPR spectroscopy and substantiated by theoretical calculations. The analysis of this behavior in 1 indicates that the relaxation of the magnetization at low temperatures in the ground state most likely occurs through a combination of a direct and one Raman process. The magnetically isolated high-spin iron(II) ion in 2 is EPR silent and does not exhibit any SIM behavior. Our synthetic approach is suitable to obtain low-dimensional compounds containing anisotropic paramagnetic transition metal ions, magnetically isolated by the diamagnetic [Co2III(μ-2,5-dpp)(CN)8]2− nodes, that could behave as SIMs. Its use in assembling a building block towards heavier metal ions, rare-earth cations or even magnetic clusters would provide new examples of SIMs as well as SMMs. Further work along this line using this diamagnetic spacer as a complexing agent towards paramagnetic metal ions aimed at obtaining tailor-made of multifunctional magnetic systems will be developed in a near future.
Supplementary Materials
The information available online at https://www.mdpi.com/2312-7481/6/4/66/s1 is: Figure S1: IR spectrum for 1, Figure S2: IR spectrum for 2, Figure S3: TG, DTG and DSC curves for 1 and 2, Figure S4: View of a fragment of the chain structure of 1, along with the atom numbering, Figure S5: A view of the hydrogen bonding pattern in 2 (the dmso molecules were omitted for clarity) [Symmetry code: (c) = x, −1 + y, z]], Figure S6: Thermal dependence of χM” for 1 under an applied static field of Hdc = 1000 G with a ±5 G oscillating field at frequencies in the range 0–3–10 kHz, Figure S7: Cole-Cole plots in the temperature range 3.5–7.0 K for 1 under an applied static field Hdc = 1000 G (the solid lines are the best-fit curves), Figure S8: Temperature dependence of τ−1 (o) for 1 under Hdc = 1000 G showing the best fit (solid line) to the combination of a direct and one Raman approach. The inset is the Arrhenius plot (o) showing the best-fit (solid line) to one Orbach process. Table S1: Results of the SHAPE analysis of the {CoIIIC4N2} and {MIIN2O4} chromophores from the {CoIII(DPP)1/2(CN)4}− (1 and 2) and {MII(CN)2(H2O)2(DMSO)2} fragments [M = CoII (1) and FeII (2)], Table S2: Energy of the calculated quartet (Qi) and doublet (Di) excited states and their contributions to the D and E values for 2 obtained from CASSCF/NEVPTZ calculations, Table S3: Energy of all calculated quintet (Qi) and triplet (Di) excited states and their contributions to the D and E values for 2 obtained from CASSCF/NEVPT2 calculations, Table S4: Parameters of the ac magnetic susceptibility data of 1 through the Debye model.
Author Contributions
A.B. performed the organic syntheses; M.-G.A. and D.V. prepared the complexes and grew the single crystal; S.S. carried out the X-ray diffraction experiments; F.L. and J.C. performed the magnetic measurements and EPR spectra and analyzed the corresponding data; J.C. carried out the theoretical calculations and discussed their results; M.J. and M.-G.A. conceived and designed the experiments; all authors contributed to the writing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support from the Romanian National Authority for Scientific Research CNCS–UEFISCDI (Projects PN-III-P1-1.1-TE-2019-0352 and PN-III-P1-1.1-MC-2019-2199), the Ministerio Español de Economía y Competitividad (Project CTQ2016-75068P and PID2019-109735GB-I00) is gratefully acknowledged. The authors would like to thank Cristian D. Ene from the “Ilie Murgulescu” Institute of Physical Chemistry for the thermogravimetric measurements.
Acknowledgments
The authors would like to thank Cristian D. Ene from the “Ilie Murgulescu” Institute of Physical Chemistry for the thermogravimetric measurements.
Conflicts of Interest
There are no conflict to declare.
References
- Ouahab, L. (Ed.) Multifunctional Molecular Materials; Pan Stanford Publishing: Singapore, 2013. [Google Scholar]
- Launay, J.-P.; Verdaguer, M. Electrons in Molecules: From Basic Principles to Molecular Electronics; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Benelli, C.; Gatteschi, D. Introduction to Molecular Magnetism: From Transition Metals to Lanthanides; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
- Layfield, R.A.; Murugesu, M. (Eds.) Lanthanides and Actinides in Molecular Magnetism; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
- Sieklucka, B.; Pinkowicz, D. (Eds.) Molecular Magnetic Materials; Wiley-VCH: Weinheim, Germany, 2017. [Google Scholar]
- Ferrando-Soria, J.; Vallejo, J.; Castellano, M.; Martínez-Lillo, J.; Pardo, E.; Cano, J.; Castro, I.; Lloret, F.; Ruiz-García, R.; Julve, M. Molecular Magnetism, quo vadis? A historical perspective from a coordination chemist viewpoint. Coord. Chem. Rev. 2017, 339, 17–103. [Google Scholar] [CrossRef]
- Mon, M.; Bruno, R.; Ferrando-Soria, J.; Armentano, D.; Pardo, E. Metal-organic framework technologies for water remediation: Towards a sustainable ecosystem. J. Mater. Chem. A 2018, 6, 4912–4947. [Google Scholar] [CrossRef]
- Andruh, M. Heterotrimetallic complexes in molecular magnetism. Chem. Commun. 2018, 54, 3559–3577. [Google Scholar] [CrossRef] [PubMed]
- Journaux, Y.; Ferrando-Soria, J.; Pardo, E.; Ruiz-Garcia, R.; Julve, M.; Lloret, F.; Cano, J.; Li, Y.; Lisnard, L.; Yu, P.; et al. Design of Magnetic Coordination Polymers Built from Polyoxalamine Ligands: A Thirty Year Study. Eur. J. Inorg. Chem. 2018, 3–4, 228–247. [Google Scholar] [CrossRef]
- Chorazy, S.; Wyczesany, M.; Sieklucka, B. Lanthanide Photoluminescence in Heterometallic Polycyanidometallate-Based Coordination Networks. Molecules 2017, 22, 1902. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Lillo, J.; Faus, J.; Lloret, F.; Julve, M. Towards multifunctional magnetic systems through molecular-programmed self assembly of Re(IV) metalloligands. Coord. Chem. Rev. 2015, 289–290, 215–232. [Google Scholar] [CrossRef]
- Marinescu, G.; Andruh, M.; Lloret, F.; Julve, M. Bis(oxalato)chromium(III) complexes: Versatile tectons in designing heterometallic coordination compounds. Coord. Chem. Rev. 2011, 255, 161–185. [Google Scholar] [CrossRef]
- Lescouëzec, R.; Toma, L.M.; Vaissermann, J.; Verdaguer, M.; Delgado, F.S.; Ruiz-Pérez, C.; Lloret, F.; Julve, M. Design of single chain magnets through cyanide-bearing six-coordinate complexes. Coord. Chem. Rev. 2005, 249, 2691–2729. [Google Scholar] [CrossRef]
- Andruh, M. Coordination Polymers Constructed from Oligonuclear Nodes. Chimia 2013, 67, 383–387. [Google Scholar] [CrossRef]
- Andruh, M. Oligonuclear complexes as tectons in crystal engineering: Structural diversity and magnetic properties. Chem. Commun. 2007, 2565–2577. [Google Scholar] [CrossRef]
- Robson, R. Design and its limitations in the construction of bi- and poly-nuclear coordination complexes and coordination polymers (aka MOFs): A personal view. Dalton Trans. 2008, 5113–5131. [Google Scholar] [CrossRef] [PubMed]
- Vigato, P.A.; Tamburini, S. The challenge of cyclic and acyclic Schiff bases and related derivatives. Coord. Chem. Rev. 2004, 248, 1717–2128. [Google Scholar] [CrossRef]
- Janiak, C.; Vieth, J.K. MOFs, MILs and more: Concepts, properties and applications for porous coordination networks (PCNs). New J. Chem. 2010, 34, 2366–2388. [Google Scholar] [CrossRef]
- Cook, T.R.; Zheng, Y.-R.; Stang, P.J. Meta-Organic Frameworks and Self-Assembled Supramolecular Coordination Complexes: Comparing and Contrasting the Design, Synthesis, and Functionality of Metal-Organic Materials. Chem Rev. 2013, 113, 734–777. [Google Scholar] [CrossRef]
- Marvaud, V.; Decroix, C.; Scuiller, A.; Guyard-Duhayon, C.; Vaissermann, J.; Gonnet, F.; Verdaguer, M. Hexacyanometalate Molecular Chemistry: Heptanuclear Heterobimetallic Complexes; Control of the Ground Spin State. Chem. Eur. J. 2003, 9, 1677–1681. [Google Scholar] [CrossRef]
- Tanase, S.; Reedijk, J. Chemistry and Magnetism of cyanido-bridged d-f assemblies. Coord. Chem. Rev. 2006, 250, 2501–2510. [Google Scholar] [CrossRef]
- Shatruk, M.; Avendaño, C.; Dunbar, K.R. Cyanide-Bridged Complexes of Transition Metals: A Molecular Magnetism Perspective. Prog. Inorg. Chem. 2009, 56, 155–334. [Google Scholar]
- Wang, X.-Y.; Avendaño, C.; Dunbar, K.R. Molecular magnetic materials based on 4d and 5d transition metals. Chem. Soc. Rev. 2011, 40, 3213–3238. [Google Scholar] [CrossRef]
- Alexandrov, E.V.; Virovets, A.V.; Blatov, V.A.; Peresypkina, E.V. Topological Motifs in Cyanometallates: From Building Units to Three-Periodic Frameworks. Chem. Rev. 2015, 115, 12286–123192. [Google Scholar] [CrossRef]
- Pinkowicz, D.; Podgajny, R.; Nowicka, B.; Chorazy, S.; Reczyński, M.; Sieklucka, B. Magnetic clusters based on octacyanidometallates. Inorg. Chem. Front. 2015, 2, 10–27. [Google Scholar] [CrossRef]
- Visinescu, D.; Alexandru, M.-G.; Madalan, A.M.; Pichon, C.; Duhayon, C.; Sutter, J.-P.; Andruh, M. Magneto-structural variety of new 3d-4f-4(5)d heterotrimetallic complexes. Dalton Trans. 2015, 44, 16713–16727. [Google Scholar] [CrossRef] [PubMed]
- Alexandru, M.-G.; Visinescu, D.; Shova, S.; Andruh, M.; Lloret, F.; Cano, J.; Julve, M. Three different types of bridging ligands in a 3d-3d’-3d” heterotrimetallic chain. Dalton Trans. 2018, 47, 1010–1013. [Google Scholar] [CrossRef] [PubMed]
- Toma, L.; Lescöuezec, R.; Vaissermann, J.; Delgado, F.S.; Ruiz-Pérez, C.; Carrasco, R.; Cano, J.; Lloret, F.; Julve, M. Nuclearity Controlled Cyanide-Bridged Bimetallic CrIII-MnII Compounds: Synthesis, Crystal Structures, Magnetic Properties and Theoretical Calculations. Chem. Eur. J. 2004, 10, 6130–6145. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Ding, X.-H.; Zuo, J.-L.; You, X.-Z.; Huang, W. Tricyanometalate molecular chemistry: A type of versatile building blocks for the construction of cyano-bridged molecular architectures. Coord. Chem. Rev. 2011, 255, 1713–1732. [Google Scholar] [CrossRef]
- Toma, L.M.; Ruiz-Pérez, C.; Lloret, F.; Julve, M. Slow Relaxation of the Magnetization in a 4,2-Wavelike FeIII2CoII Heterobimetallic Chain. Inorg. Chem. 2012, 51, 1216–1218. [Google Scholar] [CrossRef]
- Toma, L.M.; Ruiz-Pérez, C.; Pasán, J.; Wernsdorfer, W.; Lloret, F.; Julve, M. Molecular Engineering to Control the Magnetic Interaction between Single-Chain Magnets Assembled in a Two-Dimensional Network. J. Am. Chem. Soc. 2012, 134, 15265–15268. [Google Scholar] [CrossRef]
- Toma, L.M.; Pasán, J.; Ruiz-Pérez, C.; Lloret, F.; Julve, M. [FeIII(dmbpy)(CN)4]−: A new building block for designing single-chain magnets. Dalton Trans. 2012, 41, 13716–13726. [Google Scholar] [CrossRef]
- Alexandru, M.-G.; Visinescu, D.; Madalan, A.M.; Lloret, F.; Julve, M.; Andruh, M. [W(bipy)(CN)6]−: A Suitable Metalloligand in the Design of Heterometallic Complexes. The First CuIILnIIIWV Trinuclear Complexes. Inorg. Chem. 2012, 51, 4906–4908. [Google Scholar] [CrossRef]
- Li, Y.-H.; He, W.-R.; Ding, X.-H.; Wang, S.; Cui, L.-F.; Huang, W. Cyanide-bridged assemblies constructed from capped tetracyanometalate building blocks [MA(ligand)CN)4]1−/2− (MA = Fe or Cr). Coord. Chem. Rev. 2012, 256, 2795–2815. [Google Scholar] [CrossRef]
- Visinescu, D.; Toma, L.M.; Fabelo, O.; Ruiz-Pérez, C.; Lloret, F.; Julve, M. Low-Dimensional 3d-4f Complexes Assembled by Low-Spin [FeIII(phen)(CN)4]− Anions. Inorg. Chem. 2013, 52, 1525–1537. [Google Scholar] [CrossRef]
- Alexandru, M.-G.; Visinescu, D.; Andruh, M.; Marino, N.; Armentano, D.; Cano, J.; Lloret, F.; Julve, M. Heterotrimetallic Coordination Polymers: [CuIILnIIIFeIII] Chains and [NiIILnIIIFeIII] Layers: Synthesis, Crystal Structures and Magnetic Properties. Chem. Eur. J. 2015, 21, 5429–5446. [Google Scholar] [CrossRef] [PubMed]
- Alexandru, M.-G.; Visinescu, D.; Shova, S.; Andruh, M.; Lloret, F.; Julve, M. Synthesis, Crystal Structures and Magnetic Properties of Two Novel Cyanido-Bridged Heterotrimetallic [CuIIMnIICrIII] Complexes. Inorg. Chem. 2017, 56, 2258–2269. [Google Scholar] [CrossRef] [PubMed]
- Alexandru, M.-G.; Visinescu, D.; Shova, S.; Oliveira, W.X.C.; Lloret, F.; Julve, M. Design of 3d-4f molecular squares through the [Fe{(HB(pz)3}(CN)3]− metalloligand. Dalton Trans. 2018, 47, 6005–6017. [Google Scholar] [CrossRef] [PubMed]
- Alexandru, M.-G.; Visinescu, D.; Braun-Cula, B.; Shova, S.; Lloret, F.; Julve, M. In situ generation of Ph3PO in cyanide-bridged heterometallic {FeIIILnIII}2 molecular squares. Dalton Trans. 2019, 48, 7532–7536. [Google Scholar] [CrossRef] [PubMed]
- Perlepes, P.S.; Maniaki, D.; Pilichos, E.; Katsoulakou, E.; Perlepes, S.P. Smart Ligands for Efficient 3d-, 4d-, and 5d-Metal Single-Molecule Magnets and Single-Ion Magnets. Inorganics 2020, 8, 39. [Google Scholar] [CrossRef]
- Clérac, R.; Winpenny, R.E.P. Single-Molecule Magnets and Related Phenomena. Struct. Bond. 2016, 172, 35–48. [Google Scholar]
- Frost, J.M.; Harriman, K.L.M.; Murugesu, M. The rise of 3-d single-ion magnets in molecular magnetism: Towards materials from molecules? Chem. Sci. 2016, 7, 2470–2491. [Google Scholar] [CrossRef]
- Craig, G.A.; Murrie, M. 3d single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef]
- Pedersen, K.S.; Bendix, J.; Clérac, R. Single-molecule magnet engineering building-block approaches. Chem. Commun. 2014, 50, 4396–4415. [Google Scholar] [CrossRef]
- Jia, J.-H.; Li, Q.-W.; Chen, Y.-C.; Liu, J.-L.; Tong, M.-L. Luminescent single-molecule magnets based on lanthanides: Design strategies, recent advances and magneto-luminescent studies. Coord. Chem. Rev. 2019, 378, 365–381. [Google Scholar] [CrossRef]
- Long, J.; Guari, Y.; Ferreira, R.A.S.; Carlos, L.D.; Larionova, J. Recent advances in luminescent lanthanide based Single-Molecule Magnets. Coord. Chem. Rev. 2018, 363, 57–70. [Google Scholar] [CrossRef]
- Pointillart, F.; Cador, O.; Le Guennic, B.; Ouahab, L. Uncommon lanthanide ions in purely 4f Single Molecule Magnets. Coord. Chem. Rev. 2017, 346, 150–175. [Google Scholar] [CrossRef]
- Liu, J.; Guo, M.; Tang, J. Recent Developments in Lanthanide Single-Molecule Magnets. Chem. Asian J. 2017, 12, 2772–2779. [Google Scholar] [CrossRef] [PubMed]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single molecule-magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
- Maciel, J.W.; Kalinke, L.H.G.; Valdo, A.K.; Martins, F.T.; Rabelo, R.; Moliner, N.; Cano, J.; Julve, M.; Lloret, F.; Cangussu, D. New Metal-Organic Systems with a Functionalized Oxamate-Type Ligand and MnII, FeII, CuII and ZnII. J. Braz. Chem. Soc. 2019, 30, 2413–2429. [Google Scholar]
- Maniaki, D.; Pilichos, E.; Perlepes, S.P. Coordination Clusters of 3d-Metals That Behave as Single-Molecule Magnets (SMMs): Synthetic Routes and Strategies. Front. Chem. 2018, 6, 461. [Google Scholar] [CrossRef]
- Vallejo, J.; Castro, I.; Ruiz-García, R.; Cano, J.; Julve, M.; Lloret, F.; De Munno, G.; Wernsdorfer, W.; Pardo, E. Field-Induced Slow Magnetic Relaxation in a Six-Coordinate Mononuclear Cobalt(II) Complex with a Positive Anisotropy. J. Am. Chem. Soc. 2012, 134, 15704–15707. [Google Scholar] [CrossRef]
- Pascual-Álvarez, A.; Vallejo, J.; Pardo, E.; Julve, M.; Lloret, F.; Krzystek, J.; Armentano, D.; Wernsdorfer, W.; Cano, J. Field-Induced Slow Magnetic Relaxation in a Mononuclear Manganese(III)-Porphyrin Complex. Chem. Eur. J. 2015, 21, 17299–17307. [Google Scholar] [CrossRef]
- Vallejo, J.; Pascual-Alvarez, A.; Cano, J.; Castro, I.; Julve, M.; Lloret, F.; Krzystek, J.; De Munno, G.; Armentano, D.; Wernsdorfer, W.; et al. Field-Induced Hysteresis and Quantum Tunneling of the Magnetization in a Mononuclear Manganese(III) Complex. Angew. Chem. Int. Ed. 2013, 52, 14325–14329. [Google Scholar] [CrossRef]
- Korchagin, D.V.; Palii, A.V.; Yureva, E.A.; Akimov, A.V.; Misochko, E.Y.; Shilov, G.V.; Talantsev, A.D.; Morgunov, R.B.; Shakin, A.A.; Aldoshin, S.M.; et al. Evidence of field-induced slow magnetic relaxation in cis-[Co(hfac)2(H2O)2] exhibiting tri-axial anisotropy with a negative axial component. Dalton Trans. 2017, 46, 7540–7548. [Google Scholar] [CrossRef] [PubMed]
- Nemec, I.; Herchel, R.; Svoboda, I.; Boča, R.; Trávníček, Z. Large and Negative magnetic anisotropy in pentacoordinate mononuclear Ni(II) Schiff base complexes. Dalton Trans. 2015, 44, 9551–9560. [Google Scholar] [CrossRef]
- Eichhöfer, A.; Lan, Y.; Mereacre, V.; Bodenstein, T.; Weigend, F. Slow Magnetic Relaxation in Trigonal-Planar Mononuclear Fe(II) and CoII) Bis(trimethylsilyl)amido Complexes—A Comparative Study. Inorg. Chem. 2014, 53, 1962–1974. [Google Scholar] [CrossRef] [PubMed]
- Bar, A.K.; Pichon, C.; Sutter, J.-P. Magnetic anisotropy in two- to eight-coordinated transition-metal complexes: Recent developments in molecular magnetism. Coord. Chem. Rev. 2016, 308, 346–380. [Google Scholar] [CrossRef]
- Meng, Y.-S.; Jiang, S.-D.; Wang, B.-W.; Gao, S. Understanding the Magnetic Anisotropy toward Single-Ion Magnets. Acc. Chem. Res. 2016, 49, 2381–2389. [Google Scholar] [CrossRef]
- Wu, Y.; Tian, D.; Ferrando-Soria, J.; Cano, J.; Yin, L.; Ouyang, Z.; Wang, Z.; Luo, S.; Liu, X.; Pardo, E. Modulation of the magnetic anisotropy of octahedral cobalt(II) single-ion magnets by fine-tuning the axial coordination microenvironmement. Inorg. Chem. Front. 2019, 6, 848–856. [Google Scholar] [CrossRef]
- Vallejo, J.; Pardo, E.; Viciano-Chumillas, M.; Castro, I.; Amorós, P.; Déniz, M.; Ruiz-Pérez, C.; Yuste-Vivas, C.; Krzystek, J.; Julve, M.; et al. Reversible solvatomagnetic switching in a single-ion magnet from an entatic state. Chem. Sci. 2017, 8, 3694–3702. [Google Scholar] [CrossRef]
- Świtlicka, A.; Machura, B.; Kruszynski, R.; Cano, J.; Toma, L.M.; Lloret, F.; Julve, M. Field-induced slow magnetic relaxation in pseudooctahedral cobalt(II) complexes with positive axial and large rhombic anisotropy. Dalton Trans. 2019, 48, 1404–1417. [Google Scholar] [CrossRef]
- Mondal, A.K.; Jover, J.; Ruiz, E.; Konar, S. Single-ion magnetic anisotropy in a vacant octahedral Co(II) complex. Dalton Trans. 2019, 48, 25–29. [Google Scholar] [CrossRef]
- Jeon, I.-R.; Clérac, R. Controlled association of single-molecule magnets (SMMs) into coordination networks: Towards a new generation of magnetic materials. Dalton Trans. 2012, 41, 9569–9586. [Google Scholar] [CrossRef]
- Lecren, L.; Wernsdorfer, W.; Li, Y.-G.; Vindigni, A.; Miyasaka, H.; Clérac, R. One-Dimensional Supramolecular Organization of Single-Molecule Magnets. J. Am. Chem. Soc. 2007, 129, 5045–5051. [Google Scholar] [CrossRef] [PubMed]
- Baldoví, J.; Coronado, E.; Gaita-Ariño, A.; Gamer, C.; Giménez-Marqués, M.; Mínguez-Espallargas, G. A SIM-MOF: Three-Dimensional Organization of Single-Ion Magnets with Anion-Exchange Capabilities. Chem. Eur. J. 2014, 20, 10695–10702. [Google Scholar] [CrossRef] [PubMed]
- Palion-Gazda, J.; Klemens, T.; Machura, B.; Vallejo, J.; Lloret, F.; Julve, M. Single ion magnet behaviour in a two-dimensional network of dicyanamide-bridged cobalt(II) ions. Dalton Trans. 2015, 44, 2989–2992. [Google Scholar] [CrossRef] [PubMed]
- Ion, A.E.; Nica, S.; Madalan, A.M.; Shova, S.; Vallejo, J.; Julve, M.; Lloret, F.; Andruh, M. Two-Dimensional Coordination Polymers Using, Simultaneously, Linear and Angular Spacers and Cobalt(II) Nodes. New Examples of Networks of Single-Ion Magnets. Inorg. Chem. 2015, 54, 16–18. [Google Scholar] [CrossRef]
- Liu, X.-Y.; Sun, L.; Zhou, H.-L.; Cen, P.-P.; Jin, X.-Y.; Xie, G.; Chen, S.-P.; Hu, Q.-L. Single-Ion-Magnet Behavior in a Two-Dimensional Coordination Polymer Constructed from CoII Nodes and a Pyridylhydrazone Derivative. Inorg. Chem. 2015, 54, 8884–8886. [Google Scholar] [CrossRef]
- Świtlicka-Olszewska, A.; Palion-Gazda, J.; Klemens, T.; Machura, B.; Vallejo, J.; Cano, J.; Lloret, F.; Julve, M. Single-ion magnet behavior in mononuclear and two-dimensional dicyanamide-containing cobalt(II) complexes. Dalton Trans. 2016, 45, 10181–10193. [Google Scholar] [CrossRef]
- Shao, D.; Shi, L.; Zhang, S.-L.; Zhao, X.-H.; Wu, D.-Q.; Wei, X.-Q.; Wang, X.-Y. Syntheses, structures and magnetic properties of three new chain compounds based on a pentagonal bipyramidal Co(II) building blocks. CrystEngComm 2016, 18, 4150–4157. [Google Scholar] [CrossRef]
- Brunet, G.; Safin, D.A.; Jover, J.; Ruiz, R.; Murugesu, M. A new synthesis strategy towards enhancing the structure and cycle stabilities of the LiNi0.80Co0.15Al0.05O2 cathode material. J. Mater. Chem. C 2017, 5, 835–841. [Google Scholar] [CrossRef]
- Ma, R.; Chen, Z.; Cao, F.; Wang, S.; Huang, X.; Li, Y.; Lu, J.; Li, D.; Dou, J. Two 2-D multifunctional cobalt(II) compounds: Field-induced single-ion magnetism and catalytic oxidation of benzylic C-H bonds. Dalton Trans. 2017, 46, 2137–2145. [Google Scholar] [CrossRef]
- Liu, X.; Ma, X.; Cen, P.; An, F.; Wang, Z.; Song, W.; Zhang, Y.-Q. One-dimensional cobalt(II) coordination polymer featuring single-ion-magnet-type field-induced slow magnetic relaxation. New J. Chem. 2018, 42, 9612–9619. [Google Scholar] [CrossRef]
- Chen, Z.; Yin, L.; Mi, X.; Wang, S.; Cao, F.; Wang, Z.; Li, Y.; Lu, J.; Dou, J. Field-induced slow magnetic relaxation of two 1-D compounds containing six-coordinated cobalt(II) ions: Influence of the coordination geometry. Inorg. Chem. Front. 2018, 5, 2314–2320. [Google Scholar] [CrossRef]
- Roy, M.; Adhikary, A.; Mondal, A.K.; Mondal, R. Multifunctinonal Properties of a 1D Helical Co(II) Coordination Polymer: Toward Single-Ion Magnetic Behavior and Efficient Dye Degradation. ACS Omega 2018, 3, 15315–15324. [Google Scholar] [CrossRef] [PubMed]
- Mondal, P.; Dey, B.; Roy, S.; Bera, S.P.; Nasani, R.; Santra, A.; Konar, S. Field-Induced Slow Magnetic Relaxation and Anion/Solvent Dependent Proton Conduction in Cobalt(II) Coordination Polymers. Cryst. Growth Des. 2018, 18, 6211–6220. [Google Scholar] [CrossRef]
- Kong, J.-J.; Shao, D.; Zhang, J.-C.; Jiang, Y.-X.; Ji, C.-L.; Huang, X.-C. From mononuclear two-dimensional cobalt(II) complexes based on a mixed benzimidazole-dicarboxylate strategy: Synthesis, structures, and magnetic properties. CrystEngComm 2019, 21, 749–757. [Google Scholar] [CrossRef]
- Shi, L.; Shen, F.-X.; Shao, D.; Zhang, Y.-Q.; Wang, X.-Y. Syntheses, structures and magnetic properties of three two-dimensional cobalt(II) single-ion magnets with a CoIIN4X2 octahedral geometry. CrystEngComm 2019, 21, 3176–3185. [Google Scholar] [CrossRef]
- Shao, D.; Shi, L.; Wei, H.-Y.; Wang, X.-Y. Field-Induced Single-Ion Magnet Behaviour in Two New Cobalt(II) Coordination Polymers with 2,4,6-Tris(4pyridyl)-1,3,5-triazine. Inorganics 2017, 5, 90. [Google Scholar] [CrossRef]
- Zhu, Y.-Y.; Zhu, M.-S.; Yin, T.-T.; Meng, Y.-S.; Wu, Z.-Q.; Zhang, Y.-Q.; Gao, S. Cobalt(II) Coordination Polymer Exhibiting Single-Ion-Magnet-Type Field-Induced Slow Relaxation Behavior. Inorg. Chem. 2015, 54, 3716–3718. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, S.; Chen, S.; Yin, B.; Sun, Y.; Wang, Z.; Ouyang, Z.; Ren, J.; Wang, W.; Wei, Q.; et al. A two-dimensional(II) network with a remarkable positive axial anisotropy parameter exhibiting field-induced single-ion magnet behavior. J. Mater. Chem. C 2016, 4, 7798–7808. [Google Scholar] [CrossRef]
- Vallejo, J.; Fortea-Pérez, F.-R.; Pardo, E.; Benmansour, S.; Castro, I.; Krzystek, J.; Armentano, D.; Cano, J. Guest-dependent single-ion magnet behaviour in a cobalt(II) metal-organic framework. Chem. Sci. 2016, 7, 2286–2293. [Google Scholar] [CrossRef]
- Alexandru, M.-G.; Visinescu, D.; Shova, S.; Lloret, F.; Julve, M.; Andruh, M. Two-Dimensional Coordination Polymers Constructed by [NiIILnIII] Nodes and [WIV(bpy)(CN)6]2- Spacers: A Network of [NiIIDyIII] Single Molecule Magnets. Inorg. Chem. 2013, 52, 11627–11637. [Google Scholar] [CrossRef] [PubMed]
- Alexandru, M.-G.; Visinescu, D.; Marino, N.; De Munno, G.; Lloret, F.; Julve, M. {CoIIIMnIII}n corrugated chains based on heteroleptic cyanide metalloligands. RSC Adv. 2015, 5, 95410–95420. [Google Scholar] [CrossRef]
- Mondal, A.K.; Khatua, S.; Tomar, K.; Konar, S. Field-Induced Single-Ion-Magnetic Behavior of Octahedral CoII in a Two-Dimensional Coordination Polymer. Eur. J. Inorg. Chem. 2016, 2016, 3545–3552. [Google Scholar] [CrossRef]
- Shao, D.; Shi, L.; Shen, F.-X.; Wang, X.-Y. A cyano-bridged coordination nanotube showing field-induced slow magnetic relaxation. CrystEngComm 2017, 19, 5707–5711. [Google Scholar] [CrossRef]
- Shao, D.; Zhou, Y.; Pi, Q.; Shen, F.-X.; Yang, S.-R.; Zhang, S.-L.; Wang, X.-Y. Two-dimensional frameworks formed by pentagonal bipyramidal cobalt(II) ions and hexacyanometallates: Antiferromagnetic ordering, metamagnetism and slow magnetic relaxation. Dalton Trans. 2017, 46, 9088–9096. [Google Scholar] [CrossRef]
- Alexandru, M.-G.; Marino, N.; Visinescu, D.; De Munno, G.; Andruh, M.; Bentama, A.; Lloret, F.; Julve, M. A novel octacyanido dicobalt(II) building block for the construction of heterometallic compounds. New J. Chem. 2019, 43, 6675–6682. [Google Scholar] [CrossRef]
- Alexandru, M.-G.; Visinescu, D.; Marino, N.; De Munno, G.; Vallejo, J.; Lloret, F.; Julve, M. Cyanido-Bearing Cobalt(II/III) Metalloligands-Synthesis, Crystal Structures and Magnetic Properties. Eur. J. Inorg. Chem. 2014, 4564–4572. [Google Scholar] [CrossRef]
- Llunell, M.; Casanova, D.; Cirera, J.; Bofill, J.M.; Alemany, P.; Alvarez, S.; Pinsky, M.; Avnir, D. SHAPE: Continuous Shape Measures of Polygonal and Polyhedral Molecular Fragments; Version 1.1b; University of Barcelona: Barcelona, Spain, 2005. [Google Scholar]
- Casanova, D.; Llunell, M.; Alemany, P.; Alvarez, S. The Rich Stereochemistry of Eight-Vertex Polyhedra: A Continuous Shape Measures Study. Chem. Eur. J. 2005, 11, 1479–1494. [Google Scholar] [CrossRef] [PubMed]
- Carlin, R.L. Magnetochemistry; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Lloret, F.; Julve, M.; Cano, J.; Ruiz-García, R.; Pardo, E. Magnetic properties of six-coordinated high-spin cobalt(II) complexes: Theoretical background and its application. Inorg. Chim. Acta 2008, 361, 3432–3445. [Google Scholar] [CrossRef]
- Herrera, J.M.; Bleuzen, A.; Dromzée, Y.; Julve, M.; Lloret, F.; Verdaguer, M. Crystal Structures and Magnetic Properties of Two Octacyanotungstate(IV) and (V)-Cobalt(II) Three-Dimensional Bimetallic Frameworks. Inorg. Chem. 2003, 42, 7052–7059. [Google Scholar] [CrossRef] [PubMed]
- Cano, J. VPMAG; University of Valencia: Valencia, Spain, 2003. [Google Scholar]
- Fabelo, O.; Pasán, J.; Lloret, F.; Julve, M.; Ruiz-Pérez, C. 1,2,4,5-Benzenetetracarboxylate- and 2,2′-Bipyrimidine-Containing Cobalt(II) Coordination Polymers: Preparation, Crystal Structure, and Magnetic Properties. Inorg. Chem. 2008, 47, 3568–3576. [Google Scholar] [CrossRef] [PubMed]
- Fabelo, O.; Pasán, J.; Cañadillas-Delgado, L.; Delgado, F.S.; Lloret, F.; Julve, M.; Ruiz-Pérez, C. Cobalt(II) Sheet-Like Systems Based on Diacetic Ligands: From Subtle Structural Variances to Different Magnetic Behaviors. Inorg. Chem. 2009, 48, 6086–6095. [Google Scholar] [CrossRef] [PubMed]
- Sakiyama, H.; Ito, R.; Kumagai, H.; Inoue, K.; Sakamoto, M.; Nishida, Y.; Yamasaki, M. Dinuclear Cobalt(II) Complexes of an Acyclic Phenol-Based Dinucleating Ligand with Four Methoxyethyl Chelating Arms-First Magnetic Analyses in an Axially Distorted Octahedral Field. Eur. J. Inorg. Chem. 2001, 2001, 2027–2032. [Google Scholar] [CrossRef]
- Mabbs, F.E.; Machin, D.J. Magnetism and Transition Metal: Complexes; Chapman and Hall: London, UK, 1973; p. 160. [Google Scholar]
- Kahn, O. Molecular Magnetism; VCH Wiley: New York, NY, USA, 1993. [Google Scholar]
- Weismann, D.; Sun, Y.; Lan, Y.; Wolmershäuser, G.; Powell, A.K.; Sitzmann, H. High-Spin Cyclopentadienyl Complexes: A Single-Molecule Magnet Based on the Aryl-Iron(II) Cyclopentadienyl Type. Chem. Eur. J. 2011, 17, 4700–4704. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Mathonière, C.; Jeon, I.-R.; Rouzières, M.; Ozarowski, A.; Aubrey, M.L.; González, M.I.; Clérac, R.; Long, J.R. Tristability in a Light-Actuated Single-Molecule Magnet. J. Am. Chem. Soc. 2013, 135, 15880–15884. [Google Scholar] [CrossRef]
- Banci, L.; Bencini, A.; Benelli, C.; Gatteschi, D.; Zanchini, C. Spectral-structural correlations in high-spin cobalt(II) complexes. Struct. Bond. 1982, 52, 37–86. [Google Scholar]
- Yuste, C.; Bentama, A.; Stiriba, S.-E.; Armentano, D.; De Munno, G.; Lloret, F.; Julve, M. Ligand effects on the structures and magnetic properties of tricyanomethanide-containing copper(II) complexes. Dalton Trans. 2007, 5190–5200. [Google Scholar] [CrossRef]
- Stoll, S.; Schweiger, A. Easy Spin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Res. 2006, 178, 42–45. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Intediscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Schafer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis set for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Schafer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis set of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Eichkorn, K.; Treutler, O.; Ohm, H.; Haser, M.; Ahlrichs, R. Auxiliary basis sets to approximate Coulomb potentials. Chem. Phys. Lett. 1995, 240, 283–290. [Google Scholar] [CrossRef]
- Eichkorn, K.; Treutler, O.; Ohm, H.; Haser, M.; Ahlrichs, R. Auxiliary basis sets to approximate Coulomb potentials. Chem. Phys. Lett. 1995, 242, 652–660. [Google Scholar] [CrossRef]
- Eichkorn, K.; Weigend, F.; Treutler, O.; Ohm, H.; Ahlrichs, R. Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials. Theor. Chem. Acc. 1997, 97, 119–124. [Google Scholar] [CrossRef]
- Vancoillie, S.; Chalupský, J.; Ryde, U.; Solomon, E.I.; Pierloot, K.; Neese, F.; Rulišek, A. Multireference Ab Initio Calculations of g Tensors for Trinuclear Copper Clusters in Multicopper Oxidases. J. Phys. Chem. B 2010, 114, 7692–7702. [Google Scholar] [CrossRef] [PubMed]
- Kossmann, S.; Neese, F. Efficient Structure Optimization with Secon-Order Many-Body Perturbation Theory: The RIJCOSX-MP2 Method. J. Chem. Theory Comput. 2010, 6, 2325–2338. [Google Scholar] [CrossRef]
- Kossmann, S.; Neese, F. Comparison of two Efficient Approximate Hartree-Fock Approaches. Chem. Phys. Lett. 2009, 481, 240–243. [Google Scholar] [CrossRef]
- CrysAlisPro Software System v40; Rigaku Corporation: Oxford, UK, 2015.
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H.J. OLEX2: A complete structure solution, refinement and analysis program. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Brandenburg, K.; Putz, H. Diamond—Crystal and Molecular Structure Visualization; Crystal Impact: Bonn, Germany.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).