Multinuclear Magnetic Resonance Study of Sodium Salts in Water Solutions
Abstract
1. Introduction
2. Results
3. Discussion
3.1. ABMR Experiments with Sodium Atoms
3.2. NMR Evaluation of μ(23Na)
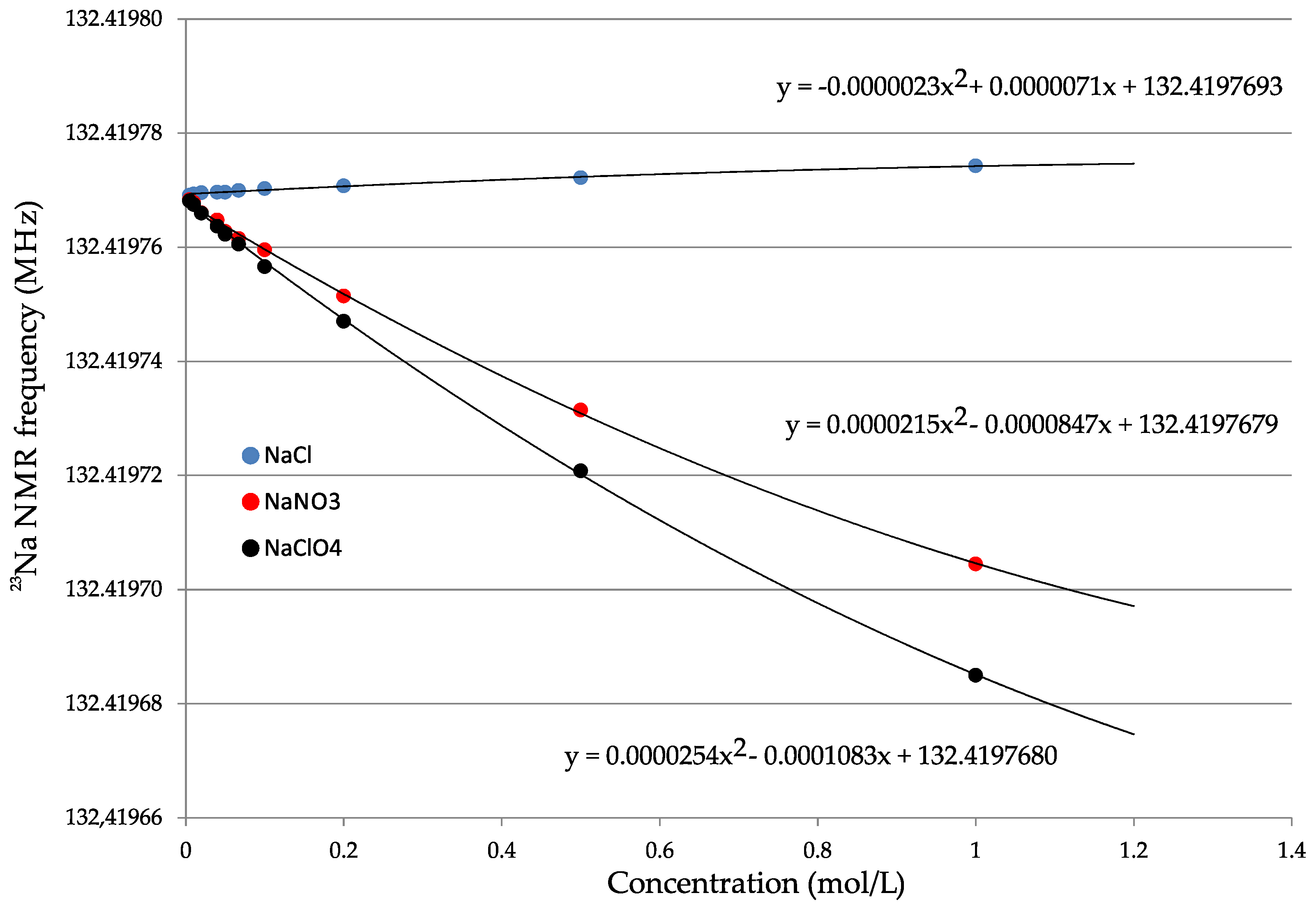
3.3. Nuclear Shielding from Aqueous Solutions
3.4. Theoretical Predictions of Nuclear Moments
4. Materials and Methods
5. Conclusions and Outlook
Funding
Acknowledgments
Conflicts of Interest
References
- Antušek, A.; Jackowski, K.; Jaszuński, M.; Makulski, W.; Wilczek, M. Nuclear magnetic dipole moments from NMR spectra. Chem. Phys. Lett. 2005, 411, 111–116. [Google Scholar] [CrossRef]
- Jaszuński, M.; Antušek, A.; Garbacz, P.; Jackowski, K.; Makulski, W.; Wilczek, M. The determination of accurate nuclear magnetic dipole moments and direct measurement of NMR shielding constants. Prog. Nucl. Magn. Reson. Spectrosc. 2012, 67, 49–63. [Google Scholar] [CrossRef] [PubMed]
- Lutz, O. The gI-factors and the magnetic moments of alkali nuclei and the shielding of Rb+ by water. Phys. Lett. 1967, 25, 440–441. [Google Scholar] [CrossRef]
- Lutz, O. Untersuchungen über die magnetische Kernresonanz von Alkalikernen in wäßriger Lösung. Z. Nat. A 1968, 23, 1202–1209. [Google Scholar] [CrossRef]
- Beckmann, A.; Böklen, K.D.; Elke, D. Precision Measurements of the Nuclear Magnetic Moments of 6Li, 7Li, 23Na, 39K and 41K. Z. Phys. 1974, 270, 173–186. [Google Scholar] [CrossRef]
- Antušek, A.; Kędziera, D.; Kaczmarek-Kędziera, A.; Jaszuński, M. Coupled cluster study of NMR shielding of alkali metal ions in water complexes and magnetic moments of alkali metal nuclei. Chem. Phys. Lett. 2012, 532, 1–8. [Google Scholar] [CrossRef]
- Baum, E.M.; Ernesti, M.C.; Knox, H.D.; Miller, T.R.; Watson, A.M. Nuclides and Isotopes. Chart of the Nuclides, 17th ed.; Bechtel: Reston, VA, USA, 2010; Available online: https://www.nuclidechart.com/xcart/ (accessed on 2 November 2019).
- Bloor, E.G.; Kidd, R.G. Solvation of sodium ions studied by 23Na nuclear magnetic resonance. Can. J. Chem. 1968, 46, 3425–3430. [Google Scholar] [CrossRef]
- Gauß, W.; Günter, S.; Haase, A.R.; Kerber, M.; Kessler, D.; Kronenbitter, J.; Krüger, H.; Lutz, O.; Nolle, A.; Schrade, P.; et al. NMR Spectra of Alkali and Halogen Nuclei in Alkali and Halogen Salts. Z. Nat. A 1978, 33, 934–939. [Google Scholar] [CrossRef]
- Makulski, W. The Radiofrequency NMR Spectra of Lithium Salts in Water: Reevaluation of Nuclear Magnetic Moments for 6Li and 7Li Nuclei. Magnetochemistry 2018, 4, 9. [Google Scholar] [CrossRef]
- Adrian, B.; Makulski, W.; Jackowski, K.; Demissie, T.B.; Ruud, K.; Antušek, A.; Jaszuński, M. NMR absolute shielding scale and nuclear magnetic dipole moment of 207Pb. Phys. Chem. Chem. Phys. 2016, 18, 16483–16490. [Google Scholar] [CrossRef]
- Jaszuński, M.; Repisky, M.; Demissie, T.B.; Komorovsky, S.; Malkin, E.; Ruud, K.; Garbacz, P.; Jackowski, K.; Makulski, W. Spin-rotation and NMR shielding constants in HCl. J. Chem. Phys. 2013, 139, 234302. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, T.; Boero, M.; Terakura, K. Hydration of alkali ions from first principles molecular dynamics revisited. J. Chem. Phys. 2007, 126, 01B611. [Google Scholar] [CrossRef] [PubMed]
- Stone, N.J. Table of Nuclear Magnetic Dipole and Electric Quadrupole Moments; IAEA Nuclear Data Section; Vienna International Centre: Vienna, Austria, 2014; Available online: http://www-nds.iaea.org/publications (accessed on 8 December 2019).
- Stone, N.J. Table of Nuclear Magnetic Dipole and Electric Quadrupole Moments. At. Data Nucl. Data Tables 2005, 90, 75–176. [Google Scholar] [CrossRef]
- Stone, N.J. Nuclear Magnetic Dipole and Electric Quadrupole Moments: Their Measurement and Tabulations as Accessible Data. J. Phys. Chem. Ref. Data 2015, 44, 031215. [Google Scholar] [CrossRef]
- Kush, P.; Millman, S.; Rabi, I.I. The Nuclear Magnetic Moment of N14, Na23, K39 and Cs133. Phys. Rev. 1939, 55, 1176. [Google Scholar] [CrossRef]
- Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA Recommended Values of the Fundamental Physical Constants: 2014. J. Phys. Chem. Ref. Data 2016, 45, 043102. Available online: http://physics.nist.gov/constants (accessed on 8 December 2019). [CrossRef]
- Mason, J. (Ed.) Multinuclear NMR; Plenum Press: New York, NY, USA, 1987; p. 56. ISBN 978-1-4613-1783-8. [Google Scholar] [CrossRef]
- Akitt, J.W. The Alkali and Alkaline Earth Metals: Lithium, Sodium Potassium, Rubidium, Cesium, Beryllium, Magnesium, Calcium, Strontium and Barium, Chapter 7, 189–220. In Multinuclear NMR; Mason, J., Ed.; Plenum Press: New York, NY, USA, 1987; ISBN 978-1-4613-1783-8. [Google Scholar]
- Lincoln, S.F.; Richens, D.T.; Sykes, A.G. Metal Aqua Ions. In Comprehensive Coordination Chemistry II: From Biology to Nanotechnology; McCleverty, J.A., Meyer, T.J., Eds.; Elsevier Ltd.: Amsterdam, The Netherlands, 2003; Volume 1, pp. 515–555. ISBN 978-0-08-043748-4. [Google Scholar]
- Mähler, J.; Persson, I. A Study of the Alkali Metal Ions in Aqueous Solution. Inorg. Chem. 2012, 51, 425–438. [Google Scholar] [CrossRef]
- Frey, U.; Merbach, A.E. Dynamics of Solutions and Fluid Mixtures by NMR; Delpuech, J.J., Ed.; Wiley: Chichester, UK, 1995; ISBN 0-471-95411-X. [Google Scholar]
- Helm, L.; Merbach, A.E. Water exchange on metal ions: experiments and simulations. Coord. Chem. Rev. 1999, 187, 151–181. [Google Scholar] [CrossRef]
- Smirnov, P.; Trostin, V. Structure of the nearest surrounding of the Na+ ion in aqueous solutions of its salts. Russ. J. Gen. Chem. 2007, 77, 844–850. [Google Scholar] [CrossRef]
- Grzybkowski, W. Nature and Properties of Metal Cations in Aqueous Solutions. Pol. J. Environ. Stud. 2006, 15, 655–663. [Google Scholar]
- Templeman, G.J.; Van Geet, A.L. Sodium magnetic resonance of aqueous salt solutions. J. Am. Chem. Soc. 1972, 94, 5578–5582. [Google Scholar] [CrossRef]
- Varma, S.; Rempe, S.B. Coordination numbers of alkali metal ions in aqueous solutions. Biophys. Chem. 2006, 124, 192–199. [Google Scholar] [CrossRef] [PubMed]
- Galib, M.; Baer, M.D.; Skinner, L.B.; Mundy, C.J.; Hutwelker, T.; Schenter, G.K.; Benmore, C.J.; Govind, N.; Fulton, J.L. Revisiting the hydration structure of aqueous Na+. J. Chem. Phys. 2017, 146, 084504. [Google Scholar] [CrossRef] [PubMed]
- Bucher, D.; Guidoni, L.; Carloni, P.; Rothlisberger, U. Coordination Numbers of K+ and Na+ Ions Inside the Selectivity Filter of the KcsA Potassium Chanel: Insights from First Principles Molecular Dynamics. Biophys. J. 2010, 98, L47–L49. [Google Scholar] [CrossRef] [PubMed]
- Rao, J.S.; Dinadayalane, T.C.; Leszczyński, J.; Sastry, G.N. Comprehensive Study on Solvation of Mono- and Divalent Metal Cations: Li+, Na+, K+, Be2+, Mg2+ and Ca2+. J. Phys. Chem. A 2008, 112, 12944–12953. [Google Scholar] [CrossRef] [PubMed]
- Rudziński, A.; Puchalski, M.; Pachucki, K. Relativistic, QED, and nuclear mass effects in the magneticshielding of 3He. J. Chem. Phys. 2009, 130, 244102. [Google Scholar] [CrossRef] [PubMed]
- Jackowski, K.; Jaszuński, M.; Wilczek, M. Alternative Approach to the Standardization of NMR Spectra. Direct Measurement of Nuclear Magnetic Shielding in Molecules. J. Phys. Chem. A 2010, 114, 2471–2475. [Google Scholar] [CrossRef]
- Saxena, A.; Srivastava, P.C. First-principles results for electromagnetic properties of sd shell nuclei. Phys. Rev. C 2017, 96, 024316. [Google Scholar] [CrossRef]
- Puchalski, M.; Komasa, J.; Pachucki, K. Deuteron and triton magnetic moments from NMR spectra of the hydrogen molecule. Phys. Rev. A 2015, 92, 0200501. [Google Scholar] [CrossRef]
- Aucar, G.A. Private Communication. Available online: http://imit.unne.edu.ar (accessed on 6 November 2019).

| Water | Nuclide | ν0 (Radiofrequency) | δ0/ppm | δ1/ppm mL mol−1 | σ/ppm | Reference |
|---|---|---|---|---|---|---|
| Solutions | MHz | δ2/ppm mL mol−2 | ||||
| NaCl | (23Na+)aqua | 132.4197693(5) | −0.045 | 0.0532 | 581.20 | [6] |
| −0.0146 | ||||||
| 35Cl‒ | 49.0491387(2) | 4.632 | 0.3928 | 998.36 | [This work] | |
| −0.0748 | ||||||
| 3He | 381.3564668(30) | −2.748 | −0.0522 | 59.709 | [This work] | |
| NaNO3 | (23Na+)aqua | 132.4197679(6) | −0.055 | −0.6459 | 581.20 | [6] |
| 0.1676 | ||||||
| 15NO3‒ | 50.7450281(5) | −5.589 | 0.132 | −137.31 | [This work] | |
| −0.0715 | ||||||
| 3He | 381.3564680(30) | −2.745 | −0.0161 | 59.706 | ||
| NaClO4 | (23Na+)aqua | 132.419768(7) | −0.055 | −0.8174 | 581.20 | [6] |
| 0.1914 | ||||||
| 35ClO4‒ | 49.0983353(4) | 1007.643 | −0.295 | −4.64 | [This work] | |
| 0.070 | ||||||
| 3He | 381.3564673(35) | −2.747 | −0.0173 | 59.708 | ||
| μ(23Na)/μN | Method/System | Nucleus | σ(23Na)aqua | Reference |
|---|---|---|---|---|
| 2.2175029(111) | NMR-3He/NaCl | 580.12 | [6] Theory | |
| 35Cl− | 580.47 | Experiment | ||
| [This work] | ||||
| 2.2175029(111) | NMR-3He/NaNO3 | 15NO3− | 575.37 | |
| 2.2175029(111) | NMR-3He/NaClO4 | 35ClO4− | 579.49 | |
| 2.2174964(111) | NMR-2H/NaCl | 35Cl− | 577.55 | Experiment |
| [This work] | ||||
| 2.2174964(111) | NMR-2H/NaNO3 | 15NO3− | 572.4 | |
| 2.2174964(111) | NMR-2H/NaClO4 | 35ClO4− | 576.56 | |
| 2.2174997(111) | NMR-average | 35Cl− | 579.00 | [This work] |
| 35ClO4− | 578.02 | |||
| 2.2174982(233) | NMR | 35Cl− | 578.35 | [6] This work |
| 35ClO4− | 577.37 | |||
| 2.2175019(133) | ABMR* | 35Cl− | 580.02 | [5] This work |
| 35ClO4− | 579.03 | |||
| 2.217522(2) | ABMR | 35Cl− | 589.08 | [20] This work |
| 35ClO4− | 588.09 | |||
| 2.2176556(6) | NMR | 35Cl− | 649.29 | [20] This work |
| 35ClO4− | 648.30 |
| Nuclide | Iπ | Abundance % [7] | μ/μN | Reference | gI | γX × 107 | Q/Barn [14] |
|---|---|---|---|---|---|---|---|
| 23Na | 3/2+ | 100 | 2.2174997(111) | [This work] | 1.478333(7) | 7.08035(4) | 0.1045(10) |
| 2.2175019(133) | ABMR* [5] | ||||||
| 2.217522(2) | ABMR [14] | ||||||
| 2.2176556(6) | NMR [14] | ||||||
| 35Cl | 3/2+ | 75.78(4) | 0.821721(5) | [12] | 0.547814(3) | 2.62371(1) | 0.0850(11) |
| 15N | 1/2− | 0.37 | −0.2830571(10) | [1,2] | 0.5661142(2) | 2.7113568(5) | |
| 3He | 1/2− | 0.000134 | 2.127625308(25) | [32] | 4.2552506(1) | 20.3801695(2) | |
| 2H(D) | 1+ | 0.0156 | 0.8574382346(53) | [35] | 0.857438235(5) | 41.0662919(2) | 0.00286(2) |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makulski, W. Multinuclear Magnetic Resonance Study of Sodium Salts in Water Solutions. Magnetochemistry 2019, 5, 68. https://doi.org/10.3390/magnetochemistry5040068
Makulski W. Multinuclear Magnetic Resonance Study of Sodium Salts in Water Solutions. Magnetochemistry. 2019; 5(4):68. https://doi.org/10.3390/magnetochemistry5040068
Chicago/Turabian StyleMakulski, Włodzimierz. 2019. "Multinuclear Magnetic Resonance Study of Sodium Salts in Water Solutions" Magnetochemistry 5, no. 4: 68. https://doi.org/10.3390/magnetochemistry5040068
APA StyleMakulski, W. (2019). Multinuclear Magnetic Resonance Study of Sodium Salts in Water Solutions. Magnetochemistry, 5(4), 68. https://doi.org/10.3390/magnetochemistry5040068




