The Role of Vibrational Anharmonicity in the Computational Study of Thermal Spin Crossover
Abstract
1. Introduction
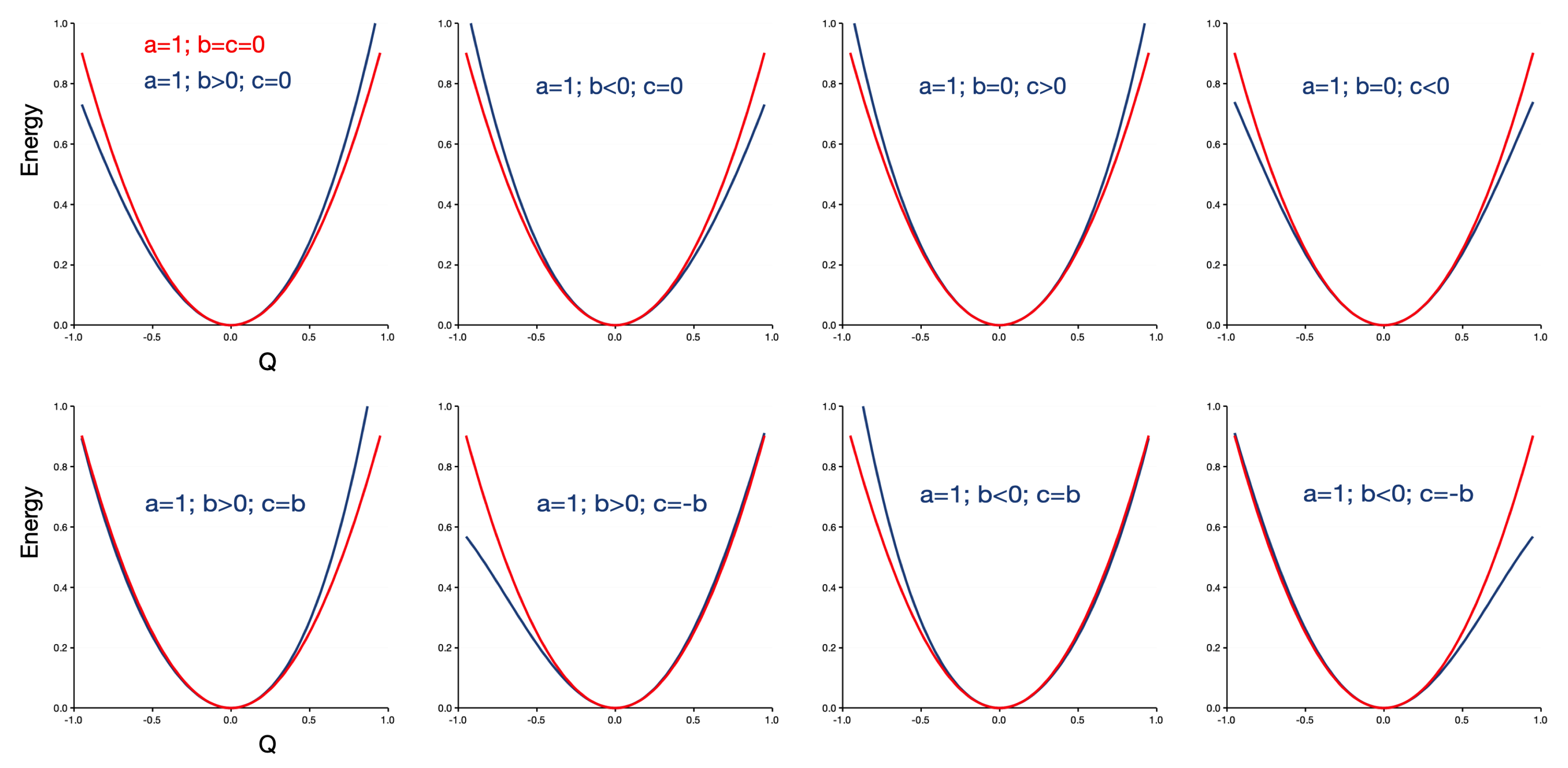
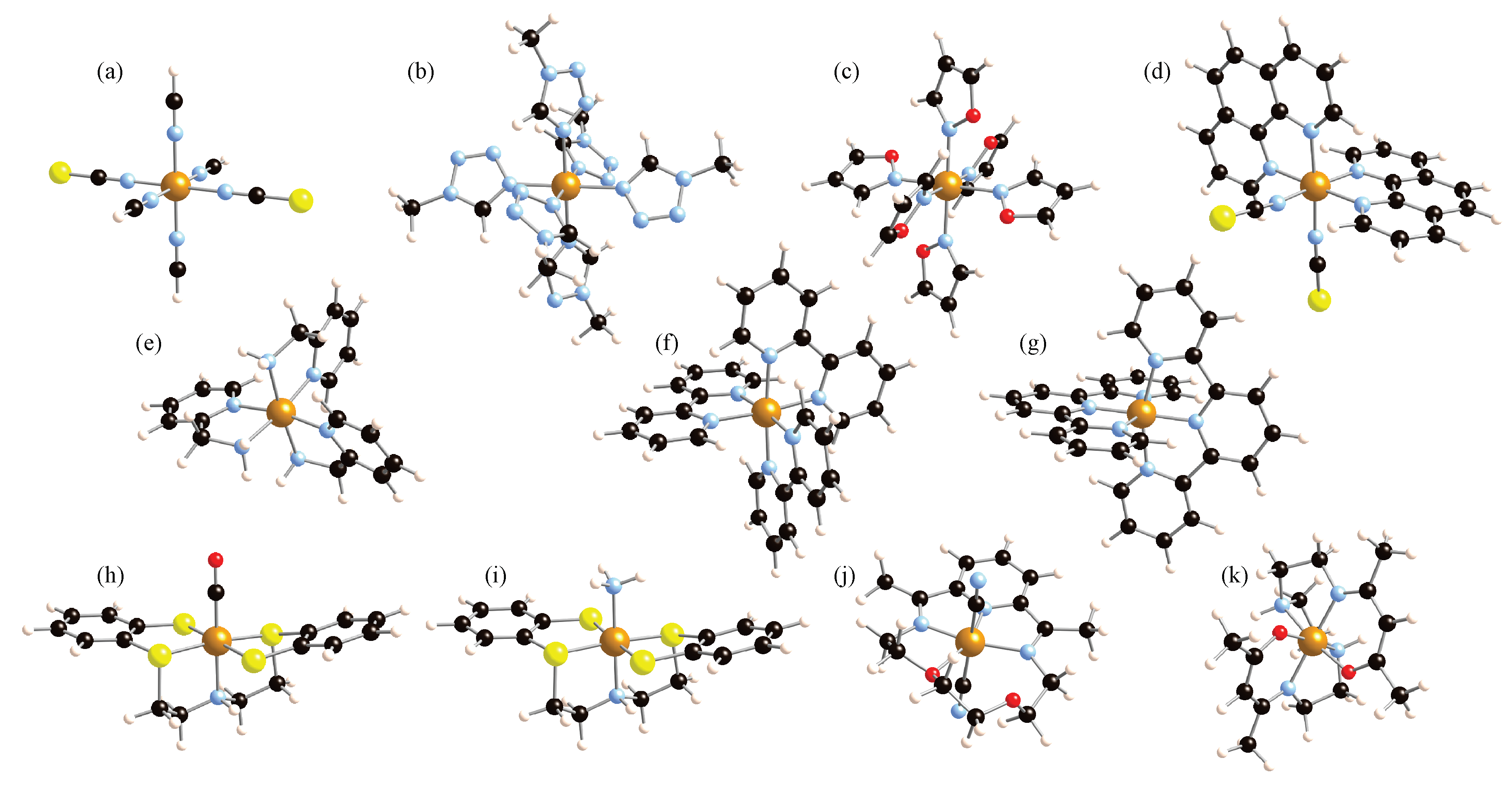
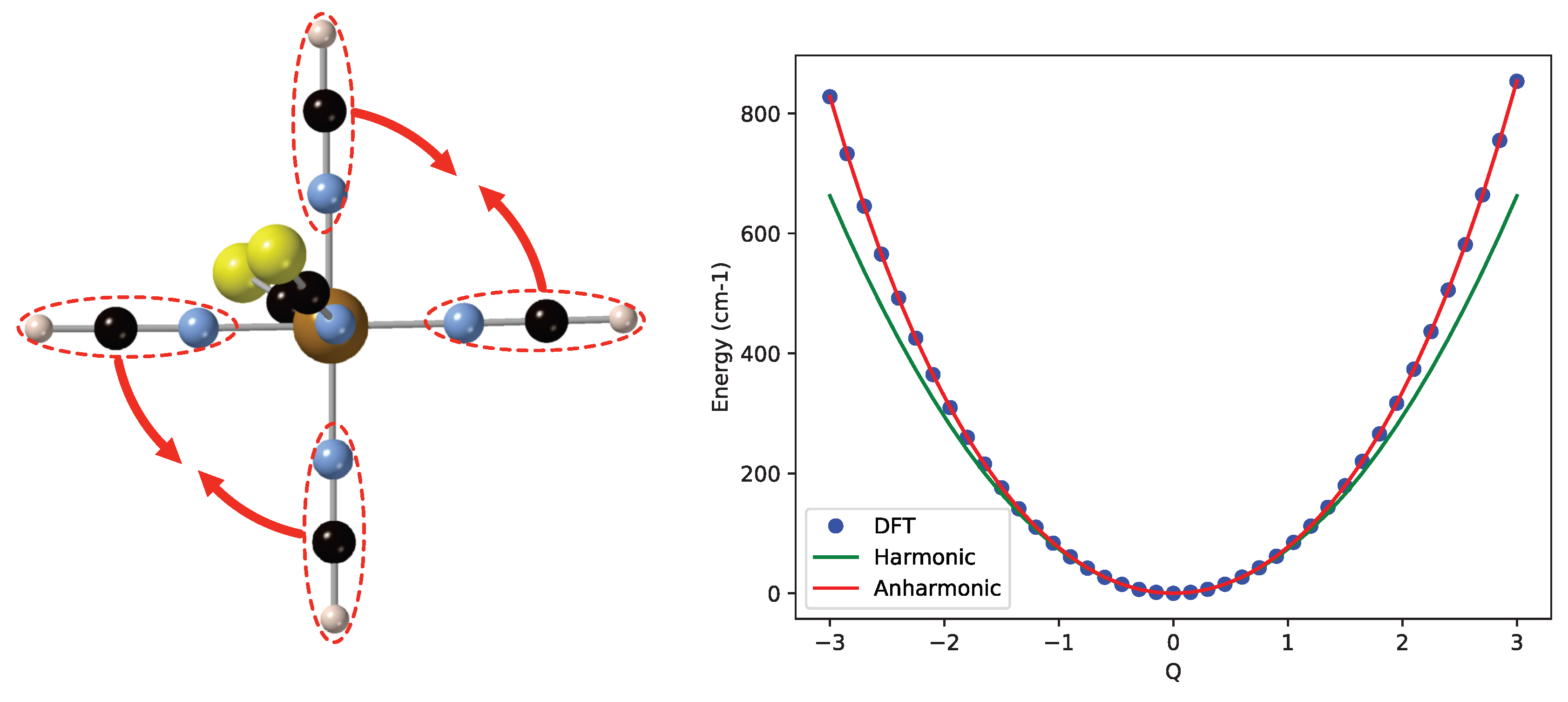
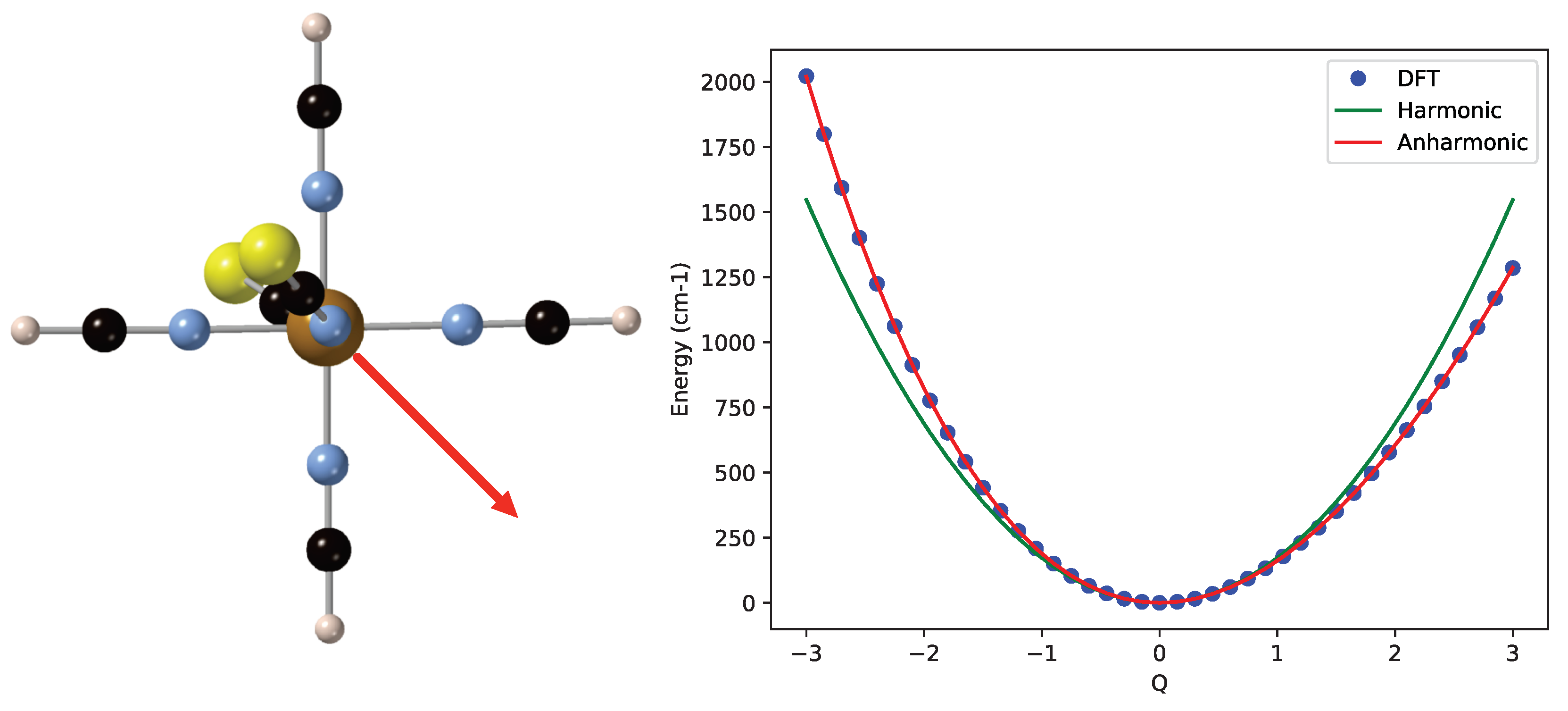
2. Results and Discussion
3. Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cambi, L.; Szego, L. The magnetic susceptibility of complex compounds. Ber. Dtsch. Chem. Ges. B 1931, 64, 2591–2598. [Google Scholar] [CrossRef]
- Cambi, L.; Cagnasso, A. Iron dithiocarbamates and nitroso dithiocarbamates. Atti. Accad. Naz. Lincei CI. Sci. Fis. Mat. Nut. Rend 1931, 13, 809–813. [Google Scholar]
- Hauser, A. Light-Induced spin-crossover and the high-spin → low-spin relaxation. In Spin Crossover in Transition Metal Compounds II; Gütlich, P., Goodwin, H.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 234, pp. 155–198. [Google Scholar]
- McGarvey, J.; Lawthers, I. Photochemically-induced perturbation of the 1A⇌5T equilibrium in FeII complexes by pulsed laser irradiation in the metal-to-ligand charge-transfer absorption band. J. Chem. Soc. Chem. Commun. 1982, 16, 906. [Google Scholar] [CrossRef]
- Decurtins, S.; Gütlich, P.; Köhler, C.P.; Spiering, H.; Hauser, A. Light-Induced excited spin state trapping in a transition metal complex: The hexakis (1-propyltetrazole) iron(II) tetrafluoroborate spin-crossover system. Chem. Phys. Lett. 1984, 105, 1–4. [Google Scholar] [CrossRef]
- Hauser, A. Intersystem crossing in the [Fe(ptz)6](BF4)2 spin crossover system (ptz=1-propyltetrazole). J. Chem. Phys. 1991, 94, 2741–2748. [Google Scholar] [CrossRef]
- Halcrow, M.A. The spin-states and spin-transitions of mononuclear iron(II) complexes of nitrogen-donor ligands. Polyhedron 2007, 26, 3523–3576. [Google Scholar] [CrossRef]
- Dîrtu, M.M.; Rotaru, A.; Gillard, D.; Linares, J.; Codjovi, E.; Tinant, B.; Garcia, Y. Prediction of the Spin Transition Temperature in FeII One-Dimensional Coordination Polymers: An Anion Based Database. Inorg. Chem. 2009, 48, 7838–7852. [Google Scholar] [CrossRef] [PubMed]
- Yamada, M.; Hagiwara, H.; Torigoe, H.; Matsumoto, N.; Kojima, M.; Dahan, F.; Tuchagues, J.P.; Re, N.; Iijima, S. A Variety of Spin-Crossover Behaviors Depending on the Counter Anion: Two-Dimensional Complexes Constructed by NH···Cl− Hydrogen Bonds, [FeIIH3LMe]Cl·X (X = PF6−, AsF6−, SbF6−, CF3SO3−; H3LMe = Tris[2-[(2- methylimidazol-4-yl)methylidene]aminoethyl]amine). Chem. Eur. J. 2006, 12, 4536–4549. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Velamazan, J.A.; Carbonera, C.; Castro, M.; Palacios, E.; Kitazawa, T.; Létard, J.F.; Burriel, R. Two-Step Thermal Spin Transition and LIESST Relaxation of the Polymeric Spin-Crossover Compounds Fe(X-py)2[Ag(CN)2]2 (X=H, 3-methyl, 4-methyl, 3,4-dimethyl, 3-Cl). Chem. Eur. J. 2010, 16, 8785–8796. [Google Scholar] [CrossRef] [PubMed]
- Bousseksou, A.; McGarvey, J.J.; Varret, F.; Real, J.A.; Tuchagues, J.P.; Dennis, A.C.; Boillot, M.L. Raman spectroscopy of the high- and low-spin states of the spin crossover complex Fe(phen)2(NCS)2: An initial approach to estimation of vibrational contributions to the associated entropy change. Chem. Phys. Lett. 2000, 318, 409–416. [Google Scholar] [CrossRef]
- Wolny, J.A.; Paulsen, H.; Trautwein, A.X.; Schünemann, V. Density functional theory calculations and vibrational spectroscopy on iron spin-crossover compounds. Coord. Chem. Rev. 2009, 253, 2423–2431. [Google Scholar] [CrossRef]
- Brehm, G.; Reiher, M.; Schneider, S. Estimation of the Vibrational Contribution to the Entropy Change Associated with the Low- to High-Spin Transition in Fe(phen)2(NCS)2 Complexes: Results Obtained by IR and Raman Spectroscopy and DFT Calculations. J. Phys. Chem. A 2002, 106, 12024–12034. [Google Scholar] [CrossRef]
- Ronayne, K.L.; Paulsen, H.; Höfer, A.; Dennis, A.C.; Wolny, J.A.; Chumakov, A.I.; Schünemann, V.; Winkler, H.; Spiering, H.; Bousseksou, A.; et al. Vibrational spectrum of the spin crossover complex [Fe(phen)2(NCS)2] studied by IR and Raman spectroscopy, nuclear inelastic scattering and DFT calculations. Phys. Chem. Chem. Phys. 2006, 8, 4685–4693. [Google Scholar] [CrossRef] [PubMed]
- Cirera, J.; Paesani, F. Theoretical Prediction of Spin-Crossover Temperatures in Ligand- Driven Light-Induced Spin Change Systems. Inorg. Chem. 2012, 51, 8194–8201. [Google Scholar] [CrossRef] [PubMed]
- Rudavskyi, A.; Sousa, C.; de Graaf, C.; Havenith, R.W.A.; Broer, R. Computational approach to the study of thermal spin crossover phenomena. J. Chem. Phys. 2014, 140, 184318. [Google Scholar] [CrossRef] [PubMed]
- Cirera, J.; Via-Nadal, M.; Ruiz, E. Benchmarking Density Functional Methods for Calculation of State Energies of First Row Spin-Crossover Molecules. Inorg. Chem. 2018, 57, 14097–14105. [Google Scholar] [CrossRef] [PubMed]
- Siig, O.S.; Kepp, K.P. Iron(II) and Iron(III) Spin Crossover: Toward an Optimal Density Functional. J. Phys. Chem. A 2018, 122, 4208–4217. [Google Scholar] [CrossRef]
- Kepp, K.P. Theoretical Study of Spin Crossover in 30 Iron Complexes. Inorg. Chem. 2016, 55, 2717–2727. [Google Scholar] [CrossRef]
- Ye, S.; Neese, F. Accurate Modeling of Spin-State Energetics in Spin-Crossover Systems with Modern Density Functional Theory. Inorg. Chem. 2010, 49, 772–774. [Google Scholar] [CrossRef]
- Swart, M. Spin States of (Bio)inorganic Systems: Successes and Pitfalls. Int. J. Quantum Chem. 2013, 113, 2–7. [Google Scholar] [CrossRef]
- Swart, M. Accurate Spin-State Energies for Iron Complexes. J. Chem. Theory Comput. 2008, 4, 2057–2066. [Google Scholar] [CrossRef] [PubMed]
- Jensen, K.P.; Cirera, J. Accurate Computed Enthalpies of Spin Crossover in Iron and Cobalt Complexes. J. Phys. Chem. A 2009, 113, 10033–10039. [Google Scholar] [CrossRef] [PubMed]
- Kepp, K.P. Consistent descriptions of metal–ligand bonds and spin-crossover in inorganic chemistry. Coord. Chem. Rev. 2013, 257, 196–209. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Pierloot, K.; Vancoillie, S. Relative energy of the high-(5T2g) and low-(1A1g) spin states of [Fe(H2O)6]2+, [Fe(NH3)6]2+, and [Fe(bpy)3]2+: CASPT2 versus density functional theory. J. Chem. Phys. 2006, 125, 124303. [Google Scholar] [CrossRef] [PubMed]
- Pierloot, K.; Vancoillie, S. Relative energy of the high-(5T2g) and low-(1A1g) spin states of the ferrous complexes [Fe(L)(NHS4)]: CASPT2 versus density functional theory. J. Chem. Phys. 2008, 128, 034104. [Google Scholar] [CrossRef] [PubMed]
- Vancoillie, S.; Zhao, H.; Radoń, M.; Pierloot, K. Performance of CASPT2 and DFT for Relative Spin-State Energetics of Heme Models Performance of CASPT2 and DFT for Relative Spin-State Energetics of Heme Models. J. Chem. Theory Comput. 2010, 6, 576–582. [Google Scholar] [CrossRef]
- Ordejón, B.; de Graaf, C.; Sousa, C. Light-Induced Excited-State Spin trapping in Tetrazole-Based Spin Crossover Systems. J. Am. Chem. Soc. 2008, 130, 13961–13968. [Google Scholar] [CrossRef]
- Lawson Daku, L.M.; Aquilante, F.; Robinson, T.W.; Hauser, A. Accurate Spin-State Energetics of Transition Metal Complexes. 1. CCSD(T), CASPT2, and DFT Study of [M(NCH)6]2+ (M = Fe, Co). J. Chem. Theory Comput. 2012, 8, 4216–4231. [Google Scholar] [CrossRef]
- Barone, V.; Biczysko, M.; Bloino, J. Fully anharmonic IR and Raman spectra of medium-size molecular systems: accuracy and interpretation. Phys. Chem. Chem. Phys. 2014, 16, 1759–1787. [Google Scholar] [CrossRef]
- Barone, V.; Biczysko, M.; Borkowska-Panek, M.; Bloino, J. A Multifrequency Virtual Spectrometer for Complex Bio-Organic Systems: Vibronic and Environmental Effects on the UV/Vis Spectrum of Chlorophyll a. ChemPhysChem 2014, 15, 3355–3364. [Google Scholar] [CrossRef] [PubMed]
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 2005, 122, 014108. [Google Scholar] [CrossRef] [PubMed]
- Escalera-Moreno, L.; Baldoví, J.J.; Gaita-Ariño, A.; Coronado, E. Spin states, vibrations and spin relaxation in molecular nanomagnets and spin qubits: A critical perspective. Chem. Sci. 2018, 9, 3265–3275. [Google Scholar] [CrossRef] [PubMed]
- Liddle, S.T.; van Slageren, J. Improving f-element single molecule magnets. Chem. Soc. Rev. 2015, 44, 6655–6669. [Google Scholar] [CrossRef] [PubMed]
- Escalera-Moreno, L.; Suaud, N.; Gaita-Ariño, A.; Coronado, E. Determining Key Local Vibrations in the Relaxation of Molecular Spin Qubits and Single-Molecule Magnets. J. Phys. Chem. Lett. 2017, 8, 1695–1700. [Google Scholar] [CrossRef] [PubMed]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.S.; Yu, K.X.; Reta, D.; Ortu, F.; Winpenny, R.E.P.; Zheng, Y.Z.; Chilton, N. Field- and temperature-dependent quantum tunnelling of the magnetisation in a large barrier single-molecule magnet. Nat. Commun. 2018, 9, 3134. [Google Scholar] [CrossRef]
- Lunghi, A.; Totti, F.; Sessoli, R.; Sanvito, S. The role of anharmonic phonons in under-barrier spin relaxation of single molecule magnets. Nat. Commun. 2017, 8, 14620. [Google Scholar] [CrossRef]
- Yagi, K.; Hirao, K.; Taketsugu, T.; Schmidt, M.W.; Gordon, M.S. Ab initio vibrational state calculations with a quartic force field: Applications to H2CO, C2H4, CH3OH, CH3CCH, and C6H6. J. Chem. Phys. 2004, 121, 1383–1389. [Google Scholar] [CrossRef]
- Bloino, J.; Biczysko, M.; Barone, V. Anharmonic Effects on Vibrational Spectra Intensities: Infrared, Raman, Vibrational Circular Dichroism, and Raman Optical Activity. J. Phys. Chem. A 2015, 119, 11862–11874. [Google Scholar] [CrossRef]
- Barnes, L.; Schindler, B.; Compagnon, I.; Allouche, A.R. Fast and accurate hybrid QM//MM approach for computing anharmonic corrections to vibrational frequencies. J. Mol. Model. 2016, 22, 285. [Google Scholar] [CrossRef] [PubMed]
- Barnes, L.; Schindler, B.; Compagnon, I.; Allouche, A.R. iGVPT2: An interface to computational chemistry packages for anharmonic corrections to vibrational frequencies. arXiv 2017, arXiv:1704.02144v1. [Google Scholar]
- Domingo, A.; Carvajal, M.A.; de Graaf, C. Spin crossover in Fe(II) complexes: An ab initio study of ligand -donation. Int. J. Quantum Chem. 2010, 110, 331–337. [Google Scholar] [CrossRef]
- Sorai, M. Calorimetric Investigations of Phase Transitions Occurring in Molecule-Based Materials in Which Electrons Are Directly Involved. Bull. Chem. Soc. Jpn. 2001, 74, 2223–2253. [Google Scholar] [CrossRef]
- Gallois, B.; Real, J.A.; Hauw, C.; Zarembowitch, J. Structural Changes Associated with the Spin Transition in Fe(phen)2( NCS)2:A Single-Crystal X-ray Investigation. Inorg. Chem. 1990, 29, 1152–1158. [Google Scholar] [CrossRef]
- Reiher, M.; Salomon, O.; Hess, A. Reparameterization of hybrid functionals based on energy differences of states of different multiplicity. Theor. Chem. Acc. 2001, 107, 48–55. [Google Scholar] [CrossRef]
- Reiher, M. Theoretical Study of the Fe(phen)2(NCS)2 spin-crossover coplex with reparametrized Density functionals. Inorg. Chem. 2002, 41, 6928–6935. [Google Scholar] [CrossRef]
- Sellmann, D.; Soglowek, W.; Knoch, F.; Ritter, G.; Dengler, J. Transition-Metal Complexes with Sulfur Ligands. 88.* 1 Dependence of Spin State, Structure, and Reactivity of [FeII(L)(’NHS4’)] Complexes on the Coligand L (L = CO, N2H2, N2H4, NH3, Pyridine, NHCH3NH2, CH3OH, THF, P(OCH2)3, P(OPh)3): Model Complexes for Iron Nitrogenases (’NHS4’2- = Dianion of 2,2’-Bis[(2-mercaptophenyl)thio]diethylamine). Inorg. Chem. 1992, 31, 3711–3717. [Google Scholar]
- Gruden, M.; Stepanović, S.; Swart, M. Spin state relaxation of iron complexes: The case for OPBE and S12g. J. Serb. Chem. Soc. 2015, 80, 1399–1410. [Google Scholar] [CrossRef]
- Guionneau, P.; Le Gac, F.; Kaiba, A.; Sánchez Costa, J.; Chasseau, D.; Létard, J.F. A reversible metal–ligand bond break associated to a spin-crossover. Chem. Commun. 2007, 3723–3725. [Google Scholar] [CrossRef]
- Dose, E.V.; Murphy, K.M.M.; Wilson, L.J. Synthesis and Spin-State Studies in Solution of 7-Substituted Tris(l8-diketonato)iron(III) Complexes and Their Spin-Equilibrium /3-Ketoimine Analogues Derived from Triethy lenetetramine. Inorg. Chem. 1976, 15, 2622–2630. [Google Scholar] [CrossRef]
- Hinek, R.; Gütlich, P.; Hauser, A. Cooperative effects in the [Fe(mtz)6](BF4)2 Spin-Crossover system: Fine tuning the energy gap. Inorg. Chem. 1994, 33, 567–572. [Google Scholar] [CrossRef]
- Kusz, J.; Spiering, H.; Gütlich, P. X-ray structure study of the light-induced metastable states of the spin-crossover compound [Fe(mtz)6](BF4)2. J. Appl. Crystallogr. 2001, 34, 229–238. [Google Scholar] [CrossRef]
- Hibbs, W.; van Koningsbruggen, P.J.; Arif, A.M.; Shum, W.W.; Miller, J.S. One- and Two-Step Spin-Crossover Behavior of [FeII(isoxazole)6]2+ and the Structure and Magnetic Properties of Triangular [FeIII3O(OAc)6(isoxazole)3][ClO4]. Inorg. Chem. 2003, 42, 5645. [Google Scholar] [CrossRef] [PubMed]
- Nakamoto, T.; Tan, Z.C.; Sorai, M. Heat Capacity of the Spin Crossover Complex [Fe(2-pic)3]Cl2·MeOH: A Spin Crossover Phenomenon with Weak Cooperativity in the Solid State. Inorg. Chem. 2001, 40, 3805–3809. [Google Scholar] [CrossRef]
- Köppen, H.; Müller, E.W.; Köhler, C.P.; Spiering, H.; Meissner, E.; Gütlich, P. Unusual spin-transition anomaly in the spin crossover system [Fe(2-pic)3]Cl2·EtOH. Chem. Phys. Lett. 1982, 91, 348–352. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 2018, 8. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A `chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Petrenko, T.; Kossmann, S.; Neese, F. Efficient time-dependent density functional theory approximations for hybrid density functionals: Analytical gradients and parallelization. J. Chem. Phys. 2011, 134, 054116. [Google Scholar] [CrossRef]
- Latouche, C.; Palazzetti, F.; Skouteris, D.; Barone, V. High-Accuracy Vibrational Computations for Transition-Metal Complexes Including Anharmonic Corrections: Ferrocene, Ruthenocene, and Osmocene as Test Cases. J. Chem. Theory Comput. 2014, 10, 4565–4573. [Google Scholar] [CrossRef] [PubMed]
- Aquilante, F.; Autschbach, J.; Carlson, R.K.; Chibotaru, L.; Delcey, M.G.; De Vico, L.; Fernández-Galván, I.; Ferré, N.; Frutos, L.M.; Gagliardi, L.; et al. MOLCAS 8: New Capabilities for Multiconfigurational Quantum Chemical Calculations across the Periodic Table. J. Comput. Chem. 2016, 37, 506–541. [Google Scholar] [CrossRef] [PubMed]
- Vela, S.; Fumanal, M.; Ribas-Ariño, J.; Robert, V. Towards an accurate and computationally-efficient modelling of Fe(II)-based spin crossover materials. Phys. Chem. Chem. Phys. 2015, 17, 16306–16314. [Google Scholar] [CrossRef] [PubMed]
- Fumanal, M.; Jiménez-Grávalos, F.; Ribas-Ariño, J.; Vela, S. Lattice-Solvent Effects in the Spin-Crossover of an Fe(II)-Based Material. The Key Role of Intermolecular Interactions between Solvent Molecules. Inorg. Chem. 2017, 56, 4474–4483. [Google Scholar] [CrossRef] [PubMed]
- Kreutzberg, L.; Hübner, C.G.; Paulsen, H. Cooperativity of Spin Crossover Complexes: Combining Periodic Density Functional Calculations and Monte Carlo Simulations. Materials 2017, 10, 172. [Google Scholar] [CrossRef] [PubMed]
- Bertoni, R.; Collet, E.; Cailleau, H.; Boillot, M.L.; Tissot, A.; Laisney, J.; Enachescu, C.; Lorenc, M. Temperature dependence of the cooperative out-of-equilibrium elastic switching in a spin-crossover material. Phys. Chem. Chem. Phys. 2019, 21, 6606–6612. [Google Scholar] [CrossRef] [PubMed]
| System | LS | HS | HS-LS |
|---|---|---|---|
| [Fe(mtz) | 690 | 645 | −46 |
| [Fe(iso) | −312 | −160 | 152 |
| [Fe(phen)(NCS)] | 298 | 177 | −122 |
| [Fe(pic) | 97 | 142 | 45 |
| [Fe(bpy) | 31 | −143 | −174 |
| [Fe(terpy) | 123 | −69 | −192 |
| [Fe(CO)(NS)] | 1014 | 1166 | 153 |
| [Fe(NH)(NS)] | 213 | 247 | 35 |
| [FeL(CN)]·HO | 667 | −191 | −857 |
| [Fe(acac)trien] | 511 | 446 | −65 |
| ZPE | (298 K) | ||||||
|---|---|---|---|---|---|---|---|
| Harm | Anharm | Harm | Anharm | Harm | Anharm | ||
| [Fe(mtz) | 1051 | −966 | −1012 | 85 | 39 | 88.5 | 83.8 |
| [Fe(iso) | 1062 | −920 | −68 | 142 | 294 | 87.9 | 147.1 |
| [Fe(phen)(NCS)] | 1362 | −754 | −875 | 608 | 487 | 60.8 | 23.1 |
| [Fe(pic) | 1320 | −981 | −937 | 339 | 383 | 68.4 | 66.8 |
| [Fe(bpy) | 5807 | −515 | −689 | 5292 | 5118 | 54.6 | 88.2 |
| [Fe(terpy) | 7919 | −501 | −692 | 7418 | 7227 | 59.5 | 84.2 |
| [Fe(CO)(NS)] | 9154 | −867 | −714 | 8287 | 8440 | 63.3 | 38.9 |
| [Fe(NH)(NS)] | 2595 | −818 | −783 | 1776 | 1811 | 78.0 | 65.0 |
| [FeL(CN)]·HO | 3998 | −847 | −1704 | 3151 | 2293 | 41.4 | 42.2 |
| [Fe(acac)trien] | 3642 | −11 | −877 | 2831 | 2766 | 38.8 | 36.8 |
| Experiment | ||||||||
|---|---|---|---|---|---|---|---|---|
| Harm | Anharm | Harm | Anharm | Harm | Anharm | |||
| [Fe(mtz) | 85 | 39 | 34.8 | 26.5 | 30 | 19 | 120 [53] | 78 [54] |
| [Fe(iso) | 142 | 294 | 38.2 | 70.7 | 44 | 49 | - | 91 [55] |
| [Fe(phen)(NCS)] | 608 | 487 | 54.4 | 22.0 | 134 | 264 | 719 [45] | 176 [46] |
| [Fe(pic) | 339 | 383 | 49.6 | 46.8 | 82 | 98 | 744 [56] | 114–121 [57] |
| [Fe(acac)trien] | 827 | 761 | 37.8 | 35.6 | 262 | 256 | 700–1200 [52] | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Sousa, C.; de Graaf, C. The Role of Vibrational Anharmonicity in the Computational Study of Thermal Spin Crossover. Magnetochemistry 2019, 5, 49. https://doi.org/10.3390/magnetochemistry5030049
Wu J, Sousa C, de Graaf C. The Role of Vibrational Anharmonicity in the Computational Study of Thermal Spin Crossover. Magnetochemistry. 2019; 5(3):49. https://doi.org/10.3390/magnetochemistry5030049
Chicago/Turabian StyleWu, Jianfang, Carmen Sousa, and Coen de Graaf. 2019. "The Role of Vibrational Anharmonicity in the Computational Study of Thermal Spin Crossover" Magnetochemistry 5, no. 3: 49. https://doi.org/10.3390/magnetochemistry5030049
APA StyleWu, J., Sousa, C., & de Graaf, C. (2019). The Role of Vibrational Anharmonicity in the Computational Study of Thermal Spin Crossover. Magnetochemistry, 5(3), 49. https://doi.org/10.3390/magnetochemistry5030049






