Abstract
First-order phase transitions (FOPT) and second-order phase transitions (SOPT) are commonly observed in Cu alloys containing lanthanide elements, due to their electronic configuration, and have an important effect on the optimization of their magnetocaloric effect (MCE). Alloys containing rare earths have the best magnetocaloric response; however, these elements are very expensive, due to their obtaining and processing methods. The present work reports the effect of using 3d transition elements and thermal treatments on the microstructure and MCE of Cu–11Al–9Zn alloys with 6.5 wt % Ni and 2.5 wt % Fe. It was found that thermal treatments of quenching and normalizing, as well as the use of Ni and Fe, have an important influence on both the resulting phases and MCE of the investigated alloy. MCE was calculated indirectly from the change in the magnetic entropy (–ΔSm) under isothermal conditions, using Maxwell´s relation; it was found that samples subjected to normalizing presented a higher magnetocaloric effect than samples with quenching, which was related to the greater disorder in the alloy, due to the coexistence of β1 + β phases.
1. Introduction
The magnetocaloric effect (MCE) in magnetic materials is of great importance for solving fundamental problems of magnetism and solid-state physics, as well as for technological applications [1]. These phenomena have a strong influence on such physical values as entropy, heat capacity, and thermal conductivity, and themselves reflect transformations taking place in the spin structure of a magnetic material [2,3]. MCE displays itself in the emission or absorption of heat by a magnetic material under the action of a magnetic field. Under adiabatic conditions, a magnetic field can cause cooling or heating of the material as a result of variation of its internal energy. The term of MCE can be considered more widely, by its application not only to temperature variation of the material, but also to the variation of the entropy of its magnetic subsystem under the effect of the magnetic field [1,2,3,4].
The entropy of such a system can be considered as the sum of two contributions: the entropy related to magnetic ordering and the entropy related to the temperature of the system. Application of a magnetic field will order the magnetic moments comprising the system, which are disordered by the thermal agitation energy, and consequently, the entropy depending on the magnetic ordering (the magnetic entropy, Sm) will be lowered. If a magnetic field is applied under adiabatic conditions, when any heat exchange with the surroundings is absent, then the entropy related to the temperature should increase in order to maintain constant the total entropy of the system constant. Increasing this entropy implies that the system heats up and increases its temperature [5].
Unlike conventional refrigeration, magnetic refrigeration (MR) does not use gases that can contribute to the global heating and the deterioration of the ozone layer. However, so far only a few prototype refrigeration machines have been presented worldwide, and there are still many scientific and technological challenges to overcome [6,7]. While in conventional refrigeration a fluid undergoes compression/evaporation processes, causing a change in the temperature of the system, MR is based on a magnetization/demagnetization process. Therefore, the efficiency of the equipment used in MR depends strongly on the magnetic behavior of the solid refrigerant [8,9]. MCE can be obtained by promoting first-order transitions (for example, the martensitic transformation) due to a high crystal lattice disorder, which results in an increase of the total system entropy that leads to better cooling capacity [9]. When the material exhibits a ferromagnetic–paramagnetic transition (second-order transition) during service, the refrigeration capacity can be also improved, since the disorder of the system increases in the transition of both, causing an increase of the total system entropy [3,10,11,12]. These types of transitions are commonly observed in alloys containing lanthanide elements (rare earths), due to their electronic configuration [13,14]. Alloys based on these elements have the best magnetocaloric response; however, these materials are very expensive, due to their obtaining and processing methods.
The use of 3d transition elements has also attracted considerable attention, due to their unique physical properties and promising applications, such as magnetic field-induced shape memory effect, magnetic field-induced strain, magnetocaloric effect, and magnetoresistance [15,16,17,18]. The magnetocaloric effect in Ni–Mn and Ni–Mn–Z (Z = Ni, Cu, Co, Fe, Mn, and Cr) Heusler alloys leads to an existing field, which is considerably less expensive and higher effective than conventional rare-earth-based magnetocaloric alloys [15]. It has been found that the magnetic properties and phase stability of these systems are sensitive to small changes in the concentrations of the parent components and the substitution of Ni, Mn, or In by an additional element Z [15,16,17,18]. The phenomena related to the magneto–structural transitions are highly dependent on the weighted average radius of the constituent ions [16]. The enhancement of a magnetic moment and magnetocaloric effect in the Ni–Mn–Sn alloys by 3d transition elements was observed when a part of Ni was substituted by Co. In this case, the martensitic phase transformation from the ferromagnetic parent phase to the antiferromagnetic-like martensite phase was detected [16]. Since martensitic transformation plays an important role in the magnetocaloric effect, thermal treatments become also important to optimize the MCE [18,19].
On the other hand, magnetic Cu-based alloys with 3d transition metals have attracted a special scientific interest. Although their magnetocaloric response is much lower than that observed in rare-earths Cu alloys, they are also considered for the development of new applications in the field of MR [12]. Some elements, such as Zn and Al, have been used to promote a martensitic transformation (first-order transition) in Cu–Zn and Cu–Al alloys, but it has been demonstrated that they are paramagnetic. Since materials for MR materials require magnetic characteristics, ferromagnetic elements, such as Fe, Ni, Mn, and Co, have been used in Cu alloys to promote SOPT, which in addition to FOPT can optimize the MCE [10].
Sarkar fabricated magnetic Cu alloys with additions of Ni [20]. Lee obtained magnetic alloys of Cu with additions of Co [21], and Zhang with additions of Fe [22]. Although the chemical composition plays an important role in the development of Cu magnetic alloys, it must be highlighted that magnetic characteristics may also be achieved if appropriate phase transformations are promoted [12]. Yoo et al. [23,24] and Jeen et al. [25] developed Cu magnetic alloys by additions of Fe or Mn in Cu–17.25Zn–15Al–1Fe (at %) and Cu–17.5Zn–15Al–1.5Mn (at %) alloys, respectively (at % is atomic percent.
The non-magnetic behavior of the Cu–Zn–Al system was modified to be magnetic by the additions of 1.0% Fe and 1.5% Mn (wt %), respectively. In addition, a martensitic phase (FOPT) was observed in that work. The importance of the martensitic transformation on the magnetic properties of Cu–Mn–Al alloys has been also reported [26].
One advantage of the Cu-based alloys containing transition elements is that their magnetic behavior can be modified by changes in chemical composition or microstructure [12,24,26,27], in addition to the lower cost compared to rare earths [13,14,28]. Thermal treatments may also cause microstructural changes in Cu-based alloys, offering the possibility to modify their magnetic behavior. The present work reports the effects of quenching and normalizing on the microstructure, magnetic behavior, and magnetocaloric effect of a Cu–11Al–9Zn alloy with a 6.5 wt % Ni–2.5 wt % Fe alloy (3d transition elements). Ni and Fe were used to promote second-order phase transformations (SOPT).
2. Experimental Procedure
The investigated alloy was obtained by fusion in an induction furnace pillar and casting in metal molds. The raw materials used were Cu (C11000-series), Fe (iron powder), Al (1000-series), Ni, and Zn (electrolytic grade). After the fusion of raw materials, the molten metal was casted in graphite molds to obtain cylindrical bars of 2 cm in diameter and 10 cm in length, which were cut to obtain samples of 1.5 cm in length. Homogenization heat treatment was conducted at 850 °C for 24 h, which was followed by further quenching and normalizing. The cooling medium was a water–ice mixture and still air for quenching and normalizing, respectively. Chemical composition of the studied alloy was determined by optical emission spectrometry (Spectro LabS). The resulting phases were identified by X-ray diffraction (XRD) in a Rigaku DMAX-2200 diffractometer, using Cu Kα (λ = 0.154 nm) radiation. The diffraction patterns were obtained in a 2θ range of 30°–100° with a step of 0.02° s−1. The microstructure of the heat-treated samples was characterized by optical microscopy (OM) and scanning electron microscopy (SEM). Observations were conducted in an Olympus GX51 optical microscope and a Philips XL30 scanning electron microscope, respectively. Intermetallic compounds were analyzed by SEM–EDXS (energy dispersive spectrometry). Metallographic preparation and etching with FeCl3 + HCl were performed according to specifications of ASTM (American Society for Testing and Materials) E407 [29]. The magnetic properties were determined in a vibrating sample magnetometer (VSM) (Versalab Quantum Design), using samples with dimensions of 2.0 mm long × 2.0 mm wide × 1.0 mm thick. The thermal demagnetization curves were obtained at a constant magnetic field of 100 oersted (Oe) from 50 K to 380 K. The Curie temperature was determined from the first derivative of these demagnetization curves. Isothermal curves were determined for a variable magnetic field ranging from 0 to 3 Tesla (T). The temperature range for these experiments was 135 to 195 K and 75 to 135 K for samples with quenching and normalizing, respectively. Finally, the MCE was calculated indirectly from the magnetic entropy (−ΔSm) under isothermal conditions, using Maxwell´s relation.
3. Results and Discussion
Table 1 shows the chemical composition of the investigated alloy; Zn and Al were added to promote a martensitic transformation (first-order transition), as reported for Cu–Zn, Cu–Al and Cu–Zn–Al and Cu–Al–Zn [30,31]. Ni and Fe were added to promote ferromagnetic behavior (second-order phase transitions) in the experimental alloy.

Table 1.
Chemical composition of the experimental alloy (wt %).
Figure 1 shows the XRD patterns corresponding to the heat-treated samples. As can be seen, β1 (CuAl) is the main phase present in the microstructure of quenched samples (Figure 1a); while the phases coexisting in normalized samples are β (CuZn) + β1 (CuAl) (Figure 1b). These results suggest a possible segregation of Al and Zn during cooling at a slower rate, which promote the presence of Al-rich and Zn-rich regions favoring the formation of β1 (CuAl) and β (CuZn). Vilarinho [32] reported that the high-temperature phase, β, is retained during quenching in a Cu–Zn system with around 3 wt % Al. This result is similar to the one reported by Moroni [33] in a Cu–Zn–Al–Ni system with about 4 wt % Al. Al is intentionally added to Cu–Zn alloys to promote the displacement of the martensite start temperature above room temperature.
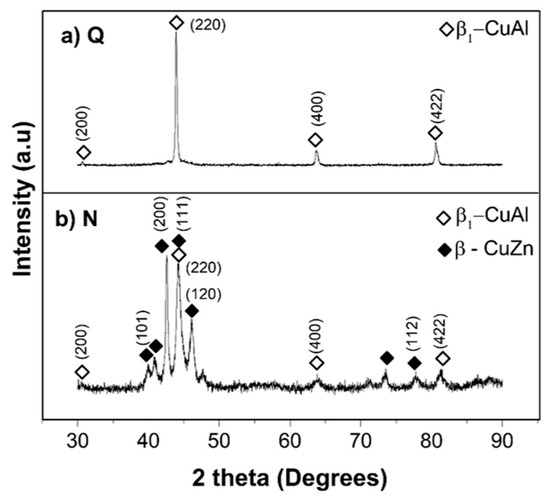
Figure 1.
X-ray diffraction (XRD) patterns corresponding to samples subjected to (a) quenching and (b) normalizing.
Figure 2 shows the microstructure of heat-treated samples. In general, the microstructure obtained after quenching is characterized by the presence of β phase, with polygonal morphology and small particles uniformly distributed in the matrix (Figure 2a,b). This morphology is characteristic of the high-temperature phase (β) commonly observed in Cu-based alloys [34]. As mentioned above, Al is added intentionally to the Cu–Zn system to promote the martensite transformation. Therefore, the result obtained suggests that even with 11.5 wt % Al, the martensite start temperature was not increased above room temperature, leading to the retention of the high-temperature phase as a result. This implies the absence of martensite in samples subjected to fast cooling (quenching), and is consistent with the result obtained by X-ray diffraction (Figure 1).
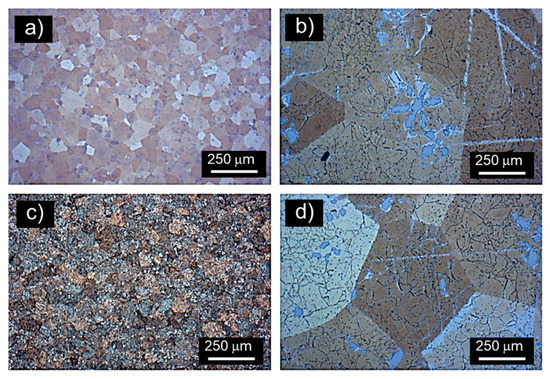
Figure 2.
Microstructure of the samples thermally treated by (a,b) quenching and (c,d) normalizing.
Samples subjected to normalizing exhibit a similar microstructure (Figure 2c,d), meaning that the size and morphology of grains is very similar to the ones obtained by quenching.
As can be seen in Figure 2b,d, the intermetallic compounds exhibit a rosette-like morphology independently on the thermal treatment, which suggests that they form during solidification, as reported by Pisarek [35].
Figure 3 illustrates the elemental mapping corresponding to intermetallic compounds observed in samples subjected to quenching. As can be observed, the intermetallic compounds are constituted mainly by Fe, Al, and Ni. In addition, Table 2 shows the results of local analysis obtained in intermetallic compounds as a function of thermal treatment. Al, Ni, and Fe contents in the intermetallic compounds are very similar, independent of the heat treatment.

Figure 3.
Elemental mapping obtained by scanning electron microscopy (SEM) with energy-dispersive X-ray spectrometry (EDXS) in quenched samples: (a) SEM image, (b) Al, (c) Fe, (d) Ni, (e) Cu, and (f) Zn.

Table 2.
Chemical composition of intermetallic compounds as a function of heat treatment.
Figure 4 shows the thermal demagnetization curves of the alloy investigated as a function of the thermal treatment. In general, samples demagnetize as the temperature increases. Quenched samples suffer demagnetization from 0.40 emu g−1 to 0.28 emu g−1 when the temperature increases from 50 K to 150 K. Magnetization decreases up to 0.08 emu g−1 when the temperature increases to 200 K. The lowest magnetization values are observed at temperatures above 250 K (Figure 4a). This behavior is associated with higher atom vibrations with the increase in temperature, which causes the unalignment of magnetic spins, which finally reduces the material magnetization. Samples subjected to normalizing exhibit a similar behavior, although in this case, magnetization decreases from 0.42 emu g−1 to 0.32 emu g−1 when the temperature increases from 50 K to 105 K (Figure 4b). Increments in temperature up to 150 K cause a decrease in magnetization up to 0.7 emu g−1. Finally, the lowest magnetization values are obtained above 175 K. The Curie temperature (Tcurie) of the investigated alloys, which represents the transition from ferromagnetic to paramagnetic, was obtained from the first derivative of the thermal demagnetization curves. The Tcurie of the samples subjected to quenching and normalizing was 170 K and 125 K, respectively.
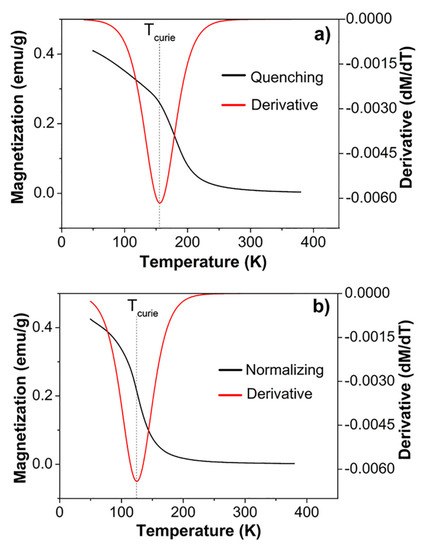
Figure 4.
Curie temperature (Tcurie) as a function of thermal treatment: (a) quenching and (b) normalizing.
The MCE is represented by the magnetic entropy change (∆Sm), which results from coupling between material magnetic moments and the magnetic field.
The relation between magnetic entropy (), magnetic field (), magnetization of material (M) and temperature (T), to the MCE, is given by the Maxwell’s relationship, as follows [3,36]:
where is used to distinguish partial derivatives from ordinary derivatives. A partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant. The following Equation is obtained by integrating Equation (1) for an isothermal (and isobaric) process:
This Equation indicates that the magnetic entropy change is proportional to both the derivative of magnetization with respect to temperature at constant field and to the field variation.
Since magnetization was obtained at discrete magnetic fields and temperature intervals, then Equation (3) can be expressed numerically as follows [36]:
where Mi and Mi+1 are the magnetization values measured at temperatures Ti and Ti+1, respectively, and at a magnetic field H. Ti corresponds to an initial temperature, while Ti+1 corresponds to a higher temperature close to Ti. It is important to mention that calculations are progressive, and thus Ti+1 becomes Ti in the next calculation, which also applies to Mi and Mi+1. Equation (3) represents the area comprised between two magnetic isothermals (change in free energy) divided by the change in temperature, according to the following equation [36]:
where ΔSm is the change in the magnetic entropy, T is temperature, H is the magnetic field, M is magnetization, Ti is temperature of the initial magnetic isothermal, and Tf = Ti+1.
Figure 5 shows the isothermal magnetization curves corresponding to samples subjected to quenching and normalizing. In general, magnetization increases with increments in intensity of the applied magnetic field. The maximum magnetization is reached at lower temperatures; however, it decreases with increasing temperature. The maximum magnetization of samples subjected to quenching for the lowest (135 K) and the highest (195 K) temperatures is 2.11 emu g−1 and 1.70 emu g−1, respectively. Samples subjected to normalizing exhibit a similar behavior, although in this case the maximum magnetization achieved at 75 K (minimum temperature) and 135 K (maximum temperature) was 2.62 emu g−1 and 2.06 emu g−1, respectively.
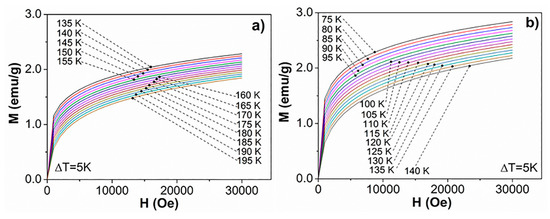
Figure 5.
Isothermal magnetization curves of samples subjected to (a) quenching and (b) normalizing. The magnetic field varied from 0 to 3 Tesla, and ∆T = 5 K.
Figure 6 shows the magnetic entropy as a function of the applied magnetic field. As can be observed, entropy is higher for a higher magnetic field. The maximum values obtained in quenched and normalized samples for a magnetic field of 3 Tesla (3 T) were 0.0020 J Kg−1 K−1 and 0.0027 J Kg−1 K−1, respectively, occurring at their respective Curie temperature (Tcurie). The highest magnetic entropy obtained in normalized samples is associated with the greatest disorder in the system, due to the simultaneous presence of β1 and β (see Figure 1).
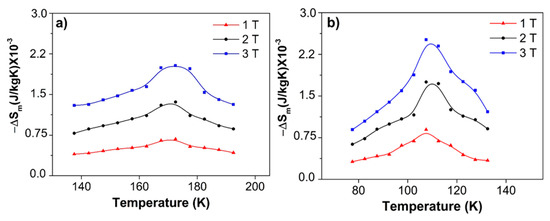
Figure 6.
−∆Sm as a function of the temperature and magnetic field in samples subjected to (a) quenching and (b) normalizing.
Belyea [37] reported the magnetocaloric effect in NiFeCoCrPd in the cold-rolled and annealed samples as a function of Pd concentrations (0.12, 0.74, 1.48, 2.91, 5.88, and 11.11 at %). The highest peak entropy values in cold-rolled samples were about 0.9 and 0.86 J Kg−1 K−1 for Pd concentrations of 5.88 and 11.11 at %, respectively. These values were higher than the one obtained in the sample without Pd (0.74 J Kg−1K−1). In the case of annealed samples, peak entropy values of about 0.74 were obtained independent of the Pd concentration [37]. Results obtained by Belyea showed that cold rolling causes an increase of lattice defects, resulting in a higher magnetic entropy. After annealing, the amount of lattice defects decreases, reducing the total magnetic entropy in the alloy to about 0.8 J Kg−1 K−1 [37]. Tcurie did not exhibit a significant change with the processing condition; however, it exhibited a strong dependence with Pd concentration. The Tcurie in samples without Pd was about 100 K, but it increased to about 225 K and 300 K for Pd concentrations of 5.88 and 11.11 at %, respectively. These results show that the magnetic behavior of NiFeCoCrPd alloys is sensitive to small changes in chemical composition [37].
Some authors have reported magnetic alloys of Cu for applications in magnetic refrigeration [38,39]. Akhter et al. [39] reported values of magnetic entropy of 1.25 J Kg−1 K−1 for the Cu0.3Zn0.7Fe2O4 alloy, with a magnetic field intensity of 3 Tesla at 370 K. The magnetocaloric effect of these alloys was correlated with the sensitivity to chemical composition and the existence of a SOPT.
The magnetic entropy of the analyzed alloys in the present work is significantly lower than that reported in the work described above. Therefore, the obtained results suggest that the investigated alloy could be used in MR applications only under magnetic fields higher than 3 Tesla and at lower temperatures. The MCE in samples with normalizing is higher than that in quenched samples for the same magnetic field intensity. Such a difference can be attributed to lattice disorder, due to the presence of β1 and β phases.
Figure 7 shows the magnetic entropy as a function of heat treatment for a magnetic field of 3 Tesla (3 T). It is clear that in both cases, the highest entropy is obtained near Tcurie. Samples subjected to normalizing exhibit the maximum entropy value at a lower temperature when compared with the quenched samples. Considering that intermetallic compounds in both conditions have similar morphology and chemical compositions, it can be suggested that such a difference relates to the presence of β1 and β phases, as mentioned above.
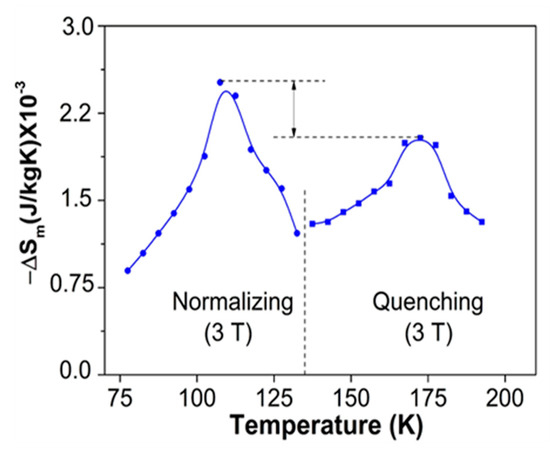
Figure 7.
−ΔSm obtained at 3 Tesla as a function of temperature in samples subjected to quenching and normalizing.
It has been reported that β phase in Cu–Zn–Al alloys is disordered at high temperatures and has a body centered cubic (bcc) lattice. During cooling processes, and depending on the alloy composition, the parent β phase can order into two different structures: B2 and L21 [31]. The presence of this ordered phase in the present work can explain the low values of entropy observed in Figure 6. B2 or L21 structures can transform to martensite phases by stress or thermally [31], which can improve the MCE of Cu-based alloys [26]. Therefore, the results of the present investigation open the possibility to improve the MCE by further transformation of the parent β phase to martensite.
4. Conclusions
The following conclusions can be drawn from the results of the present investigation:
- The high content of Zn in the investigated alloy promotes the retention of the high-temperature β phase. Apparently, the Al content in the studied alloy is not enough to displace the martensite start temperature above room temperature, precluding the transformation of the martensitic phase (FOPT).
- The use of Ni and Fe in a Cu–11Al–9Zn alloy promotes ferromagnetic–paramagnetic behavior (SOPT), and to a certain extent, MCE in the investigated alloy.
- Samples subjected to normalizing present higher magnetic entropy than those with quenching. This behavior relates with the coexistence of the β1 and β phases, which result in greater system disorder.
- The investigated alloy could be used in the MR area only under the application of magnetic fields higher than 3 Tesla and low temperatures, i.e 125 K for samples with normalizing and 170 K for samples with quenching.
Author Contributions
E.J.G.C. is the responsible of the project administration and prepared the original draft; R.E.B.C. conducted the experimental work and contributed with the formal analysis; A.C.B., A.S.R. and A.A.T.C. assisted with formal analysis and reviewed the manuscript; B.F.A., J.T.E.G. and S.A.P.S. helped with formal analysis and editing.
Funding
This research received no external funding.
Acknowledgments
E. J. Gutiérrez Castañeda thanks CONACYT (National Council of Science and Technology) for the Cátedra assigned at The Institute of Metallurgy of the Autonomous University of San Luis Potosi (IM-UASLP). The technical assistance from Dra. Nubia Arteaga, Francisco Botello, Rogelio Deaquino, L. Q. Claudia Hernández, and M. M. I. M. Rosa L. Tovar is also recognized. The facilities to carry out the experimental work at the IM-UASLP, Autonomous University of Ciudad Juarez (UACJ), and Center for Research and Advances Studies (CINVESTAV) are in the same manner appreciated and recognized. B. Fernández Arguijo and A. Contreras Briseño extend a special acknowledgment to CONACYT for the postdoctoral fellowship at the IM-UASLP.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tishin, A.M.; Spichkin, Y.I. The Magnetocaloric Effect and Its Applications; CRS Press: Boca Raton, FL, USA; Taylor and Francis Group: Didcot, UK, 2003; ISBN 978-1-4200-3337-3. [Google Scholar]
- Kitanovski, A.; Tusek, J.; Tomc, U.; Plaznik, U.; Ozbolt, M.; Poredos, A. Magnetocaloric Energy Conversion: From Theory to Applications; Springer International Publishing: Basel, Switzerland, 2015; ISBN 978-3-319-08741-2. [Google Scholar]
- Olivera, N.A.; Ranke, P.J. Theoretical aspects of the magnetocaloric effect. Phys. Rep. 2010, 489, 89–159. [Google Scholar] [CrossRef]
- Mozharivskyj, Y. Magnetocaloric Effect and Magnetocaloric Materials. In Reference Module in Chemistry, Molecular Sciences and Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 978-0-12-409547-2. [Google Scholar]
- Oliveira, N.A. Magnetocaloric effect in transition metals based compounds: A theoretical approach: A theoretical approach. Eur. Phys. J. B Condens. Matter Complex Syst. 2004, 40, 259–264. [Google Scholar] [CrossRef]
- Franco, V.; Blázquez, J.S.; Opus, J.J.; Law, J.Y.; Moreno, L.M.; Conde, A. Magnetocaloric effect: From materials research to refrigeration devices. Prog. Mater. Sci. 2018, 93, 112–232. [Google Scholar] [CrossRef]
- Romero, J.; Ferreiro, R.; De Miguel, A.; Romero, M. Magnetocaloric effect: A review of the thermodynamic cycles in magnetic refrigeration. Renew. Sustain. Energy Rev. 2013, 17, 74–82. [Google Scholar] [CrossRef]
- Kuhn, L.T.; Pryds, N.; Bahl, C.R.H.; Smith, A. Magnetic refrigeration at room temperature—From magnetocaloric materials to a prototype. J. Phys. Conf. Ser. 2011, 303, 012082. [Google Scholar] [CrossRef]
- Kanluang, T.; Hanlumyuang, Y.; Techapiesancharoenkij, R. Design and development of magnetic refrigeration prototype for the performance analysis of magnetocaloric materials. J. Phys. Conf. Ser. 2018, 1144, 012065. [Google Scholar] [CrossRef]
- Stefanita, C.G. Magnetism Basics and Applications; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 978-3-642-22976-3. [Google Scholar]
- Dincer, I.; Yuzuak, E.; Elerman, Y. The effect of the substitution of Cu for Ni on magnetoresistance and magnetocaloric properties of Ni50Mn34In16. J. Alloys Compd. 2011, 509, 794–799. [Google Scholar] [CrossRef]
- Graf, T.; Felser, C.; Parkin, S.S.P. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
- Yuan, Y.; Wu, Y.; Tong, X.; Zhang, H.; Wang, H.; Liu, X.J.; Ma, L.; Suo, H.L.; Lu, Z.P. Rare earth high-entropy alloys with giant magnetocaloric effect. Acta Mater. 2017, 125, 481–489. [Google Scholar] [CrossRef]
- Hazarika, S.; Suchismita, P.; Mohanta, D.; Nirmala, R. Magnetocaloric effect of Gd2O3 with 5% Eu-substitution. Appl. Surf. Sci. 2019, 491, 779–783. [Google Scholar] [CrossRef]
- Wang, X.; Xiang, J.; Wang, F.; Jiang, C.; Xu, H. Effect of 3d transition elements substitution for Ni in Ni2Mn1+xSn1−x on the phase stability and magnetic properties: A first principle investigation. J. Magn. Magn. Mater. 2014, 368, 286–294. [Google Scholar] [CrossRef]
- Dubenko, I.; Quetz, A.; Pandey, S.; Aryal, A.; Eubank, M.; Rodionov, I.; Prudnikov, V.; Granovsky, A.; Lahderanta, E.; Samanta, T.; et al. Multifunctional properties related to magnetostructural transitions in ternary and quaternary Heusler alloys. J. Magn. Magn. Mater. 2015, 383, 186–189. [Google Scholar] [CrossRef]
- Pandey, S.; Quetz, A.; Aryal, A.; Dubenko, I.; Blionov, M.; Rodionov, I.; Prudinkov, V.; Mazumdar, D.; Granovsky, A.; Stadler, S.; et al. Giant field-induced adiabatic temperature changes in In-based off-stoichiometric Heusler alloys. J. Appl. Phys. 2017, 121, 133901. [Google Scholar] [CrossRef]
- Pandey, S.; Quetz, A.; Ibarra, G.; Sanchez, V.; Aryal, A.; Dubenko, I.; Mazumdar, D.; Sanchez, J.; Stadler, S.; Ali, N. Effects of annealing on the magnetic properties and magnetocaloric effects of B doped Ni-Mn-In melt-spun ribbons. J. Alloys Compd. 2018, 731, 678–684. [Google Scholar] [CrossRef]
- Jiang, Z.; Wu, Y.; Wang, J.; Jiang, C. Influence of cooling rate on magneto-structural transition and magnetocalorific effect of Ni30Cu8Co12Mn37Ga13 alloy. J. Iron Steel Res. Int. 2017, 24, 711–717. [Google Scholar] [CrossRef]
- Sarkar, S.K.; Babu, P.D.; Biswas, A.; Siruguri, V.; Krishnan, M. Giant magnetocaloric effect from reverse martensitic transformation in Ni–Mn–Ga–Cu ferromagnetic shape memory alloys. J. Alloys Compd. 2016, 670, 281–288. [Google Scholar] [CrossRef]
- Lee, D.H.; Moriki, T.; Takeda, M.; Kang, S.; Bae, D.S.; Mizuguchi, M.; Takanashi, K. Relationship between the microstructure and the magnetic properties of nano-scale magnetic particles formed in a Cu-10 at% Ni-5 at% Co alloy. J. Korean Phys. Soc. 2013, 63, 555–558. [Google Scholar] [CrossRef]
- Zhang, M.; Cui, Y.; Liu, Z.; Liu, G.; Chen, J.; Wu, G.; Sui, Y.; Liu, Y.; Qian, Z.; Brück, E.; et al. A new Heusler compound Cu2FeAl: Electronic structure, magnetism and transport properties. Phys. Status Solidi 2004, 201, 1570–1577. [Google Scholar] [CrossRef]
- Yoo, P.K.; Jeen, G.S.; Park, H.Y.; Son, M.H.; Han, S.K. Martensitic and spin glass transitions of a Cu-Zn-Al-Fe shape-memory alloy single crystal. Synth. Met. 1995, 71, 2271–2272. [Google Scholar] [CrossRef]
- Yoo, P.K.; Jeen, G.S.; Park, H.Y. Spin glass behaviour of a quarternary Cu-Zn-Al-Fe shape-memory single crystal. J. Mater. Sci. Lett. 1994, 13, 23–24. [Google Scholar] [CrossRef]
- Jeen, G.S.; Yoo, P.K.; Park, H.Y.; Kim, H.K.; Park, S.T.; Lee, H.C.; Park, J.B. Spin glass behavior and martensitic transformation of Cu-Zn-Al-Mn shape memory alloys. J. Korean Phys. Soc. 1997, 31, 173–176. [Google Scholar]
- Prado, M.O.; Lovey, F.C.; Civale, L. Magnetic properties of Cu-Mn-Al alloys with shape memory effect. Acta Mater. 1998, 6, 137–147. [Google Scholar] [CrossRef]
- Lanzini, F.; Romero, R.; Rubiolo, G. Relative stability of ordered phases in bcc Cu–Al–Zn. Calphad 2011, 35, 396–402. [Google Scholar] [CrossRef]
- Gschneidner, K.A.; Pecharsky, V.K. Rare Earths and Magnetic Refrigeration. J. Rare Earths. 2006, 24, 641–647. [Google Scholar] [CrossRef]
- Standard Practice for Microetching Metals and Alloys, ASTME407-07e1. 2015. Available online: https://edisciplinas.usp.br/pluginfile.php/4313805/mod_resource/content/1/NORMA_ASTM_ATAQUE_E407-99.28400.pdf (accessed on 24 August 2019).
- Ahlers, M. Martensite and equilibrium phases in Cu-Zn and Cu-Zn-Al alloys. Prog. Mater. Sci. 1986, 30, 135–186. [Google Scholar] [CrossRef]
- Stosic, Z.; Manasijevic, D.; Valanovic, L.; Tamara, H.; Stamenkovic, U.; Premovic, M.; Minic, D.; Gorgievski, M.; Todorovic, R. Effects of composition and thermal treatment of Cu-Al-Zn alloys with low content of Al on their shape-memory properties. Mater. Res. 2017, 20, 1425–1431. [Google Scholar] [CrossRef]
- Vilarinho, C.; Soares, D.; Castro, F. Phase equilibria of the Al-Cu-Zn system for compositions close to brass alloys. J. Phase Equilibria 2003, 24, 236–239. [Google Scholar] [CrossRef][Green Version]
- Moroni, M.O.; Saldivia, R.; Sarrazin, M.; Sepúlveda, A. Damping characteristics of a CuZnAlNi shape memory alloy. Mater. Sci. Eng. A 2002, 335, 313–319. [Google Scholar] [CrossRef]
- Suarez, L.; Rodriguez, P.; Cabrera, J.M.; Martinez, A.; Majuelos, D.; Coma, A. Hot working analysis of a CuZn40Pb2 brass on the monophasic (beta) and intercritical (alpha plus beta) regions. Mater. Sci. Eng. A 2015, 627, 42–50. [Google Scholar] [CrossRef]
- Pisarek, B.P. Model of Cu-Al-Fe-Ni bronze crystallization. Arch. Foundry Eng. 2013, 13, 72–79. [Google Scholar] [CrossRef]
- Amaral, J.S.; Amaral, V.S. On estimating the magnetocaloric effect from magnetization measurements. J. Magn. Magn. Mater. 2010, 322, 1552–1557. [Google Scholar] [CrossRef]
- Belyea, D.; Lucas, M.; Michel, E.; Horwath, J.; Casey, C. Tunable magnetocaloric effect in transition metal alloys. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Spaldin, N.A. Magnetic Materials: Fundamentals and Applications, 2nd ed.; Cambridge University Press: New York, NY, USA, 2010; ISBN 978-052-188-669-7. [Google Scholar]
- Akhter, S.; Paul, D.P.; Hoque, S.M.; Hakim, M.A.; Hudl, M.; Mathieu, R.; Nordblad, P. Magnetic and magnetocaloric properties of Cu1−xZnxFe2O4 (x = 0.6, 0.7, 0.8) ferrites. J. Magn. Magn. Mater. 2014, 367, 75–80. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).