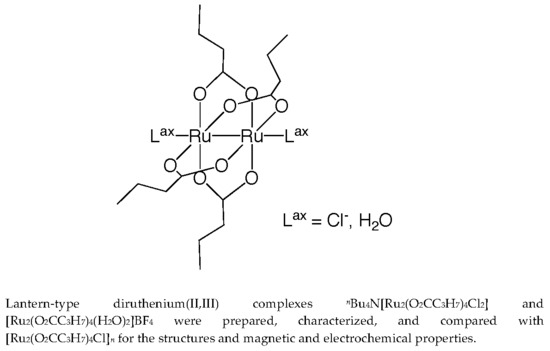
Magnetic and Electrochemical Properties of Lantern-Type Dinuclear Ru(II,III) Complexes with Axial Chloride Ions or Water Molecules
Abstract
:1. Introduction
2. Results and Discussion
2.1. Synthesis and Characterizations
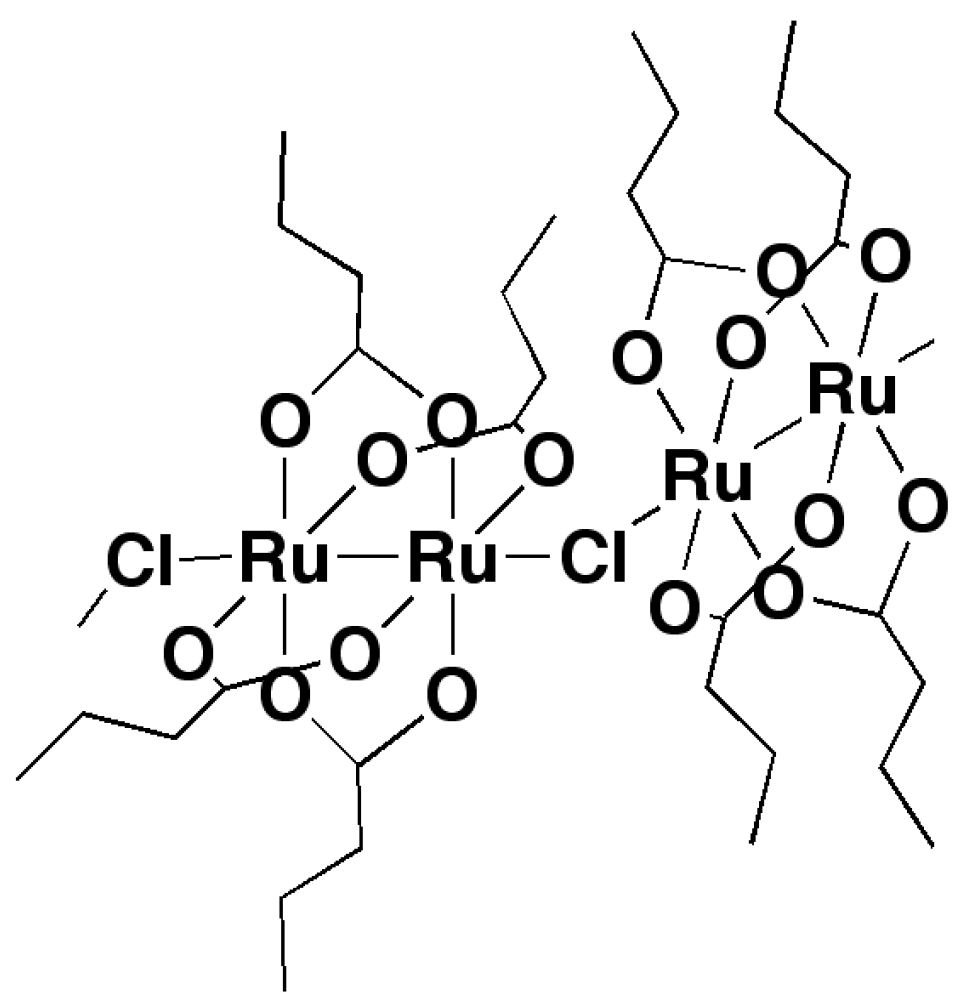
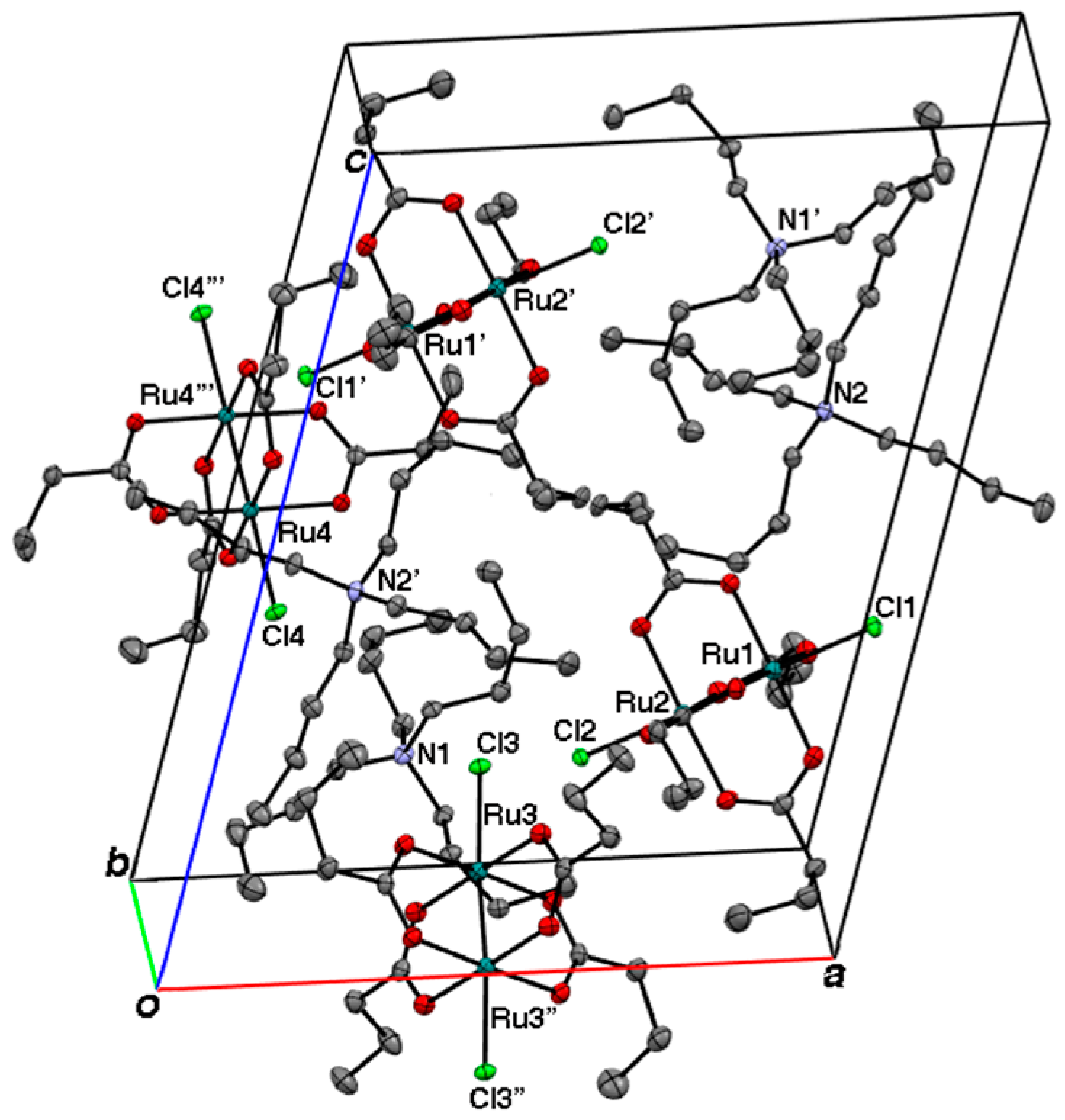
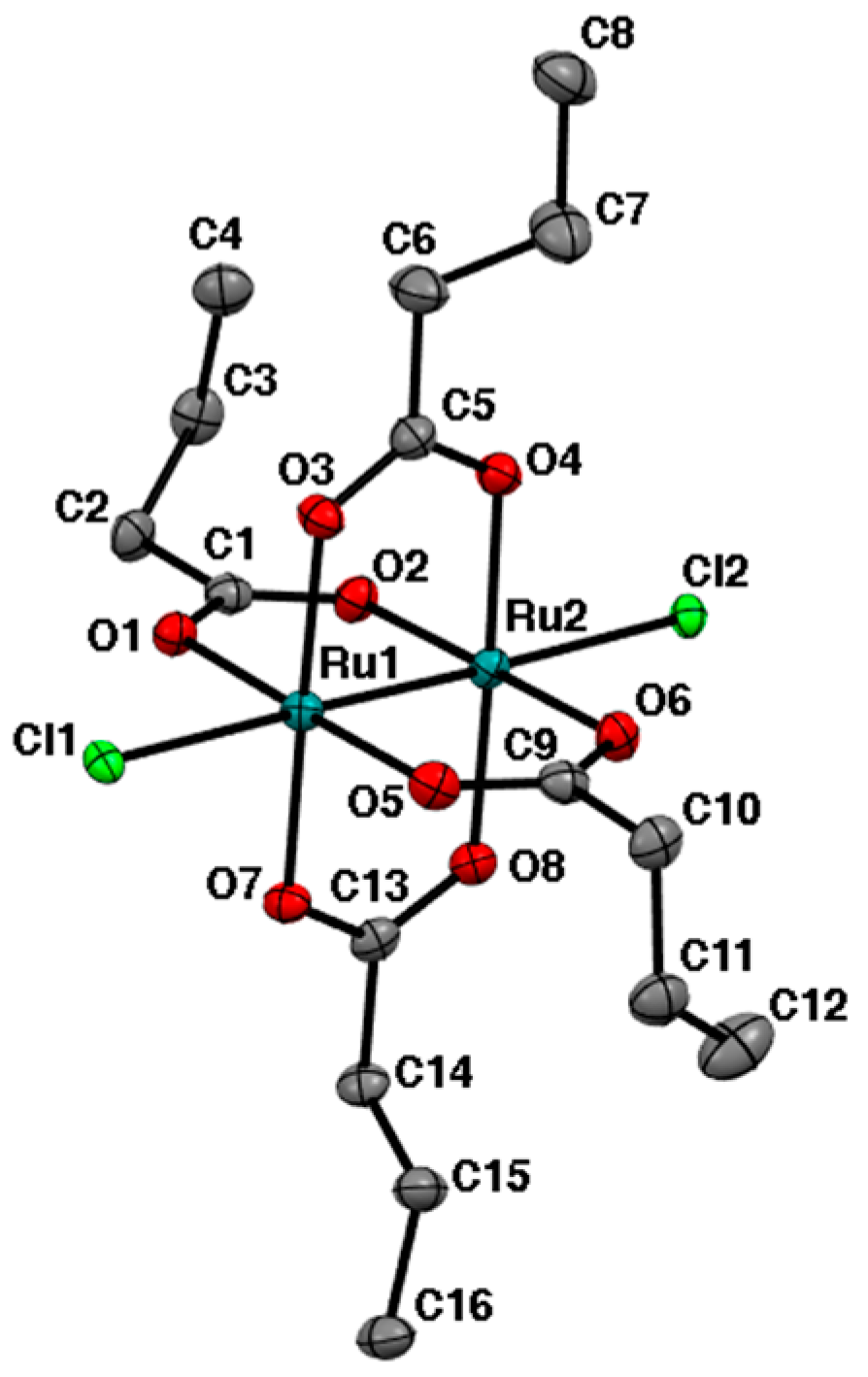
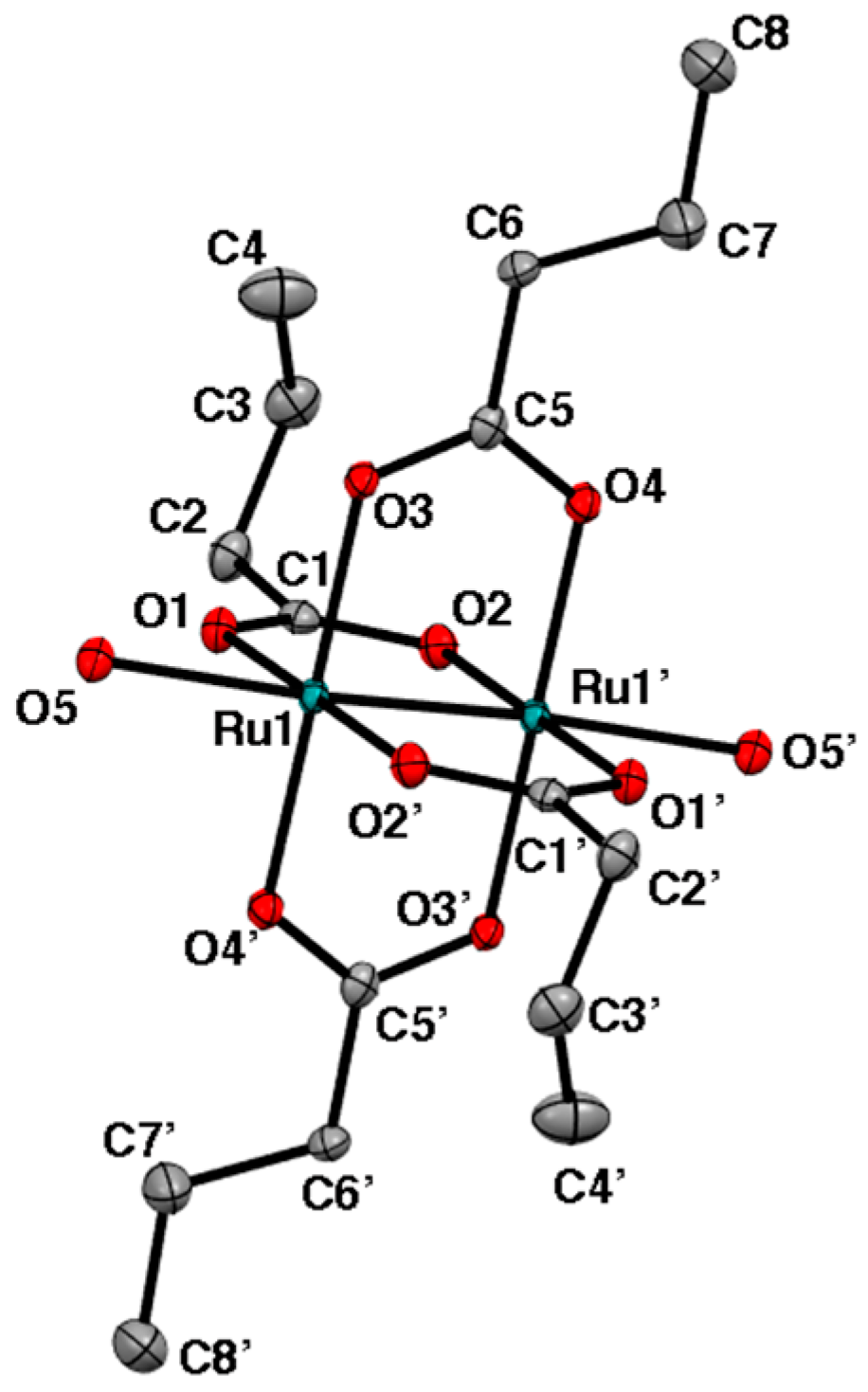
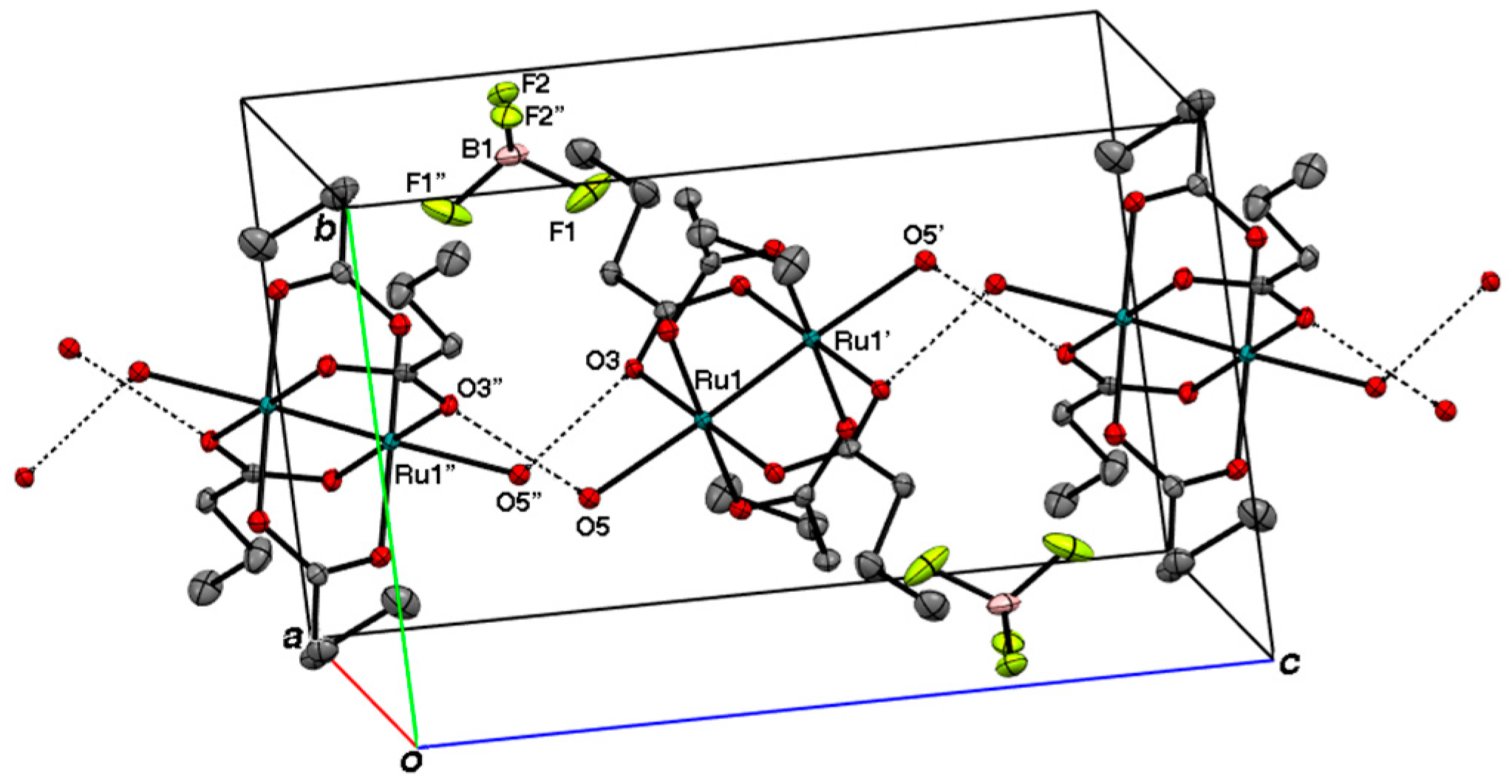
2.2. Crystal Structures
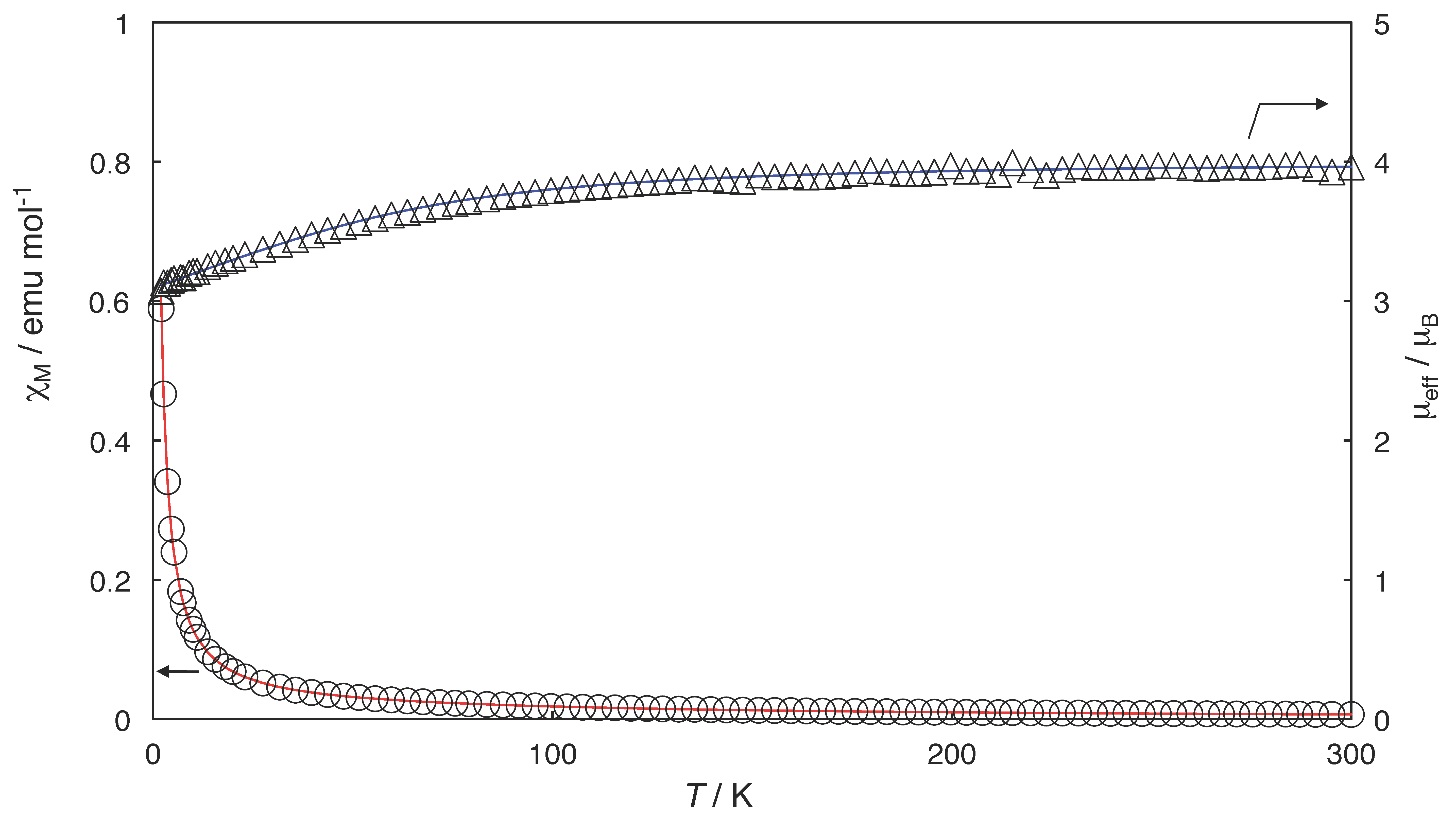
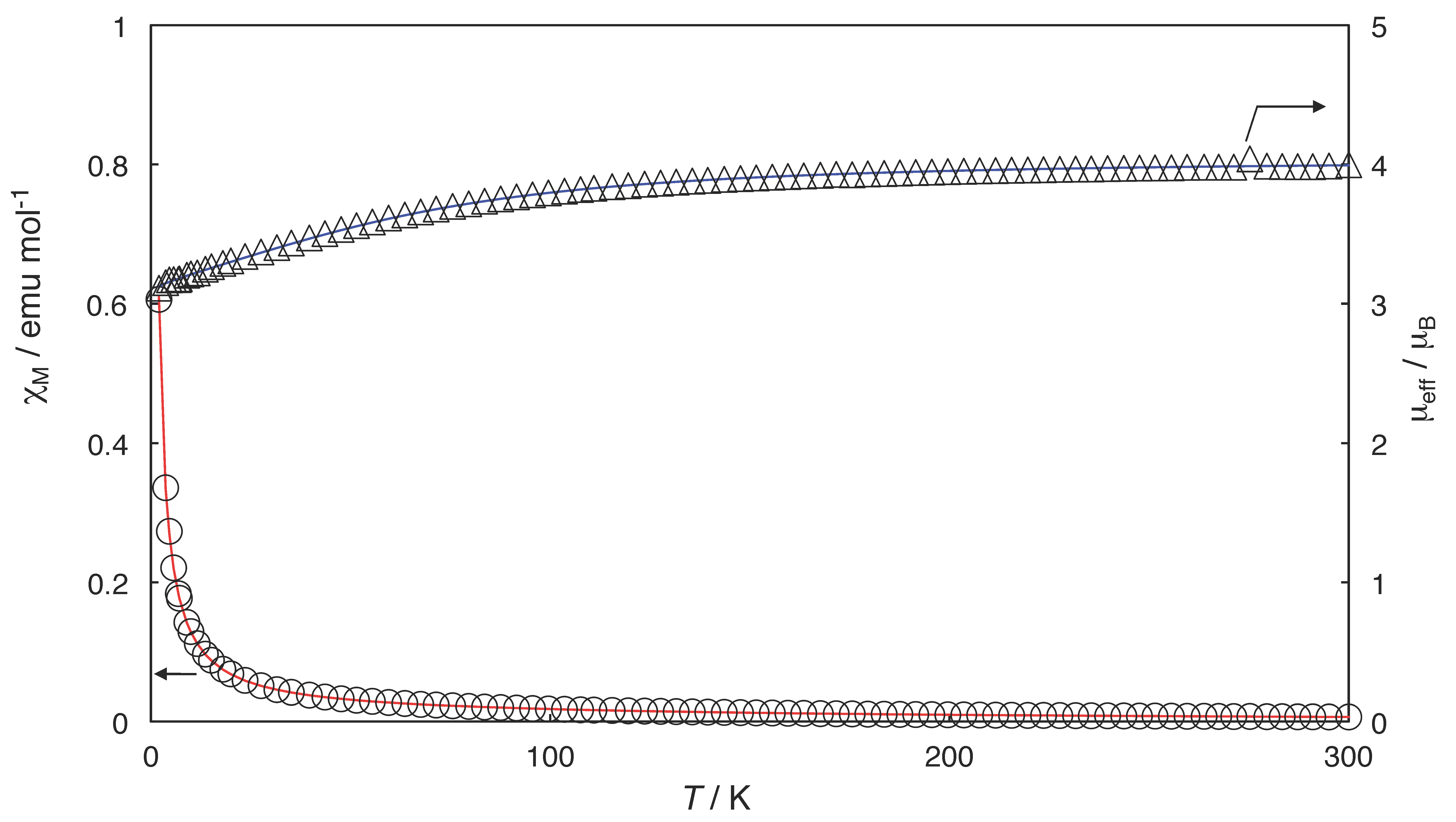
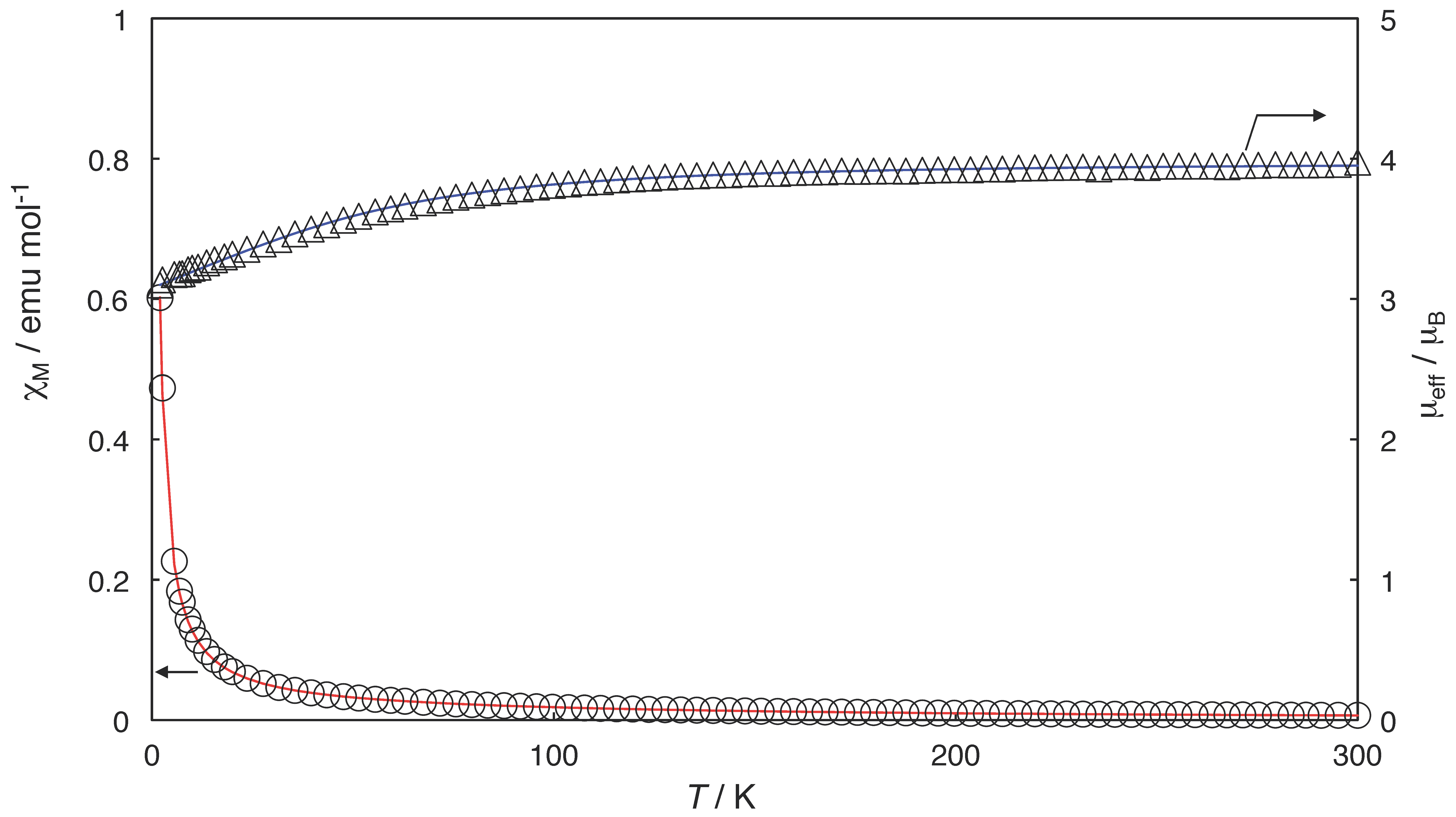
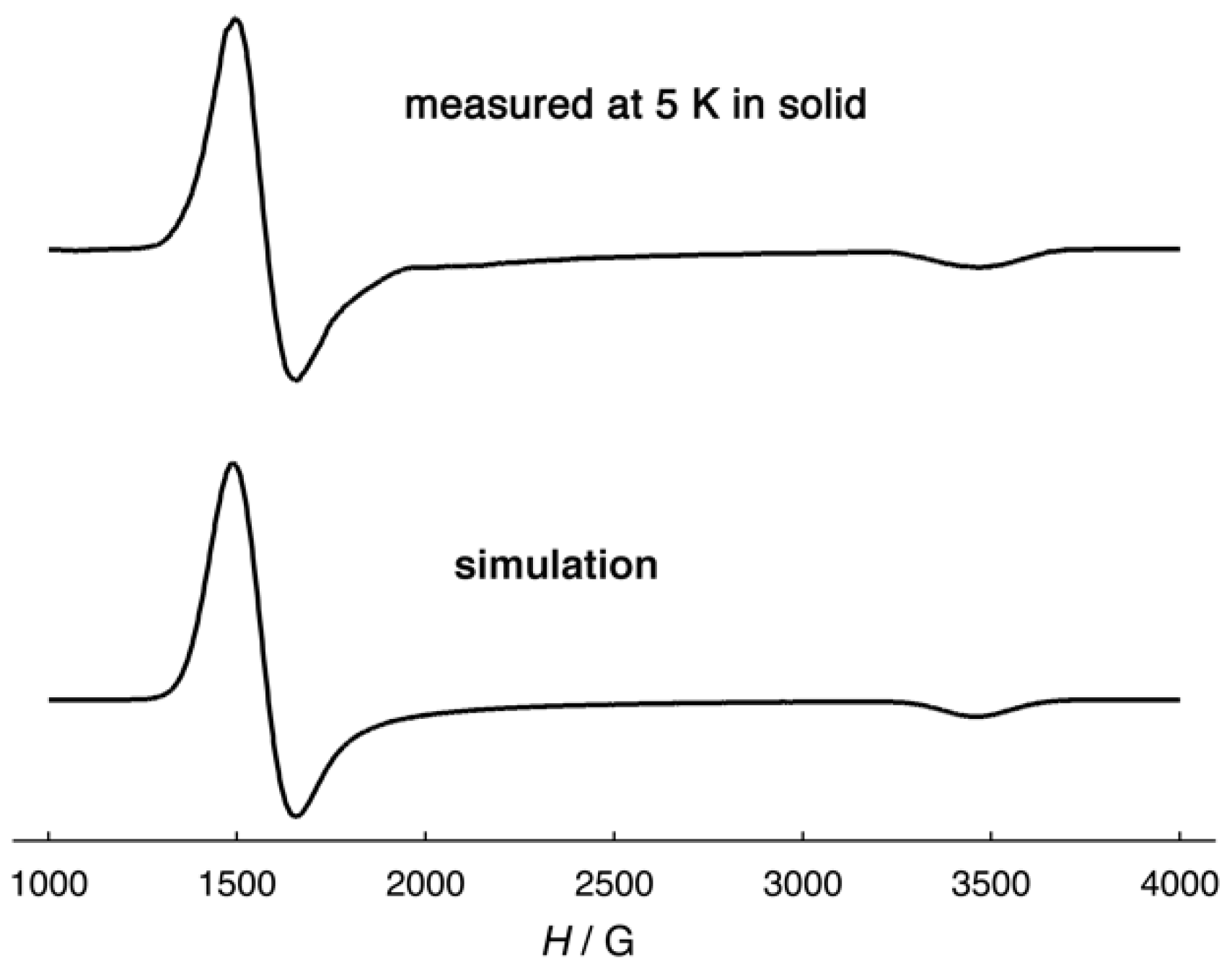
2.3. Magnetic Properties
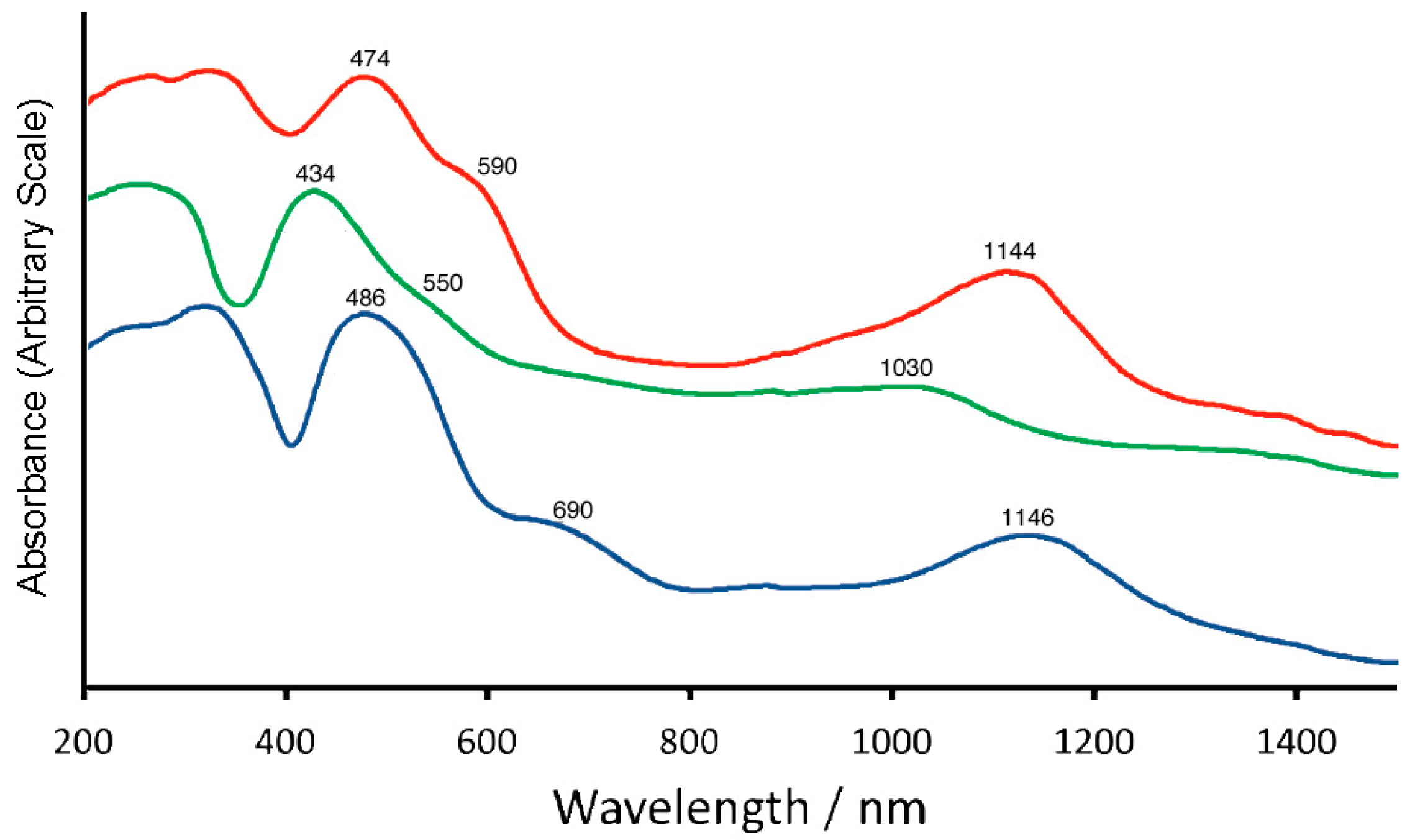
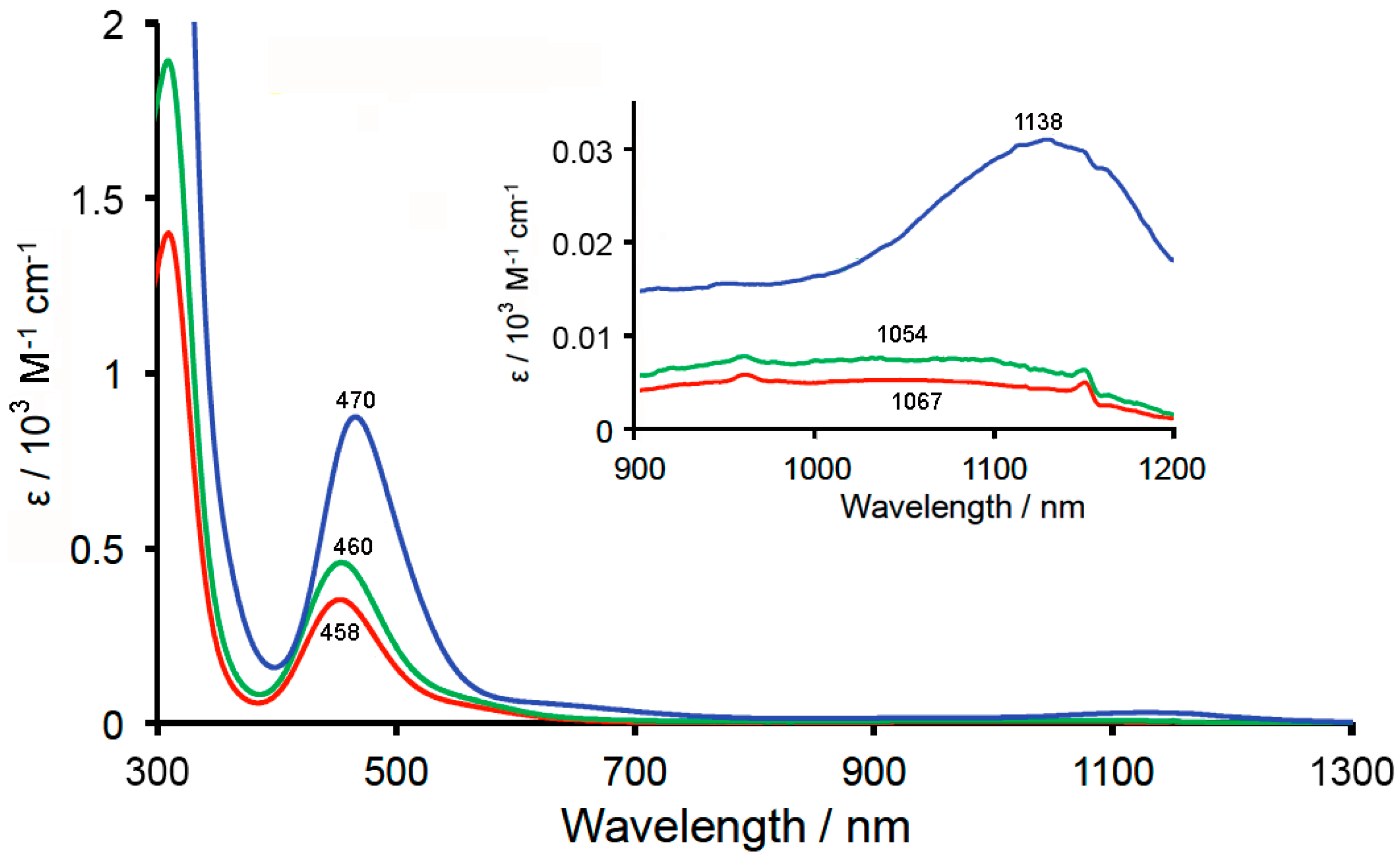
2.4. Reflectance and Absorption Spectra
2.5. Cyclic Voltammogram (CV)
3. Materials and Methods
3.1. General Aspects
3.2. Syntheses of Complexes
3.2.1. Synthesis of nBu4N[Ru2(O2CC3H7)4Cl2] (2)
3.2.2. Synthesis of [Ru2(O2CC3H7)4(H2O)2]BF4 (3)
3.3. Crystal Structure Determination
3.4. Computational Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cotton, F.A.; Murillo, C.A.; Walton, R.A. Multiple Bonds between Metal Atoms, 3rd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Liddle, S.T. Molecular Metal-Metal Bonds, Compounds, Synthesis, Properties; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
- Aquino, M.A.S. Diruthenium and diosmium tetracarboxylates: Synthesis, physical properties and applications. Coord. Chem. Rev. 1998, 170, 141–202. [Google Scholar] [CrossRef]
- Aquino, M.A.S. Recent developments in the synthesis and properties of diruthnium tetracarboxylates. Coord. Chem. Rev. 2004, 248, 1025–1045. [Google Scholar] [CrossRef]
- Mikuriya, M.; Yoshioka, D.; Handa, M. Magnetic interactions in one-, two-, and three-dimensional assemblies of dinuclear ruthenium carboxylates. Coord. Chem. Rev. 2006, 250, 2194–2211. [Google Scholar] [CrossRef]
- Bennett, M.J.; Caulton, K.G.; Cotton, F.A. The structure of tetra-n-butyratodiruthenium chloride, a compound with a strong metal-metal bond. Inorg. Chem. 1969, 8, 1–6. [Google Scholar] [CrossRef]
- Telser, J.; Drago, R.S. Reinvesigation of the Electronic and Magnetic Properties of Ruthenium Butyrate Chloride. Inorg. Chem. 1984, 23, 3114–3120, Erratum in 1985, 24, 4765, doi:10.1021/ic00220a601. [Google Scholar] [CrossRef]
- Cotton, F.A.; Pedersen, E. Magnetic and electrochemical properties of transition metal complexes with multiple metal-to-metal bonds. II. [Ru2(C3H7COO)4]n+ with n = 0 and 1. Inorg. Chem. 1975, 14, 388–391. [Google Scholar] [CrossRef]
- Nakamoto, K. Infrared and Raman Spectra, 4th ed.; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Hiraoka, Y.; Ikeue, T.; Sakiyama, H.; Guégan, F.; Luneau, D.; Gillon, B.; Hiromitsu, I.; Yoshioka, D.; Mikuriya, M.; Kataoka, Y.; et al. An unprecedented up-field shift in the 13C NMR spectrum of the carboxyl carbons of the lantern-type dinuclear complex TBA[Ru2(O2CCH3)4Cl2] (TBA+ = tetra(n-butyl)ammonium cation. Dalton Trans. 2015, 44, 13439–13443. [Google Scholar] [CrossRef] [PubMed]
- Bino, A.; Cotton, F.A.; Felthouse, T.R. Structural studies of some multiply bonded diruthenium tetracarboxylate compounds. Inorg. Chem. 1979, 18, 2599–2604. [Google Scholar] [CrossRef]
- Drysdale, K.D.; Beck, E.J.; Cameron, T.S.; Robertson, K.N.; Aquino, M.A.S. Crystal structures and physico-chemical properties of a series of [Ru2(O2CCH3)4L2](PF6) adducts (L = H2O, DMF, DMSO). Inorg. Chim. Acta 1997, 256, 243–252. [Google Scholar] [CrossRef]
- Sayama, Y.; Handa, M.; Nukada, R.; Hiromitsu, I.; Kasuga, K. Mixed-Valent Ruthenium Pivalate and Its Nitroxide Adduct. In Coordination Chemistry at the Turn of The Chemistry; Ondrejovic, G., Sirota, A., Eds.; Slovak Technical Universty Press: Bratislava, Slovakia, 1999; pp. 447–452. [Google Scholar]
- O’Connor, C.J. Magnetochemistry—Advances in Theory and Experimentaion. Prog. Inorg. Chem. 1982, 29, 203–283. [Google Scholar] [CrossRef]
- Delgado-Martinez, P.; González-Prieto, R.; Gómez-García, C.J.; Jiménez-Aparicio, R.; Priego, J.L.; Torres, M.R. Structural, magnetic and electrical properties of one-dimensional tetraamidatodiruthnium compounds. Dalton Trans. 2014, 43, 3227–3237. [Google Scholar] [CrossRef] [PubMed]
- Cukiernik, F.D.; Luneau, D.; Machon, J.-C.; Maldivi, P. Mixed-Valent Diruthenium Long-Chain Carboxylates. 2. Magnetic Properties. Inorg. Chem. 1998, 37, 3698–3704. [Google Scholar] [CrossRef] [PubMed]
- Handa, M.; Sayama, Y.; Mikuriya, M.; Nukada, R.; Hiromitsu, I.; Kasuga, K. Structure and Magnetic Properties of a Nitroxide Diruthenium(II,III) Complex, [Ru2(O2CCMe3)4(tempo)2][Ru2(O2CCMe3)4(H2O)2] (BF4)2 (tempo = 2,2,6,6-Tetramethylpiperidine-1-oxyl). Bull. Chem. Soc. Jpn. 1995, 68, 1647–1653. [Google Scholar] [CrossRef]
- Yoshioka, D.; Mikuirya, M.; Handa, M. Synthsis and Characterization of Polynuclear Chain and Tetranuclear Complexes of Mixed-Valent Ruthenium(II,III) Pivalate with N,N’-Didentate Ligands. Bull. Chem. Soc. Jpn. 2004, 77, 2205–2211. [Google Scholar] [CrossRef]
- Miskowski, V.M.; Gray, H.B. Electronic spectra of Ru2(carboxylate)4+ complexes. Higher energy electronic excited states. Inorg. Chem. 1988, 27, 2501–2506. [Google Scholar] [CrossRef]
- Kahn, O. Molecular Magnetism; VCH: Cambridge, UK, 1993; Chapter 1. [Google Scholar]
- Hagen, W.R. Biomolecular EPR Spectroscopy; CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Access Structures. Available online: www.ccdc.cam.ac.uk/data_request/cif (accessed on 5 March 2019).
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Li, J.; Fisher, C.L.; Chen, J.L.; Bashford, D.; Noodleman, L. Calculation of Redox Potentials and pKa Values of Hydrated Transition Metal Cations by a Combined Density Functional and Continuum Dielectric Theory. Inorg. Chem. 1996, 35, 4694–4702. [Google Scholar] [CrossRef]
- Trasatti, S. The Absolute Electrode Potential: An Explanatory Note. Pure Appl. Chem. 1986, 58, 955–966. [Google Scholar] [CrossRef]

| 2 | 3 | |
|---|---|---|
| Empirical formula | C32H64Cl2NO8Ru2 | C16H32BF4O10Ru2 |
| Formula mass | 863.88 | 673.37 |
| Temperature | 90 K | 90 K |
| Crystal system | Triclinic | Monoclinic |
| Space group | P 2/c | |
| a | 16.0297(11) Å | 12.600(4) Å |
| b | 16.0936(11) Å | 8.808(3) Å |
| c | 18.6813(13) Å | 13.968(4) Å |
| α | 68.4640(10)° | 90° |
| β | 68.5090(10)° | 106.581(4)° |
| γ | 64.3420(10)° | 90° |
| Unit-cell volume, V | 3915.3(5) Å3 | 1485.7(8) Å3 |
| Formula per unit cell, Z | 4 | 2 |
| Density, Dcalcd | 1.466 g cm−3 | 1.505 g cm−3 |
| Crystal size | 0.330 × 0.300 × 0.200 mm3 | 0.300 × 0.160 × 0.060 mm3 |
| Absorption coefficient, µ | 0.953 mm−1 | 1.080 mm−1 |
| θ range for data collection | 1.641–28.500° | 2.768–24.496° |
| Reflections collected/unique | 25828/18244 | 8821/2430 |
| R indices [I > 2σ(I)] b | R1 = 0.0348, wR2 = 0.0867 | R1 = 0.0265, wR2 = 0.0783 |
| Goodness-of-fit on F2 | 1.072 | 1.164 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Handa, M.; Yairi, H.; Yano, N.; Mitsumi, M.; Sakiyama, H.; Kitashima, M.; Inoue, K.; Mitsuhashi, R.; Mikuriya, M.; Akashi, H.; et al. Magnetic and Electrochemical Properties of Lantern-Type Dinuclear Ru(II,III) Complexes with Axial Chloride Ions or Water Molecules. Magnetochemistry 2019, 5, 18. https://doi.org/10.3390/magnetochemistry5010018
Handa M, Yairi H, Yano N, Mitsumi M, Sakiyama H, Kitashima M, Inoue K, Mitsuhashi R, Mikuriya M, Akashi H, et al. Magnetic and Electrochemical Properties of Lantern-Type Dinuclear Ru(II,III) Complexes with Axial Chloride Ions or Water Molecules. Magnetochemistry. 2019; 5(1):18. https://doi.org/10.3390/magnetochemistry5010018
Chicago/Turabian StyleHanda, Makoto, Haruki Yairi, Natsumi Yano, Minoru Mitsumi, Hiroshi Sakiyama, Masaharu Kitashima, Kazuhito Inoue, Ryoji Mitsuhashi, Masahiro Mikuriya, Haruo Akashi, and et al. 2019. "Magnetic and Electrochemical Properties of Lantern-Type Dinuclear Ru(II,III) Complexes with Axial Chloride Ions or Water Molecules" Magnetochemistry 5, no. 1: 18. https://doi.org/10.3390/magnetochemistry5010018
APA StyleHanda, M., Yairi, H., Yano, N., Mitsumi, M., Sakiyama, H., Kitashima, M., Inoue, K., Mitsuhashi, R., Mikuriya, M., Akashi, H., & Kataoka, Y. (2019). Magnetic and Electrochemical Properties of Lantern-Type Dinuclear Ru(II,III) Complexes with Axial Chloride Ions or Water Molecules. Magnetochemistry, 5(1), 18. https://doi.org/10.3390/magnetochemistry5010018