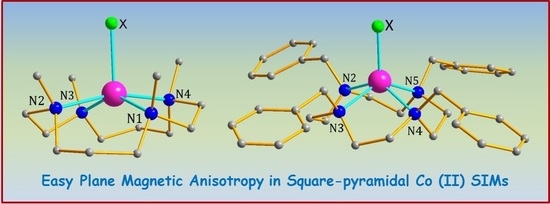
Field Induced Single Ion Magnetic Behaviour in Square-Pyramidal Cobalt(II) Complexes with Easy-Plane Magnetic Anisotropy
Abstract
1. Introduction
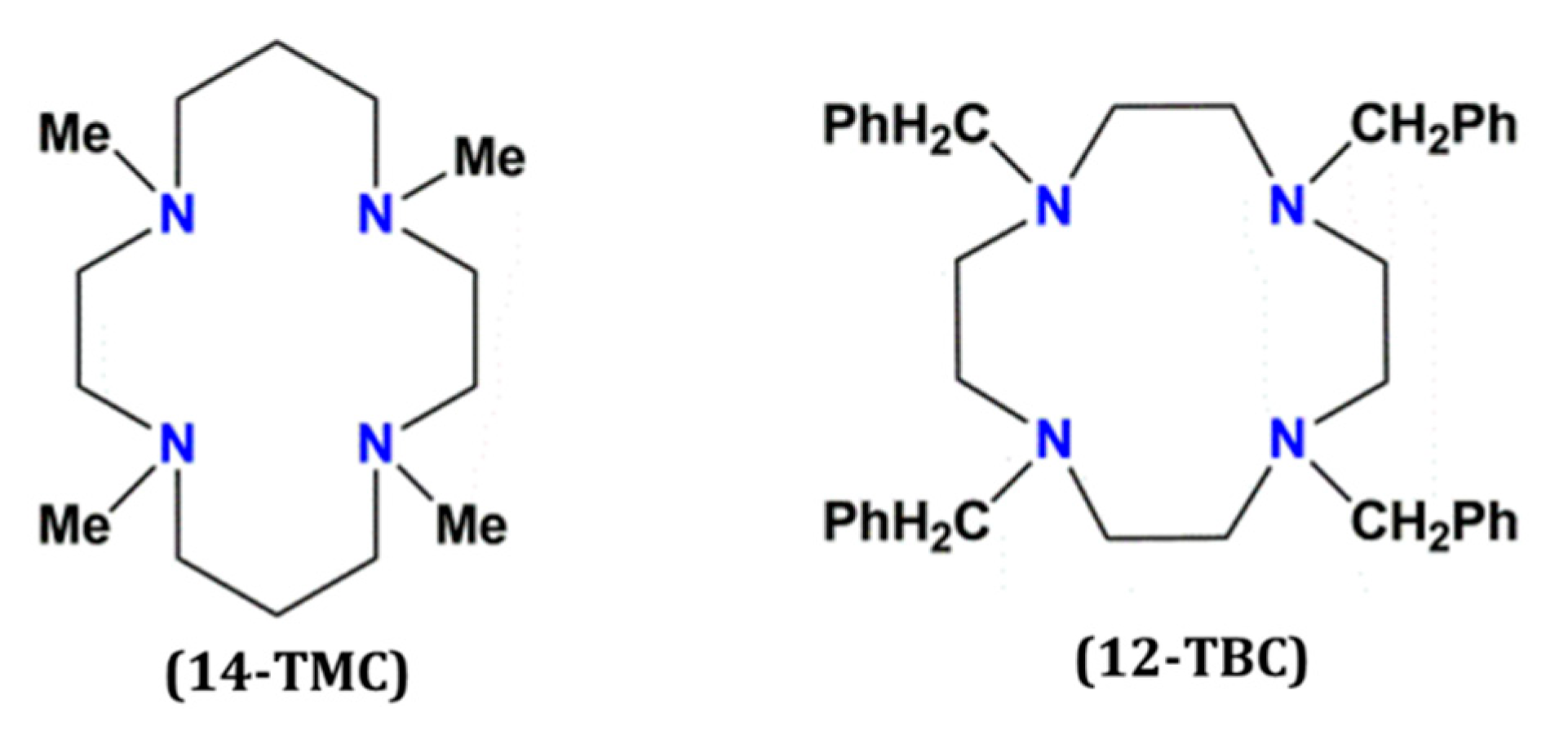
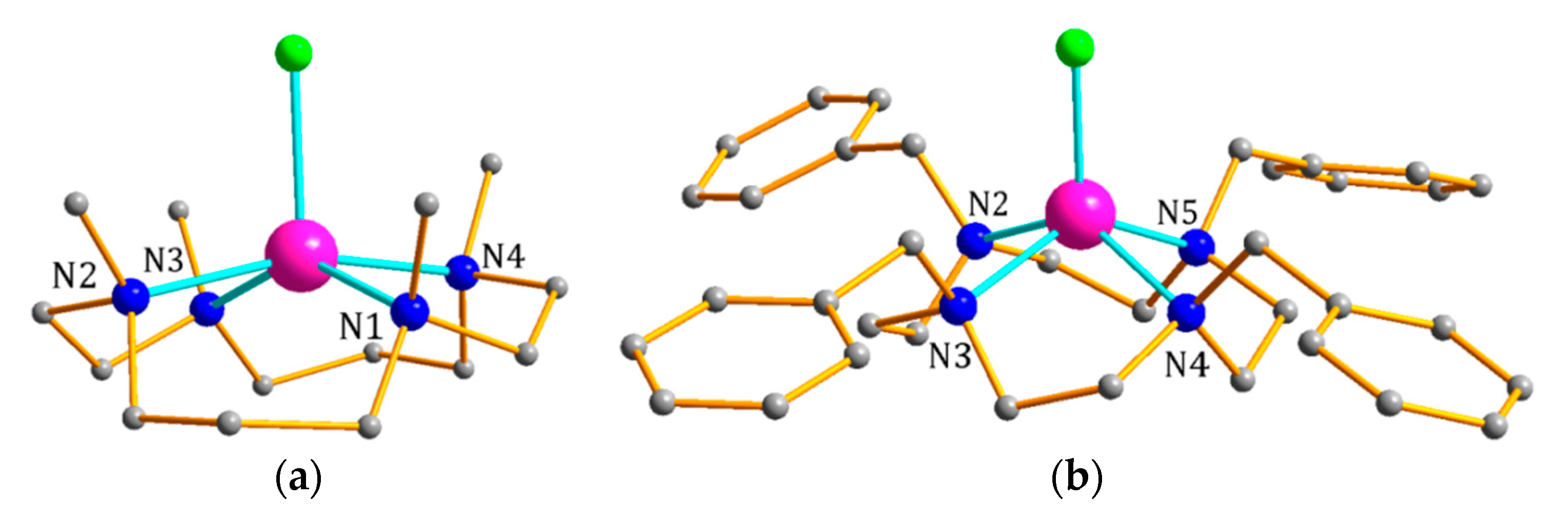
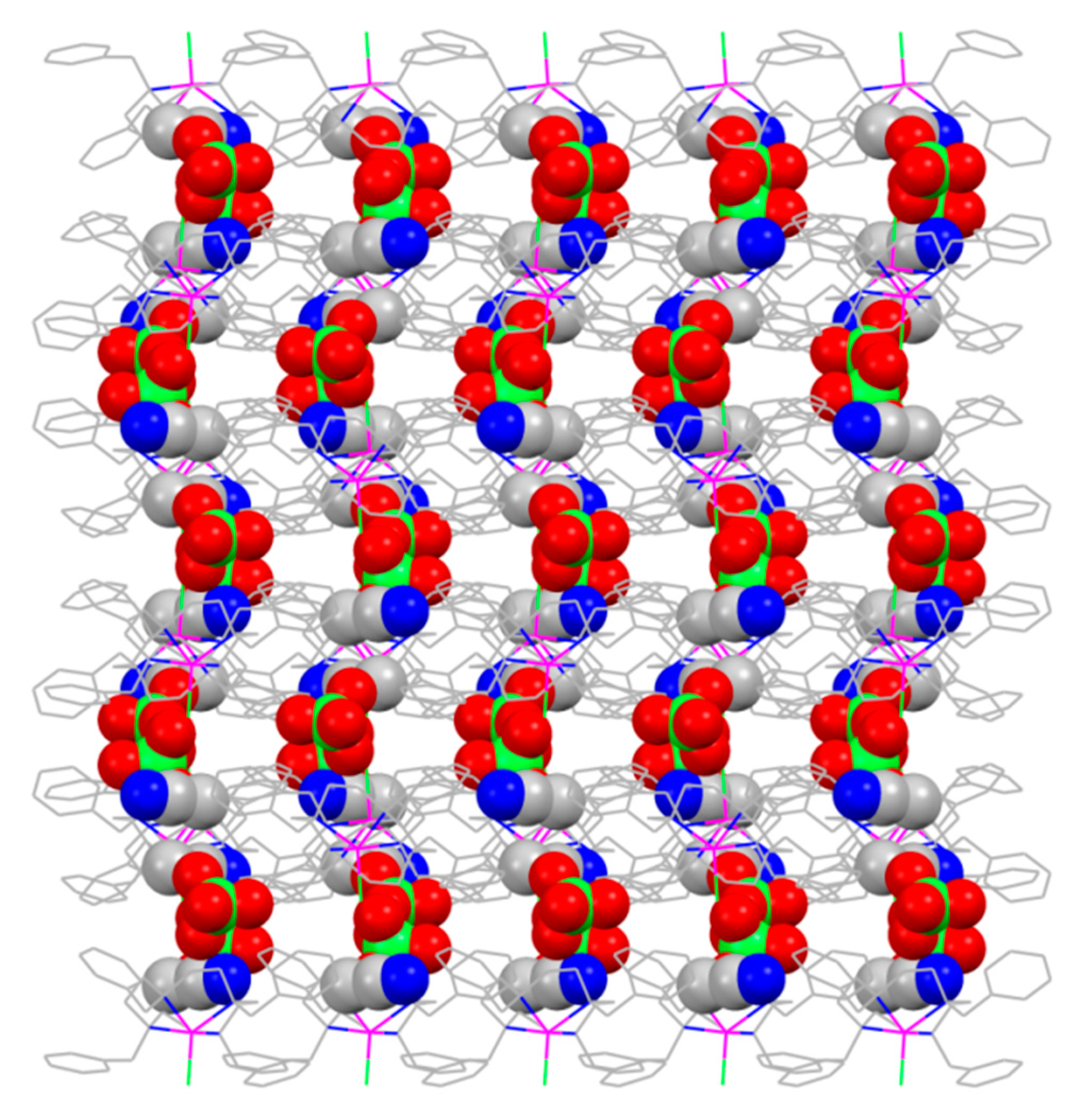
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Caneschi, A.; Gatteschi, D.; Sessoli, R.; Barra, A.L.; Brunel, L.C.; Guillot, M. Alternating current susceptibility, high field magnetization, and millimeter band EPR evidence for a ground S = 10 state in [Mn12O12(Ch3COO)16(H2O)4]·2CH3COOH·4H2O. J. Am. Chem. Soc. 1991, 113, 5873–5874. [Google Scholar] [CrossRef]
- Sessoli, R.; Tsai, H.L.; Schake, A.R.; Wang, S.Y.; Vincent, J.B.; Folting, K.; Gatteschi, D.; Christou, G.; Hendrickson, D.N. High-spin molecules: [Mn12O12(O2CR)16(H2O)4]. J. Am. Chem. Soc. 1993, 115, 1804–1816. [Google Scholar] [CrossRef]
- Brechin, E.K.; Wernsdorfer, C.W.; Yoo, J.; Yamaguchi, A.; Saňudo, E.C.; Concolino, T.R.; Rheingold, A.L.; Ishimoto, H.; Hendrickson, D.N.; Christou, G. Quantum Tunneling of Magnetization in a New [Mn18]2+ Single-Molecule Magnet with S = 13. J. Am. Chem. Soc. 2002, 124, 9710–9711. [Google Scholar] [CrossRef] [PubMed]
- Dey, A.; Kalita, P.; Chandrasekhar, V. Lanthanide(III)-Based Single-Ion Magnets. ACS Omega 2018, 3, 9462–9475. [Google Scholar] [CrossRef]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
- Goswami, S.; Mondal, A.K.; Konar, S. Nanoscopic molecular magnets. Inorg. Chem. Front. 2015, 2, 687–712. [Google Scholar] [CrossRef]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef]
- Guo, F.-S.; Day, B.M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit. Angew. Chem. Int. Ed. 2017, 56, 11445–11449. [Google Scholar] [CrossRef]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Meng, Y.-S.; Jiang, S.-D.; Wang, B.-W.; Gao, S. Understanding the Magnetic Anisotropy toward Single-Ion Magnets. Acc. Chem. Res. 2016, 49, 2381–2389. [Google Scholar] [CrossRef]
- Craig, G.A.; Murrie, M. 3d single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Coca, S.; Aravena, D.; Morales, R.; Ruiz, E. Large magnetic anisotropy in mononuclear metal complexes. Coord. Chem. Rev. 2015, 289, 379–392. [Google Scholar] [CrossRef]
- Habib, F.; Luca, O.R.; Vieru, V.; Shiddiq, M.; Korobkov, I.; Gorelsky, S.I.; Takase, M.K.; Chibotaru, L.F.; Hill, S.; Crabtree, R.H.; et al. Influence of the Ligand Field on Slow Magnetization Relaxation versus Spin Crossover in Mononuclear Cobalt Complexes. Angew. Chem. Int. Ed. 2013, 52, 11290–11293. [Google Scholar] [CrossRef] [PubMed]
- Bar, A.K.; Pichon, C.; Sutter, J. Magnetic anisotropy in two- to eight-coordinated transition−metal complexes: Recent developments in molecular magnetism. Coord. Chem. Rev. 2016, 308, 346–380. [Google Scholar] [CrossRef]
- Woods, T.J.; Ballesteros-Rivas, M.F.; Gómez-Coca, S.; Ruiz, E.; Dunbar, K.R. Relaxation Dynamics of Identical Trigonal Bipyramidal Cobalt Molecules with Different Local Symmetries and Packing Arrangements: Magnetostructural Correlations and ab inito Calculations. J. Am. Chem. Soc. 2016, 138, 16407–16416. [Google Scholar] [CrossRef] [PubMed]
- Mondal, A.K.; Jover, J.; Ruiz, E.; Konar, S. Investigation of easy plane magnetic anisotropy in P-ligand square-pyramidal CoII single ion magnets. Chem. Commun. 2017, 53, 5338–5341. [Google Scholar] [CrossRef] [PubMed]
- Mondal, A.K.; Sundararajan, M.; Konar, S. A new series of tetrahedral Co(II) complexes [CoLX2] (X = NCS, Cl, Br, I) manifesting single-ion magnet features. Dalton Trans. 2018, 47, 3745–3754. [Google Scholar] [CrossRef] [PubMed]
- Mathonière, C.; Lin, H.-J.; Siretanu, D.; Clérac, R.; Smith, J.M. Photoinduced Single-Molecule Magnet Properties in a Four-Coordinate Iron(II) Spin Crossover Complex. J. Am. Chem. Soc. 2013, 135, 19083–19086. [Google Scholar] [CrossRef]
- Feng, X.; Mathonière, C.; Jeon, I.-R.; Rouzières, M.; Ozarowski, A.; Aubrey, M.L.; Gonzalez, M.I.; Clérac, R.; Long, J.R. Tristability in a Light-Actuated Single-Molecule Magnet. J. Am. Chem. Soc. 2013, 135, 15880–15884. [Google Scholar] [CrossRef]
- Mondal, A.K.; Goswami, T.; Misra, A.; Konar, S. Probing the Effects of Ligand Field and Coordination Geometry on Magnetic Anisotropy of Pentacoordinate Cobalt(II) Single-Ion Magnets. Inorg. Chem. 2017, 56, 6870–6878. [Google Scholar] [CrossRef]
- Mondal, A.K.; Jover, J.; Ruiz, E.; Konar, S. Quantitative Estimation of Ising-Type Magnetic Anisotropy in a Family of C3-Symmetric CoII Complexes. Chem. Eur. J. 2017, 23, 12550–12558. [Google Scholar] [CrossRef]
- Goómez-Coca, S.; Cremades, E.; Aliaga-Alcalde, N.; Ruiz, E. Mononuclear Single-Molecule Magnets: Tailoring the Magnetic Anisotropy of First-Row Transition-Metal Complexes. J. Am. Chem. Soc. 2013, 135, 7010–7018. [Google Scholar] [CrossRef] [PubMed]
- Yao, X.-N.; Du, J.-Z.; Zhang, Y.-Q.; Leng, X.-B.; Yang, M.-W.; Jiang, S.-D.; Wang, Z.-X.; Ouyang, Z.-W.; Deng, L.; Wang, B.-W.; et al. Two-Coordinate Co(II) Imido Complexes as Outstanding Single-Molecule Magnets. J. Am. Chem. Soc. 2017, 139, 373–380. [Google Scholar] [CrossRef]
- Mondal, A.K.; Mondal, A.; Dey, B.; Konar, S. Influence of the Coordination Environment on Easy-Plane Magnetic Anisotropy of Pentagonal Bipyramidal Cobalt(II) Complexes. Inorg. Chem. 2018, 57, 9999–10008. [Google Scholar] [CrossRef]
- Jurca, T.; Farghal, A.; Lin, P.H.; Korobkov, I.; Murugesu, M.; Richeson, D.S. Single-Molecule Magnet Behavior with a Single Metal Center Enhanced through Peripheral Ligand Modifications. J. Am. Chem. Soc. 2011, 133, 15814–15817. [Google Scholar] [CrossRef] [PubMed]
- Murrie, M. Cobalt(II) single-molecule magnets. Chem. Soc. Rev. 2010, 39, 1986–1995. [Google Scholar] [CrossRef] [PubMed]
- Mondal, A.K.; Jover, J.; Ruiz, E.; Konar, S. Single-ion magnetic anisotropy in a vacant octahedral Co(II) complex. Dalton Trans. 2019, 48, 25–29. [Google Scholar] [CrossRef]
- Zadrozny, J.M.; Long, J.R. Slow magnetic relaxation at zero field in the tetrahedral complex [Co(SPh)4]2−. J. Am. Chem. Soc. 2011, 133, 20732–20734. [Google Scholar] [CrossRef]
- Novikov, V.V.; Pavlov, A.A.; Nelyubina, Y.V.; Boulon, M.E.; Varzatskii, O.A.; Voloschin, Y.Z.; Winpenny, R.E.P. A trigonal prismatic mononuclear cobalt(II) complex showing single-molecule magnet behavior. J. Am. Chem. Soc. 2015, 137, 9792–9795. [Google Scholar] [CrossRef]
- Vaidya, S.; Upadhyay, A.; Singh, S.K.; Langley, S.K.; Walsh, J.P.S.; Murray, K.S.; Rajaraman, G.; Shanmugam, M. A synthetic strategy for switching the single ion anisotropy in tetrahedral cobalt(II) complexes. Chem. Commun. 2014, 51, 3739–3742. [Google Scholar] [CrossRef]
- Rigamonti, L.; Bridonneau, N.; Poneti, G.; Tesi, L.; Sorace, L.; Pinkowicz, D.; Jover, J.; Ruiz, E.; Sessoli, R.; Cornia, A. A Pseudo-Octahedral Cobalt(II) Complex with Bispyrazolylpyridine Ligands Acting as a Zero-Field Single-Molecule Magnet with Easy Axis Anisotropy. Chem. Eur. J. 2018, 24, 8857. [Google Scholar] [CrossRef] [PubMed]
- Vallejo, J.; Castro, I.; Garcia, R.R.; Cano, J.; Julve, M.; Lloret, F.; Munno, G.D.; Wernsdorfer, W.; Pardo, E. Field-Induced Slow Magnetic Relaxation in a Six-Coordinate Mononuclear Cobalt(II) Complex with a Positive Anisotropy. J. Am. Chem. Soc. 2012, 134, 15704–15707. [Google Scholar] [CrossRef] [PubMed]
- Mondal, A.K.; Khatua, S.; Tomar, K.; Konar, S. Field-Induced Single-Ion-Magnetic Behavior of Octahedral CoII in a Two-Dimensional Coordination Polymer. Eur. J. Inorg. Chem. 2016, 3545–3552. [Google Scholar] [CrossRef]
- Kieber-Emmons, M.T.; Annaraj, J.; Seo, M.S.; Van Heuvelen, K.M.; Tosha, T.; Kitagawa, T.; Brunold, T.C.; Nam, W.; Riordan, C.G. Identification of an “end-on” nickel-superoxo adduct, [Ni(tmc)(O2)]+. J. Am. Chem. Soc. 2006, 128, 14230–14231. [Google Scholar] [CrossRef] [PubMed]
- Cho, J.; Woo, J.; Nam, W. An “End-On” Chromium(III)-Superoxo Complex: Crystallographic and Spectroscopic Characterization and Reactivity in C−H Bond Activation of Hydrocarbons. J. Am. Chem. Soc. 2010, 132, 5958–5959. [Google Scholar] [CrossRef] [PubMed]
- Cho, J.; Sarangi, R.; Annaraj, J.; Kim, S.Y.; Kubo, M.; Ogura, T.; Solomon, E.I.; Nam, W. Geometric and electronic structure and reactivity of a mononuclear “side-on” nickel(III)-peroxo complex. Nat. Chem. 2009, 1, 568. [Google Scholar] [CrossRef]
- Annaraj, J.; Suh, Y.; Seo, M.S.; Kim, S.O.; Nam, W. Mononuclear nonheme ferric-peroxo complex in aldehyde deformylation. Chem. Commun. 2005, 36, 4529–4531. [Google Scholar] [CrossRef] [PubMed]
- Cahier, B.; Perfetti, M.; Zakhia, G.; Naoufal, D.; ElKhatib, F.; Guillot, R.; Rivière, E.; Sessoli, R.; Barra, A.L.; Guihéry, N.; et al. Magnetic Anisotropy in Pentacoordinate NiII and CoII Complexes: Unraveling Electronic and Geometrical Contributions. Chem. Eur. J. 2017, 23, 3648–3657. [Google Scholar] [CrossRef]
- Cui, H.-H.; Wang, J.; Chen, X.-T.; Xue, Z.-L. Slow magnetic relaxation in five-coordinate spin-crossover cobalt(II) complexes. Chem. Commun. 2017, 53, 9304–9307. [Google Scholar] [CrossRef]
- Alvarez, S.; Alemany, P.; Casanova, D.; Cirera, J.; Llunell, M.; Avnir, D. Shape maps and polyhedral interconversion paths in transition metal chemistry. Coord. Chem. Rev. 2005, 249, 1693–1708. [Google Scholar] [CrossRef]
- Addison, A.W.; Rao, T.N.; Reedijk, J.; Vanrijn, J.; Verschoor, G.C. Synthesis, structure, and spectroscopic properties of copper(II) compounds containing nitrogen–sulphur donor ligands; the crystal and molecular structure of aqua[1,7-bis(N-methylbenzimidazol-2′-yl)-2,6-dithiaheptane]copper(II) perchlorate. J. Chem. Soc. Dalton Trans. 1984, 7, 1349–1356. [Google Scholar] [CrossRef]
- Mabbs, F.E.; Machin, D.J. Magnetism and Transition Metal Complexes; Dover Publications: Mineola, NY, USA, 2008. [Google Scholar]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef] [PubMed]
- Atanasov, M.; Aravena, D.; Suturina, E.; Bill, E.; Maganas, D.; Neese, F. First principles approach to the electronic structure, magnetic anisotropy and spin relaxation in mononuclear 3d-transition metal single molecule magnets. Coord. Chem. Rev. 2015, 289, 177–214. [Google Scholar] [CrossRef]
- Bartolome, J.; Filoti, G.; Kuncser, V.; Schinteie, G.; Mereacre, V.; Anson, C.E.; Powell, A.K.; Prodius, D.; Turta, C. Magnetostructural correlations in the tetranuclear series of {Fe3LnO2} butterfly core clusters: Magnetic and Mössbauer spectroscopic study. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 80, 014430. [Google Scholar] [CrossRef]
- Lin, P.H.; Burchell, T.J.; Ungur, L.; Chibotaru, L.F.; Wernsdorfer, W.; Murugesu, M. A Polynuclear Lanthanide Single-Molecule Magnet with a Record Anisotropic Barrier. Angew. Chem. Int. Ed. 2009, 48, 9489–9492. [Google Scholar] [CrossRef] [PubMed]
- Gamer, M.T.; Lan, Y.; Roesky, P.W.; Powell, A.K.; Clerac, R. Pentanuclear Dysprosium Hydroxy Cluster Showing Single-Molecule-Magnet Behavior. Inorg. Chem. 2008, 47, 6581–6583. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.F.; Wang, Q.L.; Gamez, P.; Ma, Y.; Clerac, R.; Tang, J.; Yan, S.P.; Cheng, P.; Liao, D.Z. A promising new route towards single-molecule magnets based on the oxalate ligand. Chem. Commun. 2010, 46, 1506–1508. [Google Scholar] [CrossRef]
- Mondal, A.K.; Parmar, V.S.; Konar, S. Modulating the Slow Relaxation Dynamics of Binuclear Dysprosium(III) Complexes through Coordination Geometry. Magnetochemistry 2016, 2, 35. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Guo, Y.-N.; Xu, G.-F.; Guo, Y.; Tang, J. Relaxation dynamics of dysprosium(III) single molecule magnets. Dalton Trans. 2011, 40, 9953–9963. [Google Scholar] [CrossRef]
- Colacio, E.; Ruiz, J.; Ruiz, E.; Cremades, E.; Krzystek, J.; Carretta, S.; Cano, J.; Guidi, T.; Wernsdorfer, W.; Brechin, E.K. Slow magnetic relaxation in a Co(II)-Y(III) single-ion magnet with positive axial zero-field splitting. Angew. Chem. Int. Ed. 2013, 52, 9300–9304. [Google Scholar] [CrossRef]
- Campbell, V.E.; Guillot, R.; Rivière, E.; Brun, P.-T.; Wernsdorfer, W.; Mallah, T. Subcomponent Self-Assembly of Rare-Earth Single-Molecule Magnets. Inorg. Chem. 2013, 52, 5194–5200. [Google Scholar] [CrossRef] [PubMed]
- Ungur, L.; Thewissen, M.; Costes, J.-P.; Wernsdorfer, W.; Chibotaru, L.F. Interplay of Strongly Anisotropic Metal Ions in Magnetic Blocking of Complexes. Inorg. Chem. 2013, 52, 6328–6337. [Google Scholar] [CrossRef] [PubMed]
- Mondal, A.K.; Jena, H.S.; Malviya, A.; Konar, S. Lanthanide-Directed Fabrication of Four Tetranuclear Quadruple Stranded Helicates Showing Magnetic Refrigeration and Slow Magnetic Relaxation. Inorg. Chem. 2016, 55, 5237–5244. [Google Scholar] [CrossRef] [PubMed]
- Kahn, O. Molecular Magnetism; VCH Publishers: Weinheim, Germany, 1993. [Google Scholar]
- Sheldrick, G.M. SHELXTL Program for the Solution of Crystal of Structures; University of Göttingen: Göttingen, Germany, 1993. [Google Scholar]
- Sheldrick, G.M. SHELXL 97, Program for Crystal Structure Refinement; University of Göttingen: Göttingen, Germany, 1997. [Google Scholar]
- Spek, A.L. Single-crystal structure validation with the program PLATON. J. Appl. Crystallogr. 2003, 36, 7–13. [Google Scholar] [CrossRef]
- Farrugia, L.J. WinGX suite for small-molecule single-crystal crystallography. J. Appl. Crystallogr. 1999, 32, 837–838. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
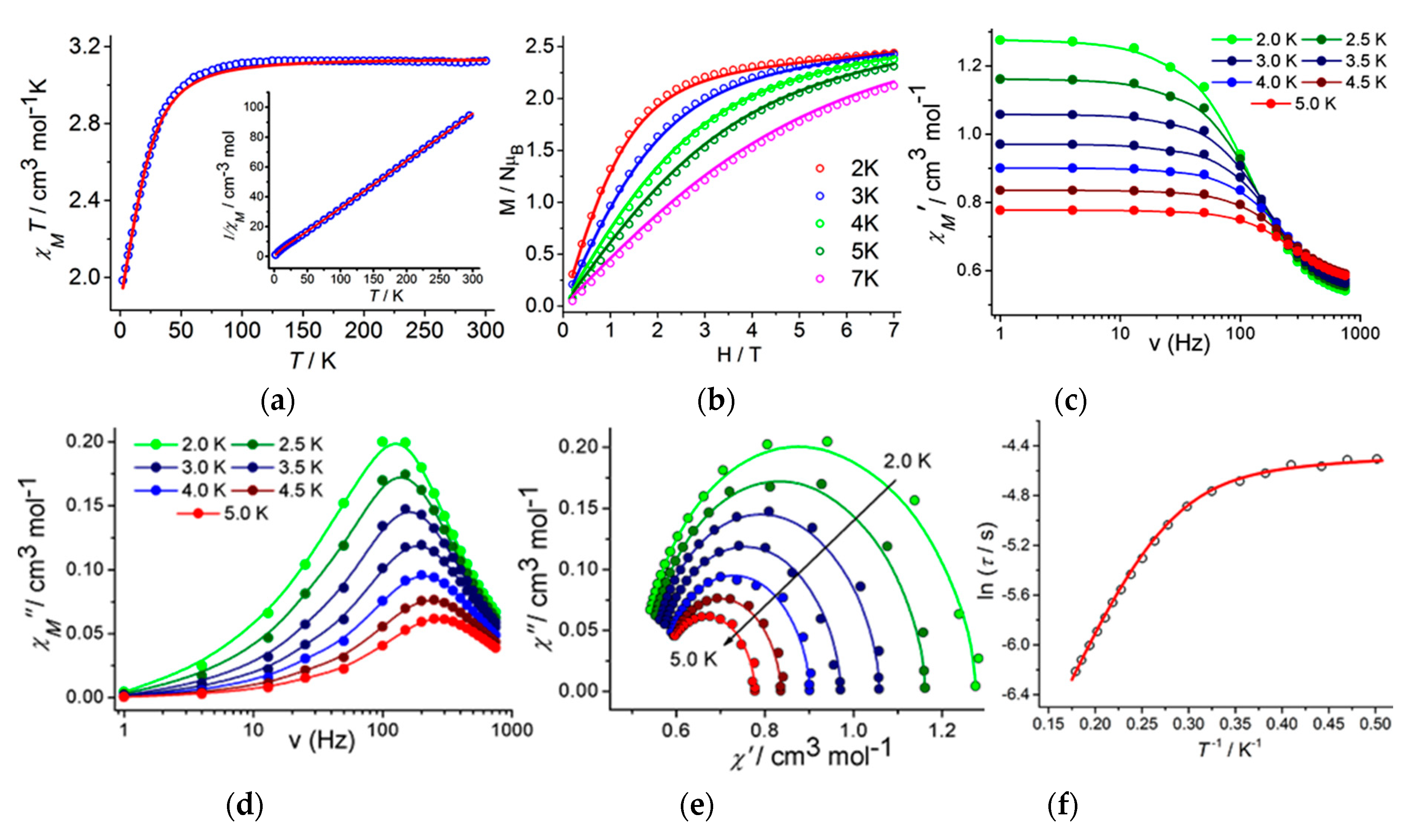
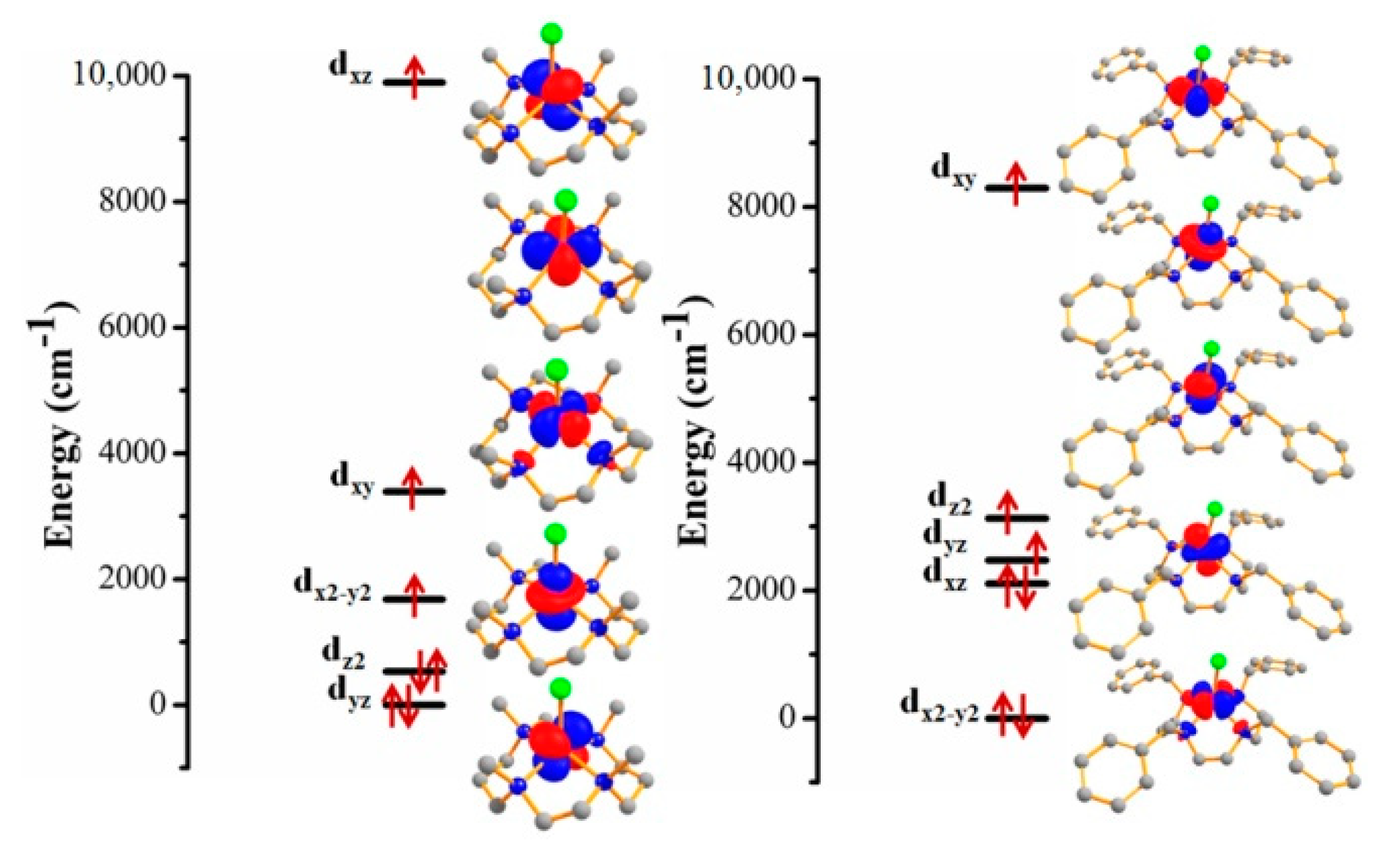
| Complex | Dexpt (cm−1) | |E|expt (cm−1) | Dcalc (cm−1) | |E|calc (cm−1) | (gx, gy, gz)cal |
|---|---|---|---|---|---|
| 1 | 45.1(6) | 9.9(1) | 46.5 | 14.3 | 2.32, 2.63, 2.01 |
| 2 | 52.3(5) | 10.1(7) | 49.1 | 11.2 | 2.70, 2.90, 1.99 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mondal, A.K.; Mondal, A.; Konar, S. Field Induced Single Ion Magnetic Behaviour in Square-Pyramidal Cobalt(II) Complexes with Easy-Plane Magnetic Anisotropy. Magnetochemistry 2019, 5, 12. https://doi.org/10.3390/magnetochemistry5010012
Mondal AK, Mondal A, Konar S. Field Induced Single Ion Magnetic Behaviour in Square-Pyramidal Cobalt(II) Complexes with Easy-Plane Magnetic Anisotropy. Magnetochemistry. 2019; 5(1):12. https://doi.org/10.3390/magnetochemistry5010012
Chicago/Turabian StyleMondal, Amit Kumar, Arpan Mondal, and Sanjit Konar. 2019. "Field Induced Single Ion Magnetic Behaviour in Square-Pyramidal Cobalt(II) Complexes with Easy-Plane Magnetic Anisotropy" Magnetochemistry 5, no. 1: 12. https://doi.org/10.3390/magnetochemistry5010012
APA StyleMondal, A. K., Mondal, A., & Konar, S. (2019). Field Induced Single Ion Magnetic Behaviour in Square-Pyramidal Cobalt(II) Complexes with Easy-Plane Magnetic Anisotropy. Magnetochemistry, 5(1), 12. https://doi.org/10.3390/magnetochemistry5010012