Analysis of Artifacts Caused by Pulse Imperfections in CPMG Pulse Trains in NMR Relaxation Dispersion Experiments
Abstract
:1. Introduction
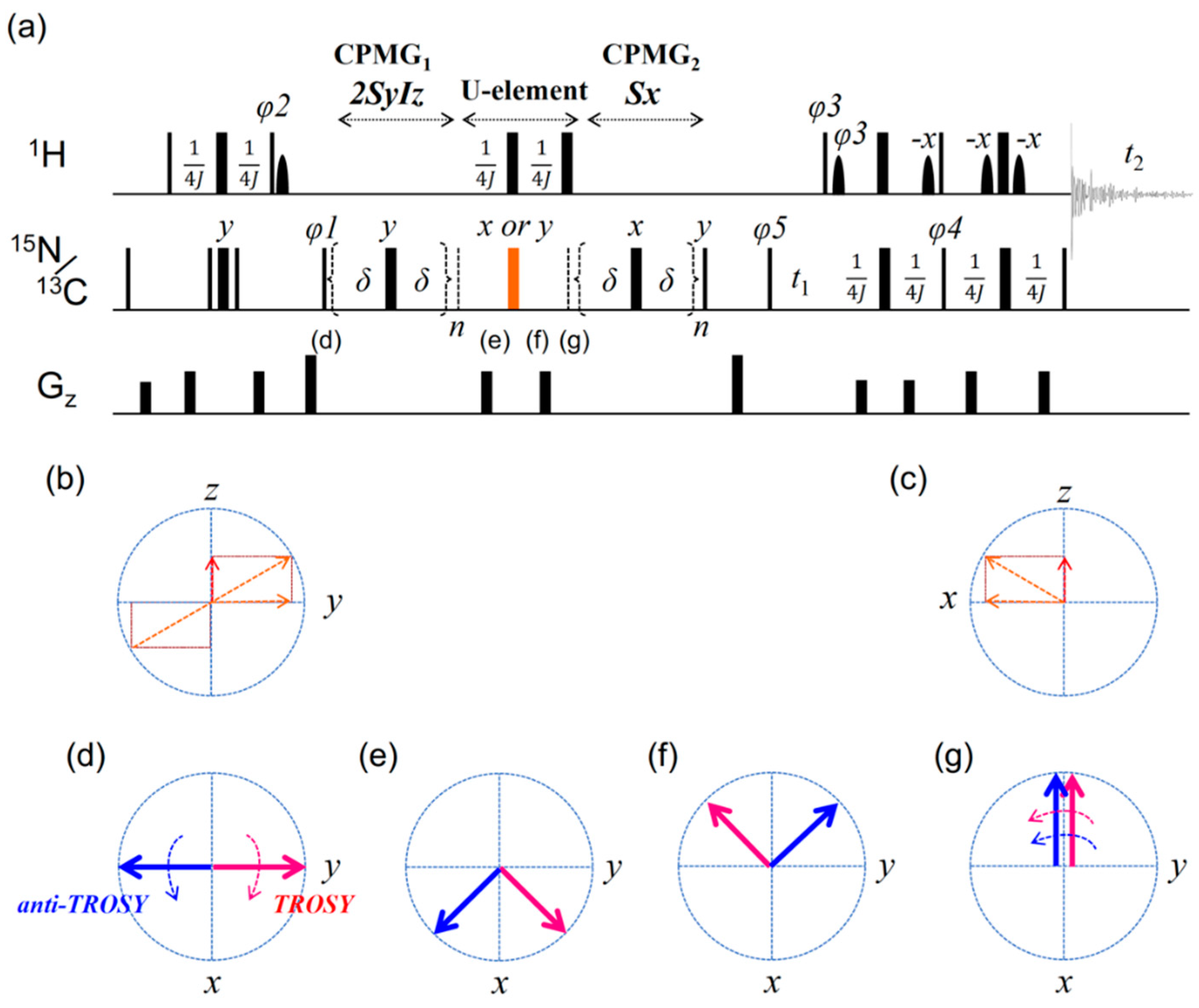
2. Results
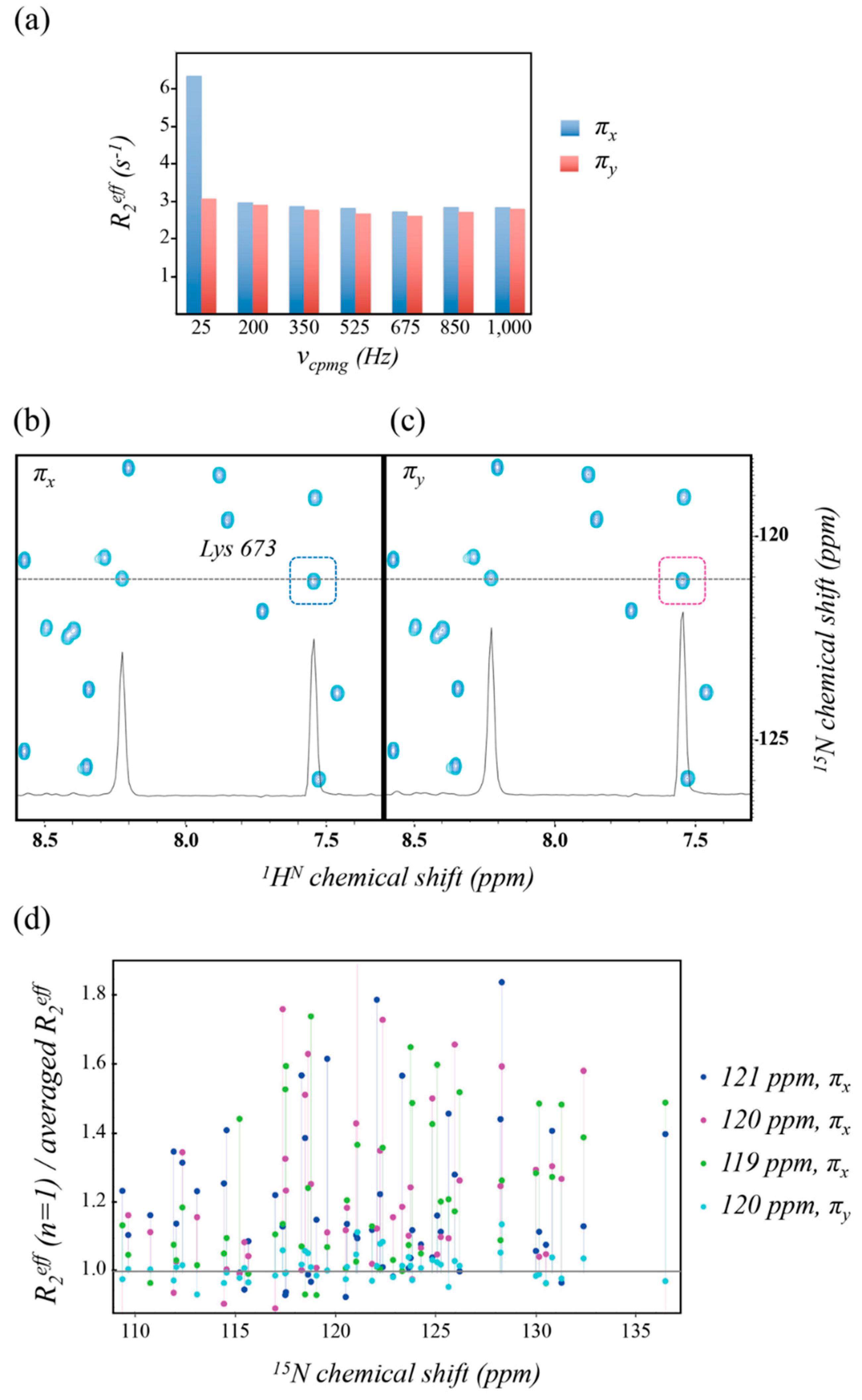
2.1. Artifacts Observed in Amide 15N Spin rd Experiments
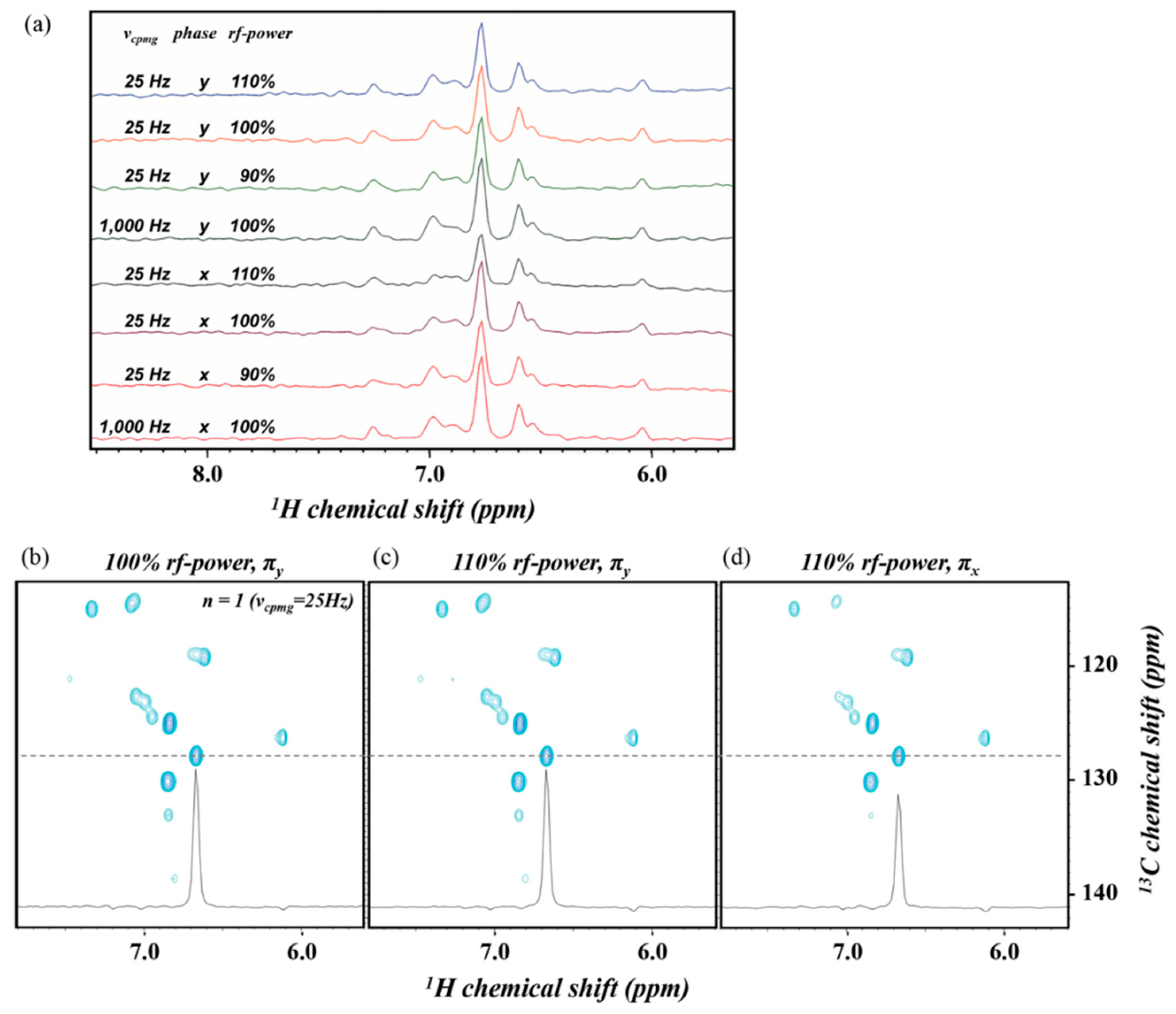
2.2. TROSY-Based Aromatic 13C Spin rd Experiments
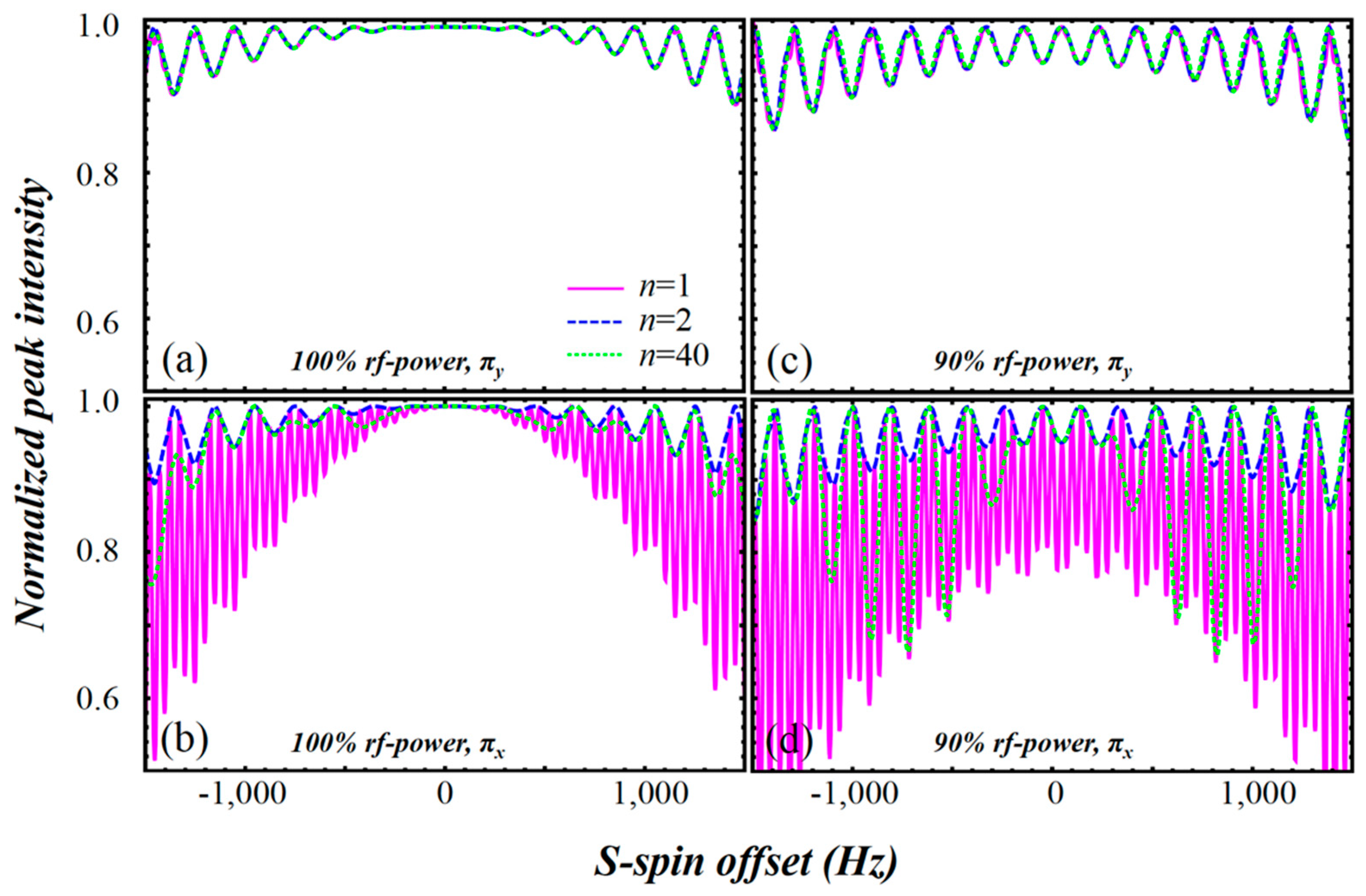
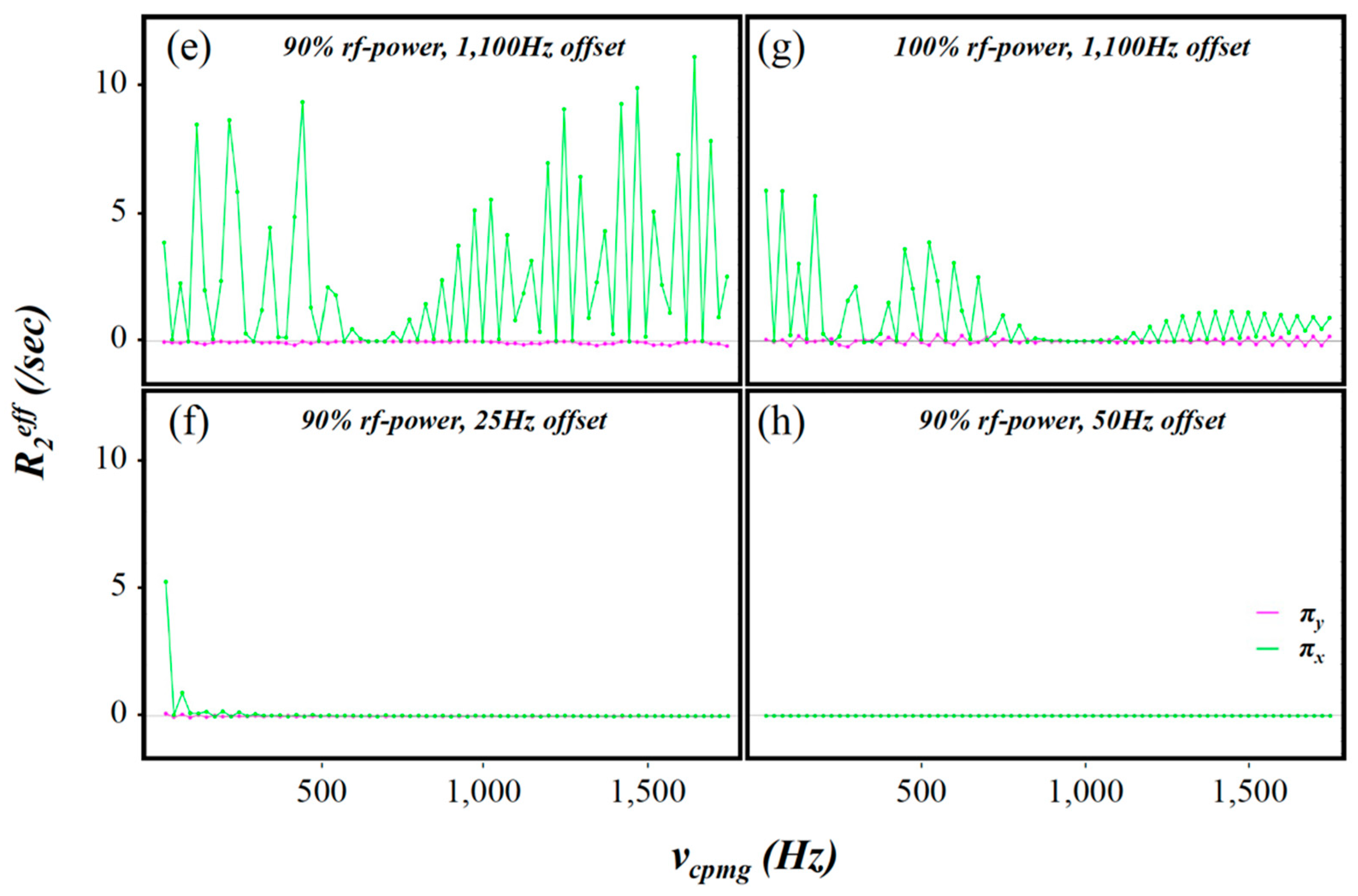
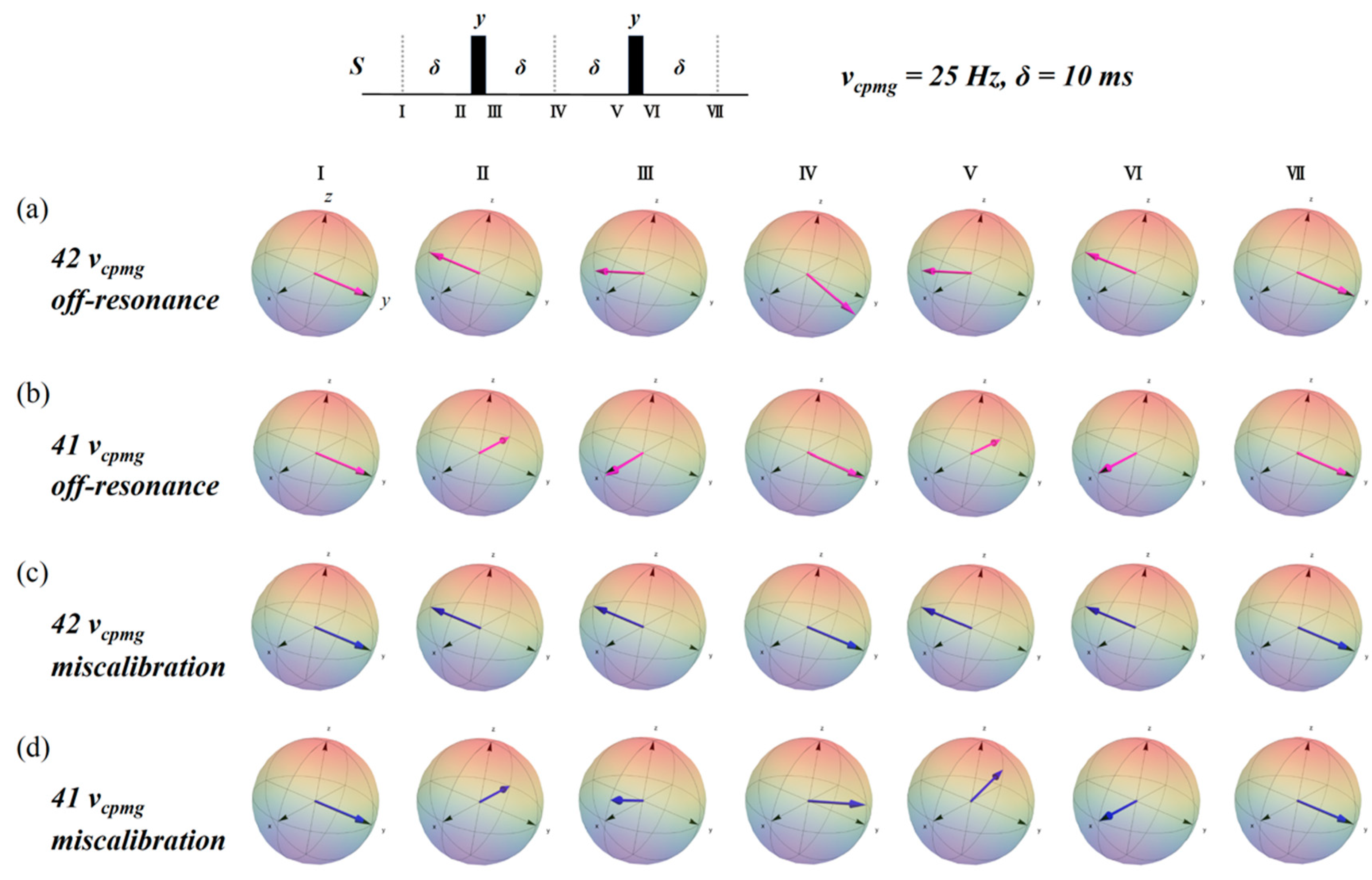
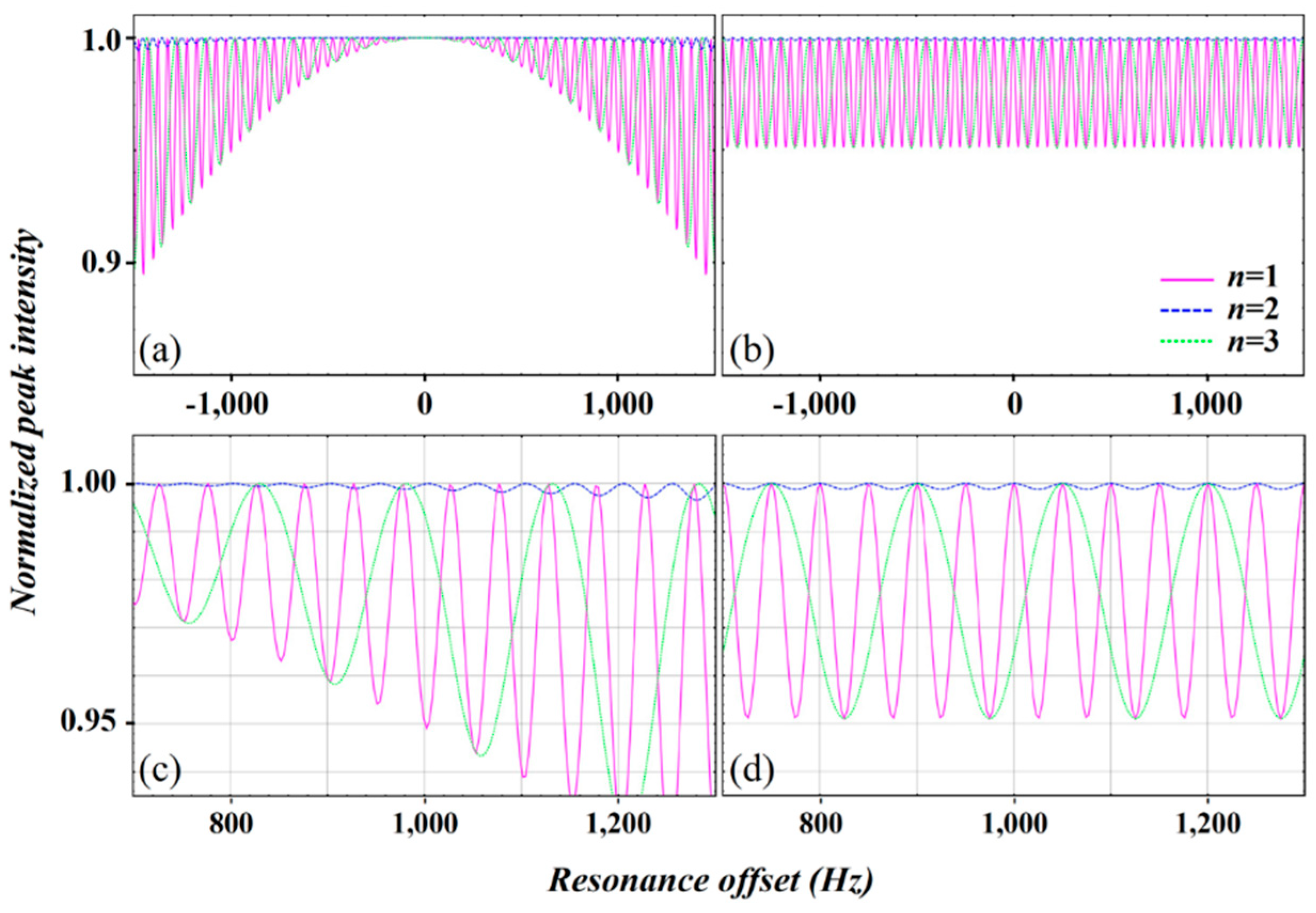
2.3. Simulation of the rc CPMG Pulse Sequence
3. Discussion
4. Materials and Methods
4.1. Sample Preparation and NMR Measurements
4.2. Simulation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akke, M.; Palmer, A.G. Monitoring macromolecular motions on microsecond to millisecond time scales by R1ρ–R1 constant relaxation time NMR spectroscopy. J. Am. Chem. Soc. 1996, 118, 911–912. [Google Scholar] [CrossRef]
- Mulder, F.A.; Mittermaier, A.; Hon, B.; Dahlquist, F.W.; Kay, L.E. Studying excited states of proteins by NMR spectroscopy. Nat. Struct. Biol. 2001, 8, 932–935. [Google Scholar] [CrossRef] [PubMed]
- Sugase, K.; Dyson, H.J.; Wright, P.E. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature 2007, 447, 1021–1025. [Google Scholar] [CrossRef] [PubMed]
- Sauerwein, A.C.; Hansen, D.F. Relaxation Dispersion NMR Spectroscopy. In Protein NMR: Biological Magnetic Resonance; Springer: Boston, MA, USA, 2015; pp. 75–132. ISBN 978-1-4899-7620-8. [Google Scholar]
- Smith, C.A.; Ban, D.; Pratihar, S.; Giller, K.; Schwiegk, C.; de Groot, B.L.; Becker, S.; Griesinger, C.; Lee, D. Population shuffling of protein conformations. Angew. Chem. Int. Ed. Engl. 2015, 54, 207–210. [Google Scholar] [CrossRef] [PubMed]
- Pratihar, S.; Sabo, T.M.; Ban, D.; Fenwick, R.B.; Becker, S.; Salvatella, X.; Griesinger, C.; Lee, D. Kinetics of the antibody recognition site in the third IgG-binding domain of protein G. Angew. Chem. Int. Ed. Engl. 2016, 55, 9567–9570. [Google Scholar] [CrossRef] [PubMed]
- Ban, D.; Smith, C.A.; de Groot, B.L.; Griesinger, C.; Lee, D. Recent advances in measuring the kinetics of biomolecules by NMR relaxation dispersion spectroscopy. Arch. Biochem. Biophys. 2017, 628, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Ikeya, T.; Ban, D.; Lee, D.; Ito, Y.; Kato, K.; Griesinger, C. Solution NMR views of dynamical ordering of biomacromolecules. Biochim. Biophys. Acta 2018, 1862, 287–306. [Google Scholar] [CrossRef] [PubMed]
- Korzhnev, D.M.; Orekhov, V.Y.; Dahlquist, F.W.; Kay, L.E. Off-resonance R1ρ relaxation outside of the fast exchange limit: An experimental study of a cavity mutant of T4 lysozyme. J. Biomol. NMR 2003, 26, 39–48. [Google Scholar] [CrossRef] [PubMed]
- Carr, H.Y.; Purcell, E.M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 1954, 94, 630–638. [Google Scholar] [CrossRef]
- Meiboom, S.; Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 1958, 29, 688–691. [Google Scholar] [CrossRef]
- Gopalan, A.B.; Hansen, D.F.; Vallurupalli, P. CPMG Experiments for Protein Minor Conformer Structure Determination. In Protein NMR: Methods in Molecular Biology; Humana Press: New York, NY, USA, 2018; pp. 223–242. ISBN 978-1-4939-7385-9. [Google Scholar]
- Chatterjee, S.D.; Ubbink, M.; van Ingen, H. Removal of slow-pulsing artifacts in in-phase 15N relaxation dispersion experiments using broadband 1H decoupling. J. Biomol. NMR 2018, 71, 69–77. [Google Scholar] [CrossRef] [PubMed]
- Loria, J.P.; Rance, M.; Palmer, A.G. A relaxation-compensated Carr−Purcell−Meiboom−Gill sequence for characterizing chemical exchange by NMR spectroscopy. J. Am. Chem. Soc. 1999, 121, 2331–2332. [Google Scholar] [CrossRef]
- Loria, J.P.; Rance, M.; Palmer, A.G. A TROSY CPMG sequence for characterizing chemical exchange in large proteins. J. Biomol. NMR 1999, 15, 151–155. [Google Scholar] [CrossRef] [PubMed]
- Ghose, R. Average Liouvillian theory in nuclear magnetic resonance—Principles, properties, and applications. Concepts Magn. Reson. 2000, 12, 152–172. [Google Scholar] [CrossRef]
- Sørensen, M.D.; Meissner, A.; Sørensen, O.W. Spin-state-selective coherence transfer via intermediate states of two-spin coherence in IS spin systems: Application to E.COSY-type measurement of J coupling constants. J. Biomol. NMR 1997, 10, 181–186. [Google Scholar] [CrossRef]
- Pervushin, K.; Riek, R.; Wider, G.; Wüthrich, K. Attenuated T2 relaxation by mutual cancellation of dipole-dipole coupling and chemical shift anisotropy indicates an avenue to NMR structures of very large biological macromolecules in solution. Proc. Natl. Acad. Sci. USA 1997, 94, 12366–12371. [Google Scholar] [CrossRef] [PubMed]
- Waluch, V.; Bradley, W.G. NMR even echo rephasing in slow laminar flow. J. Comput. Assist. Tomogr. 1984, 8, 594–598. [Google Scholar] [CrossRef] [PubMed]
- Tollinger, M.; Skrynnikov, N.R.; Mulder, F.A.; Forman-Kay, J.D.; Kay, L.E. Slow dynamics in folded and unfolded states of an SH3 domain. J. Am. Chem. Soc. 2001, 123, 11341–11352. [Google Scholar] [CrossRef] [PubMed]
- Vallurupalli, P.; Hansen, D.F.; Stollar, E.; Meirovitch, E.; Kay, L.E. Measurement of bond vector orientations in invisible excited states of proteins. Proc. Natl. Acad. Sci. USA 2007, 104, 18473–18477. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandel, A.M.; Akke, M.; Palmer, A.G. Backbone dynamics of Escherichia coli ribonuclease HI: Correlations with structure and function in an active enzyme. J. Mol. Biol. 1995, 246, 144–163. [Google Scholar] [CrossRef] [PubMed]
- Hansen, D.F.; Vallurupalli, P.; Kay, L.E. An improved 15N relaxation dispersion experiment for the measurement of millisecond time-scale dynamics in proteins. J. Phys. Chem. B 2008, 112, 5898–5904. [Google Scholar] [CrossRef] [PubMed]
- Ikegami, T.; Okada, T.; Hashimoto, M.; Seino, S.; Watanabe, T.; Shirakawa, M. Solution structure of the chitin-binding domain of Bacillus circulans WL-12 chitinase A1. J. Biol. Chem. 2000, 275, 13654–13661. [Google Scholar] [CrossRef] [PubMed]
- Yip, G.N.B.; Zuiderweg, E.R.P. A phase cycle scheme that significantly suppresses offset-dependent artifacts in the R2-CPMG 15N relaxation experiment. J. Magn. Reson. 2004, 171, 25–36. [Google Scholar] [CrossRef] [PubMed]
- Long, D.; Liu, M.; Yang, D. Accurately probing slow motions on millisecond timescales with a robust NMR relaxation experiment. J. Am. Chem. Soc. 2008, 130, 17629. [Google Scholar] [CrossRef] [PubMed]
- Myint, W.; Cai, Y.; Schiffer, C.A.; Ishima, R. Quantitative comparison of errors in 15N transverse relaxation rates measured using various CPMG phasing schemes. J. Biomol. NMR 2012, 53, 13–23. [Google Scholar] [CrossRef] [PubMed]
- Reddy, J.G.; Pratihar, S.; Ban, D.; Frischkorn, S.; Becker, S.; Griesinger, C.; Lee, D. Simultaneous determination of fast and slow dynamics in molecules using extreme CPMG relaxation dispersion experiments. J. Biomol. NMR 2018, 70, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Pervushin, K.; Riek, R.; Wider, G.; Wüthrich, K. Transverse relaxation-optimized spectroscopy (TROSY) for NMR studies of aromatic spin systems in 13C-labeled proteins. J. Am. Chem. Soc. 1998, 120, 6394–6400. [Google Scholar] [CrossRef]
- Weininger, U.; Respondek, M.; Akke, M. Conformational exchange of aromatic side chains characterized by L-optimized TROSY-selected 13C CPMG relaxation dispersion. J. Biomol. NMR 2012, 54, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Weininger, U.; Diehl, C.; Akke, M. 13C relaxation experiments for aromatic side chains employing longitudinal- and transverse-relaxation optimized NMR spectroscopy. J. Biomol. NMR 2012, 53, 181–190. [Google Scholar] [CrossRef] [PubMed]
- Weininger, U.; Brath, U.; Modig, K.; Teilum, K.; Akke, M. Off-resonance rotating-frame relaxation dispersion experiment for 13C in aromatic side chains using L-optimized TROSY-selection. J. Biomol. NMR 2014, 59, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Lundström, P.; Teilum, K.; Carstensen, T.; Bezsonova, I.; Wiesner, S.; Hansen, D.F.; Religa, T.L.; Akke, M.; Kay, L.E. Fractional 13C enrichment of isolated carbons using [1-13C]- or [2-13C]-glucose facilitates the accurate measurement of dynamics at backbone Cα and side-chain methyl positions in proteins. J. Biomol. NMR 2007, 38, 199–212. [Google Scholar] [CrossRef] [PubMed]
- Teilum, K.; Brath, U.; Lundström, P.; Akke, M. Biosynthetic 13C labeling of aromatic side chains in proteins for NMR relaxation measurements. J. Am. Chem. Soc. 2006, 128, 2506–2507. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Yu, B.; Zhang, X.; Liu, M.; Yang, D. A 15N CPMG relaxation dispersion experiment more resistant to resonance offset and pulse imperfection. J. Magn. Reson. 2015, 257, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Rance, M.; Loria, J.P.; Palmer, A.G., III. Sensitivity improvement of transverse relaxation-optimized spectroscopy. J. Magn. Reson. 1999, 136, 92–101. [Google Scholar] [CrossRef] [PubMed]
- Ishima, R. Recent developments in 15N NMR relaxation studies that probe protein backbone dynamics. Top. Curr. Chem. 2012, 326, 99–122. [Google Scholar] [CrossRef] [PubMed]
- Delaglio, F.; Grzesiek, S.; Vuister, G.W.; Zhu, G.; Pfeifer, J.; Bax, A. NMRPipe: A multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR 1995, 6, 277–293. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konuma, T.; Nagadoi, A.; Kurita, J.-i.; Ikegami, T. Analysis of Artifacts Caused by Pulse Imperfections in CPMG Pulse Trains in NMR Relaxation Dispersion Experiments. Magnetochemistry 2018, 4, 33. https://doi.org/10.3390/magnetochemistry4030033
Konuma T, Nagadoi A, Kurita J-i, Ikegami T. Analysis of Artifacts Caused by Pulse Imperfections in CPMG Pulse Trains in NMR Relaxation Dispersion Experiments. Magnetochemistry. 2018; 4(3):33. https://doi.org/10.3390/magnetochemistry4030033
Chicago/Turabian StyleKonuma, Tsuyoshi, Aritaka Nagadoi, Jun-ichi Kurita, and Takahisa Ikegami. 2018. "Analysis of Artifacts Caused by Pulse Imperfections in CPMG Pulse Trains in NMR Relaxation Dispersion Experiments" Magnetochemistry 4, no. 3: 33. https://doi.org/10.3390/magnetochemistry4030033
APA StyleKonuma, T., Nagadoi, A., Kurita, J.-i., & Ikegami, T. (2018). Analysis of Artifacts Caused by Pulse Imperfections in CPMG Pulse Trains in NMR Relaxation Dispersion Experiments. Magnetochemistry, 4(3), 33. https://doi.org/10.3390/magnetochemistry4030033




