Cu(II)–N6-Alkyladenine Complexes: Synthesis, X-ray Characterization and Magnetic Properties
Abstract
:1. Introduction
2. Results and Discussion
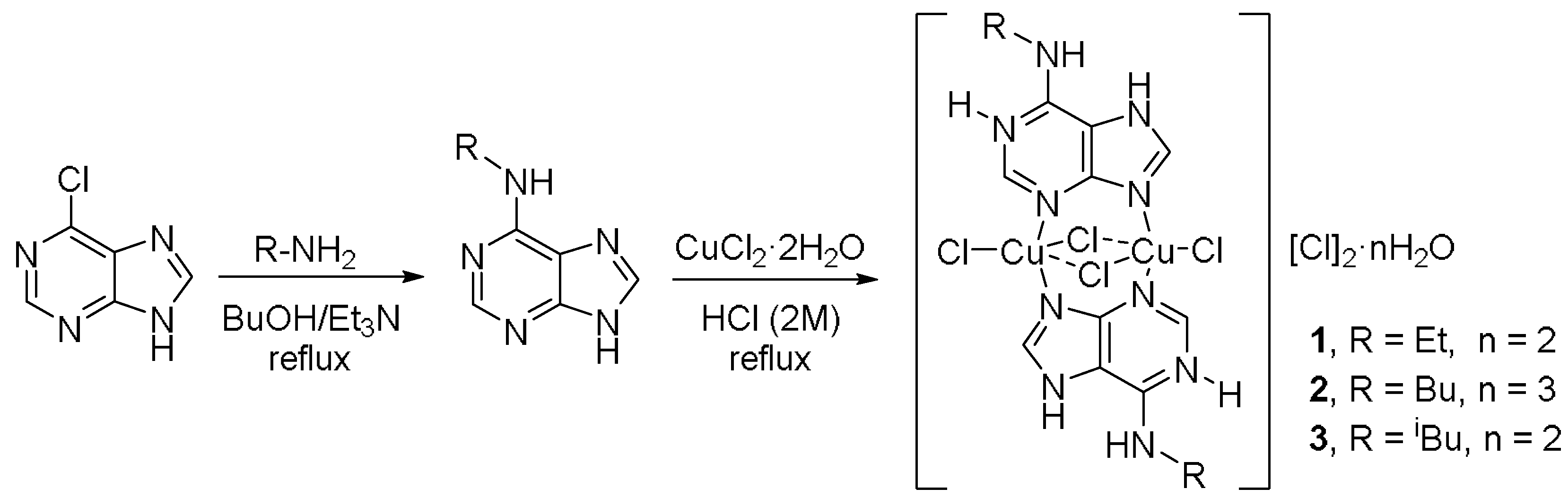
2.1. Synthesis
2.2. IR Spectra of the Complexes
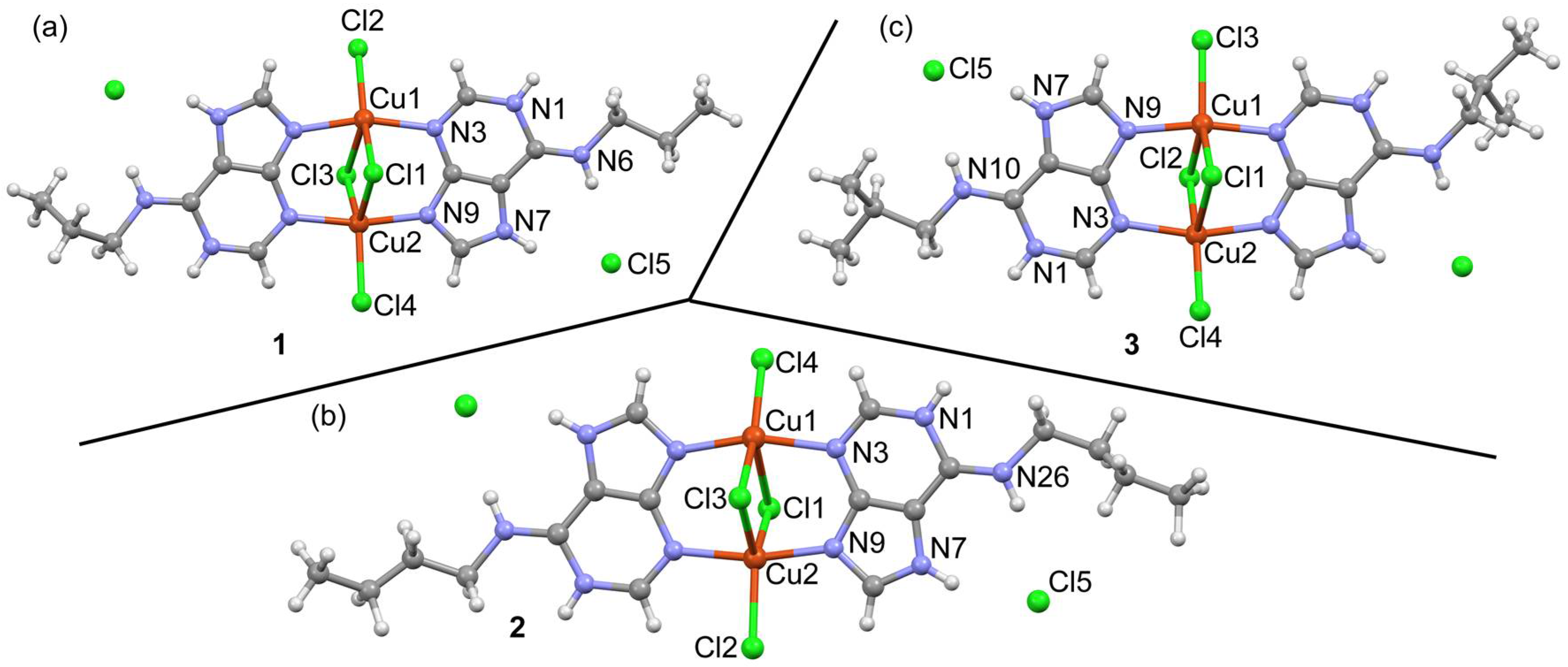
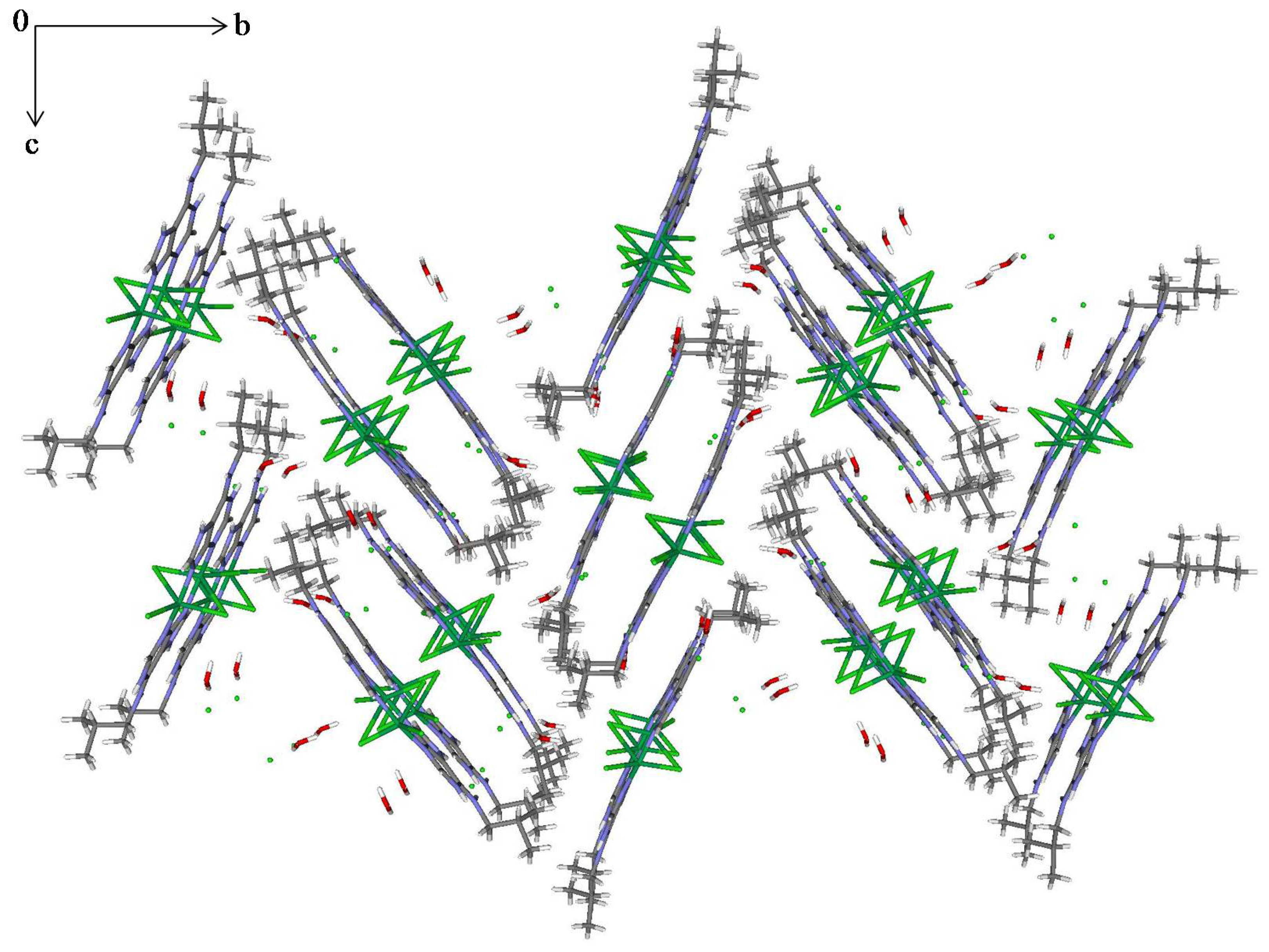
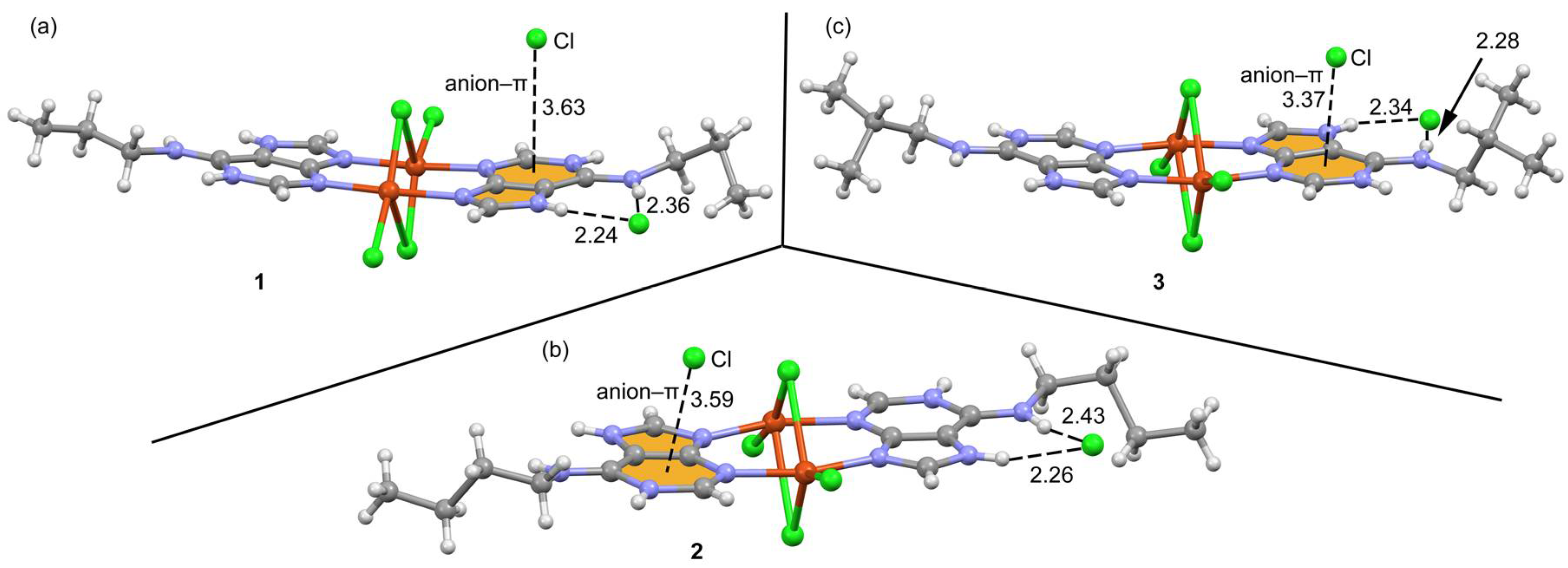
2.3. Structural Description of the Structures
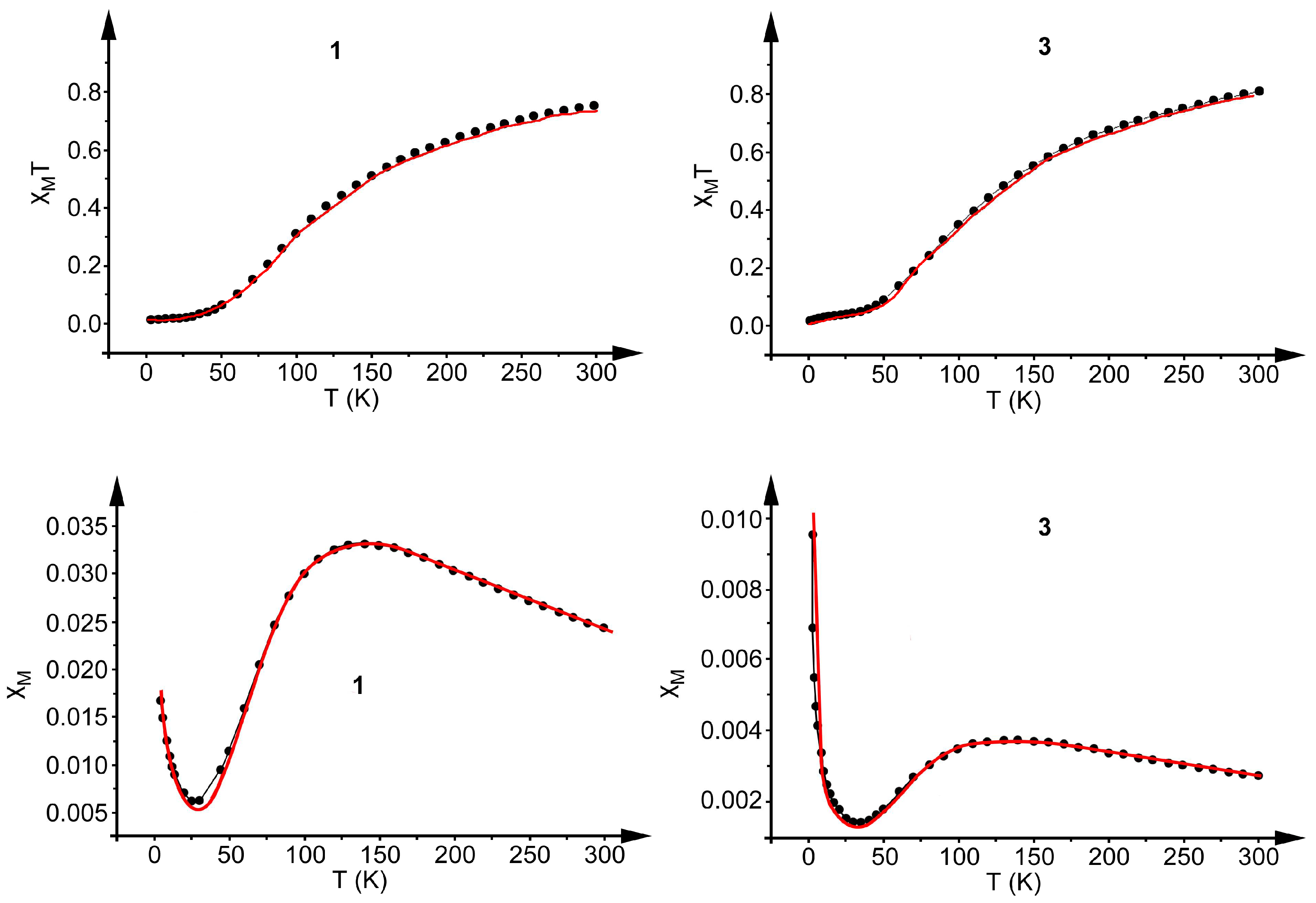
2.4. Magnetic Study
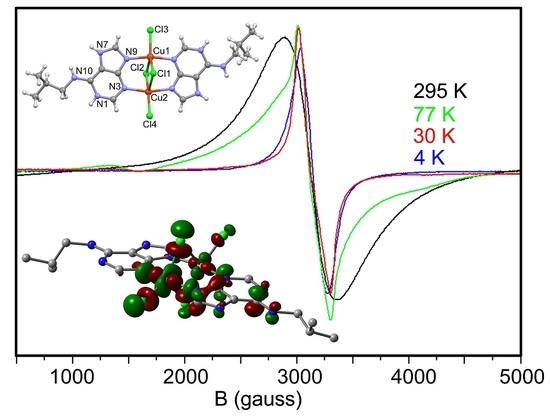
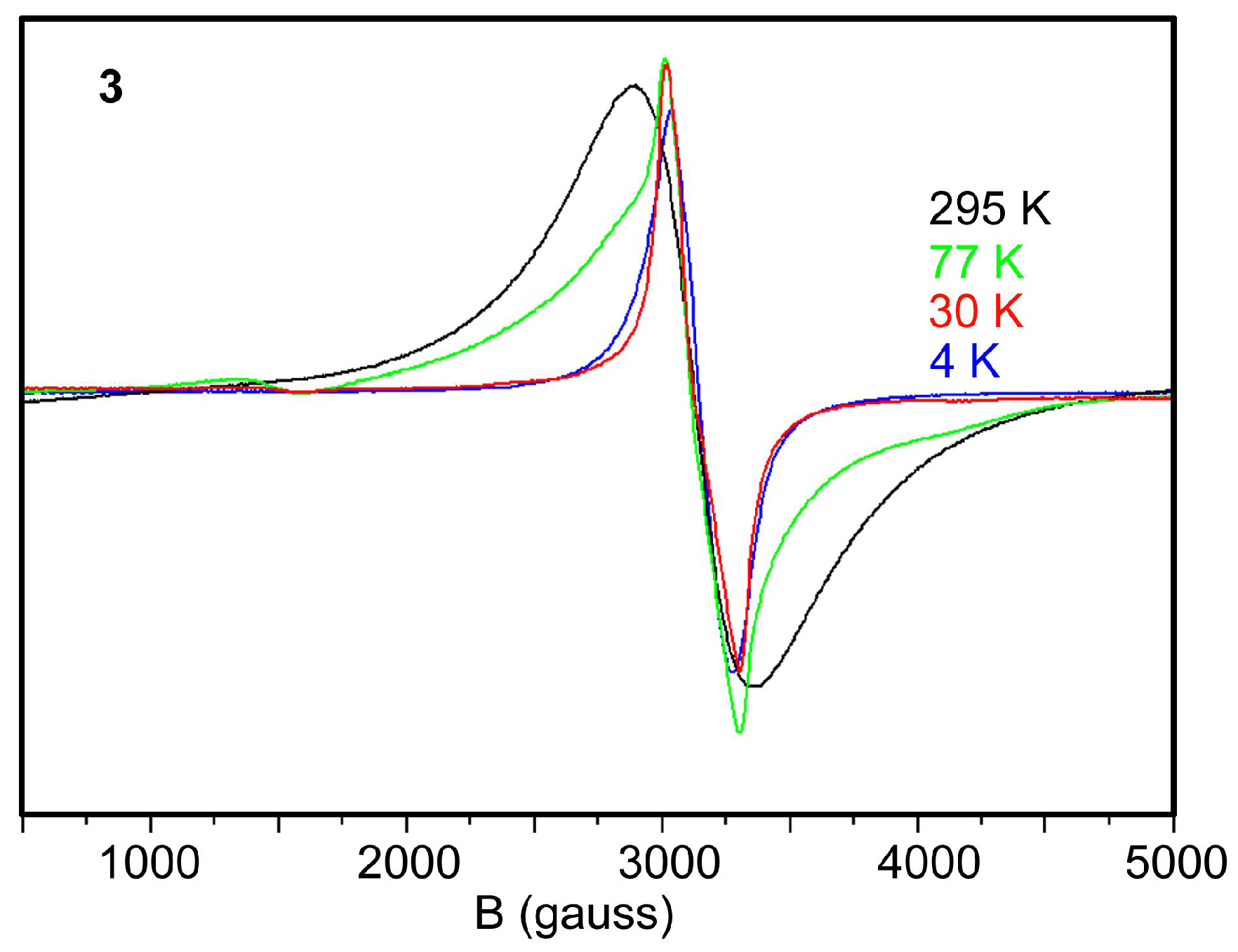
2.5. EPR Spectra
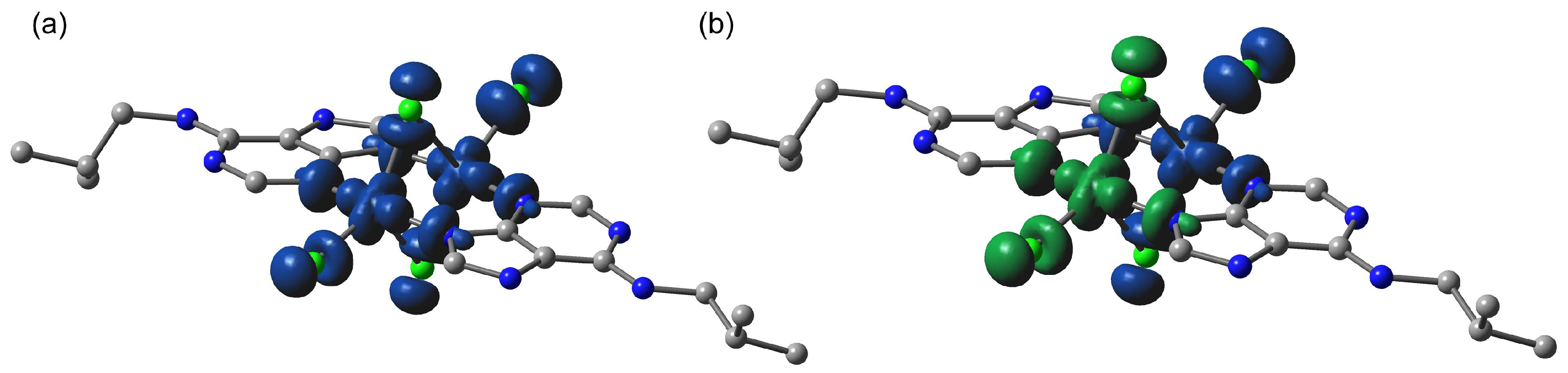
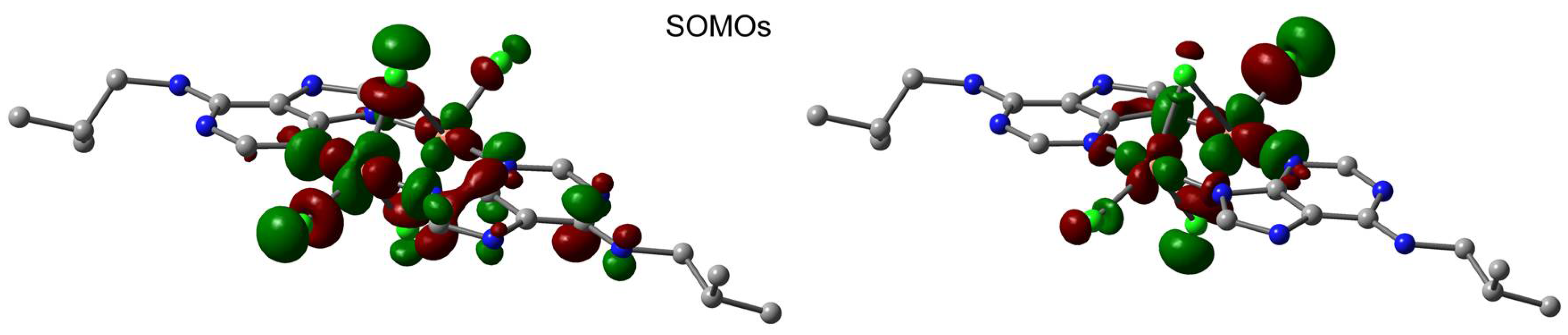
2.6. Theoretical Study
3. Materials and Methods
3.1. Starting Materials
3.2. Synthesis of the Complex [Cu2(μ–HL1)2(μ-Cl)2Cl2]Cl2·2H2O (1)
3.3. Synthesis of the Complex [Cu2(μ–HL2)2(μ-Cl)2Cl2]Cl2·3H2O (2)
3.4. Synthesis of the Complex [Cu2(μ–HL3)2(μ-Cl)2Cl2]Cl2·2H2O (2)
3.5. Physical Measurements
3.6. Computational Methodology
3.7. X-ray Crystallography
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lippert, B. Progress in Inorganic Chemistry; Karlin, K.D., Ed.; Wiley: New York, NY, USA, 2005; Volume 54, Chapter 6. [Google Scholar]
- Lippert, B. Nucleic Acid-Metal Ion Interactions; Hud, N.V., Ed.; RSC Publishing: Cambridge, UK, 2009; Chapter 2. [Google Scholar]
- Lippert, B. Multiplicity of metal ion binding patterns to nucleobases. Coord. Chem. Rev. 2000, 200–202, 487–516. [Google Scholar] [CrossRef]
- Verma, S.; Mishra, A.K.; Kumar, J. The Many Facets of Adenine: Coordination, Crystal Patterns, and Catalysis. Acc. Chem. Res. 2010, 43, 79–91. [Google Scholar] [CrossRef] [PubMed]
- Beobide, G.; Castillo, O.; Cepeda, J.; Luque, A.; Perez-Yánez, S.; Roman, P.; Thomas-Gipson, J. Metal-carboxylato-nucleobase systems: From supramolecular assemblies to 3D porous materials. Coord. Chem. Rev. 2013, 257, 2716–2736. [Google Scholar] [CrossRef]
- Yang, E.C.; Zhao, H.K.; Feng, Y.; Zhao, X.J. A Tetranuclear CuII-Based 2D Aggregate with an Unprecedented Tetradentate μ4-N1,N3,N7,N9-Adeninate Nucleobase. Inorg. Chem. 2009, 48, 3511–3513. [Google Scholar] [CrossRef] [PubMed]
- García-Teran, J.P.; Castillo, O.; Luque, A.; García-Couceiro, U.; Roman, P.; Lloret, F. One-Dimensional Oxalato-Bridged Cu(II), Co(II), and Zn(II) Complexes with Purine and Adenine as Terminal Ligands. Inorg. Chem. 2004, 43, 5761–5770. [Google Scholar] [CrossRef] [PubMed]
- Choquesillo-Lazarte, D.; Brandi-Blanco, M.P.; García-Santos, I.; Gonzalez-Perez, J.M.; Castiñeiras, A.; Niclos-Gutierrez, J. Interligand interactions involved in the molecular recognition between copper(II) complexes and adenine or related purines. Coord. Chem. Rev. 2008, 252, 1241–1256. [Google Scholar] [CrossRef]
- García-Teran, J.P.; Castillo, O.; Luque, A.; García-Couceiro, U.; Beobide, G.; Roman, P. Supramolecular architectures assembled by the interaction of purine nucleobases with metal-oxalato frameworks. Non-covalent stabilization of the 7H-adenine tautomer in the solid-state. Dalton Trans. 2006, 7, 902–911. [Google Scholar] [CrossRef] [PubMed]
- Cepeda, J.; Castillo, O.; García-Teran, J.P.; Luque, A.; Perez-Yáñez, S.; Roman, P. Supramolecular Architectures and Magnetic Properties of Self-Assembled Windmill-Like Dinuclear Copper(II) Complexes with Purine Ligands. Eur. J. Inorg. Chem. 2009, 2009, 2344–2353. [Google Scholar] [CrossRef]
- Suggs, J.W.; Dube, M.J.; Nichols, M. Synthesis and structure of a product, formed during DNA nicking with a cyclometallated nuclease, consisting of an adenine bridging two palladium(II) complexes. J. Chem. Soc. Chem. Commun. 1993, 3, 307–309. [Google Scholar] [CrossRef]
- Wei, C.H.; Jacobson, K.B. X-ray crystallographic characterization of an adenine-cadmium(II) complex, di-μ-adeninium-di-μ-aquo-tetrakis(nitrato-O,O′)dicadmium(II) dinitrate, containing a cationic nucleic acid base as a bidentate ligand. Inorg. Chem. 1981, 20, 356–363. [Google Scholar] [CrossRef]
- Gagnon, C.; Hubert, J.; Rivest, R.; Beauchamp, A.L. Crystal structure of di-μ-adeninium-disilver(I) perchlorate monohydrate. Inorg. Chem. 1977, 16, 2469–2473. [Google Scholar] [CrossRef]
- Terzis, A.; Beauchamp, A.L.; Rivest, R. Crystal and molecular structure of diaquotetra-μ-adeninediaquodicopper(I) perchlorate dihydrate, [Cu2(C5H5N5)4(H2O)2](ClO4)4+·2H2O. Inorg. Chem. 1973, 12, 1166–1170. [Google Scholar] [CrossRef]
- De Meester, P.; Skapski, A.C. Crystal structure of dichlorotetra-µ-adenine-dicopper(II) chloride hexahydrate. J. Chem. Soc. A 1971, 2167–2169. [Google Scholar] [CrossRef]
- Mastropietro, T.F.; Armentano, D.; Marino, N.; De Munno, G. Metal-nucleobase interactions in magnesium(II) and manganese(II) complexes with adenine: Influence of the anion on the non-covalent stabilization of 7H-adenine tautomer. Polyhedron 2007, 26, 4945–4954. [Google Scholar] [CrossRef]
- Gonzalez-Perez, J.M.; Alarcon-Payer, C.; Castiñeiras, A.; Pivetta, T.; Lezama, L.; Choquesillo-Lazarte, D.; Crisponi, G.; Niclós-Gutierrez, J. A Windmill-Shaped Hexacopper(II) Molecule Built Up by Template Core-Controlled Expansion of Diaquatetrakis(μ2-adeninato-N3,N9)dicopper(II) with Aqua(oxydiacetato)copper(II). Inorg. Chem. 2006, 45, 877–882. [Google Scholar] [CrossRef] [PubMed]
- Perez-Yáñez, S.; Beobide, G.; Castillo, O.; Cepeda, J.; Luque, A.; Roman, P. Directing the Formation of Adenine Coordination Polymers from Tunable Copper(II)/Dicarboxylato/Adenine Paddle-Wheel Building Units. Cryst. Growth Des. 2012, 12, 3324–3334. [Google Scholar] [CrossRef]
- Thomas-Gipson, J.; Beobide, G.; Castillo, O.; Fröba, M.; Hoffmann, F.; Luque, A.; Pérez-Yáñez, S.; Román, P. Paddle-Wheel Shaped Copper(II)-Adenine Discrete Entities as Supramolecular Building Blocks to Afford Porous Supramolecular Metal-Organic Frameworks (SMOFs). Cryst. Growth Des. 2014, 14, 4019–4029. [Google Scholar] [CrossRef]
- Reger, D.L.; Pascui, A.E.; Smith, M.D.; Jezierska, J.; Ozarowski, A. Halide and Hydroxide Linearly Bridged Bimetallic Copper(II) Complexes: Trends in Strong Antiferromagnetic Superexchange Interactions. Inorg. Chem. 2012, 51, 7966–7968. [Google Scholar] [CrossRef] [PubMed]
- Reger, D.L.; Pascui, A.E.; Smith, M.D.; Jezierska, J.; Ozarowski, A. Syntheses, Structural, Magnetic, and Electron Paramagnetic Resonance Studies of Monobridged Cyanide and Azide Dinuclear Copper(II) Complexes: Antiferromagnetic Superexchange Interactions. Inorg. Chem. 2015, 54, 1487–1500. [Google Scholar] [CrossRef] [PubMed]
- Jana, S.; Shaw, B.K.; Bhowmik, P.; Harms, K.; Drew, M.G.B.; Chattopadhyay, S.; Saha, S.K. Field-Induced Ferromagnetism and Multiferroic Behavior in End-on Pseudohalide-Bridged Dinuclear Copper(II) Complexes with Tridentate Schiff Base Blocking Ligands. Inorg. Chem. 2014, 53, 8723–8734. [Google Scholar] [CrossRef] [PubMed]
- Thomas-Gipson, J.; Pérez-Aguirre, R.; Beobide, G.; Castillo, O.; Luque, A.; Pérez-Yáñez, S.; Román, P. Unravelling the Growth of Supramolecular Metal-Organic Frameworks Based on Metal-Nucleobase Entities. Cryst. Growth Des. 2015, 15, 975–983. [Google Scholar] [CrossRef]
- Tsuboi, M.; Takahashi, S.; Harada, I. Physiochemical Properties of Nucleic Acids; Duchesne, J., Ed.; Academic Press: London, UK, 1973; Volume 2, pp. 91–145. [Google Scholar]
- Pérez-Aguirre, R.; Beobide, G.; Castillo, O.; de Pedro, I.; Pérez-Yáñez, S. Supramolecular extended systems based on discrete paddle-wheel shaped metal-adeninate entities. Inorg. Chim. Acta 2016, 452, 222–228. [Google Scholar] [CrossRef]
- Fiol, J.J.; Barcelo-Oliver, M.; Tasada, A.; Frontera, A.; Terron, A.; Garcia-Raso, A. Structural characterization, recognition patterns and theoretical calculations of long-chain N-alkyl substituted purine and pyrimidine bases as ligands: On the importance of anion–π interactions. Coord. Chem. Rev. 2013, 257, 2705–2715. [Google Scholar] [CrossRef]
- Garcia-Raso, A.; Alberti, F.M.; Fiol, J.J.; Lagos, Y.; Torres, M.; Molins, E.; Mata, I.; Estarellas, C.; Frontera, A.; Quinonero, D.; et al. A Combined Experimental and Theoretical Study of Anion–π Interactions in N6- and N9-Decyladenine Salts. Eur. J. Org. Chem. 2010, 2010, 5171–5180. [Google Scholar] [CrossRef]
- Garcia-Raso, A.; Alberti, F.M.; Fiol, J.J.; Tasada, A.; Barcelo-Oliver, M.; Molins, E.; Escudero, D.; Frontera, A.; Quinonero, D.; Deya, P.M. Anion–π Interactions in Bisadenine Derivatives: A Combined Crystallographic and Theoretical Study. Inorg. Chem. 2007, 46, 10724–10735. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, E.; Rodríguez-Forte, A.; Cano, J.; Alvarez, S.; Alemany, P. About the calculation of exchange coupling constants in polynuclear transition metal complexes. J. Comput. Chem. 2013, 24, 982–989. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1998, 38, 3098–3100. [Google Scholar] [CrossRef]
- Rassolov, V.A.; Ratner, M.A.; Pople, J.A.; Redfern, P.C.; Curtiss, L.A. 6-31G* Basis Set for Third-Row Atoms. J. Comput. Chem. 2001, 22, 976–984. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Baryshnikov, G.V.; Minaev, B.F.; Baryshnikova, A.A.; Ågren, H. Anion-induced exchange interactions in binuclear complexes of Cu(II) with flexible hexadentate bispicolylamidrazone ligands. Chem. Phys. Lett. 2016, 661, 48–52. [Google Scholar] [CrossRef]
- Baryshnikov, G.V.; Minaev, B.F.; Baryshnikova, A.T.; Ågren, H. A computational study of structural and magnetic properties of bi- and trinuclear Cu(II) complexes with extremely long Cu---Cu distances. Chem. Phys. 2017, 491, 48–55. [Google Scholar] [CrossRef]
- Walker, N.; Stuart, D. An empirical method for correcting diffractometer data for absorption effects. Acta Crystallogr. A 1983, 39, 158–166. [Google Scholar] [CrossRef]
- Farrugia, L.J. WinGX suite for small-molecule single-crystal crystallography. J. Appl. Crystallogr. 1999, 32, 837–838. [Google Scholar] [CrossRef]
- Burla, M.C.; Camalli, M.; Carrozzini, B.; Cascarano, G.L.; Giacovazzo, C.; Polidori, G.; Spagna, R. SIR2002: The program. J. Appl. Crystallogr. 2003, 36, 1103. [Google Scholar] [CrossRef]
- Burla, M.C.; Caliandro, R.; Camalli, M.; Carrozzini, B.; Cascarano, G.L.; De Caro, L.; Giacovazzo, C.; Polidori, G.; Spagna, R. SIR2004: An improved tool for crystal structure determination and refinement. J. Appl. Crystallogr. 2005, 38, 381–388. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. 2015, 71, 3–8. [Google Scholar] [CrossRef]
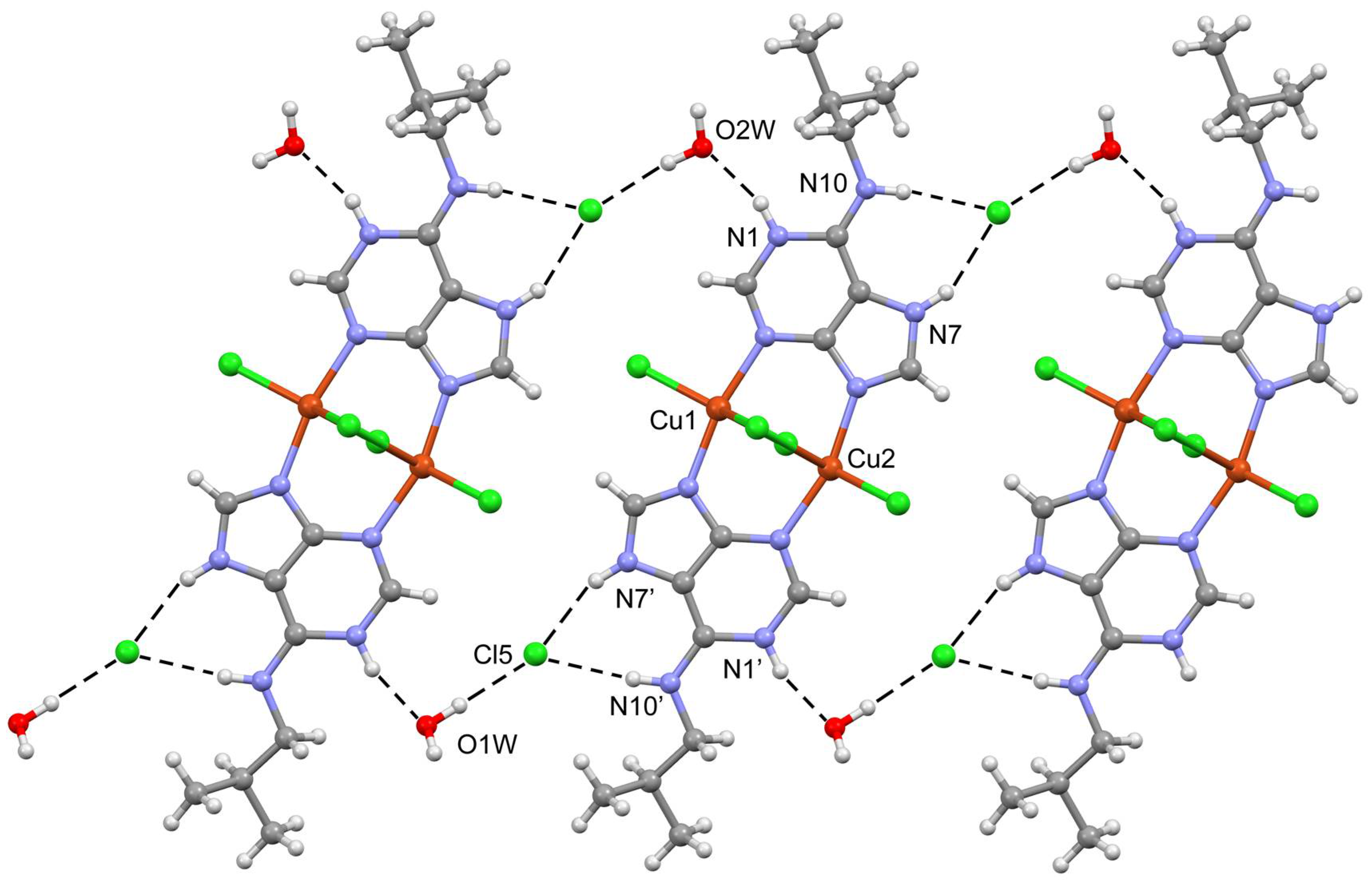
| D-H···A 1 | d(H···A) | d(D···A) | <(DHA) |
|---|---|---|---|
| N(1)-H(1)···O(1W) #1 | 1.83 | 2.671(15) | 165.2 |
| N(1′)-H(1′)···O(2W) #3 | 1.88 | 2.707(13) | 160.3 |
| N(7)-H(7)···Cl(5) #2 | 2.31 | 3.132(11) | 159.0 |
| N(7′)-H(7′)···Cl(6) #4 | 2.24 | 3.045(11) | 156.7 |
| N(10)-H(10)···Cl(5) #2 | 2.34 | 3.196(12) | 172.0 |
| N(10′)-H(10′)···Cl(6) #4 | 2.36 | 3.210(12) | 168.0 |
| O(1W)-H(1W2)···Cl(5) | 2.32(15) | 3.078(13) | 141(20) |
| O(2W)-H(2W2)···N(3′) #5 | 2.84(12) | 3.258(14) | 110(9) |
| O(2W)-H(2W1)···N(1′) #5 | 2.99(17) | 3.476(16) | 116(14) |
| O(1W)-H(1W1)···Cl(2) | 2.34(4) | 3.208(12) | 161(9) |
| O(2W)-H(2W2)···Cl(3) #5 | 2.35(3) | 3.238(11) | 173(12) |
| Atom Label | High Spin | Low Spin |
|---|---|---|
| Cu1 | 0.56 | −0.57 |
| Cu2 | 0.59 | 0.57 |
| Cl1 | 0.14 | −0.12 |
| Cl2 | 0.14 | 0.13 |
| Cl3 | 0.17 | −0.17 |
| Cl4 | 0.14 | 0.15 |
| N3/N3′ | 0.05 | 0.05/−0.05 |
| N9/N9′ | 0.07 | 0.07/−0.07 |
| C4/C4′ | 0.01 | 0.00 |
| Compound | 1 | 2 | 3 |
|---|---|---|---|
| Empirical formula | C18H34Cl6Cu2N10O3 | C16H28Cl6Cu2N10O2 | C18H32Cl6Cu2N10O2 |
| Formula weight | 778.33 | 732.26 | 760.31 |
| Temperature (K) | 294 | 294 | 294 |
| Wavelength (Å) | MoKα | MoKα | MoKα |
| Crystal system | triclinic | triclinic | monoclinic |
| Space group | P-1 | P-1 | P21/c |
| Unit cell dimensions | |||
| a (Å) | 9.508(3) | 9.529(2) | 9.521(3) |
| b (Å) | 13.341(4) | 11.482(3) | 23.356(8) |
| c (Å) | 14.067(3) | 14.226(4) | 13.621(9) |
| α (°) | 66.62(3) | 67.80(2) | 90 |
| β (°) | 73.68(2) | 75.17(2) | 99.35(4) |
| ϒ (°) | 81.53(2) | 88.03(2) | 90 |
| Volume (Å3) | 1570.5(8) | 1389.7(6) | 2989(2) |
| Z | 2 | 2 | 4 |
| Density (calculated) (Mg/m3) | 1.646 | 1.75 | 1.69 |
| Absorption coefficient (mm−1) | 1.904 | 2.143 | 1.996 |
| F(000) | 792 | 740 | 1544 |
| Crystal size (mm3) | 0.32 × 0.24 × 0.17 | 0.3 × 0.3 × 0.3 | 0.46 × 0.28 × 0.13 |
| Theta range for data collection (°) | 1.627 to 24.974 | 1.602 to 24.969 | 2.168 to 28.445 |
| Index ranges | −10 ≤ h ≤ 11 −14 ≤ k ≤ 15 0 ≤ l ≤ 16 | −10 ≤ h ≤ 11 −12 ≤ k ≤ 13 0 ≤ l ≤ 16 | −12 ≤ h ≤ 12 −31 ≤ k ≤ 0 0 ≤ l ≤ 18 |
| Reflections collected | 5520 | 4872 | 7507 |
| Independent reflections | 5520 | 4872 | 7507 |
| Completeness to final theta (%) | 100% | 99.8% | 99.5% |
| Absorption correction | Empirical (DIFABS) | Empirical (DIFABS) | Empirical (DIFABS) |
| Max. and min. transmission | 0.7235 and 0.4332 | 0.9385 and 0.5657 | 0.781 and 0.46 |
| Refinement method | Full-matrix least-squares on F2 | ||
| Data/restraints/parameters | 5520/489/506 | 4872/332/343 | 7507/6/360 |
| Goodness-of-fit on F2 | 0.944 | 0.896 | 0.892 |
| Final R indices [I > 2sigma(I)] | R1 = 0.0717, wR2 = 0.1335 | R1 = 0.0891, wR2 = 0.1469 | R1 = 0.0489, wR2 = 0.1098 |
| R indices (all data) | R1 = 0.171, wR2 = 0.1609 | R1 = 0.2495, wR2 = 0.1838 | R1 = 0.2125, wR2 = 0.1319 |
| Largest diff. peak and hole (e.Å−3) | 0.426 and −0.536 | 1.032 and −0.72 | 0.91 and −0.7 |
| CCDC code | 1840949 | 1840950 | 1840951 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez, M.S.; Bauzá, A.; Caubet, A.; García-Raso, Á.; Terrón, Á.; Fiol, J.J.; Molins, E.; Barceló-Oliver, M.; Frontera, A. Cu(II)–N6-Alkyladenine Complexes: Synthesis, X-ray Characterization and Magnetic Properties. Magnetochemistry 2018, 4, 24. https://doi.org/10.3390/magnetochemistry4020024
Martínez MS, Bauzá A, Caubet A, García-Raso Á, Terrón Á, Fiol JJ, Molins E, Barceló-Oliver M, Frontera A. Cu(II)–N6-Alkyladenine Complexes: Synthesis, X-ray Characterization and Magnetic Properties. Magnetochemistry. 2018; 4(2):24. https://doi.org/10.3390/magnetochemistry4020024
Chicago/Turabian StyleMartínez, María Soledad, Antonio Bauzá, Amparo Caubet, Ángel García-Raso, Ángel Terrón, Juan J. Fiol, Elies Molins, Miquel Barceló-Oliver, and Antonio Frontera. 2018. "Cu(II)–N6-Alkyladenine Complexes: Synthesis, X-ray Characterization and Magnetic Properties" Magnetochemistry 4, no. 2: 24. https://doi.org/10.3390/magnetochemistry4020024
APA StyleMartínez, M. S., Bauzá, A., Caubet, A., García-Raso, Á., Terrón, Á., Fiol, J. J., Molins, E., Barceló-Oliver, M., & Frontera, A. (2018). Cu(II)–N6-Alkyladenine Complexes: Synthesis, X-ray Characterization and Magnetic Properties. Magnetochemistry, 4(2), 24. https://doi.org/10.3390/magnetochemistry4020024