Electronic Structures, and Optical and Magnetic Properties of Quadruple-Decker Phthalocyanines
Abstract
:1. Introduction
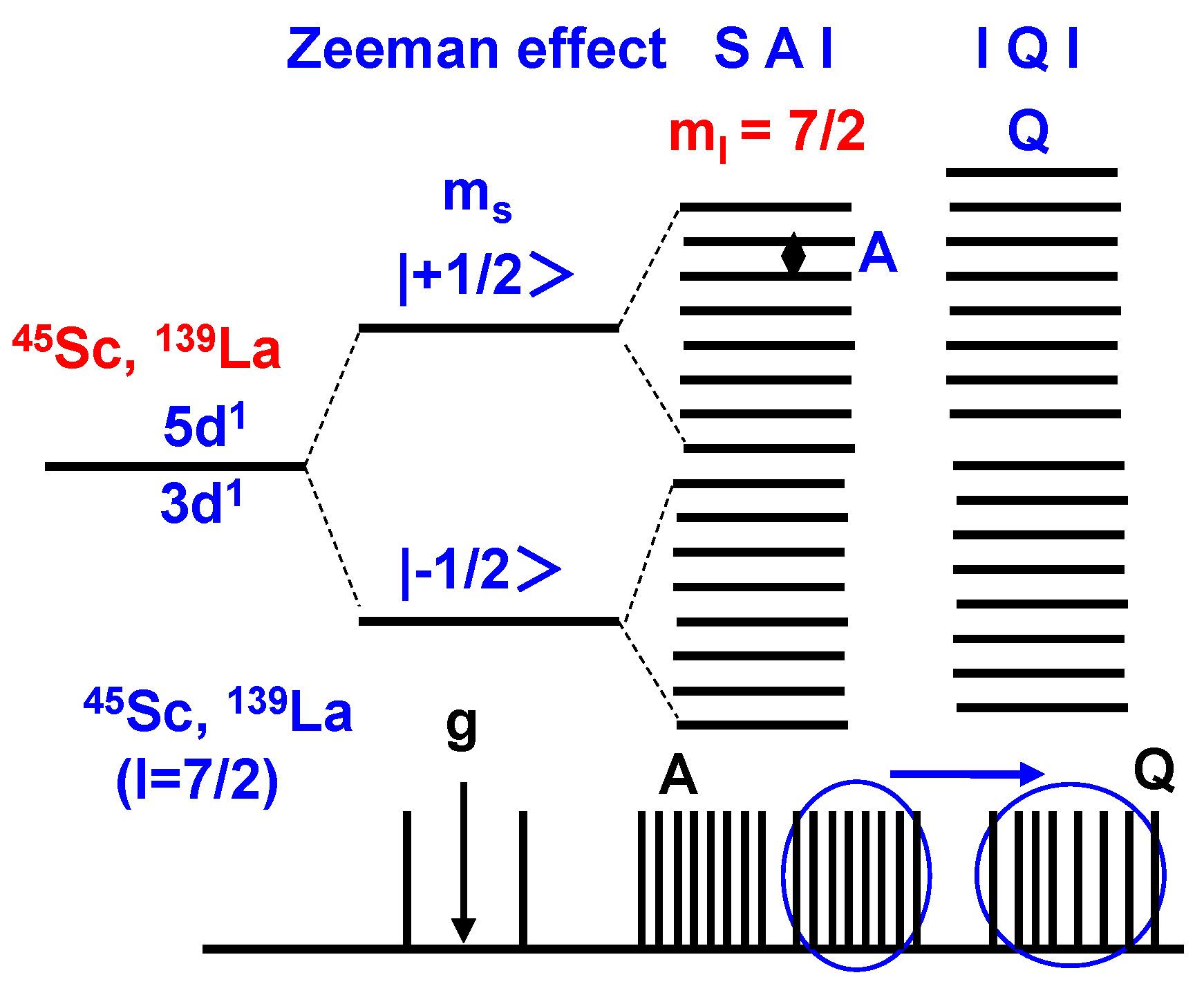
2. Results and Discussion
3. Calculation Method
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Warner, M.; Din, S.; Tupitsyn, I.S.; Morley, G.W.; Stoneham, A.M.; Gardener, J.A.; Wu, Z.; Fisher, A.J.; Heutz, S.; Kay, C.W.M.; et al. Potential for spin-based information processing in a thin-film molecular semiconductor. Nature 2013, 503, 504–508. [Google Scholar] [CrossRef] [PubMed]
- Morton, J.J.L.; Tyryshkin, A.M.; Ardavan, A.; Benjamin, S.C.; Porfyrakis, K.; Lyon, S.A.; Briggs, G.A.D. The N@C60 nuclear spin qubit: Bang-bang decoupling and ultrafast phase gates. Phys. Status Solidi B 2006, 243, 3028–3031. [Google Scholar] [CrossRef]
- Popov, A.A.; Shustova, N.B.; Svitova, A.L.; Mackey, M.A.; Coumbe, C.E.; Phillips, J.P.; Stevenson, S.; Strauss, S.H.; Boltalina, O.V.; Dunsch, L. Redox-tuning endohedral fullerene spin states: From the dication to the trianion radical of Sc3N@C80(CF3)2 in five reversible single-electron steps. Chem. Eur. J. 2010, 16, 4721–4724. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A.; Oku, T. Electronic structure and magnetic properties of endohedral metallofullerenes based on mixed metal cluster within fullerene cage with trifluoromethyl groups. J. Phys. Conf. Ser. 2013, 433, 012004. [Google Scholar] [CrossRef]
- Suzuki, A.; Oku, T. Influence of chemical substitution in ScxY3-xN@C80(CF3)n endohedral fullerenes on magnetic properties. Physica B 2013, 428, 18–26. [Google Scholar] [CrossRef]
- Svitova, A.L.; Krupskaya, Y.; Samoylova, N.; Kraus, R.; Geck, J.; Dunsch, L.; Popov, A.A. Magnetic moments and exchange coupling in nitride cluster fullerenes GdxSc3–xN@C80 (x = 1–3). Dalton Trans. 2014, 43, 7387–7390. [Google Scholar] [CrossRef] [PubMed]
- Dreiser, J.; Westerström, R.; Zhang, Y.; Popov, A.A.; Dunsch, L.; Krämer, K.; Liu, S.X.; Decurtins, S.; Greber, T. The metallofullerene field-induced single-ion magnet HoSc2N@C80. Chem. A Eur. J. 2014, 20, 13536–13540. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Krylov, D.; Rosenkranz, M.; Schiemenz, S.; Popov, A.A. Magnetic anisotropy of endohedral lanthanide ions: Paramagnetic NMR study of MSc2N@C80-Ih with M running through the whole 4f row. Chem. Sci. 2015, 6, 2328–2341. [Google Scholar] [CrossRef]
- Suzuki, A.; Oku, T. Electronic structures and magnetic properties of Sc2YN@C80(CF3)2 dimer. Jpn. J. Appl. Phys. 2014, 53, 05FN01. [Google Scholar] [CrossRef]
- Abe, Y.; Suzuki, A.; Oku, T. Electronic structures and magnetic properties of Sc4O2@C80(CF3)n (n = 2 and 4). Jpn. J. Appl. Phys. 2014, 53, 05FN02. [Google Scholar] [CrossRef]
- Valencia, R.; Fortea, A.R.; Stevenson, S.; Balch, A.L.; Poblet, J.M. Electronic structures of scandium oxide endohedral metallofullerenes, Sc4(μ3-O)n@Ih-C80 (n = 2, 3). Inorg. Chem. 2009, 48, 5957–5961. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A.; Oku, T. Geometrical effects of (14N@C60)2, 14N@C60 and C59N endohedral fullerenes within single-walled carbon nanotube as peapods on electronic structure and magnetic properties. Physica B 2011, 406, 3274–3278. [Google Scholar] [CrossRef]
- Suzuki, A.; Oku, T. Electronic structure and magnetic properties of 31P@C60-SWCNT as peapods. J. Phys. Conf. Ser. 2012, 352, 012012. [Google Scholar] [CrossRef]
- Warner, J.H.; Watt, A.A.R.; Ge, L.; Porfyrakis, K.; Akachi, T.; Okimoto, H.; Ito, Y.; Ardavan, A.; Montanari, B.; Jefferson, J.H.; et al. Dynamics of paramagnetic metallofullerenes in carbon nanotube peapods. Nano Lett. 2008, 8, 1005–1010. [Google Scholar] [CrossRef] [PubMed]
- Mizuochi, N.; Neumann, P.; Rempp, F.; Beck, J.; Jacques, V.; Siyushev, P.; Nakamura, K.; Twitchen, D.J.; Watanabe, H.; Yamasaki, S.; et al. Coherence of single spins coupled to a nuclear spin bath of varying density. Phys. Rev. B 2009, 80, 041201. [Google Scholar] [CrossRef]
- Vandersypen, L.M.K.; Steffen, M.; Breyta, G.; Yannoni, C.S.; Sherwood, M.H.; Chuang, I.L. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 2001, 414, 883–887. [Google Scholar] [CrossRef] [PubMed]
- Atzori, M.; Tesi, L.; Morra, E.; Chiesa, M.; Sorace, L.; Sessoli, R. Room-temperature quantum coherence and Rabi oscillations in vanadyl phthalocyanine: Toward multifunctional molecular spin qubits. J. Am. Chem. Soc. 2016, 138, 2154–2157. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.S.; Deng, Y.F.; Zheng, Y.Z. The rise of single-ion magnets as spin qubits. Magnetochemistry 2016, 2, 40. [Google Scholar] [CrossRef]
- Thiele, S.; Balestro, F.; Ballou, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W. Electrically driven nuclear spin resonance in single-molecule magnets. Science 2014, 344, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
- Komeda, T.; Isshiki, H.; Liu, J.; Zhang, Y.F.; Lorente, N.; Katoh, K.; Breedlove, B.K.; Yamashita, M. Observation and electric current control of a local spin in a single-molecule magnet. Nat. Commun. 2011, 2, 217. [Google Scholar] [CrossRef] [PubMed]
- Isshiki, H.; Liu, J.; Katoh, K.; Yamashita, M.; Miyasaka, H.; Breedlove, B.K.; Takaishi, S.; Komeda, T. Scanning tunneling microscopy investigation of tris(phthalocyaninato)yttrium triple-decker molecules deposited on Au(111). J. Phys. Chem. C 2010, 114, 12202–12206. [Google Scholar] [CrossRef]
- Shang, H.; Zeng, S.; Wang, H.; Dou, J.; Jiang, J. Peripheral substitution: An easy way to tuning the magnetic behavior of tetrakis(phthalocyaninato)dysprosium(III) SMMs. Sci. Rep. 2015, 5, 8838. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A.; Oku, T. Effects of central metal on electronic structure, magnetic properties, infrared and Raman spectra of double-decker phthalocyanine. Appl. Surf. Sci. 2016, 380, 127–134. [Google Scholar] [CrossRef]
- Suzuki, A.; Oku, T. Theoretical study of NMR, infrared and Raman spectra on triple-decker phthalocyanines. AIP Conf. Proc. 2016, 1709, 020013. [Google Scholar] [CrossRef]
- Katoh, K.; Komeda, T.; Yamashita, M. Surface morphologies, electronic structures, and Kondo effect of lanthanide(III)-phthalocyanine molecules on Au(111) by using STM, STS and FET properties for next generation devices. Dalton Trans. 2010, 39, 4708–4723. [Google Scholar] [CrossRef] [PubMed]
- Urdampilleta, M.; Klayatskaya, S.; Ruben, M.; Wernsdorfer, W. Magnetic interaction between a radical spin and a single-molecule magnet in a molecular spin-valve. ACS Nano 2015, 9, 4458–4464. [Google Scholar] [CrossRef] [PubMed]
- Horii, Y.; Katoh, K.; Yasuda, N.; Breedlove, B.K.; Yamashita, M. Effects of f-f interactions on the single-molecule magnet properties of terbium(III)–phthalocyaninato quintuple-decker complexes. Inorg. Chem. 2015, 54, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Horii, Y.; Katoh, K.; Cosquer, G.; Breedlove, B.K.; Yamashita, M. Weak DyIII–DyIII interactions in DyIII–phthalocyaninato multiple-decker single-molecule magnets effectively suppress magnetic relaxation. Inorg. Chem. 2016, 55, 11782–11790. [Google Scholar] [CrossRef] [PubMed]
- Morita, T.; Katoh, K.; Breedlove, B.K.; Yamashita, M. Controlling the dipole-dipole interactions between terbium(III) phthalocyaninato triple-decker moieties through spatial control using a fused phthalocyaninato ligand. Inorg. Chem. 2013, 52, 13555–13561. [Google Scholar] [CrossRef] [PubMed]
- Fukuda, T.; Matsumura, K.; Ishikawa, N. Influence of intramolecular f-f Interactions on nuclear spin driven quantum tunneling of magnetizations in quadruple-decker phthalocyanine complexes containing two terbium or dysprosium magnetic centers. J. Phys. Chem. A 2013, 117, 10447–10454. [Google Scholar] [CrossRef] [PubMed]
- Slater, J.C. Atomic Radii in Crystals. J. Chem. Phys. 2016, 41, 3199. [Google Scholar] [CrossRef]
- Sumimoto, M.; Kawashima, Y.; Horia, K.; Fujimoto, H. Theoretical study on the stability of double-decker type metal phthalocyanines, M(Pc)2 and M(Pc)2+ (M = Ti, Sn and Sc): A critical assessment on the performance of density functionals. Phys. Chem. Chem. Phys. 2015, 17, 6478–6483. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, N.; Iino, T.; Kaizu, Y. Study of 1H-NMR spectra of dinuclear complexes of heavy lanthanides with phthalocyanines based on separation of the effects of two paramagnetic centers. J. Phys. Chem. A 2003, 107, 7879–7884. [Google Scholar] [CrossRef]
- Polovkova, M.A.; Martynov, A.G.; Birin, K.P.; Nefedov, S.E.; Gorbunova, Y.G.; Tsivadze, A.Y. Determination of the structural parameters of heteronuclear(phthalocyaninato)bis(crownphthalo cyaninato)lanthanide(III)triple-deckers in solution by simultaneous analysis of NMR and single-crystal X-ray data. Inorg. Chem. 2016, 55, 9258–9269. [Google Scholar] [CrossRef] [PubMed]
- Abragam, A. Principles of Nuclear Magnetism; Oxford Clarendon Press: Oxford, UK, 1961. [Google Scholar]
- Suzuki, A.; Oku, T. Role of scandium atom in ScxY3-xN@C80(CF3)n (n = 0, 2) on nuclear quadrupole interaction, electric field gradient and asymmetric parameters. Microelectron. Eng. 2014, 126, 113–117. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1998, 98, 1372–1377. [Google Scholar] [CrossRef]
- Cheeseman, J.R.; Trucks, G.W.; Keith, T.A.; Frisch, M.J. A comparison of models for calculating nuclear magnetic resonance shielding tensors. J. Chem. Phys. 1996, 104, 5497–5509. [Google Scholar] [CrossRef]
- Liu, J.; Liang, W. Analytical approach for the excited-state Hessian in time-dependent density functional theory: Formalism, implementation, and performance. J. Chem. Phys. 2011, 135, 184111. [Google Scholar] [CrossRef] [PubMed]

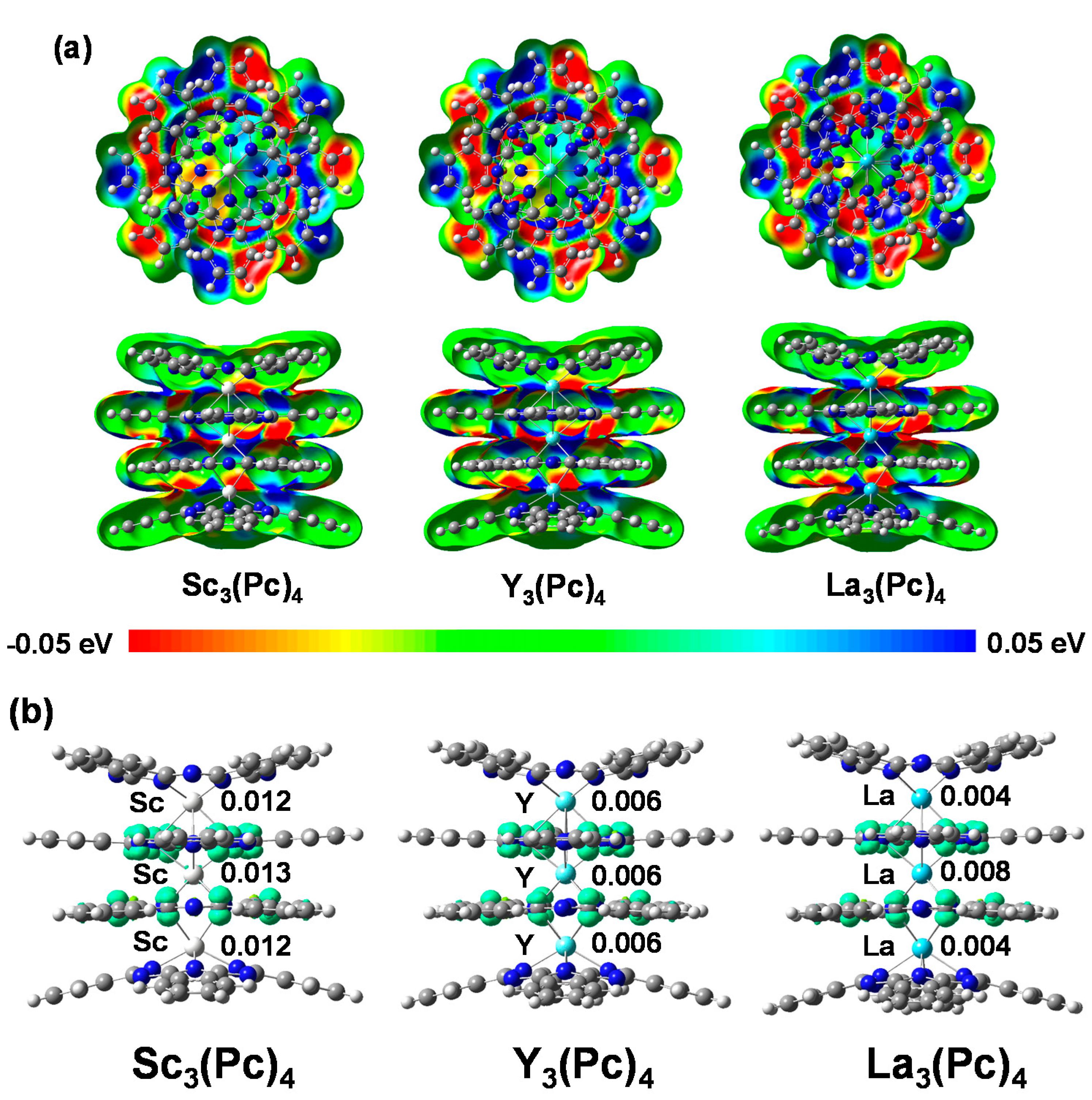
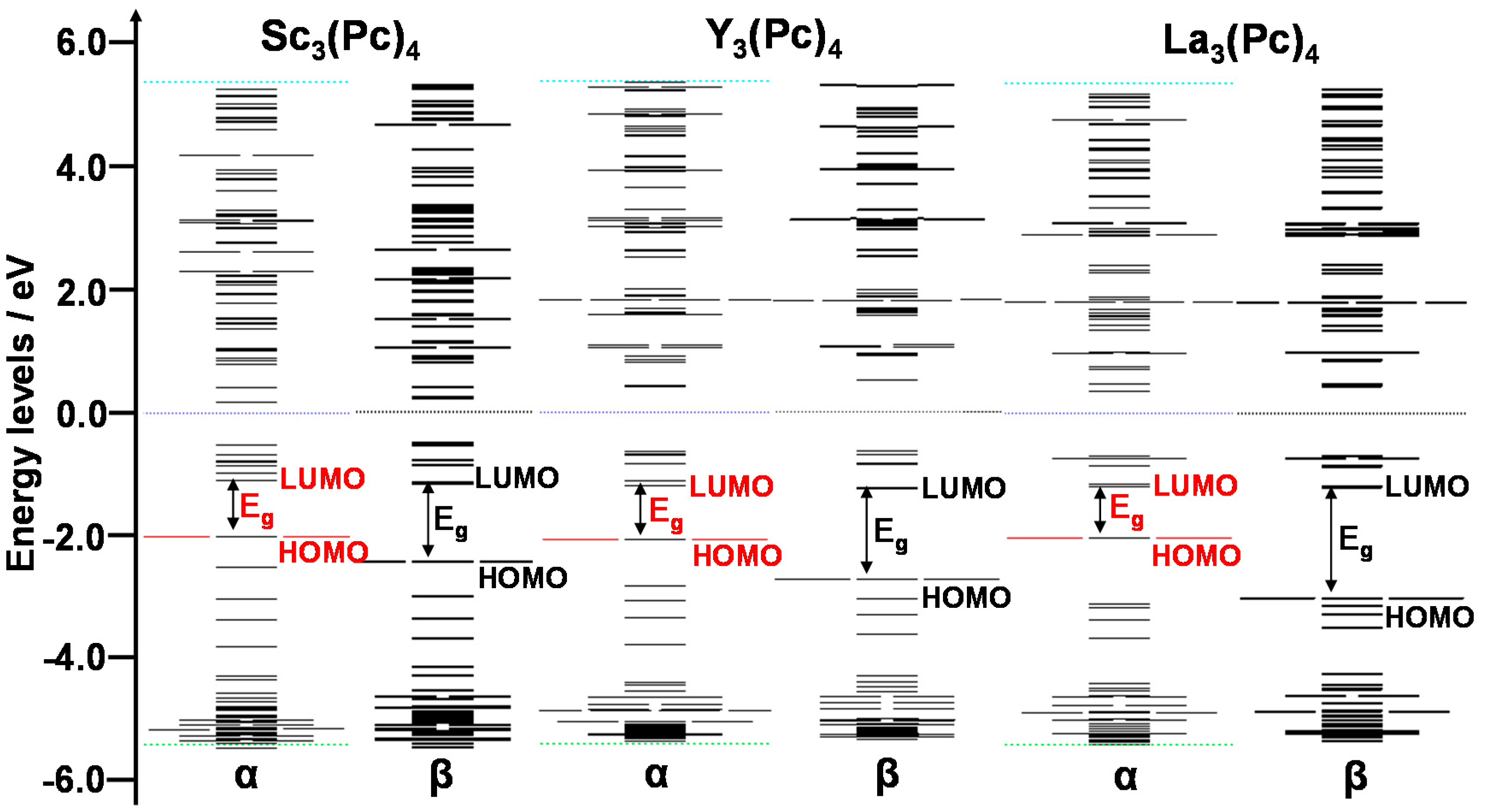

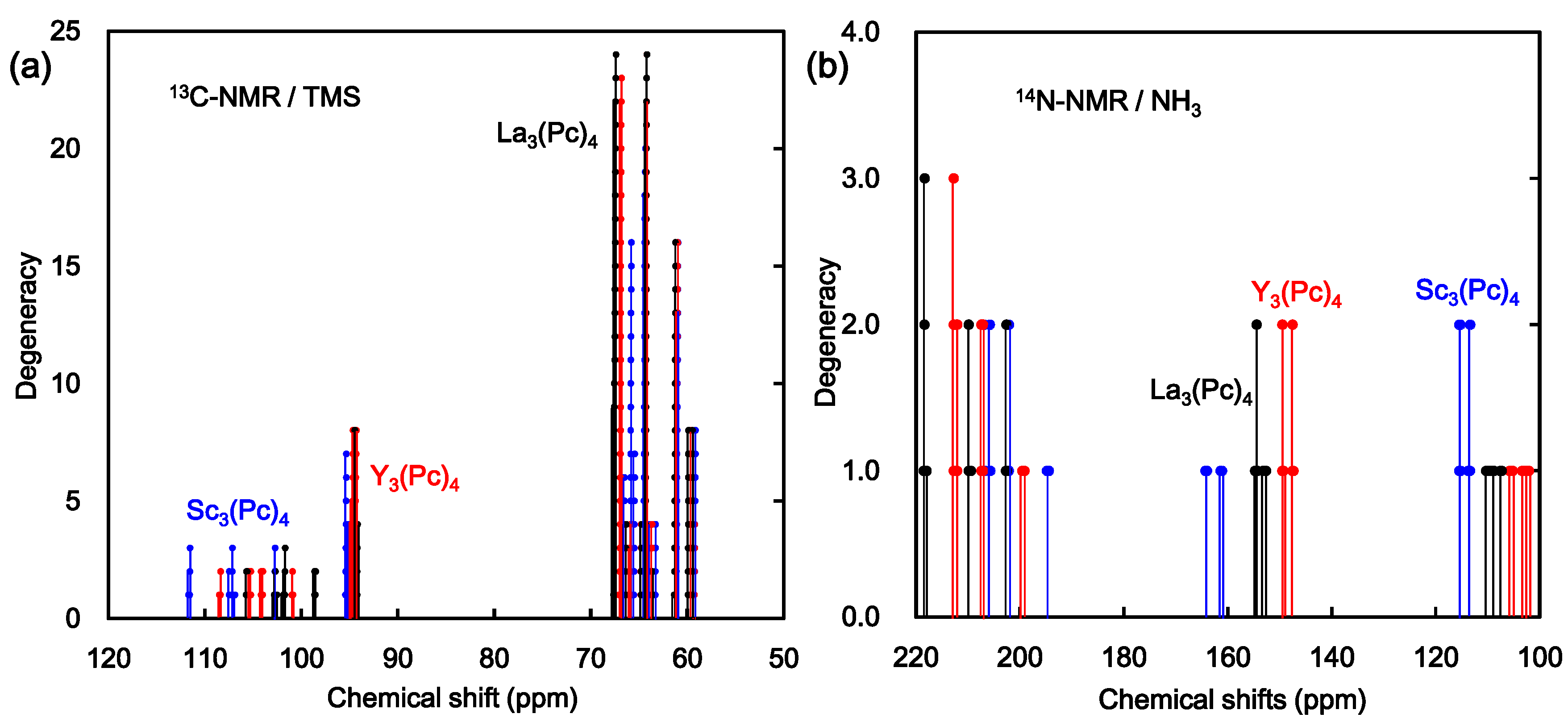
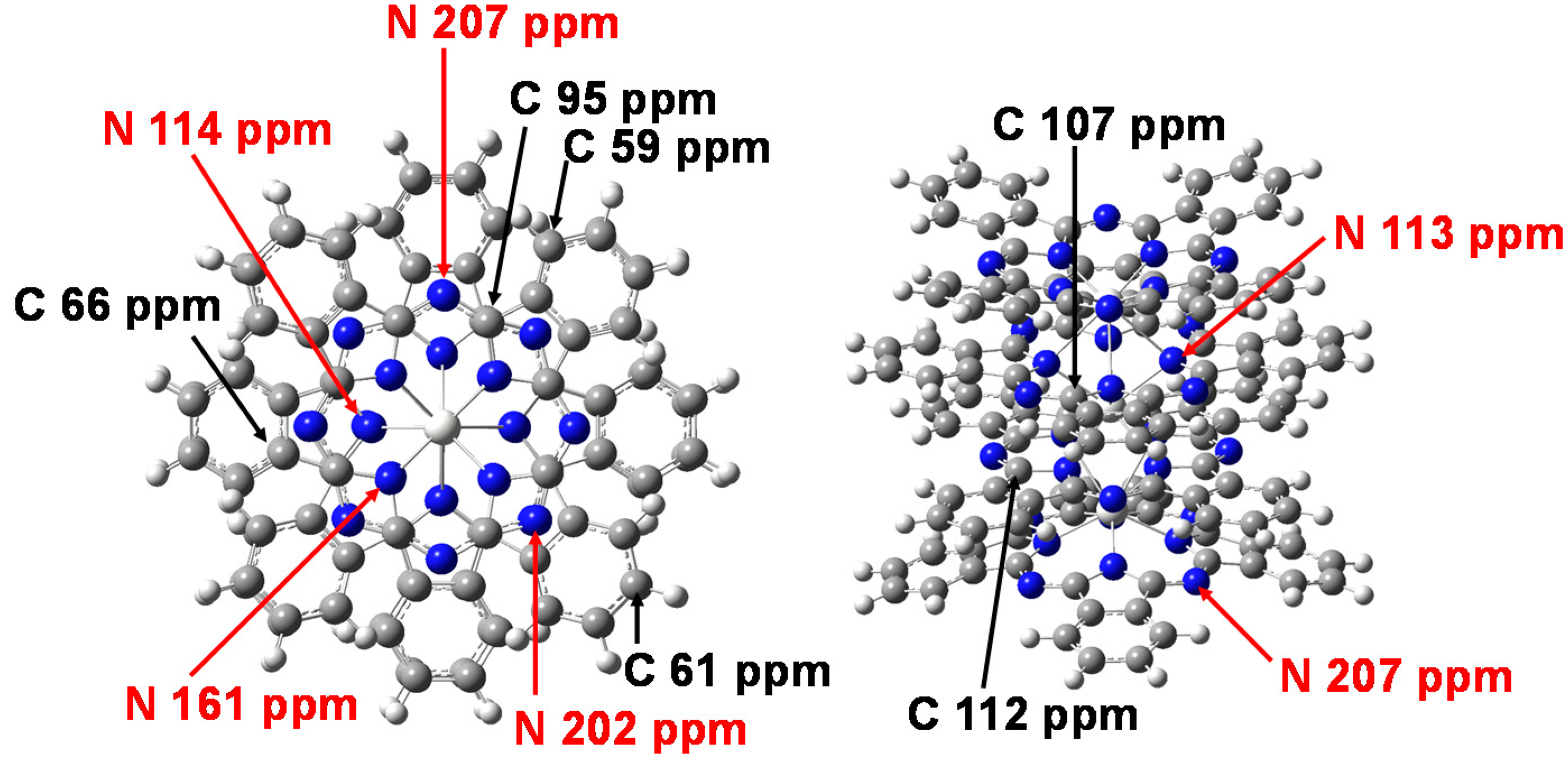
| M3(Pc)4 | Atomic Radii (pm) [31] | M–N (Å) | Angle N–M–N (°) |
|---|---|---|---|
| Sc3(Pc)4 | 160 | 2.21 | 126 |
| 2.39 | 105 | ||
| 2.21 | 126 | ||
| Y3(Pc)4 | 180 | 2.33 | 119 |
| 2.48 | 104 | ||
| 2.33 | 119 | ||
| La3(Pc)4 | 195 | 2.46 | 113 |
| 2.60 | 99 | ||
| 2.46 | 113 |
| Sc3(Pc)4 | No. | Energy (eV) | Wavelength (nm) | Oscillator Strength |
|---|---|---|---|---|
| Excited state | 1 | 0.8747 | 1417 | 0.0218 |
| Y3(Pc)4 | ||||
| Excited state | 1 | 0.6209 | 1997 | 0.0883 |
| 2 | 1.3731 | 903 | 0.0022 | |
| 3 | 1.4644 | 847 | 0.0034 |
| Sc3(Pc)4 | Mulliken Atomic Charge | Spin Density | g-tensor | EFG | η | ||||
|---|---|---|---|---|---|---|---|---|---|
| gxx | gyy | gzz | Vxx | Vyy | Vzz | ||||
| Sc1 | 0.32 | 0.0123 | 1.96695 | 2.00180 | 2.00300 | −0.0247 | −0.0356 | 0.0603 | 0.18 |
| Sc2 | 0.49 | 0.0133 | −0.0153 | −0.0370 | 0.0523 | 0.42 | |||
| Sc3 | 0.32 | 0.0122 | −0.0246 | −0.0356 | 0.0602 | 0.18 | |||
| Y3(Pc)4 | |||||||||
| Y1 | 0.31 | 0.0064 | 1.85325 | 1.99824 | 2.00298 | −0.0057 | −0.0079 | 0.0136 | 0.16 |
| Y2 | 0.53 | 0.0059 | −0.0063 | −0.0092 | 0.0155 | 0.19 | |||
| Y3 | 0.31 | 0.0064 | −0.0057 | −0.0079 | 0.0136 | 0.16 | |||
| La3(Pc)4 | |||||||||
| La1 | 0.41 | 0.0039 | 1.54111 | 1.98794 | 2.00117 | −0.0073 | −0.0087 | 0.0160 | 0.09 |
| La2 | 0.66 | 0.0078 | −0.0071 | −0.0086 | 0.0157 | 0.10 | |||
| La3 | 0.41 | 0.0039 | −0.0073 | −0.0087 | 0.0160 | 0.09 | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suzuki, A.; Oku, T. Electronic Structures, and Optical and Magnetic Properties of Quadruple-Decker Phthalocyanines. Magnetochemistry 2017, 3, 21. https://doi.org/10.3390/magnetochemistry3020021
Suzuki A, Oku T. Electronic Structures, and Optical and Magnetic Properties of Quadruple-Decker Phthalocyanines. Magnetochemistry. 2017; 3(2):21. https://doi.org/10.3390/magnetochemistry3020021
Chicago/Turabian StyleSuzuki, Atsushi, and Takeo Oku. 2017. "Electronic Structures, and Optical and Magnetic Properties of Quadruple-Decker Phthalocyanines" Magnetochemistry 3, no. 2: 21. https://doi.org/10.3390/magnetochemistry3020021
APA StyleSuzuki, A., & Oku, T. (2017). Electronic Structures, and Optical and Magnetic Properties of Quadruple-Decker Phthalocyanines. Magnetochemistry, 3(2), 21. https://doi.org/10.3390/magnetochemistry3020021






