Abstract
This work addresses the question of the identification of the excited states that are mainly responsible for the magnitude and nature of the magnetic anisotropy in high-spin mononuclear transition metal complexes. Only few states are actually responsible for the single ion magnetic anisotropy, and these states can be anticipated from rather simple rules. We show that in high-spin complexes atomic selection rules still prevail and that molecular selection rules from the symmetry point group are more selective than those of the double group. The predictive power of these rules is exemplified on a penta-coordinate Co(II) complex investigated with correlated ab initio calculations, including relativistic contributions. The electronic structure of excited states coupled to the ground state through spin-orbit coupling informs us about the nature (either axial or planar) of their contribution to the anisotropy. From this information, it is possible to anticipate the nature and strength of the ligand field and predict the magnetic anisotropy, which may guide the synthesis of improved anisotropic complexes. Such results can also be used to improve the quality of ab initio calculations of the spin Hamiltonian parameters and to reduce the computational cost.
1. Introduction
Magnetic anisotropy is at the origin of the single molecule magnet (SMM) behavior [1,2,3,4,5,6,7,8,9]. Single molecule magnets are at the forefront of the domain of molecular magnetism because of their potential applications in data storage and quantum computing. Indeed, classical SMMs have a degenerate ground state with two components of opposite magnetization that could be assimilated to the 0 and 1 states of a quantum bit, for which the quantum property of superposition of states could be exploited, paving the way to quantum computing. The property of magnetic anisotropy relates to relativistic effects that induce a lift of degeneracy of the MS components of the ground spin state S, such that the components with the largest magnetization +MS and −MS become the ground state. As this phenomenon occurs even in the absence of an external magnetic field, it is called zero-field splitting (ZFS). There are two main ZFS parameters: D and E respectively characterize the axial and rhombic anisotropies. Up to now the blocking temperatures under which the property can be observed are only of a few Kelvins. The exploitation of SMMs for practical applications—as classical or quantum bits of information, for instance—thus relies on the possibility of synthesizing molecules with higher blocking temperatures and long coherence times [10,11,12]. In order to achieve high blocking temperatures, several conditions must be fulfilled: (i) The axial parameter D of the ZFS must be negative (by convention) to ensure an easy axis of magnetization. Indeed, a positive value characterizes an easy plane of magnetization and no blocking is observed in the absence of an applied magnetic field [13]; (ii) the absolute value of D must be as large as possible, as it governs the splitting of the Ms components; and (iii) the rhombic parameter E must be strictly zero in order to prevent tunneling. Moreover, E plays also a role on the coherence time as observed experimentally [14,15]. The physical factors governing the sign and magnitude of these parameters are the amplitude of the spin-orbit coupling (SOC) and the symmetry. In symmetry point groups for which the components of the angular momentum (which transform as Rx, Ry and Rz in character tables) appear in the same irreducible representation (such as tetrahedral, octahedral, and icosahedral symmetries), the SOC does not lift the degeneracy of the MS components, and consequently no axial magnetic anisotropy can occur. A lowering of the symmetry is therefore necessary to observe the property. Molecules with the same symmetry but with different electronic configurations of the magnetic ion (different metal ions or different oxidation states) lead to completely different magnetic anisotropies (easy axis or easy plane and with or without rhombic contribution) so that the ways to improve SMMs are far from being intuitive [16,17,18,19,20].
For this purpose, theory may help in providing both analytical derivations and ab initio calculations of the anisotropy parameters in transition metal compounds [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Many papers have already been devoted to such studies and it has been shown that (i) only a few excited states significantly contribute to single ion magnetic anisotropy [21]; (ii) usually these states are not easy to anticipate from chemical intuition, and calculations are required to identify them and to rationalize their contribution to magnetic anisotropy; and (iii) the energetic order and electronic structure of the excited states can be easily correlated with the ligand field [25]. The present paper shows that as the ligand field strength is weak in high-spin compounds, the rules governing SOC in isolated transition metal ions still prevail in molecular compounds. The identification of the coupled excited states can therefore be done using the Wigner–Eckart theorem and from group theory. Correlating the electronic structure of these states with the ligand field and knowing that their contribution to the ZFS decreases in proportion to their energy difference to the ground state, it becomes possible to anticipate how to improve the property by choosing ligands with appropriate ligand fields. For such a purpose, molecular selection rules based on the symmetry point group are particularly useful as they are more selective than the double group ones, and as they allow one to anticipate which part of the SOC operator, or , is responsible for the coupling between the ground and excited states.
Another aspect of this work concerns the quality of the calculations and their computational cost. Indeed, as the method [21] usually employed to calculate the ZFS parameters goes through the optimization of average orbitals for all the computed excited states, the magnetic orbitals may not be optimal for the lowest-lying electronic states. As a consequence, the account of more excited states in the calculations does not lead to systematic improvements of the results and may even cause a decline in accuracy. The selection of those states that are responsible for magnetic anisotropy allows one to optimize average orbitals for a reduced set of states, leading to both a lower computational cost and an improvement of the quality of the results [21].
The paper is organized as follows. Section 2 sets out the theoretical basis of this study both in (i) recalling the rules that determine the SOC between the ground and excited states in atoms and molecules, and (ii) giving the computational information. Section 3 illustrates how these rules prevail in Co(II) molecular compounds. Starting from a model compound belonging to D3h symmetry point group, we have lowered its symmetry to C3v and changed the ligands to reach the situation that corresponds to a real compound for which experimental data are available. The complexes are studied by means of correlated ab initio calculations including SOC.
2. Selection Rules and Computational Information
2.1. Selection Rules for the Spin-Orbit Coupling in Atoms and Molecules
Symmetry properties of operators are used for a long time in order to improve the computational efficiency and to analyze spectroscopic data. Let us recall the main concepts leading to selection rules. The SOC Hamiltonian can be derived from the Dirac operator and used as a perturbative term in the one-component (Schrödinger) equation. Assuming a spherical potential, the so-defined SOC Hamiltonian for an N-electron system can be written as:
where is the electrostatic potential felt by electron i, , , and are, respectively, the linear momentum, the angular momentum, and the spin operator of electron i. is a radial operator proportional to the fine structure constant. It should be noted that other terms of lower magnitude such as spin-other-orbit or spin-spin couplings are often included in ab initio calculations as they impact the ZFS magnitude. Nevertheless, in many transition metal complexes, these effects are expected to be much smaller than those of the SOC and can be neglected in analytical derivations [45]. Let us just recall that in the case of small SOC contributions to the ZFS, spin-spin coupling may account for 20% of the total ZFS, e.g., in manganese(II) complexes [46].
The starting point for the derivation of selection rules is the Wigner–Eckart theorem, which allows one to separate the physical content of a tensor operator and its angular dependence.
Assuming a spherical symmetry and a Russell–Saunders coupling scheme, a first application of the Wigner–Eckart theorem on the SOC Hamiltonian allows one to re-write the SOC Hamiltonian for atoms as with , and A is the spin-orbit constant [48]. As A has no angular dependence, selection rules are only imposed by the operator. Then, the application of the Wigner–Eckart theorem leads to the expression [47]:
where J is the total angular momentum quantum number (which is a good quantum number for the atom) that parameterizes the total angular momentum resulting from the coupling of the angular and spin momenta. M is the quantum number of its associated component. Equation (3) involves 6-J symbols (in the curly brackets). Selection rules therefore arise from the Kronecker symbols and 6-J symbol properties and are written [47]:
In most cases, the fine structure of an atom can be well described by taking the SOC interaction only at the first-order of the perturbation theory (interaction of 2S+1L terms with themselves), as second-order effects are weaker by orders of magnitude. Nevertheless, as it will be shown in the next section, second-order SOC may be of crucial importance to describe the ZFS in molecules and the selection rules (see Equation (4)) will be helpful to unravel the physics governing the magnetic properties of transition metal complexes.
In molecules, SOC is much more difficult to apprehend. Indeed, the orbital angular momentum , well defined in a spherical atom, does not commute with the total Hamiltonian if the symmetry is lowered. Furthermore, one should notice that a non-spherical symmetry implies , thus the second equality in Equation (1) is not valid anymore. Nevertheless, the Hamiltonian commutes with the symmetry operators of the symmetry point group to which the molecule belongs. Information about the total orbital angular momentum of an electronic state is therefore contained in the spatial symmetry, i.e., the irreducible representation Γ of this state. The derivation of selection rules for SOC in molecules also relies on the Wigner–Eckart theorem, and can be found written in different ways. We use here the notation and the rules derived in [49]. The authors derived SOC selection rules for both the double group and point group formalisms. Despite the fact that the Co(II) complex studied here has a half-integer spin, we chose to use the symmetry point group formalism for reasons that will be clarified later. The wave functions of the spin-free electronic states can be written as where Γ is an irreducible representation of the molecular symmetry point group of the considered state, and S, MS are the spin quantum numbers. The SOC Hamiltonian used here is the phenomenological as we wish to correlate the SOC in magnetic complexes and in atoms. For symmetry based selection rules, the matrix elements to evaluate are . The application of the Wigner–Eckart theorem on the spin part of the Hamiltonian leads to the expression [49]:
where q is a component of the angular momentum operator in spherical coordinates. The spin operator in the right hand side reduced matrix element of Equation (5) is now invariant under rotation. From this expression, the following selection rules can be extracted:
The two first rules on spin quantum numbers are a consequence of the properties of the 3-J symbols. The last selection rule arises from the reduced matrix element. As the spin operator is now a scalar invariant under symmetry transformations, the selection rule only depends on the symmetry of the operator. In the double group formalism, belongs to the totally symmetric irreducible representation. Thus the selection rule for SOC in double group formalism is and it will be shown that it is less restrictive than symmetry point group rules. Another main reason for using point group rules instead of the double group ones is that our goal is to provide magneto-structural correlations, as the geometry of a molecule can be chemically controlled by the choice of appropriate ligands. Finally, one may note that the half-integer spin is fully accounted for by the Wigner–Eckart theorem [49].
In this article, we only study transition metal complexes having orbitally non-degenerate ground states, as the ZFS Hamiltonian is only defined in this context. However, it is worth noting that the rules presented above also apply to orbitally degenerate ground states.
2.2. Computational Information
Calculations have been performed with the Molcas 7.8 package [50,51,52]. The following ANO-RCC basis sets are used: (6s5p3d2f1g) for Co, (4s3p2d1f) for N, (3s2p1d) for C, (5s4p2d1f) for Cl and (2s) for H. Calculations proceed in two steps. In the first step, the energies and wave functions of the ground and excited states are computed at the CAS(7,10)SCF level, i.e., a double d shell is used, involving the 3d orbitals of the Co(II) ion and additional more diffuse d orbitals. Then the CASSCF wave function spin-components are coupled through spin-orbit interactions to form the state-interaction spin-orbit matrix (SO–SI method) [53]. The parameters of the ZFS are extracted from the computed spin-orbit energies and wave functions using the effective Hamiltonian theory [54,55], as explained in details in reference [53].
3. Results and Discussion
The main goals of this section are to illustrate: (i) How the physics of high-spin molecular complexes is reminiscent of that of the atom. For this purpose, it will be shown on a [Co(NCH)5]2+ model complex belonging to the D3h symmetry point group that the main spin-orbit coupling effects arise from electronic states issued from atomic terms, which are coupled though SOC in the Co(II) ion. (ii) How the various selection rules presented in the previous section are selective for the calculation of the ZFS of a real complex. For this second study, geometrical distortions and chemical substitutions were imposed to the model complex to reach the geometry of the real [Co(Me6tren)(Cl)]+ one [18]. Starting from the initial D3h geometry (with dCo–N fixed to 2 Å; note that dCo–N = 2.15 Å in the real compound, see Figure 1), we applied a progressive angular deformation by varying the angle α between the three equatorial NCH ligands and the xOy plane. The symmetry was thus lowered from D3h to C3v. α was increased until 9° and then the NCH ligand located on the z axis was replaced by a Cl atom.
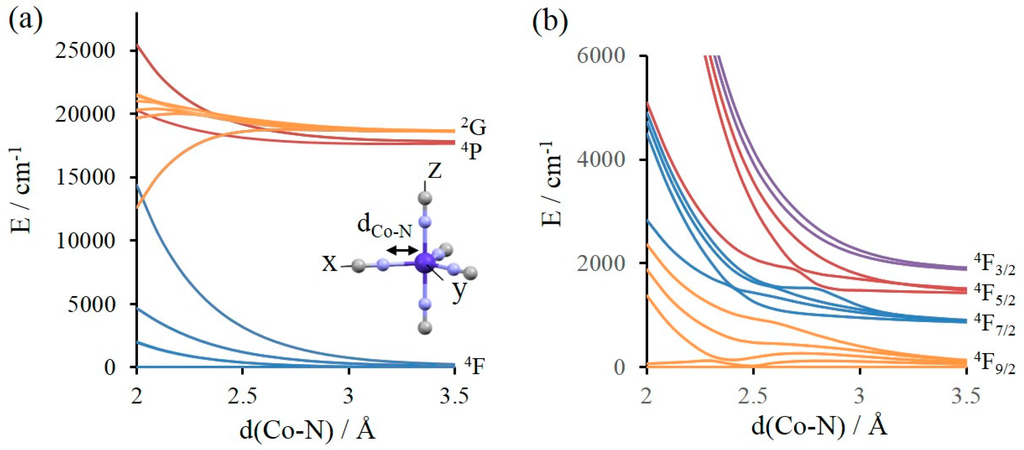
Figure 1.
(a) Lowest spin-orbit free states of [Co(NCH)5]2+ model complex of D3h symmetry computed at the CASSCF level; (b) 4F spectrum (see text) of the lowest spin-orbit states of [Co(NCH)5]2+ model complex of D3h symmetry as a function of dCo–N computed at the spin-orbit state-interaction (SO–SI) level.
3.1. Reminiscence of the Physics of the Atom in the Molecular Spectrum
As we are interested in magnetic properties, the ligand field must be weak enough to generate a high-spin ground state. In the chosen molecular compound, a weak ligand field is created by linear NCH ligands and the complex is studied for various Co–N bond lengths ranging from 2 (weak ligand field) to 3.5 Å (negligible field). Figure 1a shows the evolution of the electronic spectrum as a function of dCo–N.
Each molecular electronic state can easily be related to an atomic term. We will focus on those molecular electronic states that can be related with the 4F, 4P, and 2G atomic spectroscopic terms for different reasons. Firstly, the other excited states are higher in energy and their effect on the lowest energy spectrum through SOC is negligible (see the various spectra given in Supporting Information). Secondly, the states coming from 4F and 4P are well separated in energy, and the 4P and 2G terms, despite having different spins, possess similar energies. Finally, as the 2G is coupled to the 4F through SOC while the 4P is not (see selection rules in Equation (4)), the discussion can be limited to these terms for illustrating the idea proposed in this section, i.e., the selection rules for SOC in the isolated metal ion are not (or at least just partially) quenched by the weak applied ligand field. It can be noted that calculations have been performed with all the states of the d7 configuration and the results show that contributions of the other excited states to the low energy spin-orbit states are negligible. Since we are interested in the effect of SOC between 4F and excited states issued from the 4P and 2G atomic terms, we need first to account for the effect of SOC between the states coming from the 4F term. Let us first define what we call the 4F-SO spectrum. The 4F term is split in the four levels 4F9/2, 4F7/2, 4F5/2, and 4F3/2 by the spin-orbit coupling giving rise to 28 components that can be obtained by the diagonalization of the SOC Hamiltonian matrix when only the 7 spin-orbit free states issued from the 4F term are taken into account. In the same way, we define the (4F + 4P) SO spectrum (respectively. the (4F + 2G) SO spectrum), i.e., the lowest 28 components of the spin-orbit states (levels) obtained when the 4F + 4P (respectively 4F + 2G) states coming from 4F and 4P (respectively 2G) terms are included in the spin-orbit state-interaction matrix. The 4F SO spectrum is depicted in Figure 1b. One may notice that the 4F9/2, 4F7/2, 4F5/2, and 4F3/2 are split by the ligand field in, respectively, 5, 4, 3, and 2 molecular spin-orbit states, each of them being degenerate due to Kramer’s theorem. The three computed spectra (4F SO, (4F + 4P) SO and (4F + 2G) SO) are very similar and their plots only show small differences (the spectra are given in Tables S1–S3 in Supporting Information). We define Δ(4F+4P)−(4F) and Δ(4F+2G)−(4F) as the sum of the energy shifts (in absolute values, see Tables S4 and S5) experienced by the 14 spin-orbit states between the 4F SO spectrum and the (4F + 4P) SO and (4F + 2G) SO spectra, respectively. The values of Δ reflect the SOC effects of the states coming from the 4P or 2G terms on those issued from the 4F term. Δ(4F+4P)−(4F) and Δ(4F+2G)−(4F) as a function of dCo–N are shown in Tables S6 and S7 and Figure S1. The values of Δ when the ligand field is negligible (dCo–N = 3.5 Å) are in agreement with the selection rules for the isolated atom. Δ(4F+4P)−(4F) is equal to 0 because the 4F-4P SOC is not allowed. On the other hand, the 4F-2G coupling is allowed and Δ(4F+2G)−(4F) is quite large (≈ 600 cm−1). When the ligand field increases, Δ(4F+4P)−(4F) increases to ≈ 40 cm−1 and Δ(4F+2G)−(4F) slowly decreases to reach ≈ 450 cm−1 at dCo–N = 2 Å. For a ligand field of this magnitude, the SOC between electronic states coming from the 4F and 4P atomic terms is very small in comparison to the one between states coming from 4F and 2G atomic states. One should keep in mind that the 4P state leads to three spin-free states while the 2G leads to nine spin-free states, however these different degeneracies cannot explain alone such differences in the SOC magnitude. The main result here is that the SOC strength between the molecular ground state (GS) and excited states (ES) can be ranked as GS(4F) − ES(4F) GS(4F) − ES(2G) GS(4F) − ES(4P). In other words, the main effect of the SOC in the molecular electronic states stem from those related to the atomic 4F and 2G states, while those coming from the 4P state can be neglected.
3.2. Selection Rules for the Calculation of the ZFS in Molecular Complexes
Let us now focus on the ZFS of molecular complexes. Both model complexes (on which progressive distortions were applied) and the real complex [Co(Me6tren)(Cl)]+, previously studied by the authors [18], have been theoretically investigated. All these complexes are depicted in Figure 2 where the calculated D values are reported. The low energy spectrum and each excited-state contribution to D are also shown.
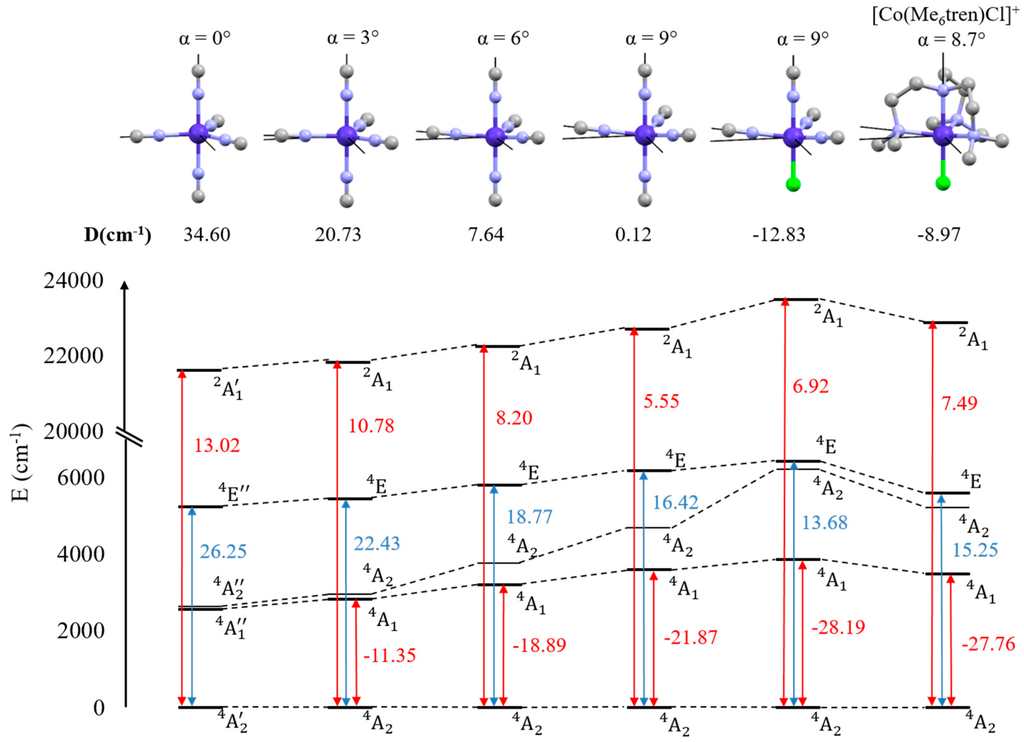
Figure 2.
Structure of studied complexes and their calculated axial anisotropy parameter D (top). Low energy spectrum of the spin-orbit free states and contributions (in cm−1) to D of each excited states (bottom). Red arrows indicate couplings between the states through the operator while blue arrows indicate couplings through the operator.
3.2.1. Molecular Selection Rules Based on the Symmetry Point Group
Let us first analyze the results on the basis of molecular selection rules (see Equation (6)). We use here the approximation that the ligand field effects are much stronger than the SOC ones, which allows us to treat SOC in a perturbative way. This is well verified for first row transition metal complexes. As we only deal with quartet and doublet states, the two first selection rules are not selective in the present case and only the last rule is important. Expressing the SOC Hamiltonian in Cartesian coordinates and noting that the operator transforms like an axial (or pseudo) vector under symmetry operations, group theory enables one to evaluate whether or not an excited state is coupled to the ground state. It also allows one to determine from which part (, or ) of the coupling occurs. In complex with an axial symmetry of order greater than two, and belong to the same irreducible representation. Furthermore, as already observed in the case of pentacoordinated Co(II) complex [18,56] with a C3 axis, for states with same (respectively different) spin multiplicity, if the coupling occurs through the part of the coupling between the ground and excited states leads to a negative (respectively positive) contribution to D, while a coupling caused by leads to a positive (respectively negative) contribution.
In the D3h symmetry point group, the model complex exhibits an easy-plane type magnetic anisotropy (D > 0). The main contribution to D comes from the SOC between the ground state and the excited state which provides a positive contribution to D. Indeed, in the D3h symmetry point group, and span the irreducible representation and the tensor product contains the totally symmetric irreducible representation. Another non-negligible contribution comes from the issued from the 2G term. The interaction is now brought by the part of ( spans the irreducible representation and ). In this symmetry (and for the four depicted excited states), no other coupling is symmetry allowed. As the symmetry is lowered to C3v, the D value decreases and becomes negative for the last complex, indicating a switch from easy plane to an easy axis type anisotropy. Note that the anisotropy of the [Co(NCH)4Cl]+ model complex with α = 9° is in quantitative agreement with that of the [Co(Me6tren)(Cl)]+ complex despite the differences between them. Electron paramagnetic resonance (EPR) spectroscopy studies on [Co(Me6tren)(Cl)]+ gave D = −8.12 cm−1. The decrease of D as the distortion increases can easily be explained by noting that, while both couplings between the GS and the excited ( in D3h) and ( in D3h) states still leads to a positive contribution to D, the coupling between the and the ( in D3h) states is now allowed through the part of ( spans the irreducible representation and ) and contributes negatively to D.
3.2.2. Molecular Selection Rules Based on the Double Group Theory
We have focused here on the [Co(NCH)5]2+ model complex with D3h symmetry but the same reasoning could be applied to the C3v complexes. Figure 3 shows the low energy electronic (O(3)) and spin-orbit (O(3)*) spectra for the isolated ion and electronic (D3h) and spin-orbit (D3h*) spectra of the molecular complex. All molecular electronic states can be correlated with an atomic term. The GS in the D3h symmetry point group is split into E1/2 and E3/2 in the D3h* double group under the effect of the SOC. The ZFS is then described by the energy difference between E1/2 (MS = ±1/2) and E3/2 (MS = ±3/2). The ground states E1/2 and E3/2 in D3h* are coming from the in O(3)* and the ground state is issued from the atomic term in D3h. As can be seen in the column D3h*, the excited states which have the same symmetry as the two lowest states in the double group are numerous and selection rules of the double group are therefore less restrictive than those of the symmetry point group.
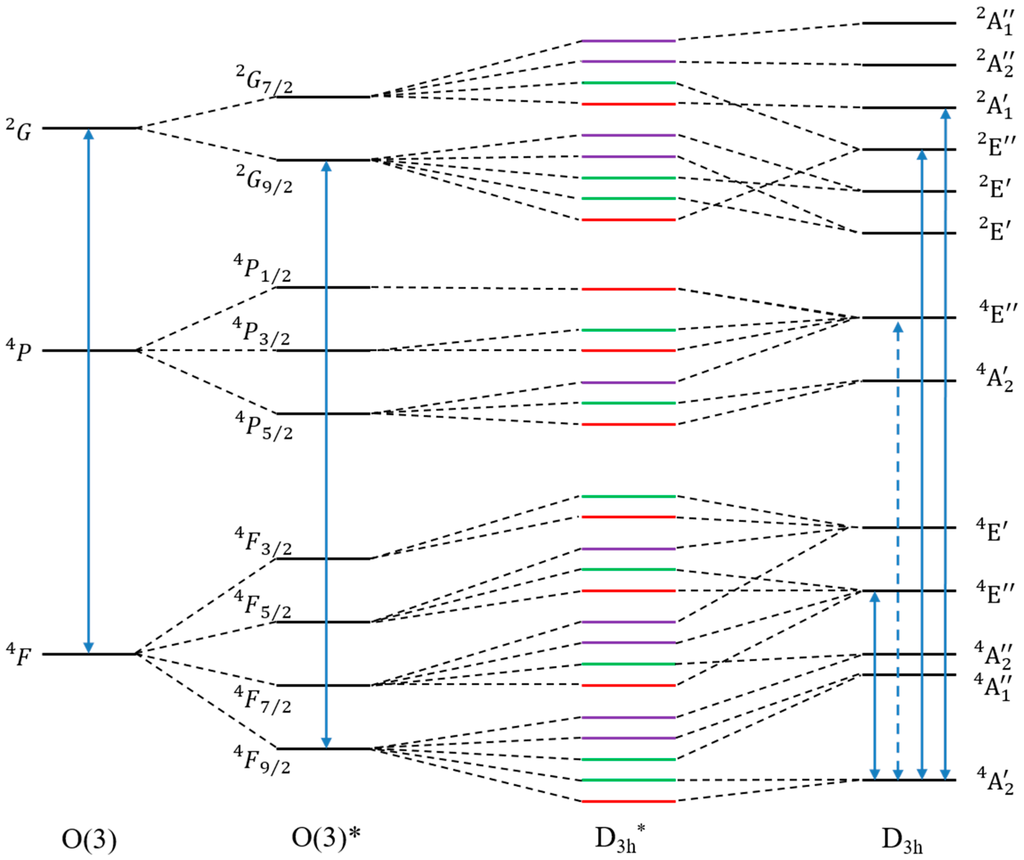
Figure 3.
Schematic (not scaled) energy spectrum. As mixing of states with same symmetry in the D3h* are possible only a few dashed lines are indicated to guide the eyes. Blue plain line arrows indicate allowed couplings between states, the dotted arrow indicates a coupling allowed at the molecular level but forbidden in the atom. Red, green and purple lines respectively indicate E1/2, E3/2 and E5/2.
3.2.3. Atomic Selection Rules
Finally, we can link the molecular selection rules for SOC with the atomic ones. In D3h symmetry point group and according to the symmetry based selection rule, the ground state can only be coupled with states of () and () symmetries. Under a D3h ligand field, the 4P term is split into . Calculations show that only the state is coupled to the GS and gives a positive contribution to D of 0.58 cm−1. The state in D3h symmetry reduces as . As expected, the and states are coupled to the GS. Their contributions to D are, respectively, 13.02 and −3.03 cm−1. The contribution of is one order of magnitude weaker than the contributions of and The SOC strength, and thus the contributions of excited states to D, therefore strongly depends on the atomic origin of the molecular state, and the almost negligible contribution of to D can be attributed to the atomic selection rules (Equation (4)). Indeed, we expect that the contribution will decrease if we lower the ligand field as the contribution of the 4P term must reach zero for negligible ligand field. These couplings are summarized in Figure 3.
3.3. Rationalization of the ZFS Nature
The energetic order of the d orbitals is given in Figure 4, as well as the excitation processes giving rise to the spin-orbit couplings and the determinants of the excited states that are coupled through SOC to the main determinant of the ground state. The information useful to improve the nature and magnitude of the ZFS can easily be extracted from the nature of the determinants involved in the SOC and the sign of their contribution to D. From a simple analysis of the here-reported theoretical results, the following recommendations can be stated:
- (i)
- If an easy axis of magnetization is needed (negative D value), the symmetry lowering from D3h to C3v is beneficial because it allows a coupling with the first excited state that brings a negative contribution to D.
- (ii)
- In order to obtain a more negative overall D value, one can decrease its positive contribution by destabilizing the 4E(C3v) excited state. As the main determinant of this state coupled to the ground state has a double occupancy in the dz2 orbital, ligands with a strong field in axial positions would be appropriate to do so.
- (iii)
- Finally, one may question the role of the chemical substitution by chlorine. To answer this query and separate the role of the distortion brought by the change of the value of the angle α from that of the electronic effect of chlorine, we have also substituted an axial NCH ligand in a slightly distorted (α = 3°) complex. In both cases (α = 3° and α = 9°), the main effect comes from the first excited state that for chlorine has a two-fold stronger coupling (see Figure S2) to the ground state, resulting in a much larger negative contribution to D. From this last observation, one may learn that not only the energy differences between the states (diagonal elements of the state interaction matrix) but also the magnitude of the coupling (off diagonal elements which are proportional to the fine structure constant and depend on the chemical nature of the ligand, i.e., electronic effect) can be tuned with the choice of appropriate ligands.
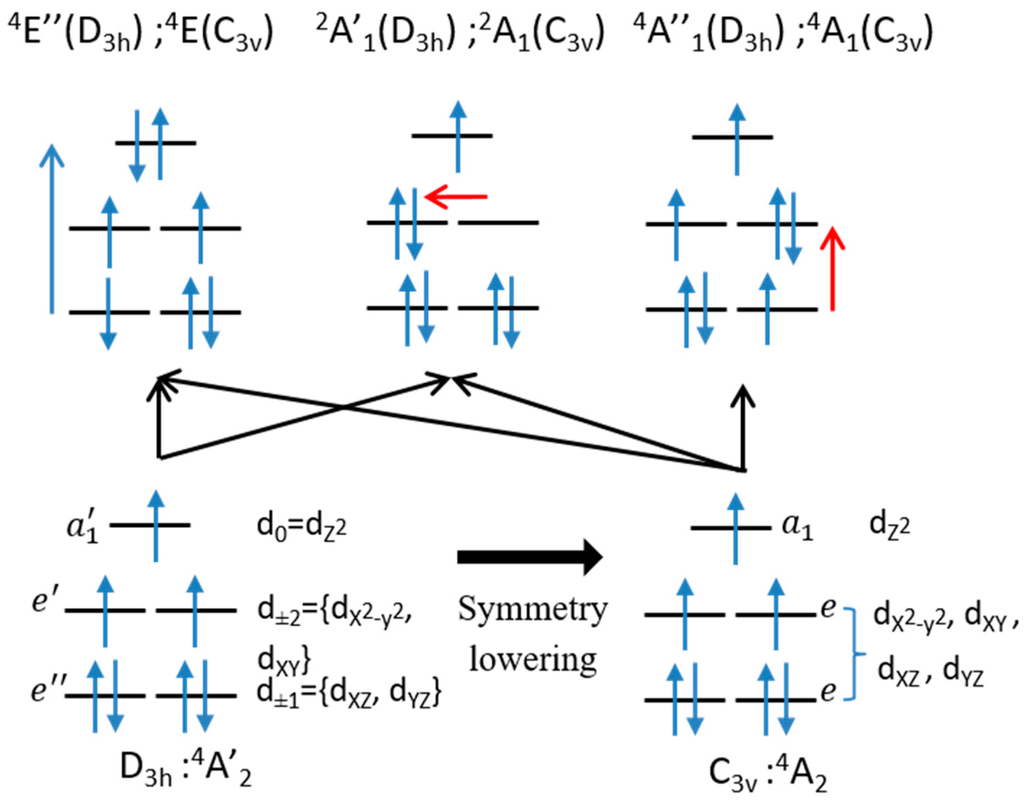
Figure 4.
All depicted excited states are multireference. Only the main determinants of the ground (bottom) and excited states coupled through SOC are represented. The labels and energetic order of the d orbitals are indicated. Only one of the two determinants equivalent by left-right symmetry is represented. The excitation leading to these excited states and the part either (purple arrow) or (red arrow) of the spin-orbit coupling (SOC) operator which is involved are also depicted.
4. Summary
For weak ligand field complexes the spin-orbit spectrum is dominated by the SOC between the states issued from the ground atomic term. The most important coupling with excited states issued from other terms essentially fulfills the atomic selection rule.
Although the ZFS is a very fine effect introducing tiny energy differences between MS components of the high-spin ground state, the reminiscence of the physics of the atom in the molecular complex is still present. An appropriate a priori selection of these states may lead to both (i) a computational gain as the size of the state-interaction matrix can be reduced, and (ii) a gain in quality of the ab initio results as the number of states used in the average optimization of the orbitals may be reduced to its bare essential. Finally, as theory may guide the synthesis of molecular complexes with targeted magnetic anisotropy, the main object of this work concerns the possible rationalization of the magnitude and nature of the ZFS from analytical derivation using second-order perturbation theory. Regarding this peculiar aspect, the selection of the states that will bring the main contributions to the ZFS is crucial. For this purpose, we have analyzed the selectivity of the various selection rules derived from the Wigner–Eckart theorem. The main conclusions are:
- (i)
- The atomic selection rules are essentially fulfilled. The contribution to D of the single excited state that is coupled to the ground state in the molecular complex but not in the atom is only 0.58 cm−1 and can be safely neglected in any attempt of rationalization of the SOC nature.
- (ii)
- The double group selection rule is less restrictive than the symmetry point group ones.
- (iii)
- From the symmetry point group selection rules, one may not only determine the excited states that are coupled to the ground state but also identify which part of the SOC operator, or , is responsible for the coupling and therefore the sign of their contribution to D.
From simple analyses of the physical content of the ground and excited states wave functions, rationalization of the magnitude and nature of the ZFS can be provided and recommendations can be drawn in order to guide synthesis and prepare molecular complexes with desired magnetic anisotropy.
Supplementary Materials
The following are available online at www.mdpi.com/2312-7481/2/3/31/s1: Table S1: 4F SO spectrum (cm−1), Table S2: (4F + 4P) SO spectrum (cm−1), Table S3: (4F + 2G) SO spectrum (cm−1), Table S4: Difference between (4F) and (4F + 4P) SO spectra (cm−1), Table S5: Difference between (4F) and (4F + 2G) SO spectra (cm−1), Table S6: Δ(4F + 4P) − (4F) (cm−1), Table S7: Δ(4F + 2G) − (4F) (cm−1), Figure S1: Δ(4F + 4P) − (4F) (blue) and Δ(4F + 2G) − (4F) (red) as a function of dCo–N, Figure S2: Most important contributions to D for the [Co(NCH)4Cl]+ (α = 3°) complex.
Acknowledgments
This work was granted access to the HPC resources of CALMIP supercomputing center under the allocation 2015-P1517. B.C. and T.M. thank The Université Paris Sud and the ANR for financial support (ANR-13-BS10-0001-03 MolQuSpin).
Author Contributions
Benjamin Cahier performed ab initio calculations. Benjamin Cahier, Rémi Maurice, Hélène Bolvin, Talal Mallah and Nathalie Guihéry analyzed the data. Benjamin Cahier and Nathalie Guihéry wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ZFS | Zero-Field Splitting |
| CASSCF | Complete Active Space Self-Consistent Field |
| SO–SI | Spin-Orbit State Interaction |
| SOC | Spin-orbit coupling |
References
- Barra, A.L.; Caneschi, A.; Cornia, A.; de Biani, F.F.; Gatteschi, D.; Sangregorio, C.; Sessoli, R.; Sorace, L. Single-molecule magnet behavior of a tetranuclear iron(iii) complex. The origin of slow magnetic relaxation in iron(III) clusters. J. Am. Chem. Soc. 1999, 121, 5302–5310. [Google Scholar] [CrossRef]
- Brechin, E.K.; Yoo, J.; Nakano, M.; Huffman, J.C.; Hendrickson, D.N.; Christou, G. A new class of single-molecule magnets: Mixed-valent [Mn4(O2CMe)2(Hpdm)6][ClO4]2 with an S = 8 ground state. Chem. Commun. 1999, 783–784. [Google Scholar] [CrossRef]
- Caneschi, A.; Gatteschi, D.; Sessoli, R.; Barra, A.L.; Brunel, L.C.; Guillot, M. Alternating-current susceptibility, high-field magnetization, and millimeter band EPR evidence for a ground S = 10 state in [Mn12O12(CH3COO)16(H2O)4].2CH3COOH.4H2O. J. Am. Chem. Soc. 1991, 113, 5873–5874. [Google Scholar] [CrossRef]
- Delfs, C.; Gatteschi, D.; Pardi, L.; Sessoli, R.; Wieghardt, K.; Hanke, D. Magnetic-properties of an octanuclear iron(III) cation. Inorg. Chem. 1993, 32, 3099–3103. [Google Scholar] [CrossRef]
- Gatteschi, D.; Caneschi, A.; Pardi, L.; Sessoli, R. Large clusters of metal-ions: The transition from molecular to bulk magnets. Science 1994, 265, 1054–1058. [Google Scholar] [CrossRef] [PubMed]
- Maheswaran, S.; Chastanet, G.; Teat, S.J.; Mallah, T.; Sessoli, R.; Wernsdorfer, W.; Winpenny, R.E. Phosphonate ligands stabilize mixed-valent {MnIII20−xMnIIx} clusters with large spin and coercivity. Angew. Chem. Int. Ed. Engl. 2005, 44, 5044–5048. [Google Scholar] [CrossRef] [PubMed]
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Sessoli, R.; Tsai, H.L.; Schake, A.R.; Wang, S.Y.; Vincent, J.B.; Folting, K.; Gatteschi, D.; Christou, G.; Hendrickson, D.N. High-spin molecules: [Mn12O12(O2CR)16(H2O)4]. J. Am. Chem. Soc. 1993, 115, 1804–1816. [Google Scholar] [CrossRef]
- Moragues-Canovas, M.; Riviere, P.; Ricard, L.; Paulsen, C.; Wernsdorfer, W.; Rajaraman, G.; Brechin, E.K.; Mallah, T. Resonant quantum tunneling in a new tetranuclear iron(III)-based single-molecule magnet. Adv. Mater. 2004, 16, 1101–1105. [Google Scholar] [CrossRef]
- Ardavan, A.; Blundell, S.J. Storing quantum information in chemically engineered nanoscale magnets. J. Mater. Chem. 2009, 19, 1754–1760. [Google Scholar] [CrossRef]
- Timco, G.A.; Carretta, S.; Troiani, F.; Tuna, F.; Pritchard, R.J.; Muryn, C.A.; McInnes, E.J.L.; Ghirri, A.; Candini, A.; Santini, P.; et al. Engineering the coupling between molecular spin qubits by coordination chemistry. Nat. Nanotech. 2009, 4, 173–178. [Google Scholar] [CrossRef] [PubMed]
- Urdampilleta, M.; Klyatskaya, S.; Cleuziou, J.P.; Ruben, M.; Wernsdorfer, W. Supramolecular spin valves. Nat. Mater. 2011, 10, 502–506. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Liu, J.; Piro, N.A.; Chang, C.J.; Hill, S.; Long, J.R. Slow magnetic relaxation in a pseudotetrahedral cobalt(II) complex with easy-plane anisotropy. Chem. Commun. 2012, 48, 3927–3929. [Google Scholar] [CrossRef] [PubMed]
- Fataftah, M.S.; Zadrozny, J.M.; Coste, S.C.; Graham, M.J.; Rogers, D.M.; Freedman, D.E. Employing forbidden transitions as qubits in a nuclear spin-free chromium complex. J. Am. Chem. Soc. 2016, 138, 1344–1348. [Google Scholar] [CrossRef] [PubMed]
- Shiddiq, M.; Komijani, D.; Duan, Y.; Gaita-Arino, A.; Coronado, E.; Hill, S. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 2016, 531, 348–351. [Google Scholar] [CrossRef] [PubMed]
- Ruamps, R.; Batchelor, L.J.; Maurice, R.; Gogoi, N.; Jimenez-Lozano, P.; Guihery, N.; de Graaf, C.; Barra, A.L.; Sutter, J.P.; Mallah, T. Origin of the magnetic anisotropy in heptacoordinate Ni-II and Co-II complexes. Chem. Eur. J. 2013, 19, 950–956. [Google Scholar] [CrossRef] [PubMed]
- Ruamps, R.; Maurice, R.; Batchelor, L.; Boggio-Pasqua, M.; Guillot, R.; Barra, A.L.; Liu, J.J.; Bendeif, E.; Pillet, S.; Hill, S.; et al. Giant ising-type magnetic anisotropy in trigonal bipyramidal Ni(II) complexes: Experiment and theory. J. Am. Chem. Soc. 2013, 135, 3017–3026. [Google Scholar] [CrossRef] [PubMed]
- Ruamps, R.; Batchelor, L.J.; Guillot, R.; Zakhia, G.; Barra, A.L.; Wernsdorfer, W.; Guihery, N.; Mallah, T. Ising-type magnetic anisotropy and single molecule magnet behaviour in mononuclear trigonal bipyramidal Co(II) complexes. Chem. Sci. 2014, 5, 3418–3424. [Google Scholar] [CrossRef]
- Gomez-Coca, S.; Cremades, E.; Aliaga-Alcalde, N.; Ruiz, E. Mononuclear single-molecule magnets: Tailoring the magnetic anisotropy of first-row transition-metal complexes. J. Am. Chem. Soc. 2013, 135, 7010–7018. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, E.; Cirera, J.; Cano, J.; Alvarez, S.; Loose, C.; Kortus, J. Can large magnetic anisotropy and high spin really coexist? Chem. Commun. 2008, 52–54. [Google Scholar] [CrossRef]
- Maurice, R.; Bastardis, R.; Graaf, C.D.; Suaud, N.; Mallah, T.; Guihéry, N. Universal theoretical approach to extract anisotropic spin hamiltonians. J. Chem. Th. Comp. 2009, 5, 2977–2984. [Google Scholar] [CrossRef] [PubMed]
- Maurice, R.; de Graaf, C.; Guihery, N. Theoretical determination of spin hamiltonians with isotropic and anisotropic magnetic interactions in transition metal and lanthanide complexes. PCCP 2013, 15, 18784–18804. [Google Scholar] [CrossRef] [PubMed]
- Batchelor, L.J.; Sangalli, M.; Guillot, R.; Guihery, N.; Maurice, R.; Tuna, F.; Mallah, T. Pentanuclear cyanide-bridged complexes based on highly anisotropic Co(II) seven-coordinate building blocks: Synthesis, structure, and magnetic behavior. Inorg. Chem. 2011, 50, 12045–12052. [Google Scholar] [CrossRef] [PubMed]
- Chibotaru, L.F.; Ungur, L. Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin hamiltonians and their derivation. J. Chem. Phys. 2012, 137, 064112. [Google Scholar] [CrossRef] [PubMed]
- Maurice, R.; de Graaf, C.; Guihery, N. Magnetostructural relations from a combined ab initio and ligand field analysis for the nonintuitive zero-field splitting in Mn(III) complexes. J. Chem. Phys. 2010, 133, 084307. [Google Scholar] [CrossRef] [PubMed]
- Maurice, R.; de Graaf, C.; Guihéry, N. Magnetic anisotropy in binuclear complexes in the weak-exchange limit: From the multispin to the giant-spin hamiltonian. Phys. Rev. B 2010, 81, 214427. [Google Scholar] [CrossRef]
- Maurice, R.; Guihery, N.; Bastardis, R.; Graaf, C. Rigorous extraction of the anisotropic multispin hamiltonian in bimetallic complexes from the exact electronic hamiltonian. J. Chem. Th. Comput. 2010, 6, 55–65. [Google Scholar] [CrossRef] [PubMed]
- Maurice, R.; Sivalingam, K.; Ganyushin, D.; Guihery, N.; de Graaf, C.; Neese, F. Theoretical determination of the zero-field splitting in copper acetate monohydrate. Inorg. Chem. 2011, 50, 6229–6236. [Google Scholar] [CrossRef] [PubMed]
- Pradipto, A.-M.; Maurice, R.; Guihéry, N.; de Graaf, C.; Broer, R. First-principles study of magnetic interactions in cupric oxide. Phys. Rev. B 2012, 85, 014409:1–014409:7. [Google Scholar] [CrossRef]
- Rechkemmer, Y.; Breitgoff, F.D.; van der Meer, M.; Atanasov, M.; Hakl, M.; Orlita, M.; Neugebauer, P.; Neese, F.; Sarkar, B.; van Slageren, J. A four-coordinate cobalt(II) single-ion magnet with coercivity and a very high energy barrier. Nat. Commun. 2016, 7, 10467. [Google Scholar] [CrossRef] [PubMed]
- Chorazy, S.; Podgajny, R.; Majcher, A.M.; Nitek, W.; Rams, M.; Suturina, E.A.; Ungur, L.; Chibotaru, L.F.; Sieklucka, B. Magnetic anisotropy of CoII–WV ferromagnet: Single crystal and ab initio study. CrystEngComm 2013, 15, 2378–2385. [Google Scholar] [CrossRef]
- Habib, F.; Long, J.; Lin, P.-H.; Korobkov, I.; Ungur, L.; Wernsdorfer, W.; Chibotaru, L.F.; Murugesu, M. Supramolecular architectures for controlling slow magnetic relaxation in field-induced single-molecule magnets. Chem. Sci. 2012, 3, 2158. [Google Scholar] [CrossRef]
- Hoeke, V.; Gieb, K.; Müller, P.; Ungur, L.; Chibotaru, L.F.; Heidemeier, M.; Krickemeyer, E.; Stammler, A.; Bögge, H.; Schröder, C.; et al. Hysteresis in the ground and excited spin state up to 10 t of a [MnIII6MnIII]3+ triplesalen single-molecule magnet. Chem. Sci. 2012, 3, 2868. [Google Scholar] [CrossRef]
- Liu, J.-L.; Chen, Y.-C.; Zheng, Y.-Z.; Lin, W.-Q.; Ungur, L.; Wernsdorfer, W.; Chibotaru, L.F.; Tong, M.-L. Switching the anisotropy barrier of a single-ion magnet by symmetry change from quasi-D5h to quasi-Oh. Chem. Sci. 2013, 4, 3310. [Google Scholar] [CrossRef]
- Chibotaru, L.F.; Ungur, L.; Aronica, C.; Elmoll, H.; Pilet, G.; Luneau, D. Structure, magnetism, and theoretical study of a mixed-valence CoII3CoIII4 heptanuclear wheel: Lack of smm behavior despite negative magnetic anisotropy. J. Am. Chem. Soc. 2008, 130, 12445–12455. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Importance of direct spin-spin coupling and spin-flip excitations for the zero-field splittings of transition metal complexes: A case study. J. Am. Chem. Soc. 2006, 128, 10213–10222. [Google Scholar] [CrossRef] [PubMed]
- Petit, S.; Pilet, G.; Luneau, D.; Chibotaru, L.F.; Ungur, L. A dinuclear cobalt(II) complex of calix[8]arenes exibiting strong magnetic anisotropy. Dalton Trans. 2007, 251, 4582–4588. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Xiao, D.J.; Atanasov, M.; Long, G.J.; Grandjean, F.; Neese, F.; Long, J.R. Magnetic blocking in a linear iron(I) complex. Nat. Chem. 2013, 5, 577–581. [Google Scholar] [CrossRef] [PubMed]
- Atanasov, M.; Zadrozny, J.M.; Long, J.R.; Neese, F. A theoretical analysis of chemical bonding, vibronic coupling, and magnetic anisotropy in linear iron(II) complexes with single-molecule magnet behavior. Chem. Sci. 2013, 4, 139–156. [Google Scholar] [CrossRef]
- Cirera, J.; Ruiz, E.; Alvarez, S.; Neese, F.; Kortus, J. How to build molecules with large magnetic anisotropy. Chem. Eur. J. 2009, 15, 4078–4087. [Google Scholar] [CrossRef] [PubMed]
- Cremades, E.; Cano, J.; Ruiz, E.; Rajaraman, G.; Milios, C.J.; Brechin, E.K. Theoretical methods enlighten magnetic properties of a family of Mn6 single-molecule magnets. Inorg. Chem. 2009, 48, 8012–8019. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Coca, S.; Urtizberea, A.; Cremades, E.; Alonso, P.J.; Camon, A.; Ruiz, E.; Luis, F. Origin of slow magnetic relaxation in kramers ions with non-uniaxial anisotropy. Nat. Commun. 2014, 5, 4300. [Google Scholar] [CrossRef] [PubMed]
- Neese, F.; Pantazis, D.A. What is not required to make a single molecule magnet. Faraday Discuss. 2011, 148, 229–238. [Google Scholar] [CrossRef] [PubMed]
- Sinnecker, S.; Neese, F.; Noodleman, L.; Lubitz, W. Calculating the electron paramagnetic resonance parameters of exchange coupled transition metal complexes using broken symmetry density functional theory: Application to a MnIII/MnIV model compound. J. Am. Chem. Soc. 2004, 126, 2613–2622. [Google Scholar] [CrossRef] [PubMed]
- Abragam, A.; Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; OUP Oxford: Oxford, UK, 2012. [Google Scholar]
- Zein, S.; Neese, F. Ab initio and coupled-perturbed density functional theory estimation of zero-field splittings in MnII transition metal complexes. J. Phys. Chem. A 2008, 112, 7976–7983. [Google Scholar] [CrossRef] [PubMed]
- Weissbluth, M. Atoms and Molecules; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Griffith, J.S. The Theory of Transition-Metal Ions; Cambridge University Press: Cambridge, UK, 1961. [Google Scholar]
- Fedorov, D.G.; Gordon, M.S. Symmetry in spin-orbit coupling. In Low-lying Potential Energy Surfaces; Hoffmann, M.R., Dyall, K.G., Eds.; Amer Chemical Soc: Washington, DC, USA, 2002; Volume 828, pp. 276–297. [Google Scholar]
- Aquilante, F.; De Vico, L.; Ferre, N.; Ghigo, G.; Malmqvist, P.A.; Neogrady, P.; Pedersen, T.B.; Pitonak, M.; Reiher, M.; Roos, B.O.; et al. Software news and update MOLCAS 7: The next generation. J. Comput. Chem. 2010, 31, 224–247. [Google Scholar] [CrossRef] [PubMed]
- Roos, B.O.; Lindh, R.; Malmqvist, P.A.; Veryazov, V.; Widmark, P.O. Main group atoms and dimers studied with a new relativistic ANO basis set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.A.; Veryazov, V.; Widmark, P.O. New relativistic ANO basis sets for transition metal atoms. J. Phys. Chem. A 2005, 109, 6575–6579. [Google Scholar] [CrossRef] [PubMed]
- Roos, B.O.; Malmqvist, P.A. Relativistic quantum chemistry: The multiconfigurational approach. PCCP 2004, 6, 2919–2927. [Google Scholar] [CrossRef]
- Bloch, C. Sur la théorie des perturbations des états liés. Nucl. Phys. 1958, 6, 329–347. [Google Scholar] [CrossRef]
- des Cloizeaux, J. Extension d’une formule de lagrange à des problèmes de valeurs propres. Nucl. Phys. 1960, 20, 321–346. [Google Scholar] [CrossRef]
- Shao, F.; Cahier, B.; Guihery, N.; Riviere, E.; Guillot, R.; Barra, A.L.; Lan, Y.; Wernsdorfer, W.; Campbell, V.E.; Mallah, T. Tuning the ising-type anisotropy in trigonal bipyramidal Co(II) complexes. Chem. Commun. 2015, 51, 16475–16478. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).