Periodic Density Functional Calculations in Order to Assess the Cooperativity of the Spin Transition in Fe(phen)2(NCS)2
Abstract
:1. Introduction
2. Results and Discussion
3. Computational Details
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Gütlich, P.; Goodwin, H.A. (Eds.) Spin Crossover in Transition Metal Compounds I, 1st ed.; Topics in Current Chemistry; Springer: Berlin, Germany; Heidelberg, Germany; New York, NY, USA, 2004; Volume 1.
- Gütlich, P.; Goodwin, H.A. (Eds.) Spin Crossover in Transition Metal Compounds II, 1st ed.; Topics in Current Chemistry; Springer: Berlin, Germany; Heidelberg, Germany; New York, NY, USA, 2004; Volume 2.
- Gütlich, P.; Goodwin, H.A. (Eds.) Spin Crossover in Transition Metal Compounds III, 1st ed.; Topics in Current Chemistry; Springer: Berlin, Germany; Heidelberg, Germany; New York, NY, USA, 2004; Volume 3.
- Decurtins, S.; Gütlich, P.; Köhler, C.; Spiering, H.; Hauser, A. Light-induced excited spin state trapping in a transition-metal complex: The hexa-1-propyltetrazole-iron (II) tetrafluoroborate spin-crossover system. Chem. Phys. Lett. 1984, 139, 1–4. [Google Scholar]
- McGarvey, J.J.; Lawthers, I. Photochemically-induced perturbation of the 1A ⇌5T equilibrium in FeII complexes by pulsed laser irradiation in the metal-to-ligand charge-transfer absorption band. J. Chem. Soc. Chem. Commun. 1982. [Google Scholar] [CrossRef]
- Slichter, C.P.; Drickamer, H.G. Pressure-induced electronic changes in compounds of iron. J. Chem. Phys. 1972, 56, 2142–2160. [Google Scholar] [CrossRef]
- Paulsen, H.; Trautwein, A. Density functional theory calculations for spin crossover complexes. Top. Curr. Chem. 2004, 235, 197–219. [Google Scholar]
- Bolvin, H. d->d spectrum and high-spin/low-spin competition in d6 octahedral coordination compounds: Ab initio study of potential energy curves. J. Phys. Chem. A 1998, 102, 7525–7534. [Google Scholar] [CrossRef]
- Paulsen, H.; Schünemann, V.; Wolny, J.A. Progress in electronic structure calculations on spin-crossover complexes. Eur. J. Inorg. Chem. 2013. [Google Scholar] [CrossRef]
- Kepp, K.P. Consistent description of metal-ligand bonds and spin-crossover in inorganic chemistry. Coord. Chem. Rev. 2013, 257, 196–209. [Google Scholar] [CrossRef]
- Deeth, R.J. Molecular discovery in spin crossover. In Spin States in Biochemistry and Inorganic Chemistry; John Wiley & Sons, Ltd.: Chichester, United Kingdom, 2015; pp. 85–102. [Google Scholar]
- Vela, S.; Fumanal, M.; Ribas-Arino, J.; Robert, V. Towards an accurate and computationally-efficient modelling of Fe(II)-based spin crossover materials. Phys. Chem. Chem. Phys. 2015, 17, 16306–16314. [Google Scholar] [CrossRef] [PubMed]
- Reiher, M.; Salomon, O.; Hess, B.A. Reparameterization of hybrid functionals based on energy differences of state of different multiplicity. Theor. Chem. Acc. 2001, 107, 48–55. [Google Scholar] [CrossRef]
- Reiher, M. Theoretical study of the Fe(phen)2(NCS)2 spin-crossover complex with reparametrized density functionals. Inorg. Chem. 2002, 41, 6928–6935. [Google Scholar] [CrossRef] [PubMed]
- Reiher, M.; Brehm, G.; Schneider, S. Assignment of vibrational spectra of 1,10-phenanthroline by comparison with frequencies and raman intensities from density functional calculations. J. Phys. Chem. A 2004, 108, 734–742. [Google Scholar] [CrossRef]
- Ronayne, K.L.; Paulsen, H.; Höfer, A.; Dennis, A.C.; Wolny, J.A.; Chumakov, A.I.; Schünemann, V.; Winkler, H.; Spiering, H.; Bousseksou, A.; et al. Vibrational spectrum of the spin-crossover complex [Fe(phen)2(NCS)2] studied by IR and Raman spectroscopy, nuclear inelastic scattering and DFT calculations. Phys. Chem. Chem. Phys. 2006, 8, 4685–4693. [Google Scholar] [CrossRef] [PubMed]
- Bučko, T.; Hafner, J.; Lebègue, S.; Ángyán, J.G. Spin crossover transition of Fe(phen)2(NCS)2: Periodic dispersion-corrected density-functional study. Phys. Chem. Chem. Phys. 2012, 14, 5389–5396. [Google Scholar] [CrossRef] [PubMed]
- Jensen, K.P.; Cirera, J. Accurate computed enthalpies of spin crossover in iron and cobalt complexes. J. Phys. Chem. A 2009, 113, 10033–10039. [Google Scholar] [CrossRef] [PubMed]
- Cirera, J.; Paesani, F. Theoretical prediction of spin-crossover temperatures in ligand-driven light-induced spin change systems. Inorg. Chem. 2012, 51, 8194–8201. [Google Scholar] [CrossRef] [PubMed]
- Swart, M. Accurate spin-state energies for iron complexes. J. Chem. Theory Comput. 2008, 4, 2057–2066. [Google Scholar] [CrossRef] [PubMed]
- Ye, S.; Neese, F. Accurate modeling of spin-state energetics in spin-crossover systems with modern density functional theory. Inorg. Chem. 2010, 49, 772–774. [Google Scholar] [CrossRef] [PubMed]
- Fouqueau, A.; Casida, M.E.; Lawson, L.M.; Hauser, A.; Neese, F. Comparison of density functionals for energy and structural differences between the high-[T:(t)(e)] and low-[A:(t)(e)] spin states of iron(II) coordination compounds: II. Comparison of results for more than ten modern functionals with ligand field theory and Ab initio results for hexaquoferrous dication, [Fe(H2O)6]2+ and hexaminoferrous dication [Fe(NH3)6]2+. J. Chem. Phys. 2005, 122, 044110. [Google Scholar]
- Fouqueau, A.; Mer, S.; Casida, M.E.; Daku, L.M.L.; Hauser, A.; Mineva, T.; Neese, F. Comparison of density funtionals for energy and structural differences between the high- [5T2g:(t2g)4(eg)2] and low- [1A1g:(t2g)6(eg)0] spin states of the hexaquoferrous cation [Fe(H2O)6]2+. J. Chem. Phys. 2004, 120, 9473–9486. [Google Scholar] [CrossRef] [PubMed]
- Lawson Daku, L.M.; Vargas, A.; Hauser, A.; Fouqueau, A.; Casida, M.E. Assessment of density functionals for the high-spin/low-spin energy difference in the low-spin iron(II) tris(2,2’-bipyridine) complex. ChemPhysChem. 2005, 6, 1393–1410. [Google Scholar] [CrossRef] [PubMed]
- Ganzenmuller, G.; Berkaine, N.; Fouqueau, A.; Casida, M.E.; Reiher, M. Comparison of density functionals for differences between the high- (5T2g) and low- (1A1g) spin states of iron(II) compounds. IV. Results for the ferrous complexes [Fe(L)(‘NHS4’)]. J. Chem. Phys. 2005, 122, 234321. [Google Scholar] [CrossRef] [PubMed]
- Slimani, A.; Yu, X.; Muraoka, A.; Boukheddaden, K.; Yamashita, K. Reparametrization approach of DFT functionals based on the equilibrium temperature of spin-crossover compounds. J. Phys. Chem. A 2014, 118, 9005–9012. [Google Scholar] [CrossRef] [PubMed]
- Paulsen, H.; Duelund, L.; Zimmermann, A.; Averseng, F.; Gerdan, M.; Winkler, H.; Toftlund, H.; Trautwein, A.X. Substituent effects on the spin-transition temperature in complexes with tris(pyrazolyl) ligands. Monatshefte Chem. 2003, 134, 295–306. [Google Scholar] [CrossRef]
- Paulsen, H.; Trautwein, A.X. Calculation of the electronic energy differences of spin crossover complexes. J. Phys. Chem. Solids 2004, 65, 793–798. [Google Scholar] [CrossRef]
- Güell, M.; Sola, M.; Swart, M. Spin-state splittings of iron(II) complexes with trispyrazolyl ligands. Polyhedron 2010, 29, 84–93. [Google Scholar] [CrossRef]
- Le Guennic, B.; Matouzenko, G.S.; Borshch, S.A. Topology of spin-crossover polymers and mutual influence of ligands. Eur. J. Inorg. Chem. 2008, 2008, 3020–3023. [Google Scholar] [CrossRef]
- Kepenekian, M.; Guennic, B.L.; Robert, V. Primary role of the electrostatic contributions in a rational growth of hysteresis loop in spin-crossover Fe(II) complexes. J. Am. Chem. Soc. 2009, 131, 11498–11502. [Google Scholar] [CrossRef] [PubMed]
- Matouzenko, G.S.; Perrin, M.; Guennic, B.L.; Genre, C.; Molnar, G.; Bousseksou, A.; Borshch, S.A. Spin crossover behavior in a family of iron(II) zigzag chain coordination polymers. Dalton Trans. 2007. [Google Scholar] [CrossRef] [PubMed]
- Rackwitz, S.; Klopper, W.; Schunemann, V.; Wolny, J.A. Quantification of intramolecular cooperativity in polynuclear spin crossover Fe(II) complexes by density functional theory calculations. Phys. Chem. Chem. Phys. 2013, 15, 15450–15458. [Google Scholar] [CrossRef] [PubMed]
- Zein, S.; Borshch, S.A. Energetics of binuclear spin transition complexes. J. Am. Chem. Soc. 2005, 127, 16197–16201. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, E. Charge transport properties of spin crossover systems. Phys. Chem. Chem. Phys. 2014, 16, 14–22. [Google Scholar] [CrossRef] [PubMed]
- Cirera, J.; Ruiz, E. Theoretical modeling of two-step spin-crossover transitions in FeII dinuclear systems. J. Mater. Chem. C 2015, 3, 7954–7961. [Google Scholar] [CrossRef]
- Saha-Dasgupta, T.; Oppeneer, P.M. Computational design of magnetic metal-organic complexes and coordination polymers with spin-switchable functionalities. MRS Bull. 2014, 39, 614–620. [Google Scholar] [CrossRef]
- Lemercier, G.; Brefuel, N.; Shova, S.; Wolny, J.A.; Dahan, F.; Verelst, M.; Paulsen, H.; Trautwein, A.X.; Tuchagues, J.P. A range of spin-crossover temperature T1/2 > 300 K results from out-of-sphere anion exchange in a series of ferrous materials based on the 4-(4-Imidazolylmethyl)-2-(2-imidazolylmethyl) imidazole (trim) ligand, [Fe(trim)2]X2 (X=F, Cl, Br, I): Comparison of experimental results with those derived from density functional theory calculations. Chem. Eur. J. 2006, 12, 7421–7432. [Google Scholar] [PubMed]
- Middlemiss, D.S.; Portinari, D.; Grey, C.P.; Morrison, C.A.; Wilson, C.C. Spin crossover in the Prussian blue analog: Phonons and thermodynamics from hybrid functionals. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Cirera, J.; Babin, V.; Paesani, F. Theoretical modeling of spin crossover in metal-organic frameworks: [Fe(pz)2Pt(CN)4] as a case study. Inorg. Chem. 2014, 53, 11020–11028. [Google Scholar] [CrossRef] [PubMed]
- Middlemiss, D.S.; Deeth, R.J. First principles calculation of a large variation in dielectric tensor through the spin crossover in the CsFe[Cr(CN)6] Prussian blue analogue. J. Chem. Phys. 2014, 140, 144503. [Google Scholar] [CrossRef] [PubMed]
- Lebègue, S.; Pillet, S.; Ángyán, J.G. Modeling spin-crossover compounds by periodic DFT+U approach. Phys. Rev. B 2008, 78. [Google Scholar] [CrossRef]
- Matar, S.F.; Létard, J.F. Ab initio molecular and solid-state studies of the spin crossover system [Fe(phen)2(NCS)2]. Z. Naturforsch. B 2010, 65, 565–570. [Google Scholar] [CrossRef]
- Zhang, Y. Predicting critical temperatures of iron(II) spin crossover materials: Density functional theory plus U approach. J. Chem. Phys. 2014, 141, 214703. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Millis, A.J.; Marianetti, C.A. Density functional plus dynamical mean-field theory of the spin-crossover molecule Fe(phen)2(NCS)2. Phys. Rev. B 2015, 91. [Google Scholar] [CrossRef]
- König, E.; Madeja, K. 5T2–1A1 Equilibriums in some iron(II)-bis(1,10-phenanthroline) complexes. Inorg. Chem. 1967, 6, 48–55. [Google Scholar] [CrossRef]
- König, E.; Madeja, K. Correction. Equilibria in some iron(II)-bis(1,10-phenanthroline) complexes. Inorg. Chem. 1968, 7, 2677. [Google Scholar] [CrossRef]
- Gallois, B.; Real, J.A.; Hauw, C.; Zarembowitch, J. Structural changes associated with the spin transition in Fe(phen)2(NCS)2: A single-crystal X-ray investigation. Inorg. Chem. 1990, 29, 1152–1158. [Google Scholar] [CrossRef]
- Legrand, V.; Pillet, S.; Weber, H.P.; Souhassou, M.; Létard, J.F.; Guionneau, P.; Lecomte, C. On the precision and accuracy of structural analysis of light-induced metastable states. J. Appl. Cryst. 2007, 40, 1076–1088. [Google Scholar] [CrossRef]
- Bousseksou, A.; McGarvey, J.J.; Varret, F.; Real, J.A.; Tuchagues, J.P.; Dennis, A.C.; Boillot, M.L. Raman spectroscopy of the high- and low-spin states of the spin crossover complex Fe(phen)2(NCS)2: An initial approach to estimation of vibrational contributions to the associated entropy change. Chem. Phys. Lett. 2000, 318, 409–416. [Google Scholar] [CrossRef]
- Palfi, V.K.; Guillona, T.; Paulsen, H.; Molnar, G.; Bousseksou, A. Isotope effects on the vibrational spectra of the Fe(Phen)2(NCS)2 spin-crossover complex studied by density functional calculation. C. R. Chim. 2005, 8, 1317–1325. [Google Scholar] [CrossRef]
- Sinitskiy, A.V.; Tchougréeff, A.L.; Dronskowski, R. Phenomenological model of spin crossover in molecular crystals as derived from atom-atom potentials. Phys. Chem. Chem. Phys. 2011, 13, 13238–13246. [Google Scholar] [CrossRef] [PubMed]
- Sorai, M.; Seki, S. Phonon coupled cooperative low-spin 1A1 high-spin 5T2 transition in [Fe(phen)2(NCS)2] and [Fe(phen)2(NCSe)2] crystals. J. Phys. Chem. Solids 1974, 35, 555–570. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comp. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Harvey, J.N. On the accuracy of density functional theory in transition metal chemistry. Annu. Rep. Prog. Chem. 2006, 102, 203–226. [Google Scholar] [CrossRef]
- Chiruta, D.; Linares, J.; Garcia, Y.; Dahoo, P.R.; Dimian, M. Analysis of the hysteretic behaviour of 3D spin crossover compounds by using an ising-like model. Eur. J. Inorg. Chem. 2013, 2013, 3601–3608. [Google Scholar] [CrossRef]
- Mebs, S.; Braun, B.; Kositzki, R.; Limberg, C.; Haumann, M. Abrupt versus gradual spin-crossover in FeII(phen)2(NCS)2 and FeIII(dedtc)3 compared by X-ray absorption and emission spectroscopy and quantum-chemical calculations. Inorg. Chem. 2015, 54, 11606–11624. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Pseudopotentials Fe.pz-sp-van_ak.upf, S.pz-van_ak.upf, N.pz-van_ak.upf, C.pz-van_ak.upf and H.pz-van_ak.upf. Available online: www.quantum-espresso.org/pseudopotentials (accessed on 10 September 2015).
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71. [Google Scholar] [CrossRef]
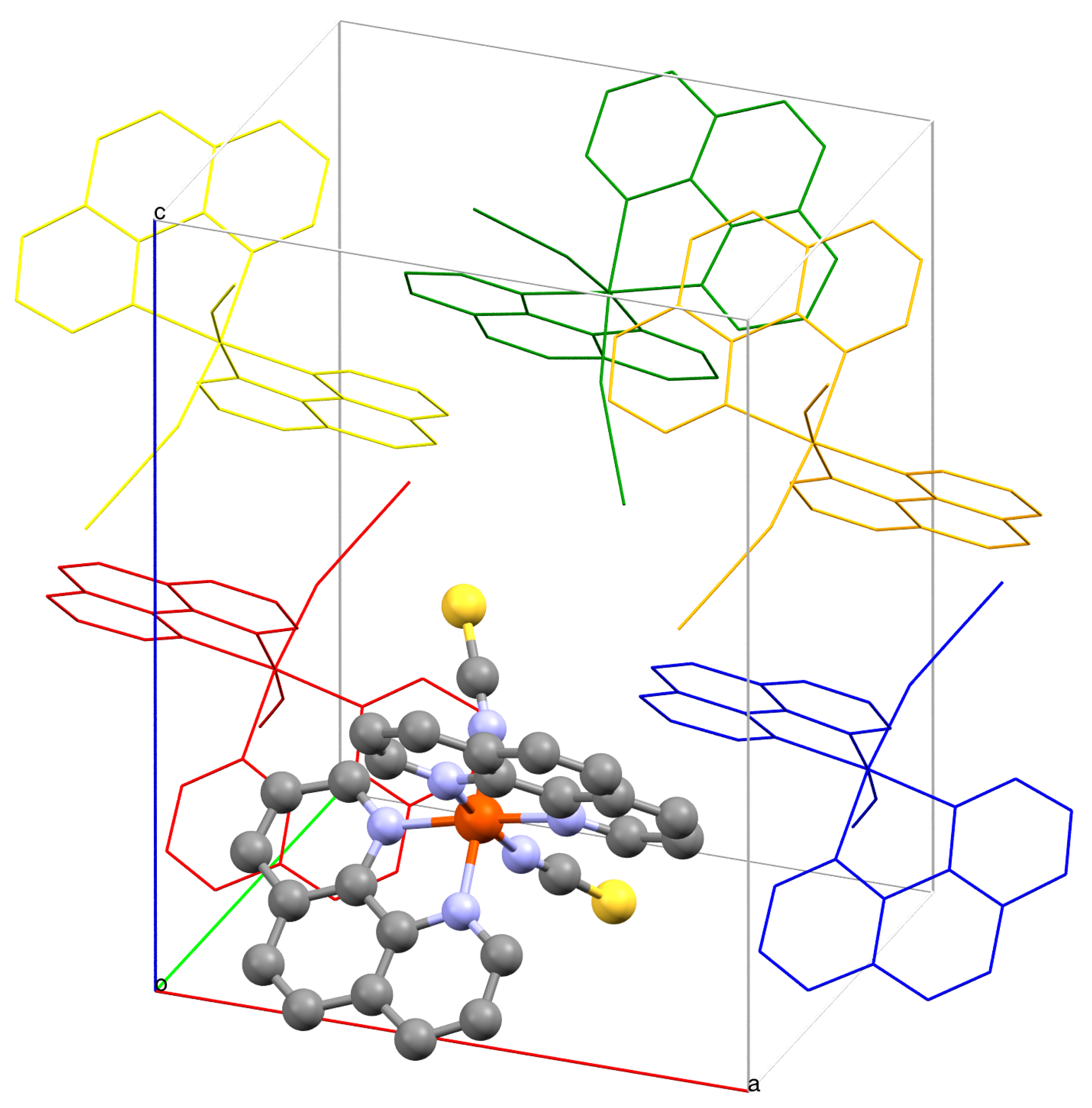
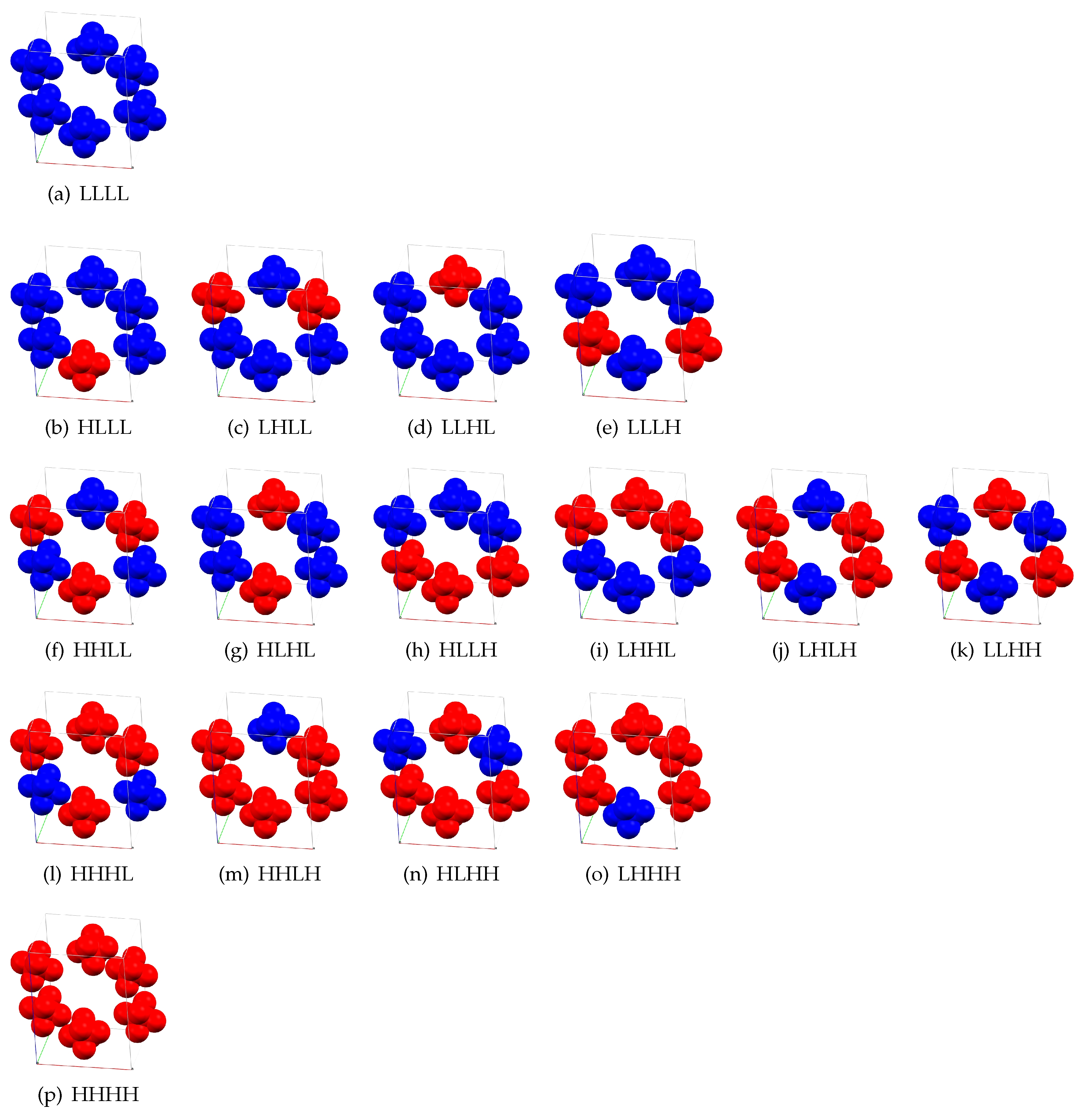
| c | c | c | c | ||||
|---|---|---|---|---|---|---|---|
| HLLL | 4.71 | HHLL | 7.55 | HHHL | 8.33 | HHHH | 9.77 |
| LHLL | 4.40 | HLHL | 6.20 | HHLH | 8.30 | ||
| LLHL | 4.61 | HLLH | 7.29 | HLHH | 8.24 | ||
| LLLH | 4.60 | LHHL | 7.71 | LHHH | 8.38 | ||
| LHLH | 6.31 | ||||||
| LLHH | 7.00 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paulsen, H. Periodic Density Functional Calculations in Order to Assess the Cooperativity of the Spin Transition in Fe(phen)2(NCS)2. Magnetochemistry 2016, 2, 14. https://doi.org/10.3390/magnetochemistry2010014
Paulsen H. Periodic Density Functional Calculations in Order to Assess the Cooperativity of the Spin Transition in Fe(phen)2(NCS)2. Magnetochemistry. 2016; 2(1):14. https://doi.org/10.3390/magnetochemistry2010014
Chicago/Turabian StylePaulsen, Hauke. 2016. "Periodic Density Functional Calculations in Order to Assess the Cooperativity of the Spin Transition in Fe(phen)2(NCS)2" Magnetochemistry 2, no. 1: 14. https://doi.org/10.3390/magnetochemistry2010014
APA StylePaulsen, H. (2016). Periodic Density Functional Calculations in Order to Assess the Cooperativity of the Spin Transition in Fe(phen)2(NCS)2. Magnetochemistry, 2(1), 14. https://doi.org/10.3390/magnetochemistry2010014






