Multi-Step in 3D Spin Crossover Nanoparticles Simulated by an Ising Model Using Entropic Sampling Monte Carlo Technique
Abstract
:1. Introduction
2. Materials and Methods
2.1. Ising Like Model
2.2. Monte Carlo Entropic Sampling
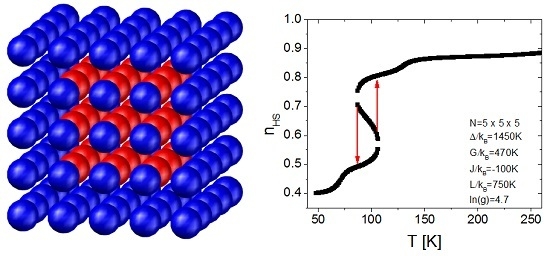
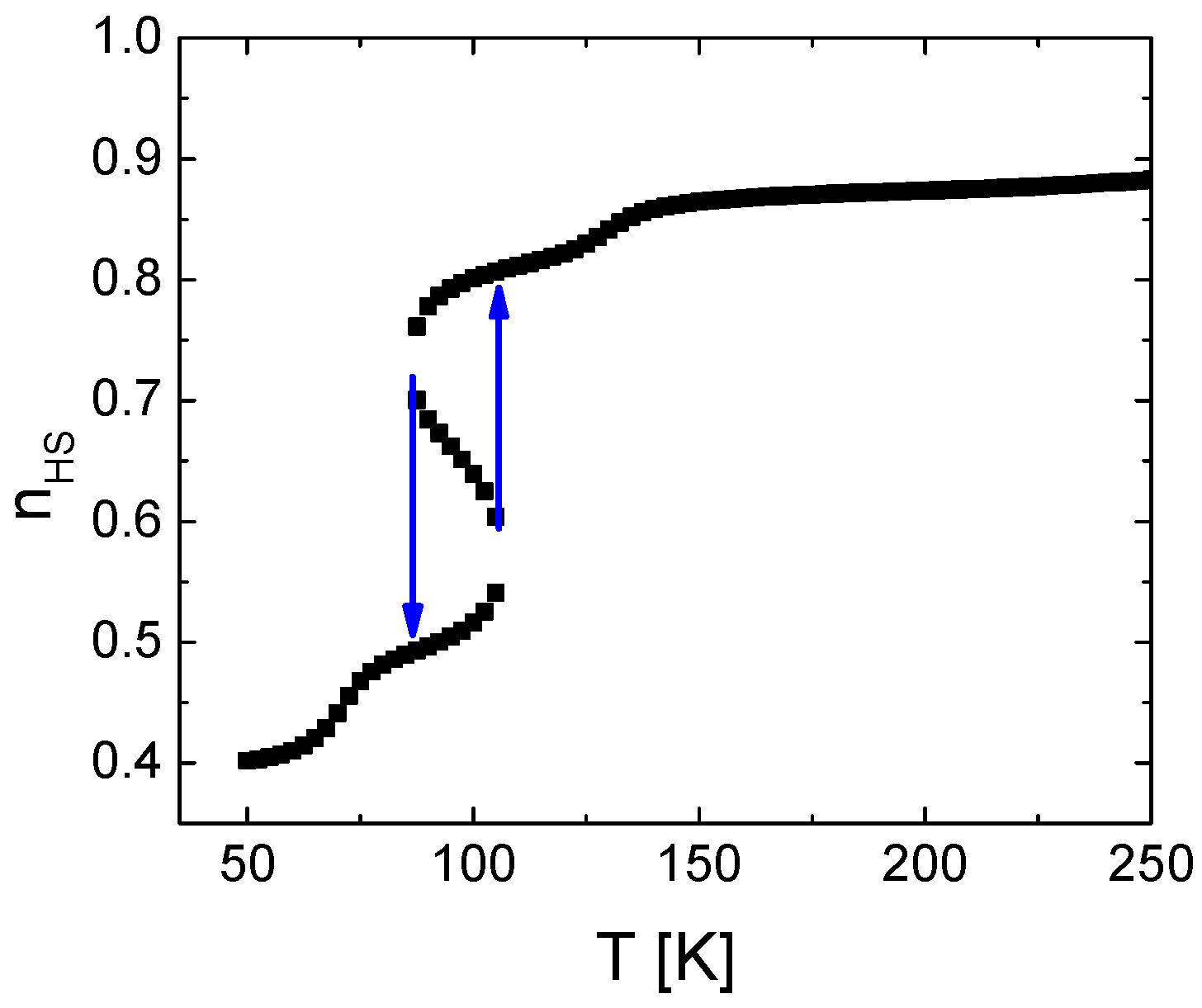
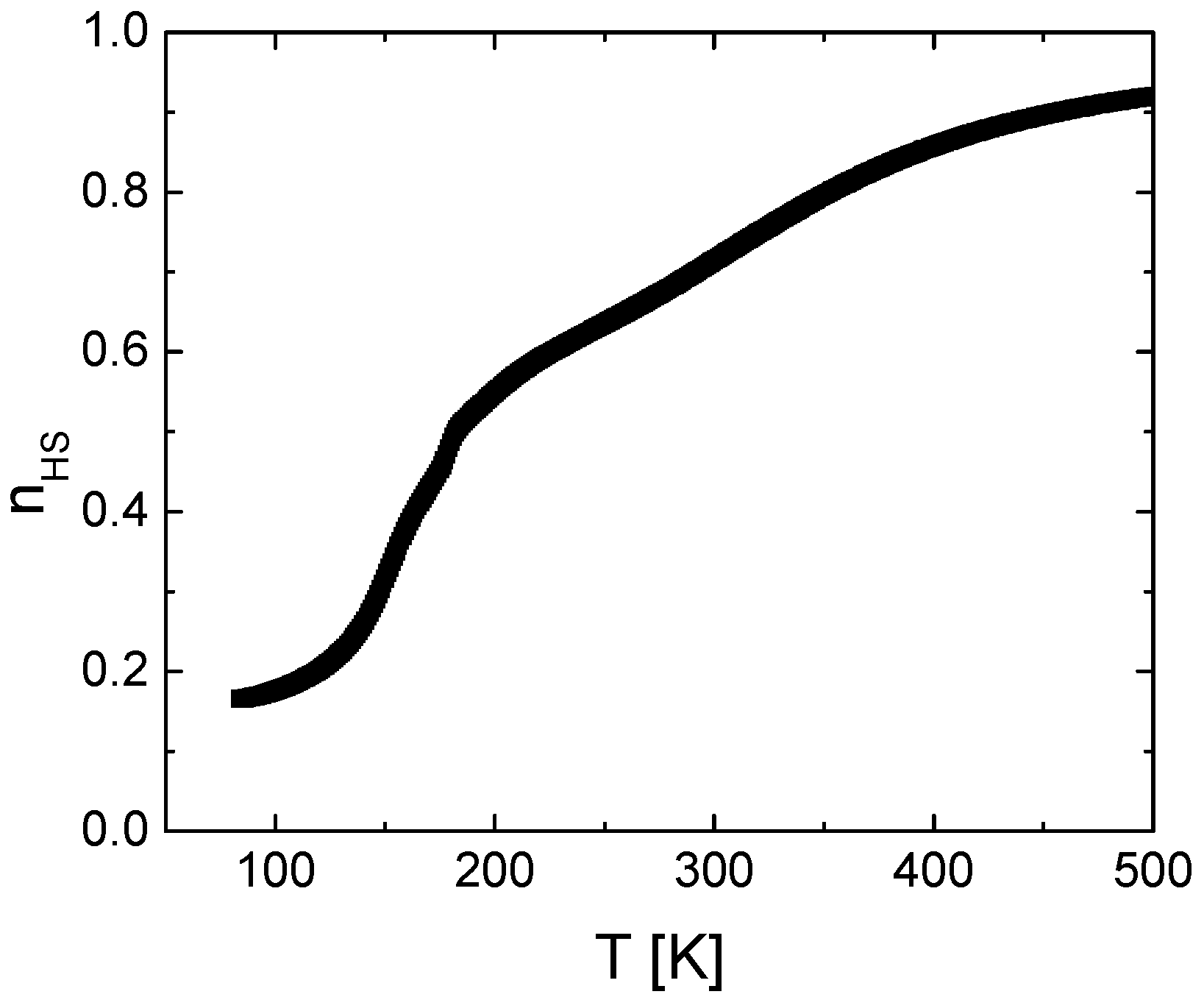
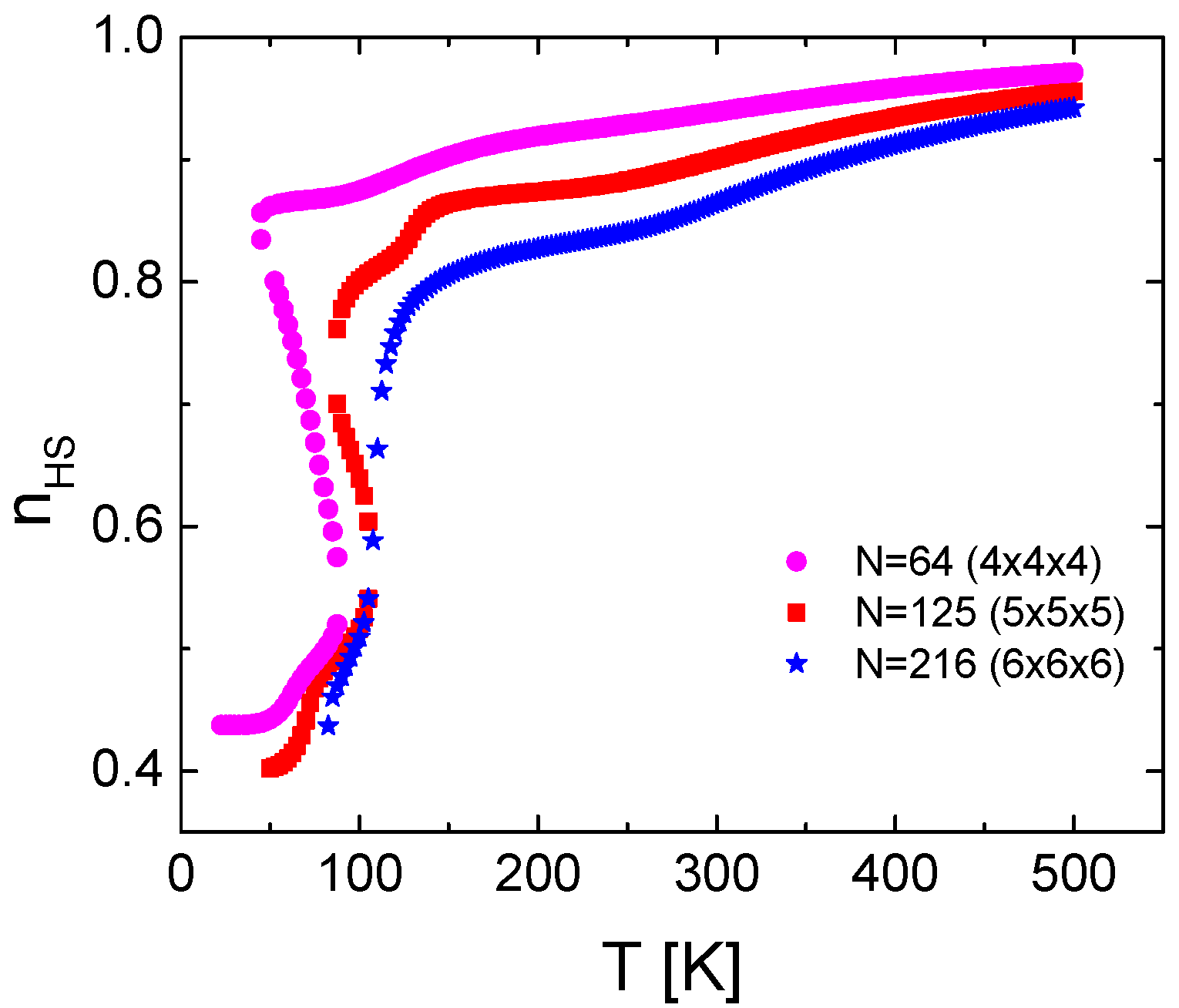
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Linares, J.; Codjovi, E.; Garcia, Y. Pressure and Temperature Spin Crossover Sensors with Optical Detection. Sensors 2012, 12, 4479–4492. [Google Scholar] [CrossRef] [PubMed]
- Jureschi, C.M.; Rusu, I.; Codjovi, E.; Linares, J.; Garcia, Y.; Rotaru, A. Thermo- and piezochromic properties of [Fe(hyptrz)]A2·H2O spin crossover 1D coordination polymer: Towards spin crossover based temperature and pressure sensors. Physica B 2014, 449, 47–51. [Google Scholar] [CrossRef]
- Jureschi, C.M.; Linares, J.; Rotaru, A.; Ritti, M.H.; Parlier, M.; Dîrtu, M.M.; Wolff, M.; Garcia, Y. Pressure sensor via optical detection based on a 1D spin transition coordination polymer. Sensors 2015, 15, 2388–2398. [Google Scholar] [CrossRef] [PubMed]
- Rotaru, A.; Dugay, J.; Tan, R.P.; Gural’skiy, I.A.; Salmon, L.; Demont, P.; Carrey, J.; Molnar, G.; Respaud, M.; Bousseksou, A. Nano-electromanipulation of Spin Crossover Nanorods: Towards Switchable Nanoelectronic Devices. Adv. Mater. 2013, 25, 1745–1749. [Google Scholar] [CrossRef] [PubMed]
- Gütlich, P.; Hauser, A.; Spiering, H. Thermal and optical switching of iron(II) complexes. Angew. Chem. Int. Ed. Engl. 1994, 33, 2024–2054. [Google Scholar] [CrossRef]
- Gütlich, P.; Garcia, Y.; Goodwin, H.A. Spin crossover phenomena in Fe(II) complexes. Chem. Soc. Rev. 2000, 29, 419–427. [Google Scholar] [CrossRef]
- Gütlich, P.; Goodwin, H.A. Spin crossover—An overall perspective. In Spin Crossover in Transition Metal Compounds I; Springer Berlin Heidelberg: Berlin, Germay, 2004; Volume 233, pp. 1–47. [Google Scholar]
- Garcia, Y.; van Koningsbruggen, P.J.; Lapouyade, R.; Fournes, L.; Rabardel, L.; Kahn, O.; Ksenofontov, V.; Levchenko, G.; Gütlich, P. Influences of temperature, pressure, and lattice solvents on the spin transition regime of the polymeric compound [Fe(hyetrz)3]A2∙3H2O, with hyetrz = 4-(2′-hydroxyethyl)-1,2,4-triazole and A− = 3-nitrophenylsulfonate. Chem. Mater. 1998, 10, 2426–2433. [Google Scholar] [CrossRef]
- Real, J.A.; Gaspar, A.B.; Munoz, M.C.; Gütlich, P.; Ksenofontov, V.; Spiering, H. Bipyrimidine-Bridged Dinuclear Iron(II) Spin Crossover Compounds. In Spin Crossover in Transition Metal Compounds I; Springer Berlin Heidelberg: Berlin, Germany, 2004; Volume 233, pp. 167–193. [Google Scholar]
- Ohba, M.; Yoneda, K.; Agusti, G.; Munoz, M.C.; Gaspar, A.B.; Real, J.A.; Yamasaki, M.; Ando, H.; Nakao, Y.; Sakaki, S.; et al. Bidirectional chemo-switching of spin state in a microporous framework. Angew. Chem. Int. Ed. 2009, 48, 4767–4771. [Google Scholar] [CrossRef] [PubMed]
- Sciortino, N.F.; Scherl-Gruenwald, K.R.; Chastanet, G.; Halder, G.J.; Chapman, K.W.; Letard, J.F.; Kepert, C.J. Hysteretic Three-Step Spin Crossover in a Thermo- and Photochromic 3D Pillared Hofmann-type Metal-Organic Framework. Angew. Chem. Int. Ed. 2012, 51, 10154–10158. [Google Scholar] [CrossRef] [PubMed]
- Kosone, T.; Tomori, I.; Kanadani, C.; Saito, T.; Mochida, T.; Kitazawa, T. Unprecedented three-step spin-crossover transition in new 2-dimensional coordination polymer {FeII(4-methylpyridine)2[Au-I(CN)2]2]. Dalton Trans. 2010, 39, 1719–1721. [Google Scholar] [CrossRef] [PubMed]
- Nishi, K.; Kondo, H.; Fujinami, T.; Matsumoto, N.; Iijima, S.; Halcrow, M.A.; Sunatsuki, Y.; Kojima, M. Stepwise Spin Transition and Hysteresis of a Tetrameric Iron(II) Complex, fac- Tris(2-methylimidazol-4-ylmethylidene-n-hexylamine) iron(II) Chloride Hexafluorophosphate, Assembled by Imidazole center dot center dot center dot Chloride Hydrogen Bonds. Eur. J. Inorg. Chem. 2013, 5–6, 927–933. [Google Scholar] [CrossRef]
- Garcia, Y.; Kahn, O.; Rabardel, L.; Chansou, B.; Salmon, L.; Tuchagues, J.P. Two-step spin conversion for the three-dimensional compound tris(4,4′-bis-1,2,4-triazole)iron(II) diperchlorate. Inorg. Chem. 1999, 38, 4663–4670. [Google Scholar] [CrossRef] [PubMed]
- Enachescu, C.; Constant-Machado, H.; Codjovi, E.; Linares, J.; Boukheddaden, K.; Varret, F. Direct access to the photo-excitation and relaxation terms in photo-switchable solids: Non-linear aspects. J. Phys. Chem. Solids 2001, 62, 1409–1422. [Google Scholar] [CrossRef]
- Jeftic, J.; Menendez, N.; Wack, A.; Codjovi, E.; Linares, J.; Goujon, A.; Hamel, G.; Klotz, S.; Syfosse, G.; Varret, F. A helium-gas-pressure apparatus with optical-reflectivity detection tested with a spin-transition solid. Meas. Sci. Tech. 1999, 10, 1059–1064. [Google Scholar] [CrossRef]
- Morscheidt, W.; Jeftic, J.; Codjovi, E.; Linares, J.; Bousseksou, A.; Constant-Machado, H.; Varret, F. Optical detection of the spin transition by reflectivity: application to [FexCo1-x(btr)2(NCS)2]∙H2O. Meas. Sci. Tech. 1998, 9, 1311–1315. [Google Scholar] [CrossRef]
- Mishra, V.; Mukherjee, R.; Linares, J.; Balde, C.; Desplanches, C.; Letard, J.F.; Collet, E.; Toupet, L.; Castro, M.; Varret, F. Temperature-dependent interactions and disorder in the spin-transition compound [Fe-II(L) 2][ClO4]2∙C7H8 through structural, calorimetric, magnetic, photomagnetic, and diffuse reflectance investigations. Inorg. Chem. 2008, 47, 7577–7587. [Google Scholar] [CrossRef] [PubMed]
- Weber, B.; Carbonera, C.; Desplanches, C.; Létard, J.F. Stepwise spin transition in a mononuclear iron(II) complex with unusually wide plateau. Eur. J. Inorg. Chem. 2008, 10, 1589–1598. [Google Scholar] [CrossRef]
- Atitoaie, A.; Tanasa, R.; Enachescu, C. Size dependent thermal hysteresis in spin crossover nanoparticles reflected within a Monte Carlo based Ising-like model. J. Mag. Mag. Mater. 2012, 324, 1596–1600. [Google Scholar] [CrossRef]
- Chiruta, D.; Linares, J.; Dimian, M.; Alayli, Y.; Garcia, Y. Role of Edge Atoms in the Hysteretic Behaviour of 3D Spin Crossover Nanoparticles Revealed by an Ising-Like Model. Eur. J. Inorg. Chem. 2013, 29, 5086–5093. [Google Scholar] [CrossRef]
- Chiruta, D.; Jureschi, C.M.; Linares, J.; Graur, A.; Dimian, M.; Rotaru, A. Analysis of Architecture Effect on Hysteretic Behavior of 3-D Spin Crossover Nanostructures. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Linares, J.; Codjovi, E.; Varret, F.; Niel, V.; Real, J.A. Dynamical Ising-like model for the two-step spin-crossover systems. J. App. Phys. 2003, 93, 7103–7105. [Google Scholar] [CrossRef]
- Enachescu, C.; Tanasa, R.; Stancu, A.; Varret, F.; Linares, J.; Codjovi, E. First-order reversal curves analysis of rate-dependent hysteresis: The example of light-induced thermal hysteresis in a spin-crossover solid. Phys. Rev. B 2005, 72. [Google Scholar] [CrossRef]
- Klokishner, S.; Linares, J.; Varret, F. Effect of hydrostatic pressure on phase transitions in spin-crossover 1D systems. Chem. Phys. 2000, 255, 317–323. [Google Scholar] [CrossRef]
- Wajnflasz, J.; Pick, R. Low-spin-high-spin transitions in Fe2+ complexes. J. Phys. Colloques 1971, 32, C1. [Google Scholar] [CrossRef]
- Bousseksou, A.; Nasser, J.; Linares, J.; Boukheddaden, K.; Varret, F. Ising-like model for the 2-step spin-crossover. J. Phys. I 1992, 2, 1381–1403. [Google Scholar] [CrossRef]
- Linares, J.; Spiering, H.; Varret, F. Analytical solution of 1D Ising-like systems modified by weak long range interaction - Application to spin crossover compounds. Eur. Phys. J. B 1999, 10, 271–275. [Google Scholar] [CrossRef]
- Chiruta, D.; Linares, J.; Dahoo, P.R.; Dimian, M. Analysis of long-range interaction effects on phase transitions in two-step spin-crossover chains by using Ising-type systems and Monte Carlo entropic sampling technique. J. Appl. Phys. 2012, 112, 7. [Google Scholar] [CrossRef]
- Chiruta, D.; Jureschi, C.M.; Linares, J.; Dahoo, P.; Garcia, Y.; Rotaru, A. On the origin of multi-step spin transition behaviour in 1D nanoparticles. Eur. Phys. J. B 2015, 88, 1–5. [Google Scholar] [CrossRef]
- Chiruta, D.; Linares, J.; Dimian, M.; Garcia, Y. Size Effect and Role of Short- and Long-Range Interactions on 1D Spin-Crossover Systems within the Framework of an Ising-Like Model. Eur. J. Inorg. Chem. 2013, 5–6, 951–957. [Google Scholar] [CrossRef]
- Chiruta, D.; Linares, J.; Garcia, Y.; Dimian, M.; Dahoo, P.R. Analysis of multi-step transitions in spin crossover nanochains. Physica B. 2014, 434, 134–138. [Google Scholar] [CrossRef]
- Jureschi, C.M.; Pottier, B.L.; Linares, J.; Richard Dahoo, P.; Alayli, Y.; Rotaru, A. Simulation of multi-steps thermal transition in 2D spin-crossover nanoparticles. Physica B 2016. [Google Scholar] [CrossRef]
- Chiruta, D.; Jureschi, C.M.; Linares, J.; Garcia, Y.; Rotaru, A. Lattice architecture effect on the cooperativity of spin transition coordination polymers. J. Appl. Phys. 2014, 115, 053523. [Google Scholar] [CrossRef]
- Peng, H.; Tricard, S.; Félix, G.; Molnár, G.; Nicolazzi, W.; Salmon, L.; Bousseksou, A. Re-Appearance of Cooperativity in Ultra-Small Spin-Crossover [Fe(pz){Ni(CN)4} Nanoparticles. Angew. Chem. 2014, 126, 11074–11078. [Google Scholar] [CrossRef]
- Muraoka, A.; Boukheddaden, K.; Linares, J.; Varret, F. Two-dimensional Ising-like model with specific edge effects for spin-crossover nanoparticles: A Monte Carlo study. Phys. Rev. B 2011, 5, 84. [Google Scholar] [CrossRef]
- Spiering, H. Elastic interaction in spin crossover compounds. In Spin Crossover in Transition Metal Compounds III; Springer: Berlin Heidelberg, Germany, 2004; Volume 235, pp. 171–195. [Google Scholar]
- Linares, J.; Enachescu, C.; Boukheddaden, K.; Varret, F. Monte Carlo entropic sampling applied to spin crossover solids: the squareness of the thermal hysteresis loop. Polyhedron 2003, 22, 2453–2456. [Google Scholar] [CrossRef]
- Shteto, I.; Linares, J.; Varret, F. Monte Carlo entropic sampling for the study of metastable states and relaxation paths. Phys. Rev. E 1997, 56, 5128–5137. [Google Scholar] [CrossRef]
- Pillet, S.; Hubsch, J.; Lecomte, C. Single crystal diffraction analysis of the thermal spin conversion in [Fe(btr)2(NCS)2](H2O): Evidence for spin-like domain formation. Eur. Phys. J. B 2004, 38, 541–552. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jureschi, C.; Linares, J.; Rotaru, A.; Garcia, Y. Multi-Step in 3D Spin Crossover Nanoparticles Simulated by an Ising Model Using Entropic Sampling Monte Carlo Technique. Magnetochemistry 2016, 2, 13. https://doi.org/10.3390/magnetochemistry2010013
Jureschi C, Linares J, Rotaru A, Garcia Y. Multi-Step in 3D Spin Crossover Nanoparticles Simulated by an Ising Model Using Entropic Sampling Monte Carlo Technique. Magnetochemistry. 2016; 2(1):13. https://doi.org/10.3390/magnetochemistry2010013
Chicago/Turabian StyleJureschi, Catalin, Jorge Linares, Aurelian Rotaru, and Yann Garcia. 2016. "Multi-Step in 3D Spin Crossover Nanoparticles Simulated by an Ising Model Using Entropic Sampling Monte Carlo Technique" Magnetochemistry 2, no. 1: 13. https://doi.org/10.3390/magnetochemistry2010013
APA StyleJureschi, C., Linares, J., Rotaru, A., & Garcia, Y. (2016). Multi-Step in 3D Spin Crossover Nanoparticles Simulated by an Ising Model Using Entropic Sampling Monte Carlo Technique. Magnetochemistry, 2(1), 13. https://doi.org/10.3390/magnetochemistry2010013