Study on Some Factors That Influence the Yield Stress in Kerosene-Based Magnetic Fluids Using an Orthogonal Experimental Design

Abstract

Magnetic fluid sealing is a novel sealing technology wherein magnetic fluids play a pivotal role in the sealing process. The yield stress of the magnetic fluid directly affectsits sealing performance and is governed by multiple interdependent factors. Conventional approaches that evaluate the effect of a single parameter while keeping other parameters constant are insufficient to fully characterize the relative contributions of each parameter to the yield stress. In this study, we investigate the preparation factors affecting the yield stress of kerosene-based magnetic fluids and propose a parameter sensitivity analysis method based on orthogonal experimental design to determine the optimal combination of factor levels within the studied range. The sensitivity of key preparation factors affecting the yield stress of kerosene-based magnetic fluids was determined via range and variance analyses of the orthogonal experimental data. The factors, ranked in descending order of sensitivity, were surfactant (C₁₈H₃₄O₂) dosage, precipitant (NH₃·H₂O) dosage, and deionized water (H₂O) volume. Moreover, the effects of different levels of the same factor were analyzed using multiple approaches. These findings provide a theoretical foundation for optimizing the preparation of magnetic fluids and enhancing their sealing performance.

1. Introduction

Magnetic fluids have numerous applications, with magnetic fluid sealing being one of the most technologically mature. These sealing systems have been widely implemented in military equipment, such as tank panoramic sight systems [1] and radar rotary joints [2], as well as in industrial equipment such as reaction vessels [3] and stirred tanks [4]. Figure 1 illustrates a typical magnetic fluid rotary seal configuration.

In addition to traditional rubber and plastic seals, magnetic fluid (ferrofluid) rotary seals utilizing this novel functional material have become a major research focus worldwide. Magnetic fluids are intelligent nanofunctional materials whose properties can be controlled using magnetic fields. Magnetic fluids consist of stable colloidal suspensions of nanoscale magnetic particles (typically 3–15 nm in diameter) coated with surfactants and dispersed in carrier liquids. The surfactant molecules, featuring long-chain structures compatible with the carrier liquid, maintain a uniform and stable dispersion of the magnetic particles via steric hindrance effects. Organic solvents or water are typically used as carrier liquids. Owing to the combination of magnetic responsiveness and fluidity, magnetic fluids are extensively applied in sealing systems, sensors, dampers, and various other fields.

Magnetic fluids exhibit unique rheological properties owing to their responsiveness to external magnetic fields. Beyond conventional rheological factors such as shear rate and temperature, their rheological behavior can be controlled by applying external magnetic fields. Thus, the rheological properties of magnetic fluids can be modulated via deliberate design and control of the applied magnetic field.

Despite these advantages, magnetic fluid sealing faces critical challenges in practical applications. The yield stress of magnetic fluids directly affects the rotational resistance torque of the seal, ultimately influencing sealing performance and potentially leading to seal failure.

The yield stress characteristics significantly affect critical performance parameters, such as the starting torque of magnetic fluid seals. However, various highly coupled factors with complex interaction mechanisms influence the yield stress, and the underlying regulatory principles remain unclear. Therefore, a systematic investigation of the yield stress behavior of magnetic fluids and their regulatory mechanisms is necessary.

Current studies on the yield stress behavior of magnetic fluids predominantly employ chain-structure models to predict yield stress. When a magnetic fluid is subjected to zero-shear conditions, its viscosity stabilizes, resulting in negligible yield stress. The yield stress under different magnetic fields can be derived by fitting the flow curves of magnetic fluids using models such as the Herschel–Bulkley model. Zubarev et al. investigated the formation of droplet-like aggregates in magnetic fluids and their elongation/fragmentation under a combination of magnetic fields and shear flow, proposing a microscopic interpretation of the yield process [5]. Shahnazian et al. reported that magnetic fluids containing cobalt particles exhibit higher yield stress than those with Fe₃O₄ particles, with the yield stress magnitude strongly correlating with the large particle content, magnetic field strength, and testing gap [6].

Liu et al. investigated the microstructural evolution of magnetic fluids under steady shear and compression via molecular dynamics simulations [7]. They reported that magnetic particles initially form chain-like structures through dipole interactions under an applied magnetic field, and that both potential energy and static yield stress increase with magnetic field strength. Under steady shear, these one-dimensional chain/columnar structures transform into layered configurations. When compressed along the field direction, the yield stress increases because of the conversion of a major portion of compression work into repulsive potential energy [7]. López-López et al. compared the rheological properties of nanoparticle- and nanofiber-based magnetic fluids and proposed a theoretical model for the static yield stress [8]. Although their model qualitatively captures experimental trends, quantitative discrepancies remain.

Xinzhi et al. [9] investigated the influence of yield stress on the sealing performance of magnetic fluids and experimentally characterized the variation in breakaway torque and pressure resistance of magnetic fluid seals as a function of resting time. They derived modified theoretical formulae for pressure resistance and drag torque that explicitly account for yield stress effects. In a complementary study, Zhenkun [10] systematically examined the magnetoviscous properties, viscoelastic behavior, and yield stress/thixotropic characteristics of magnetic fluids and explored how magnetic fluid viscosity affects the sealing performance of liquid media.

Chen & Li [11] investigated the effect of particle size distribution on the resisting torque in magnetic fluid seals. Ferrofluid samples with varying particle size distributions were prepared by applying a magnetic field gradient, and their rheological properties were analyzed using a rheometer. The variation in the starting torque of magnetic fluid seals with particle size distribution was explained in terms of field-induced structure formation and destruction using magnetoviscous effect theory. Their results suggest a feasible approach to improve the performance of magnetic fluid seals. He et al. [12] experimentally investigated the starting torque of magnetic fluid seals and four key factors, namely the temperature, ferrofluid injection volume, standing time, and external pressure applied to the ferrofluid. They analyzed the variation in seal starting torque from the perspective of ferrofluid yield stress and discussed the influence of chain-like structures within the ferrofluid on yield stress from a microscopic viewpoint, including the formation mechanisms of these chain-like structures.

The yield stress of magnetic fluids depends on multiple interdependent factors. Conventional single-factor studies have investigated individual parameters while keeping others constant. However, such approaches cannot fully characterize the relative contributions of each parameter. We address this limitation by proposing a systematic research methodology based on an orthogonal experimental design to investigate the factors affecting the yield stress of magnetic fluids.

We performed a significance analysis of the various preparation parameters affecting the yield stress, conducted comparative evaluations of different levels of the same factor, and identified the key preparation parameters that significantly influence the yield stress. The major findings include the quantitative determination of the parameter significance hierarchy, identification of optimal level combinations for critical preparation variables, and establishment of process–property relationships. This study provides both theoretical and experimental foundations for improving the application prospects of kerosene-based ferrofluids in rotary magnetic fluid seals and reducing the influence of yield stress on starting torque.

2. Yield Stress of Magnetic Fluids

2.1. Mechanism of Yield Stress Generation in Magnetic Fluids

In the absence of an external magnetic field, the magnetic particles within magnetic fluids are randomly distributed due to Brownian motion, and the fluids exhibit Newtonian behavior. Under an external magnetic field, the magnetized dipoles interact strongly, leading to a reduction in Brownian motion and causing the magnetic particles to align along the field direction to form linear chain-like structures. These structures further evolve into more complex columnar or three-dimensional networks that increase the viscosity of the magnetic fluid owing to the magnetoviscous effect. Under such conditions, the magnetic fluid demonstrates non-Newtonian behavior. At high shear rates, the shear flow disrupts these chain structures, leading to a reduction in viscosity. The stress required to break these chain structures corresponds to the yield stress of the magnetic fluid. The factors influencing the yield stress of magnetic fluids include magnetic field intensity, particle volume fraction, particle size and shape, carrier liquid type, and additives.

As shown in Figure 2a, under an applied magnetic field, the magnetic particles within the static magnetic fluid aggregate to form chain-like or network structures. When pressure p is applied on one side of the magnetic fluid (Figure 2b), these chain/network structures deform and generate a resistance force directed against the pressure. This structural resistance, which prevents complete structural failure, represents the yield stress of the magnetic fluid. In rotational sealing applications (Figure 2c), at the critical point of shaft rotation initiation, the chain structures tilt owing to the relative displacement between the upper and lower surfaces of the magnetic fluid, producing a counteracting force opposing the shaft motion. Therefore, apart from overcoming the conventional sealing friction torque, the shaft must overcome the torque required to surpass the yield stress of the magnetic fluid. Macroscopically, this phenomenon manifests as an increase in the breakaway torque of magnetic fluid-sealing devices.

Many types of magnetic fluids exhibit such yield stress behavior. When the applied shear stress exceeds a critical value, the magnetic fluid flows as a viscous liquid. Conversely, when the shear stress is below this threshold, the magnetic fluid exhibits solid-like characteristics and undergoes rigid-body motion.

The yield stress primarily originates from the formation of network structures. The number density of magnetic particles is on the order of n = 10¹⁷–10¹⁸ particles per cubic milliliter. Even if only 10% of the magnetic particles are involved in the formation of elongated chains and network structures, their total length becomes remarkably large. Assuming that the diameter of each magnetic particle is $2a_p={10}^{-8}\mathrm{m}$ ($a_p$ is the radius of each magnetic particle), the total length $\sum l_i$ of the chains and networks can be expressed as

$$\sum l_i=\left(n\times 10\%\right)2a_p={10}^8\mathrm{m}/{\mathrm{mm}}^3.$$

(1)

The total lateral surface area $\sum S_i$ can be estimated as

$$\sum S_i=2{\pi a}_p\sum l_i=3.14{\mathrm{m}}^2/{\mathrm{mm}}^3.$$

(2)

In 1 mL of a magnetic fluid, the total linear length of the chain and network structures formed by the magnetic particles can reach an order of magnitude of 10⁸ m. These elongated, particle-assembled chains bend and interlace, forming diverse structures of varying sizes and shapes that are densely distributed throughout the magnetic fluid. The combined effects of adhesive interactions at the carrier–liquid interface and intrinsic cohesive forces within the liquid collectively determine the flow characteristics of the magnetic fluid.

2.2. Calculation of Yield Stress in Magnetic Fluids

Consider a differential cubic control volume within a flowing magnetic fluid where multiple dipole chains (or network segments) penetrate all six surfaces. Focusing on the dxdy plane (Figure 3), we analyze a representative dipole chain under tensile deformation [13].

In Figure 4, the line segment AB represents one of the chains penetrating the differential plane dzdx. When the magnetic fluid approaches yielding, shear stress ${\tau }_{\mathrm{yx}}$ acts on the infinitesimal area dzdx. Given the negligible dimensions of the control volume, AB can be approximated as a straight line. Let $\gamma$ denote the angle between AB and the reference plane ${\tau }_{\mathrm{yx}}$. The stiffness of the carrier liquid under shear stress is negligible. According to the stress-partitioning principles based on relative stiffness, the entire shear stress generated by the incipient flow is borne exclusively by the magnetic particle chains. Therefore, the force balance equation is given by

$${\tau }_{\mathrm{yx}}dzdx={\sum }_{i=1}^{{\mathrm{dN}}_i}({\sigma }_1{S}_1/\cos \gamma {)}_i,$$

(3)

where ${\sigma }_1$ denotes the tensile stress acting on a single chain, $S_1$ is the cross-sectional area of the chain with $S_1$ = ${\pi a}_p^2$ (a_p is the radius of the magnetic particles), and ${dN}_i$ denotes the number of chains penetrating the differential area dzdx and subjected to tensile stress.

Let ${\left(\cos \gamma \right)}_e$ denote the mathematical expectation (statistical mean) of $\cos \gamma$, where $\cos \gamma$ follows a normal distribution:

$$(\cos \gamma {)}_e^2={\left[1-(\cos \gamma {)}_e\right]}^2,$$

(4)

or

$$(\cos \gamma {)}_e={\displaystyle \frac{1}{2}}.$$

(5)

The magnetic attraction between adjacent dipoles in a chain can be represented, to first approximation, by the diploe–dipole interaction force within a dipole pair and can be expressed as

$$({\sigma }_1{S}_1{)}_i\le (F_{d,r}{)}_i,$$

(6)

where $F_{d,r}$ represents the magnetic force between dipoles. For linearly aligned dipole pairs, we obtain

$$(F_{d,r}{)}_i={\displaystyle \frac{3{\mu }_0}{2{\pi r}^4}}{m}_{d,i}{m}_{d,i+1}.$$

(7)

If the dimensions and magnetic moments of all dipoles are identical, the strength condition can be derived as

$${\tau }_{\mathrm{yx}}\mathrm{d}z\mathrm{d}x\le \left({dN}_t\right){\displaystyle \frac{3{\mu }_0}{{\pi r}^4}}{m}_d^2.$$

(8)

Using the number of chains per unit area $n_t$, the yield stress can be expressed as

$$n_t={\displaystyle \frac{{dN}_t}{dzdx}}.$$

(9)

Therefore, the yield stress ${\tau }_s$ of the magnetic fluid is given by

$${\tau }_s=n_t{\displaystyle \frac{3{\mu }_0}{{\pi r}^4}}{m}_d^2.$$

(10)

Within the microstructures penetrating the dzdx plane, a subset comprises linearly connected polar dipole chains. In the absence of an external magnetic field, these chains are randomly oriented. When an external field is applied, a fraction of the dipole chains align along the field direction, and the degree of alignment increases with the field strength. Under a vertical external magnetic field (along the y-axis, normal to the dzdx plane), a portion of the dipole chains penetrates the dzdx surface. The number of chains penetrating the surface increases with the intensity of the applied field, thereby increasing the areal chain density in the corresponding equation. Consequently, the yield stress of the magnetic fluid is positively correlated with the external field strength.

2.3. Influence of Yield Stress on the Rotational Resistance Torque of Seals

In magnetic fluid rotary seals, the rotation of the shaft must overcome the significant yield stress generated by the magnetic fluid, resulting in a sharp increase in torque—particularly the breakaway torque. This poses significant challenges in industrial applications, where it is essential to maintain the low viscosity and low yield stress activity of the magnetic fluid in seals after prolonged storage, and to ensure reliable startup and normal operation under varying working conditions.

Various theoretical models have been developed to analyze the rotational resistance torque in magnetic fluid seals. A simplified two-dimensional model was proposed, where the magnetic fluid is confined in the gap between the rotating shaft and pole piece [14].

Figure 4 shows a schematic of the cross-sectional structure of the magnetic fluid seal. This model [14] treats the magnetic fluid as a Newtonian fluid, and the viscous shear stress for a one-dimensional flow is calculated using the Navier–Stokes equation. The resisting torque can then be calculated as

$$T=2\pi r_{1}l{\tau }_{r,\theta }=4\pi {\displaystyle \frac{\eta l\omega r_1^2{r}_2^2}{r_2^2-r_1^2}},$$

(11)

where r₁ denotes the radius of the rotating shaft, r₂ is the inner diameter of the pole piece, $\omega$ is the angular velocity of the shaft, $\eta$ is the dynamic viscosity of the magnetic fluid, and l is the total axial length of the magnetic fluid in contact with the shaft.

Based on the increment in the pressure-bearing capacity of a single-stage magnetic fluid seal and considering only rotation in the absence of external pressure, the additional resisting torque of the single-stage magnetic fluid seal is given by

$$\Delta T_{\tau }\approx 2\pi r_1^2{L}_t{\tau }_s.$$

(12)

Therefore, the total resisting torque of the magnetic fluid seal is expressed as

$$T_Z=T+n·\Delta T_r=4\pi {\displaystyle \frac{\eta l\omega r_1^2{r}_2^2}{r_2^2-r_1^2}}+n2\pi r_1^2{L}_t{\tau }_s,$$

(13)

where n denotes the number of sealing stages.

Thus, the yield stress of the magnetic fluid directly influences the rotational resistance torque in magnetic fluid rotary seals and determines the starting torque during seal startup.

2.4. Influence of Yield Stress on the Sealing Pressure-Bearing Capacity

In magnetic fluid seals, the yield stress of the magnetic fluid influences the sealing performance of the device. Inadequate sealing in certain regions can reduce the overall pressure resistance of the sealing system.

The yield stress of the magnetic fluid strongly affects the pressure resistance ${\Delta p}_{\tau }$ of the magnetic fluid seals. Let r be the radius of the magnetic fluid seal, L_t the width of the pole teeth, and L_g the sealing gap with L_g ≪ r. At the critical state when magnetic particle chains begin to rupture, the equilibrium condition yields

$$2\pi {\mathrm{rL}}_g\Delta p\tau \approx 2\pi {\mathrm{rL}}_t{\tau }_s.$$

(14)

Thus,

$${\Delta p}_{\tau }\approx {\displaystyle \frac{L_t}{L_g}}{\tau }_s.$$

(15)

Because the constitutive equations for magnetic fluids cannot be derived theoretically, the results of theoretical analyses remain qualitative. Therefore, the yield stress of magnetic fluids must be experimentally determined. During rheometer measurements, an external magnetic field is applied for characterizing magnetic fluids, and the yield stress is measured as the value of the shear stress at zero shear rate. In magnetic fluid sealing applications, the yield stress can also be calculated by measuring the breakaway torque of the seal.

3. Experimental Methods

3.1. Preparation of Magnetic Fluids

Methods for preparing magnetic fluids include mechanical grinding [15,16,17], chemical co-precipitation [18], anion exchange resin processing [19], hydrogen reduction [20], spark erosion [21], ultraviolet decomposition [20], thermal decomposition [22,23], vacuum evaporation [24], and electrodeposition [25]. Among these, chemical co-precipitation [26] has been widely adopted owing to its strong controllability, high efficiency, and excellent operational feasibility. This method was employed for synthesizing the kerosene-based magnetic fluid in the present study. The experimental procedure for chemical co-precipitation is as follows (Figure 5):

(1)

Specified quantities of FeCl₃·6H₂O and FeCl₂·4H₂O were weighed and dissolved in deionized water to obtain an iron salt solution.

(2)

The iron salt solution was heated and stirred in a water bath. Ammonium hydroxide (NH₃·H₂O), serving as the precipitating agent, was then added, and stirring was continued.

(3)

Oleic acid (C₁₈H₃₄O₂) was added as the surfactant, and the mixture was subsequently stirred to obtain a suspension.

(4)

The suspension was placed on a permanent magnet for magnetic separation. It was washed with deionized water until the supernatant pH reached 7, yielding nanosized magnetic particles.

(5)

Kerosene was used as the carrier liquid. The carrier liquid and an appropriate amount of deionized water were added to the magnetic particles. The mixture was heated in an 80 °C water bath under continuous stirring for 60 min.

(6)

The residual deionized water was removed from the product to obtain the kerosene-based magnetic fluid.

A stable kerosene-based magnetic fluid was obtained using the above-described procedure. The sources and specifications of the main reagents used are listed in

Table 1. Sources and specifications of the main reagents.

Reagent Name	Chemical Formula	Molecular Weight	Specification	Sources
Ferric chloride	FeCl3·6H2O	270.3	Analytical	ShanghaiTitan Scientific Co., Ltd., Shanghai, China.
Iron chloride tetrahydrate	FeCl2·4H2O	198.9	Analytical reagent grade	Tianjin Damao Chemical Industry Group Co., Ltd., Tianjin, China.
Ammonium hydroxide	NH3·H2O	35	Analytical reagent grade	Beijing Tongguang Fine Chemicals Company, Beijing, China.
Oleic acid	C18H34O2	282.5	Analytical reagent grade	Anhui Zesheng Technology Co., Ltd., Anqing, China.
Deionized water	H2O	18	Ultrapure water	Laboratory-Synthesized (PSDK2-20-C), Tsinghua University, Beijing, China.

. The carrier liquid, kerosene, was sourced from Macklin. The primary instruments used for magnetic fluid preparation are listed in

Table 2. Experimental instruments.

Instrument Name	Sources
YM-030S Ultrasonic Cleaner	Shenzhen Fangao Microelectronics Co., Ltd., Shenzhen, China.
HH-2 Digital Display Constant Temperature Water Bath	Shangzhou Langyue Instrument Manufacturing Co., Ltd., Shangzhou, China.
SNOES-200SH Cantilever-type Electric Stirrer	Shanghai Shangpu Instrument Equipment Co., Ltd., Shanghai, China.

.

3.2. Principles and Design of an Orthogonal Experimental Method

Orthogonal experimental design is a scientific methodology that employs orthogonal arrays to systematically investigate the influence of multiple factors on experimental outcomes. An appropriate orthogonal array is selected according to the specific requirements of the practical problems, serving both as the experimental framework and statistical basis.

The standard notation for an orthogonal array is denoted as L_N(m^k), where L denotes the orthogonal table encompassing various experimental combinations, N is the total number of experimental trials, m is the number of levels for each factor, and k denotes the maximum number of factors that can be accommodated in the experiment.

During the preparation of magnetic fluids, several factors influence the resulting yield stress. For kerosene-based magnetic fluids, the quantities of the precipitating agent (NH₃·H₂O), deionized water (H₂O), and surfactant (C₁₈H₃₄O₂) were identified as three critical process parameters. Accordingly, the dosages of the precipitant and surfactant, along with the volume of deionized water, were chosen as three variable parameters for an orthogonal experimental investigation of the yield stress of kerosene-based magnetic fluids. The amounts of other preparation materials employed are listed in

Table 3. Dosage of preparation materials.

FeCl3·6H2O (g)	FeCl2·4H2O (g)	Kerosene (mL)
32.4	20	40

.

If each parameter were to have three levels, a full factorial experiment would require 3³ = 27 preparation trials, requiring substantial human and material resources. In contrast, the orthogonal experimental design enables efficient investigation of multiple factors and levels by selecting representative test points based on orthogonality. These points exhibit “uniform dispersion and comparable regularity,” making the method a highly effective, rapid, and economical alternative. The results of each group were evaluated after configuring the factor levels using an orthogonal array. Since the yield stress of magnetic fluids can be directly measured using a rheometer, it was adopted as the evaluation metric.

Based on prior experience with the preparation of kerosene-based magnetic fluids, the following factor levels were chosen: precipitant dosage: 120 and 140 mL (two levels); deionized water volume: 400, 500, and 600 mL (three levels); and surfactant dosage: 7, 10, and 12 mL (three levels). The primary levels were selected based on common preparation conditions. The factor-level distribution is presented in

Table 4. Factor levels for orthogonal experimental design.

No.	Factor
	Precipitant (mL)	Deionized Water (mL)	Surfactant (mL)
Level 1	120	400	7
Level 2	140	500	10
Level 3	/	600	12

. To accommodate the factors with different numbers of levels, the pseudo-level method was applied. This conventional engineering technique reconciles the mixed-level conditions within the framework of a standard L9 orthogonal array, thus maintaining the required orthogonality in the experimental design. Using the orthogonal experimental design, only nine test groups were required, and these are listed in

Table 5. Orthogonal experimental design array.

No.	Factor A	Factor B	Factor C
1	Level 1	Level 2	Level 2
2	Level 1	Level 2	Level 1
3	Level 1	Level 3	Level 3
4	Level 2	Level 1	Level 2
5	Level 1	Level 3	Level 2
6	Level 2	Level 2	Level 3
7	Level 1	Level 1	Level 1
8	Level 1	Level 1	Level 3
9	Level 2	Level 3	Level 1

. Therefore, the number of experiments was significantly reduced while retaining statistical validity.

Range analysis [27] and analysis of variance (ANOVA) [28,29] were conducted to process the orthogonal experimental data and analyze the relative significance of different parameters on the experimental results [30,31].

3.3. Measurement of the Yield Stress of Magnetic Fluids

The yield stress values of the prepared kerosene-based magnetic fluid were measured using an Anton Paar MCR 301/302 rotational rheometer at the Tribology Key Laboratory of Tsinghua University, as shown in Figure 6. The magnetic field was generated using the MRD 170 accessory unit of the rheometer, which employs an electromagnetic coil installed beneath the measuring plate. The centers of the coil and plate were precisely aligned, ensuring a uniform magnetic field across the measurement region, oriented perpendicular to the velocity gradient of the sample. A current range of 0–5 A produced a magnetic field strength of 0–1 T, which was calibrated prior to the experiments. The temperature was controlled using a VT2 liquid-circulation thermostat system equipped with a rheometer. The technical specifications of the rheometer are listed in

Table 6. Technical specifications of the Anton Paar MCR 301/302 rheometer.

Technical Specifications	Numerical Data
Minimum torque	0.002 μNm
Maximum torque	200 mNm
Deflection (Preset)	0.1–∞ μrad
Minimum speed (CSS)	10−7 rpm
Minimum speed (CSR)	10−6 rpm
Maximum speed	3000 rpm
Minimum frequency	10−5 Hz
Maximum frequency	100 Hz
Normal force range	0.01–50 N
Normal force accuracy	0.002 N
Temperature range	−150–500 °C

. The MCR 301/302 rheometer employs an air-bearing system that enables both rotational and oscillatory measurements. A parallel-plate fixture with rotational measurement methodology was used to determine the yield stress of the magnetic fluid at laboratory temperature (25 °C).

The flow curve of a magnetic fluid, which depicts the relationship between shear stress (y-axis) and shear rate (x-axis), can be obtained using a rheometer. In the absence of an external magnetic field, the shear stress is proportional to the shear rate, and there is essentially no intercept on the y-axis. Under these conditions, the magnetic fluid exhibits nearly Newtonian behavior, indicating the absence of yield stress. Under an external magnetic field, the shear stress increases with the shear rate, but the rate of increase gradually diminishes. Moreover, the flow curve shows a finite intercept on the y-axis, demonstrating the non-Newtonian characteristics of the magnetic fluid. The yield stress is measured during the initial phase of measurement when the shear rate approaches zero.

4. Results

4.1. Fundamental Properties of the As-Prepared Magnetic Fluids

Based on the orthogonal experimental design, nine types of kerosene-based magnetic fluids were synthesized via chemical co-precipitation. The fundamental properties of these magnetic fluids were characterized in terms of magnetic particle dispersibility, stability, and magnetization performance.

4.1.1. Dispersibility of Magnetic Particles

The nine prepared kerosene-based magnetic fluid samples were observed using a Hitachi HT7700 transmission electron microscope (TEM, Hitachi, Japan), and the results are shown in Figure 7. The synthesized magnetic particles exhibited a predominantly spherical morphology with an average particle size of approximately 10 nm, indicating generally favorable dispersibility. A small fraction of particles showed slight agglomeration. However, as the TEM images were obtained under non-magnetic conditions, the differences in magnetic particle aggregation and chain-like alignment among the nine magnetic fluids are not distinctly demonstrated.

Statistical analysis of particle size for all samples was performed using Nano Measure software 1.2. The resulting particle size distributions are presented in

Table 7. Statistical results of particle size.

No.	1	2	3	4	5	6	7	8	9
Standard Deviation	1.27	1.18	1.37	1.27	1.03	1.18	1.03	1.09	1.01
Median (nm)	9.62	9.46	9.37	9.36	9.44	9.37	9.35	9.40	9.56
Mean (nm)	9.49	9.32	9.21	9.19	9.34	9.22	9.31	9.38	9.56

and Figure 8. The statistical results indicate that the particle size distributions of all samples conform to a normal distribution.

4.1.2. Stability

Under an applied magnetic field, magnetic particles form chain-like structures, resulting in the development of yield stress in the magnetic fluid. However, upon removal of the magnetic field, the particles undergo complete demagnetization and remain uniformly suspended within the carrier liquid. Visual inspection confirmed the absence of particle sedimentation in the magnetic fluid under such conditions. This is consistent with the relationship given in the following formula [32]:

$$C{k}_{0}T\ge ({\rho }_P-{\rho }_{ ff})V_{P1}gh,$$

(16)

where C is a constant, k₀ is the Boltzmann constant, T denotes the temperature, ${\rho }_{\mathrm{P}}$ is the density of the magnetic particles, ${\rho }_{ff}$ is the density of the magnetic fluids, g is the acceleration due to gravity, h is the height of the magnetic particle from the reference point, and $V_{\mathrm{P}1}=\pi d^3/6$ is the volume of a single magnetic particle.

The critical size of magnetic particles is given by

$$d\le \left[{\displaystyle \frac{6C{k}_{0}T}{\pi ({\rho }_{\mathrm{P}}-{\rho }_{ ff}) gh}}\right].$$

(17)

When the magnetic particle sizes are smaller than the critical dimension, a stable suspension can be formed under the influence of a gravitational field.

The stability analysis of the nine kerosene-based magnetic fluids was conducted via direct observation. Appropriate amounts of each magnetic fluid were placed in test tubes and allowed to stand for 0, 10, 30, 60, and 90 days. Freshly prepared magnetic fluid (0-day standing time) served as the reference. A comparative analysis of the magnetic fluids after different standing periods with the 0-day reference revealed no evidence of phase separation, particle agglomeration, or sedimentation in any of the nine samples. The macroscopic appearance of the magnetic fluid after being allowed to stand for 90 days under an identical applied magnetic field is shown in Figure 9. Furthermore, the saturation magnetization remained unchanged over the 90-day period. It was therefore concluded that all nine prepared kerosene-based magnetic fluids exhibit excellent stability.

4.1.3. Magnetization Properties

Under an applied magnetic field, magnetic particles within magnetic fluids assemble into chain-like or columnar microstructures. The yield stress of the fluid primarily arises from the resistance of these structures to shear deformation. This yield stress is governed by several key factors, including magnetic particle morphology, particle volume fraction, and saturation magnetization.

In this study, the kerosene-based magnetic fluids with spherical magnetic particles of relatively uniform size and distribution was used; therefore, the influence of particle morphology on the results is considered negligible. Volume fraction plays a critical role: within an appropriate range, yield stress increases with increasing particle concentration. At low volume fractions, chains are sparse and mechanically weak, leading to low yield stress. As the concentration rises, more particles contribute to microstructure formation, enhancing the yield stress. However, at excessively high volume fractions, particle aggregation occurs, colloidal stability deteriorates, and dense packing hinders the formation of well-aligned field-induced structures. This results in a diminished increase in yield stress, accompanied by a sharp rise in viscosity and loss of fluidity.

Saturation magnetization governs the magnetic dipole interactions between particles. Generally, higher saturation magnetization significantly enhances the yield stress. Since saturation magnetization is approximately linearly proportional to the magnetic particle volume fraction, it can be used as an indicator to assess the effect of concentration on yield stress. It should be noted, however, that the overall magnetorheological response is also co-determined by other factors such as the magnetization curve profile, particle size distribution, and colloidal stability.

The saturation magnetization of the magnetic fluids was characterized using a Model EZ8 vibrating sample magnetometer (MicroSense, Lowell, MA, USA) at 25 °C. The results are summarized in

Table 8. Vibrating sample magnetometer measurements for different magnetic fluids.

No.	Density (g/mL)	Saturation Magnetization (Gs)
1	1.217	473.07
2	1.220	439.91
3	1.038	332.96
4	1.119	427.79
5	1.102	346.69
6	0.986	376.81
7	0.940	332.25
8	0.926	323.16
9	0.923	321.56

, and the magnetization curves are presented in Figure 10. The results indicate that all nine samples exhibit superparamagnetic behavior under magnetic fields, with no remanent magnetization nor coercivity.

4.2. Orthogonal Test Results

The applied currents were 0, 0.5, 1, and 2 A, corresponding to magnetic field intensities of 0, 19, 36, and 65 kA/m, respectively. The yield stress of each magnetic fluid was measured under different magnetic field intensities. Three measurements were performed for each sample, and the resulting data exhibited a standard error of 2–5%. The average values of the experimental measurements are summarized in

Table 9. Yield stress measurements of different kerosene-based magnetic fluids.

No.	Factor			Yield Stress (Pa)
	Precipitant (mL)	Deionized Water (mL)	Surfactant (mL)	0 A	0.5 A	1 A	2 A
1	120	500	10	0.084	0.374	0.698	1.785
2	120	500	7	0.189	11.741	27.573	44.834
3	120	600	12	0.073	0.165	0.350	1.008
4	140	400	10	0.077	0.385	0.721	2.529
5	120	600	10	0.012	0.134	0.184	0.328
6	140	500	12	0.073	0.109	0.386	1.043
7	120	400	7	0.031	1.490	4.359	9.477
8	120	400	12	0.020	0.090	0.138	0.355
9	140	600	7	0.071	0.379	1.112	2.487

. The relationship between yield stress and magnetic field strength for the kerosene-based magnetic fluid, with error bars indicative of standard error, is illustrated in Figure 11.

5. Sensitivity Analysis of Magnetic Fluid Preparation Parameters

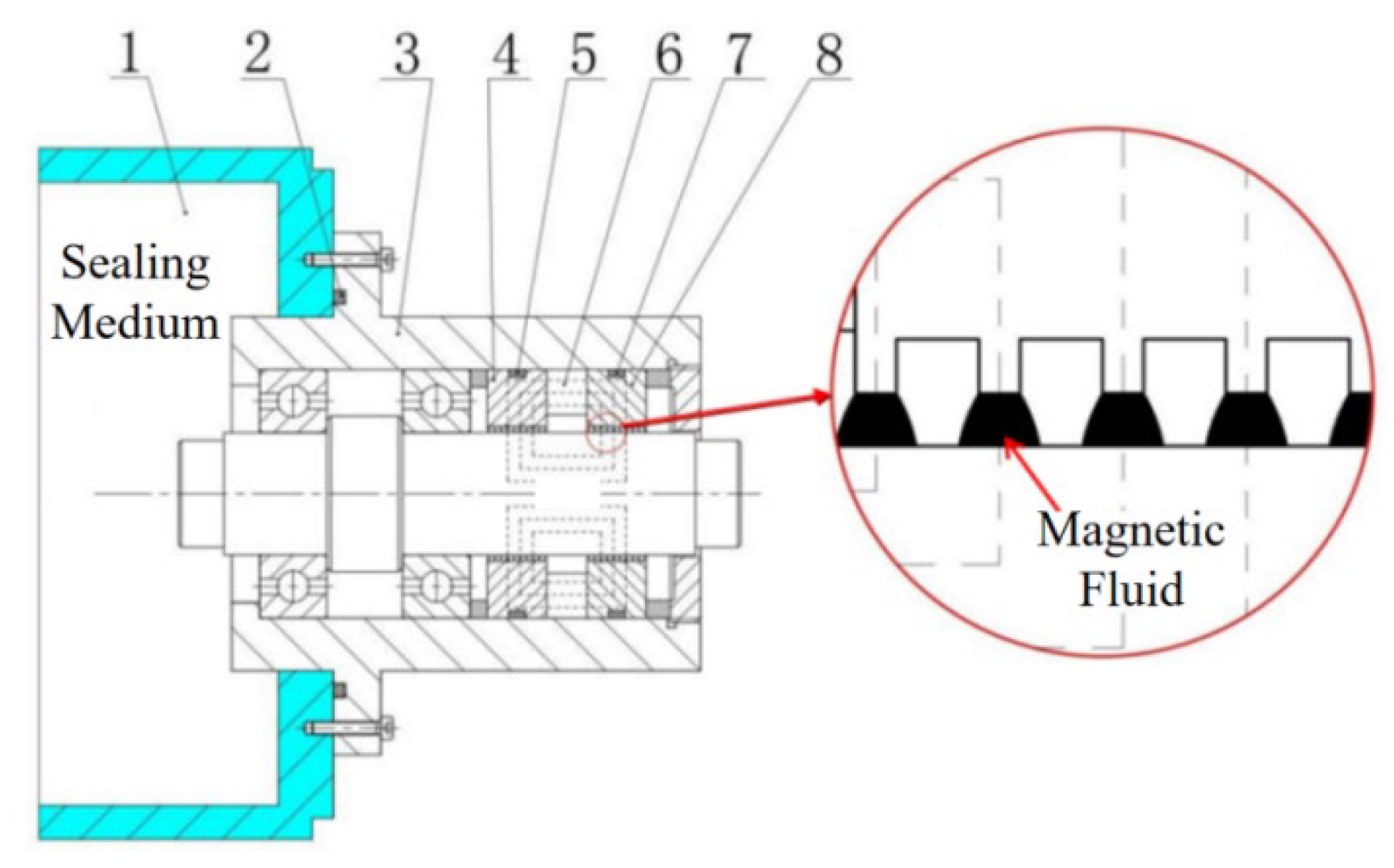
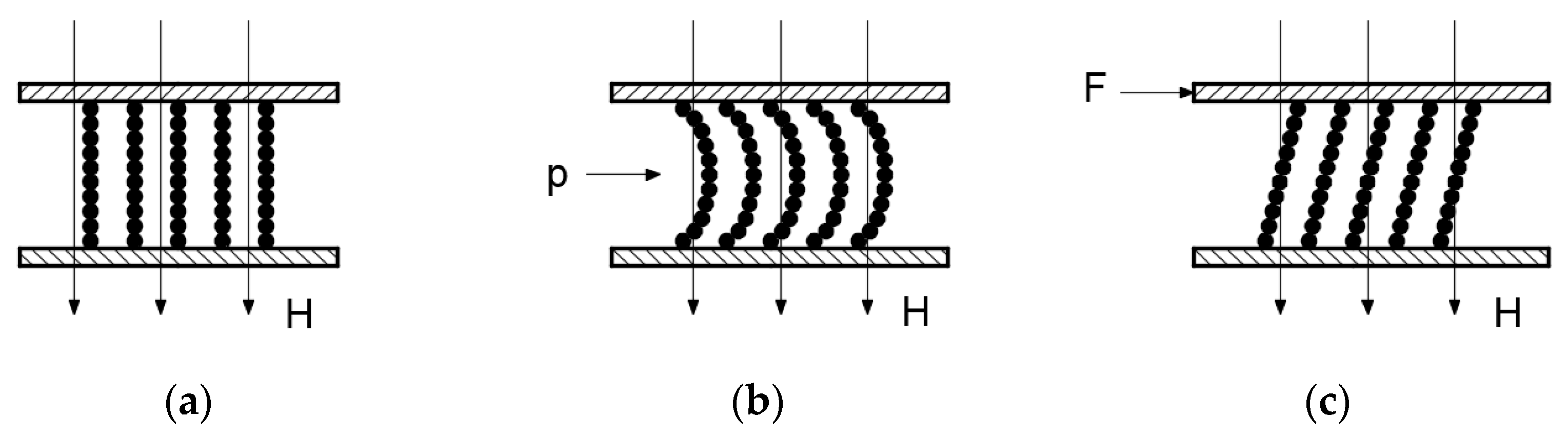
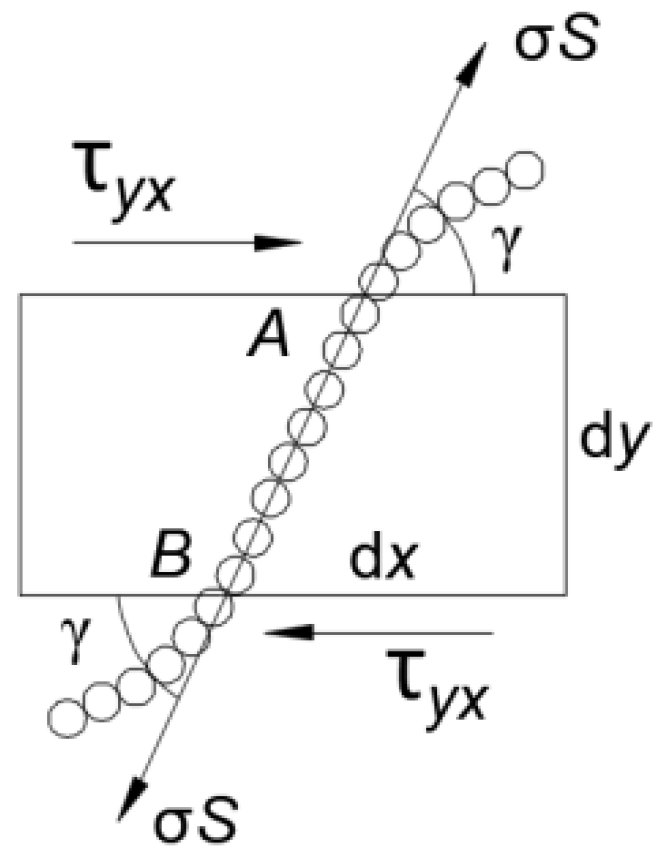
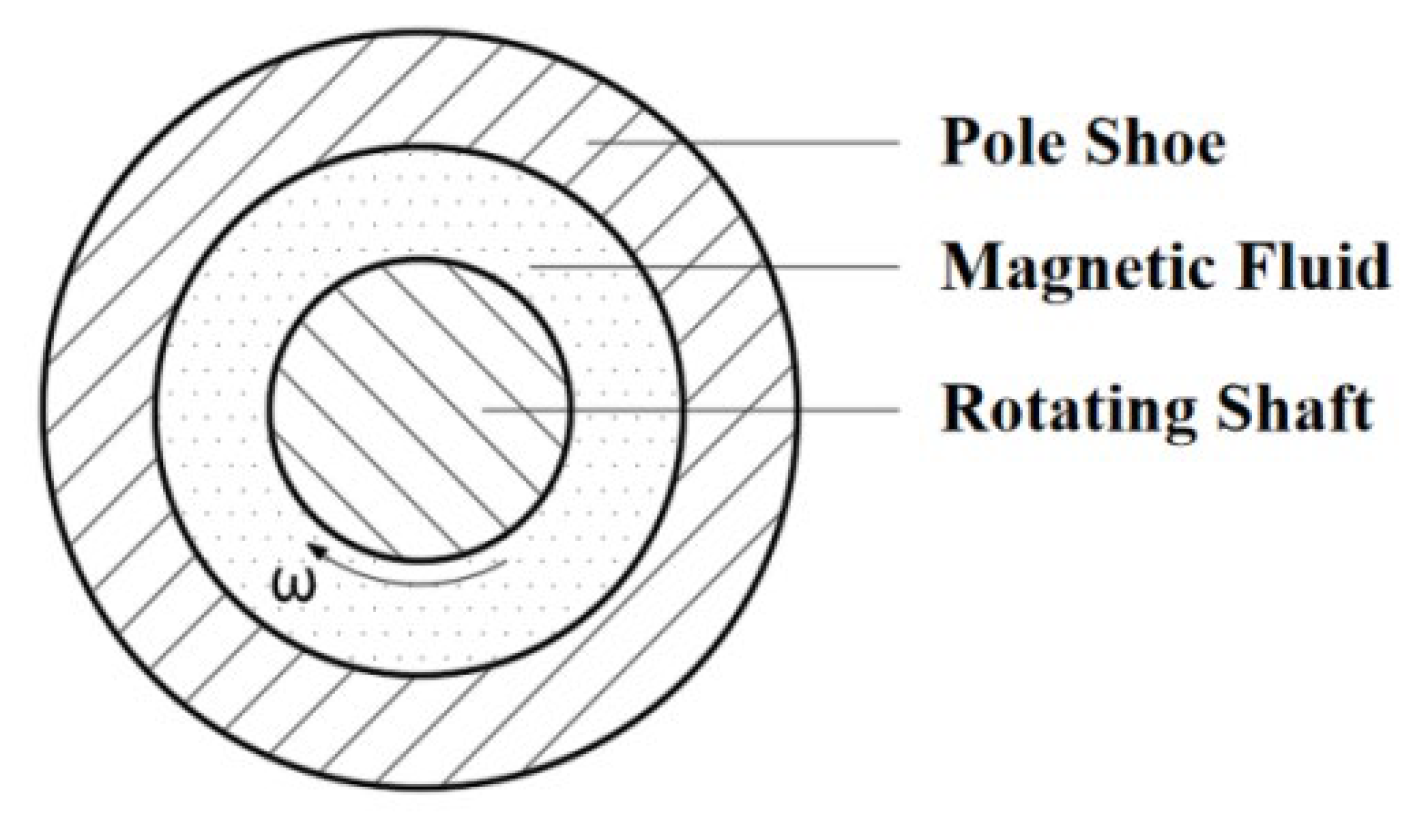
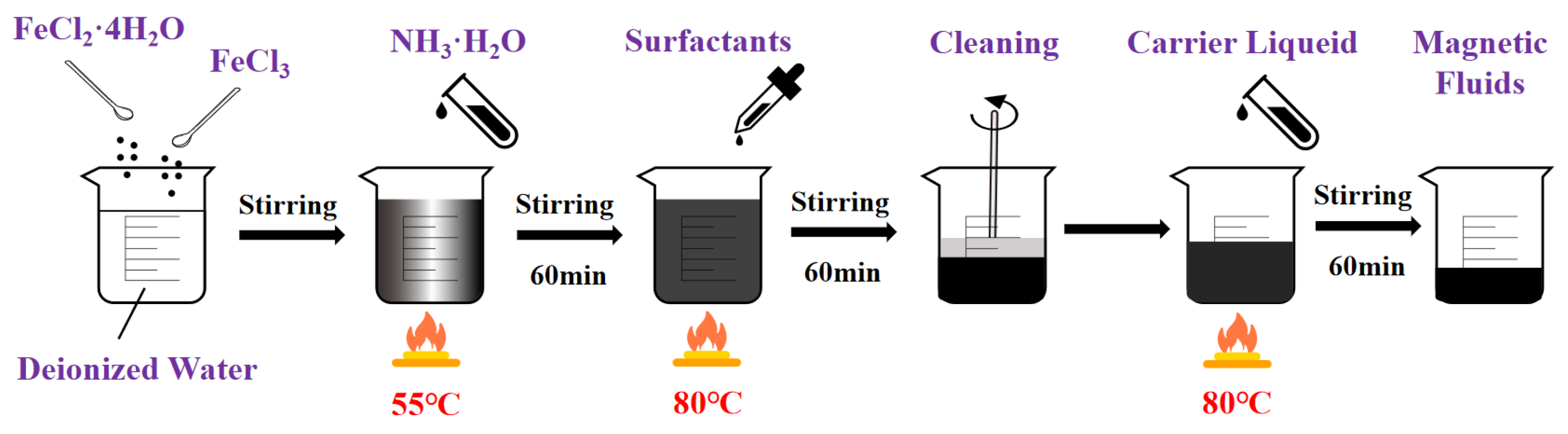
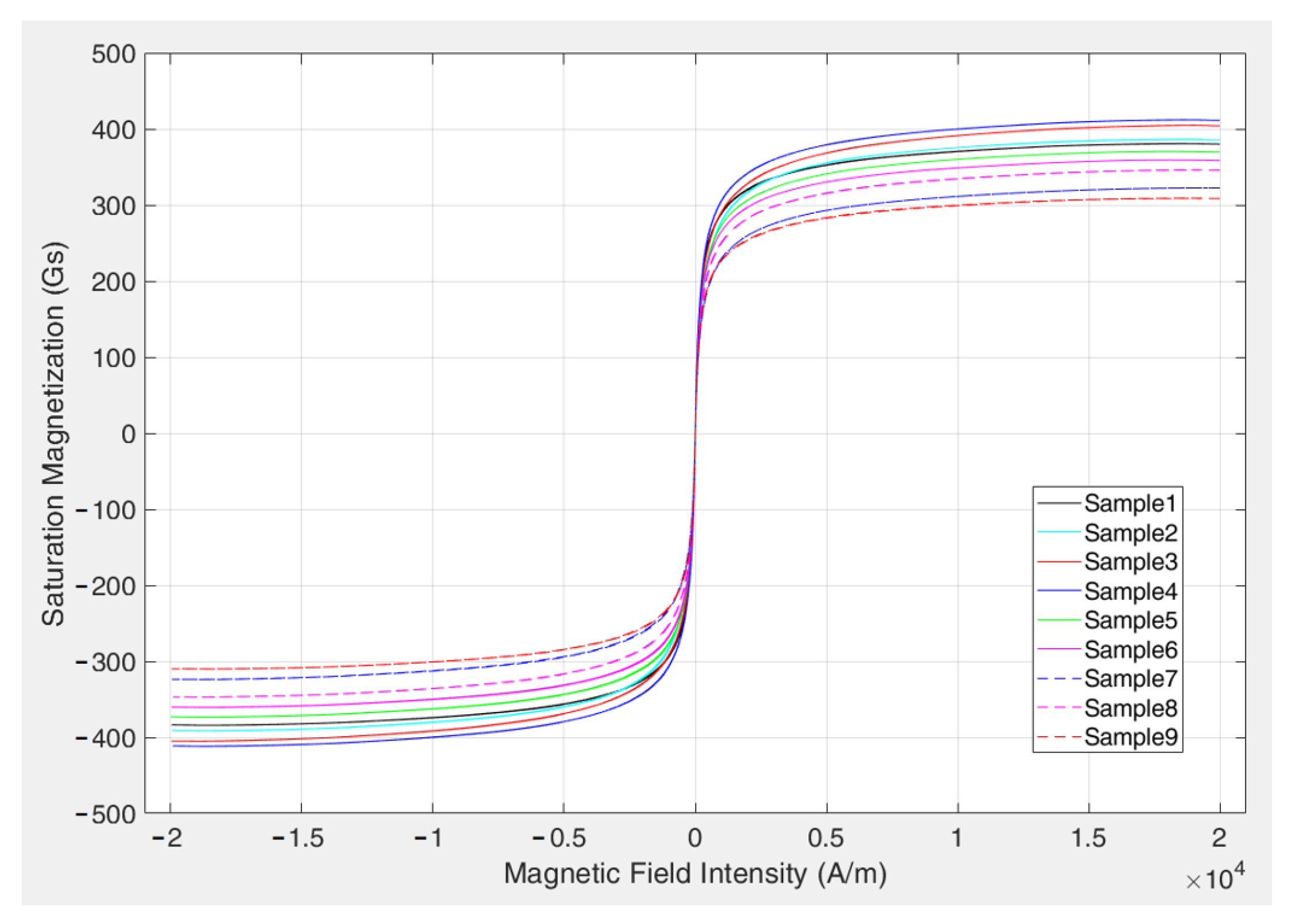
5.1. Sensitivity Analysis of Preparation Parameters Based on Range Analysis

The range analysis method employs mathematical statistics to calculate the range value for each column in an orthogonal array. By analyzing the mean values and the corresponding ranges of each factor, the optimal level combination and relative significance of the influencing parameters can be determined. The range of a factor is defined as the difference between its maximum and minimum mean values across all levels. A larger range indicates a more significant influence, and thus a primary order of importance, whereas a smaller range suggests a weaker influence and classifies the factor as secondary.

The first step in range analysis involves calculating the total value $T_{\mathrm{ij}}$ for each specific level j of a given factor i. This value is obtained by summing all experimental results ${\overline{K}}_{\mathrm{ij}}$ corresponding to the j-th level of the i-th factor. Subsequently, the level mean is computed using the formula

$${\overline{K}}_{\mathrm{ij}}={\displaystyle \frac{1}{n}}{T}_{\mathrm{ij}},$$

(18)

where n denotes the number of occurrences of level j.

The range value ${\Delta }_{\mathrm{ij}}$ for each factor can then be calculated as

$${\Delta }_{\mathrm{ij}}={\overline{K}}_{\mathrm{ijmax}}-{\overline{K}}_{\mathrm{ijmin}}.$$

(19)

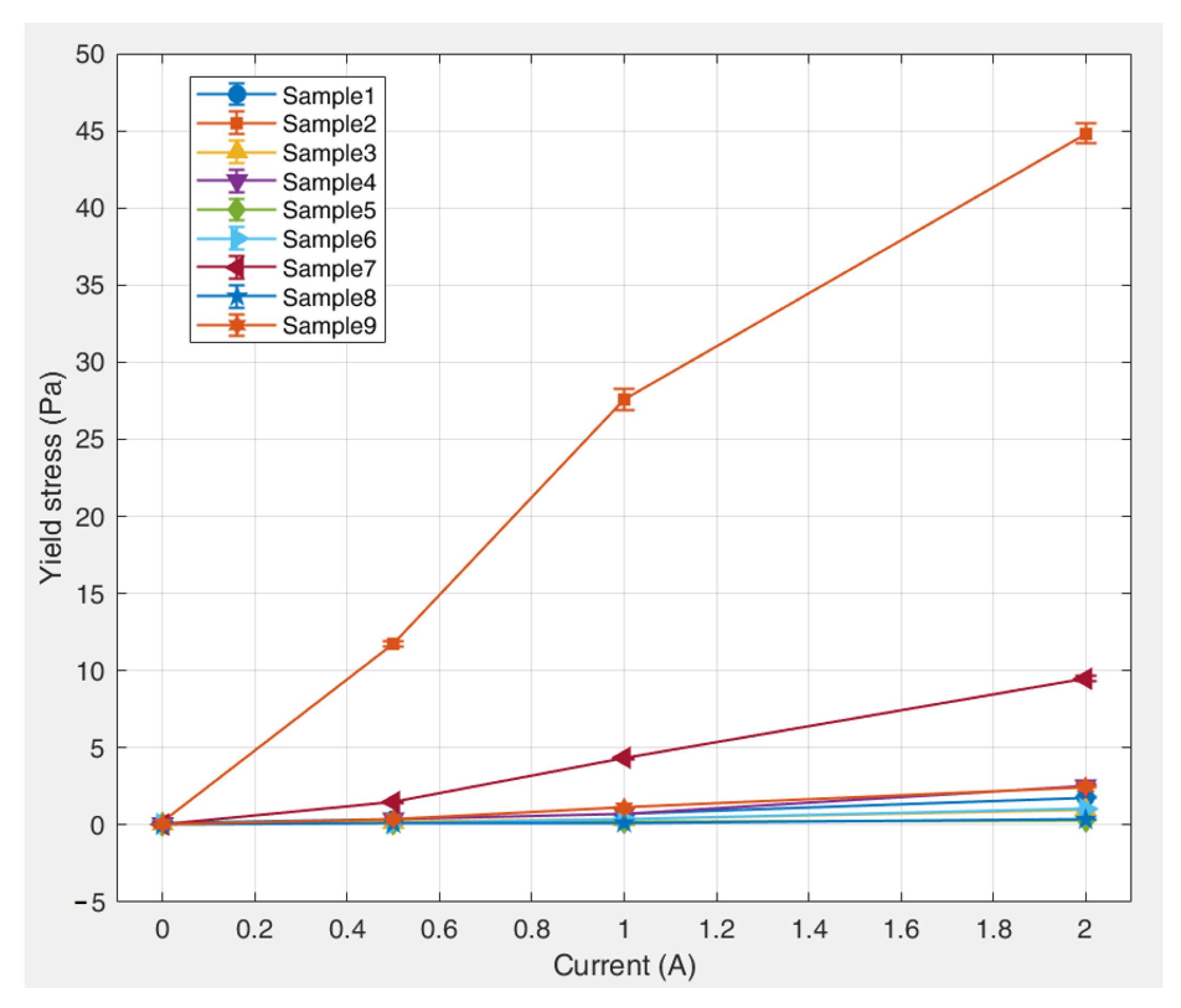
The value range for each factor was determined using the above equations. The range analysis was performed using the measured yield stress values of the kerosene-based magnetic fluids (Table 9) to evaluate the preparation parameters. The calculation results are listed in

Table 10. Range analysis of factors influencing the yield stress of kerosene-based magnetic fluids.

(a) 0 A
Range Analysis Items		Factor
		Precipitant	Deionized Water	Surfactant
Total value of levels	$T_{i1}$	0.411	0.122	0.292
	$T_{i2}$	0.215	0.347	0.167
	$T_{i3}$	0	0.156	0.167
Level mean	${\overline{K}}_{i1}$	0.068	0.04	0.097
	${\overline{K}}_{i2}$	0.072	0.116	0.056
	${\overline{K}}_{i3}$	0	0.039	0.056
Range	$\Delta$	0.003	0.077	0.042
(b) 0.5 A
Total value of levels	$T_{i1}$	13.993	1.966	13.601
	$T_{i2}$	0.865	12.223	0.893
	$T_{i3}$	0	0.670	0.364
Level mean	${\overline{K}}_{i1}$	2.332	0.655	4.534
	${\overline{K}}_{i2}$	0.288	4.074	0.298
	${\overline{K}}_{i3}$	0	0.223	0.121
Range	$\Delta$	2.044	3.851	4.412
(c) 1 A
Total value of levels	$T_{i1}$	33.301	5.215	33.044
	$T_{i2}$	2.219	28.658	1.603
	$T_{i3}$	0	1.646	0.872
Level mean	${\overline{K}}_{i1}$	5.550	1.738	11.015
	${\overline{K}}_{i2}$	0.740	9.553	0.534
	${\overline{K}}_{i3}$	0	0.549	0.291
Range	$\Delta$	4.810	9.004	10.724
(d) 2 A
Total value of levels	$T_{i1}$	57.786	12.361	56.798
	$T_{i2}$	6.059	47.662	4.641
	$T_{i3}$	0	3.822	2.405
Level mean	${\overline{K}}_{i1}$	9.631	4.120	18.933
	${\overline{K}}_{i2}$	2.020	15.887	1.547
	${\overline{K}}_{i3}$	0	1.274	0.802
Range	$\Delta$	7.612	14.613	18.131

.

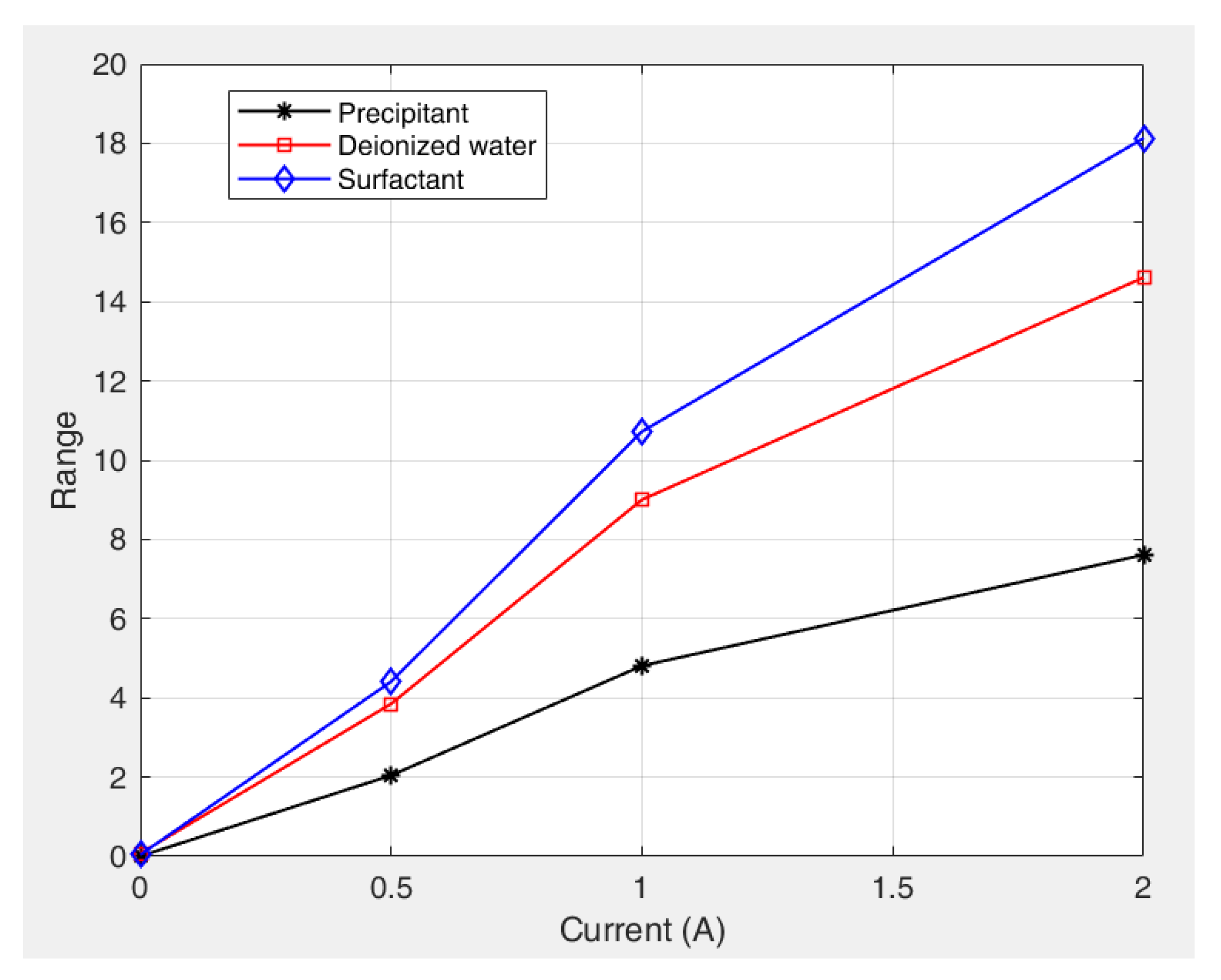
The results indicate that under an applied magnetic field, the preparation parameters of the kerosene-based magnetic fluids exhibited the following descending order of influence on the yield stress based on their range values: surfactant dosage > deionized water volume > precipitant dosage. This quantitative ranking suggests that the surfactant dosage (largest range value) is the most dominant factor governing the yield stress behavior, the deionized water volume exerts a secondary but measurable influence, and the precipitant dosage (smallest range value) exerts the least significant effect.

Figure 12 shows the variation in the range values (R) for the different factors with increasing current (magnetic field strength). The results indicate that the range values for all the factors positively correlate with the magnetic field intensity. This proportional relationship leads to more pronounced parameter effects under strong magnetic fields. Surfactant dosage remained the dominant factor and was particularly significant at higher field strengths. These trends confirm that an increase in the magnetic field strength increases the sensitivity of the yield stress to preparation parameters, especially the surfactant concentration.

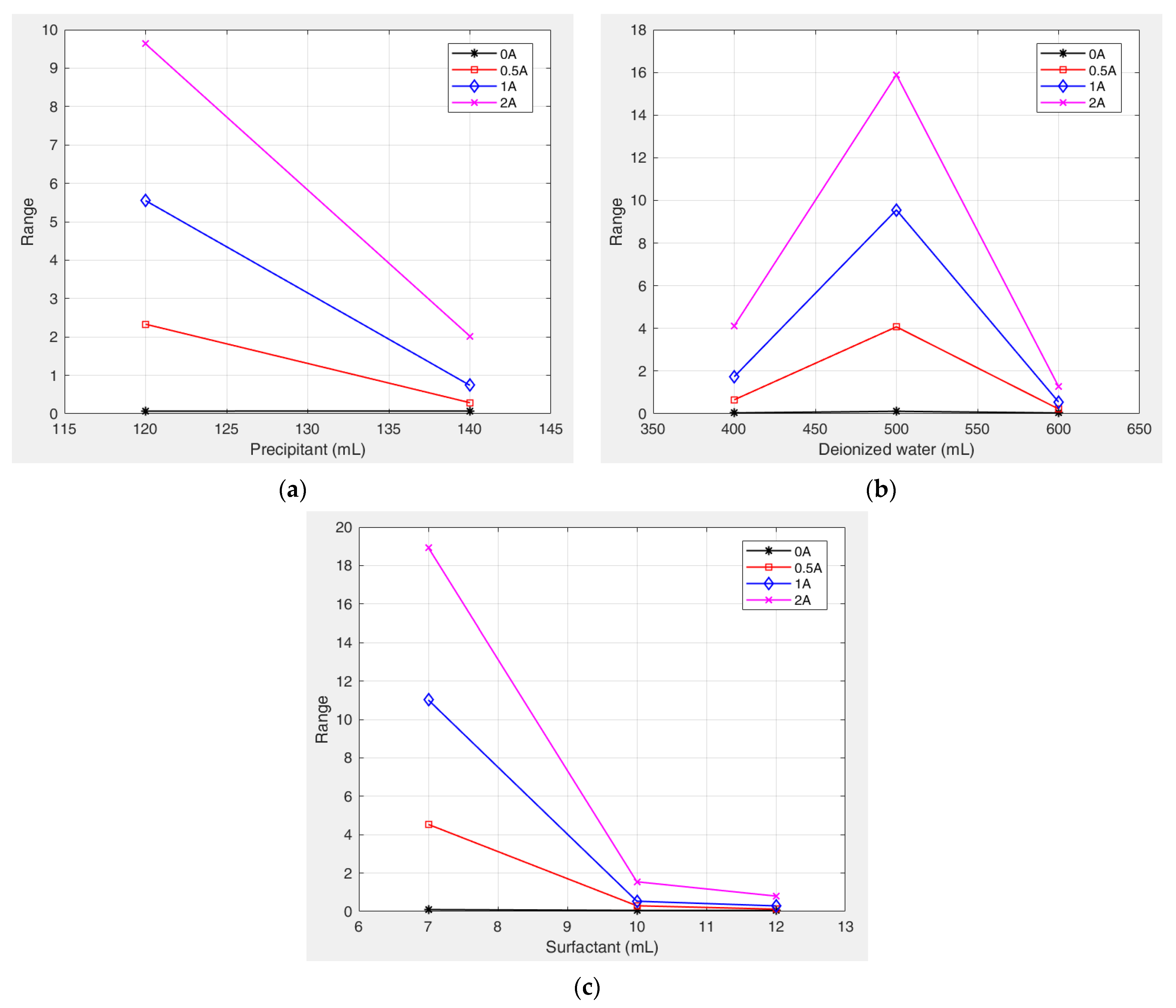
Figure 13 shows the variation trends of yield stress with different factor levels. Under the combined influence of multiple factor levels, the deionized water content exhibited an initial positive and subsequent negative correlation with the yield stress. Specifically, as the deionized water content increased, the degree of its influence on the yield stress first increased and then decreased. In contrast, both the precipitant and surfactant dosages exhibited an overall negative correlation with the yield stress of the kerosene-based magnetic fluids. With increasing dosages of these components, their influence on the yield stress decreased significantly.

5.2. Sensitivity Analysis of Preparation Parameters Based on Variance Analysis

Although range analysis can identify the relative magnitude of influence of each factor on the yield stress, it cannot assess the statistical significance of these effects or quantify the degree of significance. In contrast, ANOVA can be used to eliminate the effect of experimental errors, evaluate the effects of factor-level variations, and determine the sensitivity of different influencing factors. Thus, ANOVA enables a rigorous investigation into the statistical significance of the effects of these factors on the yield stress of kerosene-based magnetic fluids.

Accordingly, ANOVA was applied to the preparation parameter data to examine the significance of the three key factors—the precipitant dosage, deionized water volume, and surfactant dosage—on the yield stress. The parameters can be systematically adjusted based on the results to achieve targeted control over the rheological properties of the magnetic fluid.

The total value $T_{\mathrm{ij}}$ for each factor level was first calculated. Subsequently, the sum of squares $S_j$ and the corresponding degrees of freedom $f_j$ were computed as follows:

$$S_j={\displaystyle \frac{T_{i1}^2+T_{i2}^2+\dots +T_{\mathrm{ij}}^2}{r}}-{\displaystyle \frac{T^2}{N}},j=\mathrm{1,2},\dots ,k,$$

(20)

$$f_j=m-1,j=\mathrm{1,2},\dots ,k,$$

(21)

where $r={\displaystyle \frac{m}{N}}$ denotes the number of horizontal replicates, and $T$ denotes the sum of the orthogonal experimental measurement data.

Next, the error sum of squares $S_e$, defined as the sum of squares from the blank columns and several relatively small column sums of squares, was determined. The corresponding degrees of freedom $f_e$ were obtained as the sum of the degrees of freedom of these columns. In the absence of repeated trials and blank columns, the column with the smallest sums of squares may be selected to represent the error sum of squares.

The results are summarized in

Table 11. Analysis of variance (ANOVA) results.

Factor	Sum of Squares Sj	Degrees of Freedom fi	Mean Square Vj	F-Ratio
A	S1	f1	V1= S1/f1	V1/Ve
B	S2	f2	V2= S2/f2	V2/Ve
C	S3	f3	V3= S3/f3	V3/Ve
…	…	…	…	…
Error	Se	fT	Ve = Se/fe	/

, where the mean square $V_i$ and F-ratio are computed. Here, $V_e={\displaystyle \frac{S_e}{f_e}}$.

The rejection region corresponding to a given significance level α was determined, and a parameter sensitivity analysis was conducted. Generally, when F-ratio < F_0.05 (5% confidence level), the factor is considered to have no significant effect on the evaluation index. When F_0.05 < F-ratio < F_0.01 (1% confidence level), the factor is considered as a sensitive parameter with a significant influence on the evaluation index. When F-ratio > F_0.01 (1% confidence level), the factor is identified as a highly sensitive parameter that has a significant effect on the evaluation index [21]. The ANOVA results obtained from the orthogonal experimental data are presented in

Table 12. ANOVA for factors influencing the yield stress of kerosene-based magnetic fluids.

(a) 0 A
Factor	Sum of Squares Sj	Degrees of Freedom fi	F-Ratio	Significance
Precipitant	0.028157273	1	5.765
Deionized water	0.009768775	2	1
Surfactant	0.003487868	2	0.001
Error	0.009768775	2	/
(b) 0.5 A
Precipitant	40.99193984	1	3.070
Deionized water	26.70467959	2	1
Surfactant	37.44224881	2	9.361
Error	26.70467959	2	/
(c) 1 A
Precipitant	231.1069044	1	3.220
Deionized water	143.546888	2	1
Surfactant	224.8994885	2	56.225	Significant
Error	143.546888	2	/
(d) 2 A
Precipitant	672.4117578	1	3.735
Deionized water	360.1067841	2	1
Surfactant	631.5401502	2	157.885	Highly significant
Error	360.1067841	2	/

.

The F-distribution table indicates that F_0.05 (2,6) = 19.33 and F_0.01 (2,6) = 99.33. An analysis of the data shown in Table 10 indicated that, for magnetic flux densities at 0 and 0.5 A, all three factors yield F-ratios below 19.33, suggesting no significant effect on the yield stress. At 1 A, the F-ratio for the surfactant dosage lies between 19.33 and 99.33, suggesting a significant influence on the yield stress, thereby identifying it as a sensitive parameter. For a higher magnetic flux density at 2 A, the F-ratio for the surfactant dosage exceeds 99.33, indicating a highly significant effect, identifying it as an extremely sensitive parameter. Moreover, the significance of the surfactant dosage increases rapidly with increasing magnetic field strength.

Based on the magnitude of the F-ratios, the sensitivity of the parameters affecting the yield stress of the kerosene-based magnetic fluids follows the order surfactant dosage > precipitant dosage > deionized water content.

Therefore, these results are consistent with those of range analysis.

Theoretical analysis revealed that the yield stress of magnetic fluids can be determined based on the number of chains per unit area, interparticle interactions, and the size distribution of magnetic particles. Based on the experimental results, when no external magnetic field is applied or when the magnetic field strength is relatively low, the three preparation factors exhibit comparable levels of influence on the yield stress of the kerosene-based magnetic fluid. However, as the magnetic field strength increases, their impacts diverge: the surfactant demonstrates the most pronounced effect on the yield stress, followed by the precipitating agent, while the influence of deionized water remains relatively minor.

During magnetic fluid preparation, deionized water helps maintain product purity primarily by controlling the ionic strength within the system. This modulates the electrostatic interactions between particles, thereby influencing the yield stress of the magnetic fluid. Nevertheless, deionized water content exerts a relatively minor influence on the yield stress.

In this study, ammonium hydroxide (NH₃·H₂O) was used as the precipitating agent for the chemical reaction. The OH⁻ ions it provides promote the coprecipitation of metal salt solutions to form ultrafine magnetic particles, exerting a decisive influence on their size, morphology, and size distribution. Larger magnetic particles exhibit stronger magnetic attraction, facilitating the formation of robust chain-like structures, which leads to an increase in yield stress. Conversely, the uniformity of narrow particle size distributions enables the formation of highly ordered chain-like structures under a magnetic field. In such cases, the interparticle forces are more consistent, generally resulting in a higher yield stress under magnetic fields. Therefore, the precipitating agent exerts a more substantial influence on the yield stress of magnetic fluids.

Surfactants serve primarily as dispersing agents during the preparation of magnetic fluids, preventing particle agglomeration and playing a critical role in maintaining the stability of magnetic fluids in practical applications. The steric hindrance effect provided by the surfactant enables uniform and stable dispersion of magnetic particles within the carrier liquid, attenuates the van der Waals forces between particles, and suppresses magnetic dipole interactions. When the surfactant quantity is sufficient to form a complete, dense, and stable coating on the particles, each particle is effectively isolated by surfactant molecules, resulting in the lowest yield stress. If the surfactant amount is insufficient, incomplete particle coating occurs, which leads to agglomeration and the formation of robust chain-like or columnar network structures, which significantly increase the yield stress. Conversely, if an excessive amount of surfactant is used, the surplus surfactant molecules disperse within the magnetic fluid in the form of micelles or free molecules, increasing the viscosity of the magnetic fluid and consequently raising the yield stress. Therefore, the amount of surfactant exserts a more pronounced influence on the yield stress of magnetic fluids.

6. Conclusions

This study investigated the yield stress of kerosene-based magnetic fluids using a combination of theoretical and experimental approaches. The main conclusions are as follows:

(1)

The influence of yield stress on the starting torque of rotary seals using kerosene-based magnetic fluids was examined. Theoretical calculations showed that the yield stress affects both the starting torque and pressure resistance of magnetic fluid seals. These results provide a theoretical basis for optimizing the preparation of magnetic fluids and enhancing their sealing performance.

(2)

Using yield stress as the evaluation index, an orthogonal experimental design was introduced to assess parameter sensitivity. Compared with 27 preparation tests, the orthogonal experimental method required only nine sets of preparation parameters to determine the sensitivity of the preparation parameters affecting the yield stress. This approach effectively identified the key factors and optimal combination of factor levels within the studied range while reducing the number of experiments required.

(3)

Range and variance analyses of the orthogonal experimental data revealed that different preparation factors exhibit varying degrees of influence on the yield stress. Under low magnetic field intensities, all three factors show non-significant effects. As the magnetic field intensity increases, the significance of the surfactant dosage becomes markedly enhanced. The overall sensitivity order of the factors is surfactant dosage > precipitant dosage > deionized water volume. These findings provide a theoretical foundation for optimizing the preparation of magnetic fluids and enhancing their sealing performance.

Overall, the results obtained in this study provide both theoretical and experimental foundations for improving the application prospects of kerosene-based magnetic fluids in rotary seals and mitigating the impact of their yield stress on the starting torque.