Effects of Exchange, Anisotropic, and External Field Couplings on a Nanoscale Spin-2 and Spin-3/2 System: A Thermomagnetic Analysis

Abstract

In this research, an analysis of the thermomagnetic properties of a nanoscale spin-2 and spin-3/2 system is conducted. This system is modeled with as a quasi-spherical Ising-type nanoparticle with a diameter of 2 nm, in which atoms with spin-2 and spin-3/2 configured in body-centered cubic (BCC) lattices interact within their relevant nanostructures. To determine the thermomagnetic behaviors of the nanoparticle, numerical simulations using Monte Carlo techniques and thermal bath class algorithms are performed. The results exhibit the effects of exchange couplings ($J_1,J_2^{\prime }$), magnetocrystalline anisotropies ($D_{3/2}^{\prime },D_2^{\prime }$), and external magnetic fields ($h^{\prime }$) on the finite-temperature phase diagrams of magnetization ($M_T$), magnetic susceptibility (${\chi }_T$), and thermal energy ($k_B{T}^{\prime }$). The influences of the exchange, anisotropic, and external field parameters are clearly reflected in the compensation, hysteretic, and pseudocritical phenomena presented by the quasi-spherical nanoparticle. When the parameter reflecting ferromagnetic second-neighbor exchanges in the nanosphere ($J_2^{\prime }$) increases, for a given value of the external magnetic field, the compensation ($T_{comp}$) and pseudocritical ($T_{pc}$) temperatures increase. Similarly, in the ranges $0<J_2^{\prime }⩽4.5$ and $-15⩽h^{\prime }⩽15$ at a specific temperature, an increase in $J_2^{\prime }$ results in the appearance of exchange anisotropies (exchange bias) and and increased hysteresis loop areas in the nanomodel.

1. Introduction

The objective of this work is to characterize the thermal and magnetic behaviors of a fermionic–bosonic ferrimagnetic system comprising atoms with spins $S=3/2$ and $Q=2$, respectively. The spintronic configuration of the system is framed in a quasi-spherical Ising-type nanoparticle of 2 nm diameter, which contains body-centered cubic lattices as unitary cells with spins of $S=3/2$ and $Q=2$ that interact through exchange ($J_1,J_2^{\prime }$), anisotropic ($D_{3/2}^{\prime },D_2^{\prime }$), and external field ($h^{\prime }$) couplings. The question posed in this research concerns how the $J_1,J_2^{\prime },D_{3/2}^{\prime },D_2^{\prime }$, and $h^{\prime }$ couplings—especially those pertaining to $J_2^{\prime }$—influence the magnetization behavior, magnetic susceptibility, and thermal energy of the nanosystem. Recently, Madera et al. reported the diverse properties and phenomena of a quasi-spherical nanoparticle composed of spin-2 and spin-3/2 atoms, without considering the effects of second-neighbor exchanges ($J_2^{\prime }$) [1]. Considering the importance of this research, we decided to perform a thermomagnetic analysis of these couplings due to the physical situations that they entail, such as magnetic frustrations due to competition with first-neighbor exchanges and larger hysteresis loop areas, leading to hard magnetic materials, and the hysteretic response of the nanosystem at low temperatures, where the magnetization drops to zero despite the effects of crystal and anisotropic fields. Another consideration is the intrinsic relationship of $J_2^{\prime }$ with the magnetic confinement effect due to the size of the nanoparticle. From the previously mentioned considerations, this article can be regarded as a continuation of the work carried out in [1].

The great utility of intermetallic alloys configured with spin-2 and spin-3/2 is represented by the diverse properties they possess, turning them into versatile compounds under certain physical conditions for the development of fields, for example, in industrial, spintronic, and technological contexts. Among the properties exhibited by alloys containing spin-2 and spin-3/2 species, the FeCo compound is a notable example. Among these properties, the following can be particularly highlighted, among others: the magnetic behavior maintained at high temperatures, which reflects its potential for use in high-performance devices that operate at extreme temperatures; and the reduction in energy loss due to high magnetic efficiency, as in the construction of transformers [2]. Similarly, other properties characterizing this compound include its strong magnetic response, making it useful for the magnetic storage of information and in electric motors [3,4]; likewise, its effectiveness in terms of the manipulation of magnetic fields as a result of its high magnetic permeability is noteworthy [5,6]. Notably, FeCo has been applied in some mechanical devices with high performance demand in the heavy-machinery industry, where adequate resistance to wear and corrosion is required. These properties can be achieved with the use of this alloy due to its high density, hardness, and mechanical strength [7,8,9]. No less important is the utility of FeCo in the construction of high-energy and high-performance permanent magnets, with very notable uses in cutting-edge electronic devices, loudspeakers, and advanced technology such as magnetic resonators [10]. Furthermore, given its soft magnetic properties, its utility is further manifested in the construction of thin films for power frequency applications [11,12]. It is important to note that FeCo may be additionally considered as part of mixed alloys including other elements, which have exhibited important properties and phenomena both experimentally and theoretically, and have a diverse range of applications for technological development. For instance, the structural, magnetic, and electrical properties of the ternary alloy Fe-Co-Ni have been evaluated using the spark plasma sintering (SPS) method, demonstrating that Co-rich alloys exhibit high hardness, high saturation magnetizations, and higher Curie temperatures [13]. On the other hand, Can et al. investigated the structural and magnetic properties of soft magnetic composites ${\left(\mathrm{FeCo}\right)}_{84}$${\mathrm{CuB}}_{15}$ with varying Fe/Co ratios (5:1, 3:1, and 1:1) using the planar flow casting method. As a result, they observed that the linear response of the sensors to the external magnetic field broadened with increasing Fe content in the alloys [14]. Other interesting and useful results on soft alloys with FeCo have been reported by Min-Tze et al., Wang et al., and Yu et al. In their work, Min-Tze et al. verified that functional grading between Fe–Co/Fe–Ni materials refines the microstructure, thus improving the mechanical hardness of the resulting composite without the need to use a non-magnetic element [15]; meanwhile, Wang et al. and Yu et al. studied the properties and application of Fe-Co-V alloys, with Wang et al. reporting high saturation magnetic polarization and high performance in high-torque-density electric machines [16]. Furthermore, the effects of a high-pressure environment on deep-sea permanent magnet synchronous motors were studied by Yu et al. [17]. For their part, Muralles et al., in their atomistic research on the ternary compound FeCo-X (X = V, Nb, Mo, W), delved into the impact of each element “X” on the mechanical properties and microstructural evolution of equiatomic FeCo by employing the modified embedded atom method (MEAM) [18]. With this same research method, excellent results regarding the effects of size and the core–shell ratio on the magnetization of spherical FeCo nanoparticles have been reported [19]. In addition to the above, for the soft alloy FeCo, its physical properties have also been analyzed from the perspective of Co concentration, revealing that many alloys are both mechanically and dynamically stable. Likewise, this research is considered as a contribution to the development of a theoretical basis for the application of these types of alloys [20]. From a nanoscale perspective, various physical properties of the binary compound FeCo have also been analyzed. Among other previous works, it is worth highlighting the research by Patelli et al., who analyzed the structure and magnetic properties of Fe-Co alloy nanoparticles synthesized via pulsed laser inert gas condensation. Patelly et al. found that, in most nanoparticles, the composition is very uniform throughout the diameter and varies little from nanoparticle to nanoparticle [21]. Equally important are the investigations carried out by Cai et al. and Dou et al., the former involving the synthesis of a three-dimensional (3D) core–shell carbon nanofiber lattice embedded with different molar ratios of iron and cobalt (4:0, 3:1, 2:2, 1:3, 0:4) (Fe/Co@C-CNFs) via electrospinning, which were used as light absorbers of high-performance electromagnetic waves [22], while the latter focused on the use of N, O-doped walnut-type porous carbon composite microspheres loaded with Fe/Co nanoparticles for tunable electromagnetic wave absorption [23]. Regarding the use of FeCo for the degradation of organic pollutants, the utilization of nanoparticles embedded in MOF-derived nitrogen-doped porous carbon rods is a key consideration [24].

For the development of this research, the same method employed in reference [1] was used, namely Monte Carlo simulations and thermal bath-type algorithms applied to a three-dimensional quasi-spherical Ising ferrimagnet of spins 2 and 3/2, with the main purpose of analyzing the influence of second-neighbor exchanges $(S\rightleftarrows S/Q\rightleftarrows Q)$ in the nanolattice. The remainder of this paper is organized as follows. Section 2 defines the nanomodel and the method used to characterize it. The analysis and discussion of the results are presented in Section 3. Finally, Section 4 presents the conclusions.

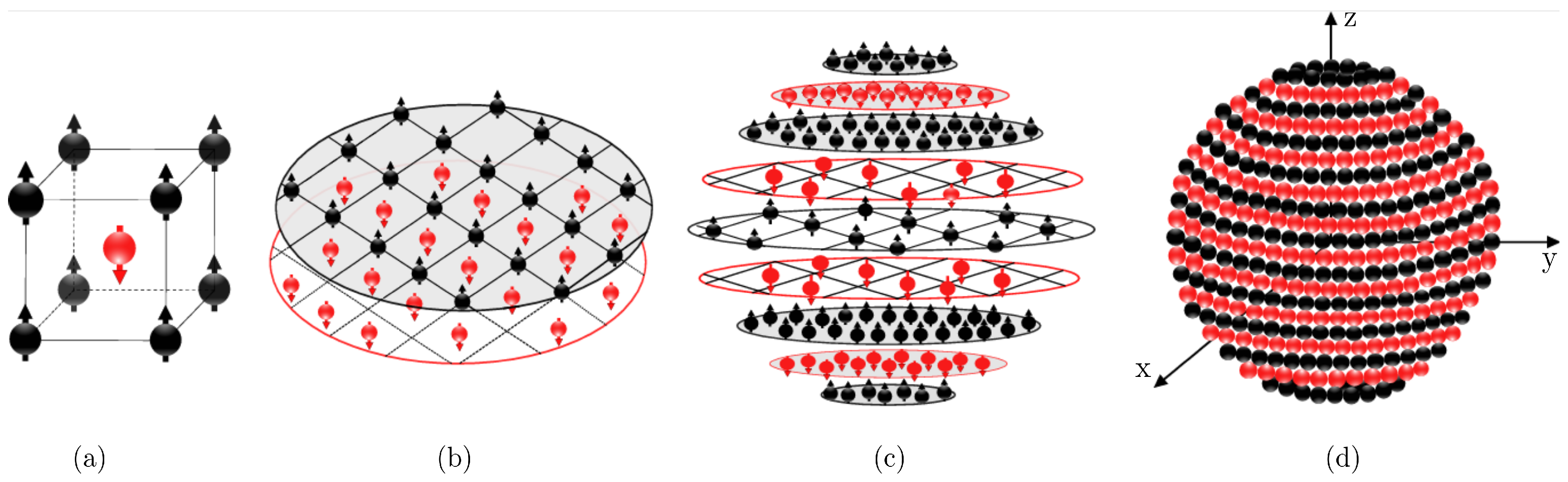
2. Model and Computational Method

2.1. Model

As in reference [1], the model in this research is represented by encapsulation inside a 2 nm diameter Ising-type quasi-nanosphere formed by crystals containing spin states 2 and 3/2 in a BCC lattice, with a spintronic configuration consisting of two sublattices: one consisting of atoms with spin $S=3/2$, while the other contains atoms with spin $Q=2$. Each sublattice accounts for approximately 50% of the total spin population. An approximate diagram of this nanoscale system is shown in Figure 1. For analysis of the interactions inside the nanomodel, the quasi-nanosphere is divided into circular planes, which separately contain the $S=3/2$ and $Q=2$ Ising particles (a $Q=2$ plane, followed in parallel by another of $S=3/2$ or vice versa), separated by the lattice constant of the FeCo compound. This modeling approach leads to a nanoparticle containing approximately 243 $S=3/2$ atoms and 244 $Q=2$ atoms.

Thermomagnetic analysis was carried out on the nanoparticle in the equiatomic B2-BCC phase—focusing on bimetallic compounds composed of spin-2 and spin-3/2 atoms—by means of the Hamiltonian of interactions, defined as

$$\begin{array}{ccc}\hfill \mathcal{H}& =& -J_1\sum _{\langle nn\rangle }{S}_i^A{Q}_j^B-J_2\{\sum _{\langle nnn\rangle }{S}_i^A{S}_k^A+\sum _{\langle nnn\rangle }{Q}_j^B{Q}_l^B\}-D_{3/2}\sum _{iϵA}{\left(S_i\right)}^2\hfill \\ & -& D_2\sum _{jϵB}{\left(Q_j\right)}^2-h\sum _{iϵA}{S}_i-h\sum _{jϵB}{Q}_j\hfill \end{array}$$

(1)

In Equation (1), $J_1<0$ represents antiferromagnetic exchange interactions between first neighbors $\left(nn\right)$ in the nanosystem ($S\rightleftarrows Q$); $J_2>0$ ferromagnetically couples the second neighbors $\left(nnn\right)$$(S\rightleftarrows S/Q\rightleftarrows Q)$; $D_{3/2}$ and $D_2$ denote the crystal or anisotropic fields generated by the A and B sublattices, respectively; and h is an external magnetic coupling to the nanosphere. The crystal and external fields act on each site on the nanoparticle. For convenience in numerical calculations, the constants in Equation (1) are parameterized dimensionlessly in this work, as a function of $|J_1|$, as follows: $D_{3/2}^{\prime }=D_{3/2}/\left|J_1\right|$, $D_2^{\prime }=D_2/\left|J_1\right|$, $h^{\prime }=h/\left|J_1\right|$, and $k_B{T}^{\prime }=k_{B}T/\left|J_1\right|$, where $k_B$ is the Boltzmann constant. The consideration of the effects of anisotropies on the surface is beyond the scope of this research, which is to be considered in subsequent studies. For the simulation, free boundary conditions were used for the atoms that are on the surface, as well as energy units in all parameters of the Hamiltonian in (1).

2.2. Monte Carlo Simulations (MCSs)

One of the widely used computational techniques for the theoretical solution of complex magnetic spintronic structures—including ferromagnets and/or ferrimagnets, both at the nanoscale and in volume—is the Monte Carlo simulation (MCS) method, which has been employed previously for the characterization of physical phenomena and thermal fluctuations from one state to another in various crystal lattices [25,26]. Its usefulness lies in the calculation of statistical averages of a physical observable in an accurate way, given the high dimensionality of the phase space, due to the large number of particles in the magnetic configurations [27,28]. In this research, an analysis of the effects of internal and external interactions in the proposed nanoparticle (via the Hamiltonian Equation (1)) was performed using an MCS method associated with thermal bath-type algorithms—an extension of the standard Metropolis algorithm for systems where the spins take more than two values. In a thermal bath algorithm, a spin is chosen and the probability of it taking another possible value—even the same one—is calculated. In this way, the rest of the system (which remains constant) acts as a thermal bath that determines the possible new value of the chosen variable. An approximate way to perform MCS is as follows: Once the initial configuration is organized, the ones that follow are randomly selected and changed according to the Boltzmann probability (${\exp }^{-\beta \mathrm{\Delta }{E}_{ij}}$), where $\mathrm{\Delta }{E}_{ij}$ represents the difference in energies between the states i and j. The transition probabilities are then calculated, taking into consideration that the number of possible changes depends on the type of particle located in the lattice. The data were obtained with $4\times {10}^6$ MCS per site, initially discarding the first ${10}^6$ steps per spin until equilibrium was reached (i.e., warming up).

The total ($M_T$) magnetization, sublattice ($M_A,M_B$) magnetization, and total magnetic susceptibility (${\chi }_T$) were calculated per lattice site, using the following expressions:

$$M_A={\displaystyle \frac{1}{L_A}}\langle \sum _i{S}_i^A\rangle M_B={\displaystyle \frac{1}{L_B}}\langle \sum _j{Q}_j^B\rangle$$

(2)

$$M_T=M_A+M_B$$

(3)

$${\chi }_T={\displaystyle \frac{\beta }{L}}\{\langle M_T^2\rangle -{\langle M_T\rangle }^2\}$$

(4)

Let $L_A$ and $L_B$ indicate the sizes of sublattices A and B, respectively (i.e., sublattice A contains 243 atoms with spins $S=3/2$ and sublattice B contains 244 atoms with spins $Q=2$). Then, $L=L_A+L_B$ is the total number of atoms of the nanosphere, and we define $\beta =1/k_{B}T$. Due to the size of the quasi-nanosphere, the location of the transition temperature is considered a pseudocritical temperature $\left(T_{pc}\right)$, which is located in a range where the magnetic susceptibility presents a maximum smooth or “flattened” contour. To locate the compensation points presented by the nanosystem, the intersection point of $M_T$ with the temperature axis was determined.

3. Results and Discussion

In this section, the results regarding the influences of the interactions modeled by the Hamiltonian (1) that defines the nanoparticle are analyzed and discussed.

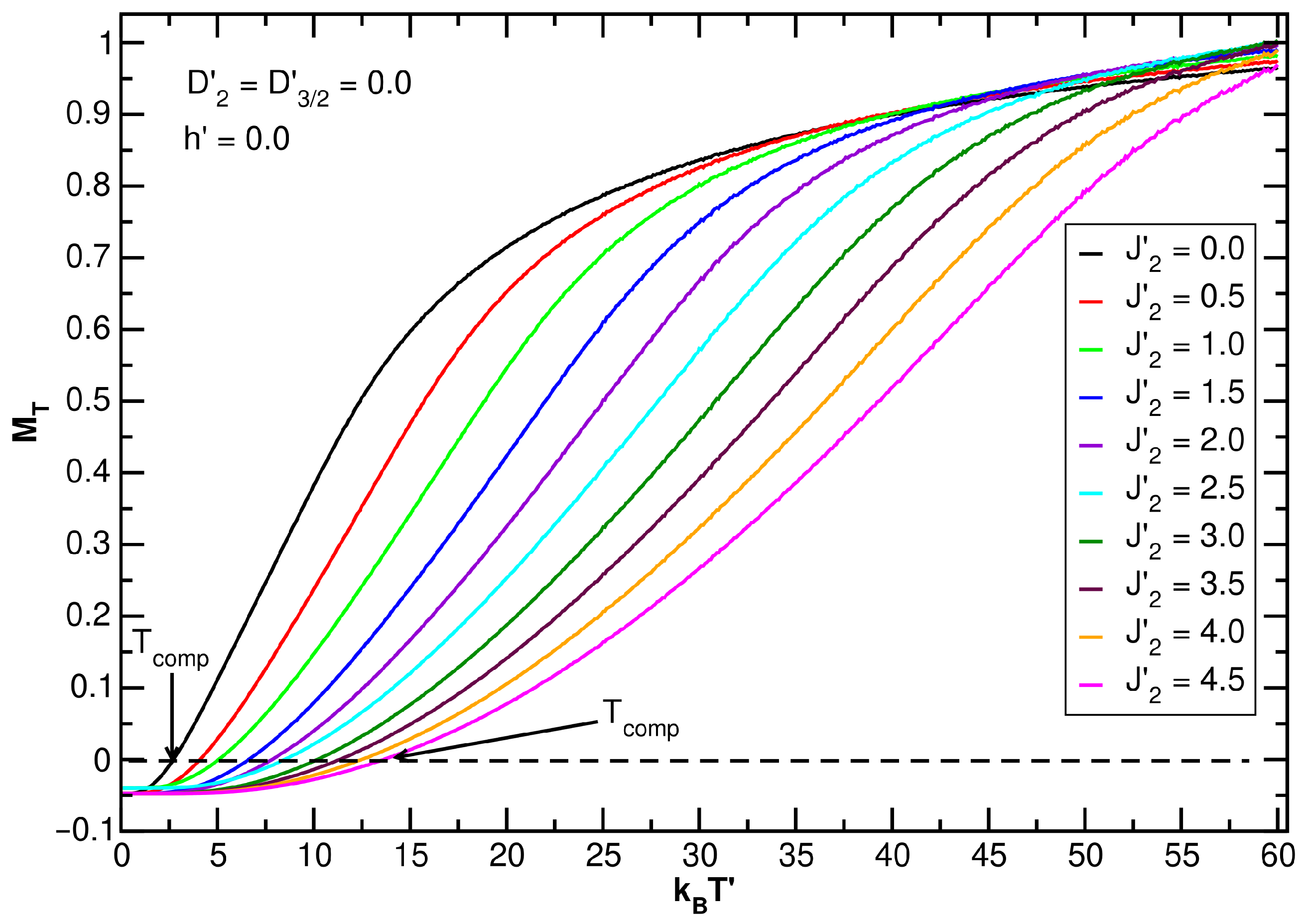
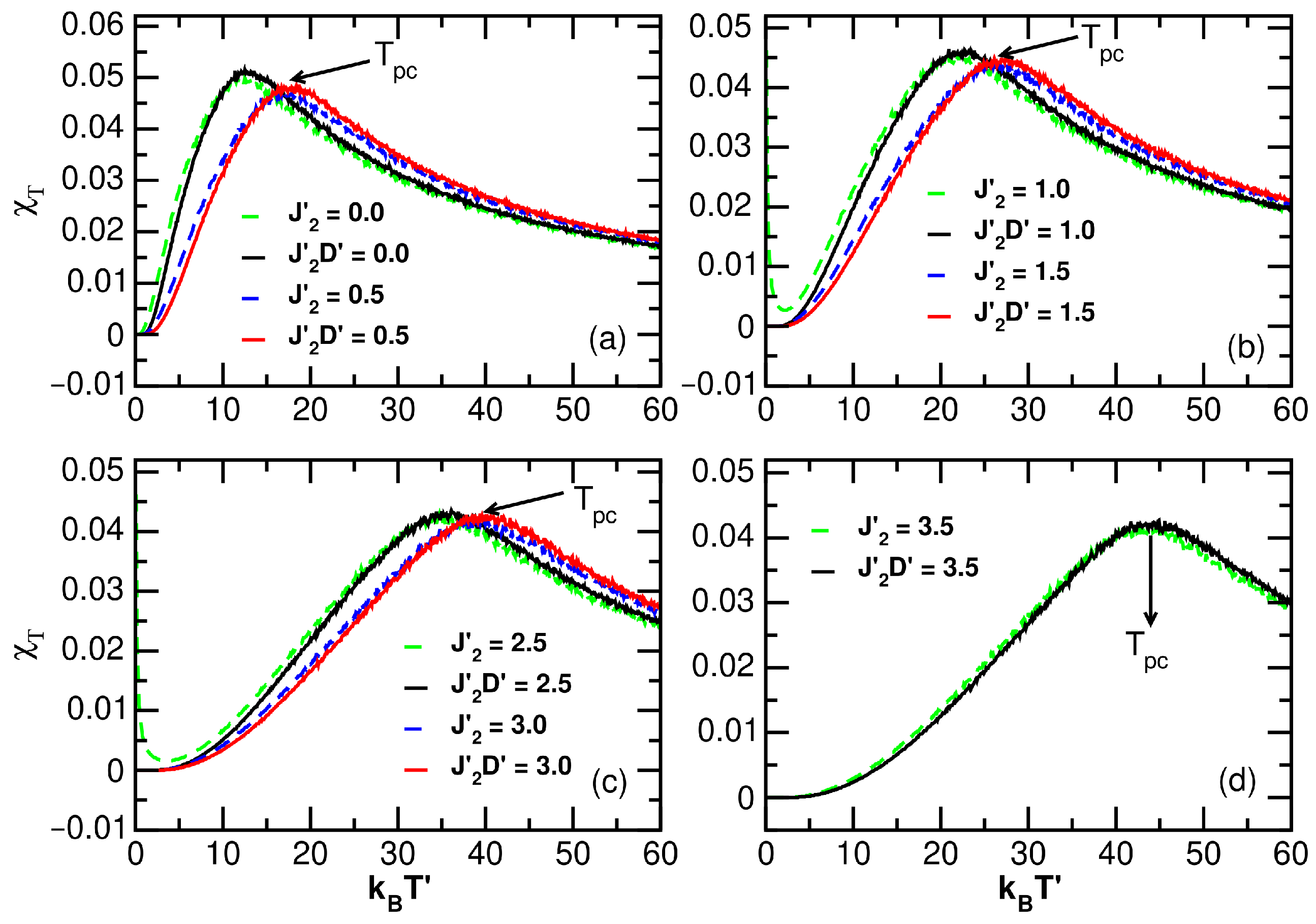
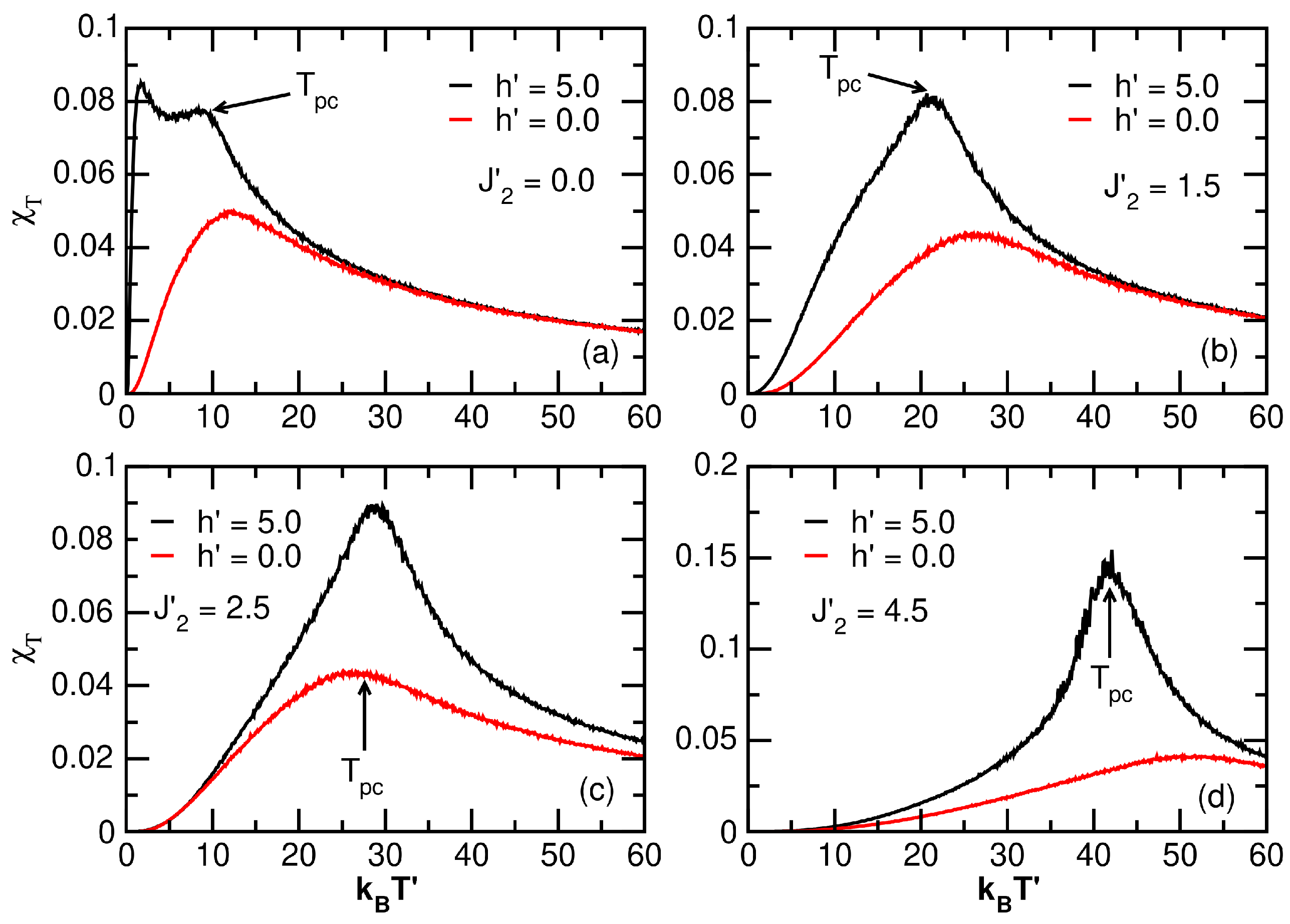
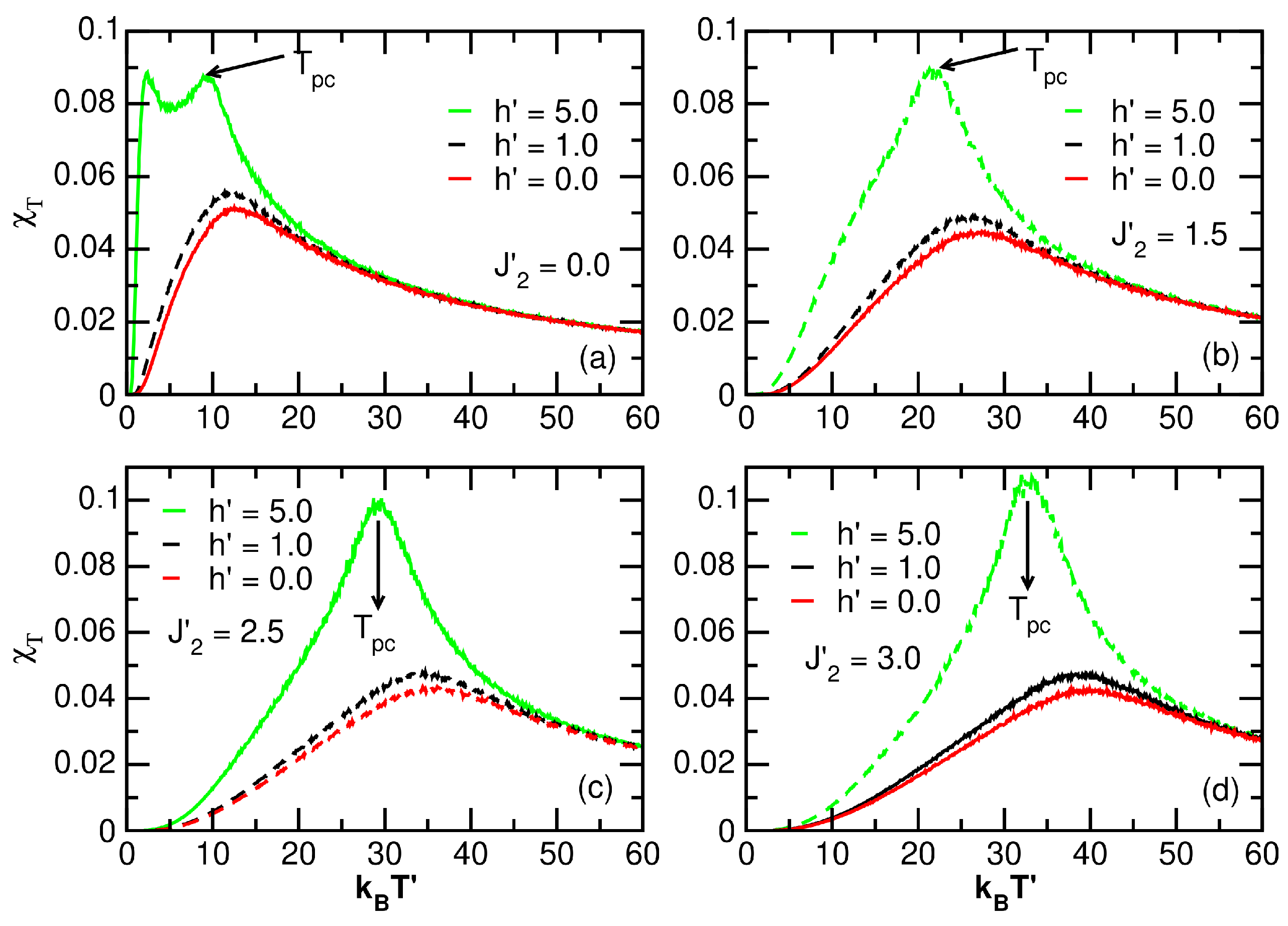
3.1. Exchange Effects

The characterization of the thermomagnetic behavior of the quasi-spherical nanoparticle begins with a study of the influence of the ferromagnetic exchange energy ($J_2^{\prime }>0$) on the system. The magnetic order (ferro, antiferro, or ferrimagnetic), according to the exchange interactions experienced by a substance, supports the discovery of various thermomagnetic phenomena benefiting techno-industrial development [29]. In the following, we consider how antiferromagnetic ($J_1<0$) and ferromagnetic ($J_2^{\prime }>0$) exchange parameters affect the magnetization, magnetic susceptibility, and hysteretic behaviors of the nanoparticle. For this purpose, the $J_1-J_2^{\prime }$ model is employed to highlight the Hamiltonian (1), considering only first-neighbor and second-neighbor exchange interactions in the nanosphere.

3.1.1. $J_1-J_2$ Model

In this case, the anisotropic interactions in the entire nanosystem are neglected, as well as the external field ($D_{3/2}^{\prime }=D_2^{\prime }=h^{\prime }=0$); here, the only couplings that affect the nanoparticle are the exchange constants $J_1=-1$ and $0⩽J_2^{\prime }⩽4.5$. Figure 2 reflects the change in magnetization behavior with increasing $k_B{T}^{\prime }$ and $J_2^{\prime }$. The compensation phenomenon can be attributed to the antiferromagnetic arrangement of spins within the crystal lattice due to the effects of the interaction $J_1<0$, making it possible to verify when $J_2^{\prime }=0$. Then, considering the ferromagnetic action on second neighbors, the compensation points increase ($T_{comp}$ in Figure 2). It is also worth noting that as the magnitude of $J_2^{\prime }$ increases, the rate of change of magnetization with respect to temperature decreases, demonstrating how $J_2^{\prime }$ influences these phenomena.

The $J_2^{\prime }$ interaction specifically influences the location and temperature increases at which compensation occurs; more precisely, the ferromagnetic interactions between second neighbors in the nanoparticle tend to parallelly order the spins, as opposed to the action of $J_1$. In some ways, the strong competition between $k_B{T}^{\prime }$, $J_1$, and $J_2^{\prime }$ causes the A (spin-2) and B (spin-3/2) sublattices to gradually become disordered at different rates until the nanosystem experiences the compensation effect. At $T=T_{comp}$, the spin-2 and spin-3/2 sublattices remain relatively ordered, leading to magnetization modules of the same magnitude; however, due to antiferromagnetism between first neighbors ($J_1<0$), they have opposite directions, leading to $M_T=0$. As the thermal energy increases, at $k_B{T}^{\prime }>T_{comp}$, the sublattices begin to become even more disordered such that, for $T=T_c$, the entire nanostructure beomes completely disordered and the total magnetization is null. This behavior cannot be noticed in this case as we have a nanoscale system in which, for $k_B{T}^{\prime }>60$, there is a tendency for $M_T$ to reach saturation. This can be considered as a kind of stabilization of magnetic states due to the nanosize of the model having consequences for magnetic fluctuations; these are caused mainly by magnetic confinement, which tends to locally redistribute the spins in the material through decreasing in the intensities of the exchange interactions $J_1$ and $J_2^{\prime }$. This situation means that no second-order transition is seen in the $M_T$ curves [1]. It is important to mention that nanoscale systems do not clearly present the transition temperature to the disordered phase, thus justifying the use of the term pseudocritical temperatures ($T_{pc}$) in this case and the approximate estimation of a region reflecting the maximum value of the system’s magnetic susceptibility. It is generally a “smoothed” curve at such a point. Bulk systems, in contrast, tend to show very sharp peaks when the system transitions to the paramagnetic state. A relevant aspect for the quasi-spherical nanoparticle investigated here, but without second-neighbor interactions, has recently been reported by Madera et al., who showed that the emergence of $T_{pc}$-type temperatures in nanoscale systems is affected by—among other factors—the coordination number (z) of the lattice that composes them. When $J_2^{\prime }=0$, $z=8$ is obtained (BCC lattice) as there are only antiferromagnetic $J_1$-type interactions ($\langle nn\rangle$), generating antiparallel alignments in the nanosphere and leading to a well-known magnetic frustration that would produce several configurations with similarly low energies [1]. When ferromagnetic coupling is considered—that is, $J_2^{\prime }>0$ ($\langle nnn\rangle$)—competition for the alignment of the atoms increases; namely, the nanosystem now experiences exchange interactions between first neighbors, with 8 different atoms (S = 3/2 ⇄ Q = 2) of the antiferromagnetic type, as well as between second neighbors of the ferromagnetic type, with 6 neighbors of the same class (S = 3/2 ⇄ S = 3/2 or Q = 2 ⇄ Q = 2). This conglomerate of internal interactions in the nanomaterial increases the pseudocriticality as $J_2^{\prime }>0$ increases, which can be observed from the behavior of the maxima of the susceptibility curves (${\chi }_T$) presented in Figure 3.

When a system experiences pseudocritical temperatures, strong spin correlations emerge on a finite scale, indicating a range in which the system exhibits large thermomagnetic fluctuations. In this case, the response function of the magnetization (susceptibility) displays flattened peaks at its maximum values without clearly revealing a true phase transition; that is, in the thermodynamic limit, the characteristic divergence of continuous phase transitions is not observed. The pseudocritical temperatures are marked as $T_{pc}$, and their shift toward the high-temperature region is observed in each as the $J_2^{\prime }$ ferromagnetic exchange increases. In the report by Madera et al. [1], the effects of crystal fields on the pseudocritical temperature of the 2 nm nanosphere was analyzed. Although the anisotropic effect has not yet been considered in this paper, it is important to note that the behavior of ${\chi }_T$ is qualitatively analogous to that reported in reference [1].

Next, Figure 4 analyzes the hysteretic manifestation of the nanosystem, through the influences of the exchange parameters and with an external field $h^{\prime }$, at a temperature of $k_B{T}^{\prime }=10$.

For small values of $J_2^{\prime }$ (Figure 4a), it is observed that the magnetization is directly correlated with the external magnetic field; in particular, when increasing the external field ($0⩽h^{\prime }⩽15$), the magnetization of the system increases almost linearly, showing a slight increase when $J_2^{\prime }=0.5$. In this case, no saturation in the magnetization is evident for the range $-15⩽h^{\prime }⩽15$, with small coercivity and remanences. The correlation between $M_T$ and $h^{\prime }$ is still evident in Figure 4b–d, owing to the competition between the couplings $J_2^{\prime }$, $h^{\prime }$, and the thermal energy $k_B{T}^{\prime }$, which cause magnetic fluctuations in the spins and lead to the system becoming irreversible. This results in the appearance of asymmetric hysteresis loops with respect to the $M_T=0$ and $h^{\prime }=0$ axes—typically termed as the exchange bias phenomenon (exchange anisotropy)—represented in this case, by horizontal displacements and widening of the hysteresis loops. In Figure 4b, it can be seen that the magnetization progressively presents a growing trend with an increase in the external field. This is a result of reorientation of the material’s magnetic domains in the $h^{\prime }$ direction and progressive breakdown of the domain walls, without achieving system saturation (i.e., the formation of a single domain). It can be observed that, when slightly increasing the exchange ($J_2^{\prime }=1.5$), apparently “discontinuous” jumps are characteristic of these loops and they present a larger internal area. On the other hand, when gradually increasing $J_2^{\prime }$, as in Figure 4c,d, the system not only reaches these jumps at smaller fields but, furthermore, achieves saturation for reduced fields, thus proportionally increasing the surface area of the loops. This is because a large value of $J_2^{\prime }$ forces the system to reach saturation more quickly, resulting in abrupt breaking of the domain walls. Analogous behaviors have been observed for the same system, resulting in positive anisotropic interactions, in a recent investigation conducted by Madera et al. [1].

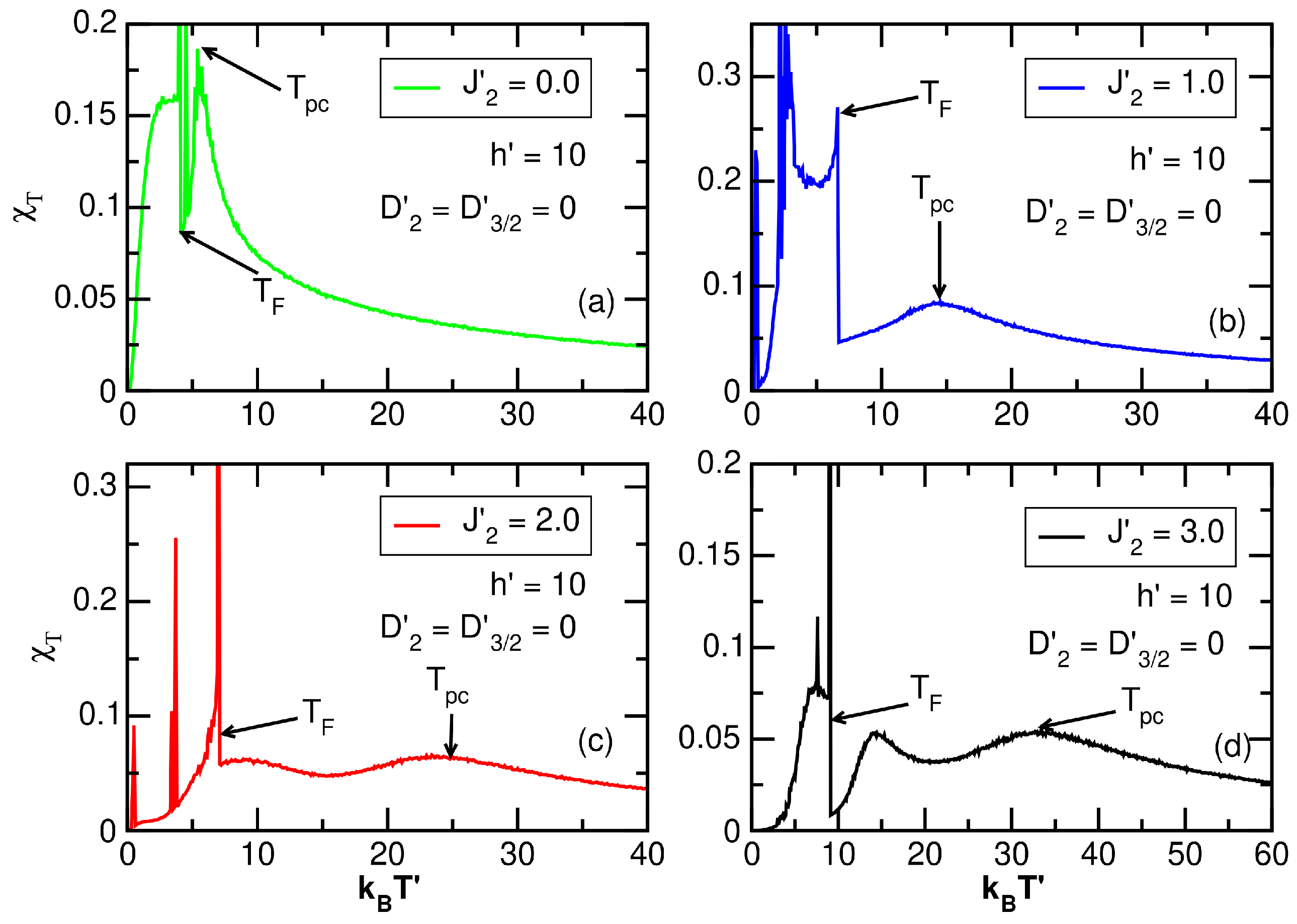
3.2. Anisotropic Effects

In this section, the influences of the crystal fields $D_{3/2}^{\prime }=1.0$ and $D_2^{\prime }=-1.0$ on the quasi-nanosphere are studied. This implies that anisotropic couplings are now added to the exchange interactions, giving rise to the model $J_1-J_2-D_{3/2}-D_2$; as a result, this case can be compared with the model in Section 3.1.1, where only the parameters $J_1-J_2$ are considered.

3.2.1. $J_1-J_2-D_{3/2}-D_2$ Model

In Figure 5 and Figure 6, the behaviors of $M_T$ and ${\chi }_T$ are presented when the nanosphere is subjected to anisotropic couplings $D_{3/2}^{\prime }$ and $D_2^{\prime }$, which are generated by the A and B sublattices, respectively. To compare the incidence of the crystal fields, the results for the $J_1-J_2$ model are plotted as dotted lines in Figure 5 and Figure 6. It is reasonable to consider that the magnetization and susceptibility curves represent how the $J_1$ and $J_2^{\prime }$ interactions generate an apparent screening effect on the anisotropies; similarly, the effects of the exchange constants prevail over those of the crystal fields. As can be seen from the figures, there are no noticeable changes in the compensation and pseudocritical temperatures. This feature can be confirmed from Figure 5d and Figure 6d as, when the intensity of $J_2^{\prime }$ is increased, the effects of the anisotropies become practically imperceptible.

The qualitative and phenomenological behaviors presented by the system in Figure 5 and Figure 6 have been explained in Section 3.1.1 regarding the $M_T$ and ${\chi }_T$ curves shown in Figure 2 and Figure 3.

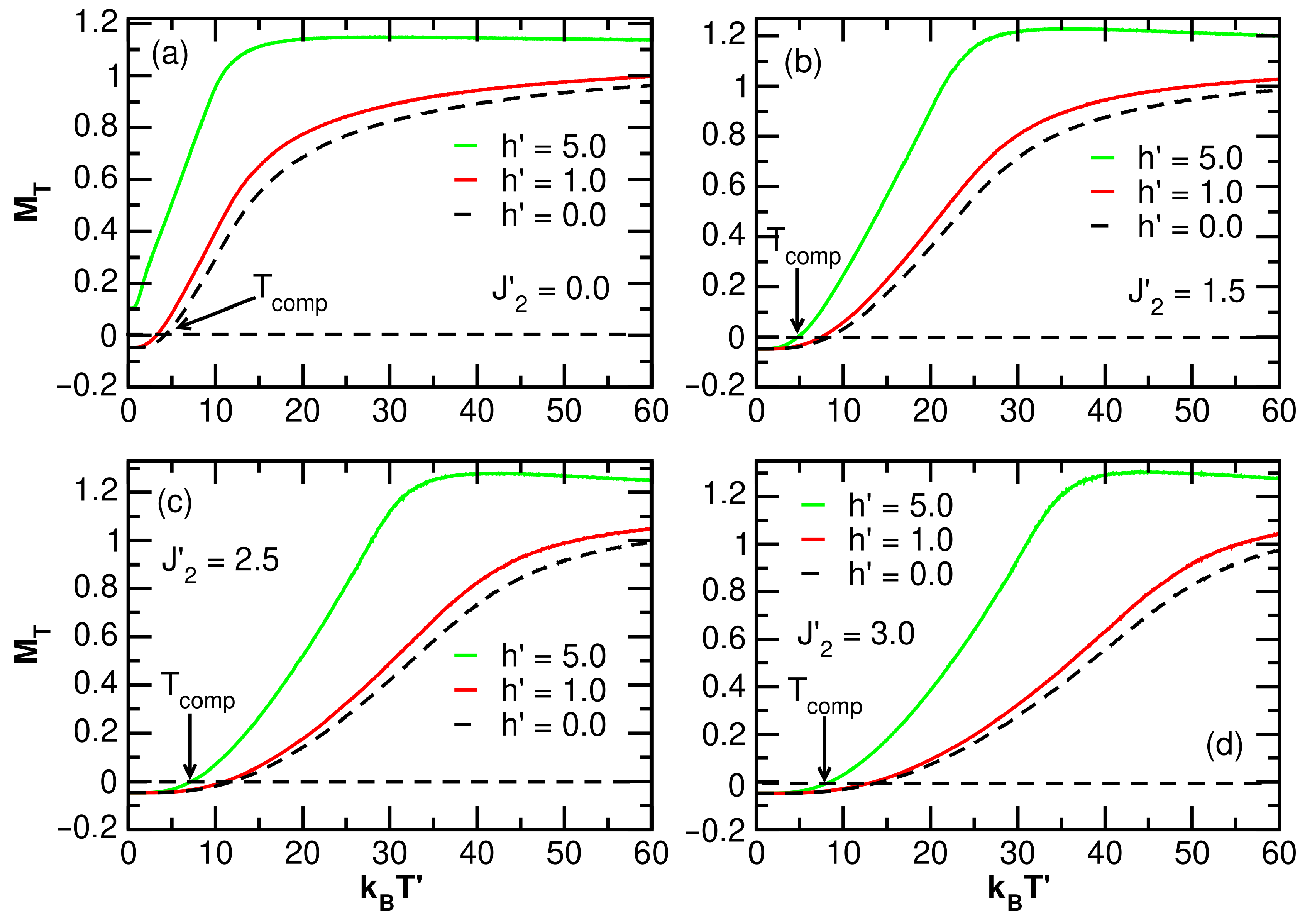
3.3. External Fields Effects

It is important to analyze how the behavior of the nanosystem changes when it is subjected to the presence of an external field $h^{\prime }$, including the effects of the bilinear exchange couplings $J_1$ and $J_2^{\prime }$. In this section, the results are compared for the $J_1-J_2$ and $J_1-J_2-h$ models; in precise terms, the physical alterations of the nanoparticle influenced by an external field $h^{\prime }$ are assessed.

3.3.1. $J_1-J_2-h$ Model

The curves in Figure 7a–d show the effects of the competition between the external field and the $J_2^{\prime }$ exchange parameter. At low temperatures $(0<k_B{T}^{\prime }\lesssim 15)$, the magnetization decreases with increasing $J_2^{\prime }$ regardless of the field applied to the nanoparticle. The change in the concavities of the $M_T$ curves can be seen for $h^{\prime }=$$\{0,1,5\}$ in Figure 7b–d. In the case $J_2^{\prime }=0$ (Figure 7a), the magnetic field tends to orient the spins in its direction, to the point that $M_T$ increases progressively, until the nanosystem experiences a possible sudden transition in the range $0\lesssim k_B{T}^{\prime }\lesssim 5$ when $h^{\prime }=10$. The tendency towards rearrangement of the nanocrystal due to the effects of the struggle between $J_1$, $J_2^{\prime }$, $h^{\prime }$, and the thermal energy is reflected in a new possible sudden transition at temperatures designated as $T_F$.

The competition between the parameters of the Hamiltonian (1) can likely be described as follows: $J_1$ gives the nanosystem its ferrimagnetic character, resulting in antiparallel orientations throughout the nanoparticle; however, the ferromagnetic action of $J_2^{\prime }$ also influences the entire nanolattice, resulting in $S=3/2$ and $Q=2$ spins seeking to maintain a parallel direction between them. Once these exchange couplings are subjected to the effect of an external field, many spins in the nanosystem with directions opposite to those of $h^{\prime }$ will try to reorient themselves toward it. Particularly when the field is large ($h^{\prime }=10$), the thermal energy comes into play, counteracting the effect of the exchange interaction to the point that the external field may suddenly orient the spins, abruptly increasing the system’s magnetization. This represents a possible sudden transition, which rises with increasing $J_2^{\prime }$, and then decreases with increasing thermal energy. Regarding the compensation temperature, it is evident that its behavior remains the same—proving to be a consequence of the exchange interactions rather than the external field.

Figure 8 presents the total susceptibility of the nanosphere and shows that the approximate regions of the pseudocritical transitions with $T_{pc}$ are demarcated. It can be seen that the temperature $T_{pc}$ increases proportionally with the $J_2^{\prime }$ value when ignoring the effect produced by the field $h^{\prime }$. The special case of the behavior of the magnetic susceptibility (${\chi }_T$) for $h^{\prime }=10$ is shown in Figure 9, where $T_F$ and $T_{pc}$ denote the approximate temperatures at which the nanosystem experiences possible sudden transitions and pseudocritical transitions, respectively. The temperatures $T_F$ coincide with the values indicated in the $M_T$ curves shown in Figure 7.

3.3.2. $J_1-J_2-D_{3/2}-D_2-h^{\prime }$ Model

In Section 3.2.1, the influence of anisotropies on the nanosystem was analyzed based on the model $J_1-J_2-D_{3/2}-D_2$. In this section, the $h^{\prime }$ external field interaction is further included, giving rise to the model $J_1-J_2-D_{3/2}-D_2-h$, with the purpose of analyzing its influence on $M_T$ and ${\chi }_T$. Notably, the same values for the anisotropies and the magnetic field are used: $D_{3/2}^{\prime }=1$; $D_2^{\prime }=-1$; $h^{\prime }=0,1,5,10$; and $0⩽J_2^{\prime }⩽4.5$.

The magnetic behaviors due to the effects of $h^{\prime }$ are depicted in Figure 10 via the $M_T$ vs. $k_B{T}^{\prime }$ curves. It can be noted that, for a fixed value of the field $h^{\prime }$, the $T_{comp}$ value increases with increasing intensity of $J_2^{\prime }$, but with values slightly lower than for the case $J_1-J_2-D_{3/2}-D_2$ ($h^{\prime }=0$). This indicates that the presence of the external field causes the rates at which the sublattices A and B become disordered to increase. As shown in Figure 5, the anisotropies do not make a significant contribution in this case as a consequence of the “screening” of the exchange couplings, to which the appearance of the compensation phenomenon can be attributed.

The external field $h^{\prime }$ directly influences the decrease in $M_T$ at low temperatures and the appearance of possible sudden transitions for large fields ($h^{\prime }=10$), as can be observed in Figure 11. Regarding the pseudocritical temperatures ($T_{pc}$), indicated approximately at the maxima of the ${\chi }_T$ curves in Figure 12, it is asserted that, for a fixed value of $J_2^{\prime }$, the temperature $T_{pc}$ decreases while $h^{\prime }$ increases. This implies that the nanosystem reaches a possible transition more quickly due to the tendency of the spins to seek the direction of the field, together with the increase in thermal energy. Furthermore, for a fixed value of $h^{\prime }$, an increase in $J_2^{\prime }$ implies an increase in $T_{pc}$, that is, the exchange coupling has a greater impact on the ordering of the spins in the nanoparticle.

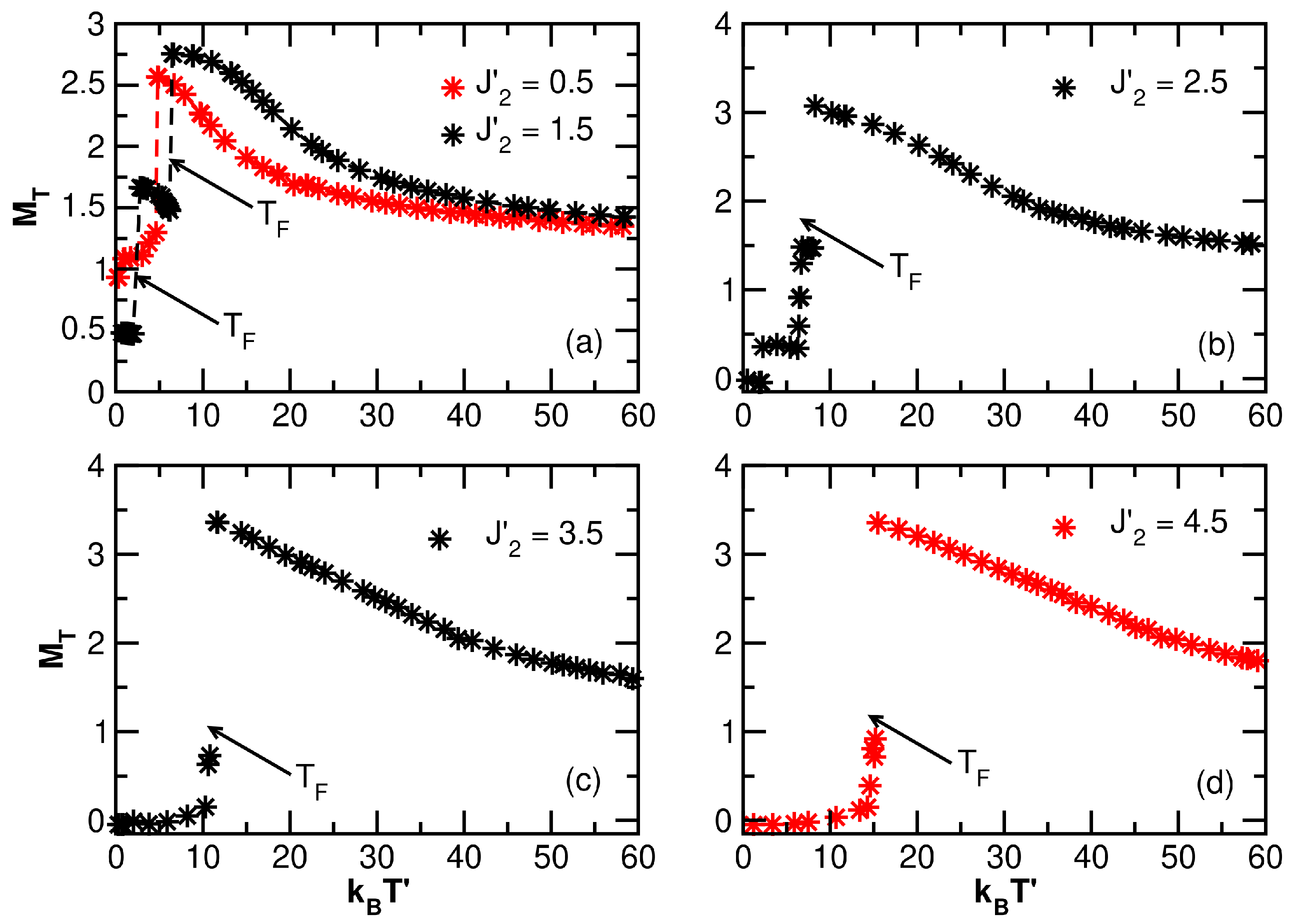
3.4. Thermal Effects

The effects produced by the thermal energy $k_B{T}^{\prime }$ on the nanosphere are just as important as the exchange, external field, and anisotropic effects. In this section, the hysteretic behaviors of the nanosystem are analyzed for different temperatures with various values of $J_2^{\prime }$, $D_{3/2}^{\prime }=1$, and $D_2^{\prime }=-1$. Similarly, the influence of the parameter $J_2^{\prime }$ on the temperatures $T_{pc}$, $T_{comp}$, and $T_F$ is studied.

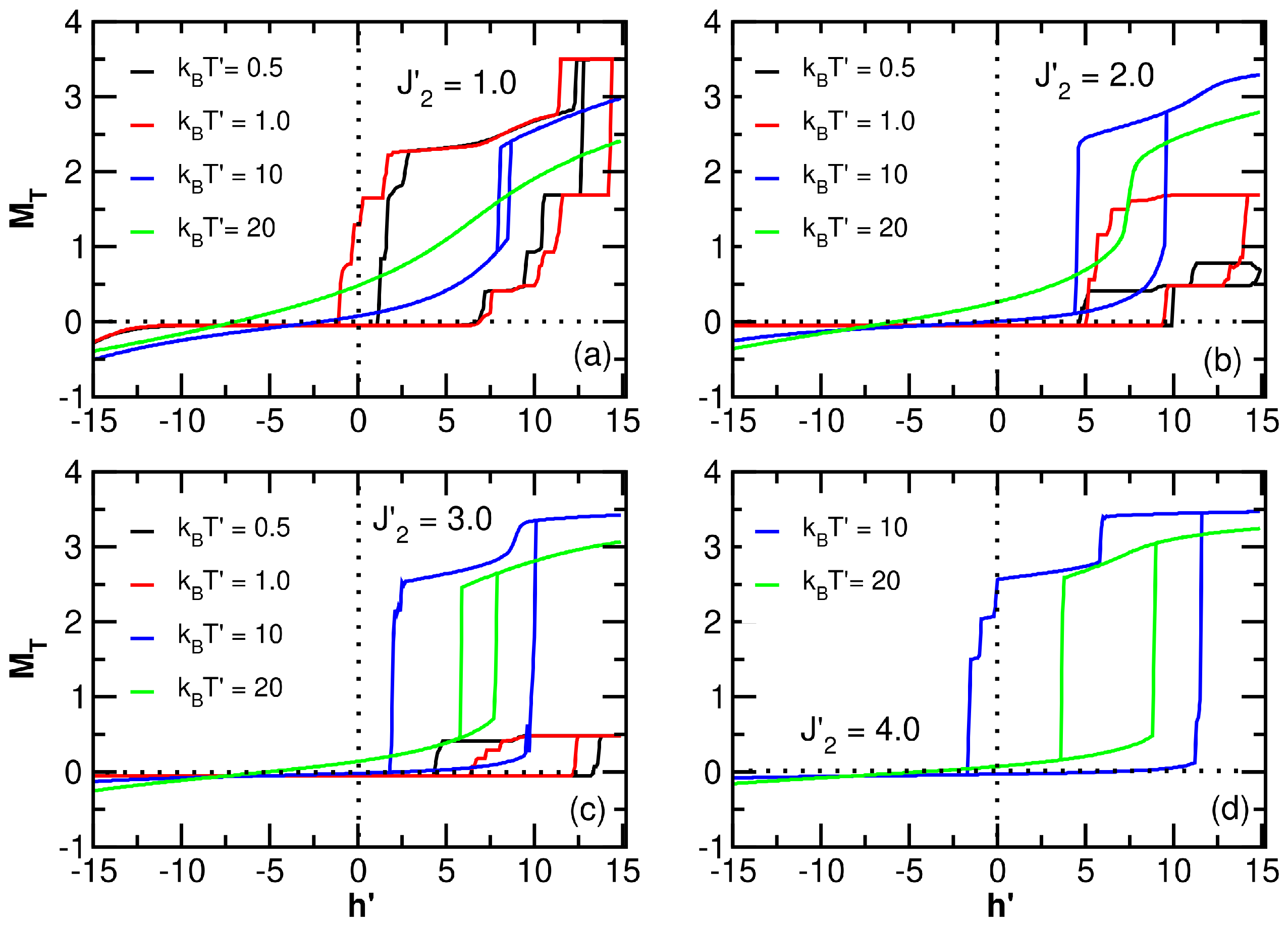
3.4.1. $J_1-J_2-D_{3/2}-D_2^{\prime }$ Model: Magnetic Hysteresis

Hysteresis processes within a material are important for memory retention in magneto-optical systems, such as hard disks and magnetic tapes, among others. The area of the hysteresis loop directly reflects the energy needed to reverse the magnetization of the system. One of the most important phenomena in the hysteresis processes of a magnetic system is exchange or unidirectional anisotropy (exchange bias), which occurs when a ferromagnetic substance interacts with an antiferromagnetic substance, thus producing an interfacial exchange. There are certain physical conditions for a material to experience this phenomenon: first, the Curie temperature of the ferromagnet must be greater than the Neel temperature ($T_c>T_N$); second, the ferromagnetic material must have a specific or adequate thickness; third, it is necessary to cool the system with an external field through $T_N$. Once these conditions are satisfied, a horizontal or vertical displacement of the hysteresis loop can be observed due to the emergence of exchange anisotropy, which can be interpreted as a supposed magnetic field, $H_{exc}$, which is distinct from the external magnetic field $h^{\prime }$. When $H_{exc}$ appears, the ferromagnet would be favorably magnetized in the direction in which the system is cooled. The fields $h^{\prime }$ and $H_{exc}$ compete, in a parallel or perpendicular manner, leading to the potential of the hysteresis loop to shift with respect to the axes $h^{\prime }=0$ and $M_T=0$, with a total magnetic energy $-M_T(h^{\prime }+H_{exc})$. It is certainly notable that, when $h^{\prime }$ and $H_{exc}$ are perpendicular, it is more difficult to shift the hysteresis loop due to the system’s tendency to magnetize toward a difficult axis. This situation results in greater energy expenditure to achieve magnetization reversal, encouraging larger and more coercive hysteresis loops; in other words, the material exerts greater resistance to the reorientation of its spins. Even so, for each value of the external field, there is an orientation angle of $M_T$ that minimizes the energy of the system [30,31].

In relation to the case of this investigation, as there is a nanoparticle with an antiferromagnetic arrangement formed by all the spins coupled to first neighbors (coupling $J_1$), and another ferromagnetic arrangement involving the interactions with second neighbors (coupling $J_2^{\prime }$), the system presents the exchange bias phenomenon, which is described in Figure 13a–d for various values of temperature and the exchange parameter $J_2^{\prime }$. It is important to mention that the hysteresis loops in a system occur due to the magnetic ordering of the sublattices that compose it, as well as to the constant competition between the internal parameters of the system, its thermal energy, and the applied external magnetic field. In the hysteretic analysis of the nanosystem, the effects of the thermal energy ($k_B{T}^{\prime }$) will be considered initially, and then those of the coupling parameter $J_2^{\prime }>0$, when $D_2^{\prime }=-1$, $D_{3/2}^{\prime }=1$, and $k_B{T}^{\prime }=0.5,1,10,20$.

For a fixed value of $J_2^{\prime }$—for instance, in Figure 13a, where ($J_2^{\prime }=1.0$)—it can be observed that at a high thermal energy value of the system, it prevails over the effects of the other couplings of the nanosystem ($J_1,J_2^{\prime },D_{3/2}^{\prime },D_2^{\prime }$), in such a way that it facilitates reorientation of the spins in the direction of $h^{\prime }$, as can be seen when $k_B{T}^{\prime }=20$. In this case, the system experiences a “superparamagnetic” state. Consistent with the above, as the temperature gradually decreases ($k_B{T}^{\prime }=10,1,0.5$), the effects of the exchange parameters become more noticeable. Hence, in this case, it becomes difficult for the external field to magnetically order the nanosystem. This can be observed in terms of the discontinuous jumps of the hysteresis loops in Figure 13a–d.

Next, the influence of $J_2^{\prime }$ on the exchange bias behavior is analyzed for the $M_T$ curves in Figure 13, with a fixed value of $T=10$. In Figure 13a, the exchange interactions $J_1$ (antiferromagnetic) and $J_2^{\prime }$ (ferromagnetic) have the same intensity, such that the unidirectional anisotropy effect at the interface is not as noticeable, when compared with more intense values of $J_2^{\prime }$ (see Figure 13b–d); in particular, the fields $h^{\prime }$ and $H_{exc}$ tend to be oriented perpendicularly, which implies that displacement of the hysteresis loop is more difficult and presents a relatively small area (see Figure 13a). When increasing $J_2^{\prime }$, the ferromagnetic interaction increases, further reinforcing the effect of the perpendicular orientation of $h^{\prime }$ and $H_{exc}$, which is reflected both in the enlargement of the area of the loops and in the coercivity (see Figure 13c,d).

Another aspect worth assessing is the thermomagnetic response of the nanosystem at low temperatures. It is noticeable, from Figure 13a–d, that the increase in the $J_2^{\prime }$ ferromagnetic interaction generates a noticeable decrease in the loop area when $k_B{T}^{\prime }=0.5,1$—to the point that, for $J_2^{\prime }=4$ (Figure 13d), the exchange bias phenomenon disappears at $M_T=0$. In contrast, in the case of $k_B{T}^{\prime }=10,20$, the loops can be seen to expand. One might wonder why this behavior occurs at low temperatures, given how striking the phenomenon is. A brief explanation is as follows: When $k_B{T}^{\prime }\to 0$, the spins in the nanoparticle will be oriented in the direction of the strongest coupling which, in this case, is $J_2^{\prime }>0$. This affects the two sublattices in such a way that ferromagnetic second-neighbor interactions between atoms with spin-2 and spin-3/2 ($S\rightleftarrows S/Q\rightleftarrows Q$) prevail in the nanolattice, even in the presence of an external field. Despite all this, there are other factors influencing the performed analysis, which cannot be ruled out. For example, a certain magnetic frustration is caused by the antiferromagnetic effect of $J_1$, which prevents the spins of the nanosystem from aligning preferentially in a single or more favorable direction, indicating that the various couplings within the nanosystem are not satisfied simultaneously by the magnetic confinement effect produced by the nanosize of the system [1]. In summary, magnetic frustration also contributes to the cancellation of magnetization at low temperatures, as there is no minimum-energy spintronic order in the nanoparticle that leads to an appreciable $M_T\ne 0$, despite coupling with an external field. Finally, it is essential to comment on the analysis of Figure 13, where the effect of the magnetocrystalline anisotropies $D_{3/2}^{\prime }$ and $D_2^{\prime }$ is only minorly relevant, given that the nanoparticle presents hysteretic behavior very similar to that in the case of the $J_1-J_2$ model, in which the action of the crystal fields was not considered (see Figure 4). This observation corroborates the idea that the parameter with the greatest effect on the system is really $J_2^{\prime }$.

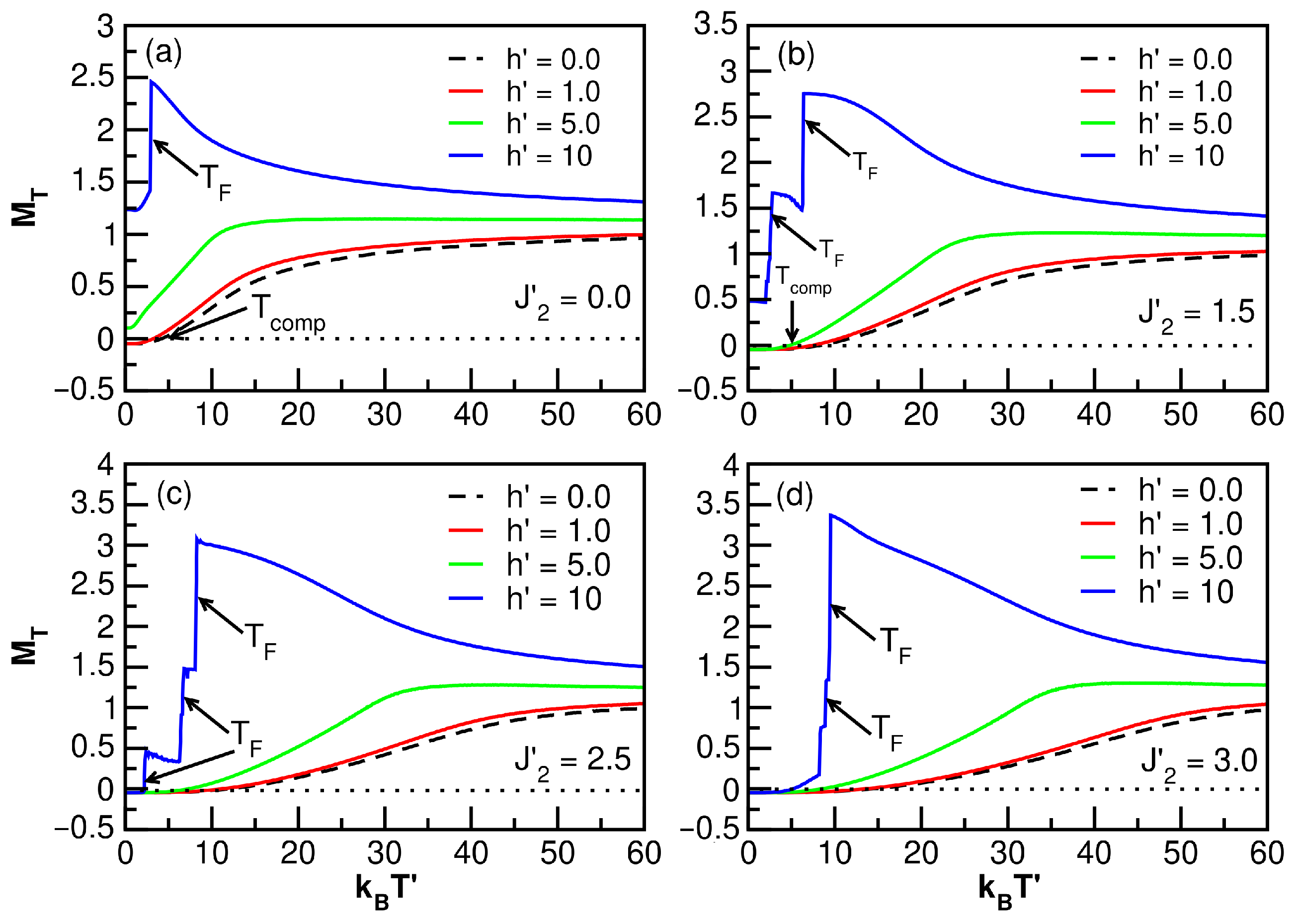
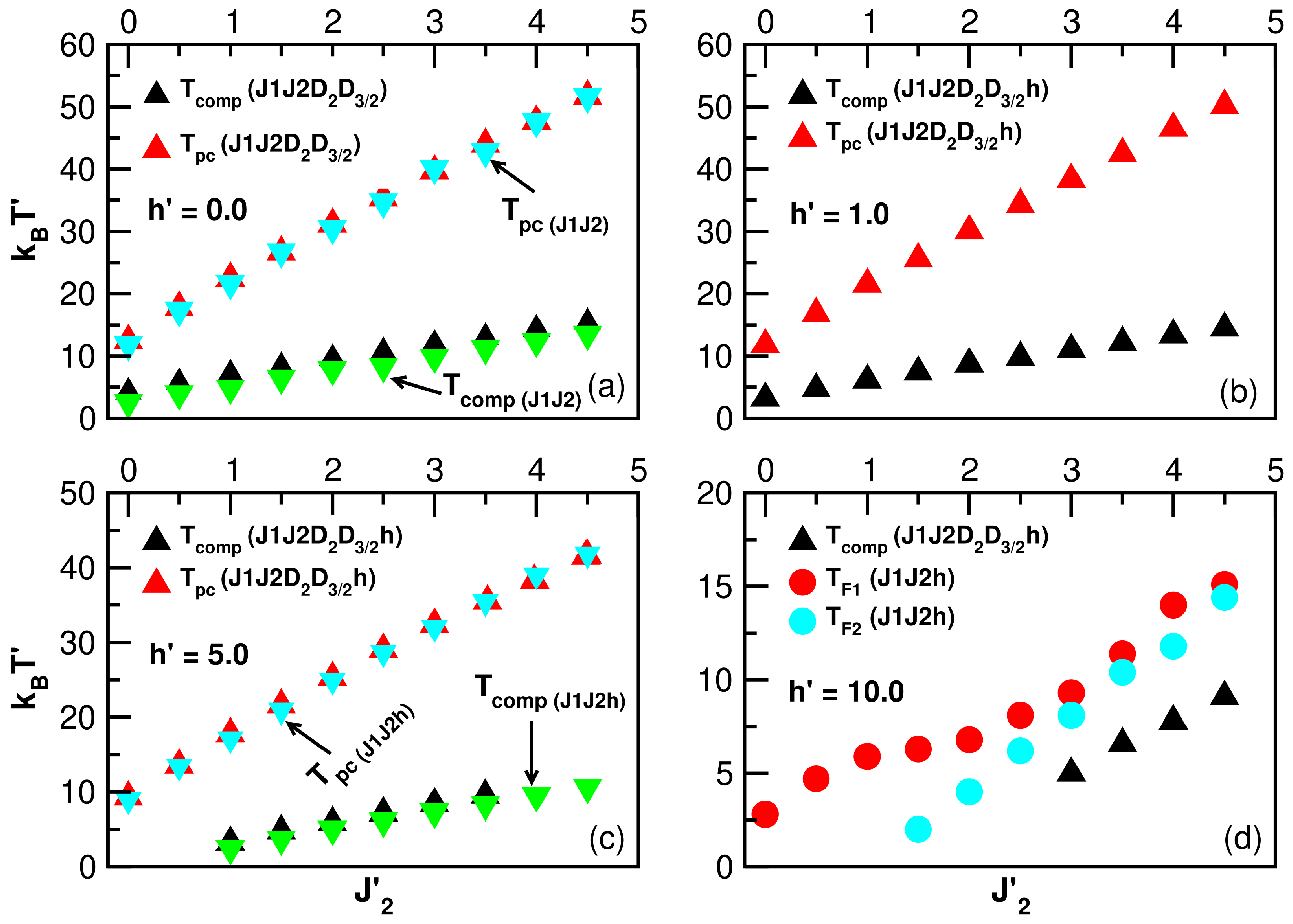
3.4.2. Exchange Effects on Temperature

In order to analyze the effects of the exchange parameter $J_2^{\prime }>0$ on the pseudocritical, compensation, and discontinuous transition temperatures ($T_{pc}$, $T_{comp}$, and $T_F$), a summary of the thermal behaviors of the nanoparticle for $h^{\prime }=0,1,5,10$ is presented in Figure 14, including the models $J_1-J_2$, $J_1-J_2-h$, $J_1-J_2-D_{3/2}-D_2$, and $J_1-J_2-D_{3/2}-D_2-h$.

The following points can be observed:

• In Figure 14a, in the absence of an external field, the pseudocritical and compensation temperatures are compared for the $J_1-J_2$ and $J_1-J_2-D_{3/2}-D_2$ models. For both models, $T_{pc}$ and $T_{comp}$ grow proportionally with $J_2^{\prime }$. Furthermore, the presence of the $D_{3/2}^{\prime }$ and $D_2^{\prime }$ fields only slightly affects $T_{comp}$, leading to a slight increase, while the behavior of $T_{pc}$ in both cases was similar.
• Figure 14b, with $h^{\prime }=1$, proportional increases in $T_{pc}$ and $T_{comp}$ with respect to an increase in the $J_2^{\prime }$ ferromagnetic interaction can be seen for the $J_1-J_2-D_{3/2}-D_2-h$ model. Comparing this result to that in the absence of crystal fields (i.e., $J_1-J_2-h$ model), it can be seen that the behaviors of the temperatures $T_{pc}$ and $T_{comp}$ are analogous to those in Figure 14a. This confirms that the crystal fields only slightly affect $T_{comp}$.
• When increasing the external field to $h^{\prime }=5$ for the same models ($J_1-J_2-D_{3/2}-D_2-h$ and $J_1-J_2-h$), as shown in Figure 14c, it is possible to establish that the direct proportionality between $T_{pc}$ and $T_{comp}$ is maintained with respect to $J_2^{\prime }$. There is a similarity in the $T_{pc}$ values, and the interval in which the system experiences compensation points when the anisotropic effect is not considered ($D_{3/2}^{\prime }=D_2^{\prime }=0$) is slightly widened.
• In the $J_1-J_2-D_{3/2}-D_2-h$ model for larger magnetic fields ($h^{\prime }=10$), as shown in Figure 14d, although $T_{comp}$ exists, it occurs in a larger and different range ($J_2^{\prime }$, $3⩽J_2^{\prime }⩽4.5$) compared to the case in Figure 14c. The most relevant observation in this situation is the appearance of double possible sudden transitions, which are proportional to $J_2^{\prime }$, when anisotropic couplings are not considered ($D_{3/2}^{\prime }=D_2^{\prime }=0$) in the $J_1-J_2-h$ model.

It is worth highlighting that the phenomena discussed in this research regarding the $M_T$ and ${\chi }_T$ phase diagrams (i.e., possible sudden transition, compensation points, pseudocritical temperatures, exchange bias) are relevant, due to their potential technological and spintronic applications. In reference to the possible sudden transitions, these are closely linked to magnetic reversals—either by jumps or abrupt drops. These are useful in the cooling of the solid state of matter, which occurs due to the intense caloric response in the presence of small magnetic fields [32]. Similarly, they are necessary for the production of large magnetocaloric effects for which a sudden change in magnetization with temperature is required, resulting in a possible discontinuity which is generally related to irreversibilities in thermomagnetic hysteretic processes [33]. In addition to the abovementioned applications of magnetic discontinuities, there are also notable uses relating to magnetostriction and magnetoresistance, originating when (dis)order-to-order transitions are experienced by a material in parallel with changes in the underlying crystal lattice, giving rise to magnetostructural transformations associated with the production of thermomagnetic hysteresis [34]. Equally significant among the uses of discontinuous transitions are their applications in the manipulation and storage of magnetic information [35,36]. In particular, it is well established that unidirectional exchange anisotropy (exchange bias) is very useful in magnetic applications such as memory, sensor, and spin valve devices, where the hardest reference layer is set in read heads and MRAM memory circuits, which utilize giant magnetoresistance or the magnetic tunnel effect [37,38]. On the other hand, exchange bias has also been used to control the voltage in multiferroic materials, as it provides an energy-efficient way to achieve a rapid 180° magnetization reversal—a key aspect for the fabrication of fast, compact, and ultra-low-power magnetoelectric devices [39]. In short, the exchange bias phenomenon has been involved in the development of many technological advances through the advanced characterization of materials, as well as in the development of various scientific fields, including surface science, spin dynamics, and spin electronics [40]. With respect to the compensation points experienced by ferrimagnetic systems at atomic scale, these are critical parameters that characterize their magnetic properties and are considered a preponderant factor in modern technological applications, as seen in fields such as magnetic storage, magneto-optical devices, and antiferromagnetic spintronics [41]. It is worth noting that the compensation phenomenon strongly penetrates through microscopic ferrimagnetic configurations, revealing electron spin interactions.

When comparing the results of this research with theoretical and experimental works on FeCo nanosystems, some interesting aspects were found in relation to the reported phenomena. For example, using a hydrothermal experimental method, FeCo nanoparticles in the BCC phase with different percentages of constituent elements have been generated, allowing for the analysis of the effects of unidirectional exchange anisotropies on the magnetic properties of the compounds. As in this study, it was shown that the FC and ZFC magnetization curves increased with temperature and that the behaviors of $M_T$ were qualitatively analogous to those observed here [42]. Likewise, another qualitative behavior analogous to ours in terms of the magnetization of an FeCo nanoparticle has been reported in the experimental work of reference [43], in which exchange bias phenomena and anisotropies at the nanocrystalline FeCo interface were investigated. As in the present investigation, in [43], no critical temperatures were found with respect to the magnetization nor the magnetic susceptibility. Theoretically, in an atomistic simulation of FeCo nanoparticles [44], critical temperatures were reported for different concentrations of the alloy, which contrasts with the results of the present work, in which only $T_{pc}$ values were found. In addition, in [44], the system did not present compensation and exchange bias phenomena, as observed in this investigation.

In theoretical Monte Carlo studies reported by Wang et al., Shi et al., Liu et al., and Jerrari et al. [45,46,47,48], which focused on the thermomagnetic characterization of Ising-type nanoparticles of spin 1-3/2 and 2-3/2 with exchange, anisotropic, and external field couplings, thermomagnetic phenomena such as compensation temperatures, hysteresis loops, and exchange bias were reported, being qualitatively similar to those observed with the nanoparticle analyzed in the present work. Likewise, in experimental work on an FeCo system with 2-3/2 spins, Gupta et al. reported exchange bias with a displacement of the loops toward the negative axis of the magnetic field—a behavior similar to that reported regarding the hysteresis curves of the quasi-spherical system considered in this study [49].

To conclude the analysis, the reports by Madera et al. [1] on the same nanosystem are considered, in comparison with the results of the present work. In [1], $T_{pc}$, $T_{comp}$, and hysteretic behaviors in the presence of exchange bias were reported, highlighting the anisotropic effects in the FeCo nanoparticle above all. When comparing the two investigations, important differences were found; especially regarding the influence of the ferromagnetic second-neighbor interaction, $J_2^{\prime }$, as detailed below. In [1], in the absence of crystal and external fields ($D_2^{\prime }=D_{3/2}^{\prime }=D^{\prime }=0,h^{\prime }=0$), they found $T_{comp}$ and $T_{pc}$ only for antiferromagnetic first-neighbor interactions ($J_1<0$) (see Figures 7 and 11 in [1]), with lower values than those obtained when considering $J_2^{\prime }>0$ (see Figure 2 and Figure 3). The consideration of negative and positive anisotropies in [1], with zero external fields, resulted in an increase in the $M_T$ vs. temperature curves, with downward concavities (see Figures 2 and 4 in [1]); meanwhile, in the current work, as $J_2^{\prime }$ increased the concavities turned upwards—notably, this situation led to smaller $M_T$ values at low temperatures (see Figure 5). Certain qualitative similarities were observed regarding the behavior of the magnetization curves in both works (increasing with temperature and concave upwards), when considering increases in anisotropy in [1] ($0⩽D^{\prime }⩽9$) (Figure 9) and increases in $J_2^{\prime }$ ($0⩽J_2^{\prime }⩽4$) (Figure 5) in the present work. Here, an increase in $T_{comp}$ became evident due to the action of $J_2^{\prime }$. A key aspect of the influence of $J_2^{\prime }$ on the nanoparticle is the appearance of possible sudden transitions in $M_T$ and ${\chi }_T$ for large external fields (see Figure 7 and Figure 11), which were not reported in reference [1]. Regarding the hysteretic behavior in the two cases, it can be observed that, in [1], at low temperatures ($k_B{T}^{\prime }$ = 1.0) (Figure 18), an increase in negative anisotropy generates exchange bias phenomena. This is in contrast to the present work, in which larger loops were formed at low values of $J_2^{\prime }$ and the same temperature; however, when $J_2^{\prime }⟶4$, the exchange bias phenomenon disappeared (see Figure 13). For $h^{\prime }=0$ and non-zero crystal fields ($D_2^{\prime }\ne D_{3/2}^{\prime }\ne 0$), $T_{pc}$ and $T_{comp}$ are higher when the 2 and 3/2 spins couple with the $J_2^{\prime }$ ferromagnetic exchange; that is, the effect of $J_2^{\prime }$ generates increases in these temperatures, as evidenced in Figure 13 of [1] and Figure 14 of this paper.

4. Conclusions

In summary, the effects of second-neighbor exchange couplings, crystal fields, and external fields on the thermomagnetic behavior of a quasi-spherical nanoparticle comprising spin-2 and spin-3/2 atoms were investigated. Simulations revealed that, under null crystal and external fields, the ferromagnetic second-neighbor exchange parameter, $J_2^{\prime }$, plays an important role in the emergence of larger temperatures (i.e., $T_{pc}$ and $T_{comp}$) than when its effect is not considered (as in [1]), indicating its higher-order effect on the nanosystem. Furthermore, the consideration of $J_2^{\prime }$ is essential to capture the nanosystem undergoing possible sudden transitions when subjected to large external fields. Additionally, as in reference [1], the nanoparticle exhibited exchange bias phenomena: as a result of the action of $J_2^{\prime }$, at low temperatures, the hysteresis loops disappear as it increases; meanwhile, at high temperatures, the loop areas increase progressively. Overall, it was demonstrated that, due to the size of the nanoparticle, magnetic confinement effects, the coordination number, and magnetic frustration, the newly considered ferromagnetic exchange parameter $J_2^{\prime }$ notably influences the nanosystem, causing it to experience decreased impacts on its thermomagnetic fluctuations and magnetic order, as demonstrated in terms of the observed pseudocritical temperatures and possible sudden transitions. This research is considered a continuation of the work presented in [1].