The Origin of Homochirality by Rotational Magnetoelectrochemistry
Abstract
:1. Introduction
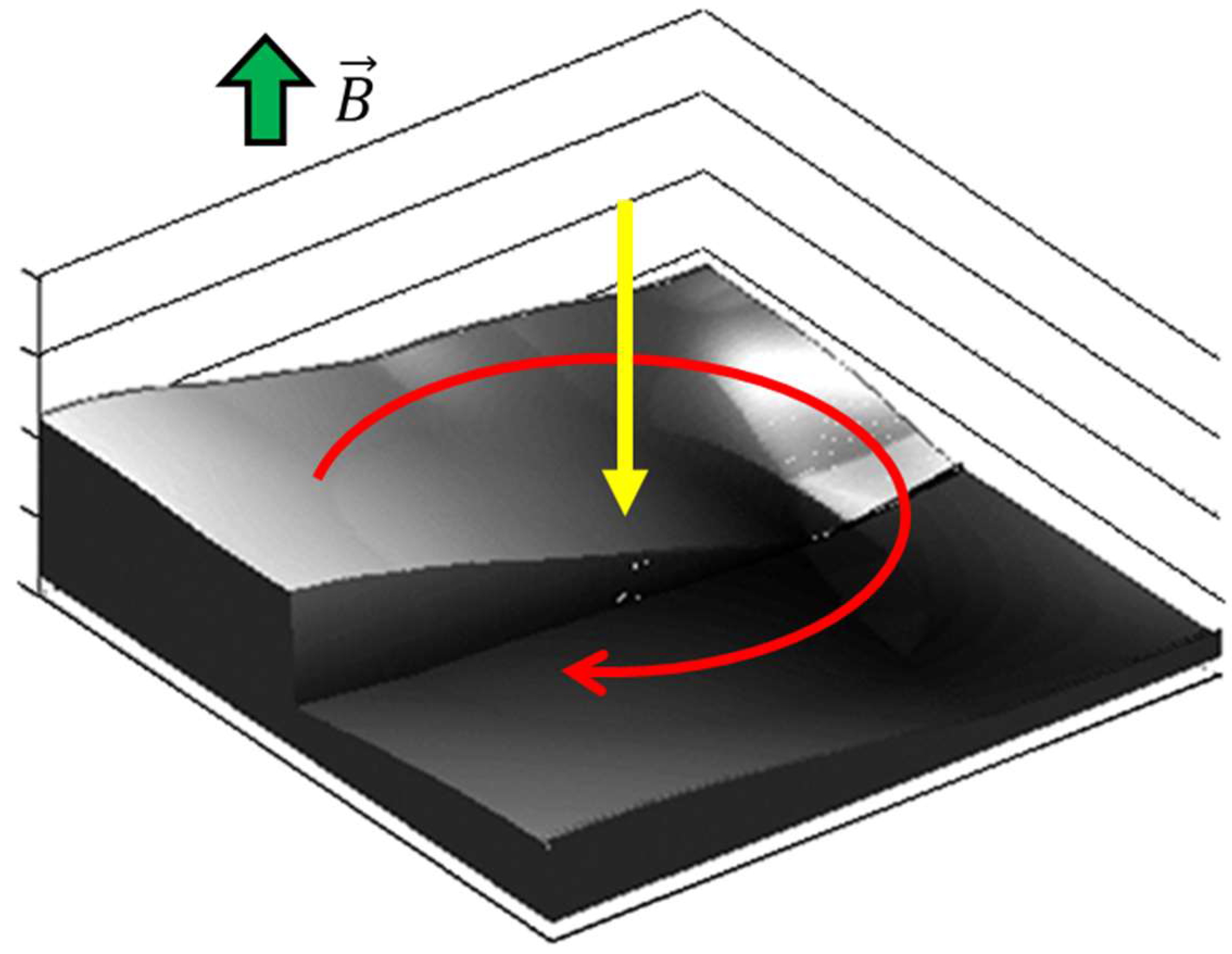
2. Theory
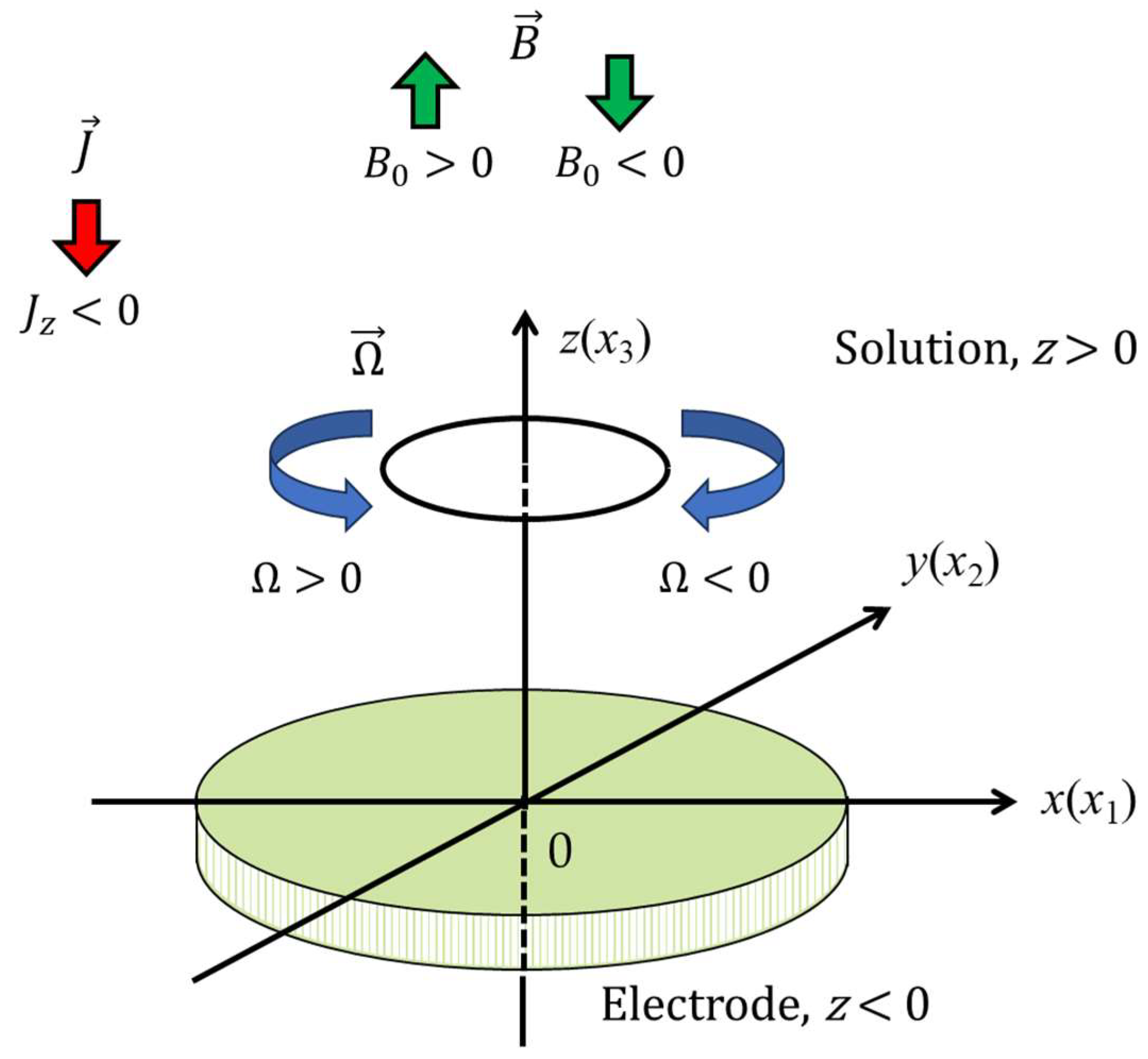
2.1. Basic Equations
2.2. Equations of the Nonequilibrium Fluctuations
2.3. Amplitude Equations of the Fluctuations
2.4. Boundary Conditions of the Fluctuations on the Rigid and Free Surfaces
2.4.1. Rigid Surface on Which No Slip Occurs
2.4.2. Free Surface Where No Tangential Stress Acts
2.5. General Solution of
2.6. Solutions of on the Rigid and Free Surfaces and
2.6.1. Amplitude of the Vorticity Fluctuation on the Rigid Surfaces
2.6.2. Amplitude of the Vorticity Fluctuation on the Free Surfaces
2.7. General and Special Solutions of the Amplitude of the Velocity Fluctuation
2.7.1. The General Solution
2.7.2. The Special Solution
2.8. Solutions of the Rigid- and Free-Surface Amplitudes and
2.8.1. The Rigid-Surface Solution
2.8.2. The Free-Surface Solution
2.9. Solutions of the Amplitudes of the Rigid- and Free-Surface Concentration Fluctuations and
2.9.1. The Rigid-Surface Solution
2.9.2. The Free-Surface Solution
2.10. Vortex Filter Functions on the Rigid and Free Surfaces and
2.10.1. Rigid-Surface Vortex (RV) Filter Function
2.10.2. Free-Surface Vortex (FV) Filter Function
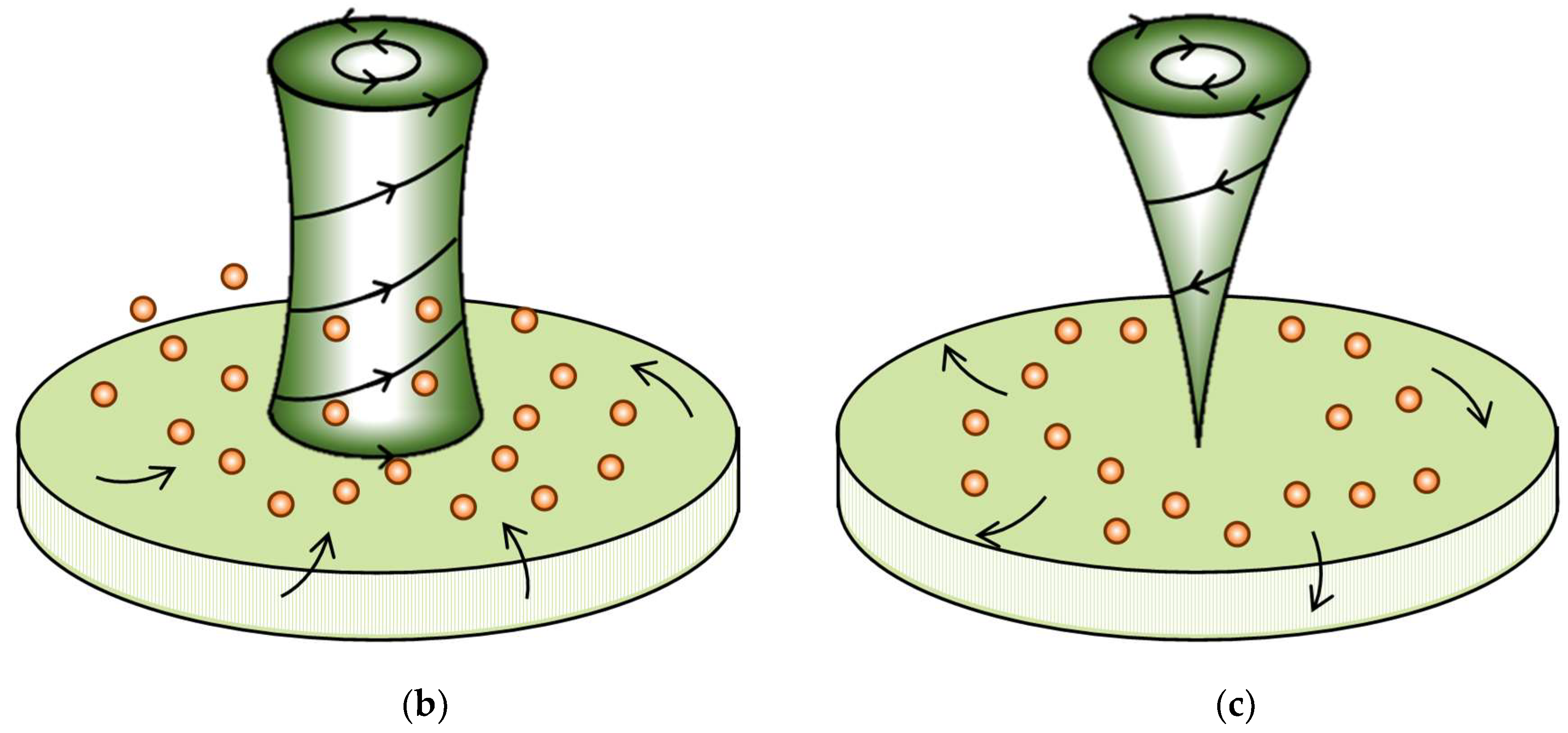
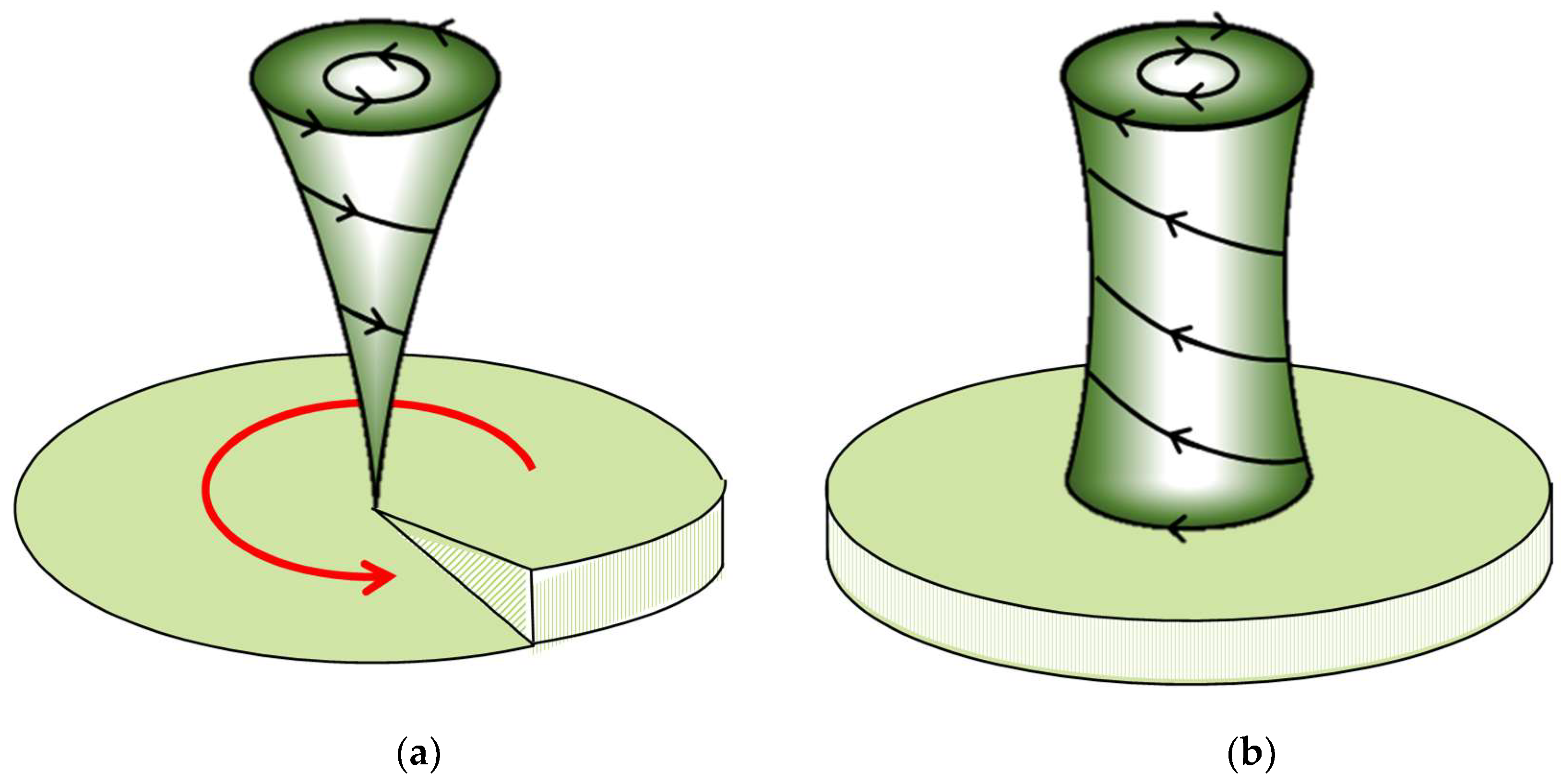
2.11. Precessional Conditions of the Microscopic RMHD Vortices
2.12. Critical Condition of the Precessional Rotation
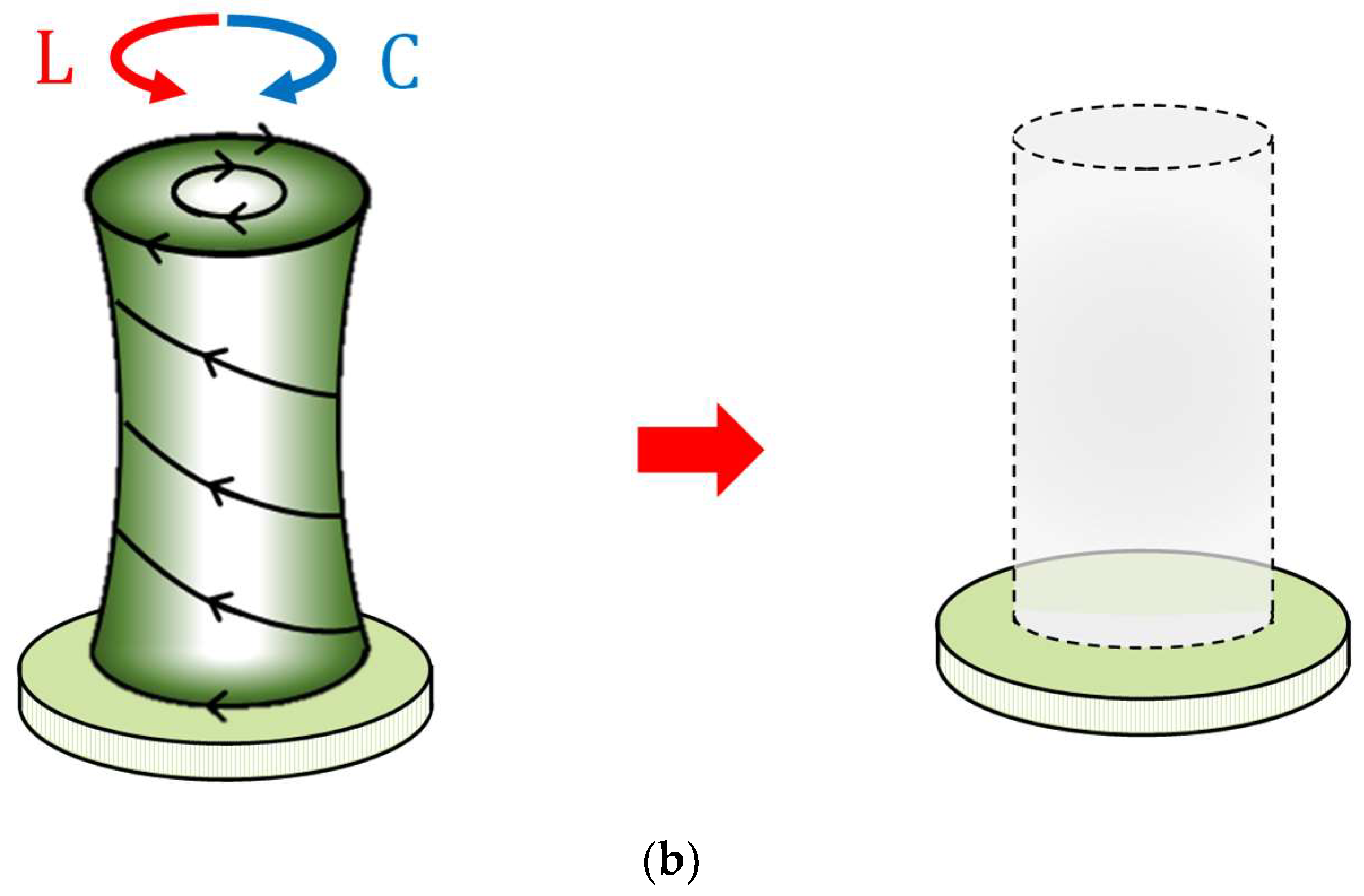
2.13. Precessional Motions of RMHD Vortices by the System Rotation
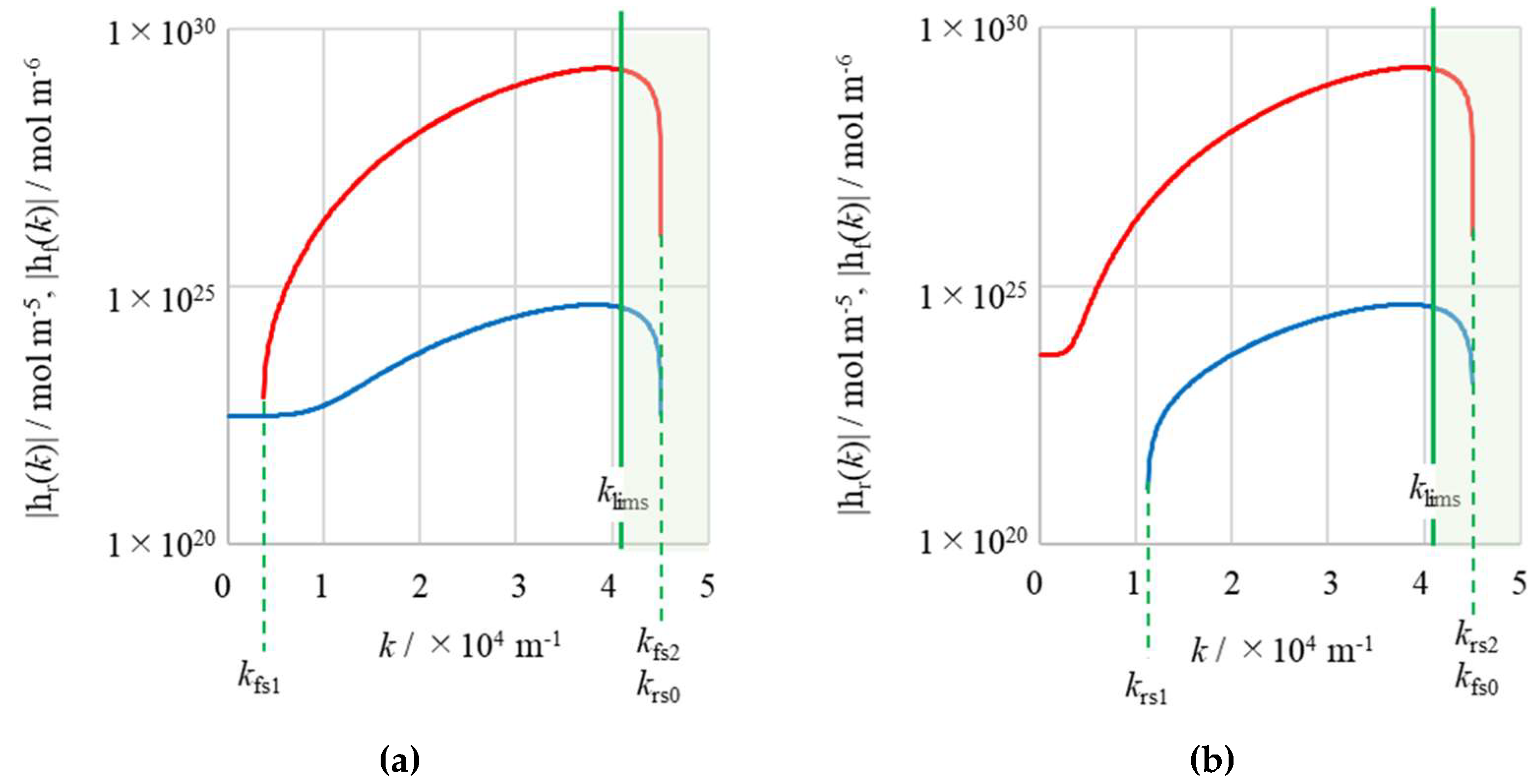
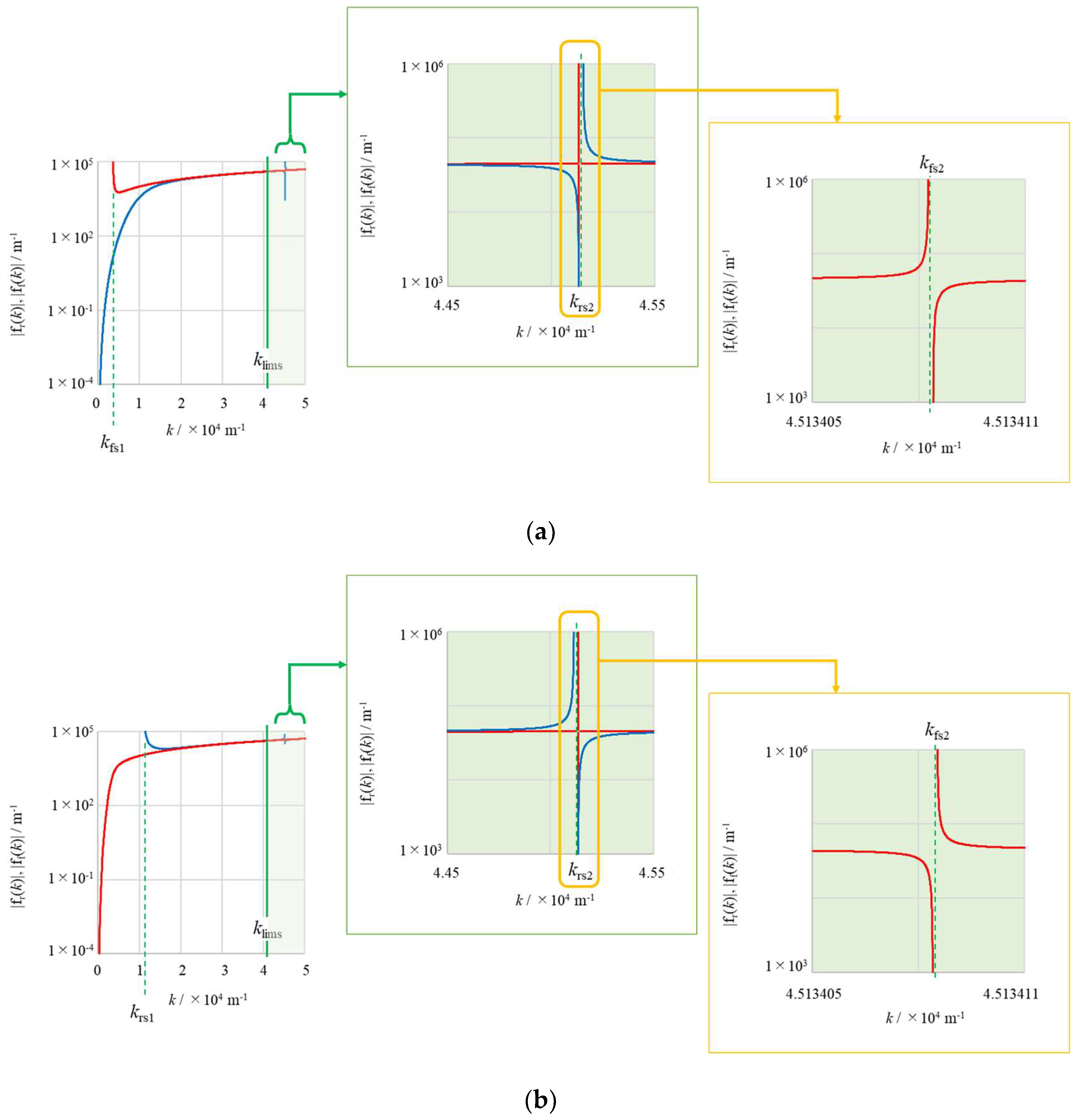
2.13.1. Singular Points of the Rigid-Surface Vortex (RV) for the Range
2.13.2. Singular Points of the Free-Surface Vortex (FV) for the Range
2.13.3. Singular Points of the Filter Functions for the Range
2.13.4. Occurrence of Homochirality
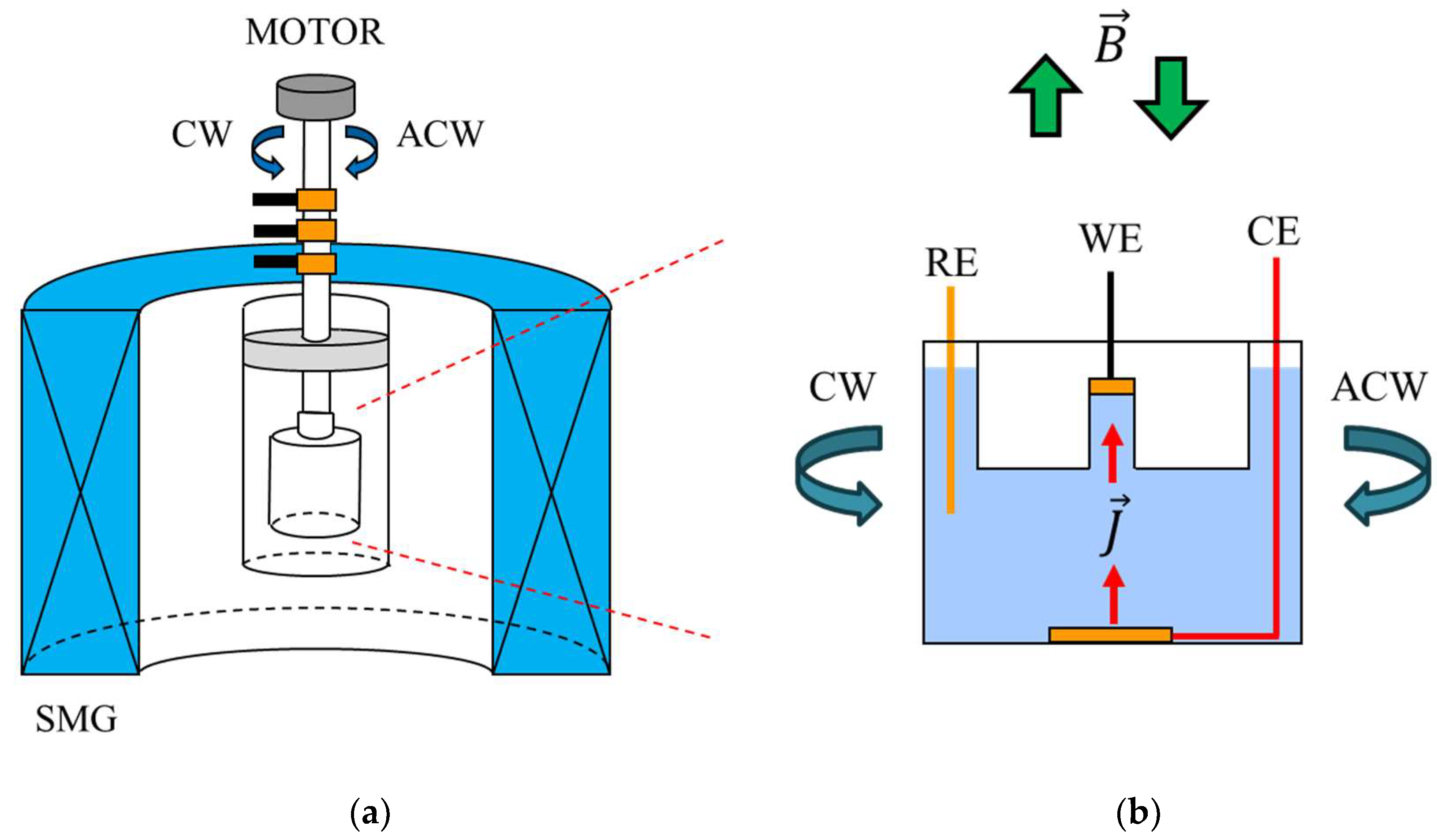
3. Experiment
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| the vector of position (m). | |
| x, y, z | coordinates of the system (m). |
| another expression of x, y, z (m). | |
| (m−1). | |
| (m−2). | |
| operator defined by (m−1). | |
| Levi Civita symbol (transposition of tensor). | |
| , | Kronecker’s deltas used in Equation (B10b). |
| wavenumber in the x-direction (m−1). | |
| wavenumber in the y-direction (m−1). | |
| wavenumber defined by (m−1). | |
| d | representative length (m). |
| t | time (s). |
| magnetic flux density (T). | |
| external magnetic flux density in the absence of the reaction (T). | |
| z-component of (T). | |
| fluctuation of by the reaction (T). | |
| z-components of (T). | |
| rotational velocity (angular velocity) (s−1). | |
| z-component of (s−1). | |
| rotational frequency (s−1, Hz). | |
| z-components of vorticity (s−1). | |
| current density vector (A m−2). | |
| z-component of (A m−2). | |
| without fluctuation (A m−2). | |
| fluctuation of (A m−2). | |
| fluid velocity (m s−1). | |
| u, v | x- and y-components of (m s−1). |
| z-components of (m s−1) | |
| P | pressure (Pa). |
| pressure fluctuation (Pa). | |
| magnetic permeability (4). | |
| kinematic viscosity (m2 s−1). | |
| kinematic viscosity in the 1st generation (m2 s−1). | |
| fluid density (kg m−3). | |
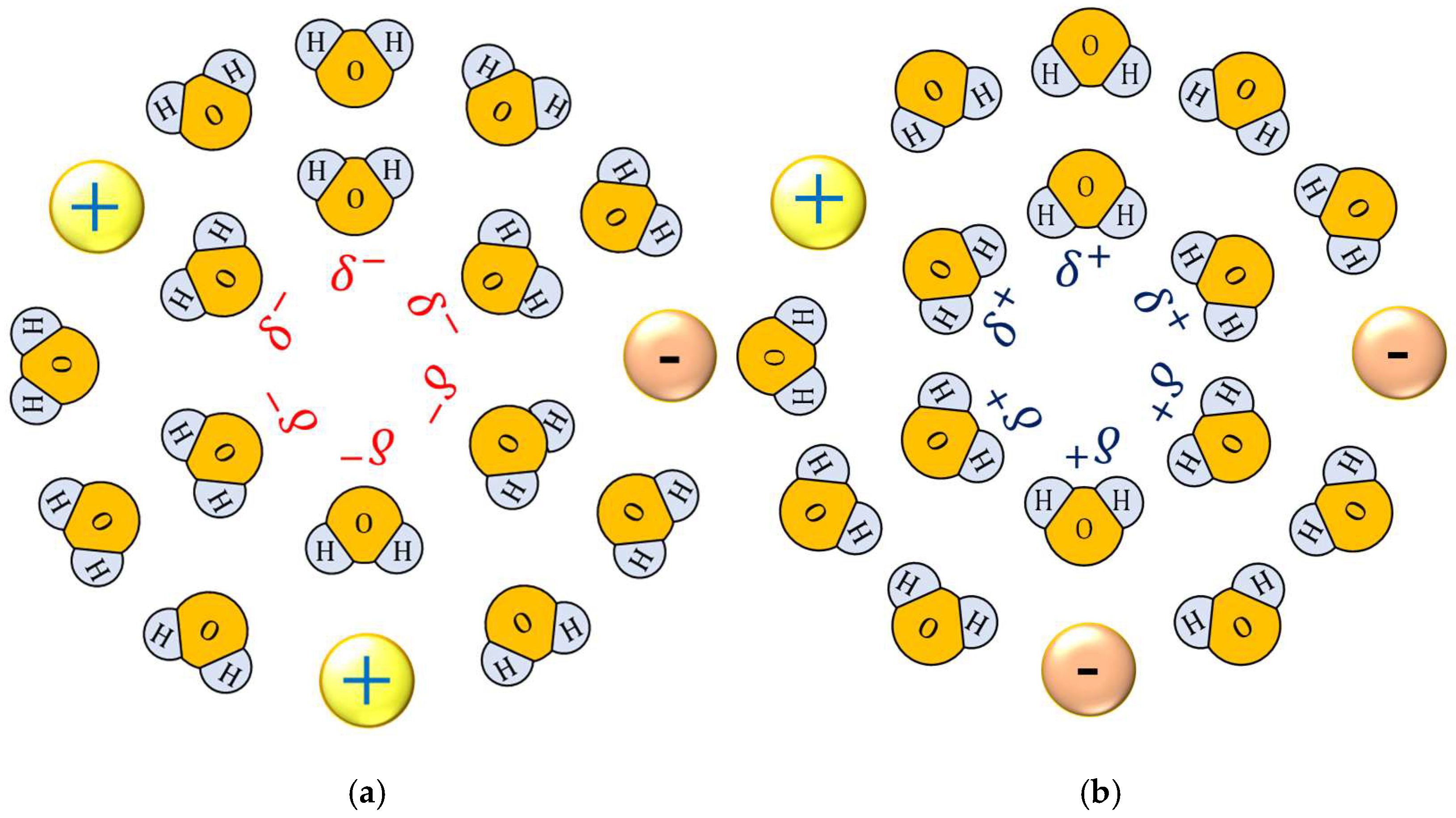
| electric field (V). | |
| electrical conductivity (S m−1). | |
| charge number including the sign of ionic species i. | |
| mobility of ionic species i (m2 V−1 s−1). | |
| F | Faraday constant (96,500 C mol−1). |
| molar concentration of ionic species i (mol m−3). | |
| molar concentration of the metallic ion (mol m−3). | |
| molar concentration of in the absence of fluctuation (mol m−3). | |
| bulk concentration of the metallic ion (mol m−3). | |
| surface concentration of the metallic ion (mol m−3). | |
| concentration difference (mol m−3). | |
| fluctuation of (mol m−3). | |
| average diffusion layer thickness (m). | |
| average concentration gradient of the metallic ion (mol m−4). | |
| diffusion coefficient of ionic species i (m2 s−1). | |
| diffusion coefficient of the metallic ion (m2 s−1). | |
| resistivity (magnetic viscosity) (m2 s−1) defined by Equation (A15). | |
| amplitude of the fluctuation (m s−1). | |
| amplitude of the fluctuation (s−1). | |
| amplitude of the fluctuation (T). | |
| amplitude of the fluctuation (A m−2). | |
| amplitude of the fluctuation (mol m−3). | |
| magneto-induction coefficient defined by Equation (C4b) (m−2). | |
| nondimensional form of defined by Equation (C6b). | |
| Coriolis force coefficient defined by Equation (C4c) (m−2). | |
| Tayler number defined by Equation (C6a). | |
| mass transfer coefficient defined by Equation (58) (mol s m−6). | |
| MHD coefficient defined by Equation (63b) (T m s kg−1). | |
| viscous stress tensor defined by Equation (8a) (Pa). | |
| viscous stress tensor defined by Equation (8b) (Pa). | |
| viscosity (Pa s). | |
| function of defined by Equation (D2). | |
| arbitrary quasi-static constants of , which are functions of t. | |
| , ,, | parameters of the solution of given by Equation (D5b). |
| solution of on the rigid surfaces (s−1). | |
| solution of on the free surfaces (s−1). | |
| vorticity coefficient of the rigid-surface vortex defined by Equation (22). | |
| vorticity coefficient of the free-surface vortex defined by Equation (26). | |
| general solution of (m s−1). | |
| function of defined by Equation (30). | |
| , , , | arbitrary coefficients of , which are functions of . |
| special solution of (m s−1). | |
| function of defined by Equation (37). | |
| , , , | arbitrary coefficients of , which are functions of . |
| solution of the rigid-surface amplitude of (m s−1). | |
| solution of the free-surface amplitude of (m s−1). | |
| , | arbitrary coefficients of , which are functions of . |
| general solution of (mol m−3). | |
| arbitrary constant of as a function of t. | |
| special solution of (mol m−3). | |
| solution of the amplitude of the rigid-surface (mol m−3). | |
| solution of the amplitude of the free-surface (mol m−3). | |
| rigid-surface vortex filter function defined by (m−1). | |
| denominator function of defined by Equation (73b) (m−5). | |
| numerator function of defined by Equation (73c) (m−6). | |
| free surface vortex filter functions defined by (m−1). | |
| denominator function of defined by Equation (75b) (m−6). | |
| numerator function of defined by Equation (75c) (m−7). | |
| parameter defined by in Equation (71b). | |
| in the 1st generation. | |
| parameter defined by in Equation (71c). | |
| Coriolis vorticity defined by Equation (76) (m−2 s−1). | |
| amplitude of (m−2 s−1). | |
| modified current density fluctuation expressed by Equation (84) (A m−1). | |
| amplitude of defined by Equations (80a) or (80b) (A m−1). | |
| Sign | function representing the sign of x. |
| power spectrum of the asymmetrical fluctuation in the 1st generation. | |
| autocorrelation distance of fluctuation (m). | |
| autocorrelation distance of the asymmetrical fluctuation (m). | |
| upper limit of the wavenumber of the asymmetrical fluctuations defined by Equation (90) (m−1). | |
| constant defined by Equation (94c) (T2 s2). | |
| singular point of the numerator function of the rigid-surface vortex (m−1). | |
| singular point of the numerator function of the free-surface vortex (m−1). | |
| limiting singular point defined by Equation (82a) (m−1). | |
| parameter expressed by Equation (96). | |
| maximum wavenumber defined by Equation (98b) (m−1). | |
| wavenumber defined by Equation (99b) (m−1). | |
| single singular point defined by Equation (100b) (m−1). | |
| the smaller one of two singular points expressed by Equation (101b) (m−1). | |
| the larger one of two singular points expressed by Equation (101c) (m−1). | |
| maximum wavenumber defined by Equation (104b) (m−1). | |
| the smaller one of two roots of the equation (m−1). | |
| the larger one of two roots of the equation (m−1). | |
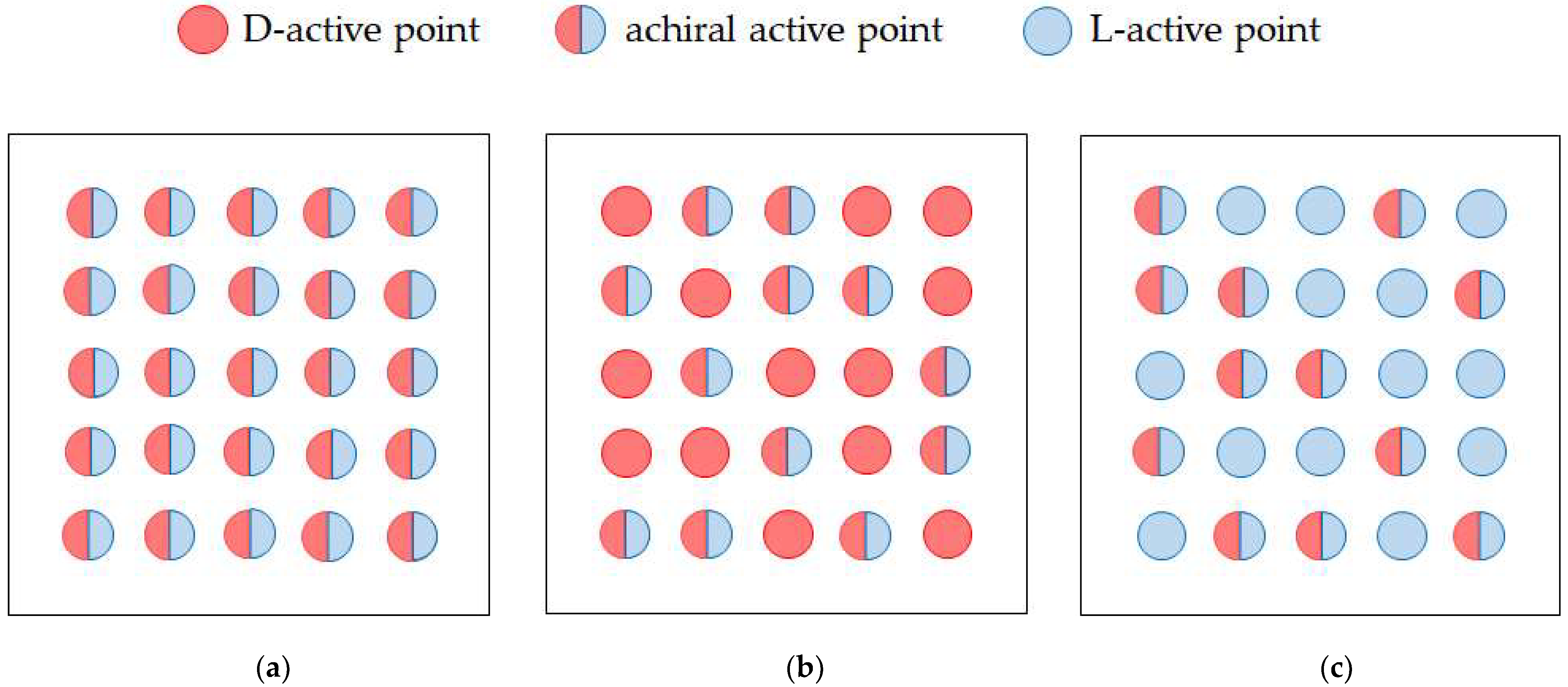
| ee | enantiomeric excess defined by Equation (106). |
| ipL | peak current of L-alanine (A m−2). |
| ipD | peak current of D-alanine (A m−2). |
| total current of the electrode covered with only achiral complex active points (A). | |
| total current active for either of enantiomeric reagents (A). | |
| total current inactive for the reagent, but active for the other one (A). | |
| evolution ratio of chiral screw dislocation. | |
| Lorentz force per unit mass defined by Equation (A4) (m s−2). | |
| i-component of the fluctuation of define by Equation (B2a) (m s−2). | |
| rotational force per unit mass defined by Equation (A7) (m s−2). | |
| i-component of the fluctuation of defined by Equation(B2b) (m s−2). | |
| fluctuation defined by Equation (B3b) (N m kg−1). |
Appendix A. Basic MHD Equations in a Rotating Electrolysis Cell Under a Static Magnetic Field
Appendix B. Non-Equilibrium Fluctuations Activated in Electrolysis
Appendix C. Derivation of the Amplitude Equations of the Fluctuations
Appendix D. General Solution of
Appendix E. Determination of the Evolution Ratio of Chiral Screw Dislocation by the Electrolytic Current of Enantiomeric Reagent
References
- Viedma, C. Chiral Symmetry Breaking During Crystallization: Complete Chiral Purity Induced by Nonlinear Autocatalysis and Recycling. Phys. Rev. Lett. 2005, 94, 065504. [Google Scholar] [CrossRef] [PubMed]
- Flores, J.J.; Bonner, W.A.; Massey, G.A. Asymmetric Photolysis of (RS)-Leucine with Circularly Polarized Ultraviolet Light. J. Am. Chem. Soc. 1977, 99, 3622–3625. [Google Scholar] [CrossRef] [PubMed]
- Rikken, G.L.J.A.; Raupach, E. Enantioselective Magnetochiral Photochemistry. Nature 2000, 405, 932–935. [Google Scholar] [CrossRef] [PubMed]
- Noorduim, W.L.; Bode, A.A.C.; van der Meijden, M.; Meekes, H.; van Etteger, A.F.; van Enckevort, W.J.P.; Christianen, P.C.M.; Kaptein, B.; Kellogg, R.M.; Rasing, T.; et al. Complete Chiral Symmetry Breaking of an Amino Acid Derivative Directed by Circularly Polarized Light. Nat. Chem. 2009, 1, 729–732. [Google Scholar] [CrossRef]
- Micali, M.; Engelkamp, H.; van Rhee, P.G.; Christianen, P.C.M.; Scolaro, L.M.; Maan, J.C. Selection of Supramolecular Chirality by Application of Rotational and Magnetic Forces. Nat. Chem. 2012, 4, 201–207. [Google Scholar] [CrossRef]
- Kondepudi, D.K.; Kaufman, R.J.; Singh, N. Chiral Symmetry Breaking in Sodium Chloride Crystallization. Science 1990, 250, 975–976. [Google Scholar] [CrossRef]
- Ribó, J.M.; Crusats, J.; Sagués, F.; Claret, J.; Rubires, R. Chiral Sign Induction by Vortices During the Formation of Mesophases in Stirred Solutions. Science 2001, 292, 2063–2066. [Google Scholar] [CrossRef]
- Tsujimoto, Y.; Ie, M.; Ando, Y.; Yamamoto, T.; Tsuda, A. Spectroscopic Visualization of Right- and Left-Handed Helical Alignments of DNA in Chiral Vortex Flows. Bull. Chem. Soc. Jpn. 2011, 84, 1031–1038. [Google Scholar] [CrossRef]
- Bolm, C.; Bienewald, F.; Seger, A. Asymmetric Autocatalysis with Amplification of Chirality. Angew. Chem. Int. Ed. Engl. 1996, 35, 1657–1659. [Google Scholar] [CrossRef]
- Uwaha, M. A Model for Complete Chiral Crystallization. J. Phys. Soc. Jpn. 2004, 73, 2601–2603. [Google Scholar] [CrossRef]
- Bargueño, P. Chirality and Gravitational Parity Violation. Chirality 2015, 27, 375–381. [Google Scholar] [CrossRef] [PubMed]
- Avalos, M.; Babiano, R.; Cintas, P.; Jiménes, J.L.; Palacios, J.C.; Barron, L.D. Absolute Asymmetric Synthesis under Physical Fields: Facts and Fictions. Chem. Rev. 1998, 98, 2391–2404. [Google Scholar] [CrossRef] [PubMed]
- Wächtershäuser, G. Before Enzymes and Templates: Theory of Surface Metabolism. Microbiol. Rev. 1988, 52, 452–484. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, M.; Nakamura, R.; Kasaya, T.; Kumagai, H.; Suzuki, K.; Takai, K. Spontaneous and Widespread Electricity Generation in Natural Deep-Sea Hydrothermal Fields. Angew. Chem. Int. Ed. 2017, 56, 5725–5728. [Google Scholar] [CrossRef]
- Burton, W.K.; Cabrera, N.; Frank, F.C. Role of Dislocations in Crystal Growth. Nature 1949, 163, 398–399. [Google Scholar] [CrossRef]
- Burton, W.K.; Cabrera, N.; Frank, F.C. The Growth of Crystals and the Equilibrium Structure of their Surfaces. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1951, 243, 299–358. [Google Scholar] [CrossRef]
- Yanson, Y.I.; Rost, M.J. Structural Accelerating Effect of Chloride on Copper Electrodeposition. Angew. Chem. Int. Ed. 2013, 52, 2454–2458. [Google Scholar] [CrossRef]
- Morimoto, R.; Miura, M.; Sugiyama, A.; Miura, M.; Oshikiri, Y.; Mogi, I.; Yamauchi, Y.; Takagi, S.; Aogaki, R. Theory of Chiral Electrodeposition by Chiral Micro-Nano-Vortices under a Vertical Magnetic Field -1: 2D Nucleation by Micro-Vortices. Magnetochemistry 2022, 8, 71. [Google Scholar] [CrossRef]
- Morimoto, R.; Miura, M.; Sugiyama, A.; Miura, M.; Oshikiri, Y.; Mogi, I.; Yamauchi, Y.; Aogaki, R. Theory of Chiral Electrodeposition by Micro-Nano-Vortexes under a Vertical Magnetic Field-2: Chiral Three-Dimensional (3D) Nucleation by Nano-Vortexes. Magnetochemistry 2024, 10, 25. [Google Scholar] [CrossRef]
- Rikken, G.L.J.A.; Fölling, J.; Wyder, P. Electrical Magnetochiral Anisotropy. Phys. Rev. Lett. 2001, 87, 236602. [Google Scholar] [CrossRef]
- Mogi, I.; Aogaki, R.; Takahashi, K. Chiral symmetry breaking in magnetoelectrochemical etching with chloride additives. Molecules 2018, 23, 19. [Google Scholar] [CrossRef]
- Takagi, S.; Asada, T.; Oshikiri, Y.; Miura, M.; Morimoto, R.; Sugiyama, A.; Mogi, I.; Aogaki, R. Nanobubble formation from ionic vacancies in an electrode reaction on a fringed electrode under a uniform vertical magnetic field—1. Formation process in a vertical magnetohydrodynamic (MHD) flow. J. Electroanal. Chem. 2022, 914, 116291. [Google Scholar] [CrossRef]
- Takagi, S.; Asada, T.; Oshikiri, Y.; Miura, M.; Morimoto, R.; Sugiyama, A.; Mogi, I.; Aogaki, R. Nanobubble formation from ionic vacancies in an electrode reaction on a fringed electrode under a uniform vertical magnetic field—2. Measurement of the angular velocity of a vertical magnetohydrodynamic (MHD) flow by the microbubbles originating from ionic vacancies. J. Electroanal. Chem. 2022, 916, 116375. [Google Scholar] [CrossRef]
- Aogaki, R. Theory of stable formation of ionic vacancy in a liquid solution. Electrochemistry 2008, 76, 458–465. [Google Scholar] [CrossRef]
- Aogaki, R.; Sugiyama, A.; Miura, M.; Oshikiri, Y.; Miura, M.; Morimoto, R.; Takagi, S.; Mogi, I.; Yamauchi, Y. Origin of nanobubbles electrochemically formed in a magnetic field: Ionic vacancy production in electrode reaction. Sci. Rep. 2016, 6, 28297. [Google Scholar] [CrossRef]
- Aogaki, R.; Motomura, K.; Sugiyama, A.; Morimoto, R.; Mogi, I.; Miura, M.; Asanuma, M.; Oshikiri, Y. Measurement of the lifetime of ionic vacancy by the cyclotron-MHD electrode. Magnetohydrodynamics 2012, 48, 289–297. [Google Scholar] [CrossRef]
- Sugiyama, A.; Morimoto, R.; Osaka, T.; Mogi, I.; Asanuma, M.; Miura, M.; Oshikiri, Y.; Yamauchi, Y.; Aogaki, R. Lifetime of ionic vacancy created in redox electrode reaction measured by cyclotron MHD electrode. Sci. Rep. 2016, 6, 19795. [Google Scholar] [CrossRef]
- Mogi, I.; Morimoto, R.; Aogaki, R.; Takahashi, K. Surface chirality in rotational magnetoelectrodeposition of copper films. Magnetochemistry 2019, 5, 53–60. [Google Scholar] [CrossRef]
- Mogi, I.; Morimoto, R.; Aogaki, R.; Watanabe, K. Surface chirality induced by rotational electrodeposition in magnetic fields. Sci. Rep. 2013, 3, 2574. [Google Scholar] [CrossRef]
- Mogi, I.; Morimoto, R.; Aogaki, R.; Takahashi, K. Effects of vertical MHD flows and cell rotation on surface chirality in magnetoelectrodeposition. IOP Conf. Ser. Mater. Sci. Eng. 2018, 424, 012024. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Oxford University Press: London, UK, 1961; pp. 87–148. [Google Scholar]
- Mogi, I.; Aogaki, R.; Takahashi, K. Fluctuation effects of magnetohydrodynamic micro-vortices on odd chirality in magnetoelectrolysis. Magnetochemistry 2020, 6, 43–51. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morimoto, R.; Mogi, I.; Miura, M.; Sugiyama, A.; Miura, M.; Oshikiri, Y.; Takahashi, K.; Yamauchi, Y.; Aogaki, R. The Origin of Homochirality by Rotational Magnetoelectrochemistry. Magnetochemistry 2025, 11, 51. https://doi.org/10.3390/magnetochemistry11060051
Morimoto R, Mogi I, Miura M, Sugiyama A, Miura M, Oshikiri Y, Takahashi K, Yamauchi Y, Aogaki R. The Origin of Homochirality by Rotational Magnetoelectrochemistry. Magnetochemistry. 2025; 11(6):51. https://doi.org/10.3390/magnetochemistry11060051
Chicago/Turabian StyleMorimoto, Ryoichi, Iwao Mogi, Miki Miura, Atsushi Sugiyama, Makoto Miura, Yoshinobu Oshikiri, Kohki Takahashi, Yusuke Yamauchi, and Ryoichi Aogaki. 2025. "The Origin of Homochirality by Rotational Magnetoelectrochemistry" Magnetochemistry 11, no. 6: 51. https://doi.org/10.3390/magnetochemistry11060051
APA StyleMorimoto, R., Mogi, I., Miura, M., Sugiyama, A., Miura, M., Oshikiri, Y., Takahashi, K., Yamauchi, Y., & Aogaki, R. (2025). The Origin of Homochirality by Rotational Magnetoelectrochemistry. Magnetochemistry, 11(6), 51. https://doi.org/10.3390/magnetochemistry11060051





