Experimental Study on Thermal Conductivity of Hybrid Magnetic Fluids Under External Magnetic Field
Abstract
1. Introduction
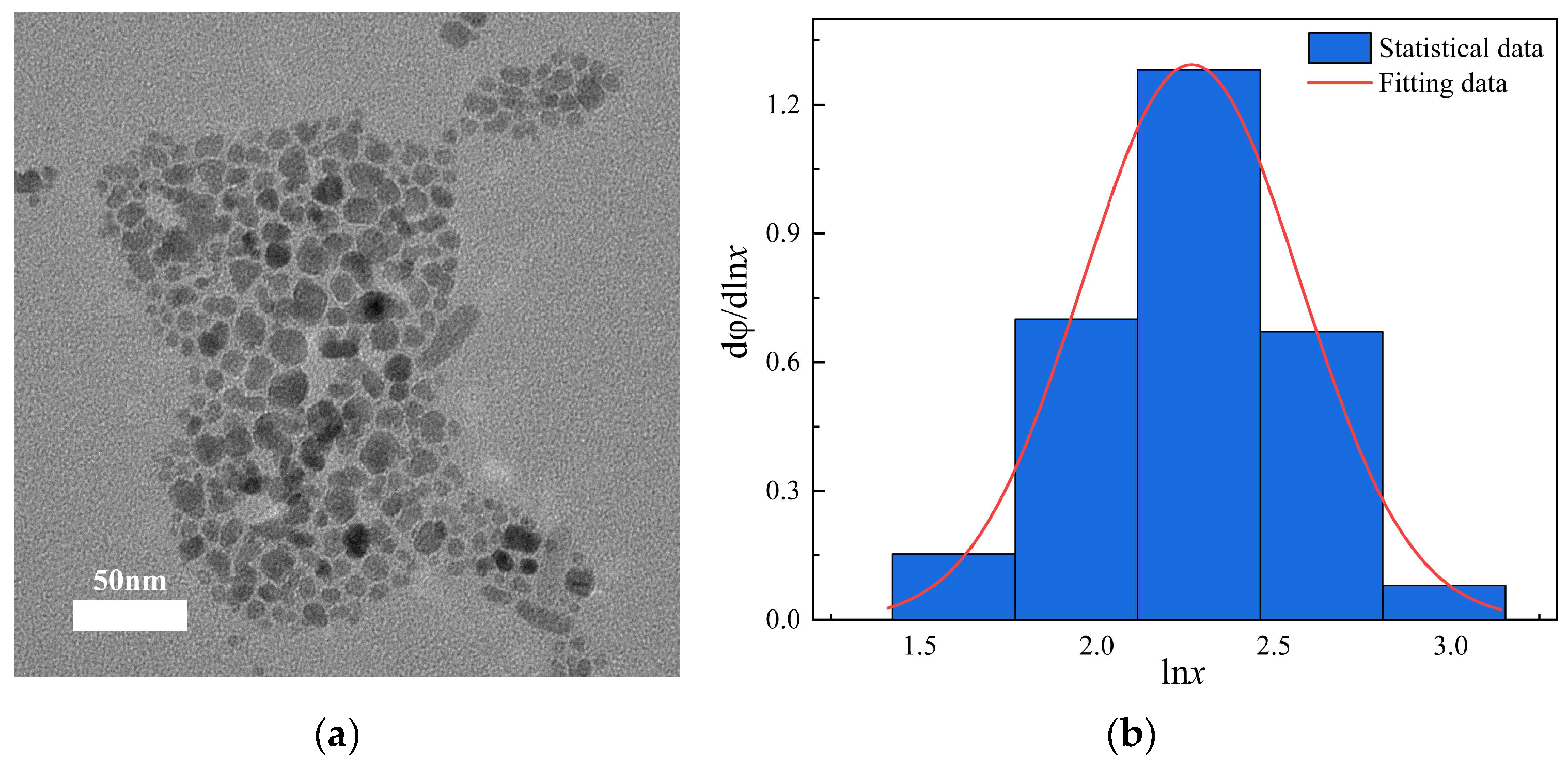
2. Preparation of Hybrid Kerosene-Based Magnetic Fluids
3. Thermal Conductivity Measurement Apparatus and Methodology
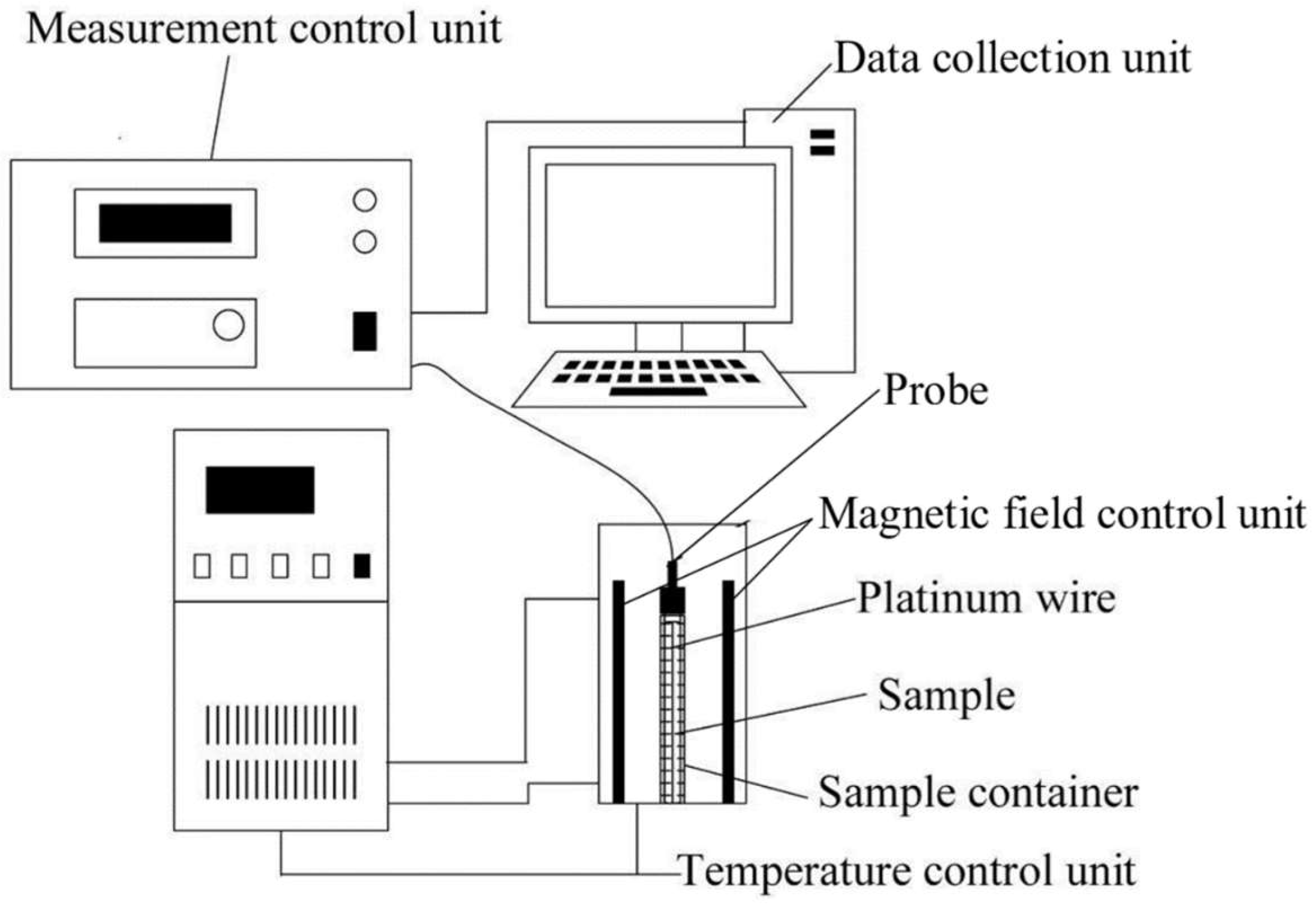
3.1. Thermal Conductivity Measurement System
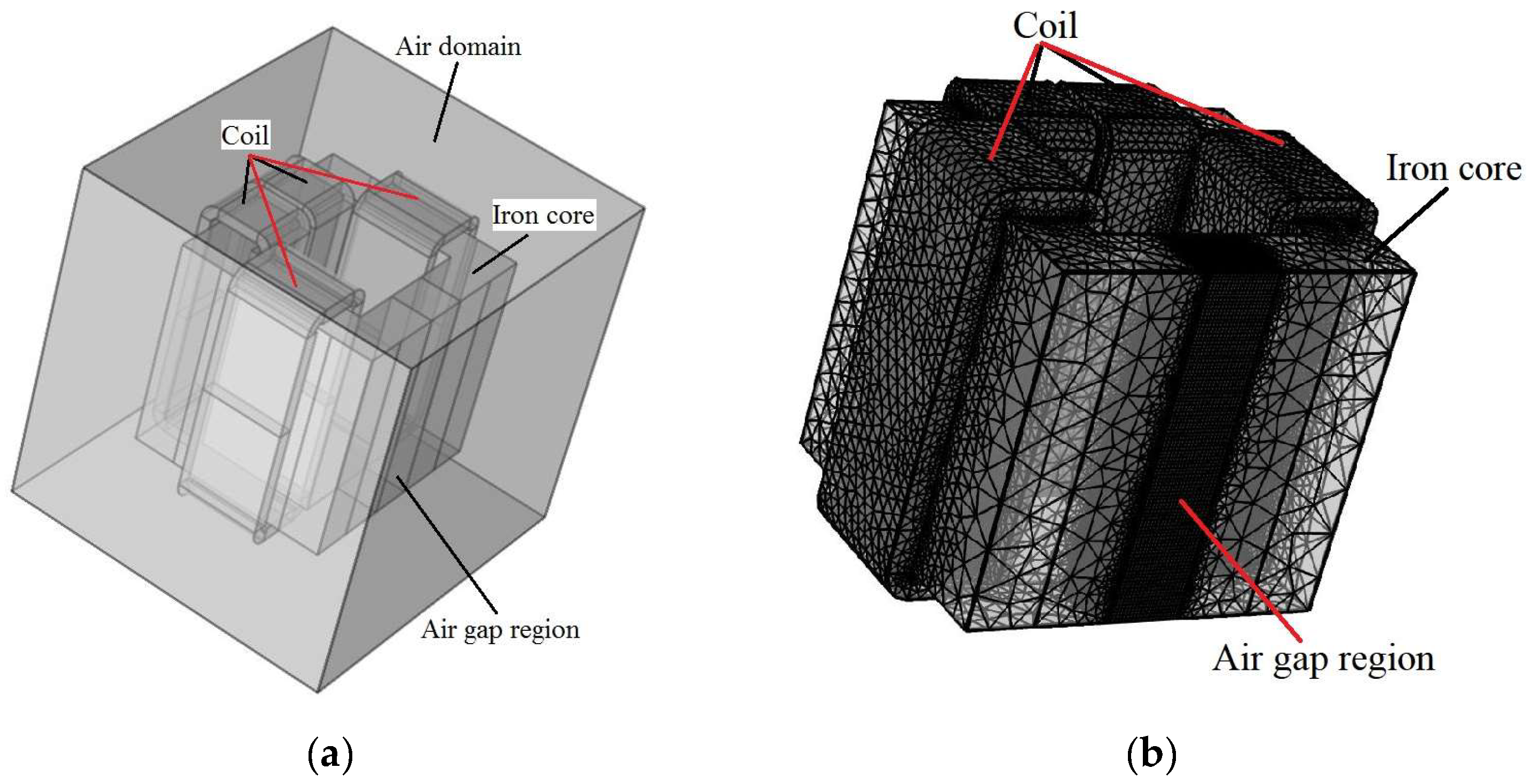
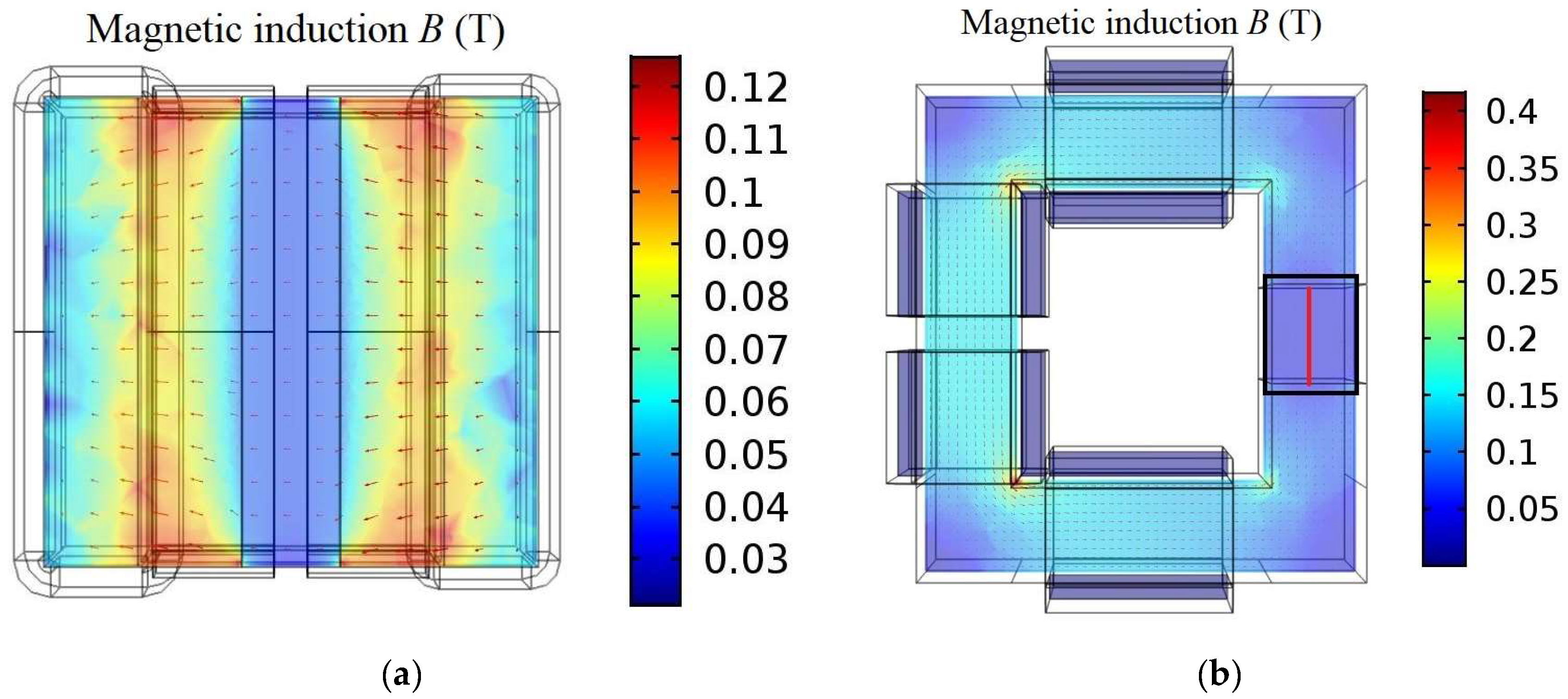
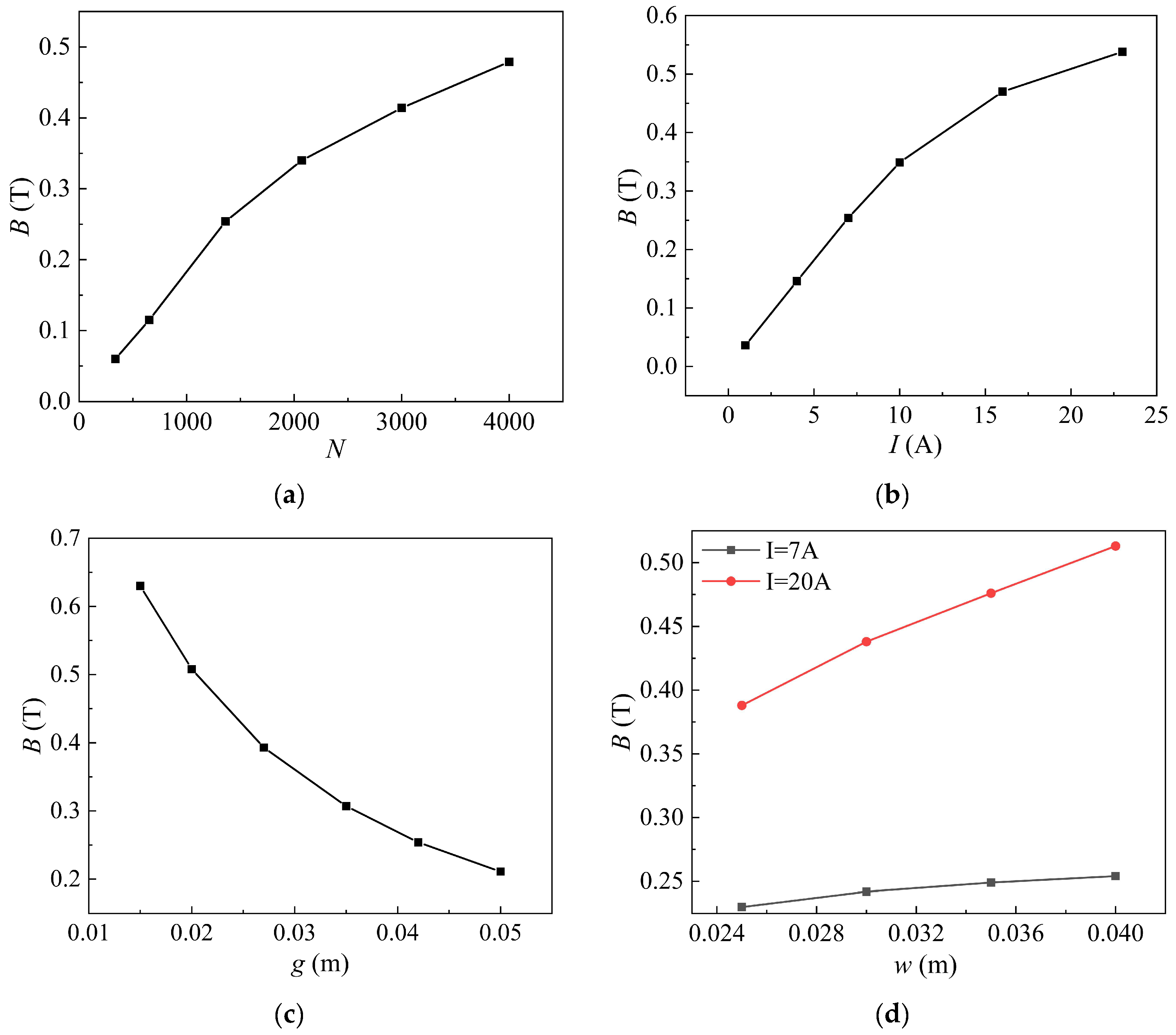
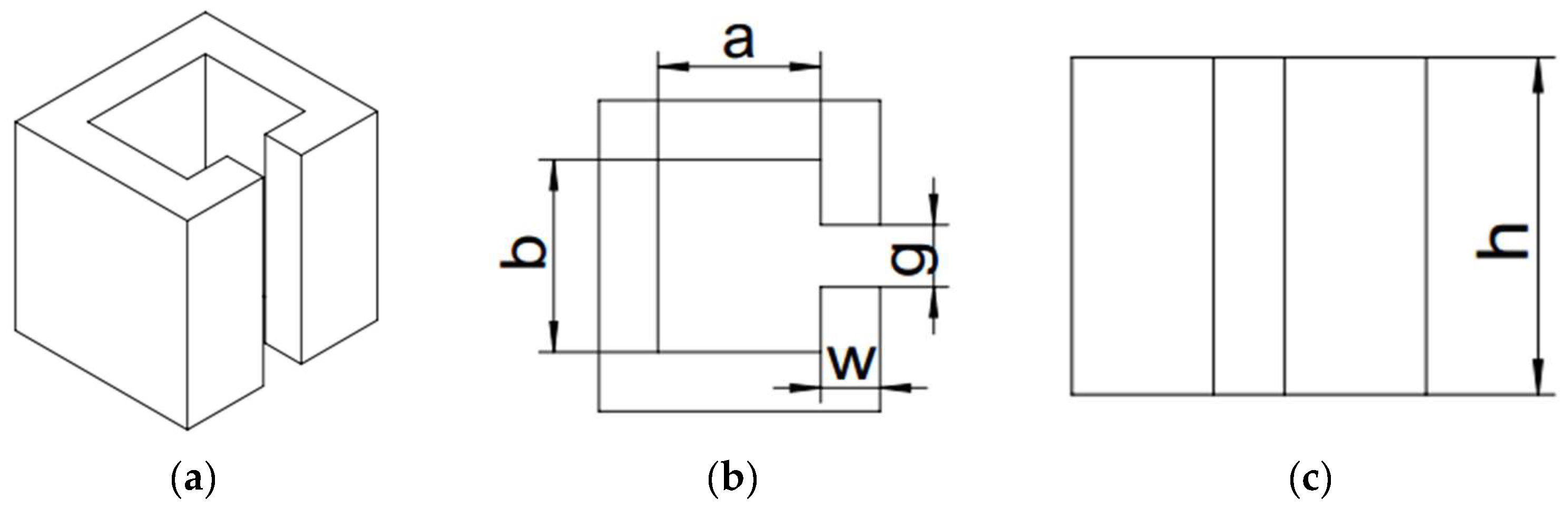
3.2. Electromagnetic Design and Simulation
3.3. Comparison of Electromagnet Performance: Theoretical, Simulated, and Experimental Result
3.3.1. Theoretical Magnetic Induction
3.3.2. Simulated Magnetic Induction
3.3.3. Comparison
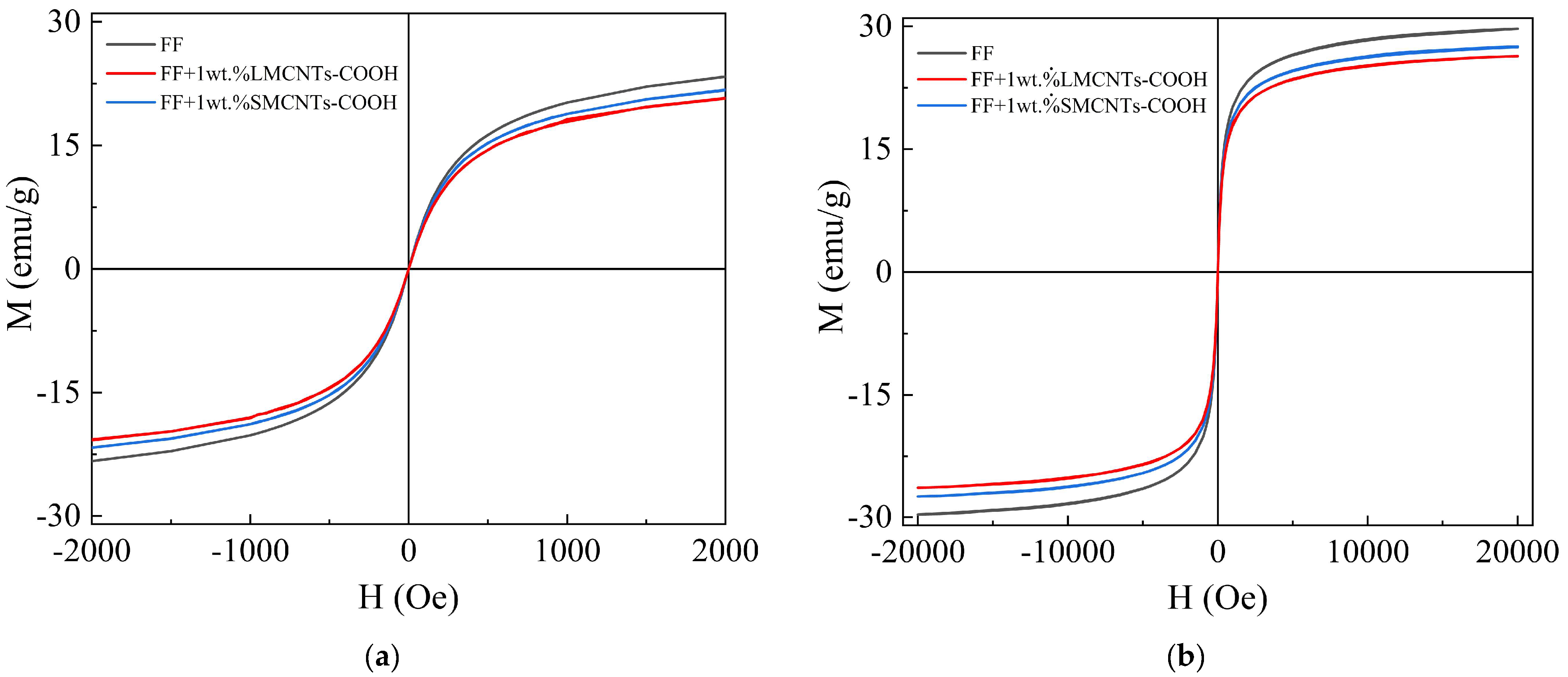
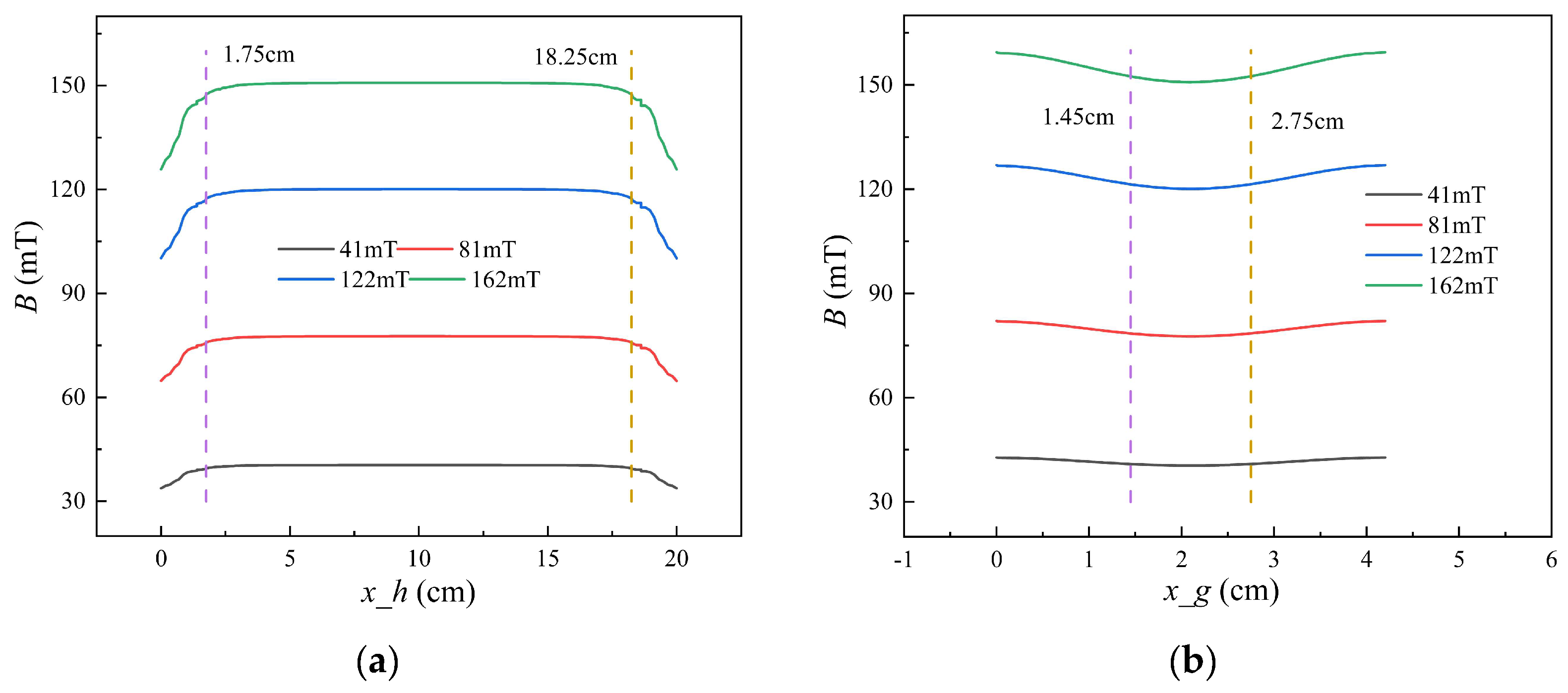
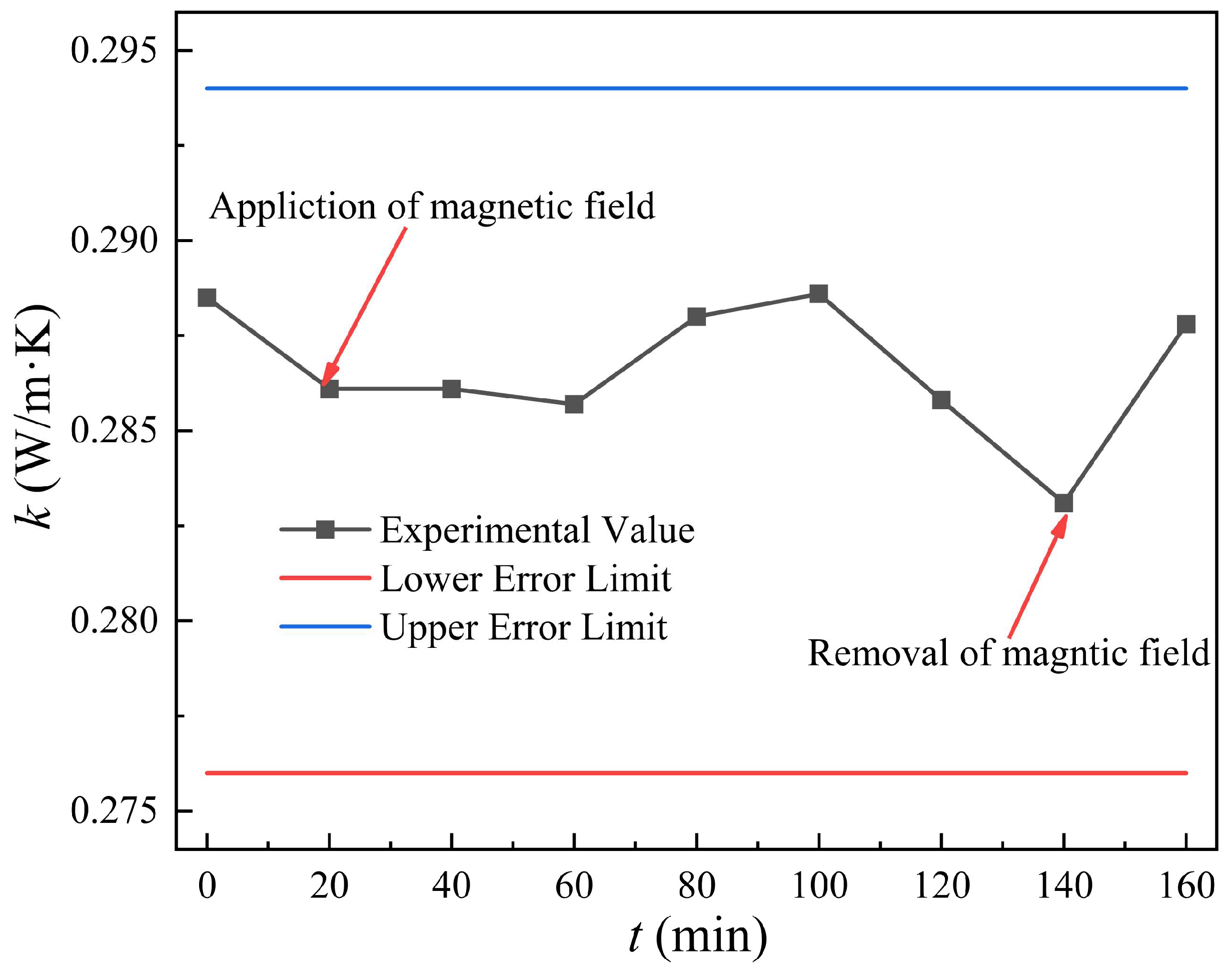
3.4. Verification of Magnetic Field Independence of the Measurement System
4. Thermal Conductivity Analysis
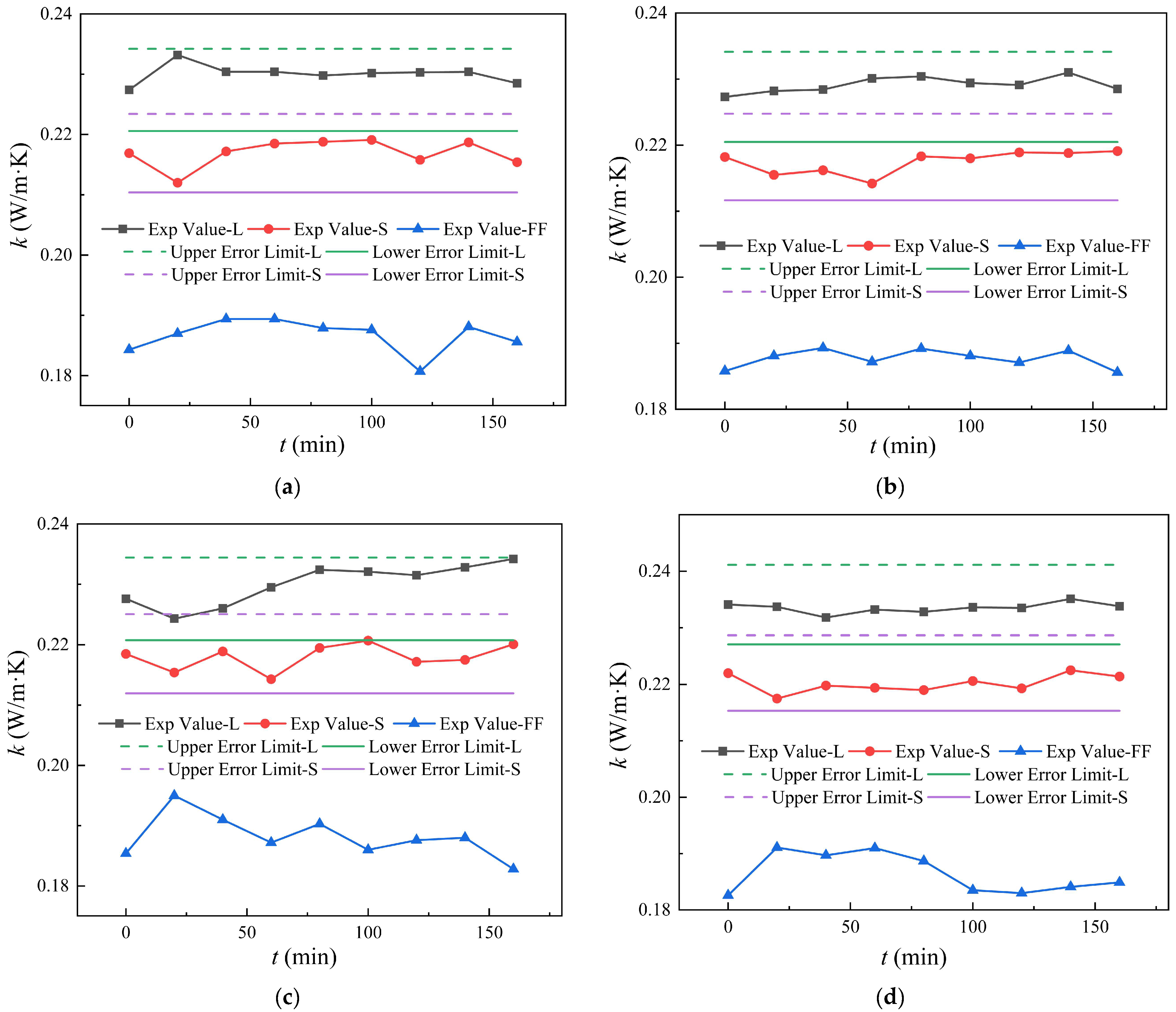
4.1. Carbon Nanotube Length Effects
4.2. Magnetic Field Effects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Decai, L.I. Theory and Application of Magnetic Fluid; Science Press: Beijing, China, 2003. (In Chinese) [Google Scholar]
- Decai, L.I. Theory and Application of Magnetic Fluid Sealing; Science Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Li, Q.; Xuan, Y.; Wang, J. Experimental investigation on transport properties of magnetic fluids. Therm. Fluid Sci. 2005, 30, 109–116. [Google Scholar]
- Fang, X.; Xuan, Y.; Li, Q. Anisotropic thermal conductivity of magnetic fluids. Prog. Nat. Sci. 2009, 19, 205–211. [Google Scholar]
- Gavili, A.; Zabihi, F.; Isfahani, T.D.; Sabbaghzadeh, J. The thermal conductivity of water base ferrofluids under magnetic field. Exp. Therm. Fluid Sci. 2012, 41, 94–98. [Google Scholar]
- Bunoiu, O.M.; Matu, G.; Marin, C.N.; Malaescu, I. Investigation of some thermal parameters of ferrofluids in the presence of a static magnetic field. J. Magn. Magn. Mater. 2020, 498, 166132. [Google Scholar]
- Vinod, S.; Philip, J. Impact of field ramp rate on magnetic field assisted thermal transport in ferrofluids. J. Mol. Liq. 2020, 298, 112047. [Google Scholar]
- Hong, H.; Wright, B.; Wensel, J.; Jin, S.; Ye, X.R.; Roy, W. Enhanced thermal conductivity by the magnetic field in heat transfer nanofluids containing carbon nanotube. Synth. Met. 2007, 157, 437–440. [Google Scholar]
- Theres Baby, T.; Sundara, R. Surfactant free magnetic nanofluids based on core-shell type nanoparticle decorated multiwalled carbon nanotubes. J. Appl. Phys. 2011, 110, 064325. [Google Scholar]
- Shahsavar, A.; Salimpour, M.R.; Saghafian, M.; Shafii, M.B. An experimental study on the effect of ultrasonication on thermal conductivity of ferrofluids loaded with carbon nanotubes. Thermochim. Acta 2015, 617, 102–110. [Google Scholar]
- Shahsavar, A.; Saghafian, M.; Salimpour, M.R.; Shafii, M.B. Effect of temperature and concentration on thermal conductivity and viscosity of ferrofluids loaded with carbon nanotubes. Heat. Mass. Transf. 2016, 52, 2293–2301. [Google Scholar]
- Yavari, M.; Mansourpour, Z.; Shariaty-Niassar, M. Controlled assembly and alignment of CNTs in ferrofluid, Application in tunable heat transfer. J. Magn. Magn. Mater. 2019, 479, 170–178. [Google Scholar]
- Liu, W.I.; Alsarraf, J.; Shahsavar, A.; Rostamzadeh, M.; Afrand, M.; Nguyen, T.K. Impact of oscillating magnetic field on the thermal-conductivity of water-Fe3O4 and water-Fe3O4/CNT ferro-fluids: Experimantal study. J. Magn. Magn. Mater. 2020, 479, 258–265. [Google Scholar] [CrossRef]
- Xing, M.; Jing, D.; Chen, H.; Zhang, H.; Wang, R. Ice thermal energy storage enhancement using aligned carbon nanotubes under external magnetic field. J. Energy Storage 2022, 56, 105931. [Google Scholar] [CrossRef]
- Afrand, M.; Toghraie, D.; Ruhani, B. Effect of magnetic field on thermal conductivity of water-based Fe3O4/CNT hybrid nanofluids. Phys. A Stat. Mech. Its Appl. 2023, 619, 128739. [Google Scholar]
- Su, Z.; Cheng, Y.; Liu, Z.; Zhou, J.; Li, D.; Li, Y. Experimental study on thermal conductivity of water-based magnetic fluid loaded with different nanoparticles. Nanomaterials 2023, 13, 2952. [Google Scholar] [CrossRef]
- Sidik NA, C.; Adamu, I.M.; Jamil, M.M.; Kefayati GH, R.; Mamat, R.; Najafi, G. Recent progress on hybrid nanofluids in heat transfer applications: A comprehensive review. Int. Commun. Heat. Mass. Transf. 2016, 78, 68–79. [Google Scholar] [CrossRef]
- Atashafrooz, M.; Sajjadi, H.; Delouei, A.A. Simulation of combined convective-radiative heat transfer of hybrid nanofluid flow inside an open trapezoidal enclosure considering the magnetic force impacts. J. Magn. Magn. Mater. 2023, 567, 170354. [Google Scholar] [CrossRef]
- Rashed, A.S.; Mahmoud, T.A.; Mabrouk, S.M. Enhanced flow and temperature profiles in ternary hybrid nanofluid with gyrotactic microorganisms: A study on magnetic field, Brownian motion, and thermophoresis phenomena. J. Appl. Comput. Mech. 2024, 10, 597–609. [Google Scholar]
- Li, Q.; Zhao, J.; Jin, L.; Li, D. Experimental study on thermal conductivity and magnetization behaviors of Kerosene-based ferrofluid loaded with multiwalled carbon nanotubes. ACS Omega 2020, 5, 13052–13063. [Google Scholar] [CrossRef]
- Allen, T. Particle Size Measurement; Chapman and Hall: London, UK, 1981. [Google Scholar]
- Li, J.; Gong, X.M.; Lin, Y.Q.; Liu, X.D.; Chen, L.L.; Li, J.M.; Mao, H.; Li, D.C. Investigation into loss in ferrofluid magnetization. Aip Adv. 2014, 4, 077123. [Google Scholar] [CrossRef]
- Zhang, G.S.; Lu, J. Electromagnet and Automatic Electromagnetic Components; China Machine Press: Beijing, China, 1982. (In Chinese) [Google Scholar]
- NDT personnel technical qualification examination committee of ordnance industry. In Handbook of Magnetic Characteristic Curves of Common Steel; China Machine Press: Beijing, China, 2003. (In Chinese)
- Jiarong, Z.; Tingyuan, Z. Handbook of Thermophysical Properties of Materials Commonly Used in Engineering; New Times Press: Beijing, China, 1987. (In Chinese) [Google Scholar]
- Qiu, L.; Zhu, N.; Feng, Y.; Michaelides, E.E.; Żyła, G.; Jing, D.; Zhang, X.; Norris, P.M.; Markides, C.N.; Mahian, O. A review of recent advances in thermophysical properties at the nanoscale: From solid state to colloids. Phys. Rep.-Rev. Sect. Phys. Lett. 2020, 843, 1–81. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O.K. Thermal conductivity of heterogeneous two-component systems. J. Ind. Eng. Chem. Fundam. 1962, 1, 27–40. [Google Scholar]
- Walvekar, R.; Faris, I.A.; Khalid, M. Thermal conductivity of carbon nanotube nanofluid—Experimental and theoretical study. Heat. Transf.—Asian Res. 2012, 41, 145–163. [Google Scholar] [CrossRef]
- Kúdelčík, J.; Hardoň, Š.; Bury, P.; Timko, M.; Kopčanský, P.; Mitróová, Z. Acoustic spectroscopy of sunctionalized carbon nanotubes in magnetic fluid. J. Magn. Magn. Mater. 2020, 502, 166538. [Google Scholar] [CrossRef]
- Hardoň, Š.; Kúdelčík, J.; Jahoda, E.; Kúdelčíková, M. The magneto-dielectric anisotropy effect in the oil-based ferrofluid. Int. J. Thermophys. 2019, 40, 24. [Google Scholar] [CrossRef]
- Takegoshi, E.; Imura, S.; Hirasawa, Y.; Takenaka, T. A Method of measuring the thermal conductivity of solid materials by transient hot wire method of comparison. Bull. JSME 1982, 25, 395–402. [Google Scholar] [CrossRef]
- Carson, J.K.; Lovatt, S.J.; Tanner, D.J.; Cleland, A.C. Thermal conductivity bounds for isotropic, porous materials. Int. J. Heat. Mass. Tran. 2005, 48, 2150–2158. [Google Scholar] [CrossRef]
- Vinod, S.; Philip, J. Role of field-induced nanostructures, zippering and size polydispersity on effective thermal transport in magnetic fluids without significant viscosity enhancement. J. Magn. Magn. Mater. 2017, 444, 29–42. [Google Scholar] [CrossRef]





| Name of the Samples | Weight Fraction of MCNTs-COOH (%) |
|---|---|
| FF + 0.1 wt.% LMCNTs-COOH | 0.1 |
| FF + 0.5 wt.% LMCNTs-COOH | 0.5 |
| FF + 1 wt.% LMCNTs-COOH | 1 |
| FF + 0.1 wt.% SMCNTs-COOH | 0.1 |
| FF + 0.5 wt.% SMCNTs-COOH | 0.5 |
| FF + 1 wt.% SMCNTs-COOH | 1 |
| W (m) | 0.03 | 0.035 | 0.04 |
|---|---|---|---|
| Γ at I = 7 A | 9.6% | 7.1% | 4.6% |
| Γ at I = 20 A | 9.9% | 7.4% | 4.9% |
| I1 (A) | I2 (A) | BEmid (mT) | BTave (mT) | BSmid (mT) | ξT_E (%) | ξS_E (%) | Γ (%) |
|---|---|---|---|---|---|---|---|
| 1.85 | 0.99 | 41 | 41.67 | 40.45 | 1.64 | −1.35 | 4.53 |
| 3.55 | 1.90 | 81 | 79.99 | 77.62 | −1.25 | −4.17 | 4.53 |
| 5.49 | 2.94 | 122 | 123.61 | 120.07 | 1.32 | −1.58 | 4.53 |
| 6.90 | 3.69 | 162 | 155.39 | 150.79 | −4.08 | −6.92 | 4.53 |
| BEmid (mT) | 41 (mT) | 81 (mT) | 122 (mT) | 162 (mT) |
|---|---|---|---|---|
| Δk/k(%) | 1.46 | 3.09 | 5.81 | 3.69 |
| Δk║/k(%) | 17.96 | 21.05 | 26.21 | 22.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, L.; Yang, J.; Li, Q.; Tian, X.; Li, D. Experimental Study on Thermal Conductivity of Hybrid Magnetic Fluids Under External Magnetic Field. Magnetochemistry 2025, 11, 30. https://doi.org/10.3390/magnetochemistry11040030
Jin L, Yang J, Li Q, Tian X, Li D. Experimental Study on Thermal Conductivity of Hybrid Magnetic Fluids Under External Magnetic Field. Magnetochemistry. 2025; 11(4):30. https://doi.org/10.3390/magnetochemistry11040030
Chicago/Turabian StyleJin, Licong, Jixian Yang, Qian Li, Xin Tian, and Decai Li. 2025. "Experimental Study on Thermal Conductivity of Hybrid Magnetic Fluids Under External Magnetic Field" Magnetochemistry 11, no. 4: 30. https://doi.org/10.3390/magnetochemistry11040030
APA StyleJin, L., Yang, J., Li, Q., Tian, X., & Li, D. (2025). Experimental Study on Thermal Conductivity of Hybrid Magnetic Fluids Under External Magnetic Field. Magnetochemistry, 11(4), 30. https://doi.org/10.3390/magnetochemistry11040030






