Next Article in Journal / Special Issue
An Organic–Inorganic Hybrid Semiconducting Quantum Spin Liquid Candidate: (BEDT-TTF)3[Cu2(μ-C2O4)3·CH3CH2OH·1.2H2O]
Previous Article in Journal / Special Issue
Positive and Negative Exchange Bias in N-, P- and Q-Type Ferri-Magnets of Niccolite Metal Formates [CH3NH2CH3]n[CrIII1−xFeIIIxFeII(HCO2)6]n
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 11
Issue 2
10.3390/magnetochemistry11020011
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Magnetic Anisotropy and Slow Magnetic Relaxation in Two Mononuclear Octahedral Cobalt(II) Complexes

by
Hui-Hui Cui
,
Dou-Zun Wang
,
Shixiang Li
,
Leixin Wang
,
Xinrui Yu
,
Xiancong Liu
,
Jin Wang
*,
Miao Wang
* and
Yanfeng Tang
*
School of Chemistry and Chemical Engineering, Nantong University, Nantong 226019, China
*
Authors to whom correspondence should be addressed.
Magnetochemistry 2025, 11(2), 11; https://doi.org/10.3390/magnetochemistry11020011
Submission received: 6 January 2025 / Revised: 29 January 2025 / Accepted: 6 February 2025 / Published: 11 February 2025
(This article belongs to the Special Issue Molecular Magnetism: A Themed Issue in Honor of Professor Dai-Zheng Liao on the Occasion of His 85th Birthday)
Browse Figures
Versions Notes

Abstract

:
Two mononuclear octahedral Co(II) complexes, [Co(L)X2] (L = 1-(prop-2-en-1-yl)-1H-imidazole, X = NCS− (1) and NCSe− (2)), have been synthesized and characterized. The central Co(II) ions in two complexes adopt an octahedral geometry, coordinated by four N atoms from the ligand and two N atoms from the anion. Direct-current magnetic data revealed large easy-plane magnetic anisotropy in both 1 and 2. Dynamic magnetic measurements demonstrated that 1 and 2 display field-induced slow magnetic relaxation. For 1 and 2, the Raman mechanism is found to the dominant process in the whole temperature range. Compared to 1, the magnetic relaxation of 2 is faster, likely due to the presence of the hydrogen bonding system in 2.

1. Introduction

Single-molecule magnets (SMMs) are a fascinating class of materials which can retain magnetization after removing the external magnetic field due to the existence of an energy barrier. SMMs derive their magnetic properties from individual metal ions. This unique characteristic makes them particularly interesting for applications in high-density data storage [1], quantum computing [2] and molecular electronics [3]. Single-ion magnets (SIMs) are a unique subclass of SMMs [4,5]. The simplicity of SIMs, which have only one metal center, facilitates the study of their magneto-structural relationships. Additionally, their design flexibility allows for precise optimization of magnetic properties by adjusting ligands and coordination environments. The molecular magnetism in SIMs originates from the energy barrier (U) that prevents the reversal of magnetization between the ‘spin up’ (MS = +S) and ‘spin down’ (MS = −S) states. This barrier depends on the ground spin state (S) and magnetic anisotropy (D) with U = |D|S2 for integer S and U = |D|(S2 − 1/4) for non-integer S [1].
Since Ishikawa et al. reported the first SIM based on the lanthanide ion [6], numerous mononuclear compounds containing lanthanide ions have been documented. Additionally, several SIMs including 3d-transition metals such as Mn(III) [7], Fe(II) [8], Co(II) [9,10,11,12,13,14] and Ni(I) [15] have been found to exhibit slow magnetic relaxation. Experimental and theoretical studies suggest that Co(II) ions with high spin are excellent candidates for constructing SIMs. This system can exhibit significant magnetic anisotropy with a flexible zero-field splitting (ZFS) parameter by modulating the polyhedron geometry [16,17,18,19].
For hexa-coordinate high spin Co(II) complexes with SIM properties, both negative and positive magnetic anisotropies can be observed [20,21,22,23,24,25,26]. Of these, Co(II) complexes with trigonal prismatic geometry usually show negative axial magnetic anisotropy. By employing a macrocyclic ligand, Novikov et al. reported easy-axis magnetic anisotropy for a cobalt(II) cage [22]. In contrast, most Co(II) complexes with distorted octahedral geometry typically exhibit high easy-plane magnetic anisotropy due to the unquenched orbital contribution of the t2g level and low-lying excited states [16]. For example, the first octahedral Co(II)-SIM, the cis-[Co(dmphen)2(NCS)2] complex (dmphen = 2,9-dimethyl-1,10-phenanthroline) reported by Vallejo et al., exhibits positive magnetic anisotropy with D = +98 cm−1, which results in field-induced slow magnetic relaxation [20]. Indeed, the mechanism of slow relaxation in positive D systems remains incompletely understood, despite attempts to explain it [21].
The above results clearly indicate that magnetic anisotropy can be modulated by changing the coordination environment of the Co(II) complexes. For most reported hexa-coordinate Co(II)-SIMs, bidentate or multidentate ligands are utilized to introduce distortions due to the chelate effect. Conversely, certain monodentate ligands containing N atoms can provide a weak ligand field, resulting in significant magnetic anisotropy for Co(II)-SIMs [26]. To explore this further, we synthesized two hexa-coordinate Co(II) complexes in this study using a monodentate nitrogen-containing ligand, 1-(prop-2-en-1-yl)-1H-imidazole. Both complexes exhibit distorted octahedral geometry. For 1, no significant intermolecular interactions are observed, while for 2, weak C–H∙∙∙Se hydrogen bonding interactions link the molecules, forming a supermolecular chain. Magnetic measurements revealed significant easy-plane magnetic anisotropy, with D values of +70.4(7) cm−1 for 1 and +64.0(2) cm−1 for 2, respectively. Additionally, both complexes display field-induced SIM behavior, with the Raman mechanism identified as the dominant process in both cases.

2. Materials and Methods

2.1. Materials

All chemicals were purchased from commercial sources (J&K Scientific, Beijing, China) and used as received without additional purification. Powder X-ray diffraction (PXRD) data for the polycrystalline samples were recorded at room temperature on a Bruker D8 ADVANCE diffractometer (Bruker, Berlin, Germany) in a 2θ range of 5.0–50.0°. The PXRD patterns verified the purity of the samples used in the magnetic measurements, consistent with the simulated data derived from single-crystal X-ray diffraction, as presented in Figures S1 and S2 of the Supplementary Materials. Elemental analyses were carried out on an Elementar Vario ELIII elemental analyzer.

2.2. Synthesis of [Co(L)(NCS)2] (1)

CoCl2 (0.065 g, 0.5 mmol) and KSCN (0.097 g, 1 mmol) were dissolved in 10 mL of ethanol and stirred for 30 min. Then, another 5 mL of dichloromethane solution containing L (0.18 g, 1 mmol) was added. The solution was stirred for 1 h and filtered. The diffusion of diethyl ether into the above solution over one week gave red crystals of 1 at 60 %. Elemental analysis (%) calcd. for C26H32CoN10S2: C, 51.39; H, 5.31; N, 23.05. Found: C, 51.37; H, 5.33; N, 23.06.

2.3. Synthesis of [Co(L)(NCSe)2] (2)

Red crystals of complex 2 were synthesized using a procedure similar to that of complex 1, except that an equivalent amount of KSeCN was used in place of KSCN. Yield: 63%. Elemental analysis (%) calcd. for C26H32CoN10Se2: C, 44.52; H, 4.60; N, 19.97. Found: C, 44.51; H, 4.63; N, 19.94.

2.4. X-Ray Single-Crystal Structure Determination

Single-crystal X-ray diffraction data for 1 and 2 were obtained at 296 K using a Bruker APEX II diffractometer (Bruker, Germany) with a CCD area detector and Mo Kα radiation (λ = 0.71073 Å) [27]. The APEXII program was utilized to determine unit cell parameters and collect the data. Integration of the data was performed using the SAINT program [28], applying corrections for Lorentz factor and polarization. Absorption corrections were processed with SADABS [29]. The structures were solved via the direct method, and refinements were conducted with full-matrix least-squares on F2 using the SHELXTL software package [30]. Non-hydrogen atoms were refined anistropically. The hydrogen atoms were positioned based on calculations and refined isotropically, with their vibration parameters linked to their associated non-hydrogen atoms.

2.5. Magnetic Measurements

Magnetic susceptibility measurements for complexes 1 and 2 were carried out using a Quantum Design SQUID VSM magnetometer (Quantum Design, San Diego, CA, USA) on finely ground powders obtained from single crystals. Direct-current (dc) susceptibility data were recorded over a temperature range of 2–300 K under dc fields up to 70 kOe. Alternating current (ac) susceptibility measurements were performed under different external fields with frequencies ranging from 1 to 1000 Hz. The magnetic susceptibility data were corrected for the diamagnetic contributions of the sample holder and the samples themselves by using Pascal’s constants [31].

3. Results and Discussion

3.1. Structural Description

The molecular structures of complexes 1 and 2 were determined through single-crystal X-ray diffraction analysis. The crystallographic and structure refinement data are listed in Table 1. The selected bond lengths and angles are presented in Table 2.
Both compounds are crystalized in the triclinic system with the P-1 space group. The structures of both complexes are highly similar. As shown in Figure 1, the asymmetric unit of complexes 1 and 2 each contain one crystallographic independent Co2+ ion, four L ligands and two pseudohalide coligands. The cobalt center in both complexes adopts a hexa-coordinate geometry featuring a [CoN6] coordination mode. The average Co–N bond length is about 2.16 Å for complex 1 and 2.15 Å for complex 2. The Co–NSCN bond length in 1 (~2.16 Å) is slightly longer than the Co–NSeCN bond length in 2 (~2.14 Å). Both the average Co-N bond length and the Co–NX (X = SCN or SeCN) bond lengths in 1 and 2 are slightly longer than those reported for other mononuclear octahedral Co(II) complexes with imidazole ligands (Table S1). In 1 and 2, the angles formed by two diagonal atoms and the central cobalt ion are equal to 180°, indicating that the geometry of both complexes closely approaches an ideal octahedral polyhedron. In both 1 and 2, the CoN6 unit is slightly compressed along the N4–Co1–N41 bond, which will be referred to as the Z-axis. Additionally, a geometric analysis was conducted using the SHAPE program to evaluate deviations from ideal symmetry [32,33]. The deviation values from a perfect octahedron for most octahedral Co(II) complexes with imidazole ligands, as summarized in Table S1, are all relatively small. For complexes 1 and 2, the values are 0.053 and 0.050 (Table S2), respectively, indicating a slight distortion from the ideal geometry.
It is well established that intermolecular interactions have a substantial impact on the magnetic behavior of mononuclear complexes. A detailed analysis of the crystal packing in 1 and 2 shows a considerable difference between them. As illustrated in Figures S3 and S4, no significant intermolecular interactions are observed in 1, while in 2, the molecules form supermolecular chains along the b-axis through weak C–H∙∙∙Se hydrogen bonding interactions. The shortest distances between neighboring Co(II) ions in complexes 1 and 2 are 8.875 Å and 8.917 Å, respectively (Figures S5 and S6).
The IR spectra confirm the proposed structures of the complexes (Figure S7). The IR spectra revealed a strong absorption band at 1520 cm⁻1 in both 1 and 2, which were assigned to the ν (C=N) of the imidazole ring [34]. The vibration of νC≡N was observed around 2085 cm⁻1 in both complexes, confirming the presence of the pseudohalide ion [35].

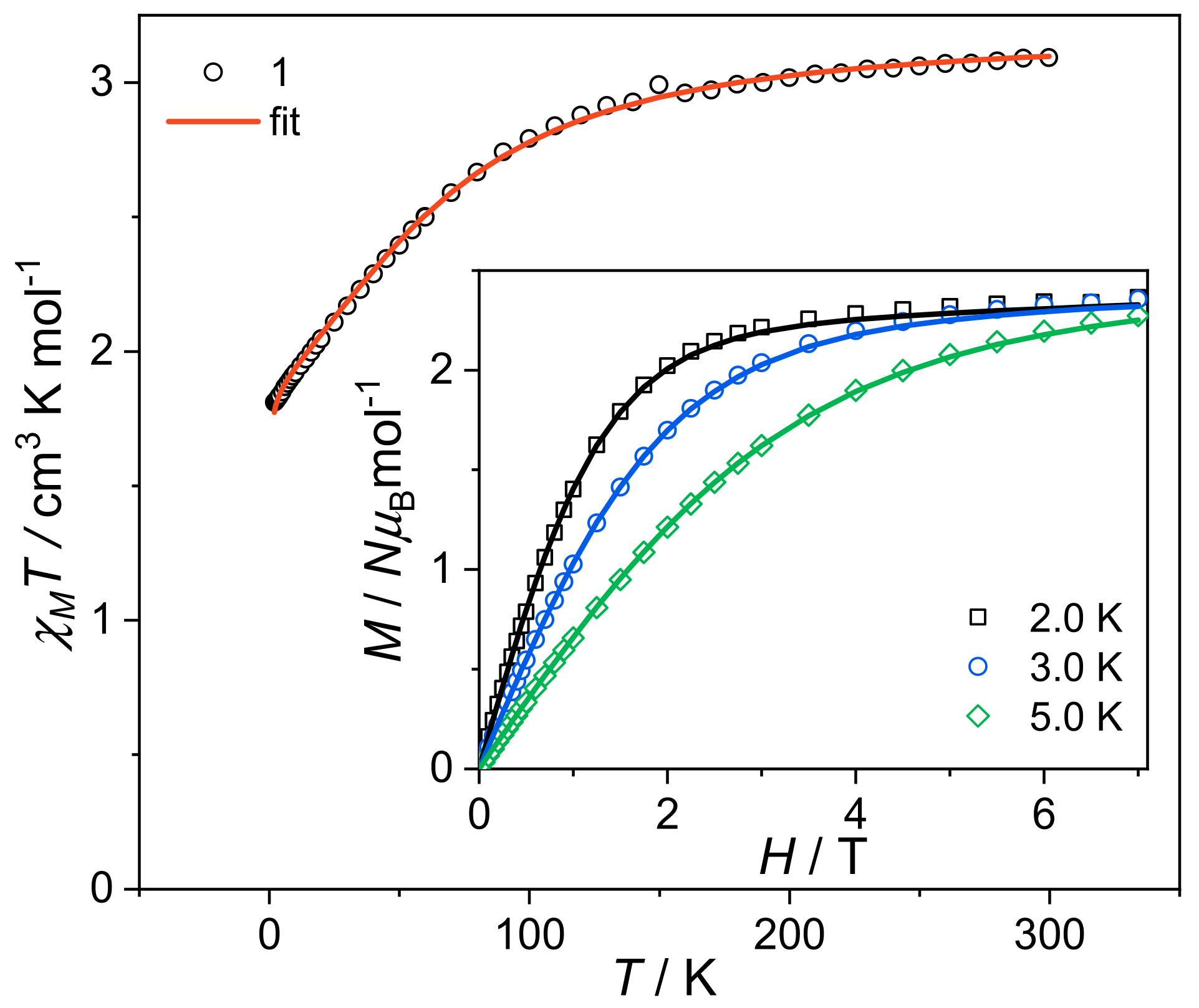
3.2. Static Magnetic Properties

Variable-temperature dc magnetic susceptibility measurements were performed on polycrystalline samples of 1 and 2. As shown in Figure 2 and Figure S8, at room temperature, the χMT values for 1 and 2 are 3.09 and 3.17 cm3 K mol−1, respectively. These values exceed the theoretical spin-only value of 1.875 cm3 K mol−1 for a mononuclear high-spin Co(II) center with S = 3/2 and g = 2.0. Comparable χMT values have been observed in previously studied Co(II) complexes featuring an octahedral coordination geometry [36,37,38,39]. For complexes 1 and 2, the χMT values show a smooth decrease as the temperature decreases, remaining stable until around 100 K. Below this point, they drop sharply, reaching final values of 1.81 cm3 K mol⁻1 at 2 K and 1.96 cm3 K mol⁻1 at 2.5 K, respectively. This reduction is most likely due to the spin–orbit coupling effects. Moreover, the field-dependent magnetizations of both complexes were measured from 0 to 7 T (Figure 2 and Figure S8).
To investigate the magnitude and sign of the anisotropy parameter, the magnetic susceptibilities and field-dependent magnetization data were analyzed simultaneously using the PHI program [40] according to the following spin Hamiltonian [Equation (1)]:
H = D ( S ^ z 2 − S ( S + 1 ) / 3 ) + E ( S ^ x 2 − S ^ y 2 ) + μ B g S ^ ⋅ H
where D and E are the axial and rhombic ZFS parameters, respectively. The optimal parameters are summarized in Table 3. Although the derived magnitudes of the ZFS parameters are not highly precise, the large positive D values (+70.4(7) cm−1 for 1; +64.0(2) cm−1 for 2) have been definitively determined, indicating the easy-plane anisotropy for both complexes.

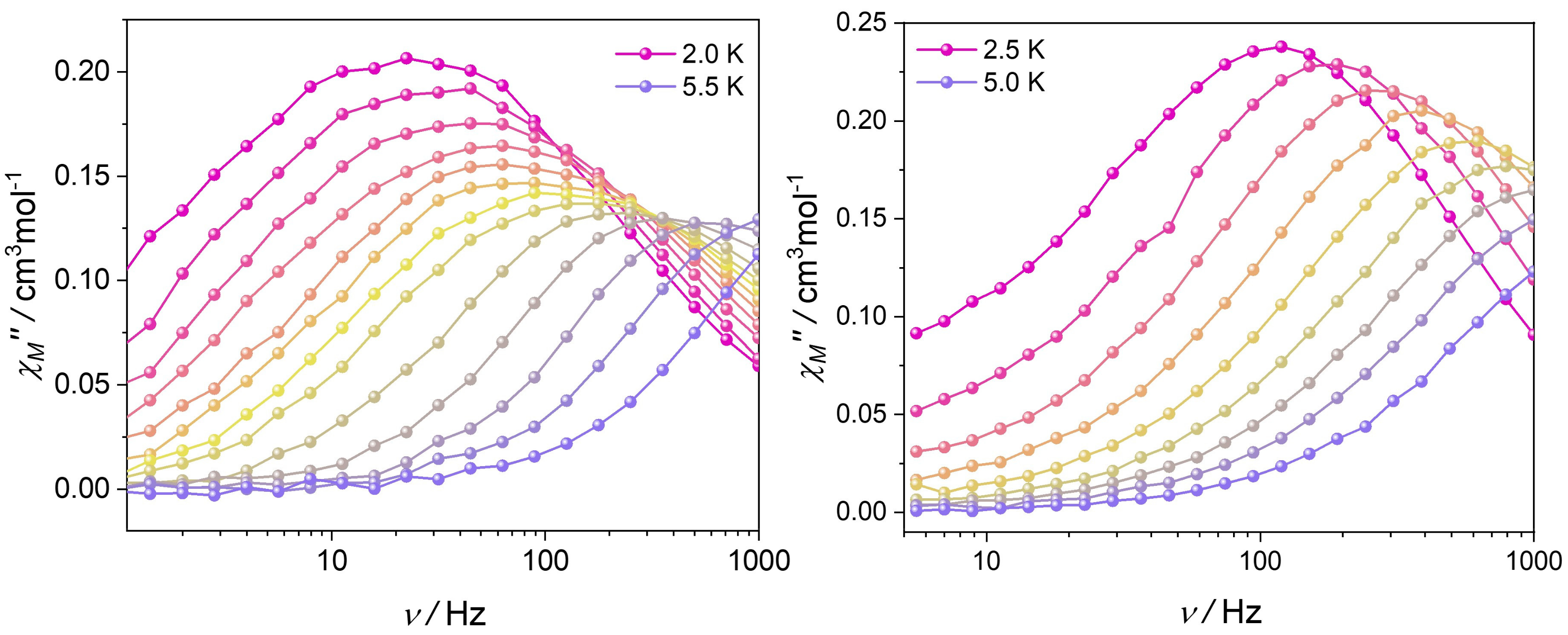
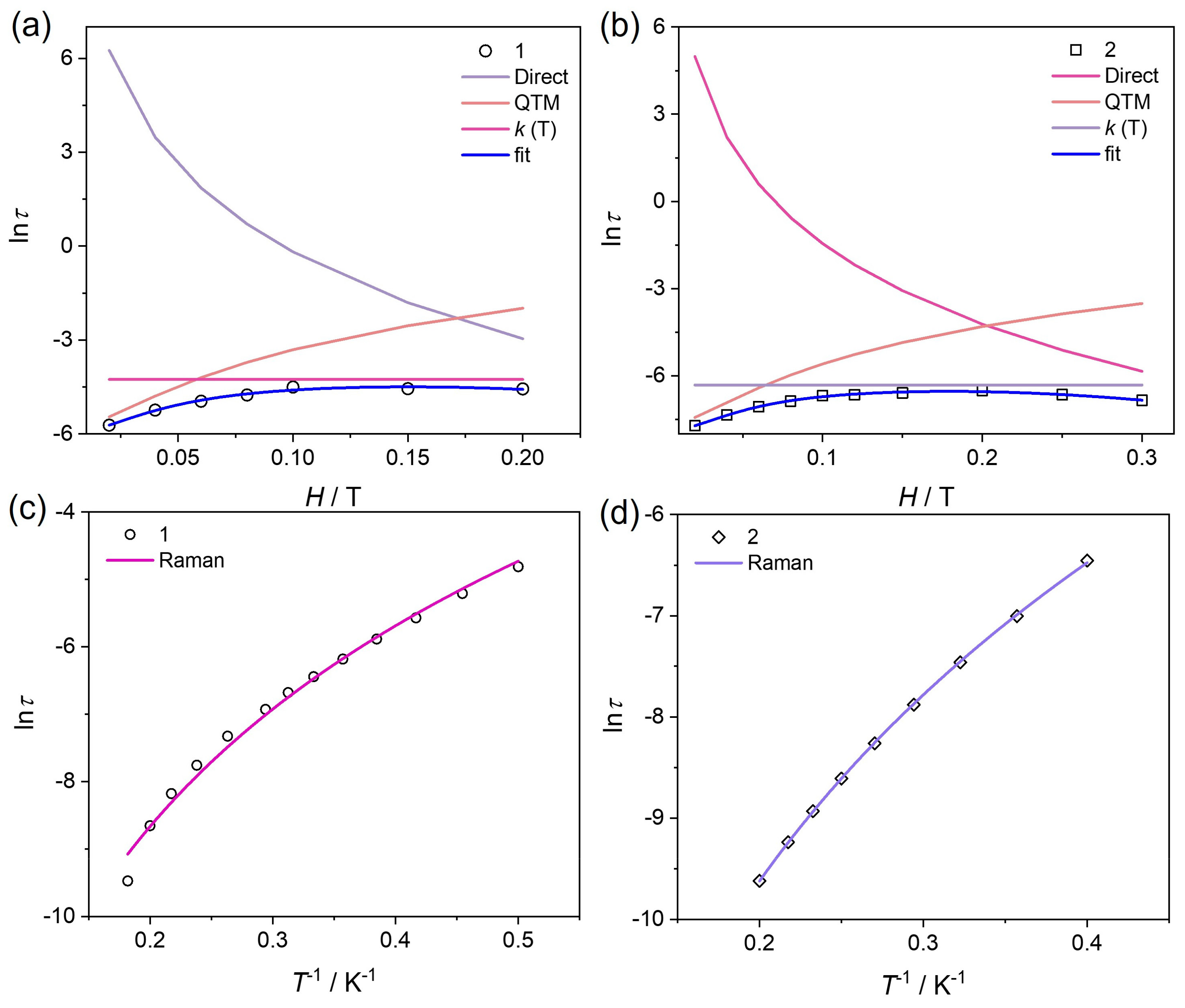
3.3. Dynamic Magnetic Properties

AC susceptibility measurements were conducted on powdered samples of 1 and 2. Figure S9 illustrates the frequency-dependent behavior of the out-of-phase component of the AC susceptibility at 1.8 K under different external dc fields. No slow magnetic relaxation was observed under a zero dc field for both 1 and 2. Under applied magnetic fields, a peak in χ″ initially shifted to lower frequencies until reaching 1000 Oe for 1 and 2000 Oe for 2, after which it began to shift to higher frequencies. To determine the optimal applied dc field, the plot of ln(τ) vs. H was derived from the variable-frequency AC susceptibility data collected under different dc fields (Figure S10). It can be observed that when the applied dc field is 1000 Oe for 1 and 2000 Oe for 2, the ln(τ) reaches its maximum value. Therefore, 1000 Oe and 2000 Oe were identified as the optimal fields for observing slow magnetic relaxation in 1 and 2, respectively. As shown in Figure 3 and Figure S11–S14, both complexes exhibit frequency and temperature dependence in their χ″ and χ′ signals.
Assuming that the Raman and Orbach processes are considered a constant k(T) due to their weak field-dependence, the ln(τ) vs. H curves of 1 and 2 were fitted using Equation (2):
τ − 1 = A H 4 T + B 1 1 + B 2 H 2 + k ( T )
where the first term represents the direct process, the second term corresponds to the quantum tunneling of magnetization (QTM), and the last term accounts for the combination of Raman and Orbach processes. The fitting curve agrees well with the experimental data, giving reasonable parameters, which are listed in Table 4. As illustrated in Figure 4a,b, the QTM process dominates the magnetic relaxation for both 1 and 2 at low fields. However, at the optimal field (1000 Oe for 1 and 2000 Oe for 2), the temperature-dependent combination process (k(T)) becomes the prevailing mechanism. It is worth noting that the direct process does not dominate across the entire field range studied.
At fixed temperatures for 1 (2.0–5.5 K) and 2 (2.5–5.0 K), semicircular Cole–Cole plots were generated and fitted using the generalized Debye model [41] (Figure S15), assuming a single relaxation pathway to determine the magnetization relaxation time (τ) and the α parameter. The α parameter ranged from 0.44 to 0.08 for complex 1 and from 0.24 to 0.11 for complex 2, indicating a broad distribution of relaxation times at lower temperatures that narrows as the temperature increases. The relaxation times extracted from the Debye fits were utilized to construct the ln(τ) vs. T−1 plots for 1 and 2. It is noteworthy that a Raman process plays an important role in most reported Co(II)-based SIMs with octahedral geometry, while a direct one-phonon contribution cannot be ignored at low temperatures [26]. Therefore, a model including both direct and Raman relaxation mechanisms was initially employed. However, the results, which are consistent with the findings obtained from fitting the ln(τ) vs. H curve, indicate that the direct mechanism is not the main contributor to the relaxation process. Consequently, the Raman process alone, described as τ−1 = CTn, was used to fit the ln(τ) vs. T−1 data (Figure 4c,d). The best-fit parameters were C = 5.7 s−1 K−n and n = 4.3 for 1, and C = 10.1 s−1 K−n and n = 4.5 for 2.
The cobalt(II) ions in complexes 1 and 2 show the same donor set and exhibit very similar bond lengths and angles, with comparable degrees of distortion. However, the AC magnetic properties demonstrate that the peaks in out-of-phase susceptibilities for 2 appear at higher frequencies than those for 1, suggesting a faster relaxation process in 2. Since the experimental magnetic data show that the magnetic anisotropies of 1 and 2 are very similar, the differences in their dynamic susceptibility behavior are attributed to the distinct pseudohalide ions. The substitution of SCN− in 1 with SeCN− in 2 leads to a significant change in the crystal packing. In 1, there are no significant intermolecular interactions, while in 2, weak C–H∙∙∙Se hydrogen bonding interactions link the molecules to form supermolecular chains along the b-axis. As reported by Boča et al., differences in hydrogen bonding may contribute to the difference in dynamic magnetic properties [42,43]. For instance, the hydrogen boding systems can enhance coupling of the dimeric units within the supramolecular chains, leading to the absence of the out-of-phase component and ultimately preventing the system from behaving as single molecule magnets [42]. Moreover, Song et al. have reported that the structural rigidity significantly impacts the slow magnetic relaxation process in the SIM system [44]. Increased structural rigidity can enhance spin–phonon coupling, which will accelerate the magnetic relaxation. Consequently, the hydrogen boding systems in 2, which provide additional stabilization to the crystal structure, may be responsible for its faster relaxation process compared to 1.

4. Conclusions

We synthesized two new mononuclear compounds, [Co(L)(NCS)2] (1) and [Co(L)(NCSe)2] (2), where L represents 1-(prop-2-en-1-yl)-1H-imidazole. Both complexes feature a similar octahedral Co(II) center, coordinated by four N atoms from the ligand L and two N atoms from the anion. Analysis of the dc magnetic data indicates the presence of easy-plane magnetic anisotropy with significant positive D values (+70.4 cm−1 for 1 and +64.0 cm−1 for 2). Ac magnetic susceptibility measurements confirm that both complexes exhibit field-induced slow magnetic relaxation behavior. Moreover, the Raman mechanism is found to be the dominant relaxation process across the entire temperature range for both complexes.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/magnetochemistry11020011/s1. Figures S1 and S2: XRD patterns for complexes 1 and 2; Table S1: Selected previously obtained mononuclear octahedral Co(II) complexes supported by imidazole ligands; Table S2: The results of the continuous shape measure (CSM) analyses of 1 and 2 by SHAPE software; Figure S3: View of the crystal packing along the a-axis in 1; Figure S4: View of the crystal packing along the a-axis in 2; Figures S5 and S6: The intermolecular Co–Co distances in 1 and 2; Figure S7: The IR spectra of complexes 1 and 2; Figure S8: Variable-temperature dc susceptibility data of 2; Table S3: The fitting results of the magnetization data with Equation (3) for 1 and 2; Figure S9: Frequency dependence of out-of-phase (χM″) ac susceptibility under the different applied static fields for 1 and 2; Figure S10: Field dependence of the magnetization relaxation rates for 1 and 2; Figures S11 and S12: Frequency dependence of in-phase (χM′) ac susceptibility under applied dc field of 1000 Oe for 1 and 2000 Oe for 2; Figures S13 and S14: Temperature dependence of in-phase (χM′) and out-of-phase (χM″) ac susceptibility at different ac frequencies for 1 and 2; Figure S15: Cole–Cole plot obtained from the ac susceptibility data under a different temperature range for 1 and 2.

Author Contributions

The manuscript was prepared with the contributions of all authors. They specifically contributed as follows: H.-H.C.—Investigation, writing—original draft; D.-Z.W.—Investigation; S.L.—Formal analysis; L.W.—Formal analysis; X.Y.—Formal analysis; X.L.—Formal analysis; J.W.—Project administration, supervision; M.W.—Review and editing; Y.T.—Supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (22101144), the Natural Science Foundation of Jiangsu Province (BK20210835) and the Natural Science Research Project of Jiangsu Colleges and Universities (21KJB150003).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

CCDC 2414366 and 2414367 contain the supplementary crystallographic data for compounds 1 and 2, respectively. These data can be obtained free of charge via https://www.ccdc.cam.ac.uk/structures/ (accessed on 5 February 2025) or from Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: (+44) 1223-336-033; or e-mail: deposit@ccdc.cam.ac.uk. The original contributions presented in this study are included in the article and Supplementary Materials; further inquiries can be directed to the corresponding authors.

Acknowledgments

We are very grateful to the Nantong University Analytical Testing Center for its support for testing.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press, Inc.: New York, NY, USA, 2006. [Google Scholar]
  2. Clemente-Juan, J.M.; Coronado, E.; Gaita-Arino, A. A magnetic polyoxometalates: From molecular magnetism to molecular spintronics and quantum computing. Chem. Soc. Rev. 2012, 41, 7464–7478. [Google Scholar] [CrossRef] [PubMed]
  3. Sanvito, S. Molecular spintronics. Chem. Soc. Rev. 2011, 40, 3336–3355. [Google Scholar] [CrossRef] [PubMed]
  4. Craig, G.A.; Murrie, M. 3d single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef] [PubMed]
  5. Feng, M.; Tong, M.-L. Single ion magnets from 3d to 5f: Developments and strategies. Chem. Eur. J. 2018, 24, 7574–7594. [Google Scholar] [CrossRef]
  6. Naoto, I.; Sugita, M.; Ishikawa, T.; Koshihara, A.S.; Kaizu, Y. Lanthanide double-decker complexes functioning as magnets at the single-molecular level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar]
  7. Vallejo, J.; Pascual-Álvarez, A.; Cano, J.; Castro, I.; Julve, M.; Lloret, F.; Krzystek, J.; De Munno, G.; Armentano, D.; Wernsdorfer, W.; et al. Field-induced hysteresis and quantum tunneling of the magnetization in a mononuclear manganese(III) complex. Angew. Chem. Int. Ed. 2013, 52, 14075–14079. [Google Scholar] [CrossRef]
  8. Zadrozny, J.M.; Atanasov, M.; Bryan, A.M.; Lin, C.-Y.; Rekken, B.D.; Power, P.P.; Neese, F.; Long, J.R. Slow magnetization dynamics in a series of two-coordinate iron(ii) complexes. Chem. Sci. 2013, 4, 125–130. [Google Scholar] [CrossRef]
  9. Bunting, P.C.; Atanasov, M.; Damgaard-Moller, E.; Perfetti, M.; Crassee, I.; Orlita, M.; Overgaard, J.; van Slageren, J.; Neese, F.; Long, J.R. A linear cobalt(II) complex with maximal orbital angular momentum from a non-Aufbau ground state. Science 2018, 362, eaat7319. [Google Scholar] [CrossRef]
  10. Rechkemmer, Y.; Breitgoff, F.D.; van der Meer, M.; Atanasov, M.; Hakl, M.; Orlita, M.; Neugebauer, P.; Neese, F.; Sarkar, B.; van Slageren, J. A fourcoordinate cobalt(II) single-ion magnet with coercivity and a very high energy barrier. Nat. Commun. 2016, 7, 10467. [Google Scholar] [CrossRef]
  11. Cui, H.-H.; Lu, F.; Chen, X.-T.; Zhang, Y.-Q.; Tong, W.; Xue, Z.-L. Zero-field slow magnetic relaxation and hysteresis loop in four-coordinate CoII single-ion magnets with strong easy-axis anisotropy. Inorg. Chem. 2019, 58, 12555–12564. [Google Scholar] [CrossRef]
  12. Gupta, S.K.; Rao, S.V.; Demeshko, S.; Dechert, S.; Bill, E.; Atanasov, M.; Neese, F.; Meyer, F. Air-stable four-coordinate cobalt(II) single-ion magnets: Experimental and ab initio ligand field analyses of correlations between dihedral angles and magnetic anisotropy. Chem. Sci. 2023, 14, 6355–6374. [Google Scholar] [CrossRef] [PubMed]
  13. Ferreira, P.S.; Malta, J.F.; Bandeira, N.A.G.; Allgaier, A.; van Slageren, J.; Paixão, J.A.; Almeida, M.; Pereira, L.C.J.; Gomes, P.T. Enhancing SIM behaviour in a mononuclear tetrahedral [Co(N,N’-2-iminopyrrolyl)2] complex. Chem. Commun. 2022, 58, 9682–9685. [Google Scholar] [CrossRef]
  14. Cui, H.-H.; Xu, H.; Zhang, T.; Chen, Q.; Luo, S.; Wang, M.; Wang, J.; Chen, L.; Zhang, M.; Tang, Y. Magnetic anisotropy and relaxation in four-coordinate cobalt(II) single-ion magnets with a [CoIIO4] Core. Inorg. Chem. 2024, 63, 9050–9057. [Google Scholar] [CrossRef]
  15. Poulten, R.C.; Page, M.J.; Algarra, A.G.; Le Roy, J.J.; López, I.; Carter, E.; Llobet, A.; Macgregor, S.A.; Mahon, M.F.; Murphy, D.M.; et al. Synthesis, electronic structure, and magnetism of [Ni(6-Mes)2]+: A two-coordinate nickel(I) complex stabilized by bulky N-heterocyclic carbenes. J. Am. Chem. Soc. 2013, 135, 13640–13643. [Google Scholar] [CrossRef] [PubMed]
  16. Sahu, P.K.; Kharel, R.; Shome, S.; Goswami, S.; Konar, S. Understanding the unceasing evolution of Co(II) based single-ion magnets. Coord. Chem. Rev. 2023, 475, 214871. [Google Scholar]
  17. Sarkar, A.; Dey, S.; Rajaraman, G. Role of coordination number and geometry in controlling the magnetic anisotropy in FeII, CoII, and NiII single-ion magnets. Chem. Eur. J. 2020, 26, 14036–14058. [Google Scholar] [CrossRef]
  18. Tripathi, S.; Dey, A.; Shanmugam, M.; Narayanan, R.S.; Chandrasekhar, V. Cobalt(II) Complexes as Single-Ion Magnets in Organometallic Magnets; Chandrasekhar, V., Pointillart, F., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 35–75. [Google Scholar] [CrossRef]
  19. Juráková, J.; Šalitroš, I. Co(II) single-ion magnets: Synthesis, structure, and magnetic properties. Monatsh. Chem. 2022, 153, 1001–1036. [Google Scholar] [CrossRef]
  20. Vallejo, J.; Castro, I.; Ruiz García, R.; Cano, J.; Julve, M.; Lloret, F.; De Munno, G.; Wernsdorfer, W.; Pardo, E. Field-induced slow magnetic relaxation in a six-coordinate mononuclear cobalt(II) complex with a positive anisotropy. J. Am. Chem. Soc. 2012, 134, 15704–15707. [Google Scholar] [CrossRef]
  21. Gómez-Coca, S.; Urtizberea, A.; Cremades, E.; Alonso, P.J.; Camón, A.; Ruiz, E.; Luis, E. Origin of slow magnetic relaxation in kramers ions with non-uniaxial anisotropy. Nat. Commun. 2014, 5, 4300. [Google Scholar] [CrossRef]
  22. Novikov, V.V.; Pavlov, A.A.; Nelyubina, Y.V.; Boulon, M.E.; Varzatskii, O.A.; Voloshin, Y.Z.; Winpenny, R.E.P. A trigonal prismatic mononuclear cobalt(II) complex showing single-molecule magnet behavior. J. Am. Chem. Soc. 2015, 137, 9792–9795. [Google Scholar] [CrossRef]
  23. Zhu, Y.-Y.; Zhu, M.-S.; Yin, T.-T.; Meng, Y.-S.; Wu, Z.-Q.; Zhang, Y.-Q.; Gao, S. Cobalt(II) coordination polymer exhibiting single-ion-magnet-type field-induced slow relaxation behavior. Inorg. Chem. 2015, 54, 3716–3718. [Google Scholar] [CrossRef] [PubMed]
  24. Zhang, J.; Li, J.; Yang, L.; Zhang, Y.-Q.; Song, Y. Magnetic anisotropy from trigonal prismatic to trigonal antiprismatic Co(II) complexes: Experimental observation and theoretical prediction. Inorg. Chem. 2018, 57, 3903–3912. [Google Scholar] [CrossRef] [PubMed]
  25. Zhang, Y.-Z.; Gómez-Coca, S.; Brown, A.J.; Saber, M.R.; Zhang, X.; Dunbar, K.R. Trigonal antiprismatic Co(II) single molecule magnets with large uniaxial anisotropies: Importance of Raman and tunneling mechanisms. Chem. Sci. 2016, 7, 6519–6527. [Google Scholar] [CrossRef] [PubMed]
  26. Zhou, J.; Song, J.; Yuan, A.; Wang, Z.; Chen, L.; Ouyang, Z.-W. Slow magnetic relaxation in two octahedral cobalt(II) complexes with positive axial anisotropy. Inorg. Chim. Acta. 2018, 479, 113–119. [Google Scholar] [CrossRef]
  27. SMART & SAINT Software Reference Manuals, version 6.45; Bruker Analytical X-ray Systems, Inc.: Madison, WI, USA, 2003.
  28. SAINT, Program for Data Extraction and Reduction; Siemens Analytical X-ray Instruments: Madison, WI, USA, 1996.
  29. Sheldrick, G.M. SADABS: Software for Empirical Absorption. Correction, version 2.05; University of Göttingen: Göttingen, Germany, 2002.
  30. Sheldrick, G.M. SHELXL14: Program for Crystal Structure Refinement; University of Göttingen: Göttingen, Germany, 2014. [Google Scholar]
  31. Bain, G.A.; Berry, J.F. Diamagnetic corrections and Pascal’s constants. J. Chem. Educ. 2008, 85, 532–536. [Google Scholar] [CrossRef]
  32. Llunell, M.; Casanova, D.; Cirera, J.; Alemany, P.; Alvarez, S. SHAPE, version 2.1; Universitat de Barcelona: Barcelona, Spain, 2013.
  33. Alvarez, S.; Alemany, P.; Casanova, D.; Cirera, J.; Llunell, M.; Avnir, D. Shape maps and polyhedral interconversion paths in transition metal chemistry. Coord. Chem. Rev. 2005, 249, 1693–1708. [Google Scholar] [CrossRef]
  34. Kurdziel, K.; Głowiak, T. X-ray and spectroscopic characterization of octahedral cobalt(II) and nickel(II) complexes with 1-(prop-2-en-1-yl)-1H-imidazole in the solid state and electron-donor properties of the latter in aqueous solution. Polyhedron 2000, 19, 2183–2188. [Google Scholar] [CrossRef]
  35. Maslejova, A.; Uhrinova, S.; Mroziriski, J.; Zurowska, B.; Munoz, M.C.; Julve, M. Study of the mutual influence of ligands in cobalt(II) complexes containing thiocyanate and imidazole derivatives. Inorg. Chimi. Acta 1997, 255, 343–349. [Google Scholar] [CrossRef]
  36. Osipov, N.G.; Faraonov, M.A.; Yakushev, I.A.; Denisov, N.N.; Otsuka, A.; Kitagawa, H.; Konarev, D.V. Slow magnetic relaxation in a complex of photochromic spiropyran in a merocyanine form and cobalt(II) hexafluoroacetylacetonate. Dalton Trans. 2024, 53, 3159–3166. [Google Scholar] [CrossRef]
  37. Hu, Z.-B.; Jing, Z.-Y.; Li, M.-M.; Yin, L.; Gao, Y.-D.; Yu, F.; Hu, T.-P.; Wang, Z.; Song, Y. Important role of intermolecular interaction in cobalt(II) single-ion magnet from single slow relaxation to double slow relaxation. Inorg. Chem. 2018, 57, 10761–10767. [Google Scholar] [CrossRef]
  38. Chen, S.-Y.; Cui, H.-H.; Zhang, Y.-Q.; Wang, Z.; Ouyang, Z.-W.; Chen, L.; Yan, H.; Xue, Z.-L. Magnetic anisotropy and relaxation behavior of six-coordinate tris(pivalato)-Co(II) and -Ni(II) complexes. Dalton Trans. 2018, 47, 10162–10171. [Google Scholar] [CrossRef] [PubMed]
  39. Walsh, J.P.S.; Bowling, G.; Ariciu, A.-M.; Jailani, N.F.M.; Chilton, N.F.; Waddell, P.G.; Collison, D.; Tuna, F.; Higham, L.J. Evidence of slow magnetic relaxation in Co(AcO)2(py)2(H2O)2. Magnetochemistry 2016, 2, 23. [Google Scholar] [CrossRef]
  40. Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef] [PubMed]
  41. Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
  42. Smolko, L.; Černák, J.; Dušek, M.; Titiš, J.; Boča, R. Tetracoordinate Co(II) complexes containing bathocuproine and single molecule magnetism. New J. Chem. 2016, 40, 6593–6598. [Google Scholar] [CrossRef]
  43. Smolko, L.; Černák, J.; Kuchár, J.; Rajnák, C.; Titiš, J.; Boča, R. Field-induced slow magnetic relaxation in mononuclear tetracoordinate cobalt(II) complexes containing a neocuproine ligand. Eur. J. Inorg. Chem. 2017, 2017, 3080–3086. [Google Scholar] [CrossRef]
  44. Hu, Z.-B.; Gui, L.-A.; Li, L.-H.; Xiao, T.-T.; Hand, A.-T.; Tin, P.; Ozerov, M.; Peng, Y.; Ouyang, Z.; Wang, Z.; et al. CoII single-ion magnet and its multi-dimensional aggregations: Influence of the structural rigidity on magnetic relaxation process. Chinese Chem. Lett. 2025, 36, 109600. [Google Scholar] [CrossRef]
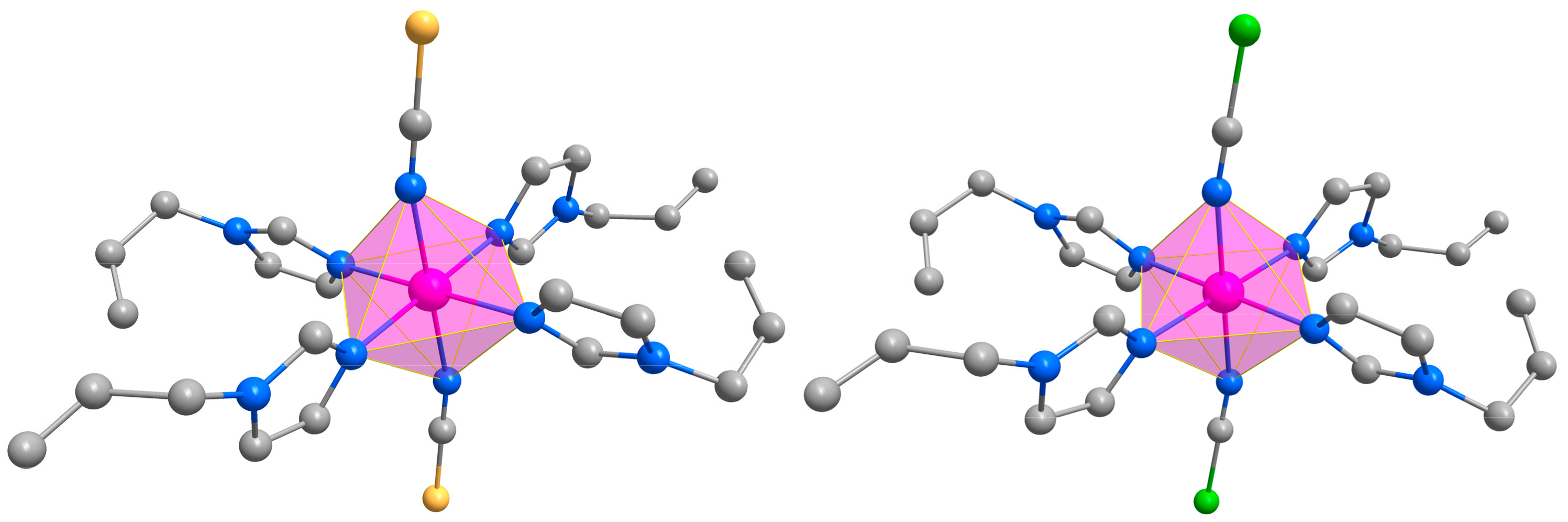
Magnetochemistry 11 00011 g001
Figure 1. Coordination geometry of 1 (left) and 2 (right). Pink, blue, yellow, green and gray spheres represent Co, N, S, Se and C atoms, respectively.
Figure 1. Coordination geometry of 1 (left) and 2 (right). Pink, blue, yellow, green and gray spheres represent Co, N, S, Se and C atoms, respectively.
Magnetochemistry 11 00011 g001
Magnetochemistry 11 00011 g002
Figure 2. The dc susceptibility data of 1. Solid lines indicate the best fits with the PHI program [40].
Figure 2. The dc susceptibility data of 1. Solid lines indicate the best fits with the PHI program [40].
Magnetochemistry 11 00011 g002
Magnetochemistry 11 00011 g003
Figure 3. Frequency dependence of the out-of-phase ac susceptibility under an applied dc field of 1000 Oe for 1 (left) and 2000 Oe for 2 (right). The solid lines are guides for the eye.
Figure 3. Frequency dependence of the out-of-phase ac susceptibility under an applied dc field of 1000 Oe for 1 (left) and 2000 Oe for 2 (right). The solid lines are guides for the eye.
Magnetochemistry 11 00011 g003
Magnetochemistry 11 00011 g004
Figure 4. Field dependence of the magnetization relaxation rates for 1 (a) and 2 (b). The blue line represents the best fit using Equation (2). The other lines represent the contribution of direct, QTM and other processes, respectively. Relaxation time of the magnetization ln(τ) vs. T−1 plots for 1 (c) and 2 (d).
Figure 4. Field dependence of the magnetization relaxation rates for 1 (a) and 2 (b). The blue line represents the best fit using Equation (2). The other lines represent the contribution of direct, QTM and other processes, respectively. Relaxation time of the magnetization ln(τ) vs. T−1 plots for 1 (c) and 2 (d).
Magnetochemistry 11 00011 g004
Table 1. Summary of crystallographic data for complexes 1 and 2.
Table 1. Summary of crystallographic data for complexes 1 and 2.
Compound12
Molecular formularC26H32CoN10S2C26H32CoN10Se2
M (g mol−1)607.66701.46
Temperature (K) 296296
Crystal systemTriclinicTriclinic
Space groupP-1P-1
a/Å8.875 (4)8.9168 (16)
b/Å9.620 (4)9.7118 (17)
c/Å10.632 (4)10.6394 (19)
α (°)69.923 (7)107.091 (3)
β (°)65.435 (6)113.791 (3)
γ (°)86.636 (6)94.205 (3)
V/Å3771.6 (6)786.2 (2)
Z11
ρcalc, g/cm31.3081.482
μ/mm−10.7242.893
F (000)317.0353.0
θ range [°]4.5/55.1766.47/55.372
Reflns collected47434896
Rint0.05230.1411
Indep. reflns33883508
Data/restr./paras3388/0/1863508/0/178
Goodness-of-fit on F21.2161.057
R1, wR2 [I > 2σ (I)] a0.0410/0.11550.0676/0.1698
R1, wR2 [all data] a0.0459/0.12770.0776/0.1794
a R1 = Σ||Fo| − |Fc||/Σ|Fo|; wR2 = [Σ[w(Fo2 − Fc2)2]/Σ[w(Fo2)2]]1/2.
Table 2. Selected bond lengths (Å) and angles (°) for complexes 1 and 2.
Table 2. Selected bond lengths (Å) and angles (°) for complexes 1 and 2.
12
Co1–N212.1656 (18)Co1–N212.163 (3)
Co1–N22.1656 (18)Co1–N22.163 (3)
Co1–N4 2.140 (2)Co1–N4 2.131 (3)
Co1–N412.1401 (19)Co1–N412.131 (3)
Co1–N32.163 (2)Co1–N32.149 (3)
Co1–N312.163 (2)Co1–N312.149 (3)
N21–Co1–N2180.0N21–Co1–N2180.00 (12)
N4–Co1–N287.23 (7)N4–Co1–N292.70 (11)
N41–Co1–N292.77 (7)N41–Co1–N287.30 (11)
N2–Co1–N391.29 (8)N2–Co1–N388.81 (12)
N4–Co1–N41180.0N4–Co1–N41180.0
N31–Co1–N3180.0N31–Co1–N3180.0
Table 3. The fitting results of the magnetization data by the PHI program [40] for 1 and 2.
Table 3. The fitting results of the magnetization data by the PHI program [40] for 1 and 2.
Fittings of the dc Magnetic Data with Equation (1)
D (cm−1)|E| (cm−1)gx,ygzzj (cm−3)
1+70.4(7)0 (1)2.53 (1)2.74 (1)−0.013 (2)
2+64.0(2)0 (8)2.60 (1)2.66 (1)/
Table 4. The parameters fit by Equation (2) for 1 and 2.
Table 4. The parameters fit by Equation (2) for 1 and 2.
A (s−1 T−4 K−1)B1 (s−1)B2 (T−2)k (T) (s−1)
16016.3340.61145.870.7
221,346.52167.2707.4554.6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Cui, H.-H.; Wang, D.-Z.; Li, S.; Wang, L.; Yu, X.; Liu, X.; Wang, J.; Wang, M.; Tang, Y. Magnetic Anisotropy and Slow Magnetic Relaxation in Two Mononuclear Octahedral Cobalt(II) Complexes. Magnetochemistry 2025, 11, 11. https://doi.org/10.3390/magnetochemistry11020011

AMA Style

Cui H-H, Wang D-Z, Li S, Wang L, Yu X, Liu X, Wang J, Wang M, Tang Y. Magnetic Anisotropy and Slow Magnetic Relaxation in Two Mononuclear Octahedral Cobalt(II) Complexes. Magnetochemistry. 2025; 11(2):11. https://doi.org/10.3390/magnetochemistry11020011

Chicago/Turabian Style

Cui, Hui-Hui, Dou-Zun Wang, Shixiang Li, Leixin Wang, Xinrui Yu, Xiancong Liu, Jin Wang, Miao Wang, and Yanfeng Tang. 2025. "Magnetic Anisotropy and Slow Magnetic Relaxation in Two Mononuclear Octahedral Cobalt(II) Complexes" Magnetochemistry 11, no. 2: 11. https://doi.org/10.3390/magnetochemistry11020011

APA Style

Cui, H.-H., Wang, D.-Z., Li, S., Wang, L., Yu, X., Liu, X., Wang, J., Wang, M., & Tang, Y. (2025). Magnetic Anisotropy and Slow Magnetic Relaxation in Two Mononuclear Octahedral Cobalt(II) Complexes. Magnetochemistry, 11(2), 11. https://doi.org/10.3390/magnetochemistry11020011

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop