Topological Rainbow Trapping in One-Dimensional Magnetoelastic Phononic Crystal Slabs
Abstract
1. Introduction
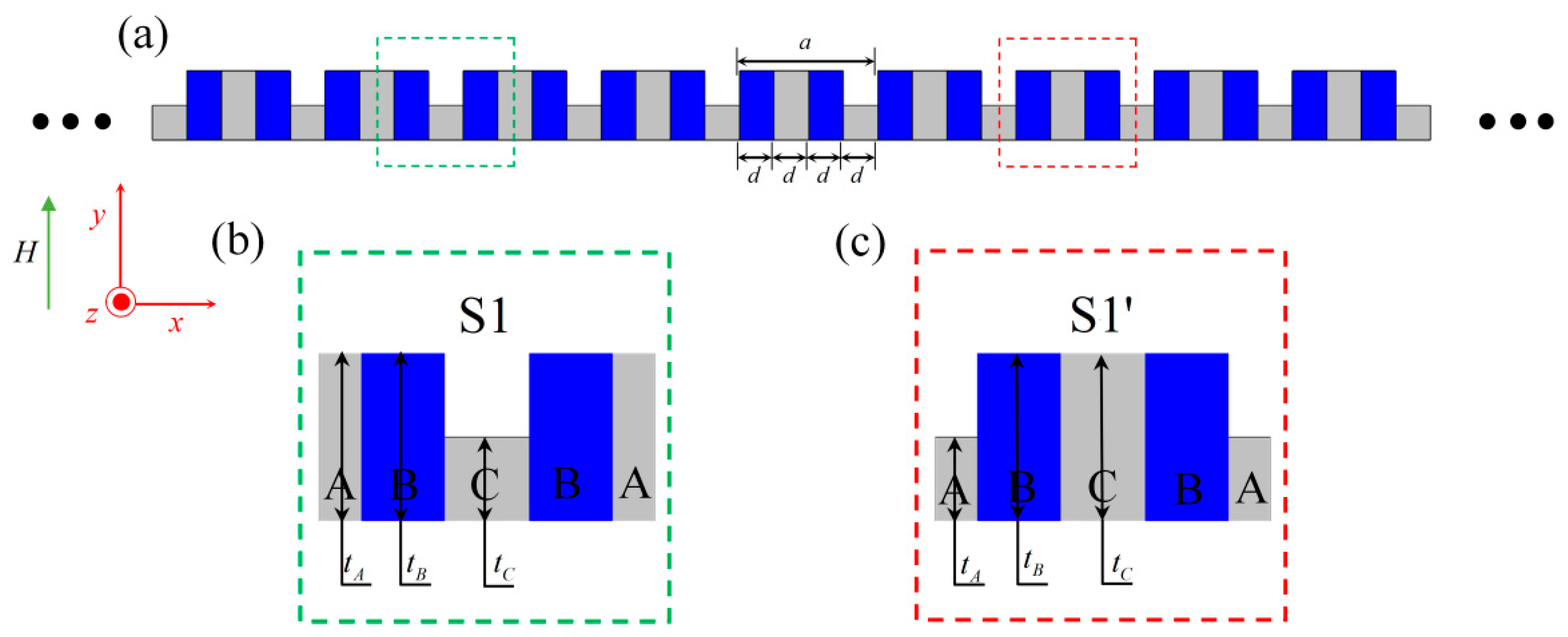
2. Models and Methods
3. Numerical Simulation
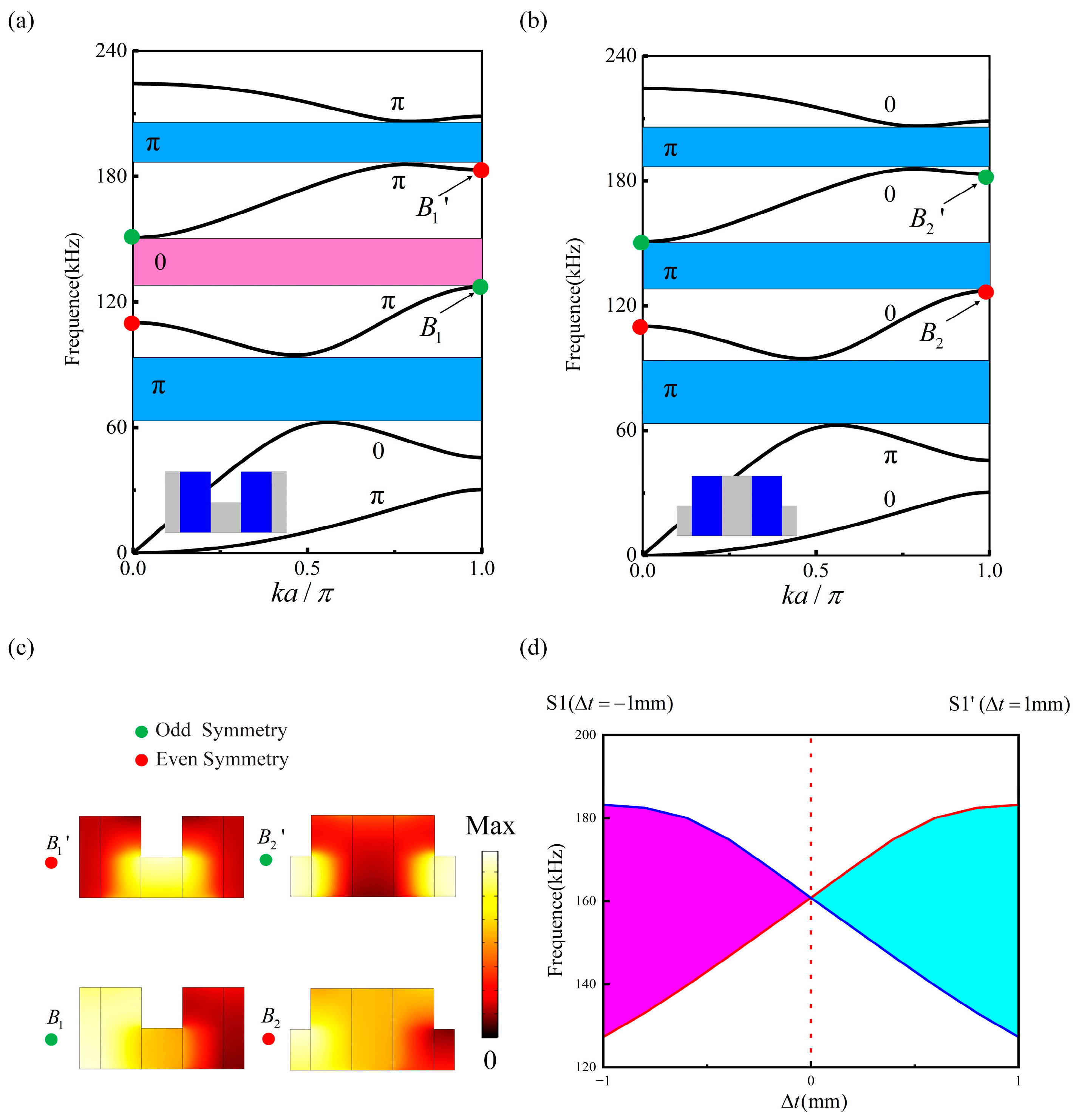
3.1. Unit Cell Band Structure and Topological Phase Transition
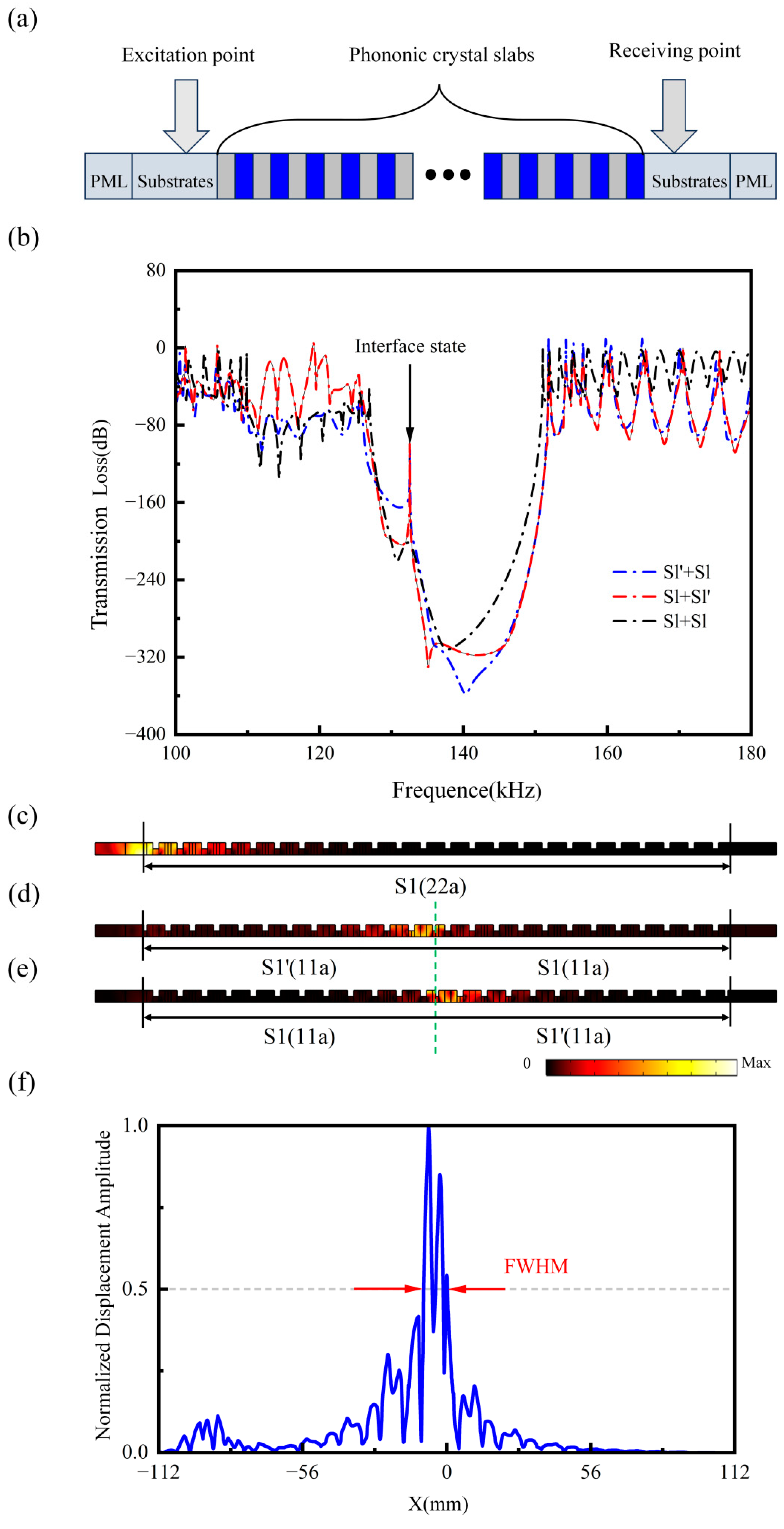
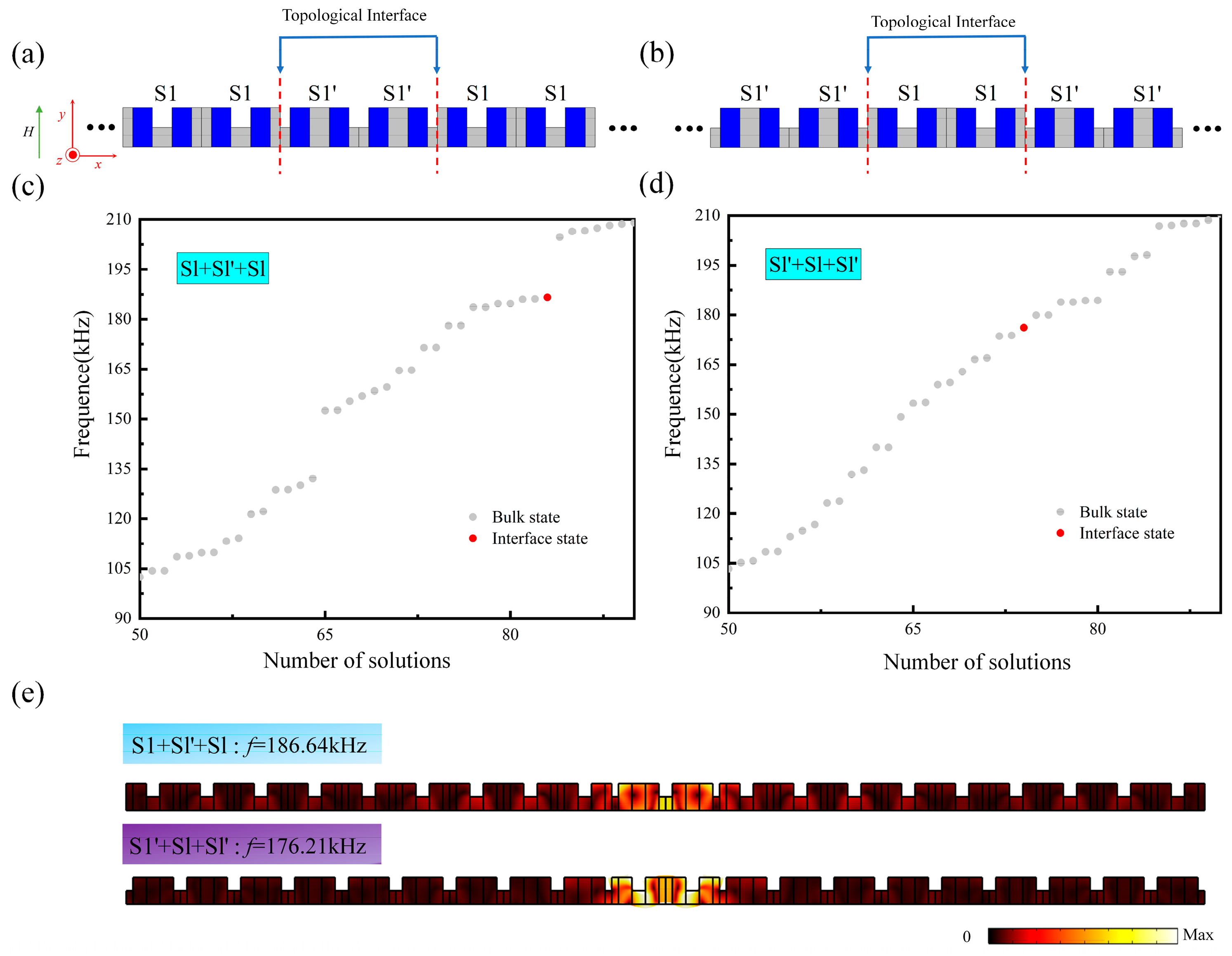
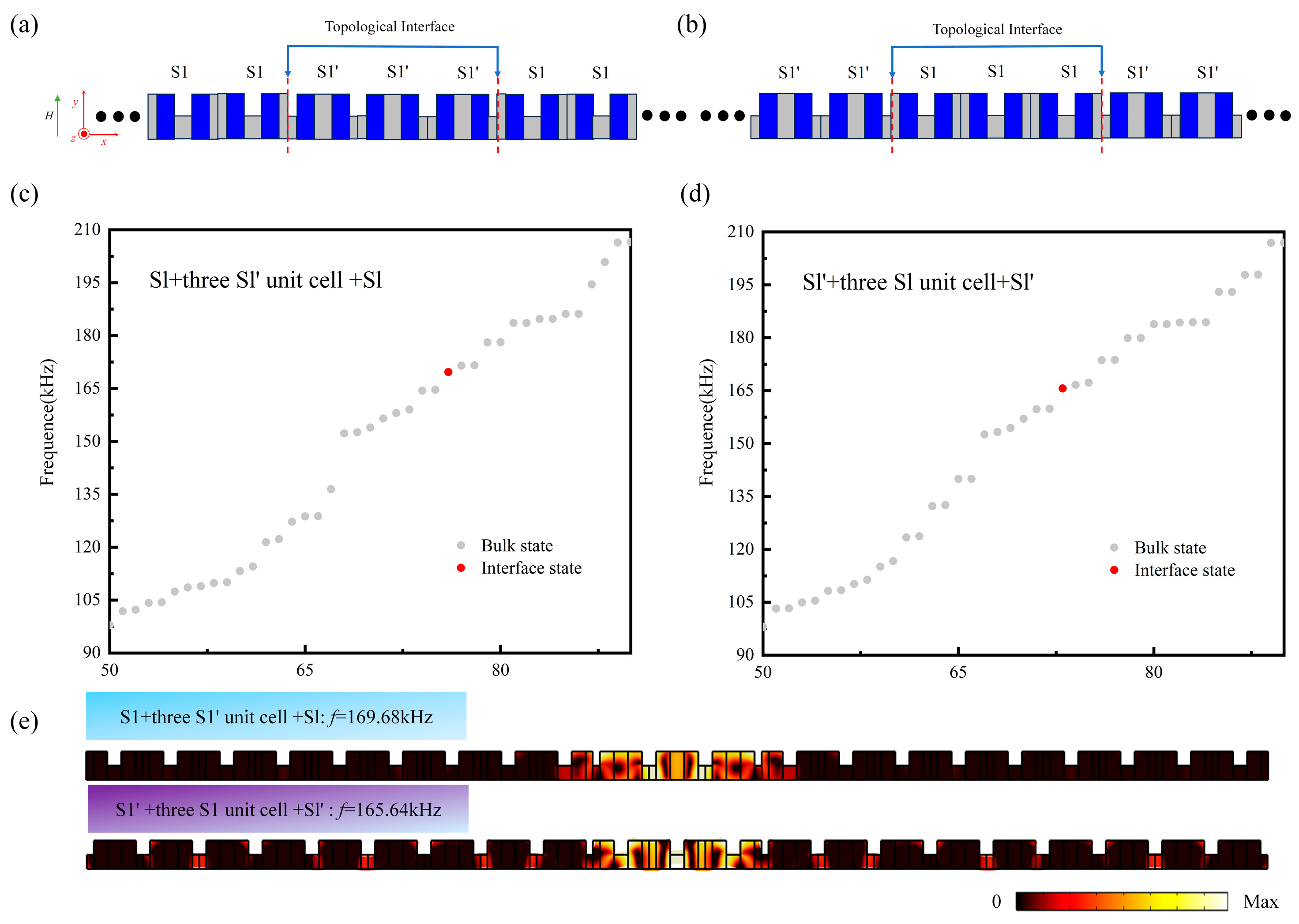
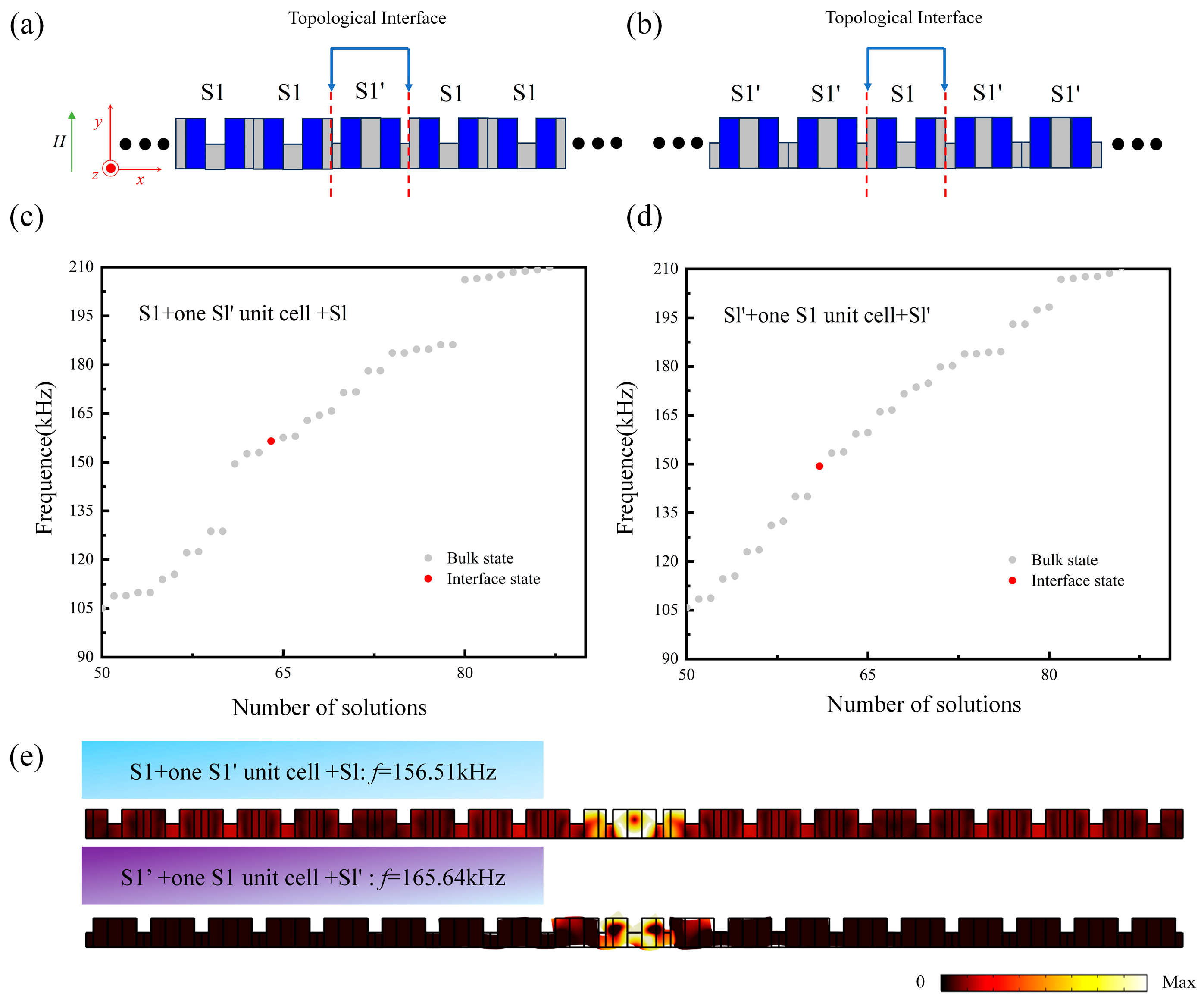
3.2. Topological Interface States in One-Dimensional Magnetoelastic Phononic Crystal Slabs
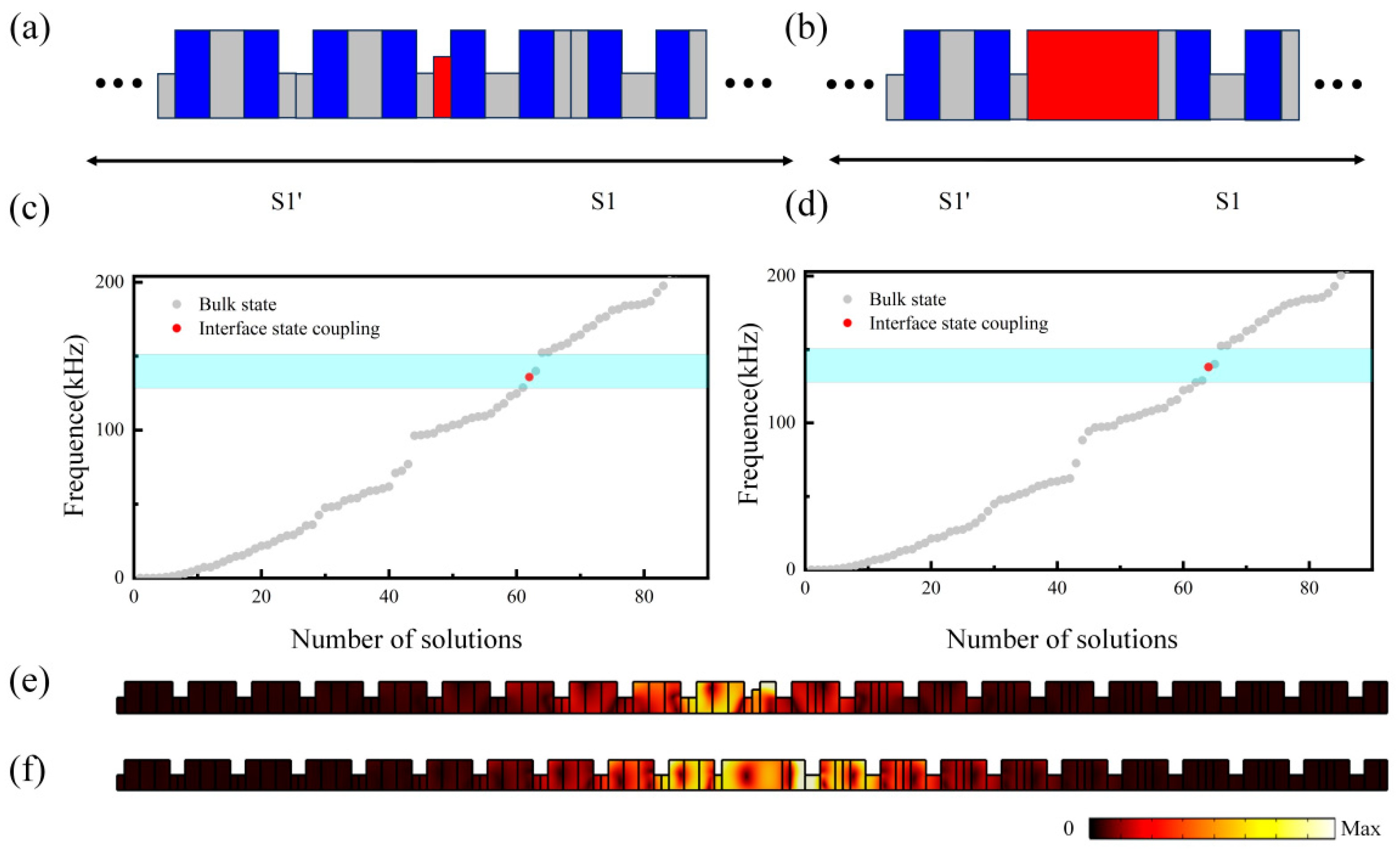
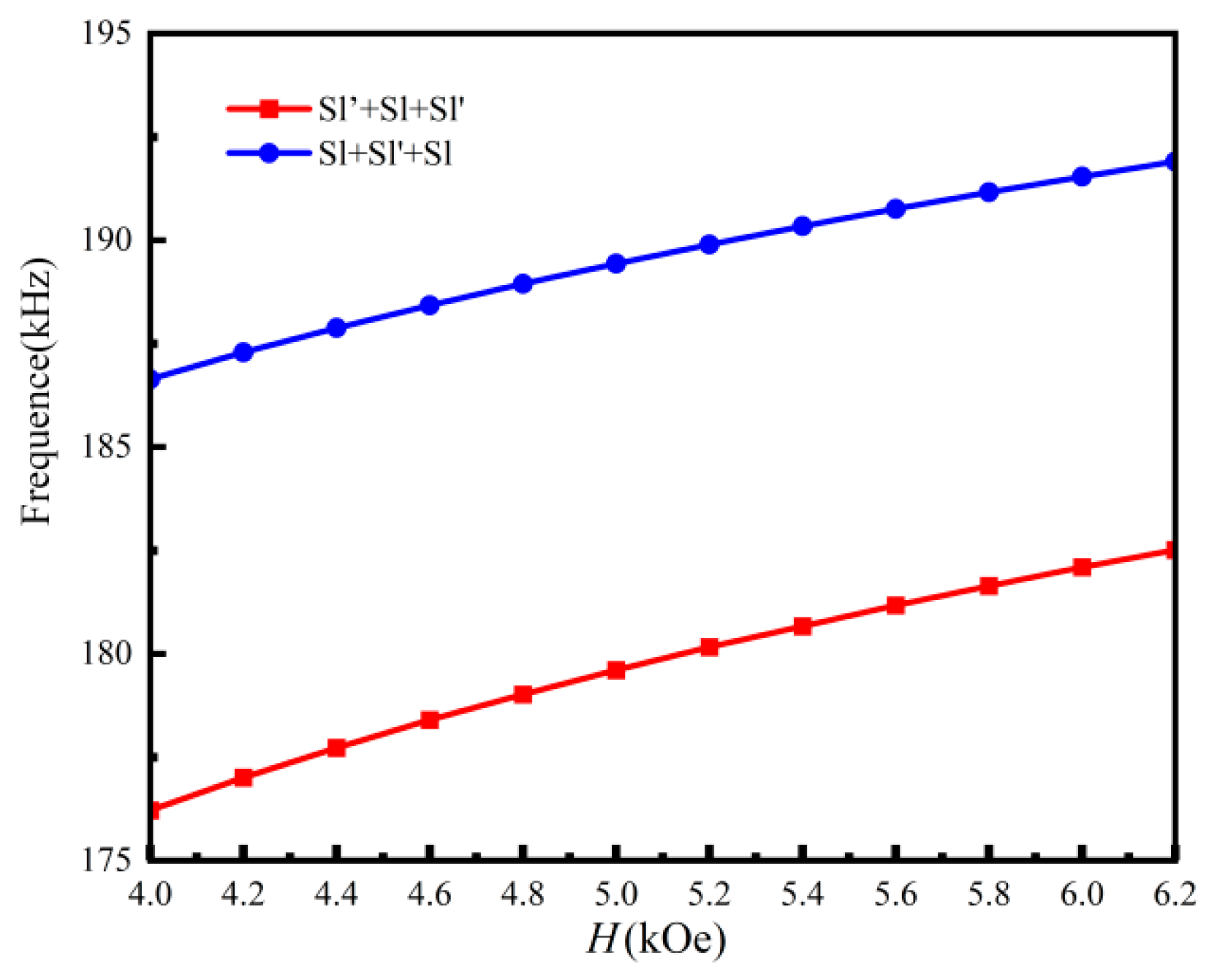
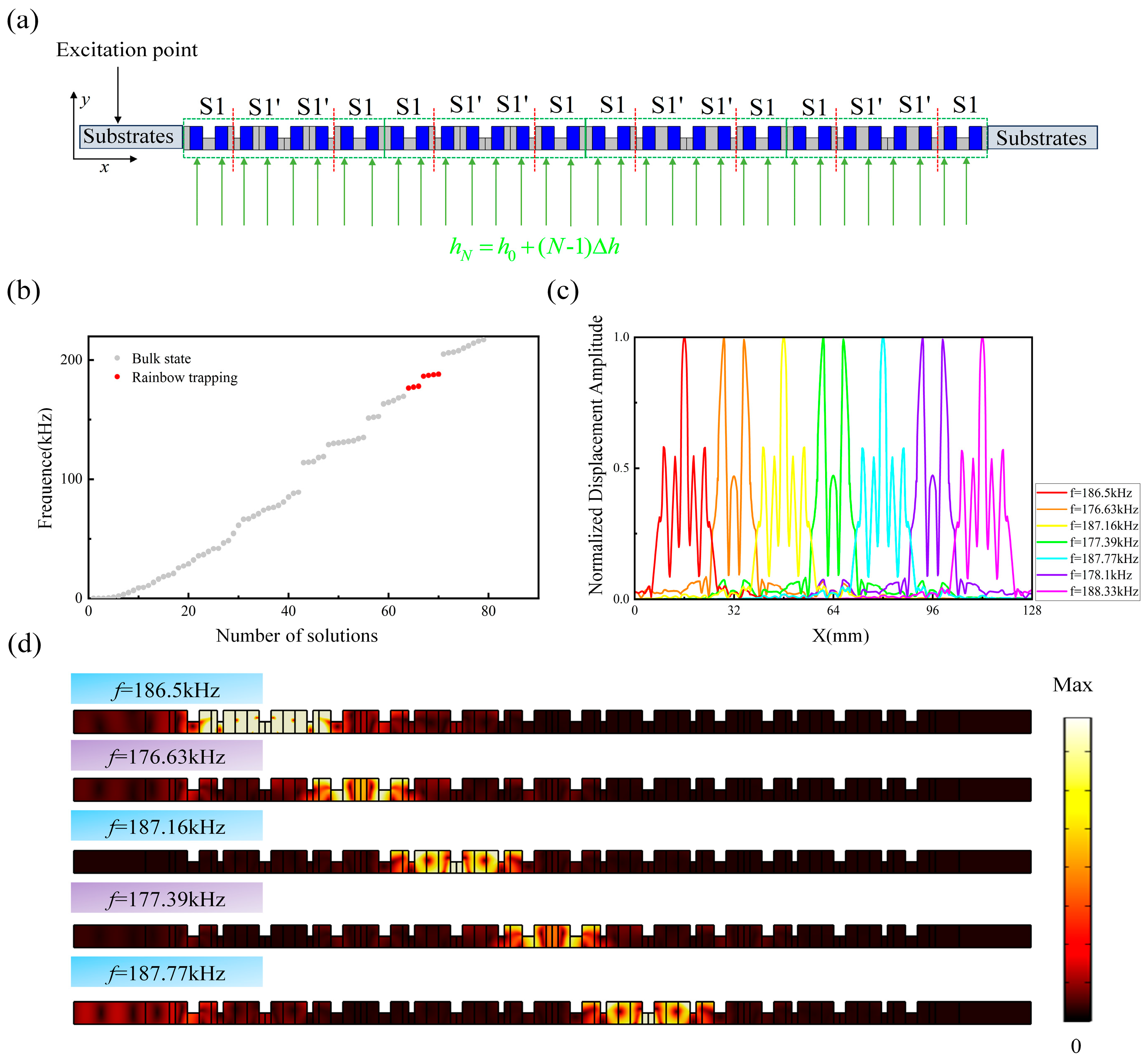
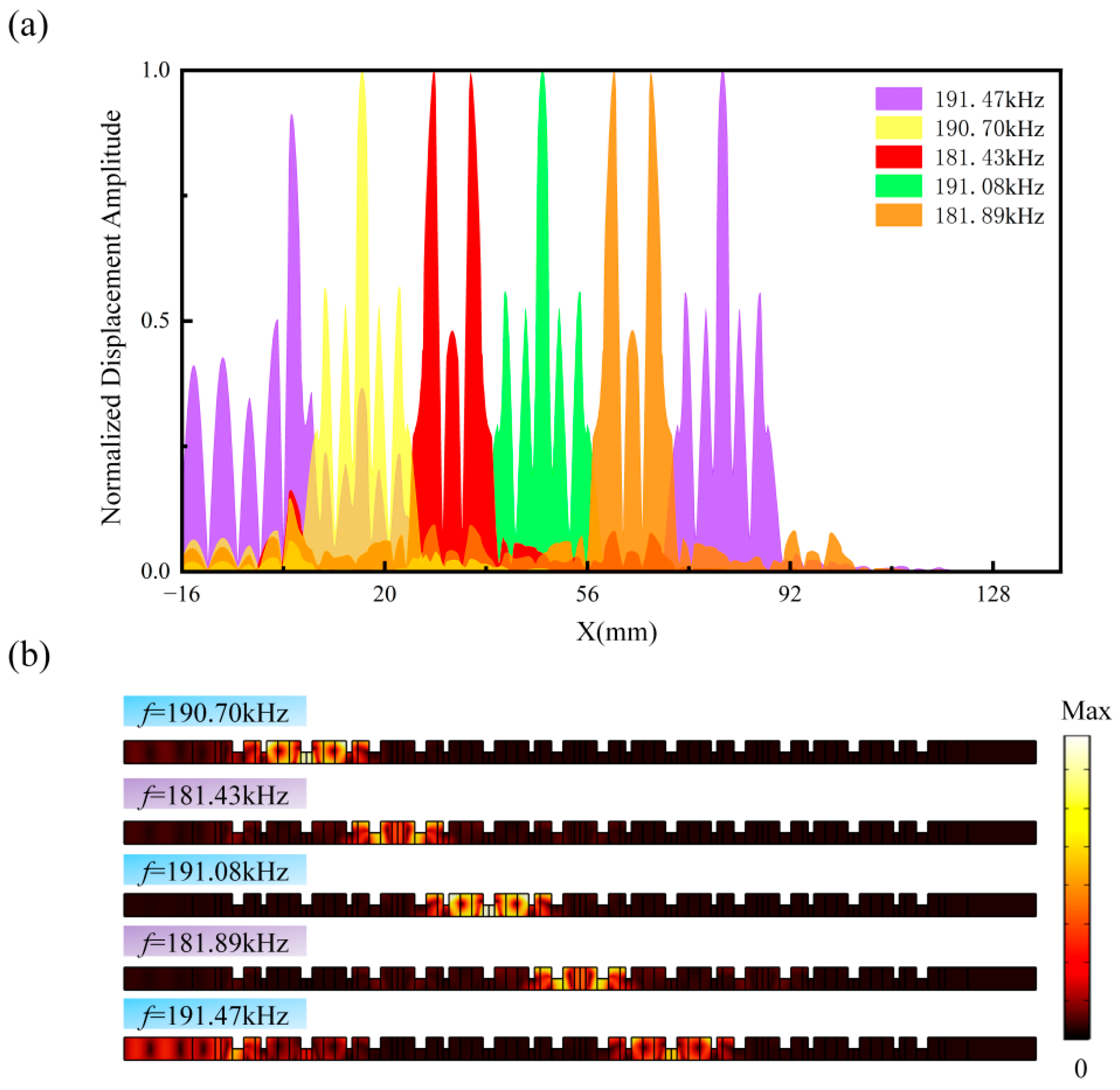
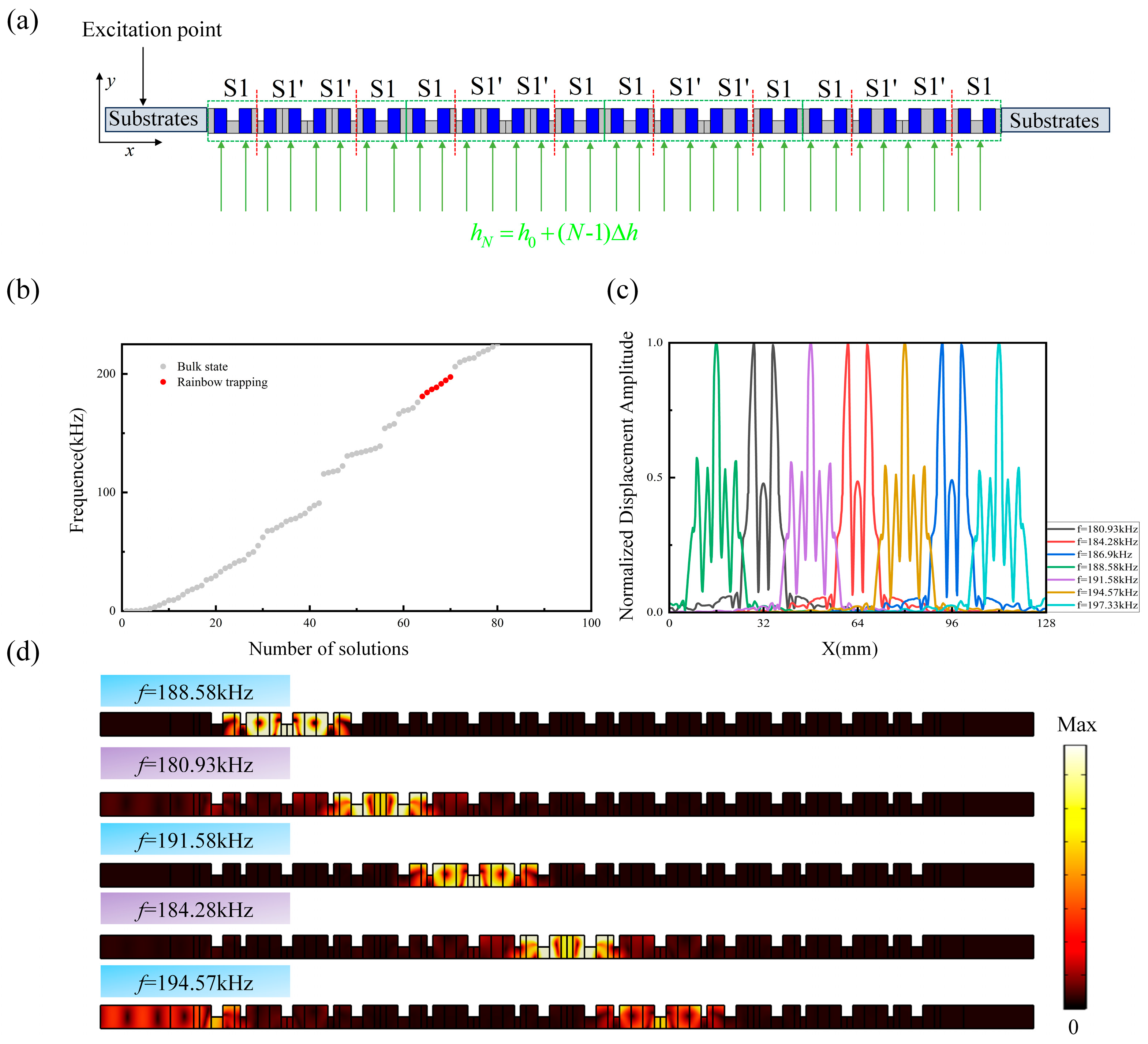
3.3. Tunable Topological Rainbow Trapping with Gradient Magnetic Field
4. Discussion and Future Perspectives
4.1. Model Limitations and Experimental Challenges
4.2. Practical Limitations and Future Perspectives
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hess, O.; Tsakmakidis, K.L. ‘Trapped rainbow’ storage of light in metamaterials. Adv. Sci. Technol.-Res. J. 2010, 75, 256–265. [Google Scholar]
- Gan, Q.; Gao, Y.; Wagner, K.; Vezenov, D.; Ding, Y.J.; Bartoli, F.J. Experimental verification of the rainbow trapping effect in adiabatic plasmonic gratings. Proc. Natl. Acad. Sci. USA 2011, 108, 5169–5173. [Google Scholar] [CrossRef]
- Hu, H.; Ji, D.; Zeng, X.; Liu, K.; Gan, Q. Rainbow Trapping in Hyperbolic Metamaterial Waveguide. Sci. Rep. 2013, 3, 1249. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Chen, Y.; Zhu, X.; Garcia-Vidal, F.J.; Yin, X.; Zhang, W.; Zhang, X. Acoustic rainbow trapping. Sci. Rep. 2013, 3, 1728. [Google Scholar] [CrossRef]
- Jang, M.S.; Atwater, H. Plasmonic Rainbow Trapping Structures for Light Localization and Spectrum Splitting. Phys. Rev. Lett. 2011, 107, 207401. [Google Scholar] [CrossRef]
- Haldane, F.D.M.; Raghu, S. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photonics 2012, 6, 782–787. [Google Scholar] [CrossRef]
- Hafezi, M.; Mittal, S.; Fan, J.; Migdall, A.L.; Taylor, J.M. Imaging topological edge states in silicon photonics. Nat. Photonics 2013, 7, 1001–1005. [Google Scholar] [CrossRef]
- Moiseev, S.; Glukhov, I. Tuning and total resonant suppression of reflection in the photonic bandgap range of Bragg reflector by two-dimensional nanoparticle array. J. Appl. Phys. 2024, 135, 083106. [Google Scholar] [CrossRef]
- Wu, L.H.; Hu, X. Scheme for Achieving a Topological Photonic Crystal by Using Dielectric Material. Phys. Rev. Lett. 2015, 114, 223901. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Page, J.H.; Liu, Z.; Cowan, M.L.; Chan, C.T.; Sheng, P. Focusing of Sound in a 3D Phononic Crystal. Phys. Rev. Lett. 2004, 93, 024301. [Google Scholar] [CrossRef]
- Wu, T.T.; Huang, Z.G.; Lin, S. Surface and bulk acoustic waves in two-dimensional phononic crystal consisting of materials with general anisotropy. Phys. Rev. B 2004, 69, 94301. [Google Scholar] [CrossRef]
- Khelif, A.; Aoubiza, B.; Mohammadi, S.; Adibi, A.; Laude, V. Complete band gaps in two-dimensional phononic crystal slabs. Phys. Rev. E 2006, 74, 046610. [Google Scholar] [CrossRef] [PubMed]
- Vasseur, J.; Deymier, P.; Djafari-Rouhani, B.; Pennec, Y.; Hladky-Hennion, A.C. Absolute forbidden bands and waveguiding in two-dimensional phononic crystal plates. Phys. Rev. B-Condens. Matter. 2009, 20, 439–446. [Google Scholar] [CrossRef]
- Khelif, A.; Choujaa, A.; Benchabane, S.; Djafari-Rouhani, B.; Laude, V. Guiding and bending of acoustic waves in highly confined phononic crystal waveguides. Appl. Phys. Lett. 2004, 84, 4400–4402. [Google Scholar] [CrossRef]
- Vasseur, J.O.; Deymier, P.A.; Khelif, A.; Lambin, P.; Djafari-Rouhani, B.; Akjouj, A.; Dobrzynski, L.; Fettouhi, N.; Zemmouri, J. Phononic crystal with low filling fraction and absolute acoustic band gap in the audible frequency range: A theoretical and experimental study. Phys. Rev. E 2002, 65, 056608. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.; Sun, T.; Zhang, Z.; Wang, Z. Thermally tunable topological transmission of elastic waves in solid phononic crystals. Appl. Phys. A-Mater. Sci. Process. 2025, 131, 259. [Google Scholar] [CrossRef]
- Swift, S.H.; El-Kady, I.F.; Kellogg, R.A.; Cillessen, D.E.; Denison, M.H. Cyclically symmetric radially self-similar phononic pseudocrystal isolator for broadband, ultrasonic vibration bandstop filtering. Appl. Phys. Lett. 2025, 126, 082201. [Google Scholar] [CrossRef]
- Tian, Z.; Yu, L. Rainbow trapping of ultrasonic guided waves in chirped phononic crystal plates. Sci. Rep. 2017, 7, 40004. [Google Scholar] [CrossRef]
- Gan, Q.; Ding, Y.J.; Bartoli, F.J. ‘rainbow’ Trapping and Releasing at Telecommunication Wavelengths. Phys. Rev. Lett. 2009, 102, 199–202. [Google Scholar] [CrossRef]
- Khelif, A.; Mohammadi, S.; Eftekhar, A.A.; Adibi, A.; Aoubiza, B. Acoustic confinement and waveguiding with a line-defect structure in phononic crystal slabs. J. Appl. Phys. 2010, 108, 084515. [Google Scholar] [CrossRef]
- Bessière, A.; Lecointre, A.; Priolkar, K.R.; Gourier, D. Role of crystal defects in red long-lasting phosphorescence of CaMgSi2O6: Mn diopsides. J. Mater. Chem. 2012, 22, 19039–19046. [Google Scholar] [CrossRef]
- Sainidou, R.; Stefanou, N.; Modinos, A. Linear chain of weakly coupled defects in a three-dimensional phononic crystal: A model acoustic waveguide. Phys. Rev. B 2006, 74, 172302. [Google Scholar] [CrossRef]
- Min, Z.; Yun-Tuan, F.; Ting-Gen, S. Study on One Dimension Phononic Crystal with Defects. J. Synth. Cryst. 2005, 34, 536–541. [Google Scholar]
- Khelif, A.; Achaoui, Y.; Aoubiza, B. In-plane confinement and waveguiding of surface acoustic waves through line defects in pillars-based phononic crystal. AIP Adv. 2011, 1, 141. [Google Scholar] [CrossRef]
- Wang, N.; Hsiao, F.L.; Palaniapan, M.; Lee, C. Silicon two-dimensional phononic crystal resonators using alternate defects. Appl. Phys. Lett. 2011, 99, 765. [Google Scholar] [CrossRef]
- Romero-Garcia, V.; Pico, R.; Cebrecos, A.; Sanchez-Morcillo, V.J.; Staliunas, K. Enhancement of sound in chirped sonic crystals. Appl. Phys. Lett. 2013, 102, 2022-R. [Google Scholar] [CrossRef]
- Ryosuke, N. Equivalence Between Non-Commutative Harmonic Oscillators and Two-Photon Quantum Rabi Models. Int. Math. Res. Notices 2025, 7, rnaf066. [Google Scholar]
- Zhou, Y.; Kong, F.; Liu, H.; Jin, Y.; Chen, H.; Sun, C. Numerical study on hydrodynamic characteristics of deep sea microfluidic eel energy capture device. Renew. Energy 2024, 225, 120325. [Google Scholar] [CrossRef]
- Masha, E.; Barbieri, L.; Skowronski, J.; Aliotta, M.; Ananna, C.; Barile, F.; Bemmerer, D.; Best, A.; Boeltzig, A.; Broggini, C. First measurement of the low-energy direct capture in 20Ne(p, γ)21Na and improved energy and strength of the Ec.m.=368 keV resonance. Phys. Rev. C 2023, 108, L052801. [Google Scholar] [CrossRef]
- Zhao, J.M.; Huo, S.Y.; Huang, H.; Chen, J. Topological Interface States of Shear Horizontal Guided Wave in One-Dimensional Phononic Quasicrystal Slabs. Phys. Status Solidi-Rapid Res. Lett. 2018, 12, 1800322. [Google Scholar] [CrossRef]
- Huang, H.B.; Chen, J.; Huo, S. Simultaneous topological Bragg and locally resonant edge modes of shear horizontal guided wave in one-dimensional structure. J. Phys. D-Appl. Phys. 2017, 50, 275102. [Google Scholar] [CrossRef]
- Ge, Z.; Sang, T.; Luo, C.; Zhang, X.; Pian, C. Configurable dual-topological-interface-states induced reflection in hybrid multilayers consisting of a Ge2Sb2Te5 film. Opt. Express 2024, 32, 16351–16361. [Google Scholar] [CrossRef]
- Elshahat, S.; Lu, C. Bidirectional rainbow trapping in 1-D chirped topological photonic crystal. Front. Phys. 2022, 10, 831203. [Google Scholar] [CrossRef]
- Chaplain, G.J.; Ponti, J.M.D.; Colombi, A.; Fuentes-Dominguez, R.; Craster, R.V. Tailored elastic surface to body wave Umklapp conversion. Nat. Commun. 2020, 11, 3267. [Google Scholar] [CrossRef] [PubMed]
- Omrani, E.M.; Nazari, F. Magnetically tunable 4 × 2 encoder utilizing Terfenol-D-embedded phononic crystal ring resonators. J. Sci. Adv. Mater. Devices 2025, 10, 100861. [Google Scholar] [CrossRef]
- Omrani, E.M.; Nazari, F. Magnetically adjustable AND/XOR logic gates using Terfenol-D in phononic crystal. Sci. Rep. 2025, 15, 12169. [Google Scholar] [CrossRef] [PubMed]
- Omrani, E.M.; Nazari, F. Magnetically tunable acoustic add-drop filter via Terfenol-D. Phys. Scr. 2024, 99, 105924. [Google Scholar] [CrossRef]
- Ranjbar, S.; Nazari, F.; Hajizadeh, R. Magnetically Controlled Bidirectional 2 × 2 Elastic Switch Using Terfenol-D in a Phononic Crystal-Based Mach-Zehnder Interferometer. J. Sci. Adv. Mater. Devices 2025, 10, 100926. [Google Scholar] [CrossRef]
- Ansari, M.H.; Attarzadeh, M.A.; Nouh, M.; Karami, A. Application of magnetoelastic materials in spatiotemporally modulated phononic crystals for nonreciprocal wave propagation. Smart Mater. Struct. 2018, 27, 015030. [Google Scholar] [CrossRef]
- Vasseur, J.O.; Matar, O.B.; Robillard, J.F.; Hladky-Hennion, A.C.; Deymier, P.A. Band structures tunability of bulk 2D phononic crystals made of magneto-elastic materials. AIP Adv. 2011, 1, 041904. [Google Scholar] [CrossRef]
- Matar, O.B.; Robillard, J.F.; Vasseur, J.O.; Hladky-Hennion, A.C.; Deymier, P.A.; Pernod, P.; Preobrazhensky, V. Band gap tunability of magneto-elastic phononic crystal. J. Appl. Phys. 2012, 111, 141. [Google Scholar] [CrossRef]
- Tartakovskaya, E.V.; Vovk, A.; Golub, V. Dipolar interaction in ordered superlattices of ferromagnetic nanoparticles. Phys. Status Solidi B-Basic. Res. 2010, 205, 1787–1789. [Google Scholar] [CrossRef]
- Turov, E.A.; Shavrov, V.G. Broken symmetry and magnetoacoustic effects in ferroand antiferromagnetics. Sov. Phys. Usp. 1983, 26, 593–611. [Google Scholar] [CrossRef]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747. [Google Scholar] [CrossRef] [PubMed]
- Delplace, P.; Ullmo, D.; Montambaux, G. The Zak phase and the existence of edge states in graphene. Phys. Rev. B-Condens. Matter. 2011, 84, 5324–5326. [Google Scholar] [CrossRef]
- Kim, I.; Iwamoto, S.; Arakawa, Y. Topologically protected elastic waves in one-dimensional phononic crystals of continuous media. Appl. Phys. Express 2018, 11, 017201. [Google Scholar] [CrossRef]
- Feng, L.; Huang, K.; Chen, J.; Luo, J.C.; Huo, S. Magnetically tunable topological interface states for Lamb waves in one-dimensional magnetoelastic phononic crystal slabs. AIP Adv. 2019, 9, 115201. [Google Scholar] [CrossRef]
- Kivelson, S. Wannier functions in one-dimensional disordered systems: Application to fractionally charged solitons. Phys. Rev. B 2008, 26, 4269–4277. [Google Scholar] [CrossRef]
- Wang, H.X.; Guo, G.Y.; Jiang, J.H. Band topology in classical waves: Wilson-loop approach to topological numbers and fragile topology. New J. Phys. 2019, 2, 093029. [Google Scholar] [CrossRef]
- Blanco-Redondo, A.; Andonegui, I.; Collins, M.J.; Harari, G.; Segev, M. Topological Optical Waveguiding in Silicon and the Transition between Topological and Trivial Defect States. Phys. Rev. Lett. 2016, 117, 129901. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Sai, Y.; Chen, J. Tunable Lamb wave band gaps in two-dimensional magnetoelastic phononic crystal slabs by an applied external magnetostatic field. Ultrasonics 2016, 71, 69–74. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, W.; Sui, F.; Chen, J.; Huang, H.; Luo, T. Topological Rainbow Trapping in One-Dimensional Magnetoelastic Phononic Crystal Slabs. Magnetochemistry 2025, 11, 83. https://doi.org/10.3390/magnetochemistry11100083
Xiao W, Sui F, Chen J, Huang H, Luo T. Topological Rainbow Trapping in One-Dimensional Magnetoelastic Phononic Crystal Slabs. Magnetochemistry. 2025; 11(10):83. https://doi.org/10.3390/magnetochemistry11100083
Chicago/Turabian StyleXiao, Wen, Fuhao Sui, Jiujiu Chen, Hongbo Huang, and Tao Luo. 2025. "Topological Rainbow Trapping in One-Dimensional Magnetoelastic Phononic Crystal Slabs" Magnetochemistry 11, no. 10: 83. https://doi.org/10.3390/magnetochemistry11100083
APA StyleXiao, W., Sui, F., Chen, J., Huang, H., & Luo, T. (2025). Topological Rainbow Trapping in One-Dimensional Magnetoelastic Phononic Crystal Slabs. Magnetochemistry, 11(10), 83. https://doi.org/10.3390/magnetochemistry11100083





